A Matrix Approach to Vertex-Degree-Based Topological Indices

Abstract

A VDB (vertex-degree-based) topological index over a set of digraphs $\mathcal{H}$ is a function $\phi :\mathcal{H}\to \mathbb{R}$, defined for each $H\in \mathcal{H}$ as

$$\phi \left(H\right)=\frac{1}{2}\sum _{uv\in E}{\phi }_{d_u^{+}{d}_v^{-}},$$

where E is the arc set of H, $d_u^{+}$ and $d_v^{-}$ denote the out-degree and in-degree of vertices u and v respectively, and ${\phi }_{ij}=f(i,j)$ for an appropriate real symmetric bivariate function f. It is our goal in this article to introduce a new approach where we base the concept of VDB topological index on the space of real matrices instead of the space of symmetric real functions of two variables. We represent a digraph H by the $p\times p$ matrix $\alpha \left(H\right)$, where ${\left[\alpha \left(H\right)\right]}_{ij}$ is the number of arcs $uv$ such that $d_u^{+}=i$ and $d_v^{-}=j$, and p is the maximum value of the in-degrees and out-degrees of H. By fixing a $p\times p$ matrix $\phi$, a VDB topological index of H is defined as the trace of the matrix ${\phi }^T\alpha \left(H\right)$. We show that this definition coincides with the previous one when $\phi$ is a symmetric matrix. This approach allows considering nonsymmetric matrices, which extends the concept of a VDB topological index to nonsymmetric bivariate functions.

1. Introduction

A directed graph (or just a digraph) D consists of a nonempty finite set V of elements called vertices and a finite set E of ordered pairs of distinct vertices called arcs. Two vertices are called adjacent if they are connected by an arc. If there is an arc from vertex u to vertex v, we indicate this by writing $uv$. The in-degree (resp. out-degree) of a vertex v, denoted by $d_v^{-}$ (resp. $d_v^{+}$) is the number of arcs of the form $uv$ (resp. $vu$), where $u\in V.$

Directed graphs arise in a natural way in many applications of graph theory. Social networks are often modeled as directed graphs, representing networks with directionality such as social media interactions [1]. The same occurs with transportation networks [2]. Moreover, specific types of digraphs, such as derivable digraphs, are used in wireless sensor networking [3].

The theory of VDB topological indices of graphs is a widely investigated topic in the mathematical and chemical literature [4,5,6,7,8,9,10,11,12,13,14]. The concept of a VDB topological index of a digraph was introduced in [15] as a generalization of VDB topological indices of graphs. Namely, a VDB topological index over a set of digraphs $\mathcal{H}$ is a function $\phi :\mathcal{H}⟶\mathbb{R}$, defined for each $H\in \mathcal{H}$ as

$$\phi \left(H\right)=\frac{1}{2}\sum _{uv\in E}{\phi }_{d_u^{+}{d}_v^{-}},$$

where ${\phi }_{ij}$ is an appropriate bivariate function which satisfies ${\phi }_{ij}={\phi }_{ji}$. In the mentioned paper, the Randić index of a digraph was obtained, and the extreme value problem of the Randić index over the set of oriented trees with n vertices was solved. More recent studies of the topic of VDB topological indices of digraphs can be found in [16,17,18,19,20].

In this article, we introduce a new matrix approach to the concept of VDB topological index, where each of these indices is defined by a real matrix $\phi$. Related to this definition, we introduce the concept of an affine subspace of a digraph providing a geometrical interpretation of the VDB topological index of a digraph.

In case the matrix $\phi$ is symmetric, we recover the concept of the VDB topological index usually induced by symmetric real functions of two variables. However, by considering nonsymmetric matrices, we obtain an extension of this concept to nonsymmetric bivariate functions. This is the main difference with the concept of a VDB topological index of a digraph introduced in [15], since it is based on a symmetric function. In Section 5, we study the general first Zagreb index over the set of orientations of a path. This index is an example of a VDB topological index induced by a nonsymmetric matrix.

Finally, we show that our approach can be used for some distance-based topological indices, such as the Szeged [21] and the Mostar [22] indices.

2. Preliminaries

Given a digraph D with vertex set V and arc set E, we denote by ${\Delta }^{+}\left(D\right)$ and ${\Delta }^{-}\left(D\right)$ the maximal out-degree and maximal in-degree, respectively, among all vertices in D. A vertex v is called an isolated vertex if $d_v^{+}=0=d_v^{-}$, a source vertex if $d_v^{-}=0<d_v^{+}$, and a sink vertex if $d_v^{+}=0<d_v^{-}$.

We say that D is an oriented graph if, whenever $uv\in E$ then $vu\notin E.$ An oriented graph D is obtained from a graph G by assigning a direction to each edge of G; D is called an orientation of G. An example of an orientation of a graph is the so-called sink-source orientation, in which every vertex is a sink vertex or a source vertex. On the other hand, we have balanced orientations of a graph, where the difference between the in-degree and out-degree of each vertex is at most 1.

Let us denote by ${\mathcal{D}}_n$ the set of digraphs with n non-isolated vertices.

Recall that a graph G can be identified with its symmetric digraph $\overline{G}$, where each edge in G is replaced by a pair of symmetric arcs in $\overline{G}$. Let us denote by ${\mathcal{G}}_n\subseteq {\mathcal{D}}_n$ the set of graphs with n vertices. The theory of symmetric VDB topological indices over a set $\mathcal{H}\subseteq {\mathcal{G}}_n$ has been studied extensively in the past decades. In fact, in this theory it is always assumed that $\phi =\left({\phi }_{ij}\right)$ is induced by a symmetric bivariate function ${\phi }_{ij}$.

The space of $p\times p$ real matrices is denoted by ${\mathcal{M}}_p\left(\mathbb{R}\right)$. If $M\in {\mathcal{M}}_p\left(\mathbb{R}\right)$, then ${\left[M\right]}_{ij}$ is the $ij$-entry of M. In this way, $tr\left(M\right)={\sum }_{i=1}^n{\left[M\right]}_{ii}$ is the trace of M. The transpose of M is denoted by $M^{\top }$. For each $M\in {\mathcal{M}}_p\left(\mathbb{R}\right)$ we have the linear functional $⟨M,-⟩:{\mathcal{M}}_p\left(\mathbb{R}\right)⟶\mathbb{R}$ defined as $⟨M,N⟩=tr\left(M^{\top }N\right)$, for every $N\in {\mathcal{M}}_p\left(\mathbb{R}\right)$.

3. Affine Subspace of a Digraph

In this section, we introduce the matrix approach to the concept of the VDB topological index and define the affine subspace of a digraph.

Definition 1.

Let $\mathcal{H}\subseteq {\mathcal{D}}_n.$ The maximal degree of $\mathcal{H}$ is the number

$$max\left\{\underset{H\in \mathcal{H}}{max}\left\{{\Delta }^{+}\left(H\right)\right\},\underset{H\in \mathcal{H}}{max}\left\{{\Delta }^{-}\left(H\right)\right\}\right\}.$$

Let $\mathcal{H}\subseteq {\mathcal{D}}_n$ with maximal degree p. We represent each graph $H\in \mathcal{H}$ by the matrix $\alpha \left(H\right)\in {\mathcal{M}}_p\left(\mathbb{R}\right)$, where ${\left[\alpha \left(H\right)\right]}_{ij}$ is the number of arcs $uv$ such that $d_u^{+}=i$ and $d_v^{-}=j$. In this way we have a representing function $\alpha :\mathcal{H}⟶{\mathcal{M}}_p\left(\mathbb{R}\right)$ of the set $\mathcal{H}$ into the space of matrices ${\mathcal{M}}_p\left(\mathbb{R}\right)$. On the other hand, fix a matrix $\phi \in {\mathcal{M}}_p\left(\mathbb{R}\right),$ and consider the linear functional $⟨\phi ,-⟩:{\mathcal{M}}_p\left(\mathbb{R}\right)⟶\mathbb{R}$ defined as $⟨\phi ,M⟩=tr\left({\phi }^{\top }M\right)$, for each $M\in {\mathcal{M}}_p\left(\mathbb{R}\right).$

Definition 2.

The function $\widehat{\phi }:\mathcal{H}⟶\mathbb{R}$ defined as $\widehat{\phi }=\frac{1}{2}⟨\phi ,-⟩\circ \alpha$ is called a VDB topological index defined over $\mathcal{H}$.

Example 1.

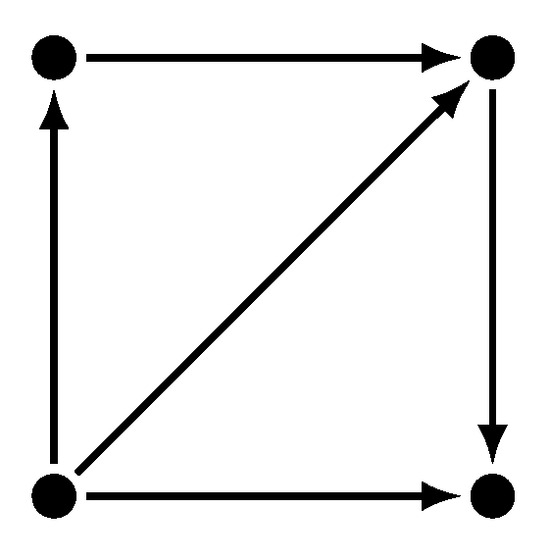
Let D denote the digraph depicted in Figure 1. The sequence of out-degrees of D is $\{1,1,0,3\}$ while the sequence of in-degrees of D is $\{1,2,2,0\}$. Consequently, D has maximal degree $p=3$ and it is represented by a $3\times 3$ matrix $\alpha \left(D\right)=\left(\begin{array}{ccc}0& 2& 0\\ 0& 0& 0\\ 1& 2& 0\end{array}\right)$.

Figure 1. Digraph used in Example 1.

Consider the matrix $\mathcal{SC}\in {\mathcal{M}}_3\left(\mathbb{R}\right)$ whose $ij$-entry is given by ${\left[\mathcal{SC}\right]}_{ij}={\left(i+j\right)}^{-\frac{1}{2}}:$

$$\mathcal{SC}=\left(\begin{array}{ccc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{3}}& \frac{1}{2}\\ \frac{1}{\sqrt{3}}& \frac{1}{2}& \frac{1}{\sqrt{5}}\\ \frac{1}{2}& \frac{1}{\sqrt{5}}& \frac{1}{\sqrt{6}}\end{array}\right)$$

The VDB topological index $\widehat{\mathcal{SC}}$ of digraph D, denoted by $\widehat{\mathcal{SC}}\left(D\right)$, is obtained by the composition

$$\mathcal{D}\stackrel{\alpha }{⟶}\alpha \left(D\right)\in {\mathcal{M}}_3\left(\mathbb{R}\right)\stackrel{⟨\mathcal{SC},-⟩}{⟶}\widehat{\mathcal{SC}}\left(D\right)\in \mathbb{R}$$

and its value is

$$\begin{array}{ccc}\hfill \widehat{\mathcal{SC}}\left(D\right)& =& \frac{1}{2}⟨\mathcal{SC},\alpha \left(D\right)⟩=\frac{1}{2}tr\left({\mathcal{SC}}^{\top }\alpha \left(D\right)\right)=\frac{1}{2}tr\left(\begin{array}{ccc}\frac{1}{2}& \frac{2}{\sqrt{2}}+1& 0\\ \frac{1}{\sqrt{5}}& \frac{2}{\sqrt{3}}+\frac{2}{\sqrt{5}}& 0\\ \frac{1}{\sqrt{6}}& 1+\frac{2}{\sqrt{6}}& 0\end{array}\right)\hfill \\ & =& \frac{1}{4}+\frac{1}{\sqrt{3}}+\frac{1}{\sqrt{5}}.\hfill \end{array}$$

We next show that Definition 2 coincides with the definition of VDB topological index of digraphs given in ([15], Definition 2.1), when matrix $\phi \in {\mathcal{M}}_p\left(\mathbb{R}\right)$ is symmetric.

Lemma 1.

Let $\widehat{\phi }$ be a VDB topological index over the set $\mathcal{H}\subseteq {\mathcal{D}}_n$ of degree p. If $H\in \mathcal{H}$, then

$$\widehat{\phi }\left(H\right)=\frac{1}{2}\sum _{i=1}^p\sum _{k=1}^p{\left[\phi \right]}_{ki}{\left[\alpha \left(H\right)\right]}_{ki}=\frac{1}{2}\sum _{uv\in E}{\phi }_{d_u^{+}{d}_v^{-}},$$

where E is the set of arcs in H.

Proof. 

If $H\in \mathcal{H}$, then

$$\begin{array}{ccc}\hfill \widehat{\phi }\left(H\right)& =& \left(\frac{1}{2}⟨\phi ,-⟩\circ \alpha \right)\left(H\right)=\frac{1}{2}⟨\phi ,\alpha \left(H\right)⟩=\frac{1}{2}tr\left({\phi }^{\top }\alpha \left(H\right)\right)\hfill \\ & =& \frac{1}{2}\sum _{i=1}^p{\left[{\phi }^{\top }\alpha \left(H\right)\right]}_{ii}=\frac{1}{2}\sum _{i=1}^p\sum _{k=1}^p{\left[{\phi }^{\top }\right]}_{ik}{\left[\alpha \left(H\right)\right]}_{ki}\hfill \\ & =& \frac{1}{2}\sum _{i=1}^p\sum _{k=1}^p{\left[\phi \right]}_{ki}{\left[\alpha \left(H\right)\right]}_{ki}=\frac{1}{2}\sum _{uv\in E}{\phi }_{d_u^{+}{d}_v^{-}}.\hfill \end{array}$$

□

Example 2.

Let $\mathcal{H}=\mathcal{O}\left(P_n\right)$ be the set of all orientations of the path $P_n$ of n vertices. Clearly, $\mathcal{H}$ has maximal degree 2. Consequently, each $H\in \mathcal{H}$ is represented by a $2\times 2$ matrix $\alpha \left(H\right)=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right),$ where $a,b,c,d$ are real nonnegative numbers such that

$$\begin{array}{ccc}\hfill a+b+c+d& =& n-1\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill a+b+c& \ge & 2.\hfill \end{array}$$

(2)

Consider the matrix $\mathcal{R}\in {\mathcal{M}}_2\left(\mathbb{R}\right)$ whose $ij$-entry is given by ${\left[\mathcal{R}\right]}_{ij}={\left(ij\right)}^{-\frac{1}{2}}:$

$$\mathcal{R}=\left(\begin{array}{cc}1& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{2}\end{array}\right)$$

Then we obtain the VDB topological index $\widehat{\mathcal{R}}$ as the composition

$$\mathcal{H}\stackrel{\alpha }{⟶}{\mathcal{M}}_2\left(\mathbb{R}\right)\stackrel{⟨\mathcal{R},-⟩}{⟶}\mathbb{R}.$$

For instance, consider the balanced orientation $H_0$ of $P_n$ given in Figure 2. Then clearly $\alpha \left(H_0\right)=\left(\begin{array}{cc}n-1& 0\\ 0& 0\end{array}\right)$ and so

$$\widehat{\mathcal{R}}\left(H_0\right)=\frac{1}{2}⟨\mathcal{R},\alpha \left(H_0\right)⟩=\frac{1}{2}\left(n-1\right).$$

On the other hand, if n is even and $H_1$ is a sink-source orientation of $P_n$ (see Figure 2), then $\alpha \left(H_1\right)=\left(\begin{array}{cc}0& 1\\ 1& n-3\end{array}\right)$. If n is odd, then $H_2$ and $H_3$ are sink-source orientations of $P_n$ (see Figure 2) with $\alpha \left(H_2\right)=\left(\begin{array}{cc}0& 2\\ 0& n-3\end{array}\right)$ and $\alpha \left(H_3\right)=\left(\begin{array}{cc}0& 0\\ 2& n-3\end{array}\right)$. In either case,

$$\widehat{\mathcal{R}}\left(H_i\right)=\frac{1}{2}⟨\mathcal{R},\alpha \left(H_i\right)⟩=\frac{1}{2}\left(\frac{2}{\sqrt{2}}+\frac{n-3}{2}\right),$$

where $i\in \{1,2,3\}$.

Figure 2. Balanced and sink-source orientations of $P_n$.

Let us assume that $\widehat{\phi }$ is a VDB topological index over the set $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p. Note that the kernel of $⟨\phi ,-⟩$, which we denote by $K_{\phi }$, is a hyperspace of ${\mathcal{M}}_p\left(\mathbb{R}\right)$. In other words, $K_{\phi }$ is a subspace of ${\mathcal{M}}_p\left(\mathbb{R}\right)$ of dimension $p^2-1$. Furthermore, let us denote by $K_{\phi }^{+}$ and $K_{\phi }^{-}$ the upper and lower open halfspaces determined by $K_{\phi }$:

$$K_{\phi }^{+}=\left\{M\in {\mathcal{M}}_p\left(\mathbb{R}\right):⟨\phi ,M⟩>0\right\},$$

(3)

and

$$K_{\phi }^{-}=\left\{M\in {\mathcal{M}}_p\left(\mathbb{R}\right):⟨\phi ,M⟩<0\right\}.$$

(4)

Definition 3.

Let $\widehat{\phi }$ be a VDB topological index over $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p and $H_0\in \mathcal{H}.$ The affine subspace of $H_0$ is denoted by $\mathcal{A}\left(H_0\right)$ and defined as

$$\mathcal{A}\left(H_0\right)=K_{\phi }+\alpha \left(H_0\right).$$

Furthermore, the affine upper and lower open halfspaces of $H_0$ are

$${\mathcal{A}}^{+}\left(H_0\right)=K_{\phi }^{+}+\alpha \left(H_0\right)and{\mathcal{A}}^{-}\left(H_0\right)=K_{\phi }^{-}+\alpha \left(H_0\right),$$

respectively.

In other words, each $H_0\in \mathcal{H}$ divides the space of matrices ${\mathcal{M}}_p\left(\mathbb{R}\right)$ into two open halfspaces: ${\mathcal{A}}^{+}\left(H_0\right)$ and ${\mathcal{A}}^{-}\left(H_0\right)$ (see Figure 3).

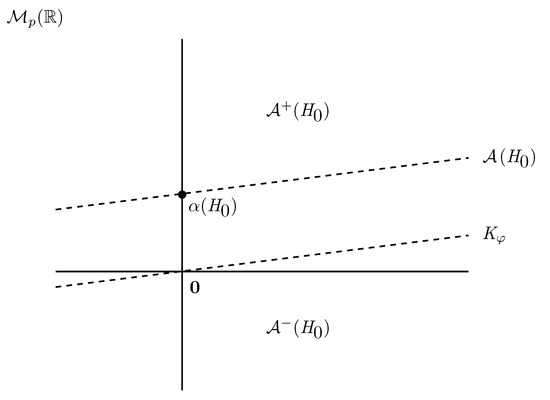
Figure 3. $H_0\in \mathcal{H}$ divides the space of matrices ${\mathcal{M}}_p\left(\mathbb{R}\right)$ into two open halfspaces.

Theorem 1.

Let $\widehat{\phi }$ be a VDB topological index over $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p and $H_0\in \mathcal{H}$. Given $H\in \mathcal{H}$, the following conditions hold:

1. 

$\widehat{\phi }\left(H\right)=\widehat{\phi }\left(H_0\right)$ if and only if $\alpha \left(H\right)\in \mathcal{A}\left(H_0\right);$

2. 

$\widehat{\phi }\left(H\right)>\widehat{\phi }\left(H_0\right)$ if and only if $\alpha \left(H\right)\in {\mathcal{A}}^{+}\left(H_0\right);$

3. 

$\widehat{\phi }\left(H\right)<\widehat{\phi }\left(H_0\right)$ if and only if $\alpha \left(H\right)\in {\mathcal{A}}^{-}\left(H_0\right).$

Proof. 1. This is a consequence of the following equivalences:

$$\begin{array}{ccc}\hfill \widehat{\phi }\left(H\right)=\widehat{\phi }\left(H_0\right)& \iff & \frac{1}{2}⟨\phi ,\alpha \left(H\right)⟩=\frac{1}{2}⟨\phi ,\alpha \left(H_0\right)⟩\iff ⟨\phi ,\alpha \left(H\right)-\alpha \left(H_0\right)⟩=0\hfill \\ & \iff & \alpha \left(H\right)-\alpha \left(H_0\right)\in K_{\phi }\iff \alpha \left(H\right)\in \mathcal{A}\left(H_0\right).\hfill \end{array}$$

2.

It follows from the equivalences

$$\begin{array}{ccc}\hfill \widehat{\phi }\left(H\right)>\widehat{\phi }\left(H_0\right)& \iff & \frac{1}{2}⟨\phi ,\alpha \left(H\right)⟩>\frac{1}{2}⟨\phi ,\alpha \left(H_0\right)⟩\iff ⟨\phi ,\alpha \left(H\right)-\alpha \left(H_0\right)⟩>0\hfill \\ & \iff & \alpha \left(H\right)-\alpha \left(H_0\right)\in K_{\phi }^{+}\iff \alpha \left(H\right)\in {\mathcal{A}}^{+}\left(H_0\right).\hfill \end{array}$$

3.

This is similar to the proof of 2.

□

Definition 4.

Let $\widehat{\phi }$ be a VDB topological index over $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p and $H_0\in \mathcal{H}.$ We say that $H_0$ is maximal (resp. minimal) in $\mathcal{H}$ with respect to $\widehat{\phi }$ if $\widehat{\phi }\left(H_0\right)\ge \widehat{\phi }\left(H\right)$ (resp. $\widehat{\phi }\left(H_0\right)\le \widehat{\phi }\left(H\right)$), for all $H\in \mathcal{H}.$

Corollary 1.

Let $\widehat{\phi }$ be a VDB topological index over $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p and $H_0\in \mathcal{H}.$ Then:

1. 

$H_0$ is maximal in $\mathcal{H}$ with respect to $\widehat{\phi }$ if and only if $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{+}\left(H_0\right)=\varnothing$;

2. 

$H_0$ is minimal in $\mathcal{H}$ with respect to $\widehat{\phi }$ if and only if $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{-}\left(H_0\right)=\varnothing$.

Proof. 

This is a direct consequence of Theorem 1. □

Example 3.

Consider the VDB topological index $\widehat{\mathcal{R}}$ over $\mathcal{H}=\mathcal{O}\left(P_n\right)$ as described in Example 2, and $H_0,H_1,H_2,H_3$ as defined in Example 2 (see Figure 2). Then

$$K_{\mathcal{R}}=\left\{\left(\begin{array}{cc}x& y\\ w& z\end{array}\right)\in {\mathcal{M}}_2\left(\mathbb{R}\right):x+\frac{y}{\sqrt{2}}+\frac{w}{\sqrt{2}}+\frac{z}{2}=0\right\}.$$

Let $H\in \mathcal{H}$ with matrix representation $\alpha \left(H\right)=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right).$ Then

$$\alpha \left(H\right)-\alpha \left(H_0\right)=\left(\begin{array}{cc}a-\left(n-1\right)& b\\ c& d\end{array}\right),$$

and by (1),

$$a-\left(n-1\right)+\frac{b}{\sqrt{2}}+\frac{c}{\sqrt{2}}+\frac{d}{2}=-b-c-d+\frac{b}{\sqrt{2}}+\frac{c}{\sqrt{2}}+\frac{d}{2}\le 0.$$

Hence, $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{+}\left(H_0\right)=\varnothing$ and so by Corollary 1, $H_0$ is maximal in $\mathcal{H}$ with respect to $\widehat{\mathcal{R}}$. Similarly,

$$\begin{array}{ccc}\hfill \alpha \left(H\right)-\alpha \left(H_1\right)& =& \left(\begin{array}{cc}a& b-1\\ c-1& d-\left(n-3\right)\end{array}\right)\hfill \\ \hfill \alpha \left(H\right)-\alpha \left(H_2\right)& =& \left(\begin{array}{cc}a& b-2\\ c& d-\left(n-3\right)\end{array}\right)\hfill \\ \hfill \alpha \left(H\right)-\alpha \left(H_3\right)& =& \left(\begin{array}{cc}a& b\\ c-2& d-\left(n-3\right)\end{array}\right),\hfill \end{array}$$

In either case by (1) and (2)

$$\begin{array}{cc}\hfill a+\frac{b+c-2}{\sqrt{2}}+\frac{d-\left(n-3\right)}{2}& =\frac{1}{2}\left[a+b(\sqrt{2}-1)+c(\sqrt{2}-1)-2(\sqrt{2}-1)\right]\hfill \\ & \ge \frac{\sqrt{2}-1}{2}\left(a+b+c-2\right)\ge 0.\hfill \end{array}$$

Consequently, $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{-}\left(H_i\right)=\varnothing$ and so by Corollary 1, $H_i$ is minimal in $\mathcal{H}$ with respect to $\widehat{\mathcal{R}}$ for each $i\in \{1,2,3\}$. Compare with ([15], Theorem 5.1).

4. Symmetric VDB Topological Indices

We begin this section defining the concept of symmetric VDB topological indices.

Definition 5.

Let $\widehat{\phi }$ be a VDB topological index over $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p. We say that $\widehat{\phi }$ is a symmetric VDB topological index if φ is a symmetric matrix, i.e., $\phi ={\phi }^{\top }.$ Otherwise, we say that $\widehat{\phi }$ is a nonsymmetric VDB topological index.

Example 4.

Let $\mathcal{H}\subseteq {\mathcal{D}}_n$ be a set of digraphs of maximal degree p and $r,s\in \mathbb{R}$. We define the general first Zagreb index ${\widehat{M}}_1^{r,s}$ to be the VDB topological index induced by the $p\times p$ matrix with $ij$-entries ${\left[{\mathcal{M}}_1^{r,s}\right]}_{ij}=i^r+j^s$. Clearly, ${\widehat{M}}_1^{r,s}$ is a symmetric VDB topological index if and only if $r=s$. Note that ${\widehat{M}}_1^{1,1}$ is the usual first Zagreb ${\widehat{\mathcal{M}}}_1$ index.

Definition 2 perfectly allows the possibility of considering nonsymmetric VDB topological indices defined over a set of graphs. However, if $\mathcal{H}\subseteq {\mathcal{G}}_n$ has maximal degree p, then the representing function $\alpha :\mathcal{H}⟶{\mathcal{M}}_p\left(\mathbb{R}\right)$ satisfies $\alpha \left(H\right)=\alpha {\left(H\right)}^{\top }$, for all $H\in \mathcal{H}$, since clearly, in this case, the number of arcs from vertices with out-degree i to vertices with in-degree j is the same as the number of arcs from vertices with out-degree j to vertices with in-degree i, for all $1\le i,j\le p$. Based on this fact, we will show next that any VDB topological index defined over a set $\mathcal{H}\subseteq {\mathcal{G}}_n$ can be reduced to a symmetric VDB topological index over $\mathcal{H}.$

Theorem 2.

Let $\widehat{\phi }$ be a VDB topological index defined over a set $\mathcal{H}\subseteq {\mathcal{G}}_n$ of maximal degree p. Let $S_{\phi }=\frac{1}{2}\left(\phi +{\phi }^{\top }\right)$ be the symmetric part of φ. Then $\widehat{\phi }\left(H\right)={\widehat{S}}_{\phi }\left(H\right)$ for all $H\in \mathcal{H}.$

Proof. 

We know that $\alpha \left(H\right)=\alpha {\left(H\right)}^{\top }$ for all $H\in \mathcal{H}$, since $\mathcal{H}\subseteq {\mathcal{G}}_n$. Consequently,

$$\begin{array}{ccc}\hfill ⟨\phi ,\alpha \left(H\right)⟩& =& tr\left({\phi }^{\top }\alpha \left(H\right)\right)=tr\left(\alpha {\left(H\right)}^{\top }\phi \right)=tr\left(\alpha \left(H\right)\phi \right)\hfill \\ & =& tr\left(\phi \alpha \left(H\right)\right)=⟨{\phi }^{\top },\alpha \left(H\right)⟩.\hfill \end{array}$$

Hence,

$$\begin{array}{ccc}\hfill 2{\widehat{S}}_{\phi }\left(H\right)& =& ⟨S_{\phi },\alpha \left(H\right)⟩=\frac{1}{2}⟨\phi +{\phi }^{\top },\alpha \left(H\right)⟩\hfill \\ & =& \frac{1}{2}⟨\phi ,\alpha \left(H\right)⟩+\frac{1}{2}⟨{\phi }^{\top },\alpha \left(H\right)⟩\hfill \\ & =& ⟨\phi ,\alpha \left(H\right)⟩=2\widehat{\phi }\left(H\right).\hfill \end{array}$$

□

Example 5.

Consider the general first Zagreb index ${\widehat{\mathcal{M}}}_1^{1,2}$ over the set ${\mathcal{T}}_n$ of all trees with $n\ge 2$ vertices. If $T\in {\mathcal{T}}_n$, then by Theorem 2,

$${\widehat{\mathcal{M}}}_1^{1,2}\left(T\right)={\widehat{S}}_{{\mathcal{M}}_1^{1,2}}\left(T\right)=\frac{1}{2}\left({\widehat{\mathcal{M}}}_1^{1,1}\left(T\right)+{\widehat{M}}_1^{2,2}\left(T\right)\right)=\frac{1}{2}\left({\widehat{\mathcal{M}}}_1\left(T\right)+\widehat{\mathcal{F}}\left(T\right)\right),$$

where ${\widehat{\mathcal{M}}}_1$ and $\widehat{\mathcal{F}}$ are the first Zagreb index and Forgotten index, respectively. In particular, using ([23], Corollaries 1 and 2) we can solve the extreme value problem of ${\widehat{M}}_1^{1,2}$ over the set of trees with $n\ge 2$ vertices:

$$\begin{array}{c}6n-10\le {\widehat{\mathcal{M}}}_1^{1,2}\left(T\right)\le \frac{1}{2}(n-1)(n^2-n+2).\end{array}$$

(5)

Equality in the left-hand side of (5) holds if and only if $T=P_n$, while equality in the right-hand side ocurrs if and only if $T=S_n$.

5. The General First Zagreb Index over Orientations of the Path

It follows from our previous section that the study of VDB topological indices over a set of graphs reduces to the study of symmetric VDB topological indices. It is our interest in this section, to analyze a VDB topological index over a set of digraphs (which are not graphs). Specifically, we study the general first Zagreb index over the set $\mathcal{H}=\mathcal{O}\left(P_n\right)$ as described in Example 2.

Let $r,s$ be two different positive real numbers and consider the general first Zagreb index ${\widehat{\mathcal{M}}}_1^{r,s}$ over $\mathcal{O}\left(P_n\right)$. Recall that $H_0$ is a balanced orientation of $P_n$ and $H_1,H_2,H_3$ are sink-source orientations of $P_n$ (see Figure 2). Note that $H_2$ is the inverse orientation of $H_3$, however, ${\widehat{\mathcal{M}}}_1^{r,s}\left(H_2\right)\ne {\widehat{\mathcal{M}}}_1^{r,s}\left(H_3\right)$, which is a consequence of the fact that ${\widehat{\mathcal{M}}}_1^{r,s}$ is a nonsymmetric VDB topological index.

Theorem 3.

Let $r,s$ be two different positive real numbers and $n>3$ an integer. Then:

1. 

$H_0$ is minimal in $\mathcal{O}\left(P_n\right)$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$.

2. 

If n is even, then $H_1$ is maximal in $\mathcal{O}\left(P_n\right)$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$.

3. 

If n is odd and $r<s$, then $H_2$ is maximal in $\mathcal{O}\left(P_n\right)$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$.

4. 

If n is odd and $r>s$, then $H_3$ is maximal in $\mathcal{O}\left(P_n\right)$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$.

Proof. 

Let $H\in \mathcal{H}=\mathcal{O}\left(P_n\right)$ with matrix representation $\alpha \left(H\right)=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$,

$${\mathcal{M}}_1^{r,s}=\left(\begin{array}{cc}2& 1+2^s\\ 1+2^r& 2^r+2^s\end{array}\right)\in {\mathcal{M}}_2\left(\mathbb{R}\right),$$

and

$$K_{{\mathcal{M}}_1^{r,s}}=\left\{\left(\begin{array}{cc}x& y\\ w& z\end{array}\right)\in {\mathcal{M}}_2\left(\mathbb{R}\right):2x+y(1+2^s)+w(1+2^r)+z(2^r+2^s)=0\right\}.$$

• $\alpha \left(H\right)-\alpha \left(H_0\right)=\left(\begin{array}{cc}a-\left(n-1\right)& b\\ c& d\end{array}\right)$. By (1),

  $$\begin{array}{ccc}\hfill ⟨{\mathcal{M}}_1^{r,s},\alpha \left(H\right)-\alpha \left(H_0\right)⟩& =& 2a-2(n-1)+b(1+2^s)+c(1+2^r)+d(2^r+2^s)\hfill \\ & =& -2b-2c-2d+b(1+2^s)+c(1+2^r)+d(2^r+2^s)\hfill \\ & =& b(2^s-1)+c(2^r-1)+(2^r+2^s-2)d\ge 0.\hfill \end{array}$$

  Hence, $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{-}\left(H_0\right)=\varnothing$. By Corollary 1, $H_0$ is minimal in $\mathcal{H}$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$ and

  $${\widehat{\mathcal{M}}}_1^{r,s}\left(H_0\right)=\frac{1}{2}⟨{\mathcal{M}}_1^{r,s},\alpha \left(H_0\right)⟩=\left(n-1\right).$$
• Let $n>3$ be even. $\alpha \left(H\right)-\alpha \left(H_1\right)=\left(\begin{array}{cc}a& b-1\\ c-1& d-\left(n-3\right)\end{array}\right)$. Using (1) we obtain,

  $$\begin{array}{ccc}\hfill ⟨{\mathcal{M}}_1^{r,s},\alpha \left(H\right)-\alpha \left(H_1\right)⟩& =& 2a+(b-1)(1+2^s)+(c-1)(1+2^r)\hfill \\ & & +(d-(n-3))(2^r+2^s)\hfill \\ & =& 2a+\left(b-1\right)\left(1+2^s\right)+\left(c-1\right)\left(1+2^r\right)\hfill \\ & & +\left(2-a-b-c\right)\left(2^r+2^s\right)\hfill \\ & =& -(a+b-1)\left(2^r-1\right)-(a+c-1)\left(2^s-1\right)\hfill \\ & \le & 0,\hfill \end{array}$$

  if $a+b\ge 1$ and $a+c\ge 1$. If $a+b=0$, by (2) $c\ge 2$, and consequently $d\le n-3$. The only orientation of $P_n$ satisfying these conditions is $H_3$, but this orientation only exists when n is odd. Similarly, if $a+c=0$, by (2) $b\ge 2$, and consequently $d\le n-3$. The only orientation of $P_n$ satisfying these conditions is $H_2$, but this orientation only exists when n is odd.
  Hence, $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{+}\left(H_1\right)=\varnothing$. By Corollary 1, $H_1$ is maximal in $\mathcal{H}$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$ and

  $${\widehat{\mathcal{M}}}_1^{r,s}\left(H_1\right)=\frac{1}{2}⟨{\mathcal{M}}_1^{r,s},\alpha \left(H_1\right)⟩=\frac{1}{2}\left(n-2\right)\left(2^r+2^s\right)+1.$$
• Let $n>3$ be odd and $r<s$. $\alpha \left(H\right)-\alpha \left(H_2\right)=\left(\begin{array}{cc}a& b-2\\ c& d-\left(n-3\right)\end{array}\right)$. Using (1) and (2) we obtain,

  $$\begin{array}{ccc}\hfill ⟨{\mathcal{M}}_1^{r,s},\alpha \left(H\right)-\alpha \left(H_2\right)⟩& =& 2a+(b-2)(1+2^s)+c(1+2^r)\hfill \\ & & +(d-(n-3))(2^r+2^s)\hfill \\ & =& 2a+\left(b-2\right)\left(1+2^s\right)+c\left(1+2^r\right)\hfill \\ & & +\left(2-a-b-c\right)\left(2^r+2^s\right)\hfill \\ & =& -(a+b+c-2)\left(2^r-1\right)-a\left(2^s-1\right)-c\left(2^s-2^r\right)\hfill \\ & \le & 0,\hfill \end{array}$$

  Hence, $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{+}\left(H_2\right)=\varnothing$. By Corollary 1, $H_2$ is maximal in $\mathcal{H}$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$ and

  $${\widehat{\mathcal{M}}}_1^{r,s}\left(H_2\right)=\frac{1}{2}⟨{\mathcal{M}}_1^{r,s},\alpha \left(H_2\right)⟩=\frac{1}{2}\left(n-1\right)\left(2^r+2^s\right)-2^r+1.$$
• Let $n>3$ be odd and $r>s$. $\alpha \left(H\right)-\alpha \left(H_3\right)=\left(\begin{array}{cc}a& b\\ c-2& d-\left(n-3\right)\end{array}\right)$. Using (1) and (2) we obtain,

  $$\begin{array}{ccc}\hfill ⟨{\mathcal{M}}_1^{r,s},\alpha \left(H\right)-\alpha \left(H_2\right)⟩& =& 2a+b(1+2^s)+(c-2)(1+2^r)\hfill \\ & & +(d-(n-3))(2^r+2^s)\hfill \\ & =& 2a+b\left(1+2^s\right)+\left(c-2\right)\left(1+2^r\right)\hfill \\ & & +\left(2-a-b-c\right)\left(2^r+2^s\right)\hfill \\ & =& -(a+b+c-2)\left(2^s-1\right)-a\left(2^r-1\right)-b\left(2^r-2^s\right)\hfill \\ & \le & 0,\hfill \end{array}$$

  Hence, $\alpha \left(\mathcal{H}\right)\cap {\mathcal{A}}^{+}\left(H_3\right)=\varnothing$. By Corollary 1, $H_3$ is maximal in $\mathcal{H}$ with respect to ${\widehat{\mathcal{M}}}_1^{r,s}$ and

  $${\widehat{\mathcal{M}}}_1^{r,s}\left(H_3\right)=\frac{1}{2}⟨{\mathcal{M}}_1^{r,s},\alpha \left(H_3\right)⟩=\frac{1}{2}\left(n-1\right)\left(2^r+2^s\right)-2^s+1.$$

□

Remark 1.

By reversing the inequalities in the proof of Theorem 3, we deduce a dual version of Theorem 3 when $r,s$ are two different negative real numbers, by simply substituting ’minimal’ by ’maximal’ and viceversa.

6. Discussion

A VDB topological index over a set of digraphs $\mathcal{H}\subseteq {\mathcal{D}}_n$ of maximal degree p is the composition

$$\mathcal{H}\stackrel{\alpha }{⟶}{\mathcal{M}}_p\left(\mathbb{R}\right)\stackrel{⟨\phi ,-⟩}{⟶}\mathbb{R},$$

where $\alpha$ is a representing function of $\mathcal{H}$ in the space of matrices ${\mathcal{M}}_p\left(\mathbb{R}\right)$ and $\phi \in {\mathcal{M}}_p\left(\mathbb{R}\right).$ What makes it a vertex-degree-based topological index is the fact that the matrix representing the digraph $H\in \mathcal{H}$ has entries containing information about the degrees of the vertices, namely, the degrees of the end-vertices of each arc in H. A natural question arises: what kind of topological indices do we obtain when we change the representing function of the set $\mathcal{H}$ of digraphs?

Let us discuss one specific example. Let G be a connected graph with vertex set V and edge set E. For $u,v\in V$, we denote by $d_G\left(u,v\right)$ the distance of u and v in G, that is, the length of the shortest path connecting u and v in G. Furthermore, we write $n_G\left(u,v\right)$ for the number of vertices in G closer to u than to v.

Consider the set ${\mathcal{C}}_n$ of all connected graphs with n vertices. Clearly, ${\mathcal{C}}_n$ has maximal degree $n-1$. We represent each graph $G\in {\mathcal{C}}_n$ by the matrix $\beta \left(G\right)\in {\mathcal{M}}_{n-1}\left(\mathbb{R}\right)$, where ${\left[\beta \left(G\right)\right]}_{ij}$ is the number of edges $e=uv$ such that $n_G\left(u,v\right)=i$ and $n_G\left(v,u\right)=j$. On the other hand, consider the matrix $S\in {\mathcal{M}}_{n-1}\left(\mathbb{R}\right)$, defined in each $ij$-entry as ${\left[S\right]}_{ij}=ij$. Then we consider the composition $\widehat{S}=\frac{1}{2}⟨S,-⟩\circ \beta .$ It turns out that for each $G\in {\mathcal{C}}_n$,

$$\widehat{S}\left(G\right)=\sum _{e=uv\in E\left(G\right)}{n}_G\left(u,v\right)n_G\left(v,u\right).$$

This is precisely the well-known Szeged index introduced by Gutman in [21]. Similarly, if we choose the matrix $M\in {\mathcal{M}}_{n-1}\left(\mathbb{R}\right)$ with $ij$-entry ${\left[M\right]}_{ij}=|i-j|$, then the composition $\widehat{M}=\frac{1}{2}⟨M,-⟩\circ \beta$ yields for each $G\in {\mathcal{C}}_n$,

$$\widehat{M}\left(G\right)=\sum _{e=uv\in E\left(G\right)}|n_G\left(u,v\right)-n_G\left(v,u\right)|.$$

In this case we obtain the well-known Mostar index introduced in [22]. More generally, given any matrix $\psi \in {\mathcal{M}}_{n-1}\left(\mathbb{R}\right),$ we can define the Szeged-like topological index $\widehat{\psi }=\frac{1}{2}⟨\psi ,-⟩\circ \beta$ over ${\mathcal{C}}_n$.

7. Conclusions

In conclusion, this new matrix approach to topological indices via a representing function of the set of digraphs into the space of matrices formalizes, unifies and gives a geometrical interpretation to the concept of a topological index. Also, it is important to emphasize that even in the case of graphs, it is possible to study nonsymmetric VDB topological indices (for instance, matrices induced by nonsymmetric bivariate functions as in the case of the general first Zagreb index), but in view of Theorem 2, these indices reduce to the study of symmetric VDB topological indices. Finally, it is important to point out that this matrix approach can be extended to different classes of topological indices, not necessarily vertex-degree-based indices.