Fuzzy-Augmented Model Reference Adaptive PID Control Law Design for Robust Voltage Regulation in DC–DC Buck Converters
Abstract
:1. Introduction
1.1. Literature Review
1.2. Main Contribution
- Formulation of a well-postulated MRAC-based PID control law for the buck converter that tracks the output of the baseline LQ-PID control law.
- Robustification of the designed MRAC-based PID control law by augmenting it with a pre-configured fuzzy self-regulating system that uses the system’s output voltage error and its relative rate to dynamically adjust the MRAC’s inner adaptation rates.
- Experimental validation of the proposed fuzzy-augmented MRAC-based PID control law by performing tailored hardware experiments on a low-power DC–DC buck converter prototype.
1.3. Innovative Features of the Proposed Control Law
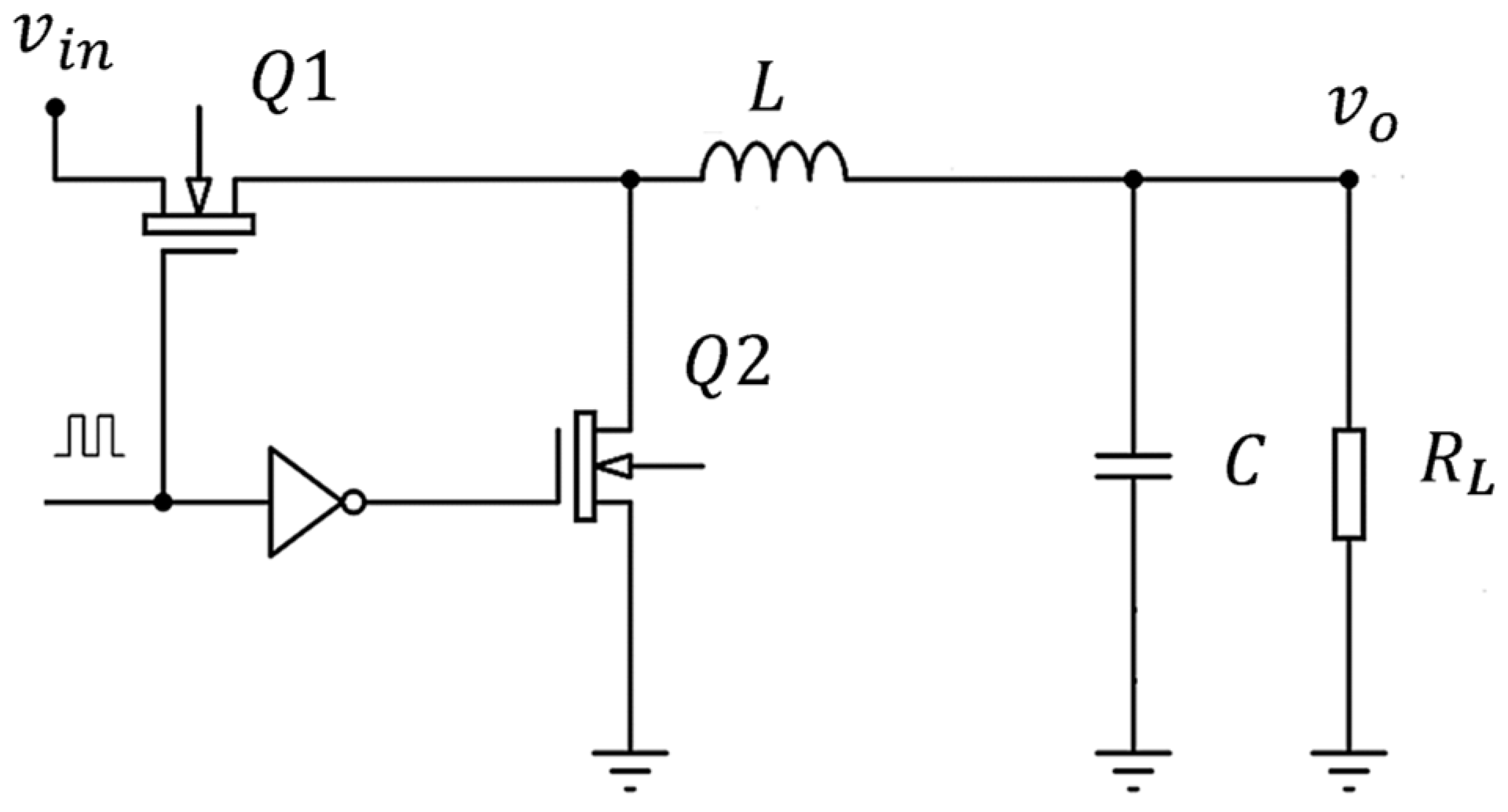
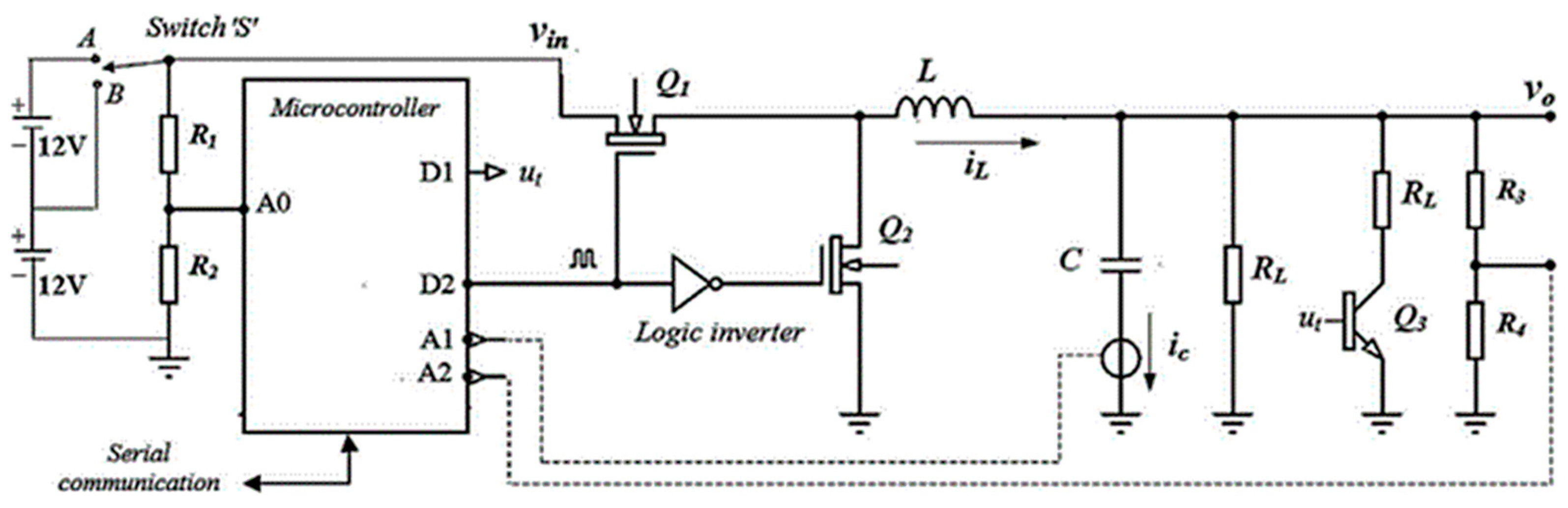
2. System Description
2.1. State Space Model
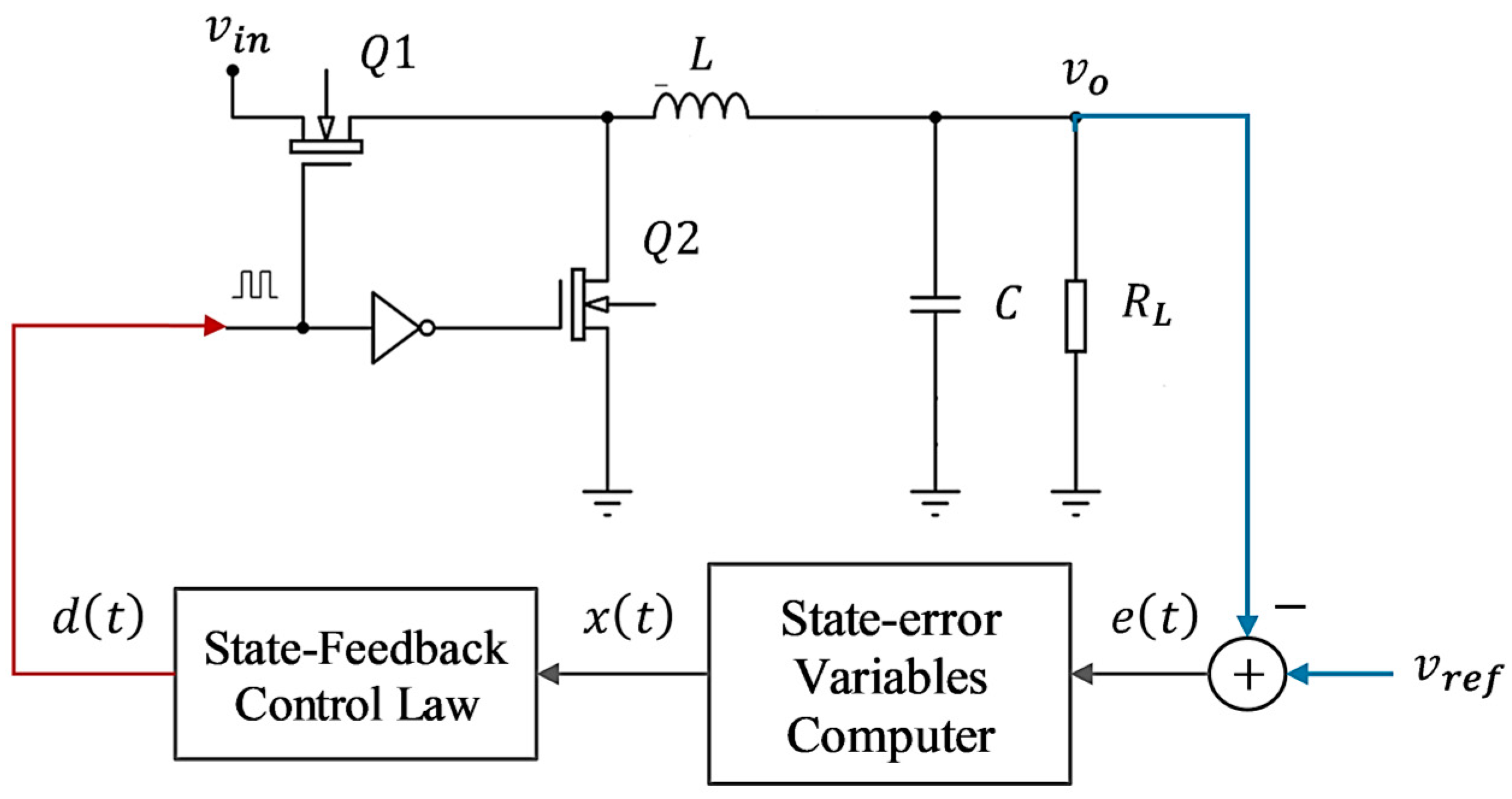
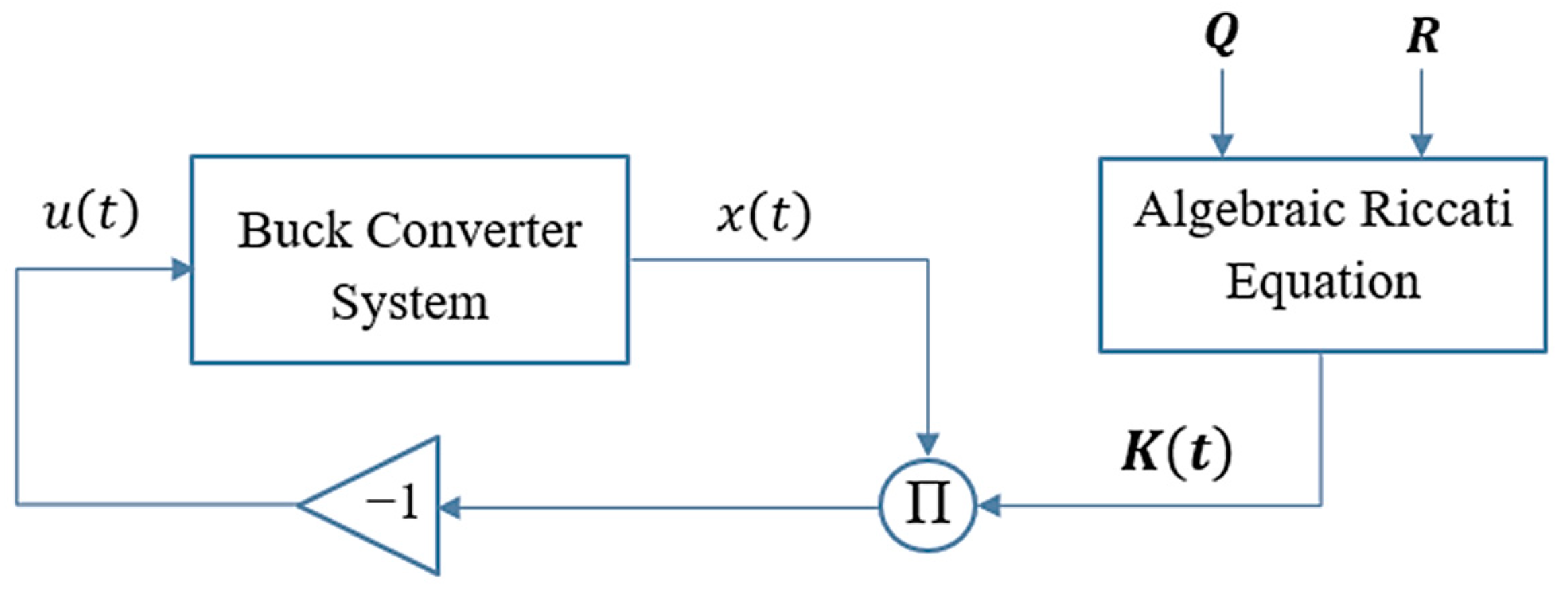
2.2. Baseline LQ-PID Compensator Design
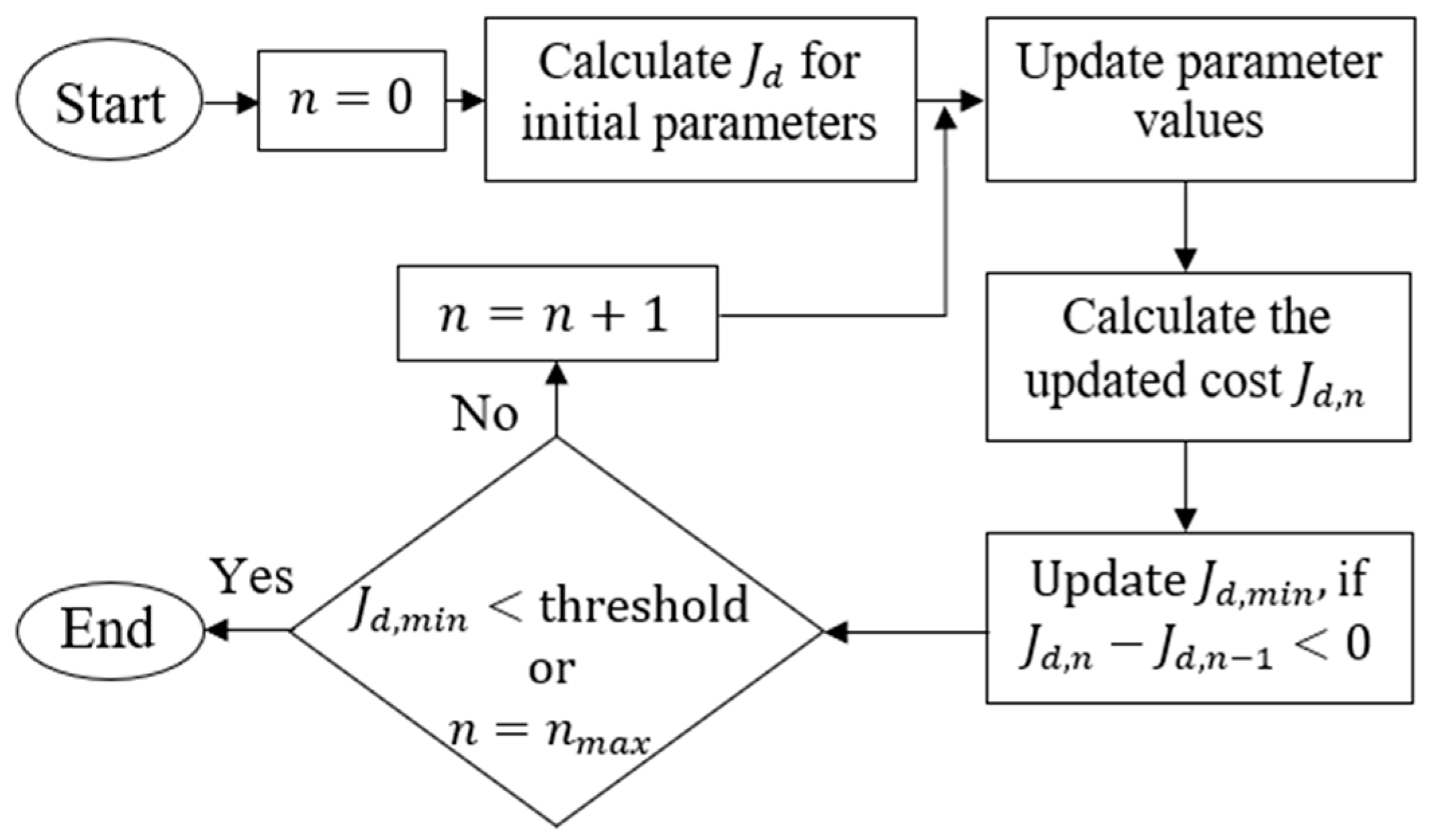
2.3. Parameter Tuning Procedure
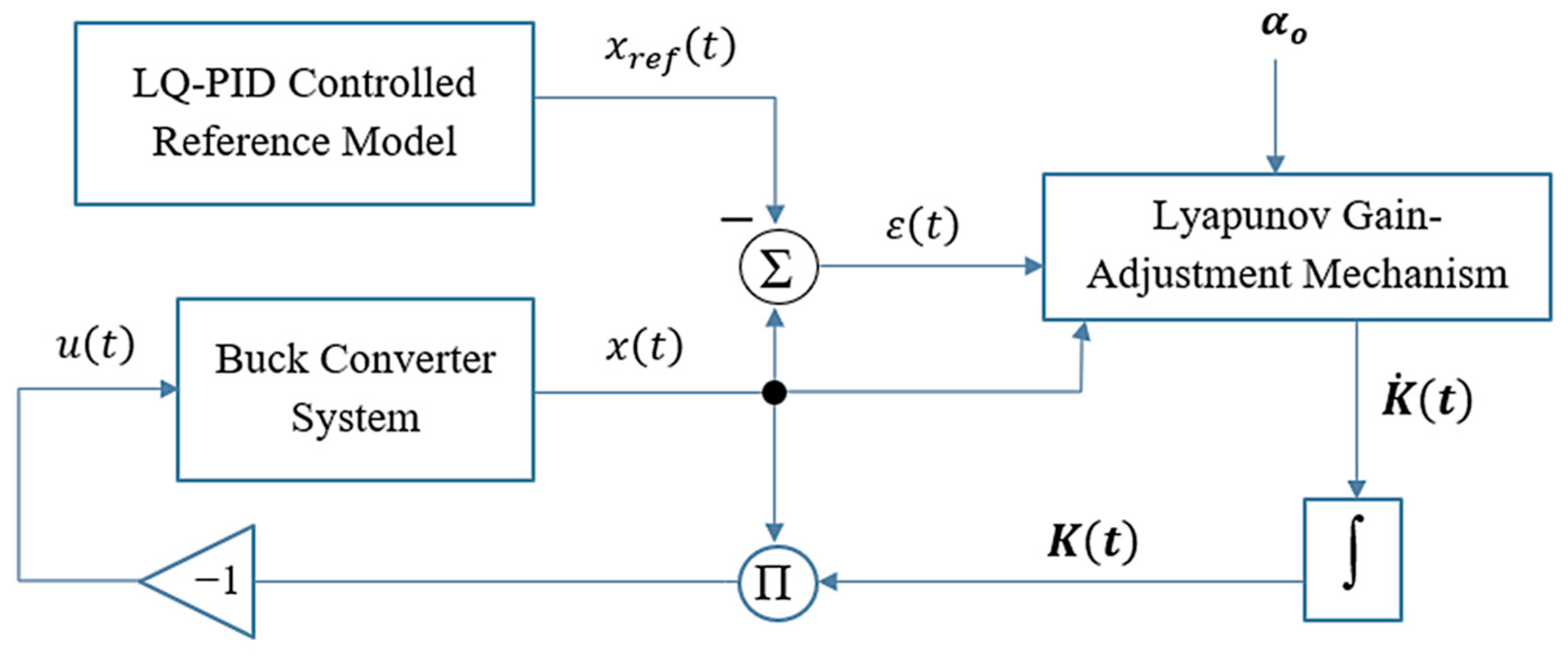
3. Basic MRAC-Based PID Control Law
4. Proposed Control Methodology
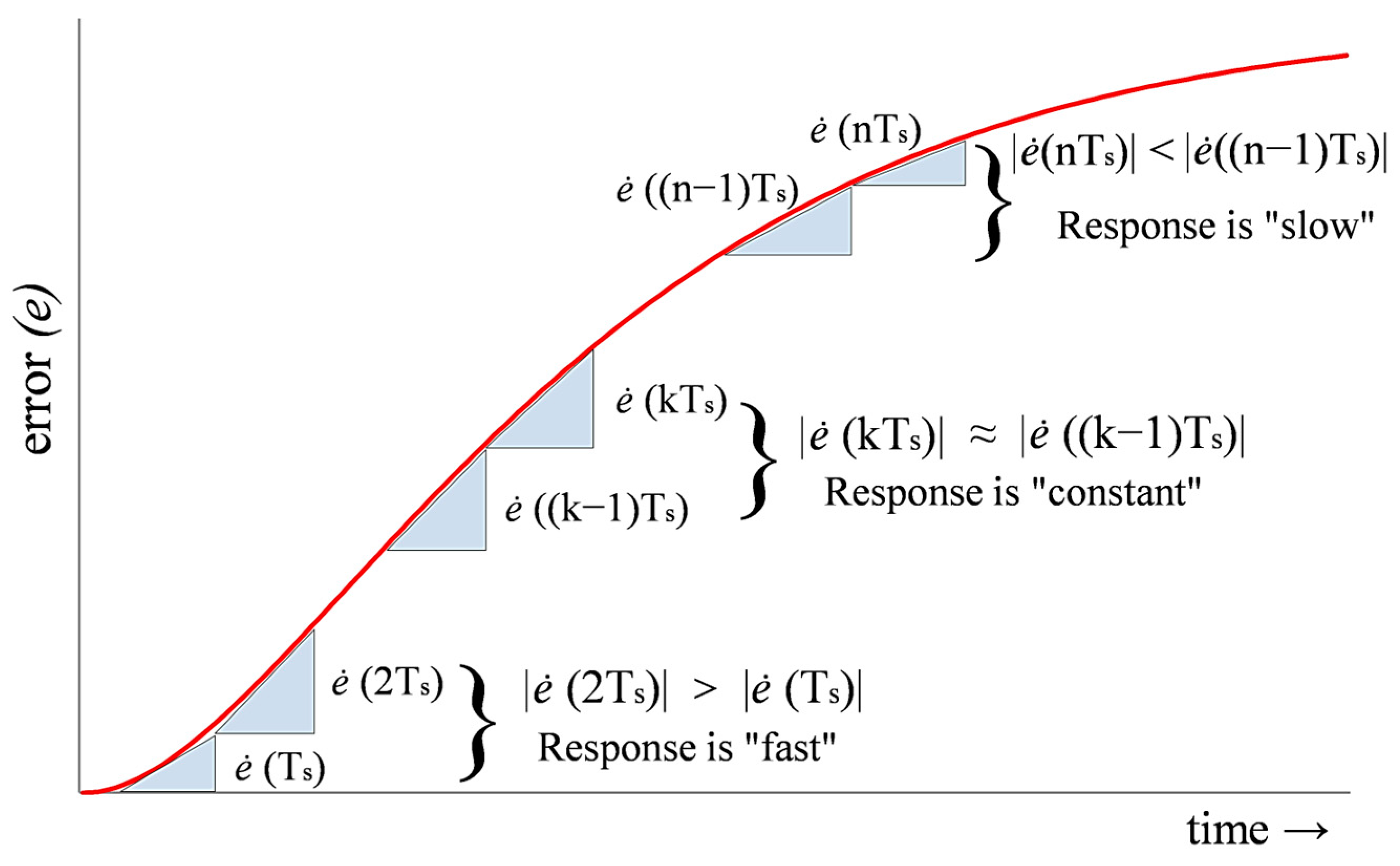
4.1. Relative Rate Calculation
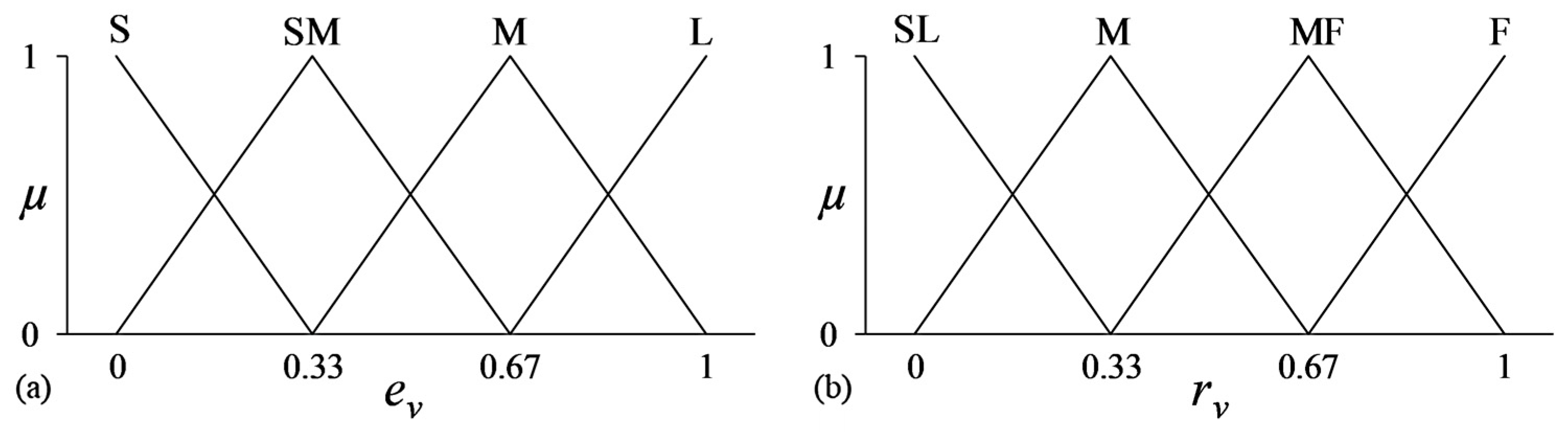
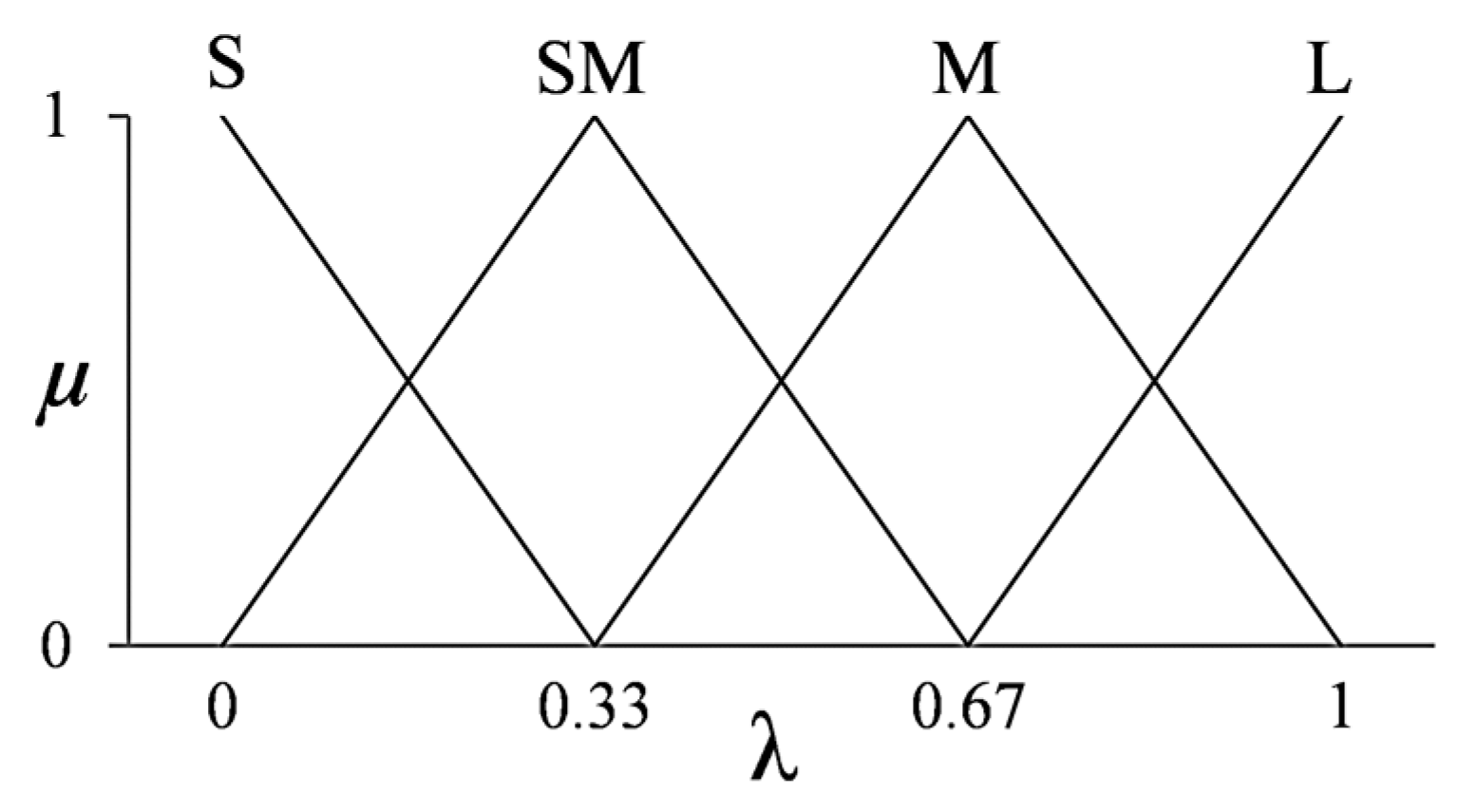
4.2. Fuzzy Self-Regulation of Adaptation Rates
- When the system response is fast, but the error magnitude is small, large adaptation rates are selected that efficiently change the controller gains to quickly counteract the disturbance by reducing the transit speed and rejecting the overshoots.
- When the error magnitude is large and the system response is also fast, moderate adaptation rates are selected to avoid highly disruptive (and aggressive) control application, which prevents unnecessary increment in the overshoot of the response that has already drifted significantly away from the reference.
- When the system response is slow, irrespective of the error magnitude, the adaptation rates are reduced to decelerate the responsiveness of the controller gains. This helps apply a gentle control effort for eliminating any residual steady-state fluctuations while maintaining an accurate and smooth tracking of the reference signal.
4.3. FA-MRAC Law Formulation
5. Experimental Evaluation and Discussion
5.1. Experimental Setup
5.2. Tests and Results
- Voltage regulation: This test case serves to analyze the control procedure’s transient response as well as its reference tracking accuracy under nominal conditions. The controllers are tasked to track the reference signal of +10.0 V DC while the and are kept constant at +24.0 V and 10 Ω, respectively. The resulting time domain profiles of yielded by each controller are illustrated in Figure 12.
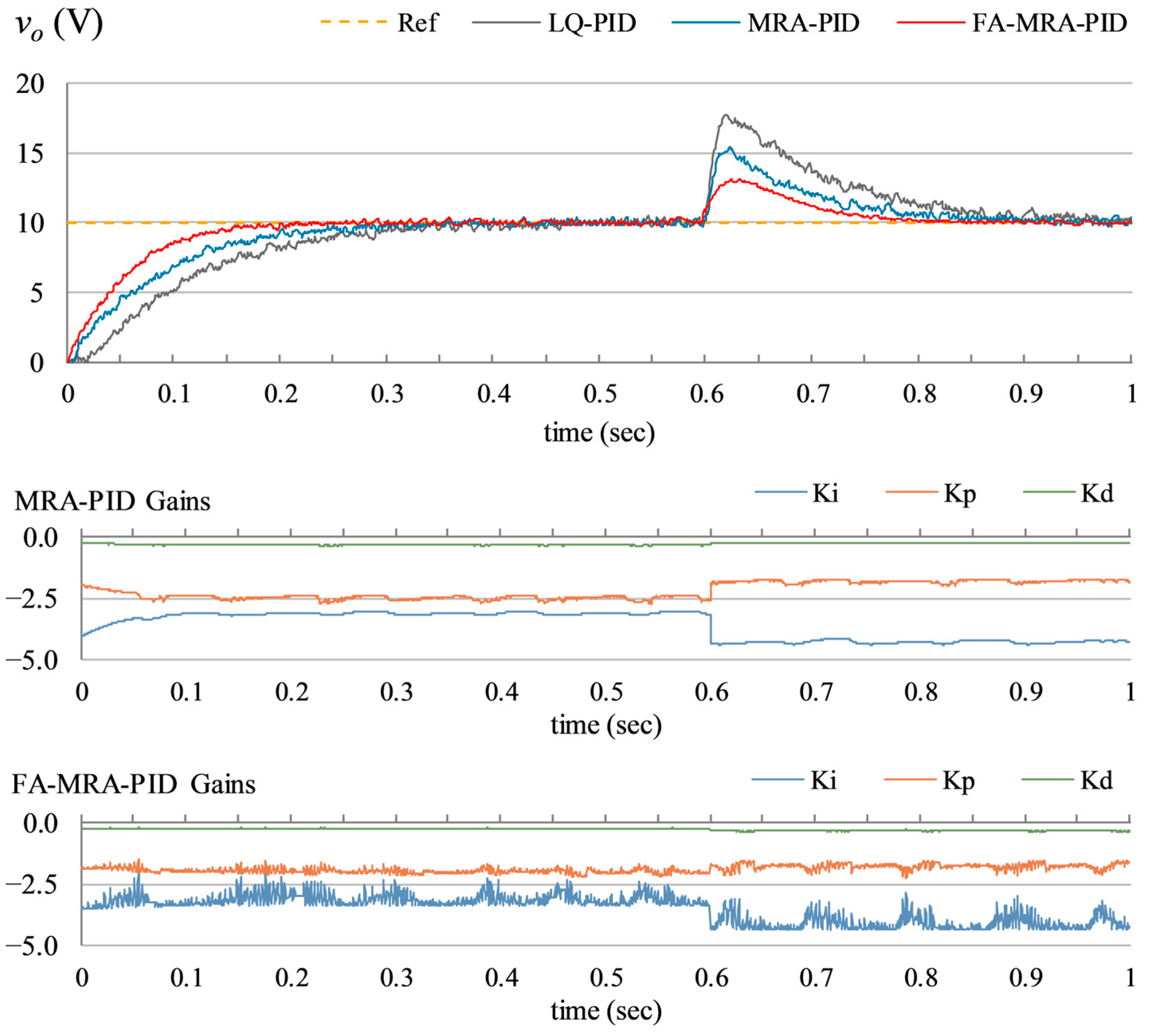
- Load disturbance rejection: This test case is used to examine the controller’s ability to reject step disturbances in the converter’s load. The said experiment is conducted by activating the switch at , which administers a 50% step decrement in the system’s load resistance. The corresponding fluctuations recorded in are shown in Figure 13.
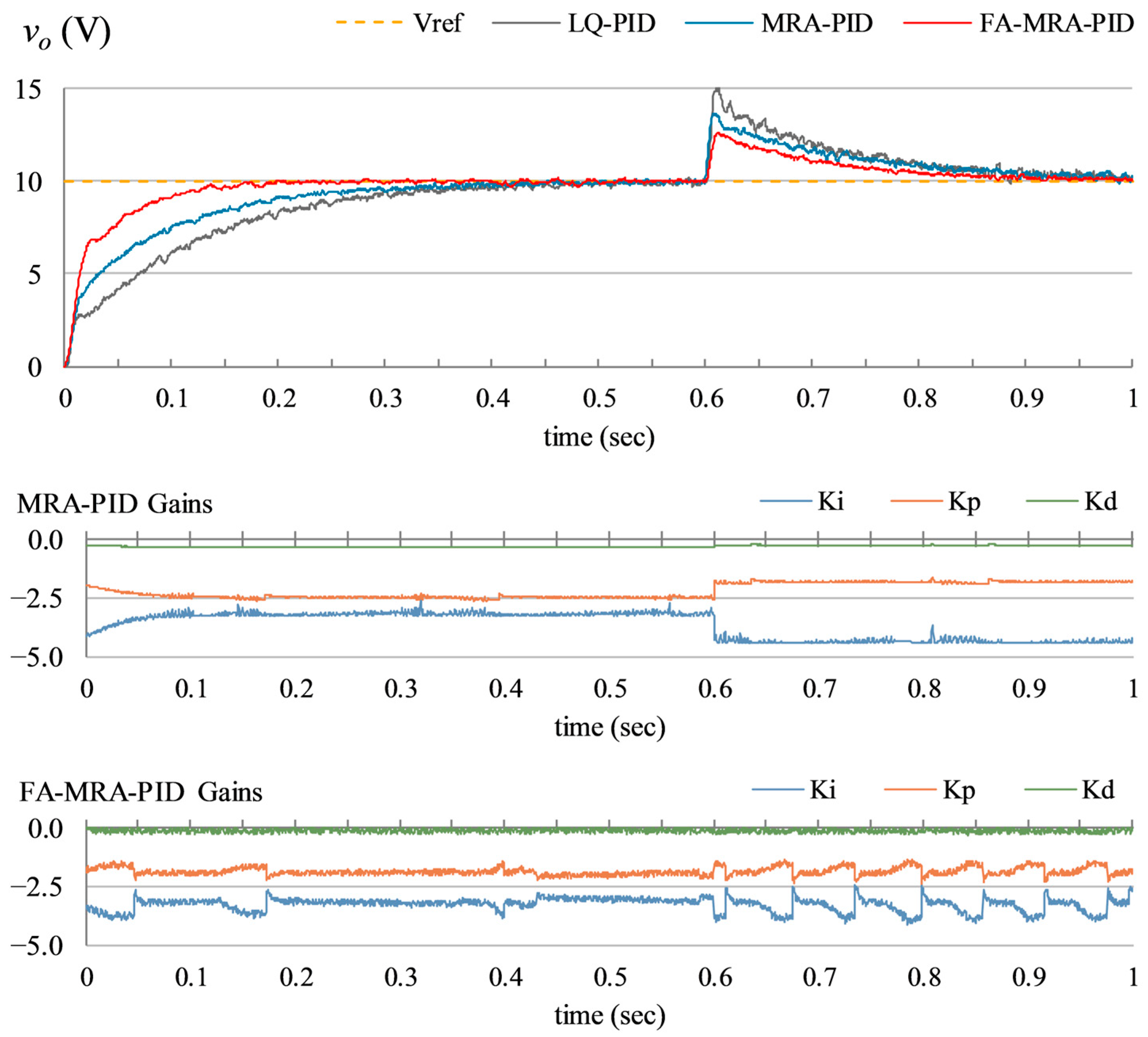
- Input disturbance compensation: This test case is used to examine the controller’s adaptability to compensate for step disturbances in the converter’s . The said experiment is conducted by flipping the switch at from the position A to position B, as shown in Figure 5, which decreases the converter’s from +24.0 V to +12.0 V. The consequent perturbations in the system’s are shown in Figure 14.
5.3. Discussion
- erms: The root mean squared value of error in , .
- trise: The time taken by to commute from 10% to 90% of the .
- tset: The time taken by to settle within of after the initial startup.
- OS: The peak overshoot in contributed by the initial startup.
- Mp: The peak overshoot in contributed by the load or input disturbance.
- trec: The time taken by to recover and settle within of after disturbance.
5.4. Comparison with a State-of-the-Art Control Law
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alfred, D.; Czarkowski, D.; Teng, J. Reinforcement Learning-Based Control of a Power Electronic Converter. Mathematics 2024, 12, 671. [Google Scholar] [CrossRef]
- Shenoy, P.S.; Amaro, M.; Morroni, J.; Freeman, D. Comparison of a Buck Converter and a Series Capacitor Buck Converter for High-Frequency, High-Conversion-Ratio Voltage Regulators. IEEE Trans. Pow. Electron. 2016, 31, 7006–7015. [Google Scholar] [CrossRef]
- Abdurraqeeb, A.M.; Al-Shamma’a, A.A.; Alkuhayli, A.; Noman, A.M.; Addoweesh, K.E. RST Digital Robust Control for DC/DC Buck Converter Feeding Constant Power Load. Mathematics 2022, 10, 1782. [Google Scholar] [CrossRef]
- Rumbo-Morales, J.Y.; Gómez-Radilla, J.; Ortiz-Torres, G.; Sorcia-Vázquez, F.D.J.; Buenabad-Arias, H.M.; López-Osorio, M.A.; Torres-Cantero, C.A.; Ramos-Martinez, M.; Juárez, M.A.; Calixto-Rodriguez, M.; et al. Geometric Control and Structure-at-Infinity Control for Disturbance Rejection and Fault Compensation Regarding Buck Converter-Based LED Driver. Mathematics 2024, 12, 1277. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Dong, J.; Hu, Y.; Jiang, L.; He, X. Integrated Multiple-Output Synchronous Buck Converter for Electric Vehicle Power Supply. IEEE Trans. Veh. Technol. 2017, 66, 5752–5761. [Google Scholar] [CrossRef]
- Bereš, M.; Kováč, D.; Vince, T.; Kováčová, I.; Molnár, J.; Tomčíková, I.; Dziak, J.; Jacko, P.; Fecko, B.; Gans, Š. Efficiency Enhancement of Non-Isolated DC-DC Interleaved Buck Converter for Renewable Energy Sources. Energies 2021, 14, 4127. [Google Scholar] [CrossRef]
- Sreekumar, C.; Agarwal, V. Hybrid control approach for the output voltage regulation in buck type DC–DC converter. IET Electr. Power Appl. 2007, 1, 897–906. [Google Scholar] [CrossRef]
- Saoudi, M.; El-Sayed, A.; Metwally, H. Design and implementation of closed-loop control system for buck converter using different techniques. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 30–39. [Google Scholar] [CrossRef]
- Wang, S.; Li, S.; Su, J.; Li, J.; Zhang, L. Extended state observer-based nonsingular terminal sliding mode controller for a DC-DC buck converter with disturbances: Theoretical analysis and experimental verification. Int. J. Control 2023, 96, 1661–1671. [Google Scholar] [CrossRef]
- Olalla, C.; Queinnec, I.; Leyva, R.; El-Aroudi, A. Robust optimal control of bilinear DC–DC converters. Control Eng. Pract. 2011, 19, 688–699. [Google Scholar] [CrossRef]
- Mariethoz, S.; Almer, S.; Baj, M.; Beccuti, A.G.; Patino, D.; Wernrud, A.; Buisson, J.; Cormerais, H.; Geyer, T.; Fujioka, H.; et al. Comparison of hybrid control techniques for buck and boost DC-DC converters. IEEE Trans. Control Syst. Technol. 2010, 18, 1126–1145. [Google Scholar] [CrossRef]
- Rajamani, M.P.E.; Rajesh, R.; Willjuice Iruthayarajan, M. Design and experimental validation of PID controller for buck converter: A multi-objective evolutionary algorithms based approach. IETE J. Res. 2023, 69, 21–32. [Google Scholar] [CrossRef]
- Kapat, S.; Krein, P.T. Formulation of PID control for DC–DC converters based on capacitor current: A geometric context. IEEE Trans. Pow. Electron. 2011, 27, 1424–1432. [Google Scholar] [CrossRef]
- Chincholkar, S.; Tariq, M.; Poshtan, M.; Sharaf, M. Normalized Error-Based PI Controller and Its Application to the DC–DC Buck Converter. Mathematics 2024, 12, 240. [Google Scholar] [CrossRef]
- Ghamari, S.M.; Narm, H.G.; Mollaee, H. Fractional-order fuzzy PID controller design on buck converter with antlion optimization algorithm. IET Control Theory Appl. 2022, 16, 340–352. [Google Scholar] [CrossRef]
- Warrier, P.; Shah, P. Design of an Optimal Fractional complex order PID controller for buck converter. J. Rob. Control 2023, 4, 243–262. [Google Scholar] [CrossRef]
- Naik, B.B.; Mehta, A.J. Sliding mode controller with modified sliding function for DC-DC Buck Converter. ISA Trans. 2017, 70, 279–287. [Google Scholar] [CrossRef] [PubMed]
- Ding, S.; Zheng, W.X.; Sun, J.; Wang, J. Second-order sliding-mode controller design and its implementation for buck converters. IEEE Trans. Ind. Inform. 2017, 14, 1990–2000. [Google Scholar] [CrossRef]
- Huangfu, Y.; Zhuo, S.; Rathore, A.K.; Breaz, E.; Nahid-Mobarakeh, B.; Gao, F. Super-twisting differentiator-based high order sliding mode voltage control design for DC-DC buck converters. Energies 2016, 9, 494. [Google Scholar] [CrossRef]
- Kaplan, O.; Bodur, F. Second-order sliding mode controller design of buck converter with constant power load. Int. J. Control 2023, 96, 1210–1226. [Google Scholar] [CrossRef]
- Dong, W.; Li, S.; Fu, X.; Li, Z.; Fairbank, M.; Gao, Y. Control of a buck DC/DC converter using approximate dynamic programming and artificial neural networks. IEEE Trans. Circuits Syst. I Reg. Papers 2021, 68, 1760–1768. [Google Scholar] [CrossRef]
- Sorouri, H.; Sedighizadeh, M.; Oshnoei, A.; Khezri, R. An intelligent adaptive control of DC–DC power buck converters. Int. J. Elect. Pow. Energy Syst. 2022, 141, 108099. [Google Scholar] [CrossRef]
- Nizami, T.K.; Mahanta, C. An intelligent adaptive control of DC–DC buck converters. J. Franklin Inst. 2016, 353, 2588–2613. [Google Scholar] [CrossRef]
- Saleem, O.; Shami, U.T.; Mahmood-ul-Hasan, K. Time-optimal control of DC-DC buck converter using single-input fuzzy augmented fractional-order PI controller. Int. Trans. Electr. Energy Syst. 2019, 29, e12064. [Google Scholar] [CrossRef]
- Behih, K.; Benmahammed, K.; Bouchama, Z.; Harmas, M.N. Real-time investigation of an adaptive fuzzy synergetic controller for a DC-DC buck converter. Eng. Technol. Appl. Sci. Res. 2019, 9, 4984–4989. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M. Performance optimization of LQR-based PID controller for DC-DC buck converter via iterative-learning-tuning of state-weighting matrix. Int. J. Numer. Mod. 2019, 32, e2572. [Google Scholar] [CrossRef]
- Junior, L.A.M.; Valle, R.L.; Ferreira, A.A.; Barbosa, P.G.; Montagner, V.F. A LQR design with rejection of disturbances and robustness to load variations applied to a buck converter. Eletrônica Potência 2016, 21, 7–15. [Google Scholar] [CrossRef]
- Danayiyen, Y.; Altas, I.; Sahin, E. Model Predictive Control of a DC-DC Buck Converter. Sigma J. Eng. & Nat. Sci. 2017, 8, 91–97. [Google Scholar]
- Chen, Y.; Lu, Y.; Luo, W. Model predictive control of double-input buck converters. J. Pow. Electron. 2021, 21, 941–950. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P.; Sayed-Mouchaweh, M. Adaptive neurofuzzy H-infinity control of DC–DC voltage converters. Neural Comput. Appl. 2020, 32, 2507–2520. [Google Scholar] [CrossRef]
- Boukerdja, M.; Chouder, A.; Hassaine, L.; Bouamama, B.O.; Issa, W.; Louassaa, K. H∞ based control of a DC/DC buck converter feeding a constant power load in uncertain DC microgrid system. ISA Trans. 2020, 105, 278–295. [Google Scholar] [CrossRef] [PubMed]
- Ghamari, S.M.; Khavari, F.; Mollaee, H. Adaptive backstepping controller design for DC/DC buck converter optimised by grey wolf algorithm. IET Energy Syst. Integr. 2024, 6, 18–30. [Google Scholar] [CrossRef]
- Saadat, S.A.; Ghamari, S.M.; Mollaee, H. Adaptive backstepping controller design on Buck converter with a novel improved identification method. IET Control Theory Appl. 2022, 16, 485–495. [Google Scholar] [CrossRef]
- He, W.; Namazi, M.M.; Guerrero, J.M. Adaptive Energy-Based Control for Buck Converter with a Class of Nonlinear Loads. IEEE Trans. Circuit Syst. II 2022, 69, 4869–4873. [Google Scholar] [CrossRef]
- Chouya, A.; Boureguig, K. Adaptive Control with MRAC Regulator for DC-DC Buck Converter. Int. J. Control Syst. Robot. 2022, 7, 13–26. [Google Scholar]
- Islam, M.; Abdul Ghaffar, A.F.; Sulaeman, E.; Ahsan, M.M.; Kouzani, A.Z.; Mahmud, M.P. Performance analysis of PI and DMRAC algorithm in buck–boost converter for voltage tracking in electric vehicle using simulation. Electronics 2021, 10, 2516. [Google Scholar] [CrossRef]
- Qureshi, M.A.; Musumeci, S.; Torelli, F.; Reatti, A.; Mazza, A.; Chicco, G. A novel model reference adaptive control approach investigation for power electronic converter applications. Int. J. Electr. Pow. Energy Syst. 2024, 156, 109722. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M.; Mahmood-ul-Hasan, K.; Ahmad, M. Performance enhancement of multivariable model reference optimal adaptive motor speed controller using error-dependent hyperbolic gain functions. Automatika 2020, 61, 117–131. [Google Scholar] [CrossRef]
- Dınakın, D.; Oluseyi, P. Fuzzy-Optimized model reference adaptive control of interacting and noninteracting processes based on MIT and Lyapunov rules. Turkish J. Eng. 2021, 5, 141–153. [Google Scholar] [CrossRef]
- Saleem, O.; Rizwan, M.; Awan, F.G. Robustification of the state-space MRAC law for under-actuated systems via fuzzy-immunological computations. Sci. Prog. 2022, 105, 1–26. [Google Scholar] [CrossRef]
- Saleem, O.; Awan, F.G.; Mahmood-ul-Hasan, K.; Ahmad, M. Self-adaptive fractional-order LQ-PID voltage controller for robust disturbance compensation in DC-DC buck converters. Int. J. Numer. Model. 2020, 33, e2718. [Google Scholar] [CrossRef]
- Tan, G.Q.; Chen, Y.H.; Gu, L. LQR based optimal PID control for buck converter. Appl. Mech. Mater. 2014, 687, 3221–3226. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Saleem, O.; Iqbal, J. Complex-order PID controller design for enhanced blood-glucose regulation in Type-I diabetes patients. Meas. Control 2023, 56, 1811–1825. [Google Scholar] [CrossRef]
- Tian, T.; Hou, X.; Yan, F. A Novel MRAC Scheme for Output Tracking. Mathematics 2022, 10, 2384. [Google Scholar] [CrossRef]
- Chen, K.Y. Model reference adaptive minimum-energy control for a mechatronic elevator system. Optim. Control Appl. Method. 2017, 38, 3–18. [Google Scholar] [CrossRef]
- Astrom, K.J.; Wittenmark, B. Adaptive Control, 3rd ed.; Pearson Education: London, UK, 1995. [Google Scholar]
- Chen, K.Y.; Tung, P.C.; Tsai, M.T.; Fan, Y.H. A self-tuning fuzzy PID-type controller design for unbalance compensation in an active magnetic bearing. Expert. Syst. Appl. 2009, 36, 8560–8570. [Google Scholar] [CrossRef]
- Saleem, O. An enhanced adaptive-LQR procedure for under-actuated systems using relative-rate feedback to dynamically reconfigure the state-weighting-factors. J. Vib. Control 2023, 29, 2316–2331. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Prasad, N.R.; Walker, C.L.; Walker, E.A. A First Course in Fuzzy and Neural Control, 1st ed; Chapman and Hall/CRC: London, UK, 2002. [Google Scholar]



| Performance Parameter | COPID [15] | HOSMC [20] | CNN [23] | LQ-PID [26] | H-inf [30] | Backstep [32] | MRAC [35] | Proposed Scheme |
|---|---|---|---|---|---|---|---|---|
| Error minimization | Good | Better | Good | Bad | Good | Fair | Good | Good |
| Asymptotic stability | Yes | Yes | Yes | Yes | Yes | Difficult | Yes | Yes |
| Control economy | Fair | Bad | Bad | Better | Fair | Bad | Fair | Better |
| Disturbance rejection | Good | Best | Better | Bad | Good | Fair | Good | Better |
| Chattering suppression | Good | Fair | Fair | Good | Good | Good | Better | Better |
| Mathematical complexity | Medium | High | High | Low | High | High | Low | Low |
| Computation burden | Medium | High | High | Low | High | High | Low | Medium |
| Parameter tuning needed | High | Medium | High | Low | Low | High | Low | Medium |
| Parameters | Description | Value | Units |
|---|---|---|---|
| Load resistor | 10 | Ω | |
| Inductor | 220 | mH | |
| Capacitor | 2700 | μF | |
| Capacitor’s ESR | 0.04 | Ω | |
| Capacitor’s ESL | 0.06 | Ω | |
| Input voltage | 24.0 | V | |
| Output voltage | 10.0 | V |
| System’s Response | ||
|---|---|---|
| Positive | Positive | Fast |
| Positive | Zero | Moderate |
| Positive | Negative | Slow |
| Negative | Positive | Slow |
| Negative | Zero | Moderate |
| Negative | Negative | Fast |
| SL | M | MF | F | |
|---|---|---|---|---|
| S | M | M | L | L |
| SM | SM | M | M | L |
| M | S | SM | M | M |
| L | S | S | SM | M |
| Experiment | KPM | Control Law | |||
|---|---|---|---|---|---|
| Symbol | Unit | LQ-PID | MRA-PID | FA-MRA-PID | |
| A | erms | V | 0.055 | 0.042 | 0.035 |
| trise | sec. | 0.21 | 0.14 | 0.10 | |
| OS | V | 0.29 | 0.46 | 0.28 | |
| tset | sec. | 0.40 | 0.30 | 0.21 | |
| B | erms | V | 0.085 | 0.062 | 0.046 |
| Mp | V | 7.74 | 5.40 | 3.09 | |
| trec | sec. | 0.26 | 0.21 | 0.16 | |
| C | erms | V | 0.054 | 0.042 | 0.029 |
| Mp | V | 5.07 | 3.65 | 2.63 | |
| trec | sec. | 0.35 | 0.31 | 0.27 | |
| Experiment | KPM | Control Law | Percentage Improvement | ||
|---|---|---|---|---|---|
| Symbol | Unit | PIαDβ [41] | FA-MRA-PID (Proposed) | ||
| A | erms,ss | mV | 6.56 | 6.15 | 6.3 % |
| trise | msec. | 0.15 | 0.10 | 33.3 % | |
| OS | V | n/a | 0.28 | n/a | |
| tset | sec. | 0.23 | 0.21 | 8.7 % | |
| B | Mp | V | 3.48 | 3.09 | 11.2 % |
| trec | sec. | 0.18 | 0.16 | 11.1 % | |
| C | Mp | V | 4.66 | 2.63 | 43.5 % |
| trec | sec. | 0.35 | 0.27 | 22.9 % | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleem, O.; Ahmad, K.R.; Iqbal, J. Fuzzy-Augmented Model Reference Adaptive PID Control Law Design for Robust Voltage Regulation in DC–DC Buck Converters. Mathematics 2024, 12, 1893. https://doi.org/10.3390/math12121893
Saleem O, Ahmad KR, Iqbal J. Fuzzy-Augmented Model Reference Adaptive PID Control Law Design for Robust Voltage Regulation in DC–DC Buck Converters. Mathematics. 2024; 12(12):1893. https://doi.org/10.3390/math12121893
Chicago/Turabian StyleSaleem, Omer, Khalid Rasheed Ahmad, and Jamshed Iqbal. 2024. "Fuzzy-Augmented Model Reference Adaptive PID Control Law Design for Robust Voltage Regulation in DC–DC Buck Converters" Mathematics 12, no. 12: 1893. https://doi.org/10.3390/math12121893
APA StyleSaleem, O., Ahmad, K. R., & Iqbal, J. (2024). Fuzzy-Augmented Model Reference Adaptive PID Control Law Design for Robust Voltage Regulation in DC–DC Buck Converters. Mathematics, 12(12), 1893. https://doi.org/10.3390/math12121893







