Two Block Splitting Iteration Methods for Solving Complex Symmetric Linear Systems from Complex Helmholtz Equation

Abstract

In this paper, we study the improved block splitting (IBS) iteration method and its accelerated variant, the accelerated improved block splitting (AIBS) iteration method, for solving linear systems of equations stemming from the discretization of the complex Helmholtz equation. We conduct a comprehensive convergence analysis and derive optimal iteration parameters aimed at minimizing the spectral radius of the iteration matrix. Through numerical experiments, we validate the efficiency of both iteration methods.

1. Introduction

In this paper, we consider the complex partial differential Equation (PDE) governing the 2D field variable $u(x,y)$:

$$-{\nabla }^{2}u+\sigma u=f,{\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2},\sigma \in \mathbb{C}$$

(1)

where, importantly, the parameter $\sigma$ is a complex-valued constant. The PDE in (1) will then be referred to as the complex Helmholtz equation. The complex Helmholtz equation arises in periodically forced systems, ranging from electrochemical impedance spectroscopy to unsteady slow viscous flows, and in a broad area that has become known as diffusion wave field theory [1]. Discretizations of the complex Helmholtz Equation (1) using, e.g., finite differences [2,3,4], finite element [5,6], or spectral element methods [7], and appropriate boundary conditions result in a large, sparse, possibly complex-valued, and highly indefinite linear system:

$$Ax\equiv (W+\mathbf{i}T)x=\mathit{b},$$

(2)

where $W,T\in {\mathbb{R}}^{n\times n}$ are symmetric positive semi-definite matrices with at least one of them being positive definite, $x,\mathit{b}\in {\mathbb{C}}^n$, and $\mathbf{i}=\sqrt{-1}$ is the imaginary unit. The above linear system is also widely used in scientific computing and engineering applications, such as electromagnetism, wave propagation, quantum mechanics, molecular scattering, and structural dynamics (see [8,9,10,11,12,13,14]).

To solve the complex linear system (2), we often transform it into the following equivalent real block two-by-two form:

$$Bz\equiv \left[\begin{array}{cc}W& -T\\ T& W\end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{c}f\\ g\end{array}\right]\equiv \tilde{\mathit{b}},$$

(3)

where $x=u+\mathbf{i}v$, $\mathit{b}=f+\mathbf{i}g$, u, v, f, $g\in {\mathbb{R}}^n$, $\tilde{\mathit{b}}\in {\mathbb{R}}^{2n}$. In this paper, ${\left(·\right)}^{*}$ denotes the conjugate transpose of a matrix or a vector, ${\left(·\right)}^Z$ denotes the transpose of a matrix or a vector, and $\rho (·)$ denotes the spectral radius of a matrix, respectively.

For solving complex symmetric linear systems, a lot of iteration methods, including stationary iteration methods and Krylov subspace iteration methods (often using preconditioners) have been proposed in the literature. In this paper, we are concerned with block splitting iteration methods with parameter acceleration. In recent years, many authors have developed the block splitting iteration methods for solving complex symmetric linear systems. In 2013, for solving the real-valued linear system (3), Bai [15] established a class of rotated block triangular preconditioners, and analyzed the eigenproperties of the corresponding preconditioned matrices. Following this, Salkuyeh et al. [16] discussed the generalized successive overrelaxation (GSOR) iteration method in 2014, with convergence analysis. Then, to improve the convergence speed of GSOR, in 2015, Edalatpour et al. [17] proposed an accelerated GSOR (AGSOR) iteration method with two parameters, and determined the optimal parameters. In 2018, Li et al. [18] constructed a symmetric block triangular splitting (SBTS) iteration method based on two splittings, and gave the convergence conditions as well as the optimal parameters. In 2019, Axelsson and Salkuyeh [19] derived the transformed matrix iteration (TMIT) method and gave the convergence conditions; they also determined that the optimal parameter of TMIT method was contained in the interval $(0, 1)$. In 2021, Siahkolaei et al. [20] gave an upper bound for the spectral radius of the iteration matrix of the TMIT method and then obtained the parameter which minimizes this upper bound.

Recently, Huang [21] studied a new block splitting (NBS) iteration method and a parameterized block splitting (PBS) iteration method to solve the real value linear system (3). In this paper, we continue to study BS iteration methods for solving (3). We will construct the improved block splitting (IBS) iteration method and give the corresponding convergence analysis. Furthermore, using the parameter accelerating technique for the IBS iteration method, we will construct the accelerated improved block splitting (AIBS) iteration method based on the split of the AGSOR iteration method.

The remainder of this paper is organized as follows. In Section 2, we construct the IBS iteration method to solve the linear system with a real value (3) and give the convergence analysis. In Section 3, we study the AIBS iteration method and give the convergence analysis. In Section 4, we present some numerical examples to demonstrate the effectiveness of the IBS and AIBS iteration methods. Finally, some conclusions are drawn in Section 5.

2. IBS Iteration Method and Its Convergence Analysis

In this section, we study the IBS iteration method for solving the real-valued linear system (3). First, we recall the NBS and PBS iteration methods. Multiply both sides of (3) from the left by the block matrix:

$$P=\left[\begin{array}{cc}I& \tilde{\alpha }I\\ 0& I\end{array}\right],$$

(4)

where $\tilde{\alpha }$ is a positive constant, and denote:

$$\left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{cc}I& I\\ 0& \tilde{\alpha }I\end{array}\right]\left[\begin{array}{c}d\\ e\end{array}\right],$$

(5)

where d, $e\in {\mathbb{R}}^n$. Then, (3) can be written as:

$$\left[\begin{array}{cc}W+\tilde{\alpha }T& (1+{\tilde{\alpha }}^2)W\\ T& \tilde{\alpha }W+T\end{array}\right]\left[\begin{array}{c}d\\ e\end{array}\right]=\left[\begin{array}{c}f+\tilde{\alpha }g\\ g\end{array}\right].$$

(6)

Split the coefficient matrix of (6) as follows:

$$\begin{array}{cc}\left[\begin{array}{cc}W+\tilde{\alpha }T& (1+{\tilde{\alpha }}^2)W\\ T& \tilde{\alpha }W+T\end{array}\right]\hfill & =\left[\begin{array}{cc}W+\tilde{\alpha }T& 0\\ T& \tilde{\alpha }W+T\end{array}\right]-\left[\begin{array}{cc}0& -(1+{\tilde{\alpha }}^2)W\\ 0& 0\end{array}\right]\hfill \\ & \equiv \tilde{M}\left(\tilde{\alpha }\right)-\tilde{N}\left(\tilde{\alpha }\right).\hfill \end{array}$$

(7)

Then, it yields the following NBS iteration:

$$\left[\begin{array}{c}{d}^{(k+1)}\\ e^{(k+1)}\end{array}\right]=\tilde{\mathsf{\Gamma }}\left(\tilde{\alpha }\right)\left[\begin{array}{c}{d}^{\left(k\right)}\\ e^{\left(k\right)}\end{array}\right]+\tilde{M}{\left(\tilde{\alpha }\right)}^{-1}\left[\begin{array}{c}f+\tilde{\alpha }g\\ g\end{array}\right],$$

(8)

where the iteration matrix is:

$$\begin{array}{cc}\tilde{\mathsf{\Gamma }}\left(\tilde{\alpha }\right)\hfill & =\tilde{M}{\left(\tilde{\alpha }\right)}^{-1}\tilde{N}\left(\tilde{\alpha }\right)\hfill \\ & =\left[\begin{array}{cc}0& -(1+{\tilde{\alpha }}^2){(W+\tilde{\alpha }T)}^{-1}W\\ 0& (1+{\tilde{\alpha }}^2){(\tilde{\alpha }W+T)}^{-1}T{(W+\tilde{\alpha }T)}^{-1}W\end{array}\right].\hfill \end{array}$$

(9)

To derive the PBS method, we multiply both sides of (3) from the left by the matrix P in (4) and denote:

$$\left[\begin{array}{c}u\hfill \\ v\hfill \end{array}\right]=\left[\begin{array}{cc}I& I\\ 0& \tilde{\beta }I\end{array}\right]\left[\begin{array}{c}\overline{d}\hfill \\ \overline{e}\hfill \end{array}\right],$$

(10)

where $\tilde{\beta }$ is a positive constant and $\overline{d},\overline{e}\in {\mathbb{R}}^n$. Then, (3) can be written as:

$$\left[\begin{array}{cc}\tilde{\alpha }T+W& (\tilde{\alpha }\tilde{\beta }+1)W+(\tilde{\alpha }-\tilde{\beta })T\\ T& \tilde{\beta }W+T\end{array}\right]\left[\begin{array}{c}\overline{d}\\ \overline{e}\end{array}\right]=\left[\begin{array}{c}f+\tilde{\alpha }g\\ g\end{array}\right].$$

(11)

The PBS method splits the coefficient matrix of (11) as follows:

$$\begin{array}{c}\left[\begin{array}{cc}\tilde{\alpha }T+W& (\tilde{\alpha }\tilde{\beta }+1)W+(\tilde{\alpha }-\tilde{\beta })T\\ T& \tilde{\beta }W+T\end{array}\right]\hfill \\ =\left[\begin{array}{cc}\tilde{\alpha }T+W& 0\\ T& \tilde{\beta }W+T\end{array}\right]-\left[\begin{array}{cc}0& -[(\tilde{\alpha }\tilde{\beta }+1)W+(\tilde{\alpha }-\tilde{\beta })T]\\ 0& 0\end{array}\right]\equiv \tilde{M}(\tilde{\alpha },\tilde{\beta })-\tilde{N}(\tilde{\alpha },\tilde{\beta }),\hfill \end{array}$$

(12)

and the iteration matrix is:

$$\begin{array}{cc}\tilde{\mathsf{\Gamma }}(\tilde{\alpha },\tilde{\beta })\hfill & =\tilde{M}{(\tilde{\alpha },\tilde{\beta })}^{-1}\tilde{N}(\tilde{\alpha },\tilde{\beta })\hfill \\ & =\left[\begin{array}{cc}0& -{(\tilde{\alpha }T+W)}^{-1}[(\tilde{\alpha }\tilde{\beta }+1)W+(\tilde{\alpha }-\tilde{\beta })T]\\ 0& {(\tilde{\beta }W+T)}^{-1}T{(\tilde{\alpha }T+W)}^{-1}[(\tilde{\alpha }\tilde{\beta }+1)W+(\tilde{\alpha }-\tilde{\beta })T]\end{array}\right].\hfill \end{array}$$

(13)

Remark 1.

For the NBS method, the optimal parameter ${\tilde{\alpha }}^{*}$, which minimizes the upper bound of the spectral radius $\rho \left(\tilde{\mathsf{\Gamma }}\left(\tilde{\alpha }\right)\right)$ is ${\tilde{\alpha }}^{*}=1$, see Theorem 2.1 in [21]. Furthermore, for the PBS method, maybe not optimal, the parameter $\tilde{\alpha }$ is still taken as ${\tilde{\alpha }}^{*}=1$, see Theorem 3.2 in [21].

By the idea of NBS and PBS methods, we take the parameter $\tilde{\alpha }=1$ directly, then (6) can be written as:

$$\left[\begin{array}{cc}W+T& 2W\\ T& W+T\end{array}\right]\left[\begin{array}{c}d\\ e\end{array}\right]=\left[\begin{array}{c}f+g\\ g\end{array}\right].$$

(14)

Split the coefficient matrix of (14) as follows:

$$\begin{array}{cc}\left[\begin{array}{cc}W+T& 2W\\ T& W+T\end{array}\right]\hfill & =\left[\begin{array}{cc}W+T& 0\\ T& \alpha (W+T)\end{array}\right]-\left[\begin{array}{cc}0& -2W\\ 0& (\alpha -1)(W+T)\end{array}\right]\hfill \\ & \equiv M\left(\alpha \right)-N\left(\alpha \right),\hfill \end{array}$$

(15)

where $\alpha$ is a positive constant. Then, it yields the following IBS iteration:

$$\left[\begin{array}{c}{d}^{(k+1)}\\ e^{(k+1)}\end{array}\right]=\mathsf{\Gamma }\left(\alpha \right)\left[\begin{array}{c}{d}^{\left(k\right)}\\ e^{\left(k\right)}\end{array}\right]+M{\left(\alpha \right)}^{-1}\left[\begin{array}{c}f+g\\ g\end{array}\right],$$

(16)

where the iteration matrix is:

$$\begin{array}{cc}\mathsf{\Gamma }\left(\alpha \right)\hfill & =M{\left(\alpha \right)}^{-1}N\left(\alpha \right)\hfill \\ & =\left[\begin{array}{cc}0& -2{(W+T)}^{-1}W\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(W+T)}^{-1}T{(W+T)}^{-1}W\end{array}\right].\hfill \end{array}$$

(17)

IBS iteration algorithm: Given initial vectors $d^{\left(0\right)},e^{\left(0\right)}\in {\mathbb{R}}^n$, for $k=0,1,2,\cdots ,$ until the sequence ${\left\{{({d^{\left(k\right)}}^Z,{e^{\left(k\right)}}^Z)}^Z\right\}}_{k=0}^{\infty }$ converges, compute:

$$\left\{\begin{array}{c}(W+T)d^{(k+1)}=-2W{e}^{\left(k\right)}+f+g,\hfill \\ \alpha (W+T)e^{(k+1)}=-T{d}^{(k+1)}+(\alpha -1)(W+T)e^{\left(k\right)}+g,\hfill \\ u^{(k+1)}=d^{(k+1)}+e^{(k+1)},v^{(k+1)}=e^{(k+1)}.\hfill \end{array}\right.$$

(18)

From the iteration scheme (18), it can be seen that two linear subsystems with respect to the symmetric positive definite coefficient matrix $T+W$ need to be solved at each iteration step. It can be solved by Cholesky factorization [22].

Next, we give the convergence analysis for the IBS method, and discuss the optimal parameter ${\alpha }^{*}$ that minimizes the spectral radius $\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)$.

Theorem 2.

Let W be symmetric positive definite and T be symmetric positive semi-definite, respectively, and $\alpha >0$. Then:

(1) 

The eigenvalues of the iteration matrix $\mathsf{\Gamma }\left(\alpha \right)$ are taken as follows:

$$\lambda =0,\lambda =1-\frac{1+u_k^2}{\alpha {(1+u_k)}^2},k=1,2,\cdots ,n,$$

(19)

where $0\le u_1\le u_2\le \dots \le u_n$ are the eigenvalues of the matrix $S=W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}$.

(2) 

$\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)<1$ if and only if α satisfies the following conditions:

(a) 

If $u_n<1$:

$$\alpha >\frac{1+u_1^2}{2{(1+u_1)}^2};$$

(20)

(b) 

If $u_1>1$:

$$\alpha >\frac{1+u_n^2}{2{(1+u_n)}^2};$$

(21)

(c) 

If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, $s\in \{1,2,\cdots ,n-1\}$, then:

$$\alpha >max\left\{\frac{1+u_1^2}{2{(1+u_1)}^2},\frac{1+u_n^2}{2{(1+u_n)}^2}\right\}.$$

(22)

(3) 

$\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)$ has the following expression:

(a) If $u_n<1$ or $u_1>1$:

$$\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|\right\};$$

(23)

(b) If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, $s\in \{1,2,\cdots ,n-1\}$, then:

$$\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|,\left|1-\frac{1+u_j^2}{\alpha {(1+u_j)}^2}\right|\right\},$$

(24)

where

$$j=\left\{\begin{array}{c}s,u_s\ge \frac{1}{u_{s+1}},\hfill \\ s+1,u_s<\frac{1}{u_{s+1}}.\hfill \end{array}\right.$$

Proof. 

Let:

$$P_1=\left[\begin{array}{cc}{W}^{-\frac{1}{2}}& 0\\ 0& W^{-\frac{1}{2}}\end{array}\right].$$

(25)

Then, by the Equation $\left(17\right)$, the following holds:

$$\begin{array}{cc}\mathsf{\Gamma }\left(\alpha \right)\hfill & =\left[\begin{array}{cc}0& -2{(W+T)}^{-1}W\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(W+T)}^{-1}T{(W+T)}^{-1}W\end{array}\right]\hfill \\ & =\left[\begin{array}{cc}0& -2W^{-\frac{1}{2}}{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}{W}^{\frac{1}{2}}\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{W}^{-\frac{1}{2}}{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}{W}^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}{W}^{\frac{1}{2}}\end{array}\right]\hfill \\ & =P_1\left[\begin{array}{cc}0& -2{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}{W}^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}\end{array}\right]{P_1}^{-1}.\hfill \end{array}$$

That is, $\mathsf{\Gamma }\left(\alpha \right)$ is similar to the following matrix $\tilde{\mathsf{\Gamma }}\left(\alpha \right)$:

$$\tilde{\mathsf{\Gamma }}\left(\alpha \right)=\left[\begin{array}{cc}0& -2{(I+S)}^{-1}\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(I+S)}^{-1}S{(I+S)}^{-1}\end{array}\right],$$

(26)

in which $S=W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}$. Then, $\mathsf{\Gamma }\left(\alpha \right)$ and $\tilde{\mathsf{\Gamma }}\left(\alpha \right)$ have the same eigenvalues. Let $S=U^Z\mathsf{\Sigma }U$ be the eigendecomposition of S, where $U\in {\mathbb{R}}^{n\times n}$ is an orthogonal matrix, $\mathsf{\Sigma }=diag(u_1,u_2,\dots ,u_n)$, and Z denotes transpose in this paper. Denote:

$$P_2=\left[\begin{array}{cc}{U}^Z& 0\\ 0& U^Z\end{array}\right],$$

(27)

and $\widehat{\mathsf{\Gamma }}\left(\alpha \right)=P_2^{-1}\tilde{\mathsf{\Gamma }}\left(\alpha \right)P_2$. Then, it holds that:

$$\begin{array}{cc}\widehat{\mathsf{\Gamma }}\left(\alpha \right)\hfill & =\left[\begin{array}{cc}U& 0\\ 0& U\end{array}\right]\left[\begin{array}{cc}0& -2{(I+S)}^{-1}\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(I+S)}^{-1}S{(I+S)}^{-1}\end{array}\right]\left[\begin{array}{cc}{U}^Z& 0\\ 0& U^Z\end{array}\right]\hfill \\ & =\left[\begin{array}{cc}0& -2{(I+\mathsf{\Sigma })}^{-1}\\ 0& \frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(I+\mathsf{\Sigma })}^{-1}\mathsf{\Sigma }{(I+\mathsf{\Sigma })}^{-1}\end{array}\right].\hfill \end{array}$$

Notice that $\mathsf{\Gamma }\left(\alpha \right)$, $\tilde{\mathsf{\Gamma }}\left(\alpha \right)$ and $\widehat{\mathsf{\Gamma }}\left(\alpha \right)$ have the same eigenvalues, and $\frac{\alpha -1}{\alpha }I+\frac{2}{\alpha }{(I+\mathsf{\Sigma })}^{-1}\mathsf{\Sigma }{(I+\mathsf{\Sigma })}^{-1}$ is a diagonal matrix with the main diagonal elements being $\frac{\alpha -1}{\alpha }+\frac{2u_k}{\alpha {(1+u_k)}^2}=1-\frac{1+{u_k}^2}{\alpha {(1+u_k)}^2}$, $k=1,2,\cdots ,n$. Then, it is easy to see that the eigenvalues of $\mathsf{\Gamma }\left(\alpha \right)$ are:

$$0,1-\frac{1+u_k^2}{\alpha {(1+u_k)}^2},k=1,2,\cdots ,n.$$

(28)

Hence, the conclusion (1) is proved.

Next, we prove conclusion (2). By the Equation $\left(28\right)$, it holds that:

$$\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)<1\iff \left.\left|1-\frac{1+u_k^2}{\alpha {(1+u_k)}^2}\right.\right|<1\iff -1<1-\frac{1+u_k^2}{\alpha {(1+u_k)}^2}<1.$$

Notice for any $\alpha >0$, $1-\frac{1+u_k^2}{\alpha {(1+u_k)}^2}<1$ holds obviously. Now, we consider the solution to $-1<1-\frac{1+u_k^2}{\alpha {(1+u_k)}^2}$, i.e., $\alpha >\frac{1+u_k^2}{2{(1+u_k)}^2}$. Define $f\left(u\right)=\frac{1+u^2}{2{(1+u)}^2}$, $u\in \left[u_1,u_n\right]$. Then, the derivative of $f\left(u\right)$ is $\frac{df\left(u\right)}{du}=\frac{u-1}{{\left(1+u\right)}^3}$. We discuss the following three cases:

(a)

If $u_n<1$, then $\frac{df\left(u\right)}{du}<0$, i.e., $f\left(u\right)$ is monotonically decreasing with respect to u, which means $\underset{1\le k\le n}{max}f\left(u_k\right)=\frac{1+u_1^2}{2{(1+u_1)}^2}$, so $\alpha >\frac{1+u_1^2}{2{(1+u_1)}^2}$;

(b)

If $u_1>1$, then $\frac{df\left(u\right)}{du}>0$, i.e., $f\left(u\right)$ is monotonically increasing with respect to u, which means $\underset{1\le k\le n}{max}f\left(u_k\right)=\frac{1+u_n^2}{2{(1+u_n)}^2}$, so $\alpha >\frac{1+u_n^2}{2{(1+u_n)}^2}$;

(c)

If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, then $f\left(u\right)$ is monotonically decreasing in $\left[u_1,u_s\right]$ and monotonically increasing in $\left[u_{s+1},u_n\right]$, respectively, so it holds that $\underset{1\le k\le n}{max}f\left(u_k\right)=max\left\{\frac{1+u_1^2}{2{(1+u_1)}^2},\frac{1+u_n^2}{2{(1+u_n)}^2}\right\}$, which yields $\alpha >max\left\{\frac{1+u_1^2}{2{(1+u_1)}^2},\frac{1+u_n^2}{2{(1+u_n)}^2}\right\}$.

Hence, conclusion (2) is proved.

Next, we prove the conclusion (3). Define $s\left(u\right)=1-\frac{1+u^2}{\alpha {(1+u)}^2}$, $u\in \left[u_1,u_n\right]$, then we have $\frac{ds\left(u\right)}{du}=-\frac{2(u-1)}{\alpha {\left(1+u\right)}^3}$. We discuss the following two cases:

(a)

If $u_n<1$, then $\frac{ds\left(u\right)}{du}>0$, $s\left(u\right)$ is monotonically increasing, and it is easy to see that:

$$\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|\right\}.$$

Similarly, when $u_1>1$, $s\left(u\right)$ is monotonically decreasing, then $\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)$ has the same form of $\left(23\right)$.

(b)

If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, then $s\left(u\right)$ is monotonically increasing in $\left[u_1,u_s\right]$ and monotonically decreasing in $\left[u_{s+1},u_n\right]$, respectively. In this case $s\left(u\right)$ has maximum $s{\left(u\right)}_{max}=max\left\{1-\frac{1+u_s^2}{\alpha {(1+u_s)}^2},1-\frac{1+u_{s+1}^2}{\alpha {(1+u_{s+1})}^2}\right\}$. Then, we consider the following two cases.

Cases I: When $\alpha \le min\left\{\frac{1+u_s^2}{{(1+u_s)}^2},\frac{1+u_{s+1}^2}{{(1+u_{s+1})}^2}\right\}$, i.e., $s{\left(u\right)}_{max}\le 0$, then we have:

$$\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|\right\}.$$

Cases II: When $\alpha > min\left\{\frac{1+u_s^2}{{(1+u_s)}^2},\frac{1+u_{s+1}^2}{{(1+u_{s+1})}^2}\right\}$, i.e., $s{\left(u\right)}_{max}>0$, then we consider the following two subcases.

If $u_s\ge \frac{1}{u_{s+1}}$, then $s\left(u_s\right)\ge s\left(u_{s+1}\right)$. When $s\left(u_{s+1}\right)\ge 0$, then $\left|s\left(u_{s+1}\right)\right|\le \left|s\left(u_s\right)\right|$. When $s\left(u_{s+1}\right)<0$, then $\left|s\left(u_{s+1}\right)\right|\le \left|s\left(u_n\right)\right|$. Thus, we have:

$$\begin{array}{cc}\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)\hfill & =max\left\{\left|s\left(u_1\right)\right|,\left|s\left(u_n\right)\right|,\left|s\left(u_s\right)\right|\right\}\hfill \\ & =max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|,\left|1-\frac{1+u_s^2}{\alpha {(1+u_s)}^2}\right|\right\}.\hfill \end{array}$$

If $u_s<\frac{1}{u_{s+1}}$, then $s\left(u_{s+1}\right)>s\left(u_s\right)$. When $s\left(u_s\right)\ge 0$, then $\left|s\left(u_s\right)\right|<\left|s\left(u_{s+1}\right)\right|$. When $s\left(u_s\right)<0$, then $\left|s\left(u_s\right)\right|\le \left|s\left(u_1\right)\right|$. Thus, we have:

$$\begin{array}{cc}\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)\hfill & =max\left\{\left|s\left(u_1\right)\right|,\left|s\left(u_n\right)\right|,\left|s\left(u_{s+1}\right)\right|\right\}\hfill \\ & =max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|,\left|1-\frac{1+u_{s+1}^2}{\alpha {(1+u_{s+1})}^2}\right|\right\}.\hfill \end{array}$$

Then, it holds by the above discussion that:

$$\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|,\left|1-\frac{1+u_j^2}{\alpha {(1+u_j)}^2}\right|\right\},$$

where

$$j=\left\{\begin{array}{c}s,u_s\ge \frac{1}{u_{s+1}},\hfill \\ s+1,u_s<\frac{1}{u_{s+1}},\hfill \end{array}\right.$$

which finishes the proof. □

Theorem 2 gives the convergence conditions for the IBS method. Now, we investigate the optimal parameter ${\alpha }^{*}$ that minimizes $\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)$.

Theorem 3.

Assume that the conditions of Theorem 2 are satisfied and $0\le u_1\le u_2\le \dots \le u_n$ are the eigenvalues of $S=W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}$. Then, the optimal parameter ${\alpha }^{*}$ which minimizes $\rho \left(\mathsf{\Gamma }\right(\alpha \left)\right)$ and the corresponding optimal convergence factor $\underset{\alpha }{min}\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)$ are given by:

(1) 

If $u_n<1$ or $u_1>1$, then:

$${\alpha }^{*}=\frac{(1+{u_1}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_1)}^2}{2{(1+u_1)}^2{(1+u_n)}^2},$$

(29)

$$\underset{\alpha }{min}\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\left\{\begin{array}{c}\frac{(1+{u_1}^2){(1+u_n)}^2-(1+{u_n}^2){(1+u_1)}^2}{(1+{u_1}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_1)}^2},u_n<1.\hfill \\ \frac{(1+{u_n}^2){(1+u_1)}^2-(1+{u_1}^2){(1+u_n)}^2}{(1+{u_1}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_1)}^2},u_1>1.\hfill \end{array}\right.$$

(30)

(2) 

If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, $s\in \{1,2,\cdots ,n-1\}$, then:

$${\alpha }^{*}=\left\{\begin{array}{c}\frac{(1+{u_1}^2){(1+u_j)}^2+(1+{u_j}^2){(1+u_1)}^2}{2{(1+u_1)}^2{(1+u_j)}^2},u_1\le \frac{1}{u_n}.\hfill \\ \frac{(1+{u_j}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_j)}^2}{2{(1+u_j)}^2{(1+u_n)}^2},u_1>\frac{1}{u_n}.\hfill \end{array}\right.$$

(31)

$$\underset{\alpha }{min}\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\left\{\begin{array}{c}\frac{(1+{u_1}^2){(1+u_j)}^2-(1+{u_j}^2){(1+u_1)}^2}{(1+{u_1}^2){(1+u_j)}^2+(1+{u_j}^2){(1+u_1)}^2},u_1\le \frac{1}{u_n},\hfill \\ \frac{(1+{u_n}^2){(1+u_j)}^2-(1+{u_j}^2){(1+u_n)}^2}{(1+{u_j}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_j)}^2},u_1>\frac{1}{u_n},\hfill \end{array}\right.$$

(32)

where

$$j=\left\{\begin{array}{c}s,u_s\ge \frac{1}{u_{s+1}}.\hfill \\ s+1,u_s<\frac{1}{u_{s+1}}.\hfill \end{array}\right.$$

Proof. 

(1) If $u_n<1$, then:

$${\alpha }^{*}=arg\underset{\alpha }{min}\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=arg\underset{\alpha }{min}max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|\right\}.$$

Define $s_u\left(\alpha \right)=1-\frac{1+u^2}{\alpha {(1+u)}^2}$, $s_{u_1}\left(\alpha \right)=1-\frac{1+{u_1}^2}{\alpha {(1+u_1)}^2},s_{u_n}\left(\alpha \right)=1-\frac{1+{u_n}^2}{\alpha {(1+u_n)}^2},$ then ${\alpha }^{*}=arg\underset{\alpha }{min}max\left\{\left|s_{u_1}\left(\alpha \right)\right|,\left|s_{u_n}\left(\alpha \right)\right|\right\}$. 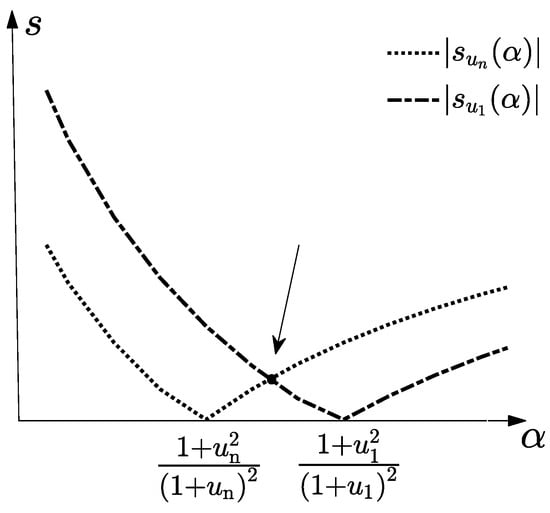Notice $\frac{d{s}_u\left(\alpha \right)}{d\alpha }=\frac{1+u^2}{{\alpha }^2{(1+u)}^2}>0$, then $s_u\left(\alpha \right)$ is monotonically increasing with respect to $\alpha$, and $-s_u\left(\alpha \right)$ is monotonically decreasing with respect to $\alpha$. As shown in Figure 1, the arrow points to the position of the optimal parameter, and it is easy to see that the optimal ${\alpha }^{*}$ satisfies: $1-\frac{1+{u_n}^2}{{\alpha }^{*}{(1+u_n)}^2}=\frac{1+{u_1}^2}{{\alpha }^{*}{(1+u_1)}^2}-1$, and after some algebra we have ${\alpha }^{*}=\frac{(1+{u_1}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_1)}^2}{2{(1+u_1)}^2{(1+u_n)}^2}$.

Substitute ${\alpha }^{*}$ into $\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|$ we have:

$$\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\frac{(1+{u_1}^2){(1+u_n)}^2-(1+{u_n}^2){(1+u_1)}^2}{(1+{u_1}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_1)}^2}.$$

Similarly, if $u_1>1$, ${\alpha }^{*}$ has the same expression as $\left(29\right)$. Substitute ${\alpha }^{*}$ into $\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\left|1-\frac{1+u_1^2}{{\alpha }^{*}{(1+u_1)}^2}\right|$ we have:

$$\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\frac{(1+{u_n}^2){(1+u_1)}^2-(1+{u_1}^2){(1+u_n)}^2}{(1+{u_1}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_1)}^2}.$$

(2) If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, let $s_{u_j}\left(\alpha \right)=1-\frac{1+{u_j}^2}{\alpha {(1+u_j)}^2},$ then:

$${\alpha }^{*}=arg\underset{\alpha }{min}\rho \left(\mathsf{\Gamma }\left(\alpha \right)\right)=arg\underset{\alpha }{min}max\left\{\left|1-\frac{1+u_1^2}{\alpha {(1+u_1)}^2}\right|,\left|1-\frac{1+u_n^2}{\alpha {(1+u_n)}^2}\right|,\left|1-\frac{1+u_j^2}{\alpha {(1+u_j)}^2}\right|\right\},$$

where

$$j=\left\{\begin{array}{c}s,u_s\ge \frac{1}{u_{s+1}}.\hfill \\ s+1,u_s<\frac{1}{u_{s+1}}.\hfill \end{array}\right.$$

(33)

Notice $s_u\left(\alpha \right)$ is monotonically increasing with respect to $\alpha$ and $-s_u\left(\alpha \right)$ is monotonically decreasing with respect to $\alpha$. We now discuss the following two cases:

When $u_1\le \frac{1}{u_n}$, then $\frac{1+{u_n}^2}{\alpha {(1+u_n)}^2}-1\le \frac{1+{u_1}^2}{\alpha {(1+u_1)}^2}-1$, i.e., $-s_{u_n}\left(\alpha \right)\le -s_{u_1}\left(\alpha \right)$:

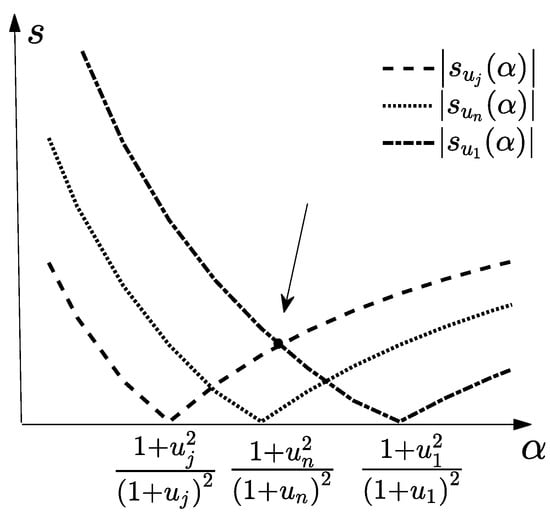
As shown in Figure 2, the image of $-s_{u_1}\left(\alpha \right)$ is above the image of $-{s_u}_n\left(\alpha \right)$, and the arrow points to the position of the optimal parameter , and it is easy to see the optimal ${\alpha }^{*}$ satisfies $1-\frac{1+{u_j}^2}{{\alpha }^{*}{(1+u_j)}^2}=\frac{1+{u_1}^2}{{\alpha }^{*}{(1+u_1)}^2}-1$, after some algebra we have ${\alpha }^{*}=\frac{(1+{u_1}^2){(1+u_j)}^2+(1+{u_j}^2){(1+u_1)}^2}{2{(1+u_1)}^2{(1+u_j)}^2}$. Substitute ${\alpha }^{*}$ into $\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\left|1-\frac{1+{u_j}^2}{{\alpha }^{*}{(1+u_j)}^2}\right|$, we have:

$$\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\frac{(1+{u_1}^2){(1+u_j)}^2-(1+{u_j}^2){(1+u_1)}^2}{(1+{u_1}^2){(1+u_j)}^2+(1+{u_j}^2){(1+u_1)}^2}.$$

When $u_1>\frac{1}{u_n}$, then $\frac{1+{u_1}^2}{\alpha {(1+u_1)}^2}-1<\frac{1+{u_n}^2}{\alpha {(1+u_n)}^2}-1$, i.e., $-s_{u_1}\left(\alpha \right)<-s_{u_n}\left(\alpha \right)$.

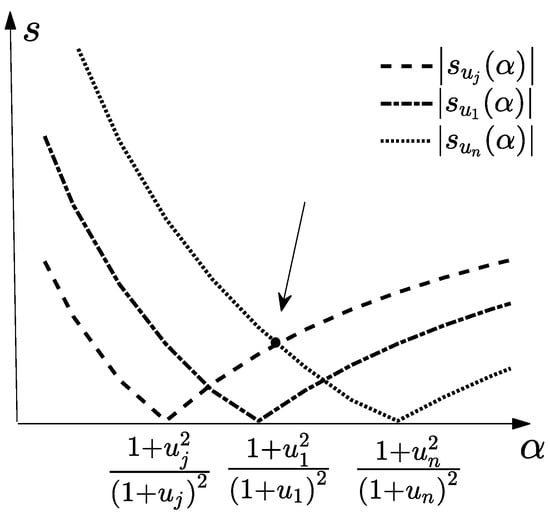
As shown in Figure 3, the image of $-s_{u_n}\left(\alpha \right)$ is above the image of $-s_{u_1}\left(\alpha \right)$, and the arrow points to the position of the optimal parameter, and the optimal ${\alpha }^{*}$ satisfies $1-\frac{1+{u_j}^2}{{\alpha }^{*}{(1+u_j)}^2}=\frac{1+{u_n}^2}{{\alpha }^{*}{(1+u_n)}^2}-1$, after some algebra, we have ${\alpha }^{*}=\frac{(1+{u_j}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_j)}^2}{2{(1+u_j)}^2{(1+u_n)}^2}$. Substitute ${\alpha }^{*}$ into $\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\left|1-\frac{1+{u_j}^2}{{\alpha }^{*}{(1+u_j)}^2}\right|$ we have:

$$\rho \left(\mathsf{\Gamma }\left({\alpha }^{*}\right)\right)=\frac{(1+{u_n}^2){(1+u_j)}^2-(1+{u_j}^2){(1+u_n)}^2}{(1+{u_j}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_j)}^2},$$

which finishes the proof. □

Remark 4.

From Theorem 3 we see that if $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, $s\in \{1,2,\cdots ,n-1\}$, then:

$${\alpha }^{*}=\left\{\begin{array}{c}\frac{(1+{u_1}^2){(1+u_j)}^2+(1+{u_j}^2){(1+u_1)}^2}{2{(1+u_1)}^2{(1+u_j)}^2},u_1\le \frac{1}{u_n}.\hfill \\ \frac{(1+{u_j}^2){(1+u_n)}^2+(1+{u_n}^2){(1+u_j)}^2}{2{(1+u_j)}^2{(1+u_n)}^2},u_1>\frac{1}{u_n}.\hfill \end{array}\right.$$

However, generally it is very expensive to compute $u_s$ and $u_{s+1}$ that satisfies $1\in [u_s,u_{s+1}]$. In our numerical experiments, when $u_1<1<u_n$, we approximate ${\alpha }^{*}$ by taking $u_j=1$, which yields the following practical optimal parameter:

$${\alpha }^{*}=\left\{\begin{array}{c}\frac{2(1+{u_1}^2)+{(1+u_1)}^2}{4{(1+u_1)}^2},u_1\le \frac{1}{u_n}.\hfill \\ \frac{2(1+{u_n}^2)+{(1+u_n)}^2}{4{(1+u_n)}^2},u_1>\frac{1}{u_n}.\hfill \end{array}\right.$$

3. AIBS Iteration Method and Its Convergence Analysis

In this section, inspired by the idea of the AGSOR iteration method, we construct the AIBS iteration method, which generalizes the IBS one and has faster convergence speed.

First, we recall the AGSOR iteration method. Multiplying both sides of $\left(3\right)$ from the left by the block matrix:

$$\mathsf{\Omega }=\left[\begin{array}{cc}\alpha I& 0\\ 0& \beta I\end{array}\right],$$

(34)

where $\beta$ is a positive constant and I is the $n\times n$ identity matrix, then $\left(3\right)$ can be written as:

$$\left[\begin{array}{cc}\alpha W& -\alpha T\\ \beta T& \beta W\end{array}\right]\left[\begin{array}{c}u\\ v\end{array}\right]=\left[\begin{array}{c}\alpha f\\ \beta g\end{array}\right].$$

(35)

Split the coefficient matrix of (35) as follows:

$$\begin{array}{cc}\left[\begin{array}{cc}\alpha W& -\alpha T\\ \beta T& \beta W\end{array}\right]=\hfill & \left[\begin{array}{cc}W& 0\\ \beta T& W\end{array}\right]-\left[\begin{array}{cc}(1-\alpha )W& \alpha T\\ 0& (1-\beta )W\end{array}\right]\equiv \tilde{M}(\alpha ,\beta )-\tilde{N}(\alpha ,\beta ).\hfill \end{array}$$

Then, it yields the AGSOR iteration, whose iteration matrix is:

$$\begin{array}{cc}\tilde{\mathsf{\Gamma }}(\alpha ,\beta )\hfill & =\tilde{M}{(\alpha ,\beta )}^{-1}\tilde{N}(\alpha ,\beta )\hfill \\ & =\left[\begin{array}{cc}(1-\alpha )I& \alpha W^{-1}T\\ (\alpha -1)\beta W^{-1}T& (1-\beta )I-\alpha \beta W^{-1}T{W}^{-1}T\end{array}\right].\hfill \end{array}$$

Now we construct the AIBS iteration method, which is just a preconditioned AGSOR (PAGSOR) iteration method. Recall $\left(14\right)$ in Section 2; the linear system $\left(3\right)$ can be written by the following form:

$$\left[\begin{array}{cc}W+T& 2W\\ T& W+T\end{array}\right]\left[\begin{array}{c}d\\ e\end{array}\right]=\left[\begin{array}{c}f+g\\ g\end{array}\right].$$

(36)

Multiplying both sides of $\left(36\right)$ from the left by the matrix $\mathsf{\Omega }$, we have:

$$\left[\begin{array}{cc}\alpha (W+T)& 2\alpha W\\ \beta T& \beta (W+T)\end{array}\right]\left[\begin{array}{c}d\\ e\end{array}\right]=\left[\begin{array}{c}\alpha (f+g)\\ \beta g\end{array}\right].$$

(37)

Similar to AGSOR, split the coefficient matrix of (37) as follows:

$$\begin{array}{cc}\left[\begin{array}{cc}\alpha (W+T)& 2\alpha W\\ \beta T& \beta (W+T)\end{array}\right]\hfill & =\left[\begin{array}{cc}W+T& 0\\ \beta T& W+T\end{array}\right]-\left[\begin{array}{cc}(1-\alpha )(W+T)& -2\alpha W\\ 0& (1-\beta )(W+T)\end{array}\right]\hfill \\ & \equiv M(\alpha ,\beta )-N(\alpha ,\beta ).\hfill \end{array}$$

Then, it yields the following AIBS (PAGSOR) iteration:

$$\left[\begin{array}{c}{d}^{(k+1)}\\ e^{(k+1)}\end{array}\right]=\mathsf{\Gamma }(\alpha ,\beta )\left[\begin{array}{c}{d}^{\left(k\right)}\\ e^{\left(k\right)}\end{array}\right]+M{(\alpha ,\beta )}^{-1}\left[\begin{array}{c}\alpha (f+g)\\ \beta g\end{array}\right],$$

where the iteration matrix is:

$$\begin{array}{cc}& \mathsf{\Gamma }(\alpha ,\beta )=M{(\alpha ,\beta )}^{-1}N(\alpha ,\beta )\hfill \\ =\hfill & \left[\begin{array}{cc}(1-\alpha )I& -2\alpha {(W+T)}^{-1}W\\ (\alpha -1)\beta {(W+T)}^{-1}T& (1-\beta )I+2\alpha \beta {(W+T)}^{-1}T{(W+T)}^{-1}W\end{array}\right].\hfill \end{array}$$

(38)

AIBS iteration algorithm: Given initial vectors $d^{\left(0\right)},e^{\left(0\right)}\in {\mathbb{R}}^n$, for $k=0,1,2,\cdots ,$ until the sequence ${\left\{{({d^{\left(k\right)}}^Z,{e^{\left(k\right)}}^Z)}^Z\right\}}_{k=0}^{\infty }$ converges, compute:

$$\left\{\begin{array}{c}(W+T)d^{(k+1)}=(1-\alpha )(W+T)d^{\left(k\right)}-2\alpha W{e}^{\left(k\right)}+\alpha f+\alpha g,\hfill \\ (W+T)e^{(k+1)}=-\beta T{d}^{(k+1)}+(1-\beta )(W+T){\mathrm{e}}^{\left(k\right)}+\beta g,\hfill \\ u^{(k+1)}=d^{(k+1)}+e^{(k+1)},v^{(k+1)}=e^{(k+1)}.\hfill \end{array}\right.$$

Remark 5.

The IBS iteration method is the special case of the AIBS one as $\alpha =1$, since they have the same iteration matrix when $\alpha =1$.

Next, we discuss the convergence properties of the AIBS iteration method.

Lemma 1

([23]). Both roots of the real quadratic equation $x^2-rx+t=0$ are less than one in the modulus if and only if $\left|t\right|<1$ and $\left|r\right|<1+t$.

Lemma 2.

Let W be symmetric positive definite and T be symmetric positive semi-definite, respectively, and $0\le u_1\le u_2\le \dots \le u_n$ are the eigenvalues of $S=W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}$. Let ${\xi }_k=\frac{2u_k}{{(1+u_k)}^2},k=1,2,\cdots ,n$, $s\in \{1,2,\cdots ,n-1\}$. Then, the maximum ${\xi }_{max}$ and the minimum ${\xi }_{min}$ of ${\xi }_k$ satisfy the following equations:

$${\xi }_{max}=\left\{\begin{array}{c}\frac{2u_n}{{(1+u_n)}^2},u_n<1,\hfill \\ \frac{2u_1}{{(1+u_1)}^2},u_1>1,\hfill \\ max\left\{\frac{2u_s}{{(1+u_s)}^2},\frac{2u_{s+1}}{{(1+u_{s+1})}^2}\right\},0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n.\hfill \end{array}\right.$$

(39)

$${\xi }_{min}=\left\{\begin{array}{c}\frac{2u_1}{{(1+u_1)}^2},u_n<1,\hfill \\ \frac{2u_n}{{(1+u_n)}^2},u_1>1,\hfill \\ min\left\{\frac{2u_1}{{(1+u_1)}^2},\frac{2u_n}{{(1+u_n)}^2}\right\},0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n.\hfill \end{array}\right.$$

(40)

Proof. 

Define $g\left(u\right)=\frac{2u}{{(1+u)}^2}$, $u\in \left[u_1,u_n\right]$, then we have $\frac{dg\left(u\right)}{du}=\frac{2(1-u)}{{\left(1+u\right)}^3}$. We now discuss the following three cases:

(1)

If $u_n<1$, then $\frac{dg\left(u\right)}{du}>0$, i.e., $g\left(u\right)$ is monotonically increasing with respect to u:

$${\xi }_{max}=\underset{1\le k\le n}{max}g\left(u_k\right)=\frac{2u_n}{{(1+u_n)}^2},$$

$${\xi }_{min}=\underset{1\le k\le n}{min}g\left(u_k\right)=\frac{2u_1}{{(1+u_1)}^2}.$$

(2)

If $u_1>1$, then $\frac{dg\left(u\right)}{du}<0$, i.e., $g\left(u\right)$ is monotonically decreasing with respect to u:

$${\xi }_{max}=\underset{1\le k\le n}{max}g\left(u_k\right)=\frac{2u_1}{{(1+u_1)}^2},$$

$${\xi }_{min}=\underset{1\le k\le n}{min}g\left(u_k\right)=\frac{2u_n}{{(1+u_n)}^2}.$$

(3)

If $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, then $g\left(u\right)$ is monotonically increasing and monotonically decreasing in $\left[u_1,u_s\right]$ and $\left[u_{s+1},u_n\right]$, respectively:

$${\xi }_{max}=\underset{1\le k\le n}{max}g\left(u_k\right)=max\left\{\frac{2u_s}{{(1+u_s)}^2},\frac{2u_{s+1}}{{(1+u_{s+1})}^2}\right\},$$

$${\xi }_{min}=\underset{1\le k\le n}{min}g\left(u_k\right)=min\left\{\frac{2u_1}{{(1+u_1)}^2},\frac{2u_n}{{(1+u_n)}^2}\right\}.$$

${\xi }_{max}$ and ${\xi }_{min}$ satisfy (39) and (40), which finishes the proof.

□

Remark 6.

In Lemma 2, when $0\le u_1\le \dots \le u_s\le 1\le u_{s+1}\le \dots \le u_n$, $s\in \{1,2,\cdots ,n-1\}$, then ${\xi }_{max}=max\left\{\frac{2u_s}{{(1+u_s)}^2},\frac{2u_{s+1}}{{(1+u_{s+1})}^2}\right\}$. Since it is difficult to compute a $u_s$ and $u_{s+1}$ that satisfy $1\in [u_s,u_{s+1}]$, in our numerical experiments, when $u_1<1<u_n$, we take ${\xi }_{max}=\frac{1}{2}$, which is equivalent to $u_s=1$ or $u_{s+1}=1$.

Theorem 7.

Assume that the conditions of Lemma 2 are satisfied. Then, the AIBS iteration method is convergent if the parameters α and β satisfy:

$$0<c<b<\frac{c(1+{\xi }_{min})}{2}+2,$$

where $b=\alpha +\beta$, $c=\alpha \beta$.

Proof. 

Let:

$$P_1=\left[\begin{array}{cc}{W}^{-\frac{1}{2}}& 0\\ 0& W^{-\frac{1}{2}}\end{array}\right].$$

Then, by Equation $\left(38\right)$, it holds that:

$$\begin{array}{cc}\mathsf{\Gamma }(\alpha ,\beta )\hfill & \left[\begin{array}{cc}=(1-\alpha )I& -2\alpha {(W+T)}^{-1}W\\ (\alpha -1)\beta {(W+T)}^{-1}T& (1-\beta )I+2\alpha \beta {(W+T)}^{-1}T{(W+T)}^{-1}W\end{array}\right]\hfill \\ & =P_1\left[\begin{array}{cc}(1-\alpha )I& -2\alpha {(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}\\ {\mathsf{\Gamma }}_1& {\mathsf{\Gamma }}_2\end{array}\right]{P_1}^{-1},\hfill \end{array}$$

where

$${\mathsf{\Gamma }}_1=(\alpha -1)\beta {(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}{W}^{-\frac{1}{2}}T{W}^{-\frac{1}{2}},$$

$${\mathsf{\Gamma }}_2=(1-\beta )I+2\alpha \beta {(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}{W}^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}{(I+W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}})}^{-1}.$$

That is, $\mathsf{\Gamma }(\alpha ,\beta )$ is similar to the following matrix $\tilde{\mathsf{\Gamma }}(\alpha ,\beta )$:

$$\tilde{\mathsf{\Gamma }}(\alpha ,\beta )=\left[\begin{array}{cc}(1-\alpha )I& -2\alpha {(I+S)}^{-1}\\ (\alpha -1)\beta {(I+S)}^{-1}S& (1-\beta )I+2\alpha \beta {(I+S)}^{-1}S{(I+S)}^{-1}\end{array}\right],$$

in which $S=W^{-\frac{1}{2}}T{W}^{-\frac{1}{2}}$. Then, $\mathsf{\Gamma }(\alpha ,\beta )$ and $\tilde{\mathsf{\Gamma }}(\alpha ,\beta )$ have the same eigenvalues. Let $S=U^Z\mathsf{\Sigma }U$ be the eigendecomposition of S, where $U\in {\mathbb{R}}^{n\times n}$ is an orthogonal matrix, $\mathsf{\Sigma }=diag(u_1,u_2,\dots ,u_n)$. Denote:

$$P_2=\left[\begin{array}{cc}{U}^Z& 0\\ 0& U^Z\end{array}\right],$$

and $\widehat{\mathsf{\Gamma }}(\alpha ,\beta )=P_2^{-1}\tilde{\mathsf{\Gamma }}(\alpha ,\beta )P_2$. Then, it holds that:

$$\widehat{\mathsf{\Gamma }}(\alpha ,\beta )=\left[\begin{array}{cc}(1-\alpha )I& -2\alpha {(I+\mathsf{\Sigma })}^{-1}\\ (\alpha -1)\beta {(I+\mathsf{\Sigma })}^{-1}\mathsf{\Sigma }& (1-\beta )I+2\alpha \beta {(I+\mathsf{\Sigma })}^{-1}\mathsf{\Sigma }{(I+\mathsf{\Sigma })}^{-1}\end{array}\right].$$

Notice that the non-zero block matrices of $\widehat{\mathsf{\Gamma }}(\alpha ,\beta )$ are all diagonal matrices; define:

$$T_k(\alpha ,\beta )=\left[\begin{array}{cc}1-\alpha & \frac{-2\alpha }{{1+u}_k}\\ \frac{(\alpha -1)\beta u_k}{{1+u}_k}& 1-\beta +\frac{{2\alpha \beta u}_k}{{\left({1+u}_k\right)}^2}\end{array}\right],$$

then it is easy to see that:

$$\rho \left(\mathsf{\Gamma }(\alpha ,\beta )\right)=\rho \left(\widehat{\mathsf{\Gamma }}(\alpha ,\beta )\right)=\underset{1\le k\le n}{max}\rho \left(T_k(\alpha ,\beta )\right).$$

The eigenvalues $\lambda$ of the matrix $T_k(\alpha ,\beta )$ satisfy the following equation:

$${\lambda }^2-(2-(\alpha +\beta )+\alpha \beta \frac{{2u}_k}{{\left({1+u}_k\right)}^2})\lambda +\alpha \beta -(\alpha +\beta )+1=0.$$

(41)

Let:

$$b=\alpha +\beta ,c=\alpha \beta ,{\xi }_k=\frac{2u_k}{{(1+u_k)}^2},k=1,2,\cdots ,n.$$

Then, (41) can be written as:

$${\lambda }^2-(2-b+c{\xi }_k)\lambda +c-b+1=0.$$

(42)

Now, by Lemma 1, $\left|\lambda \right|<1$ if and only if:

$$\left\{\begin{array}{c}\left|c-b+1\right|<1,\hfill \\ \left|2+c{\xi }_k-b\right|<c-b+2.\hfill \end{array}\right.$$

Solving the above inequality yields:

$$0<c<b<\frac{c(1+{\xi }_k)}{2}+2.$$

Noticing $\frac{c(1+\xi )}{2}+2$ is monotonically increasing with respect to $\xi$, we have:

$$0<c<b<\frac{c(1+{\xi }_{min})}{2}+2,$$

which finishes the proof. □

Remark 8.

Theorem 7 gives the convergence conditions for the AIBS iteration method. Now, we discuss the optimal parameters ${\alpha }^{*}$ and ${\beta }^{*}$ which minimize $\rho \left(\mathsf{\Gamma }\right(\alpha ,\beta \left)\right)$. It is very sophisticated when $c-b+1<0$, so in this paper and for this problem, we assume $c-b+1\ge 0$. Together with the convergence conditions in Theorem 7, we now assume $b-1\le c<b$ to investigate the local optimal parameters.

Theorem 9.

Assume that the conditions of Lemma 2 are satisfied, and $b-1\le c<b$, where $b=\alpha +\beta$, $c=\alpha \beta$. Then, the optimal parameters ${\alpha }^{*}$ and ${\beta }^{*}$ which minimize $\rho \left(\mathsf{\Gamma }\right(\alpha ,\beta \left)\right)$ are given by:

$${\alpha }^{*}=\frac{b^{*}+\sqrt{{b^{*}}^2-4c^{*}}}{2},{\beta }^{*}=\frac{b^{*}-\sqrt{{b^{*}}^2-4c^{*}}}{2},$$

where

$$b^{*}=4\frac{1+\sqrt{(1-{\xi }_{min})(1-{\xi }_{max})}}{{(\sqrt{1-{\xi }_{min}}+\sqrt{1-{\xi }_{max}})}^2},c^{*}=4\frac{1}{{(\sqrt{1-{\xi }_{min}}+\sqrt{1-{\xi }_{max}})}^2},$$

and the corresponding optimal convergence factor is given by:

$$\underset{\alpha ,\beta }{min}\rho \left(\mathsf{\Gamma }(\alpha ,\beta )\right)=\rho \left(\mathsf{\Gamma }({\alpha }^{*},{\beta }^{*})\right)=\frac{\sqrt{1-{\xi }_{min}}-\sqrt{1-{\xi }_{max}}}{\sqrt{1-{\xi }_{min}}+\sqrt{1-{\xi }_{max}}}.$$

Proof. 

The two roots of (42) are given by:

$${\lambda }_1(b,c,{\xi }_k)=\frac{1}{2}\left[\phi (b,c,{\xi }_k)+\sqrt{\phi {(b,c,{\xi }_k)}^2-4(c-b+1)}\right],$$

(43)

$${\lambda }_2(b,c,{\xi }_k)=\frac{1}{2}\left[\phi (b,c,{\xi }_k)-\sqrt{\phi {(b,c,{\xi }_k)}^2-4(c-b+1)}\right],$$

(44)

where

$$\phi (b,c,{\xi }_k)=2+c{\xi }_k-b.$$

Let $\lambda (b,c,{\xi }_k)$ be the larger modulus of the two roots ${\lambda }_1(b,c,{\xi }_k)$ and ${\lambda }_2(b,c,{\xi }_k)$, that is:

$$\lambda (b,c,{\xi }_k)=max\{\left|{\lambda }_1(b,c,{\xi }_k)\right|,\left|{\lambda }_2(b,c,{\xi }_k)\right|\}.$$

Then, we discuss the following two cases.

(1)

If $\mathsf{\Delta }={(2+c{\xi }_k-b)}^2-4(c-b+1)<0$, then:

$$\left|{\lambda }_1(b,c,{\xi }_k)\right|=\left|{\lambda }_2(b,c,{\xi }_k)\right|=\sqrt{c-b+1},$$

that is:

$$\lambda (b,c,{\xi }_k)=\sqrt{c-b+1}.$$

(2)

If $\mathsf{\Delta }={(2+c{\xi }_k-b)}^2-4(c-b+1)\ge 0$, then ${\lambda }_1(b,c,{\xi }_k)$ and ${\lambda }_2(b,c,{\xi }_k)$ are real, and it holds that:

$$\lambda (b,c,{\xi }_k)=\left\{\begin{array}{c}{\lambda }_1(b,c,{\xi }_k),2+c{\xi }_k-b\ge 0,\hfill \\ -{\lambda }_2(b,c,{\xi }_k),2+c{\xi }_k-b<0.\hfill \end{array}\right.$$

From (42), we know:

$${\lambda }_1(b,c,{\xi }_k){\lambda }_2(b,c,{\xi }_k)=c-b+1,$$

then, it is easy to see that:

$$\lambda (b,c,{\xi }_k)\ge \sqrt{c-b+1}.$$

Denote $\mathsf{\Gamma }(b,c)=\mathsf{\Gamma }(\alpha ,\beta )$, then the spectral radius of the AIBS iteration matrix can be defined by:

$$\rho \left(\mathsf{\Gamma }(b,c)\right)=\underset{1\le k\le n}{max}\left\{\lambda (b,c,{\xi }_k)\right\}.$$

Let:

$${\lambda }_i(b,c)=\underset{1\le k\le n}{max}\left\{\left|{\lambda }_i(b,c,{\xi }_k)\right|\right\},i=1,2.$$

Then, it holds that:

$$\rho \left(\mathsf{\Gamma }(b,c)\right)=max\{{\lambda }_1(b,c),{\lambda }_2(b,c)\}.$$

When $\mathsf{\Delta }\ge 0$ and $2+c{\xi }_k-b\ge 0$, i.e., $2+c{\xi }_k-b\ge 2\sqrt{c-b+1}$, then:

$$\left|{\lambda }_1(b,c,{\xi }_k)\right|\ge \left|{\lambda }_2(b,c,{\xi }_k)\right|.$$

When $\mathsf{\Delta }\ge 0$ and $2+c{\xi }_k-b<0$, i.e., $2+c{\xi }_k-b<-2\sqrt{c-b+1}$, then:

$$\left|{\lambda }_1(b,c,{\xi }_k)\right|\le \left|{\lambda }_2(b,c,{\xi }_k)\right|.$$

After some algebra, we have when $\mathsf{\Delta }\ge 0$ and $2+c{\xi }_k-b\ge 0$, then:

$$\rho \left(\mathsf{\Gamma }(b,c)\right)={\lambda }_1(b,c)=\frac{1}{2}\left[\phi (b,c,{\xi }_{max})+\sqrt{\phi {(b,c,{\xi }_{max})}^2-4(c-b+1)}\right],$$

(45)

when $\mathsf{\Delta }\ge 0$ and $2+c{\xi }_k-b<0$, then:

$$\rho \left(\mathsf{\Gamma }(b,c)\right)={\lambda }_2(b,c)=\frac{1}{2}\left[-\phi (b,c,{\xi }_{min})+\sqrt{\phi {(b,c,{\xi }_{min})}^2-4(c-b+1)}\right].$$

(46)

It is easy to see there exist two variables $\overline{\xi }$, $\widehat{\xi }$ $(0\le \widehat{\xi }\le \overline{\xi }\le \frac{1}{2})$ satisfying the following equations:

$$2+c\overline{\xi }-b=2\sqrt{c-b+1},$$

(47)

$$2+c\widehat{\xi }-b=-2\sqrt{c-b+1}.$$

(48)

Now, we prove $\overline{\xi },\widehat{\xi }\in \left[{\xi }_{min},{\xi }_{max}\right]$. Define $h\left(\xi \right)=2+c\xi -b$, $\xi \in \left[0,\frac{1}{2}\right]$, $h\left(\xi \right)$ is monotonically increasing with respect to $\xi$. If $\overline{\xi }>{\xi }_{max}$, then we have $h\left(\overline{\xi }\right)>h\left({\xi }_{max}\right)$, that is:

$$2+c\overline{\xi }-b>2+c{\xi }_{max}-b,$$

by (45) and (47), it holds that:

$$2\sqrt{c-b+1}>2+c{\xi }_{max}-b\ge 0,$$

which means $\mathsf{\Delta }<0$, then it contradicts $\mathsf{\Delta }\ge 0$; If $\widehat{\xi }<{\xi }_{min}$, then $h\left(\widehat{\xi }\right)<h\left({\xi }_{min}\right)$, that is:

$$2+c\widehat{\xi }-b<2+c{\xi }_{min}-b,$$

by (46) and (48), it holds that:

$$-2\sqrt{c-b+1}<2+c{\xi }_{min}-b<0,$$

which means $\mathsf{\Delta }<0$, then it contradicts $\mathsf{\Delta }\ge 0$. Hence, $\overline{\xi },\widehat{\xi }\in \left[{\xi }_{min},{\xi }_{max}\right]$.

From (47) and (48), by some algebra, it holds that:

$$b=4\frac{1+\sqrt{(1-\overline{\xi })(1-\widehat{\xi })}}{{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2},$$

(49)

$$c=4\frac{1}{{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2}.$$

(50)

Then, we have:

$$\left\{\begin{array}{c}{\lambda }_1(b,c)=\frac{{(\sqrt{{\xi }_{max}-\overline{\xi }}+\sqrt{{\xi }_{max}-\widehat{\xi }})}^2}{{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2},\hfill \\ {\lambda }_2(b,c)=\frac{{(\sqrt{\widehat{\xi }-{\xi }_{min}}+\sqrt{\overline{\xi }-{\xi }_{min}})}^2}{{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2}.\hfill \end{array}\right.$$

For convenience, let ${\lambda }_1(b,c)={\lambda }_1(\overline{\xi },\widehat{\xi })$, ${\lambda }_2(b,c)={\lambda }_2(\overline{\xi },\widehat{\xi })$. Without loss of generality, suppose ${\xi }_{min}<{\xi }_{max}$. In fact, if ${\xi }_{min}={\xi }_{max}$, $\overline{\xi }=\widehat{\xi }={\xi }_{min}={\xi }_{max}$, then ${\lambda }_1(\overline{\xi },\widehat{\xi })={\lambda }_2(\overline{\xi },\widehat{\xi })=0$, i.e., $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)=0$, which is the extreme trivial situation. It is easy to see that the following results hold true.:

$$\left\{\begin{array}{c}{\lambda }_1(\overline{\xi },\widehat{\xi })={\lambda }_2(\overline{\xi },\widehat{\xi }),\overline{\xi }+\widehat{\xi }={\xi }_{min}+{\xi }_{max},\hfill \\ {\lambda }_1(\overline{\xi },\widehat{\xi })<{\lambda }_2(\overline{\xi },\widehat{\xi }),\overline{\xi }+\widehat{\xi }>{\xi }_{min}+{\xi }_{max},\hfill \\ {\lambda }_1(\overline{\xi },\widehat{\xi })>{\lambda }_2(\overline{\xi },\widehat{\xi }),\overline{\xi }+\widehat{\xi }<{\xi }_{min}+{\xi }_{max}.\hfill \end{array}\right.$$

(51)

Then, we have:

$$\rho \left(\mathsf{\Gamma }(b,c)\right)=\left\{\begin{array}{c}{\lambda }_1(\overline{\xi },\widehat{\xi }),\overline{\xi }+\widehat{\xi }\le {\xi }_{min}+{\xi }_{max},\hfill \\ {\lambda }_2(\overline{\xi },\widehat{\xi }),\overline{\xi }+\widehat{\xi }>{\xi }_{min}+{\xi }_{max}.\hfill \end{array}\right.$$

(52)

Notice:

$$\left\{\begin{array}{c}\frac{\partial {\lambda }_1(\overline{\xi },\widehat{\xi })}{\partial \overline{\xi }}=\frac{\sqrt{{\xi }_{max}-\overline{\xi }}+\sqrt{{\xi }_{max}-\widehat{\xi }}}{\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }}}{Q}_1,\hfill \\ \frac{\partial {\lambda }_2(\overline{\xi },\widehat{\xi })}{\partial \overline{\xi }}=\frac{\sqrt{\widehat{\xi }-{\xi }_{min}}+\sqrt{\overline{\xi }-{\xi }_{min}}}{\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }}}{Q}_2,\hfill \end{array}\right.$$

where

$$Q_1=\frac{{\xi }_{max}-1+\sqrt{({\xi }_{max}-\overline{\xi })({\xi }_{max}-\widehat{\xi })}-\sqrt{(1-\overline{\xi })(1-\widehat{\xi })}}{\sqrt{({\xi }_{max}-\overline{\xi })(1-\overline{\xi })}{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2}<0,$$

$$Q_2=\frac{1-{\xi }_{min}+\sqrt{(\widehat{\xi }-{\xi }_{min})(\overline{\xi }-{\xi }_{min})}+\sqrt{(1-\overline{\xi })(1-\widehat{\xi })}}{\sqrt{(1-\overline{\xi })({\xi }_{min}-\overline{\xi })}{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2}>0,$$

then, it holds that:

$$\frac{\partial {\lambda }_1(\overline{\xi },\widehat{\xi })}{\partial \overline{\xi }}<0,\frac{\partial {\lambda }_2(\overline{\xi },\widehat{\xi })}{\partial \overline{\xi }}>0.$$

Analogously, it also holds that:

$$\frac{\partial {\lambda }_1(\overline{\xi },\widehat{\xi })}{\partial \widehat{\xi }}<0,\frac{\partial {\lambda }_2(\overline{\xi },\widehat{\xi })}{\partial \widehat{\xi }}>0.$$

Similar to the proof of Theorem 2.5 in [24], $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)$ has a minimum at $\overline{\xi }+\widehat{\xi }={\xi }_{min}+{\xi }_{max}$.

First, we prove $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)$ has no minimum at $\overline{\xi }+\widehat{\xi }\ne {\xi }_{min}+{\xi }_{max}$, see the following two cases.

Assume $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)$ has a minimum at $\overline{\xi }+\widehat{\xi }>{\xi }_{min}+{\xi }_{max}$. By (52), it holds that $\rho \left(\mathsf{\Gamma }(b,c)\right)={\lambda }_2(\overline{\xi },\widehat{\xi })$, let ${\xi }^{*}={\xi }_{min}+{\xi }_{max}-\widehat{\xi }$. Then, $\overline{\xi }>{\xi }^{*}$. By the above monotone property of the function ${\lambda }_2(\overline{\xi },\widehat{\xi })$, we have ${\lambda }_2(\overline{\xi },\widehat{\xi })>{\lambda }_2({\xi }^{*},\widehat{\xi })$, which contradicts the assumption.

Assume $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)$ has minimum at $\overline{\xi }+\widehat{\xi }<{\xi }_{min}+{\xi }_{max}$. By (52), it holds that $\rho \left(\mathsf{\Gamma }(b,c)\right)={\lambda }_1(\overline{\xi },\widehat{\xi })$, let ${\xi }^{**}={\xi }_{min}+{\xi }_{max}-\widehat{\xi }$, then $\overline{\xi }<{\xi }^{**}$. By the above monotone property of the function ${\lambda }_1(\overline{\xi },\widehat{\xi })$, we have ${\lambda }_1(\overline{\xi },\widehat{\xi })>{\lambda }_1({\xi }^{**},\widehat{\xi })$, which contradicts the assumption.

It is easy to see from the above two cases that $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)$ may have a minimum only at $\overline{\xi }+\widehat{\xi }={\xi }_{min}+{\xi }_{max}$.

When $\overline{\xi }+\widehat{\xi }={\xi }_{min}+{\xi }_{max}$, from (51) and (52), it holds that:

$$\begin{array}{cc}\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)\hfill & ={\lambda }_1(\overline{\xi },\widehat{\xi })={\lambda }_2(\overline{\xi },\widehat{\xi })\hfill \\ & =\frac{{(\sqrt{{\xi }_{max}-\overline{\xi }}+\sqrt{{\xi }_{max}-\widehat{\xi }})}^2}{{(\sqrt{1-\overline{\xi }}+\sqrt{1-\widehat{\xi }})}^2}\hfill \\ & =\frac{{(\sqrt{{\xi }_{max}-\overline{\xi }}+\sqrt{\overline{\xi }-{\xi }_{min}})}^2}{{(\sqrt{1-\overline{\xi }}+\sqrt{1+\overline{\xi }-{\xi }_{min}-{\xi }_{max}})}^2}\hfill \\ & =\frac{{\xi }_{max}-{\xi }_{min}+2\sqrt{-{\overline{\xi }}^2+({\xi }_{min}+{\xi }_{max})\overline{\xi }-{\xi }_{min}{\xi }_{max}}}{2-{\xi }_{max}-{\xi }_{min}+2\sqrt{-{\overline{\xi }}^2+({\xi }_{min}+{\xi }_{max})\overline{\xi }+1-{\xi }_{max}-{\xi }_{min}}}.\hfill \end{array}$$

Let $t=-{\overline{\xi }}^2+({\xi }_{min}+{\xi }_{max})\overline{\xi }\ge {\xi }_{min}{\xi }_{max}$, and define a function $\varphi \left(t\right)$:

$$\varphi \left(t\right)=\rho \left(\mathsf{\Gamma }(b,c)\right)=\frac{{\xi }_{max}-{\xi }_{min}+2\sqrt{t-{\xi }_{min}{\xi }_{max}}}{2-{\xi }_{max}-{\xi }_{min}+2\sqrt{t+1-{\xi }_{max}-{\xi }_{min}}}.$$

When $t={\xi }_{min}{\xi }_{max}$, i.e., $-{\overline{\xi }}^2+({\xi }_{min}+{\xi }_{max})\overline{\xi }={\xi }_{min}{\xi }_{max}$, it holds that

$$({\xi }_{max}-\overline{\xi })(\overline{\xi }-{\xi }_{min})=0,$$

so $\overline{\xi }={\xi }_{max}$ and $\widehat{\xi }={\xi }_{min}$.

When $t>{\xi }_{min}{\xi }_{max}$, it holds that $\frac{d\varphi \left(t\right)}{dt}>0$, which means $\varphi \left(t\right)$ is increasing with respect to t.

From the above analysis, we see that $\varphi \left(t\right)$ has minimum at $t={\xi }_{min}{\xi }_{max}$, which means $\rho \left(\mathsf{\Gamma }\right(b,c\left)\right)$ has a minimum:

$$\underset{b,c}{min}\rho \left(\mathsf{\Gamma }(b,c)\right)=\frac{\sqrt{1-{\xi }_{min}}-\sqrt{1-{\xi }_{max}}}{\sqrt{1-{\xi }_{min}}+\sqrt{1-{\xi }_{max}}}$$

at $\overline{\xi }={\xi }_{max}$ and $\widehat{\xi }={\xi }_{min}$. Furthermore, from (49) and (50), we obtain the corresponding optimal parameters:

$$b^{*}=4\frac{1+\sqrt{(1-{\xi }_{min})(1-{\xi }_{max})}}{{(\sqrt{1-{\xi }_{min}}+\sqrt{1-{\xi }_{max}})}^2},c^{*}=4\frac{1}{{(\sqrt{1-{\xi }_{min}}+\sqrt{1-{\xi }_{max}})}^2},$$

and notice $b^{*}={\alpha }^{*}+{\beta }^{*}$, $c^{*}={\alpha }^{*}{\beta }^{*}$, then it holds that:

$${\alpha }^{*}=\frac{b^{*}+\sqrt{{b^{*}}^2-4c^{*}}}{2},{\beta }^{*}=\frac{b^{*}-\sqrt{{b^{*}}^2-4c^{*}}}{2},$$

which finishes the proof. □

4. Numerical Results

In this section, we present some numerical examples to demonstrate the effectiveness of the IBS iteration method and the AIBS iteration method. All the computations are implemented in MATLAB (version R2021a) on a PC computer with 16.0 GB memory, an Intel(R) Core(TM) i5-10500 CPU @1.19 GHz, and Windows 10 as the operating system. We denote the elapsed CPU time (in second) by CPU, the iteration numbers by IT, and the norm of the relative residuals by RES, respectively. In our computations all the initial guesses are taken by zero vectors, and the computations are terminated once the stopping criterion is satisfied:

$$RES=\frac{{∥\mathit{b}-A{x}^{\left(k\right)}∥}_2}{{∥\mathit{b}∥}_2}\le {10}^{-10}$$

(53)

We compare the AIBS and IBS methods with NBS, PBS, AGSOR, and PMHSS methods, including the corresponding preconditioned GMRES methods. In each iteration of AIBS, IBS, NBS, PBS, AGSOR, and PMHSS methods, we use the Cholesky factorization to solve the subsystems. In addition, we use the preconditioned restarted GMRES(20) in our numerical tests. The iteration number k of GMRES means $k=(i-1)\times 20+p$, where i is the number of restarting, and p is the iteration number of the last restarting, respectively.

Example 1.

Consider the following complex symmetric linear system Equation [25,26]:

$$[(K+\frac{3-\sqrt{3}}{\tau }I)+\mathbf{i}(K+\frac{3+\sqrt{3}}{\tau }I)]u=\mathit{b}$$

(54)

where τ is the time step-size and K is the five-point centered difference matrix approximating the negative Laplacian operator with homogeneous Dirichlet boundary conditions, on a uniform mesh in the unit square $[0,1]\times [0,1]$ with the mesh-size $h=\frac{1}{m+1}$. The matrix $K\in {\mathbb{R}}^{n\times n}$ possesses the tensor-product form $K=I\otimes V_m+V_m\otimes I$, with $V_m=h^{-2}tridiag(-1,2,-1)\in {\mathbb{R}}^{m\times m}$. Hence, K is an $n\times n$ block tridiagonal matrix, with $n=m^2$. We take:

$$W=K+\frac{3-\sqrt{3}}{\tau }I\mathrm{and}T=K+\frac{3+\sqrt{3}}{\tau }I,$$

and the right-hand side vector $\mathit{b}$ with its $\overline{j}$th entry ${\mathit{b}}_{\overline{j}}$ is given by:

$${\mathit{b}}_{\overline{j}}=\frac{(1-\mathbf{i})\overline{j}}{\tau {(\overline{j}+1)}^2},\overline{j}=1,2,\cdots ,n.$$

Making $\tau =h$, and multiplying both sides of the system of equations by $h^2$ to regularize the coefficient matrix and the right-hand side vector at the same time.

Table 1. The optimal parameters for Example 1.

Method	m	32	64	128	256
AIBS	${\alpha }^{*}$	1.7909	1.7562	1.7354	1.7233
	${\beta }^{*}$	1.0034	1.0048	1.0058	1.0065
IBS	${\alpha }^{*}$	0.5579	0.5687	0.5754	0.5792
PBS	${\alpha }^{*}$	1	1	1	1
	${\beta }^{*}$	3.1391	2.8092	2.6385	2.5517
NBS	${\alpha }^{*}$	1	1	1	1
AGSOR	${\alpha }^{*}$	0.8283	0.7882	0.7626	0.7480
	${\beta }^{*}$	0.2438	0.2225	0.2100	0.2032
PMHSS	${\alpha }^{*}$	1	1	1	1

lists the optimal parameters for the AIBS, IBS, PBS [21], NBS [21], AGSOR [17], and PMHSS [27] methods. ${\alpha }^{*}$, ${\beta }^{*}$ represents the optimal parameters for each method.

Table 2. Numerical results of stationary iterations for Example 1.

Method	m	32	64	128	256
AIBS	IT	10	11	11	11
	CPU	0.0106	0.0307	0.1780	1.2865
	RES	5.9254$\times {10}^{-13}$	9.6256$\times {10}^{-14}$	1.2124$\times {10}^{-13}$	9.6584$\times {10}^{-14}$
IBS	IT	12	13	13	13
	CPU	0.0205	0.0298	0.1972	1.8338
	RES	4.0848$\times {10}^{-13}$	1.4752$\times {10}^{-13}$	2.0660$\times {10}^{-13}$	1.7505 $\times {10}^{-13}$
PBS	IT	17	18	19	19
	CPU	0.0126	0.0557	0.3170	2.2667
	RES	4.8159$\times {10}^{-13}$	3.9531$\times {10}^{-13}$	1.5480$\times {10}^{-13}$	1.3762$\times {10}^{-13}$
NBS	IT	34	35	35	35
	CPU	0.0153	0.0693	0.5070	3.7428
	RES	1.7149$\times {10}^{-12}$	4.7500$\times {10}^{-13}$	2.4915$\times {10}^{-13}$	1.2721$\times {10}^{-13}$
AGSOR	IT	26	29	31	33
	CPU	0.0113	0.0653	0.4588	3.9342
	RES	9.1573$\times {10}^{-13}$	4.0411$\times {10}^{-13}$	2.9290$\times {10}^{-13}$	1.2160$\times {10}^{-13}$
PMHSS	IT	36	36	36	35
	CPU	0.0156	0.0679	0.5744	3.9953
	RES	2.2443$\times {10}^{-12}$	1.0691$\times {10}^{-12}$	4.1579$\times {10}^{-13}$	2.5996$\times {10}^{-13}$

and

Table 3. Numerical results of preconditioned GMRES for Example 1.

Method	m	32	64	128	256
AIBS-GMRES	IT	9	9	10	10
	CPU	0.0462	0.0567	0.2596	1.7734
	RES	1.8233$\times {10}^{-11}$	8.2612$\times {10}^{-11}$	9.0014$\times {10}^{-12}$	3.4665$\times {10}^{-11}$
IBS-GMRES	IT	9	9	10	10
	CPU	0.0498	0.0580	0.2668	2.3085
	RES	4.7762$\times {10}^{-12}$	7.6997$\times {10}^{-11}$	1.5088$\times {10}^{-11}$	5.8511$\times {10}^{-11}$
PBS-GMRES	IT	10	12	12	13
	CPU	0.0515	0.0698	0.4258	2.9442
	RES	7.3239$\times {10}^{-11}$	5.8871$\times {10}^{-12}$	5.7710$\times {10}^{-11}$	1.6185$\times {10}^{-11}$
NBS-GMRES	IT	9	9	10	10
	CPU	0.0487	0.0593	0.3193	2.4691
	RES	2.5049$\times {10}^{-12}$	4.2859$\times {10}^{-11}$	8.4617$\times {10}^{-12}$	3.3517$\times {10}^{-11}$
AGSOR-GMRES	IT	14	16	18	20
	CPU	0.0680	0.0781	0.4317	3.6026
	RES	4.4083$\times {10}^{-11}$	5.6892$\times {10}^{-11}$	4.5164$\times {10}^{-11}$	6.8716$\times {10}^{-11}$
PMHSS-GMRES	IT	15	16	17	17
	CPU	0.0499	0.0653	0.4575	3.4580
	RES	1.8291$\times {10}^{-11}$	5.6628$\times {10}^{-11}$	2.6098$\times {10}^{-11}$	6.9464$\times {10}^{-11}$

list the IT, CPU, and RES of each iteration method for Example 1.

Example 2.

Consider the following complex Helmholtz Equation [28,29]:

$$-{\nabla }^{2}u+{\sigma }_{1}u+\mathbf{i}{\sigma }_{2}u=f$$

(55)

where ${\sigma }_1$, ${\sigma }_2$ are real coefficient functions and u satisfies Dirichlet boundary conditions in $D=[0,1]\times [0,1]$. The above equation describes the propagation of damped time-harmonic waves. We take H the five-point centered difference matrix approximating the negative Laplacian operator on an uniform mesh with meshsize $h=\frac{1}{m+1}$. The matrix $H\in {\mathbb{R}}^{n\times n}$ possesses the tensor-product form $H=I\otimes V_m+V_m\otimes I$, with $V_m=h^{-2}tridiag(-1,2,-1)\in {\mathbb{R}}^{m\times m}$. Hence, H is an $n\times n$ block-tridiagonal matrix, with $n=m^2$. This leads to the complex symmetric linear system:

$$Ax\equiv \left[\left(H+{\sigma }_{1}I\right)+\mathbf{i}{\sigma }_{2}I\right]x=\mathit{b}$$

(56)

In addition, we set ${\sigma }_1={10}^3$, ${\sigma }_2={10}^4$ and the right-hand side vector $\mathit{b}$ to be $\mathit{b}=(1+\mathbf{i})A1$, with 1 being the vector of all entries equal to 1. We normalize the system by multiplying both sides by $h^2$.

Table 4. The optimal parameters for Example 2.

Method	m	32	64	128	256
AIBS	${\alpha }^{*}$	1.4756	1.4757	1.4757	1.2826
	${\beta }^{*}$	1.0336	1.0337	1.0337	1.0934
IBS	${\alpha }^{*}$	0.6660	0.6660	0.6854	0.7318
PBS	${\alpha }^{*}$	1	1	1	1
	${\beta }^{*}$	1.4525	1.4542	1.4542	1.4542
NBS	${\alpha }^{*}$	1	1	1	1
AGSOR	${\alpha }^{*}$	0.3963	0.2370	0.1969	0.1873
	${\beta }^{*}$	0.0791	0.1420	0.1721	0.1810
PMHSS	${\alpha }^{*}$	1	1	1	1

lists the optimal parameters for the AIBS, IBS, PBS [21], NBS [21], AGSOR [17], and PMHSS [27] methods. ${\alpha }^{*}$, ${\beta }^{*}$ represents the optimal parameters for each method.

Table 5. Numerical results of stationary iterations for Example 2.

Method	m	32	64	128	256
AIBS	IT	13	13	14	14
	CPU	0.0142	0.0303	0.2544	1.6005
	RES	1.7848$\times {10}^{-11}$	2.5251$\times {10}^{-12}$	1.7833$\times {10}^{-13}$	9.0874$\times {10}^{-14}$
IBS	IT	17	17	17	19
	CPU	0.0172	0.0515	0.2861	2.2295
	RES	2.6696$\times {10}^{-11}$	3.5821$\times {10}^{-12}$	4.3296$\times {10}^{-13}$	6.9801$\times {10}^{-14}$
PBS	IT	19	24	24	24
	CPU	0.0181	0.0517	0.3498	5.0836
	RES	1.5969$\times {10}^{-11}$	2.9966$\times {10}^{-12}$	5.0604$\times {10}^{-13}$	6.6493$\times {10}^{-14}$
NBS	IT	26	31	31	30
	CPU	0.0176	0.0617	0.4955	3.4326
	RES	1.6634$\times {10}^{-11}$	2.3180$\times {10}^{-12}$	3.5384$\times {10}^{-13}$	9.3083$\times {10}^{-14}$
AGSOR	IT	98	138	143	142
	CPU	0.0430	0.2715	2.3142	25.0304
	RES	9.5904$\times {10}^{-12}$	8.8873$\times {10}^{-13}$	1.1951$\times {10}^{-13}$	1.9752$\times {10}^{-14}$
PMHSS	IT	53	53	53	57
	CPU	0.0416	0.1432	0.9691	12.1306
	RES	2.7446$\times {10}^{-11}$	3.5964$\times {10}^{-12}$	4.6031$\times {10}^{-13}$	8.7414$\times {10}^{-14}$

and

Table 6. Numerical results of preconditioned GMRES for Example 2.

Method	m	32	64	128	256
AIBS-GMRES	IT	12	12	13	14
	CPU	0.0527	0.0664	0.3105	2.4856
	RES	1.5324$\times {10}^{-11}$	4.9631$\times {10}^{-11}$	3.8500$\times {10}^{-11}$	8.9480$\times {10}^{-11}$
IBS-GMRES	IT	12	12	13	14
	CPU	0.0591	0.0638	0.3695	2.4913
	RES	1.6402$\times {10}^{-11}$	5.2164$\times {10}^{-11}$	3.6414$\times {10}^{-11}$	8.1989$\times {10}^{-11}$
PBS-GMRES	IT	12	13	13	14
	CPU	0.0650	0.0704	0.4306	3.1274
	RES	5.4437$\times {10}^{-11}$	4.3436$\times {10}^{-11}$	9.4839$\times {10}^{-11}$	2.7788$\times {10}^{-11}$
NBS-GMRES	IT	11	12	13	14
	CPU	0.0720	0.0865	0.4490	3.1868
	RES	7.4649$\times {10}^{-11}$	2.9526$\times {10}^{-11}$	2.5275$\times {10}^{-11}$	6.5381$\times {10}^{-11}$
AGSOR-GMRES	IT	41	79	103	110
	CPU	0.0540	0.4017	2.3971	16.6325
	RES	9.6830$\times {10}^{-11}$	9.8920$\times {10}^{-11}$	9.4586$\times {10}^{-11}$	8.4524$\times {10}^{-11}$
PMHSS-GMRES	IT	21	23	23	27
	CPU	0.1185	0.1212	0.7072	5.4326
	RES	8.4213$\times {10}^{-11}$	3.4984$\times {10}^{-11}$	5.4485$\times {10}^{-11}$	5.7106$\times {10}^{-11}$

list the IT, CPU, and RES of each iteration method for Example 2.

5. Conclusions

For solving a complex symmetric linear system from the complex Helmholtz equation, based on the NBS and AGSOR iteration methods, we construct the IBS and AIBS iteration methods for solving its equivalent real-valued form. We analyze the convergence of the two iteration methods, and obtain the corresponding optimal parameters that minimize the spectral radius of the iteration matrix. It can be shown in our numerical results that, both for the stationary iteration and as a preconditioner to accelerate GMRES, IBS, and AIBS methods always outperform some existing iteration methods, such as the NBS method, PBS method, AGSOR method, PMHSS method, and so forth. The technique in this paper is valid for the 2D problem, and it can be tried to solve 3D problem, which will be our future work.