Change-Point Detection in Functional First-Order Auto-Regressive Models
Abstract
:1. Introduction
2. Auxiliary Results
- (a)
- There is a continuous function such that
- (b)
- The function is bounded and has finite variation.
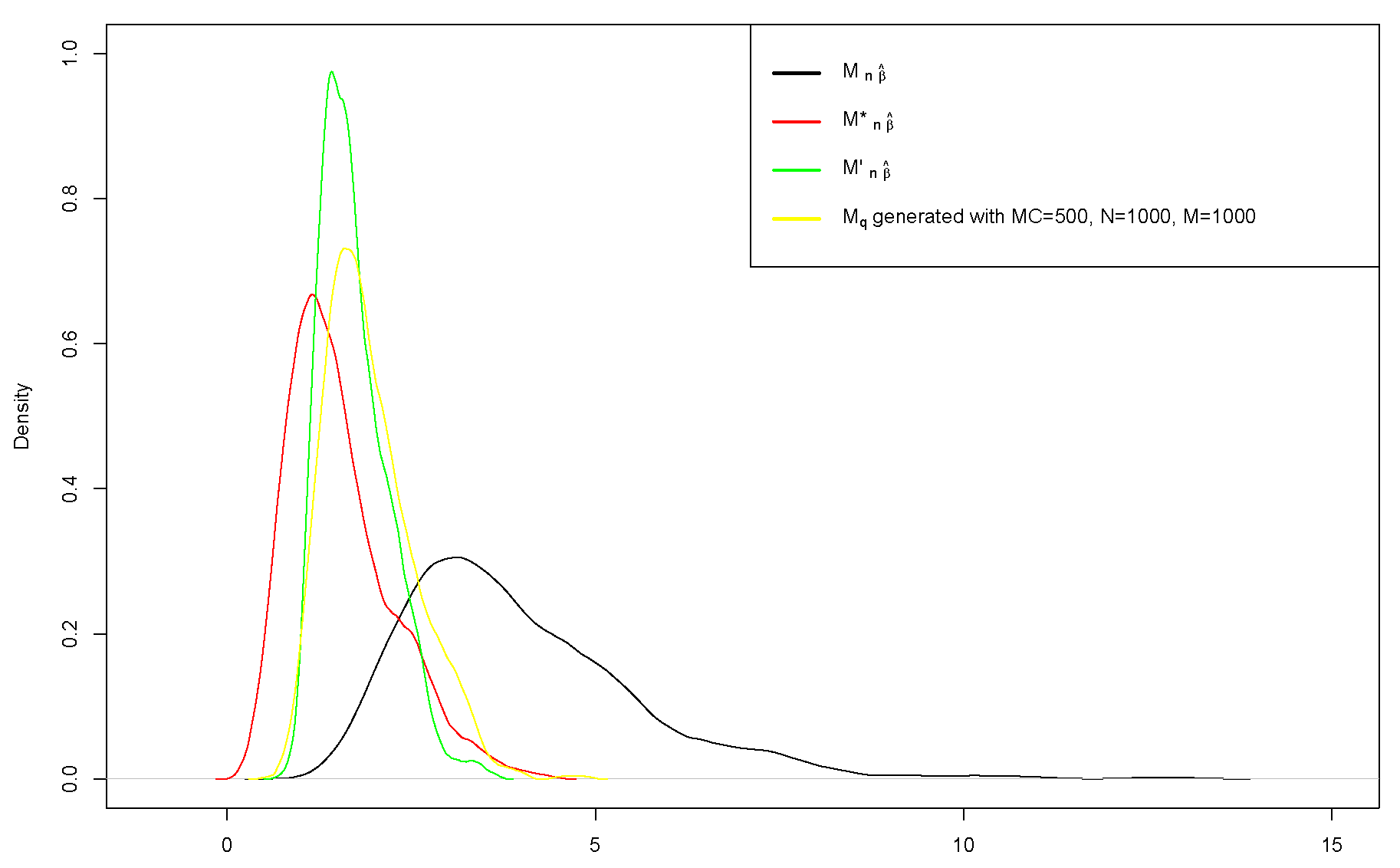
3. Test Statistics and Their Asymptoticity
4. Testing Procedure
| Algorithm 1 Block bootstrap procedure |
|
| Algorithm 2 Adjusted quantiles procedure |
|
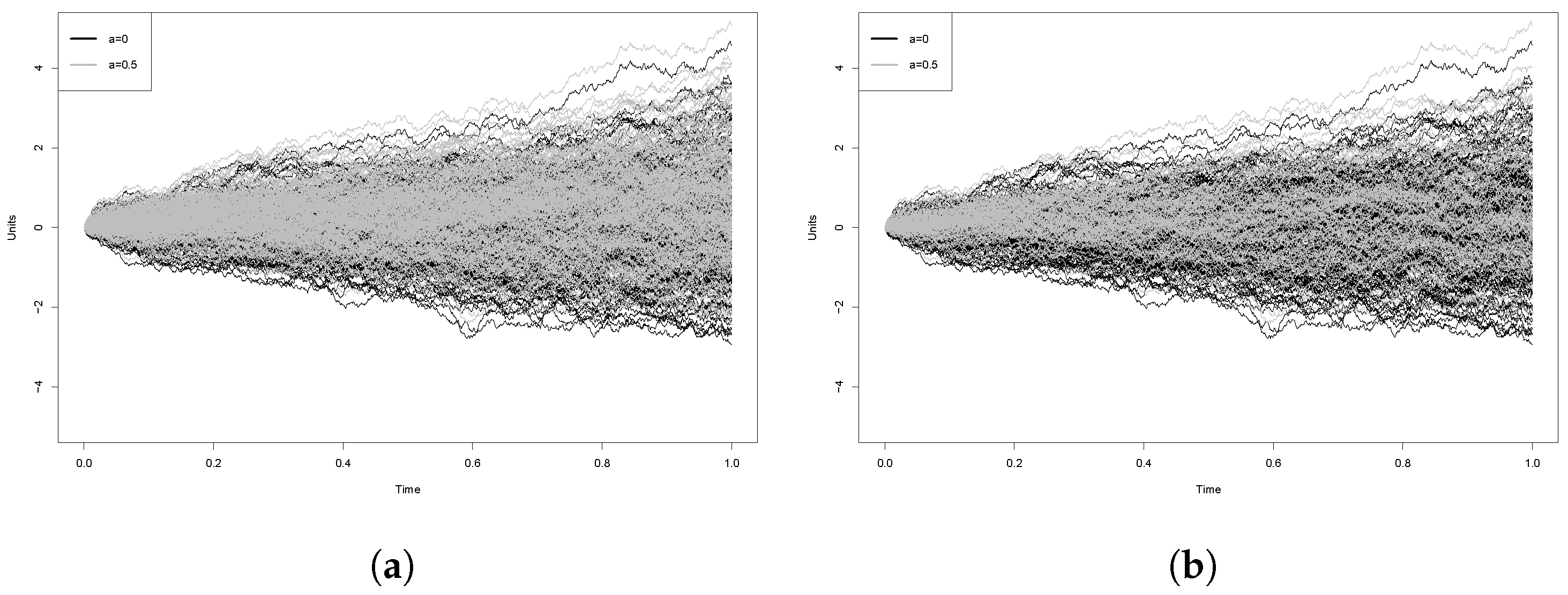
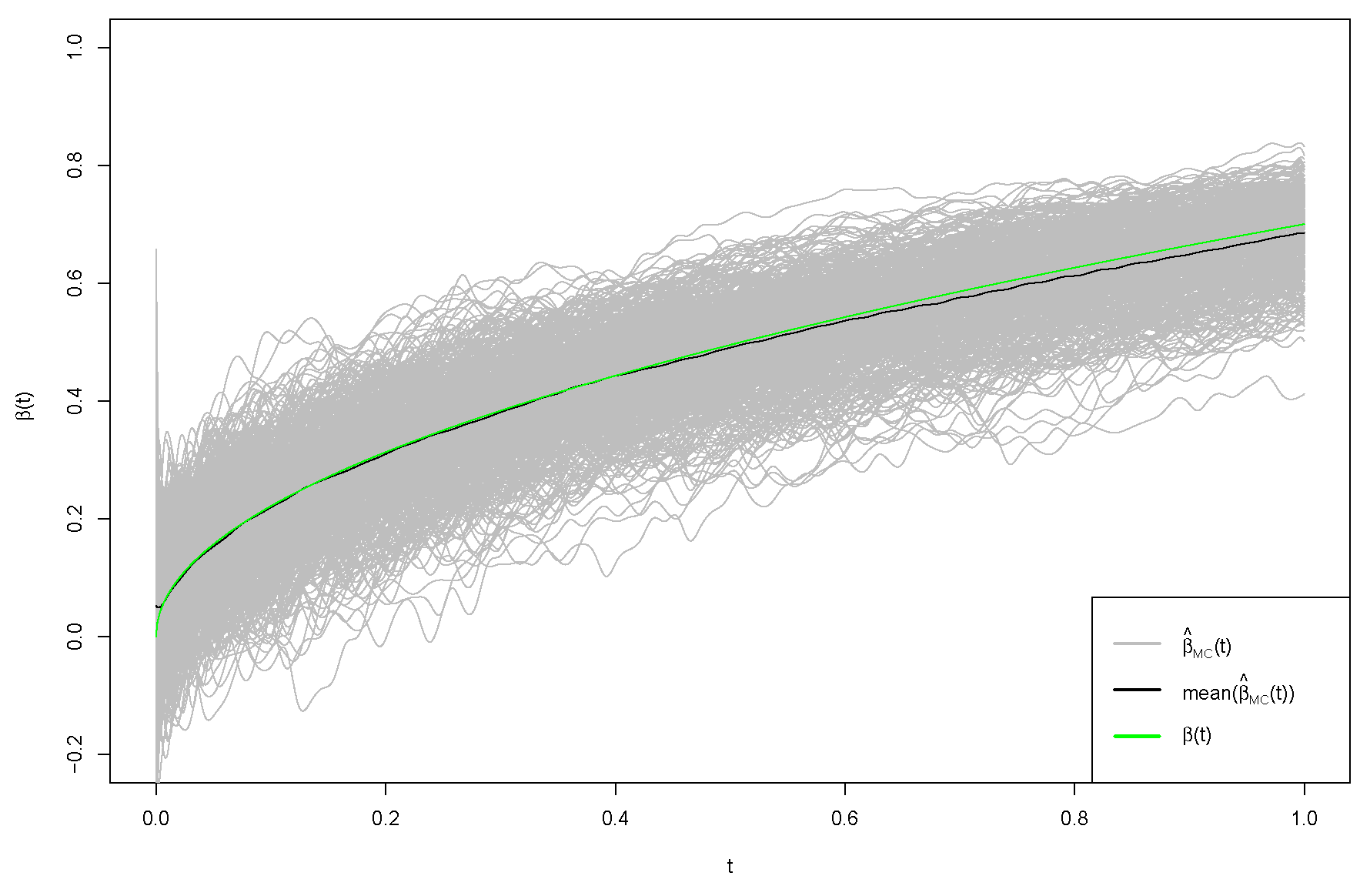
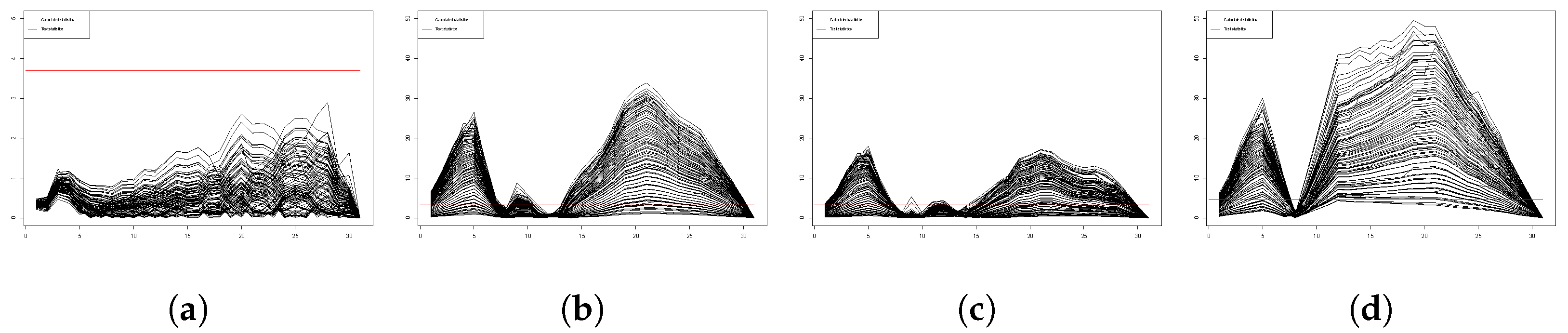
5. Simulation Study
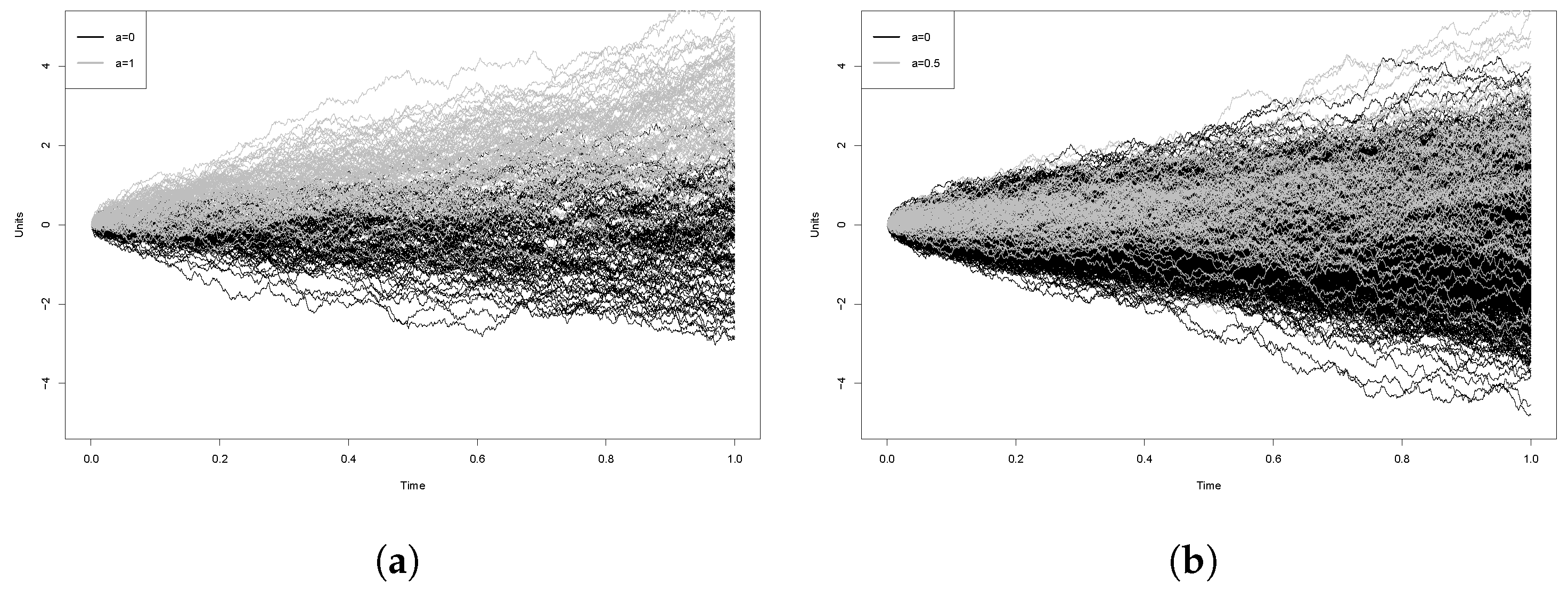
- Case 1: , with the aim to test
- Case 2: , with the aim to test
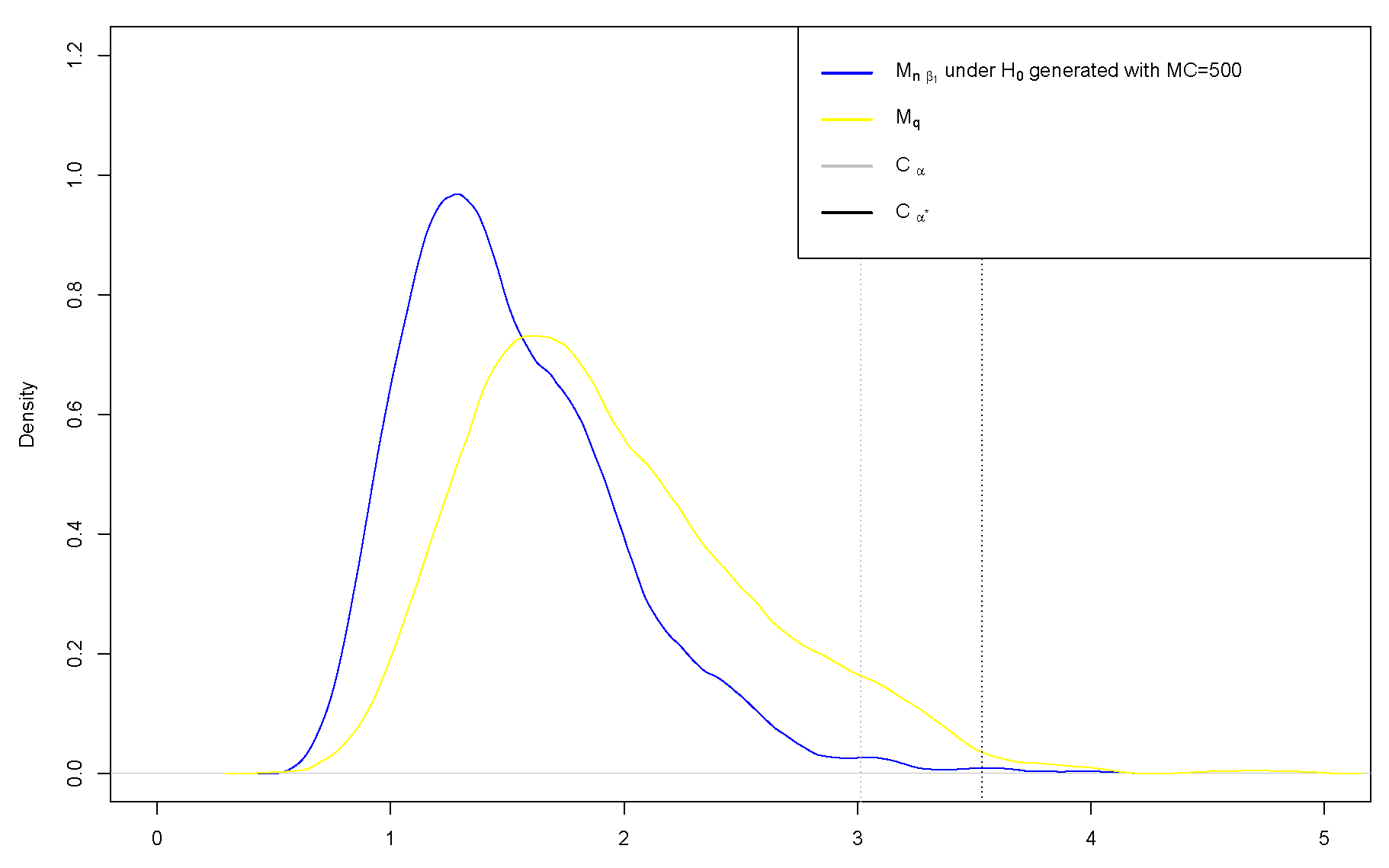
5.1. False-Positive Rate
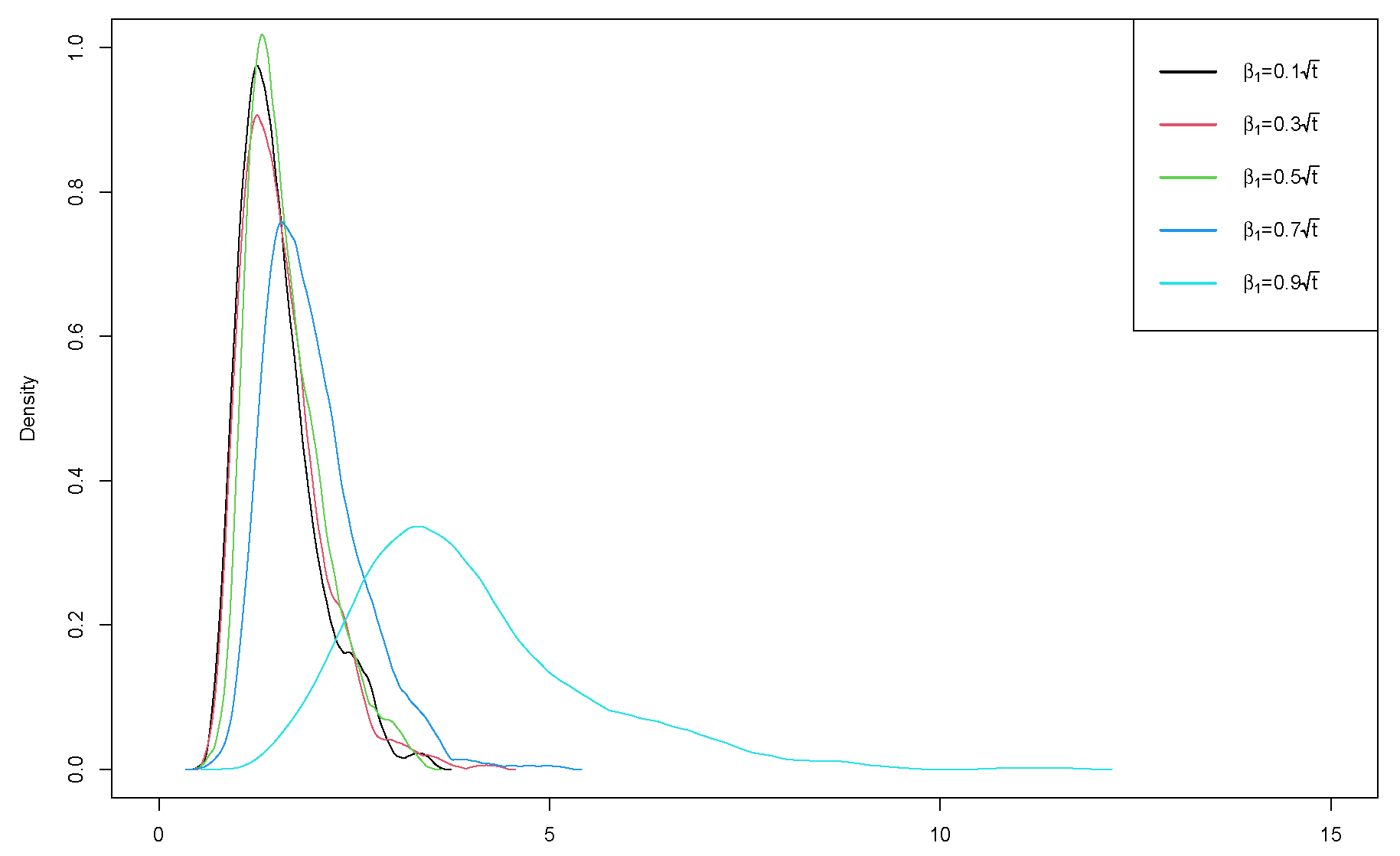
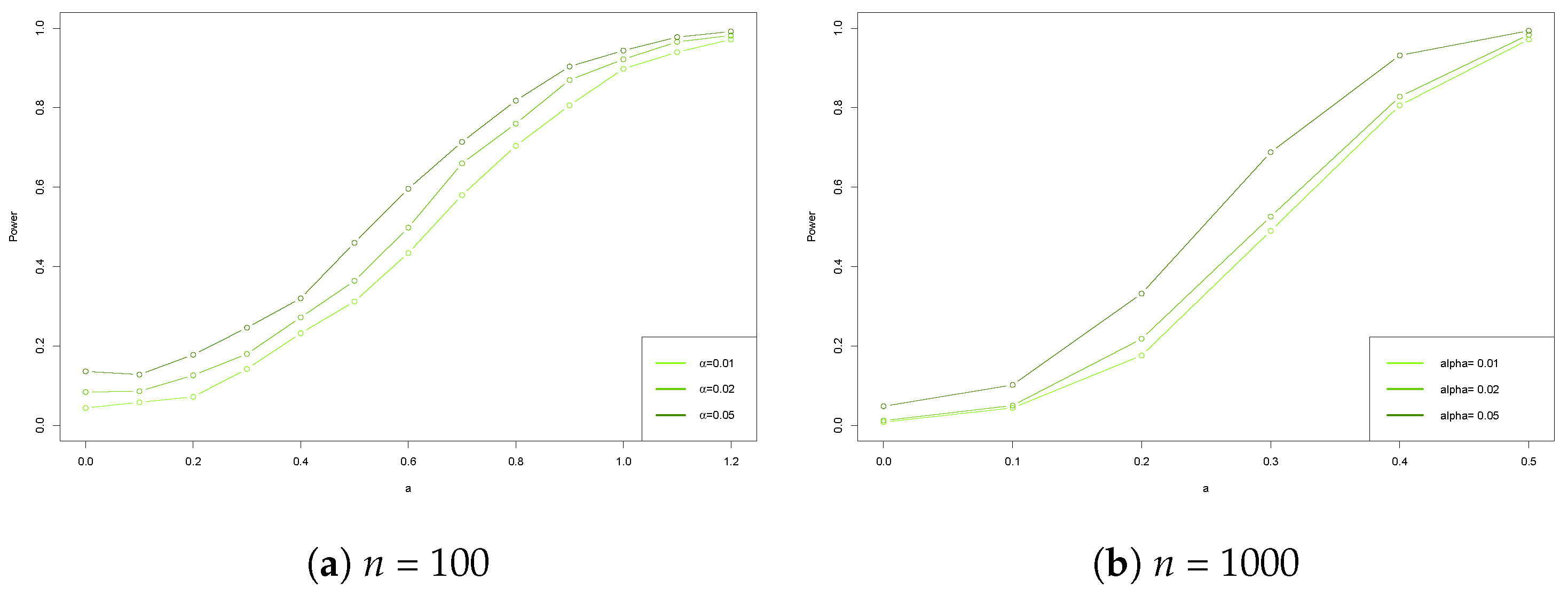
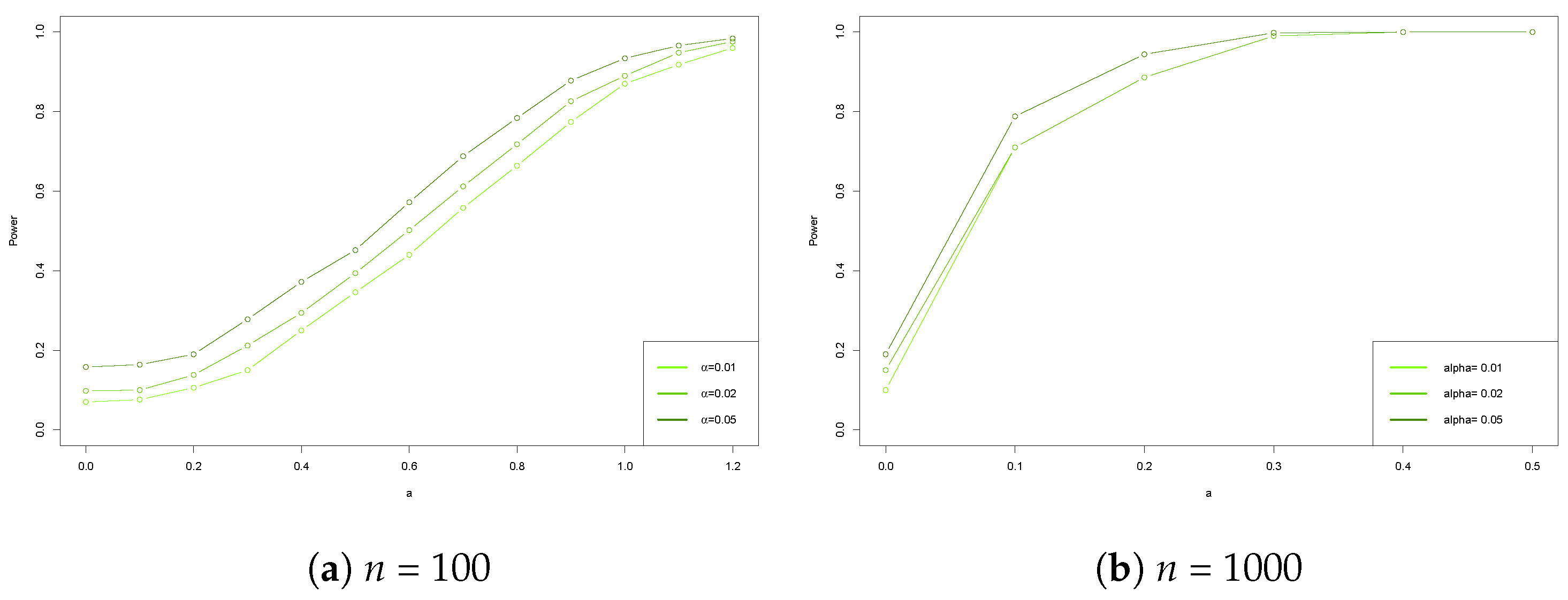
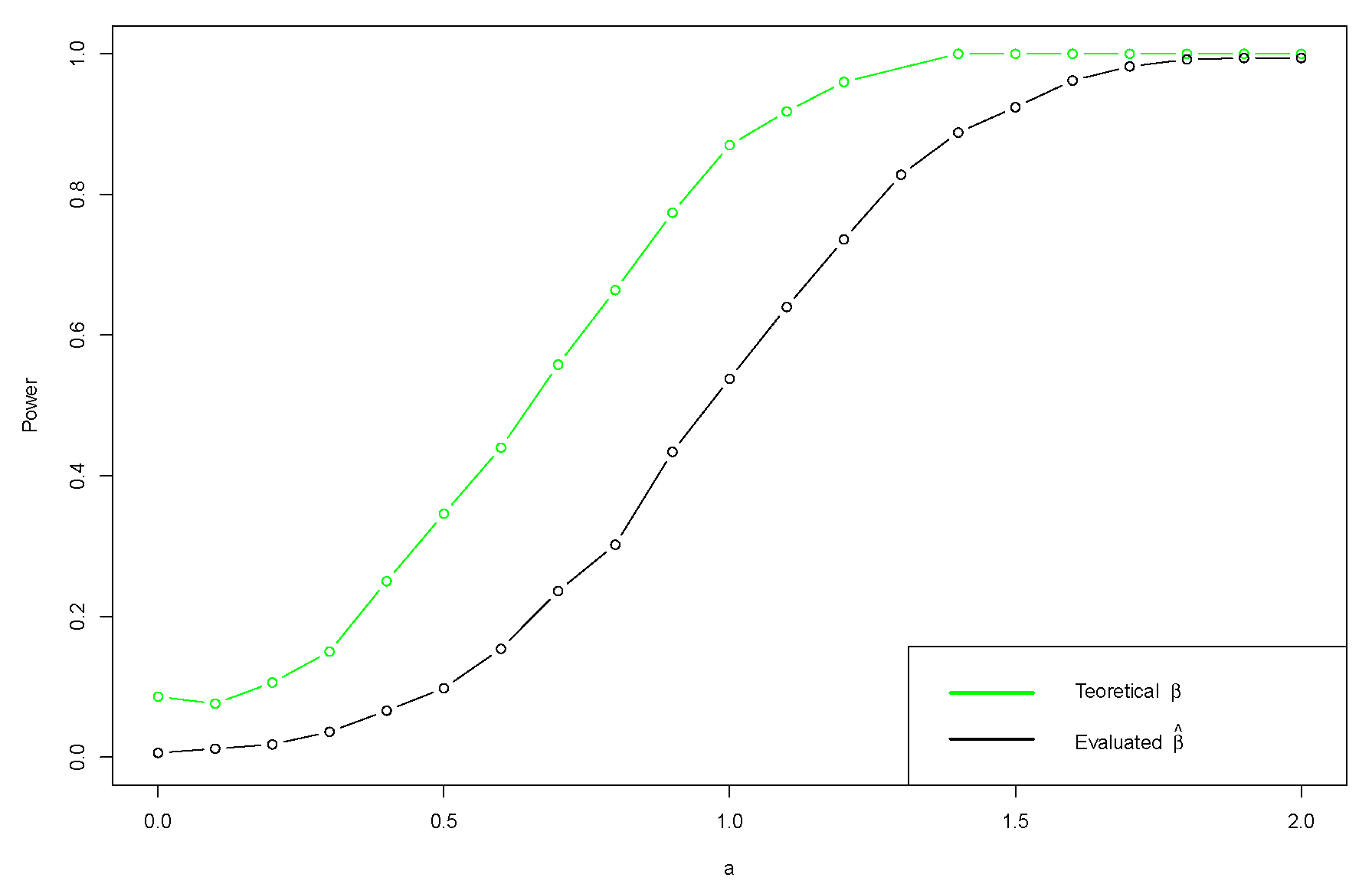
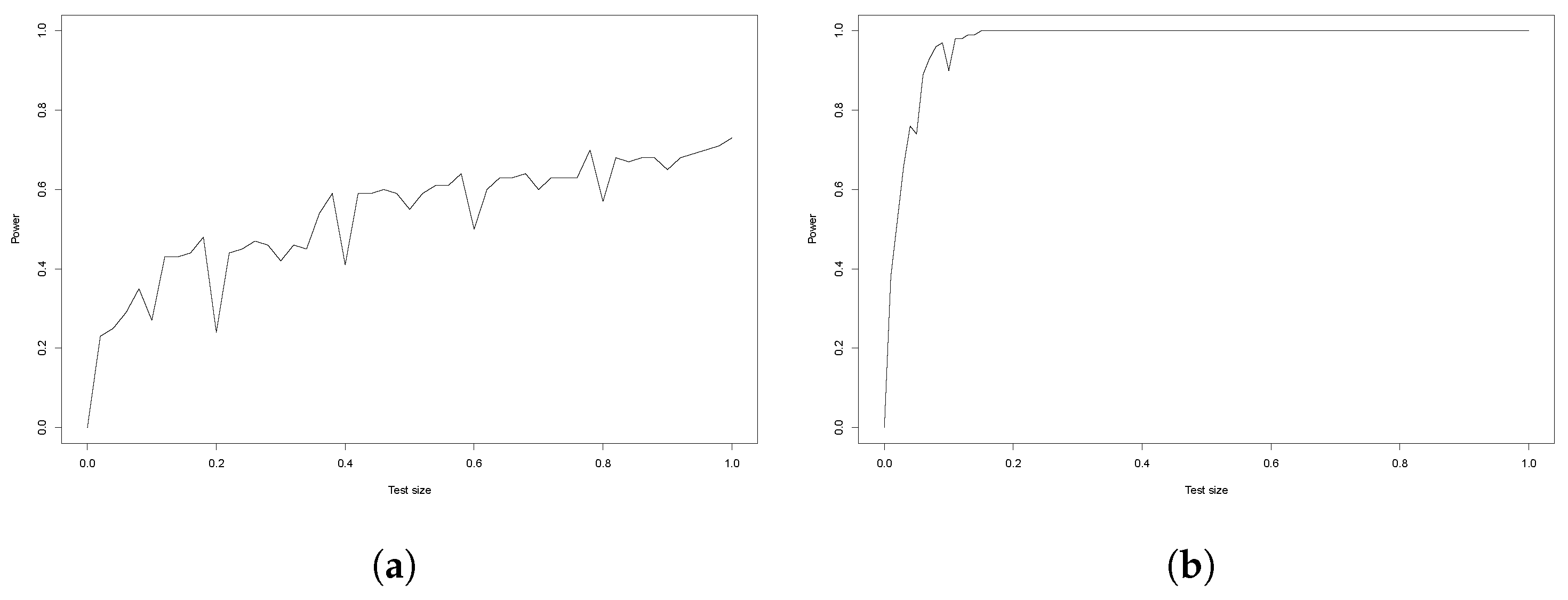
5.2. Power Analysis
- Case 1
- Case 2
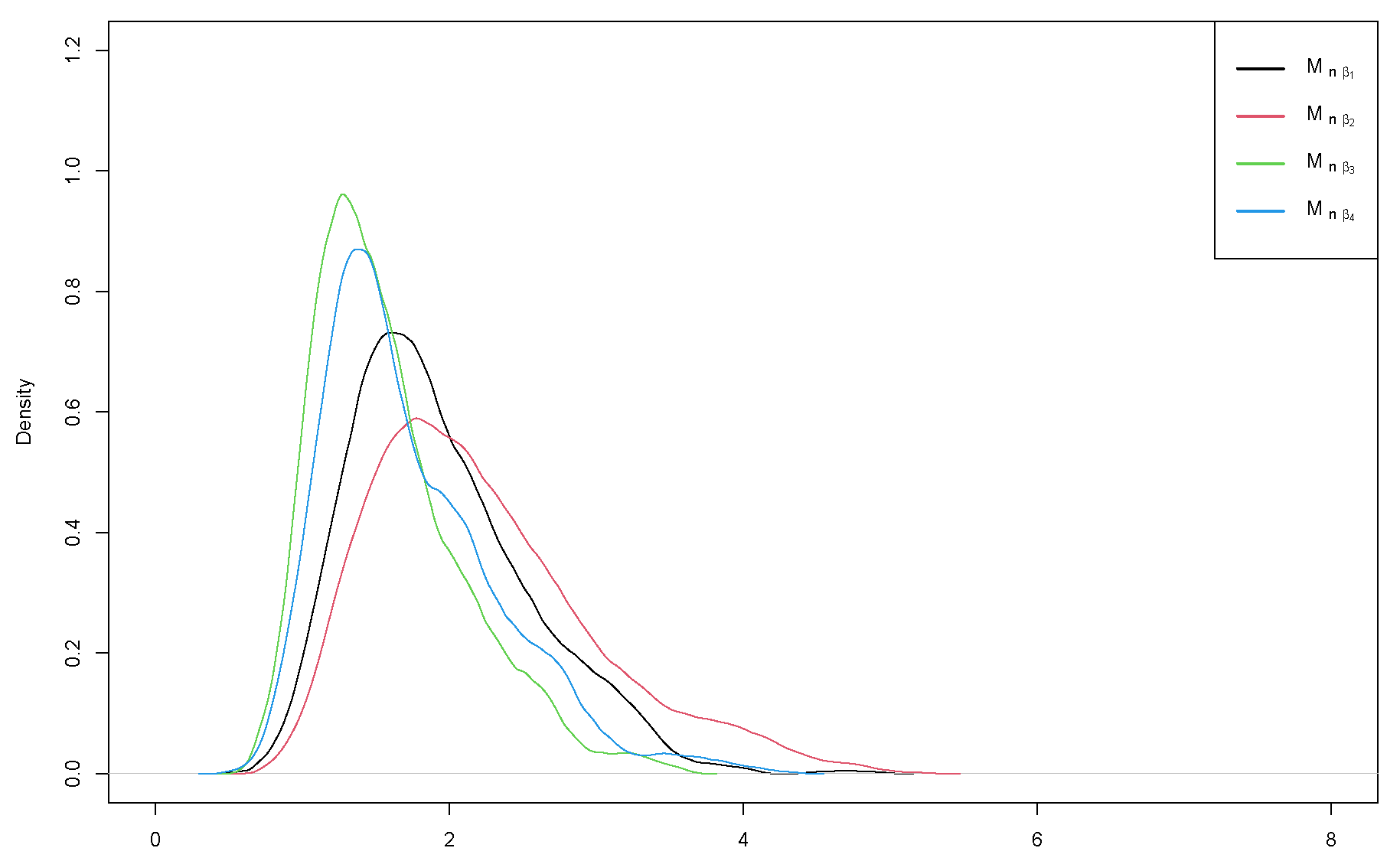
6. Case Study
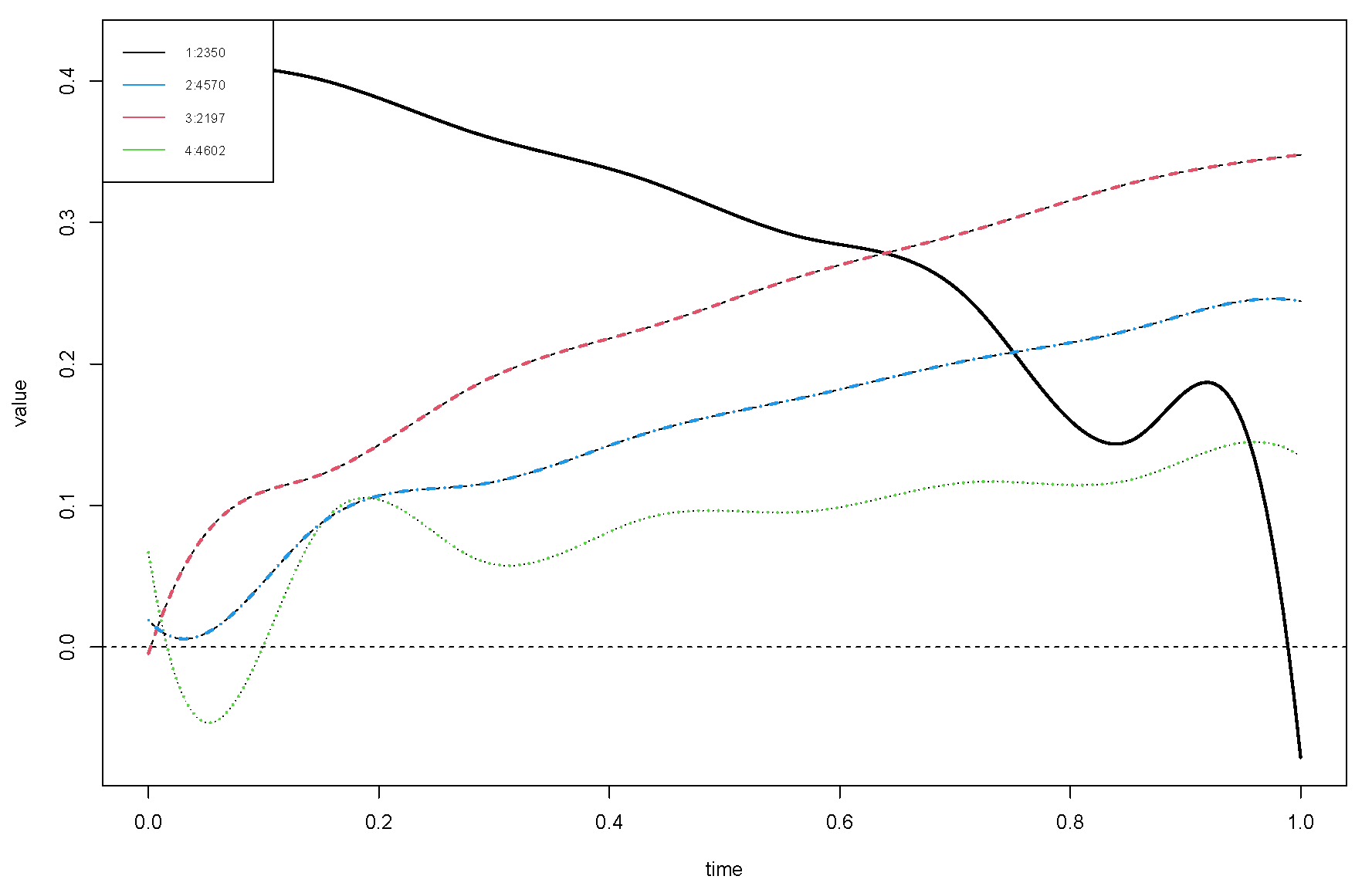
- A functional first-order auto-regression, FAR(1), is created for every subscriber. The total number of subscribers is z = 13,862.
- are taken from every FAR(1).
- are clustered into four groups using the Fisher-EM algorithm with k-means initialization. The best cluster is chosen by AIC criteria.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aue, A.; Horváth, L. Structural breaks in time series. J. Time Ser. Anal. 2013, 34, 1–16. [Google Scholar] [CrossRef]
- Zhu, X.; Li, Y.; Liang, C.; Chen, J.; Wu, D. Copula based change-point Detection for Financial Contagion in Chinese Banking. Procedia Comput. Sci. 2013, 17, 619–626. [Google Scholar] [CrossRef]
- Garcia, R.; Perron, P. An Analysis of the Real Interest Rate Under Regime Shifts. Rev. Econ. Stat. 1996, 78, 111–125. [Google Scholar] [CrossRef]
- Beaulieu, C.; Chen, J.; Sarmiento, J.L. Change-point analysis as a tool to detect abrupt climate variations. Philos. Trans. R. Soc. 2012, 370, 1228–1249. [Google Scholar] [CrossRef]
- Ramsay, J.O. When the data are functions. Psychometrika 1982, 47, 379–396. [Google Scholar] [CrossRef]
- Kokoszka, P.; Reimherr, M. Introduction to Functional Data Analysis; Chapman & Hall/CRC Texts in Statistical Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ramsay, J.O.; Hooker, G.; Graves, S. Functional Data Analysis; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ramsay, J.O.; Hooker, G.; Graves, S. Functional Data Analysis with R and MATLAB; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Aneiros, G.; Cao, R.; Vilar-Fernandez, J.M.; Munoz-San-Roque, A. Functional Prediction for the Residual Demand in Electricity Spot Markets. Recent Adv. Funct. Data Anal. Relat. Top. 2011, 1, 4201–4208. [Google Scholar] [CrossRef]
- Alaya, M.; Ternynck, C.; Dabo-Niang, S.; Chebana, F.; Ouardas, T. Change-point detection of flood events using a functional data framework. Adv. Water Resour. 2020, 137. [Google Scholar] [CrossRef]
- Koerner, F.; Anderson, J.; Fincham, J.; Kassa, R. Change-point detection of cognitive states across multiple trials in functional neuroimaging. Stat. Med. 2016, 36, 618–642. [Google Scholar] [CrossRef]
- Berkes, I.; Gabrys, R.; Horváth, L.; Kokoszka, P. Detecting changes in the mean of functional observations. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2009, 71, 927–946. [Google Scholar] [CrossRef]
- Aue, A.; Gabrys, R.; Horváth, L.; Kokoszka, P. Estimation of a change-point in the mean function of functional data. J. Multivar. Anal. 2009, 100, 2254–2269. [Google Scholar] [CrossRef]
- Horváth, L.; Kokoszka, P.; Rice, G. Testing stationarity of functional data. J. Econom. 2014, 179, 66–82. [Google Scholar] [CrossRef]
- Horváth, L.; Reeder, R. Detecting changes in functional linear models. J. Multivar. Anal. 2012, 111, 310–334. [Google Scholar] [CrossRef]
- Aue, A.; van Delft, A. Testing for stationarity of functional time series in the frequency domain. Ann. Stat. 2020, 48, 2505–2547. [Google Scholar] [CrossRef]
- Danielius, T.; Račkauskas, A. p-Variation of CUSUM process and testing change in the mean. Commun. Stat. Simul. Comput. 2020, 52, 1–13. [Google Scholar] [CrossRef]
- Aspirot, L.; Bertin, K.; Perera, G. Asymptotic normality of the Nadaraya–Watson estimator for nonstationary functional data and applications to telecommunications. J. Nonparametric Stat. 2009, 21, 535–551. [Google Scholar] [CrossRef]
- Yu, Y.; Lambert, D. Fitting Trees to Functional Data, with an Application to Time-of-Day Patterns. J. Comput. Graph. Stat. 1999, 8, 749–762. [Google Scholar] [CrossRef]
- Birbilas, A.; Račkauskas, A. Functional modelling of telecommunications data. Math. Model. Anal. 2022, 27, 117–133. [Google Scholar] [CrossRef]
- Shields, A.; Doody, P.; Scully, T. Application of multiple change-point detection methods to large urban telecommunication networks. In Proceedings of the 28th Irish Signals and Systems Conference (ISSC), Killarney, Ireland, 20–21 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Loreh, J. Changepoint Analysis in the Wireless Telecommunications Industry; Colorado School of Mines, ProQuest Dissertations Publishing: Ann Arbor, MI, USA, 2013; Available online: https://hdl.handle.net/11124/80121 (accessed on 1 February 2023).
- Aleksiejunas, R.; Garuolis, D. Usage of Published Network Traffic Datasets for Anomaly and Change Point Detection. Wireless Pers. Commun. 2023, 133, 1281–1303. [Google Scholar] [CrossRef]
- Račkauskas, A.; Suquet, C. On limit theorems for Banach-space-valued linear processes. Lith. Math. J. 2010, 50, 71–87. [Google Scholar] [CrossRef]
- Billingsley, P. Convergence of Probability Measures; John Willey & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Kuelbs, J. The invariance principle for Banach space valued random variables. J. Multivar. Anal. 1973, 3, 161–172. [Google Scholar] [CrossRef]
- Härdle, W.; Horowitz, J.; Kreiss, J.P. Bootstrap Methods for Time Series. Int. Stat. Rev. 2003, 71, 435–459. [Google Scholar] [CrossRef]
- Kunsch, H.R. The jackknife and the bootstrap for general stationary observations. Ann. Stat. 1993, 17, 1217–1261. [Google Scholar] [CrossRef]
- Liu, R.Y.; Singh, K. Moving blocks jackknife and bootstrap capture weak dependence. Explor. Limits Bootstrap 1992, 1, 225–248. [Google Scholar]
- Nyarige, E.U. The Bootstrap for the Functional Autoregressive Model FAR(1). Ph.D. Thesis, Kaiserslautern Technical University, Kaiserslautern, Germany, 2016. Available online: https://d-nb.info/1106250273/34 (accessed on 1 April 2023).
- Haynes, W. Bonferroni Correction. Encycl. Syst. Biol. 2013, 1, 154. [Google Scholar] [CrossRef]
- Sedgwick, P. Multiple significance tests: The Bonferroni correction. BMJ 2012, 344, 509. [Google Scholar] [CrossRef]
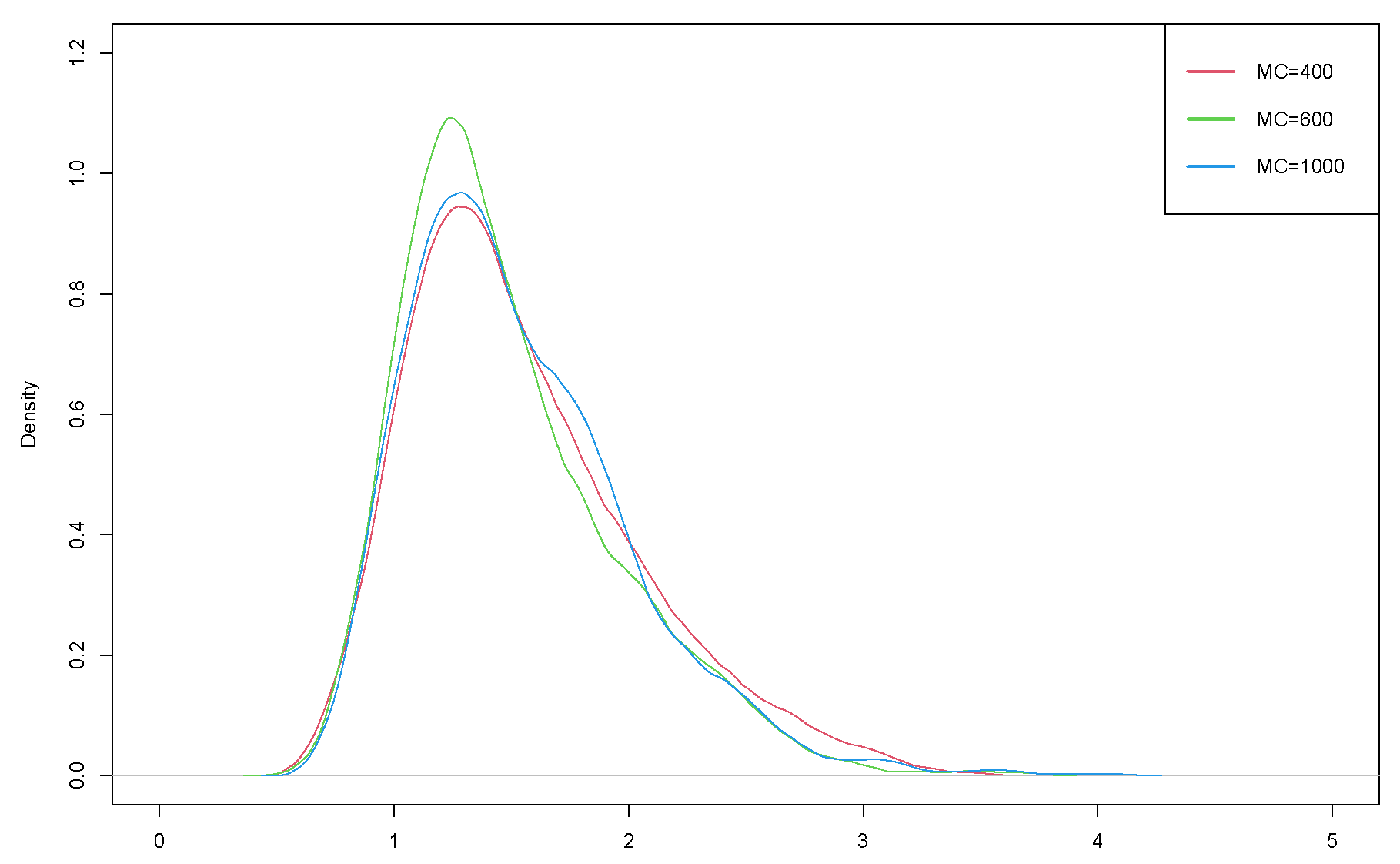




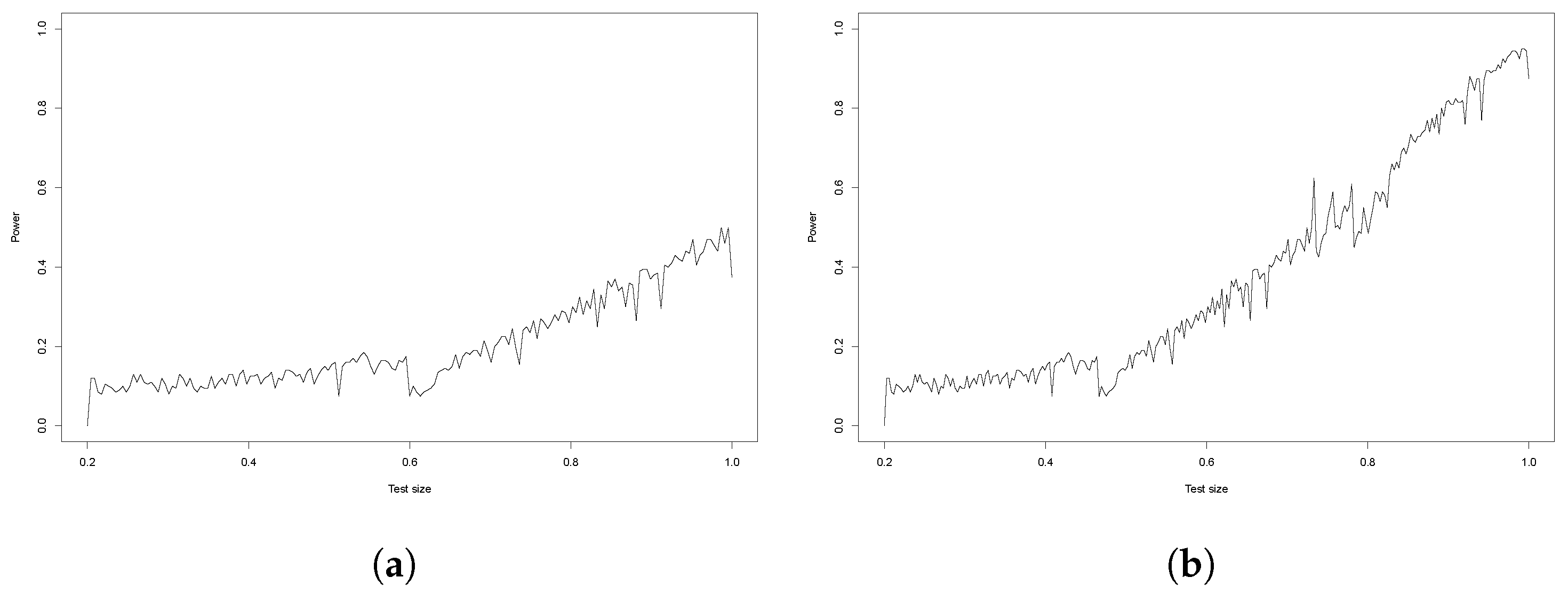
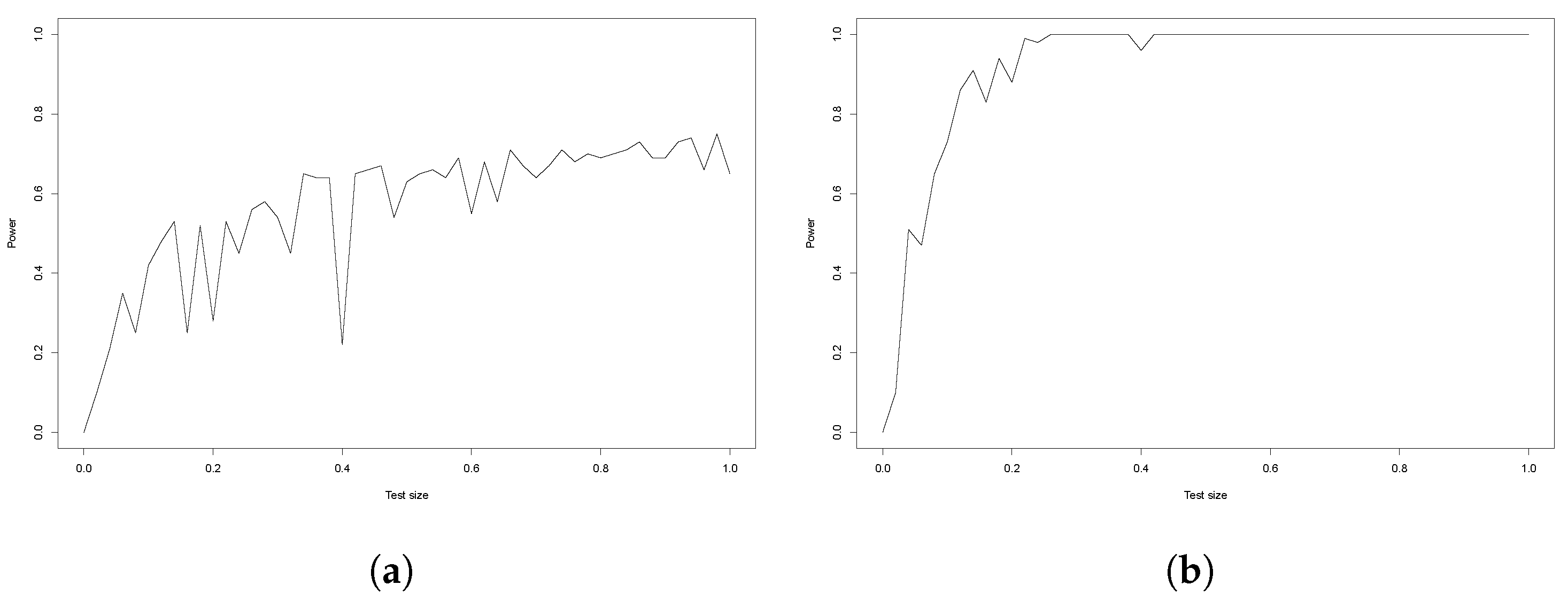




| 0.005 | 0.01 | 0.025 | 0.05 | 0.25 | 0.5 | 0.75 | 0.95 | 0.975 | 0.99 | 0.995 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MC = 400 | 0.8082 | 0.8266 | 0.8606 | 0.8982 | 1.1622 | 1.4163 | 1.7689 | 2.5414 | 2.6921 | 2.9071 | 2.9927 |
| MC = 600 | 0.8062 | 0.8562 | 0.8965 | 0.9412 | 1.1957 | 1.4358 | 1.8070 | 2.5188 | 2.7242 | 3.2369 | 3.3202 |
| MC = 800 | 0.7636 | 0.8120 | 0.8779 | 0.9413 | 1.1853 | 1.4317 | 1.7576 | 2.4568 | 2.6881 | 2.9427 | 3.1688 |
| MC = 1000 | 0.7897 | 0.8176 | 0.8857 | 0.9322 | 1.1690 | 1.4240 | 1.7919 | 2.4478 | 2.7043 | 2.9565 | 3.1000 |
| 0.005 | 0.01 | 0.025 | 0.05 | 0.25 | 0.5 | 0.75 | 0.95 | 0.975 | 0.99 | 0.995 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MC = 400 | 0.7489 | 0.7682 | 0.7988 | 0.8313 | 1.0401 | 1.2276 | 1.4700 | 1.9317 | 2.0333 | 2.1389 | 2.2285 |
| MC = 600 | 0.7509 | 0.7809 | 0.8214 | 0.8649 | 1.0425 | 1.2301 | 1.4860 | 1.9290 | 2.1213 | 2.3126 | 2.6485 |
| MC = 800 | 0.7514 | 0.7745 | 0.8266 | 0.8751 | 1.0401 | 1.2257 | 1.4606 | 1.9188 | 2.0661 | 2.2002 | 2.4172 |
| MC = 1000 | 0.7313 | 0.7520 | 0.8111 | 0.8606 | 1.0397 | 1.2230 | 1.4336 | 1.8510 | 2.0777 | 2.2900 | 2.3669 |
| for | for | for | for | |
|---|---|---|---|---|
| = 0.01 | 3.51 | 3.51 | 3.54 | 3.51 |
| = 0.02 | 3.41 | 3.41 | 3.42 | 3.41 |
| = 0.05 | 3.10 | 3.15 | 3.12 | 3.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Birbilas, A.; Račkauskas, A. Change-Point Detection in Functional First-Order Auto-Regressive Models. Mathematics 2024, 12, 1889. https://doi.org/10.3390/math12121889
Birbilas A, Račkauskas A. Change-Point Detection in Functional First-Order Auto-Regressive Models. Mathematics. 2024; 12(12):1889. https://doi.org/10.3390/math12121889
Chicago/Turabian StyleBirbilas, Algimantas, and Alfredas Račkauskas. 2024. "Change-Point Detection in Functional First-Order Auto-Regressive Models" Mathematics 12, no. 12: 1889. https://doi.org/10.3390/math12121889
APA StyleBirbilas, A., & Račkauskas, A. (2024). Change-Point Detection in Functional First-Order Auto-Regressive Models. Mathematics, 12(12), 1889. https://doi.org/10.3390/math12121889





