A Legendre Spectral-Element Method to Incorporate Topography for 2.5D Direct-Current-Resistivity Forward Modeling
Abstract
1. Introduction
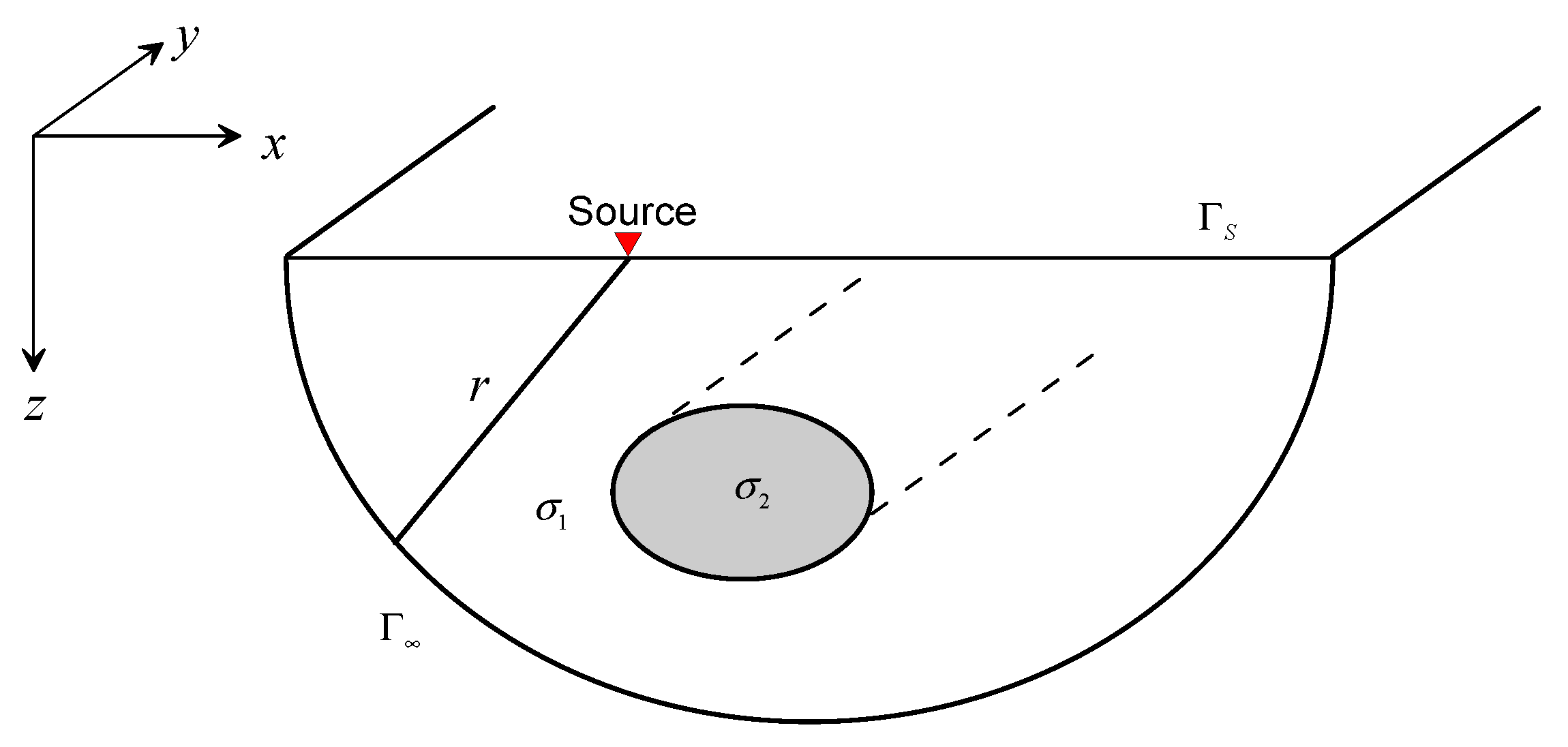
2. Mathematical Problem
3. Legendre Spectral-Element Method
3.1. Variational Problem and Discretization
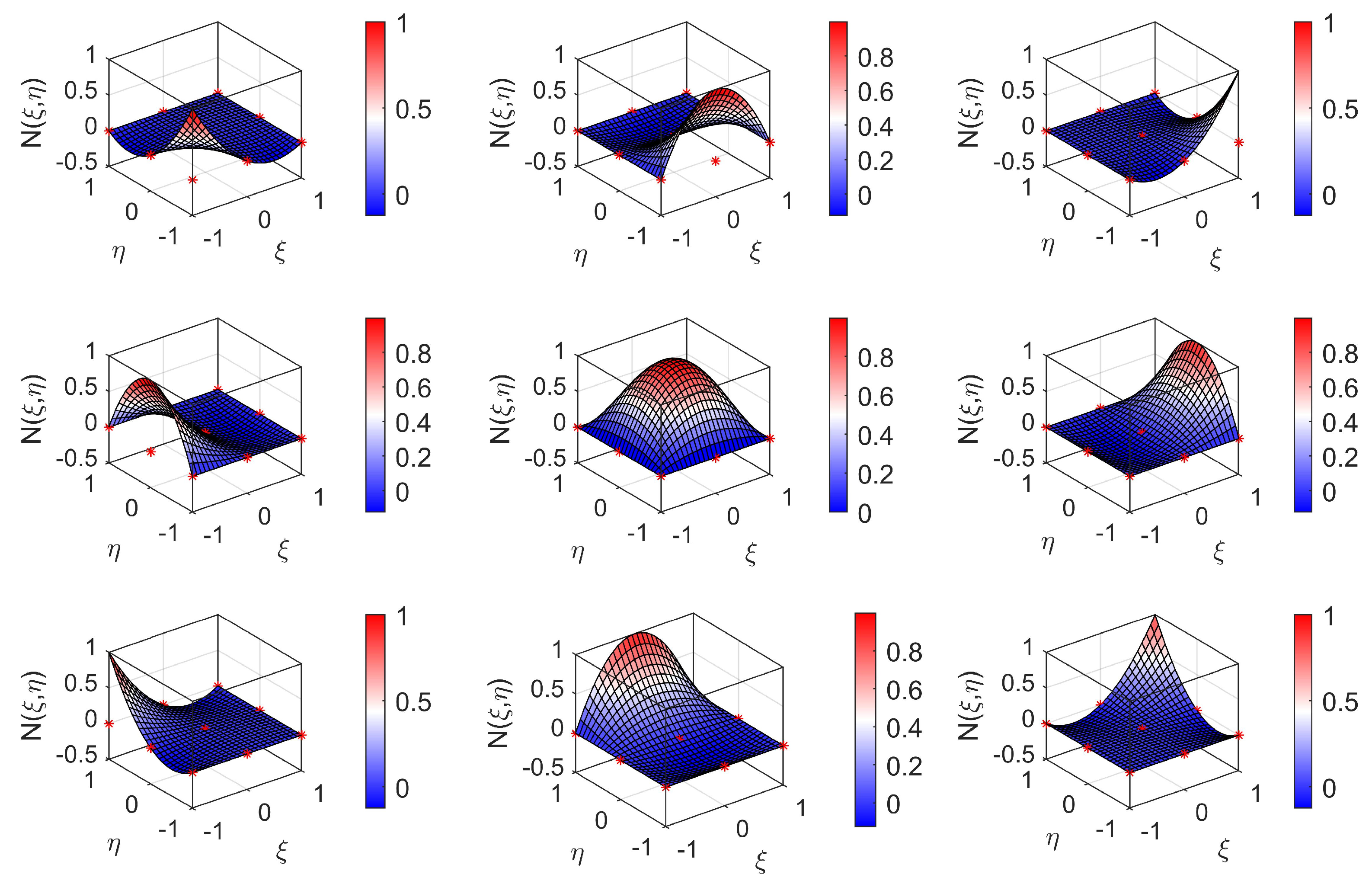
3.2. Legendre Basis Functions
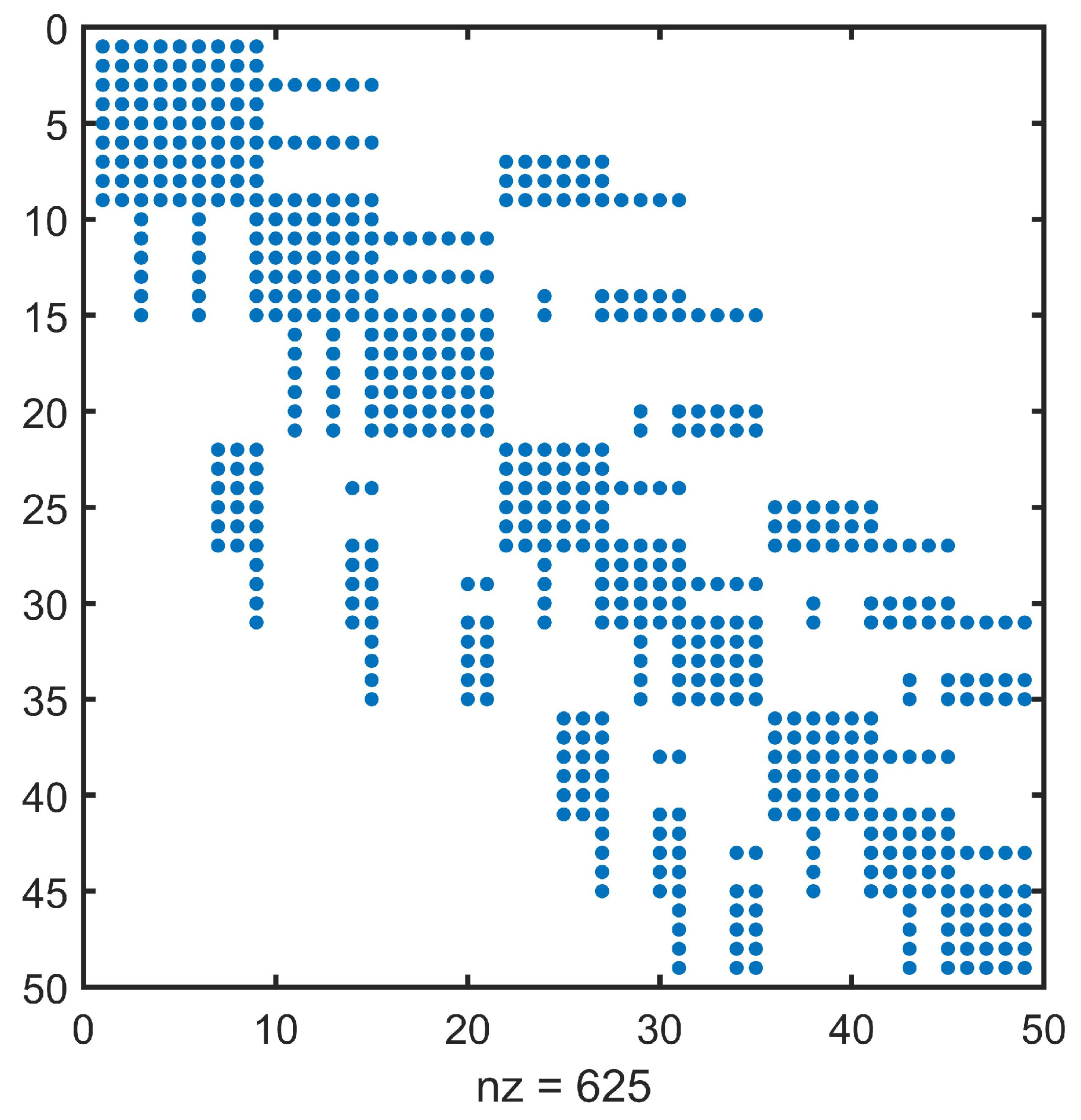
3.3. Legendre Spectral-Element Equation
3.4. Calculation of the Apparent Resistivity Response
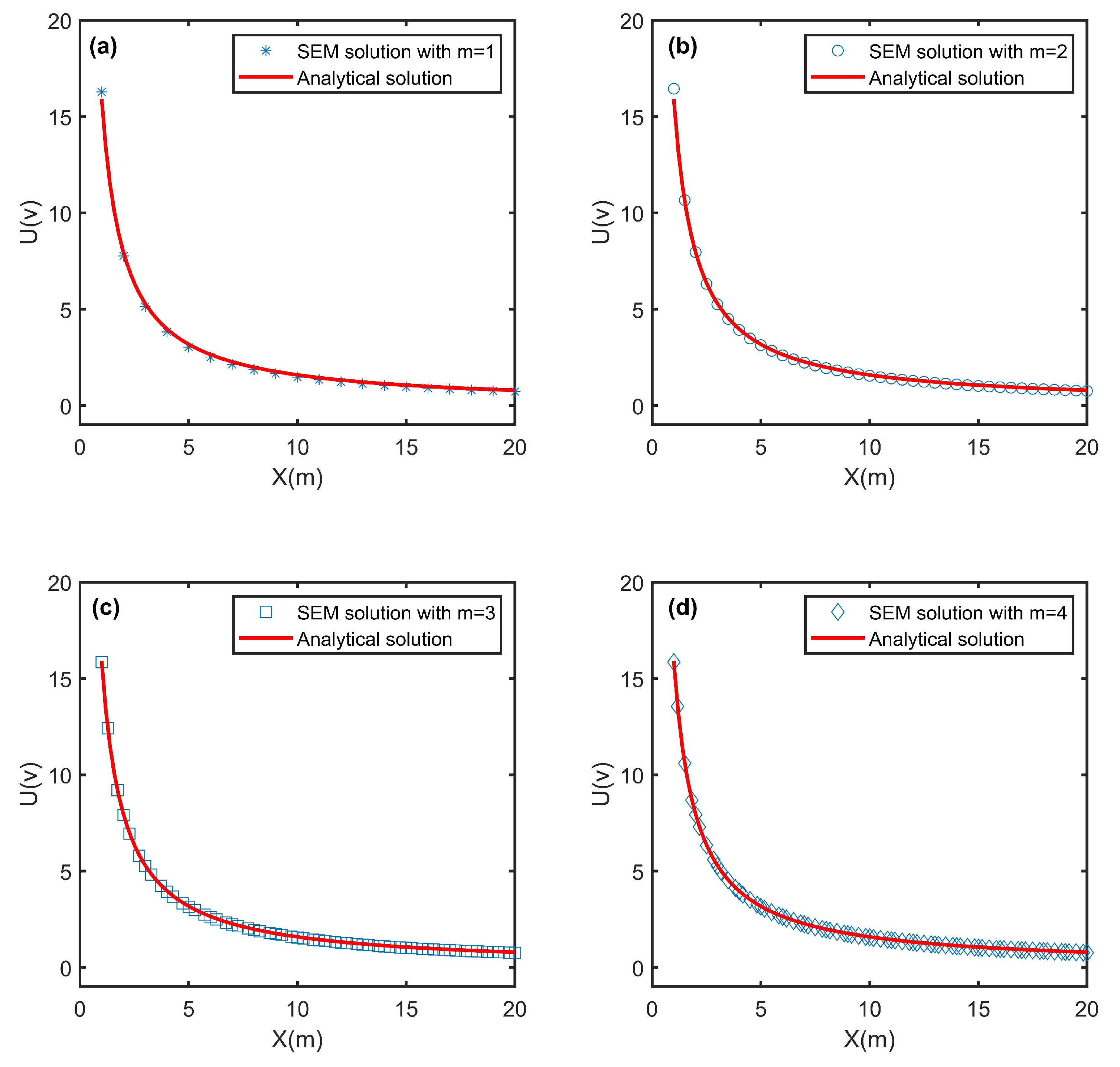
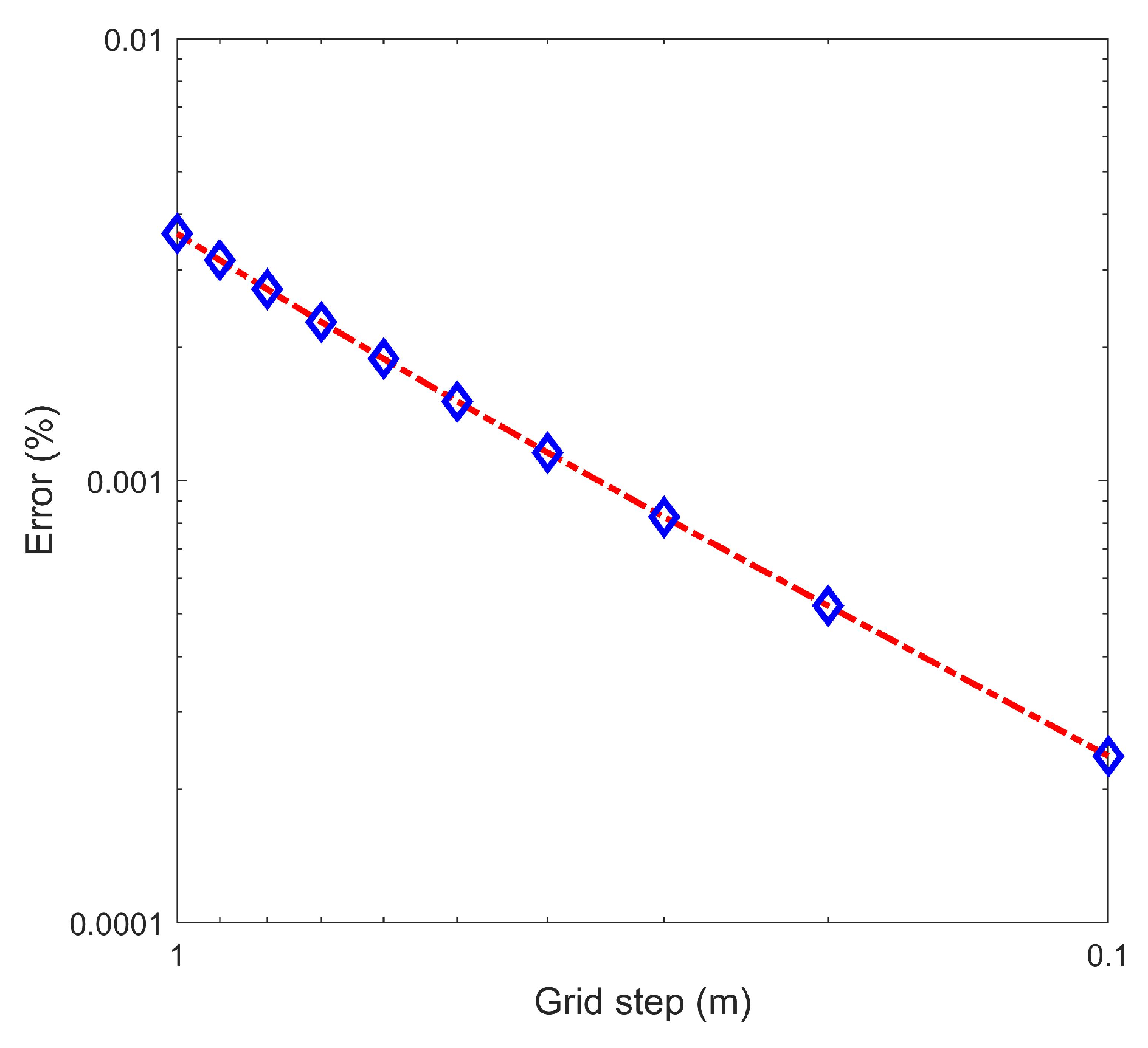
4. Accuracy Analysis of the Numerical Algorithm
4.1. Two-Dimensional Helmholtz Equation with a Homogeneous Dirichlet Boundary
4.2. Direct-Current Resistivity Modeling with a Half-Space Model
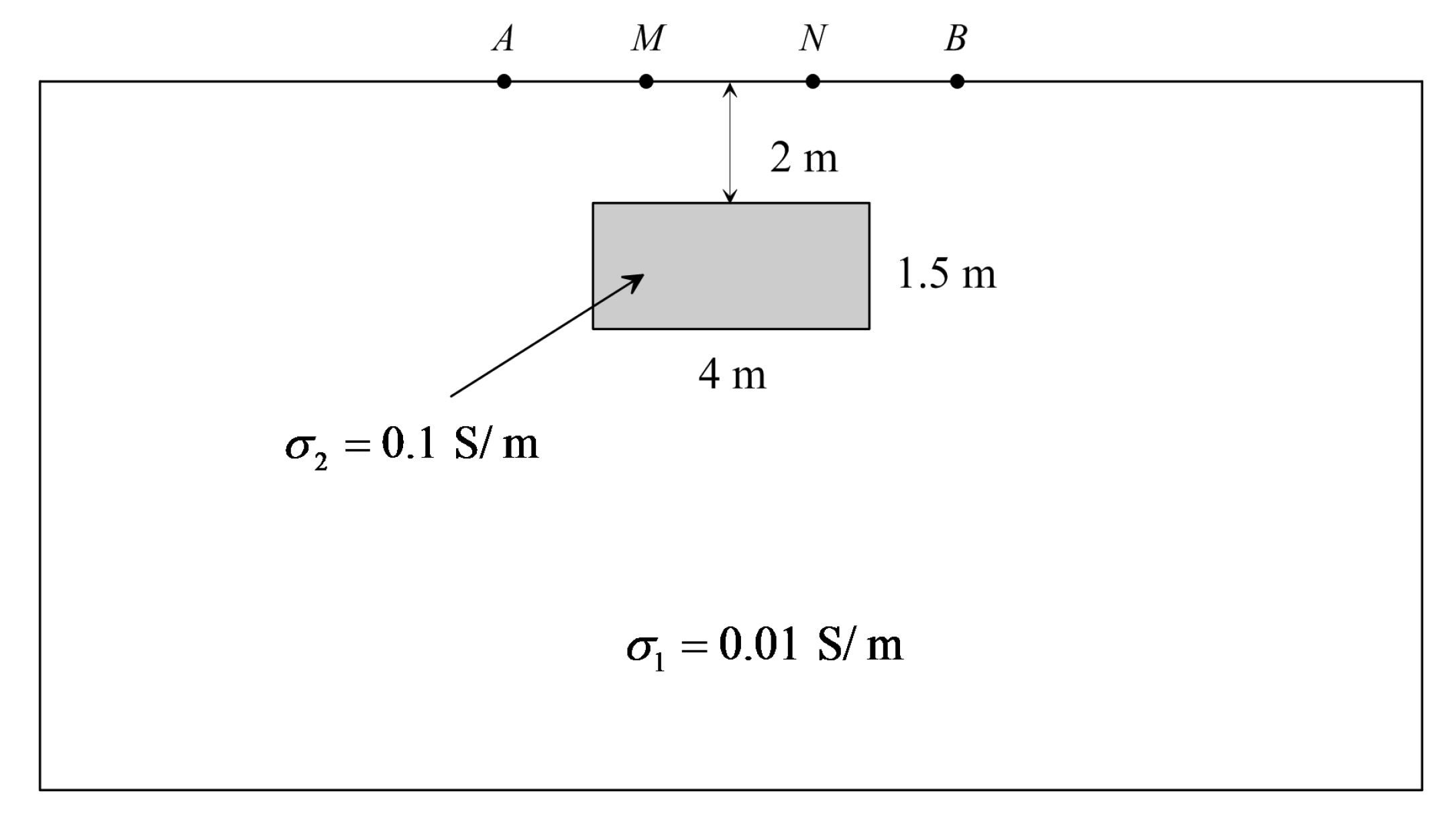
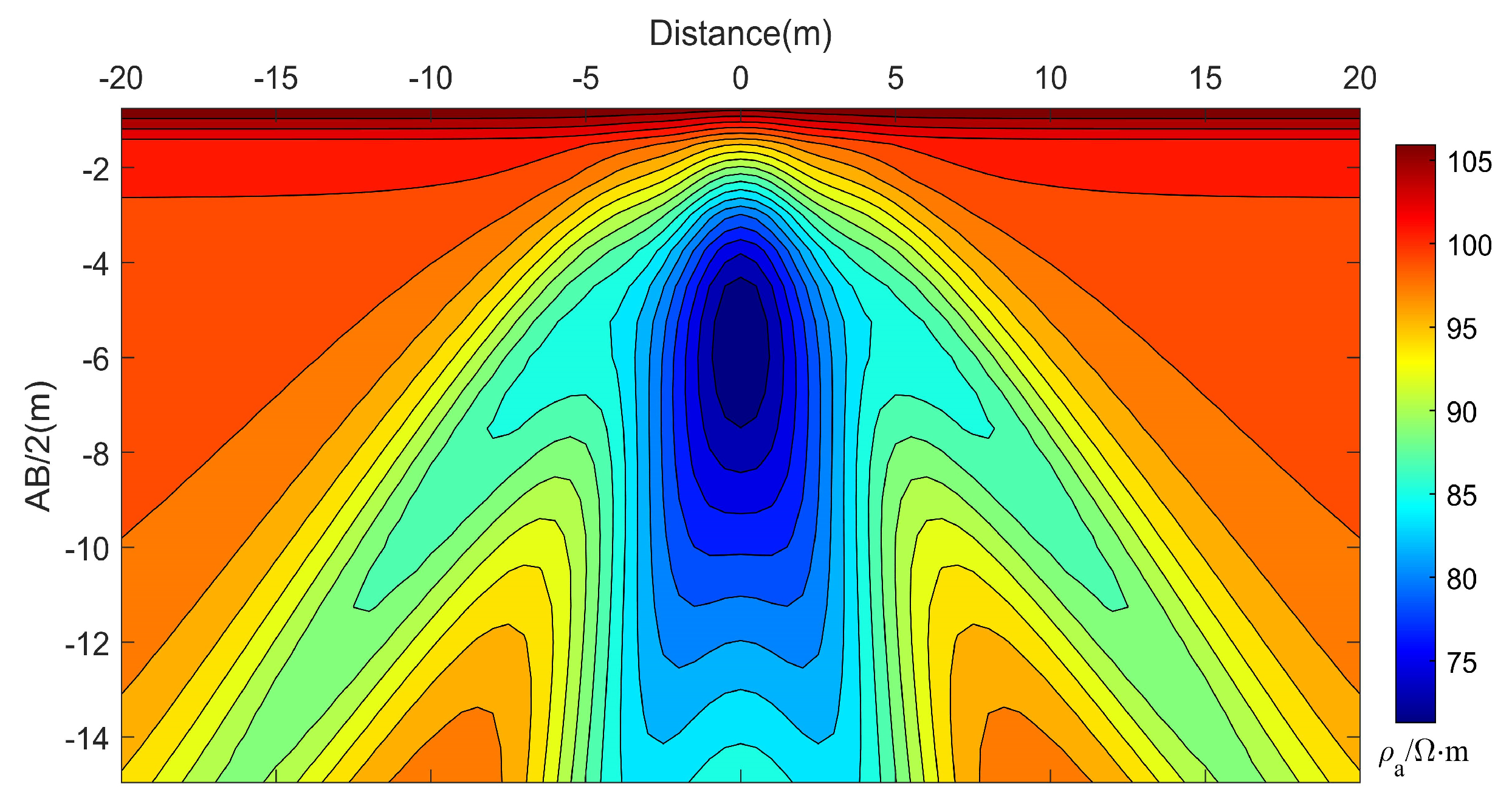
5. Model Computations and Discussion
5.1. A 2D Model with a Flat Topography
5.2. A Homogeneous Model with a Ridge Topography
5.3. A Homogeneous Model with a Valley Topography
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Appendix A. Numerical Integration
- function [x_node, w_coefficient]=gll(N)
- %Input arguments
- %N: Order or number of integration points
- %Output argument
- %x_node: GLL nodes
- %w_coefficient: GLL weights
- N_new=N+1;
- x_node=cos(pi*(0:N)/N);
- x_node=x_node’;
- P_Legendre=zeros(N_new);
- xold=2;
- while max(abs(x_node-xold))>eps
- xold=x_node;
- P_Legendre(:,1)=1;
- P_Legendre(:,2)=x_node;
- for m=2:N
- P_Legendre(:,m+1)=((2*m-1)*x_node.*P_Legendre(:,m)-(m-1)...
- *P_Legendre(:,m-1))/m;
- end
- x_node=xold-(x.*P_Legendre(:,N_new)-P_Legendre(:,N))...
- ./(N_new*P_Legendre(:,N_new));
- end
- w_coefficient=2./(N*N_new*P_Legendre(:,N_new).^2);
- end
Appendix B. Analytical Solution of Space-Domain Electrical Potential for the Homogenous Half-Space Model
References
- Yi, M.J.; Kim, J.H.; Son, J.S. Three-dimensional anisotropic inversion of resistivity tomography data in an abandoned mine area. Explor. Geophys. 2011, 42, 7–17. [Google Scholar] [CrossRef]
- Deng, Z.; Li, Z.; Nie, L.; Zhang, S.; Han, L.; Li, Y. Forward and inversion approach for direct current resistivity based on an unstructured mesh and its application to tunnel engineering. Geophys. Prospect. 2024, 72, 13510. [Google Scholar] [CrossRef]
- Mitchell, M.A.; Oldenburg, D.W. Using DC resistivity ring array surveys to resolve conductive structures around tunnels or mine-working. J. Appl. Geophys. 2023, 211, 104949. [Google Scholar] [CrossRef]
- Li, S.; Liu, B.; Nie, L.; Liu, Z.; Tian, M.; Wang, S.; Su, M.; Guo, Q. Detecting and monitoring of water inrush in tunnels and coal mines using direct current resistivity method: A review. J. Rock Mech. Geotech. Eng. 2015, 7, 469–478. [Google Scholar] [CrossRef]
- Chambers, J.C.; Kuras, O.; Meldrum, P.I.; Ogilvy, R.D.; Hollands, J. Electrical resistivity tomography applied to geologic, hydrogeologic, and engineering investigations at a former waste-disposal site. Geophysics 2006, 71, 231–239. [Google Scholar] [CrossRef]
- Ammar, A.I.; Kamal, K.A. Detection of shallow and deep conductive zones using direct current resistivity and time-domain electromagnetic methods, west El-Minia, Egypt. Groundw. Sustain. Dev. 2023, 20, 100865. [Google Scholar] [CrossRef]
- Chang, P.Y.; Doyoro, Y.G.; Lin, D.J.; Puntu, J.M.; Amania, H.H.; Kassie, L.N. Electrical resistivity imaging data for hydrogeological and geological hazard investigations in Taiwan. Data Brief 2023, 49, 109377. [Google Scholar] [CrossRef]
- Mosaad, A.H.; Farag, M.M.; Wei, Q.; Fahad, A.; Mohamed, S.A.; Hussein, A.S. Integration of electrical resistivity tomography and induced polarization for characterization and mapping of (Pb-Zn-Ag) sulfide deposits. Minerals 2023, 13, 986. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Li, Y.; Ellis, R.G. Inversion of geophysical data over a copper gold porphyry deposit: A case history for Mt. Milligan. Geophysics 1997, 62, 1419–1431. [Google Scholar] [CrossRef]
- Sirota, D.; Shragge, J.; Krahenbuhl, R.; Swidinsky, A.; Yalo, N.; Bradford, J. Development and validation of a low-cost direct current resistivity meter for humanitarian geophysics applications. Geophysics 2022, 87, WA1–WA14. [Google Scholar] [CrossRef]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Mufti, I.R. Finite-difference resistivity modeling for arbitrarily shaped two-dimensional structures. Geophysics 1976, 41, 62–78. [Google Scholar] [CrossRef]
- Gernez, S.; Bouchedda, A.; Gloaguen, E.; Paradis, D. AIM4RES, an open-source 2.5D finite difference MATLAB library for anisotropic electrical resistivity modeling. Comput. Geosci. 2020, 135, 104401. [Google Scholar] [CrossRef]
- Tong, X.; Sun, Y. Fictitious Point Technique Based on Finite-Difference Method for 2.5D Direct-Current Resistivity Forward Problem. Mathematics 2024, 12, 269. [Google Scholar] [CrossRef]
- Jahandari, H.; Lelièvre, P.; Farquharson, C.G. Forward modeling of direct-current resistivity data on unstructured grids using an adaptive mimetic finite-difference method. Geophysics 2023, 88, 123–134. [Google Scholar] [CrossRef]
- Zhou, B.; Greenhalgh, S.A. Finite element three-dimensional direct current resistivity modelling: Accuracy and efficiency considerations. Geophys. J. Int. 2001, 145, 679–688. [Google Scholar] [CrossRef]
- Yan, B.; Li, Y.; Liu, Y. Adaptive finite element modeling of direct current resistivity in 2-D generally anisotropic structures. J. Appl. Geophys. 2016, 130, 169–176. [Google Scholar] [CrossRef]
- Ren, Z.Y.; Qiu, L.; Tang, J. 3D direct current resistivity anisotropic modelling by goal-oriented adaptive finite element methods. Geophys. J. Int. 2018, 212, 76–87. [Google Scholar] [CrossRef]
- Tong, X.; Sun, Y.; Zhang, B. An efficient spectral element method for two-dimensional magnetotelluric modeling. Front. Earth Sci. 2023, 11, 1183150. [Google Scholar] [CrossRef]
- Gharti, H.N.; Tromp, J.; Zampini, S. Spectral-infinite-element simulations of gravity anomalies. Geophys. J. Int. 2018, 215, 1098–1117. [Google Scholar] [CrossRef]
- Zou, P.; Cheng, J. Pseudo-spectral method using rotated staggered grid for elastic wave propagation in 3D arbitrary anisotropic media. Geophys. Prospect. 2018, 66, 47–61. [Google Scholar] [CrossRef]
- Gharit, H.N.; Tromp, J. Spectral-infinite-element simulations of magnetic anomalies. Geophys. J. Int. 2019, 217, 1656–1667. [Google Scholar] [CrossRef]
- Weiss, M.; Kalscheuer, T.; Ren, Z. Spectral element method for 3-D controlled-source electromagnetic forward modeling using unstructured hexahedral meshes. Geophys. J. Int. 2023, 232, 1427–1454. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhuang, M.; Shi, L.; Cai, G.; Liu, N.; Liu, Q. Spectral element method with divergence-free constraint for 2.5-D marine CSEM hydrocarbon exploration. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1973–1977. [Google Scholar] [CrossRef]
- Wang, X.; Yu, T.; Feng, D.; Ding, S.; Li, B.; Liu, Y.; Feng, Z. A high-efficiency spectral element method based on CFS-PML for GPR numerical simulation and reverse time migration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1232–1243. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, L.; Huang, L.; Zhao, Z.; Ji, Y.; Liu, X.; Fang, G. An efficient 2.5-D forward algorithm based on the spectral element method for airborne transient electromagnetics data. Geophys. Prospect. 2023, 71, 1056–1069. [Google Scholar] [CrossRef]
- Spitzer, K. A 3-D finite-difference algorithm for DC resistivity modelling using conjugate gradient methods. Geophys. J. Int. 1995, 123, 903–914. [Google Scholar] [CrossRef]
- Penz, S.; Chauris, H.; Donno, D.; Mehl, C. Resistivity modelling with topography. Geophys. J. Int. 2013, 194, 1486–1497. [Google Scholar] [CrossRef]
- Pozrikidis, C. Introduction to Finite and Spectral Element Methods Using MATLAB; Chapman and Hall Press: New York, NY, USA, 2014. [Google Scholar]
- Lee, J.H.; Liu, Q.H. An efficient 3-D spectral-element method for Schrodinger equation in nanodevice simulation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2005, 24, 1848–1858. [Google Scholar] [CrossRef]
- Tong, X.; Sun, Y.; Huang, J.; Liu, J. High-accuracy gravity field and gravity gradient forward modelling based on 3D vertex-centered finite-element algorithm. J. Cent. South Unive. 2024, 31, 1–12. [Google Scholar] [CrossRef]
- Chen, J.; Haber, E.; Oldenburg, D.W. Three-dimensional numerical modelling and inversion of magnetometric resistivity data. Geophys. J. Int. 2002, 149, 679–697. [Google Scholar] [CrossRef]
- Pan, K.; Wang, J.; Hu, S.; Ren, Z.; Cui, T.; Guo, R.; Tang, J. An efficient cascadic multigrid solver for 3-D magnetotelluric forward modelling problems using potentials. Geophys. J. Int. 2022, 230, 1834–1851. [Google Scholar] [CrossRef]
- Xu, S.Z.; Duan, B.C.; Zhang, D.H. Selection of the wavenumbers k using an optimization method for the inverse Fourier transform in 2.5D electrical modeling. Geophys. Prospect. 2000, 48, 789–796. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, D.; Liu, J.; Zhang, Q. Efficient 2D modelling of magnetic anomalies using NUFFT in the Fourier domain. Pure Appl. Geophys. 2022, 179, 2311–2325. [Google Scholar] [CrossRef]
- Tsourios, P.E.; Szymanski, J.E.; Tsokas, G.N. The effect of terrain topography on commonly used resistivity arrays. Geophysics 1999, 64, 1357–1363. [Google Scholar] [CrossRef]


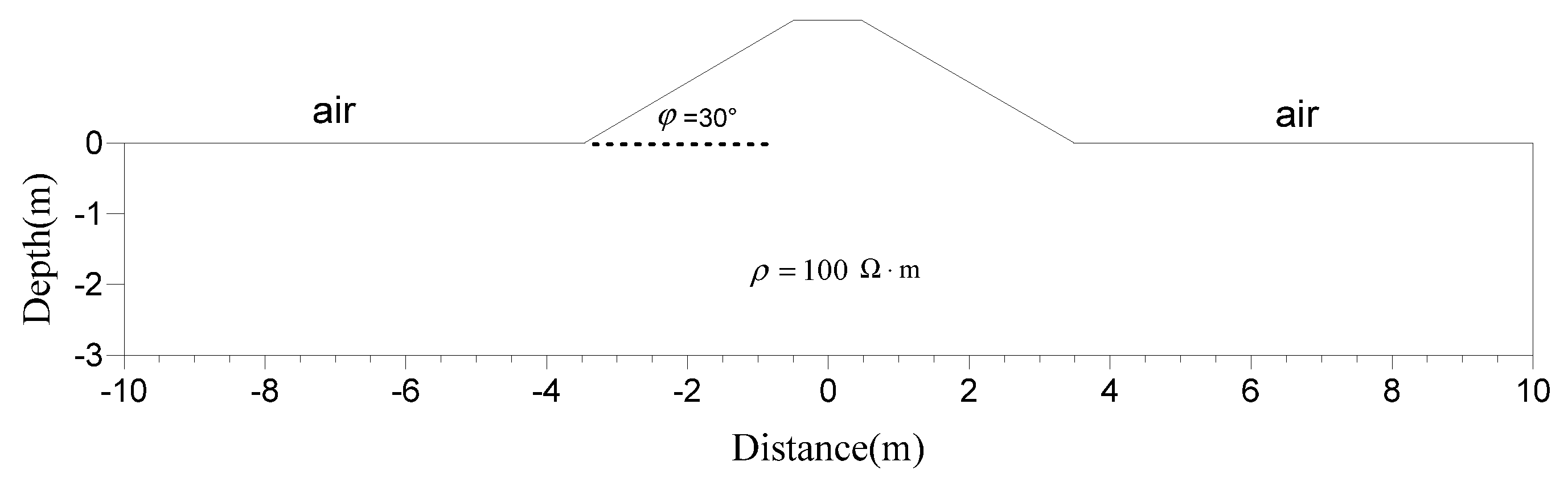


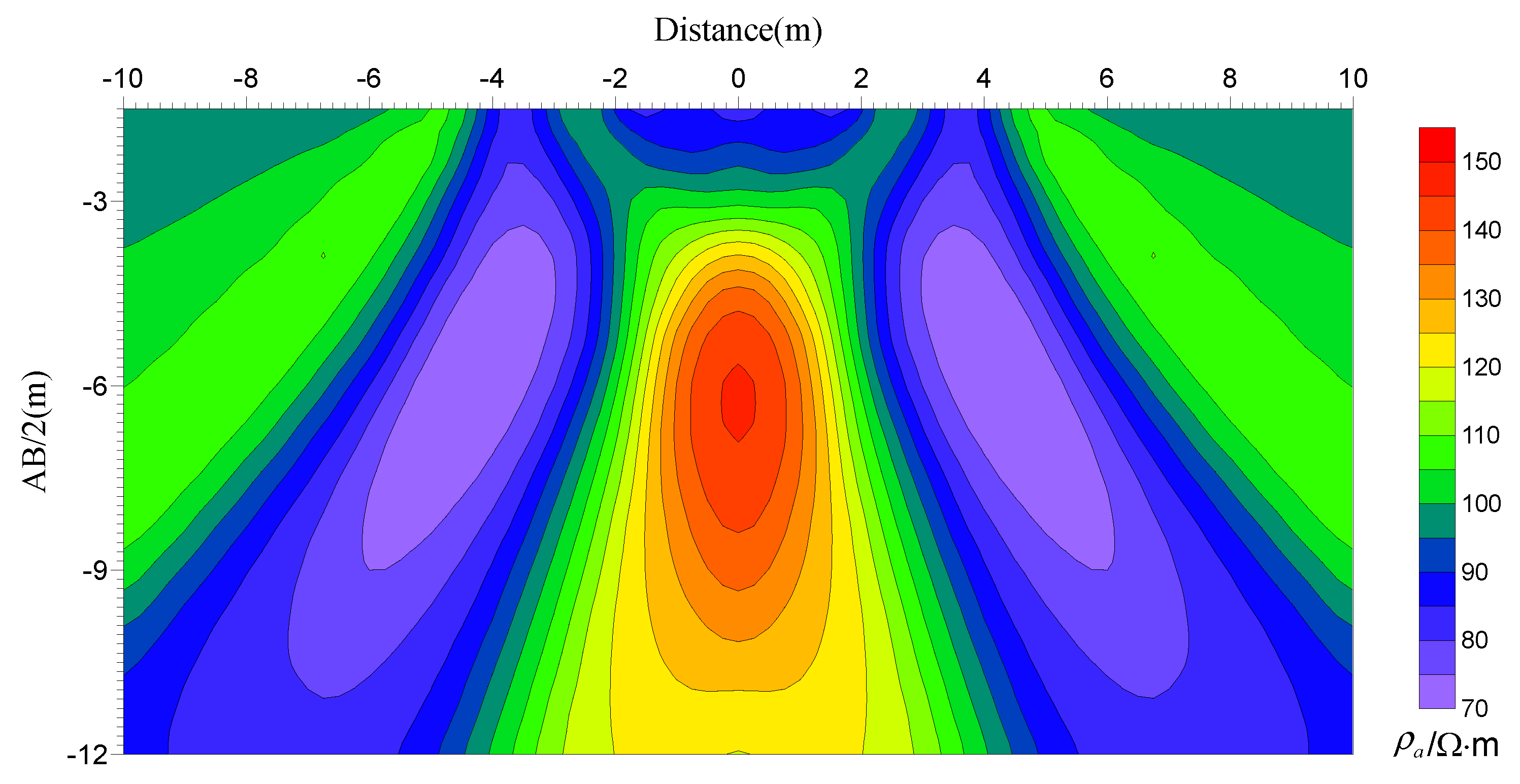
| i | ||
|---|---|---|
| 1 | 0.0113218 | 0.0176814 |
| 2 | 0.0601482 | 0.0486791 |
| 3 | 0.1856957 | 0.1227978 |
| 4 | 0.5151699 | 0.3351368 |
| 5 | 1.5271465 | 1.1654942 |
| 6 | 6.4249320 | 7.9156312 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Zhu, W.; Tong, X.; Ma, H. A Legendre Spectral-Element Method to Incorporate Topography for 2.5D Direct-Current-Resistivity Forward Modeling. Mathematics 2024, 12, 1864. https://doi.org/10.3390/math12121864
Xie W, Zhu W, Tong X, Ma H. A Legendre Spectral-Element Method to Incorporate Topography for 2.5D Direct-Current-Resistivity Forward Modeling. Mathematics. 2024; 12(12):1864. https://doi.org/10.3390/math12121864
Chicago/Turabian StyleXie, Wei, Wendi Zhu, Xiaozhong Tong, and Huiying Ma. 2024. "A Legendre Spectral-Element Method to Incorporate Topography for 2.5D Direct-Current-Resistivity Forward Modeling" Mathematics 12, no. 12: 1864. https://doi.org/10.3390/math12121864
APA StyleXie, W., Zhu, W., Tong, X., & Ma, H. (2024). A Legendre Spectral-Element Method to Incorporate Topography for 2.5D Direct-Current-Resistivity Forward Modeling. Mathematics, 12(12), 1864. https://doi.org/10.3390/math12121864







