Non-Parametric Estimation of the Renewal Function for Multidimensional Random Fields

Abstract

This paper addresses the almost sure convergence and the asymptotic normality of an estimator of the multidimensional renewal function based on random fields. The estimator is based on a sequence of non-negative independent and identically distributed ${\displaystyle (i.i.d.)}$ multidimensional random fields and is expressed as infinite sums of ${\displaystyle k}$-folds convolutions of the empirical distribution function. It is an extension of the work from the case of the two-dimensional random fields to the case of the ${\displaystyle d}$-dimensional random fields where ${\displaystyle d>2}$. This is established by the definition of a “strict order relation”. Concrete applications are given.

1. Introduction

Density and regression estimations for random fields have been widely studied in the literature. The studies of univariate or multivariate stationary-dependent random fields received increasing attention. Tran [1] establishes the uniform strong consistency and obtains rates of convergence under a mixing assumption. By considering a linear process, Tran [2] obtains similar results without a mixing assumption. Carbon et al. [3] study the uniform convergence for stationary mixing processes. Doukhan and Louichi [4] show results on the mean square, the uniform and the almost sure convergences. Bradley and Tran [5] prove the asymptotic normality for a class of strictly stationary random fields satisfying a strong mixing condition. Biau [6] studies the mean-squared error and the mean integrated squared error and shows that the both errors turn out to be asymptotically the same as in the ${\displaystyle i.i.d.}$ case. Sufficient conditions for the convergence in ${\displaystyle L1}$ are obtained by Hallin et al. [7] under general conditions. Carbon et al. [8] show an uniform convergence on compact sets under general conditions. El Machkouri [9] establishes a central limit theorem for mixing random fields and a similar result but for ${\displaystyle m}$-dependent random fields is proved by Fazekas et al. [10]. Harel et al. [11] investigate the asymptotic behavior of binned kernel density estimators for dependent and locally non-stationary random fields converging to stationary random fields. Carbon and Duchesne [12] investigate the multivariate frequency polygon as a density estimator for stationary random fields indexed by multidimensional lattice points space. Studying such models is of great practical interest. For example, in an epidemic area, the number of patients decreases from this area toward those where the number of patients is stationary(see the example given in Section 3). The same phenomenon can be observed from the beginning to the end of the epidemic. In mining research also, there may be neighboring sites wherein the soil content of a given metal is not homogeneous from one spot to another. Many other practical examples can be found in finance, ecology and many other domains. Concerning concrete applications of the random fields in dam construction, Amin Hariri-Ardebili et al. [13] propose a hybrid random field polynomial chaos expansion surrogate model for uncertainty quantification and assessment of dams while Congyong et al. [14] propose a safety risk analysis method for a gravity dam–foundation system based on random field theory.

The estimation of the renewal function for random variables is widely studied in the literature. In order to better point out our results on the asymptotic behavior of the estimator, we note some results in the literature. Frees [15] develops almost sure consistency and asymptotic normality of the estimator. Grubel and Pitts [16] discuss consistency, asymptotic normality and asymptotic validity of bootstrap confidence regions of the estimator. Then, Harel et al. [17] prove the weak convergence of the estimator on Skorohod topology. Markovich et al. [18] show almost sure convergence of the estimator while Gokpinar et al. [19] study consistency, asymptotic unbiasedness and asymptotic normality of the estimator. Harel and Ravelomanantsoa [20] show not only almost sure convergence and asymptotic normality but also weak convergence on Skorohod topology of the estimator. In the two-dimensional and bivariate case, Harel et al. [21] study almost sure convergence and asymptotic normality of the estimator while, in the multidimensional and multivariate case, Harel et al. [22] prove the weak convergence on Skorohod topology of the estimator. Andriamampionona et al. [23] study the asymptotic normality of the renewal function estimator for sequences of random fields in dimension 2. In this paper, we generalize their results in dimension ${\displaystyle d>2}$ and show the almost sure convergence and the asymptotic normality of the estimator of the renewal function. This paper is organized as follows: the general assumptions, including some notations, definitions and illustrations, are given in Section 2. Details of concrete application in the mutidimensional case are stated in Section 3. We examine, respectively, the almost sure convergence of the empirical distribution function and that of the estimator of the renewal function in Section 4 and Section 5. The asymptotic normality of these estimators are, respectively, given in Section 6 and Section 7.

2. General Assumptions

If random variables have total order, random fields only have partial order. Indeed, the renewal processes add random fields according to a certain order. The latter can be done according to the application circumstances such as the proximity of individuals to one another in the case of an epidemic. In this paper, we assume that the random fields are independent and identically distributed, so the obtained results do not depend on the order chosen. We choose an order that makes our proof easier to establish. Regarding the chosen order, we suppose that, for each component ${\displaystyle i_j,1\le j\le d}$, the set of indices is not bounded. In our example of Section 3, the second component has only two indices, namely 1 and 2. For bounded indices, the order is different.

Let ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ be a sequence of ${\displaystyle i.i.d.}$ absolutely continuous positive ${\displaystyle d}$-dimensional random fields with values on ${\displaystyle {\mathbb{R}}_{+}}$. Let ${\displaystyle {\prec }_d}$ be the order relation defined as follows: ${\displaystyle \left(i_1,i_2,\dots ,i_{d-1},i_d\right){\prec }_d\left(i_1^{\prime },i_2^{\prime },\dots ,i_{d-1}^{\prime },i_d^{\prime }\right)}$ if and only if

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{i}_1+\dots +i_d=i_1^{\prime }+\dots +i_d^{\prime }\mathrm{and}\left\{\begin{array}{c}\{i_1=i_1^{\prime },\dots ,i_{d-2}=i_{d-2}^{\prime }\mathrm{and}{i}_{d-1}<i_{d-1}^{\prime }\}\hfill \\ \dots \hfill \\ \{i_1=i_1^{\prime },i_2=i_2^{\prime }\mathrm{and}{i}_3<i_3^{\prime }\}\hfill \\ \{i_1=i_1^{\prime }\mathrm{and}{i}_2<i_2^{\prime }\}\hfill \\ \{i_1<i_1^{\prime }\}\hfill \end{array}\right.\hfill \\ i_1+\dots +i_d<i_1^{\prime }+\dots +i_d^{\prime }\hfill \end{array}\right..\end{array}$$

(1)

Remark 1.

It is a strict inequality.

According to this order, we define the set

$$\begin{array}{c}\hfill {\widehat{\mathbf{I}}}_n^d=\left\{(i_1,\dots ,i_d)\mathrm{such}\mathrm{that}{i}_1+\dots +i_d\le n+d-1,i_1=1,\dots ,n;\dots ;i_d=1,\dots ,n\right\}.\end{array}$$

(2)

As the random fields are independent, our order was chosen only to facilitate the proofs of our results.

To describe the sum of the random fields on ${\displaystyle {\widehat{\mathbf{I}}}_n^d}$ according to the order relation, define

$$\begin{array}{c}\hfill {\mathbf{S}}_l^d=\left\{{\mathbf{X}}_{(i_1,i_2,\dots ,i_d)};i_1+i_2+\dots +i_d=l+d-1,\mathrm{for}d\ge 3\mathrm{and}l\in {\mathbb{N}}^{\ast }\right\},\end{array}$$

and

$$\begin{array}{c}\hfill {\mathbf{S}}_l^{\ast d}=\sum _{{\mathbf{X}}_{\mathbf{i}}\in {\mathbf{S}}_l^d}{\mathbf{X}}_{\mathbf{i}}.\end{array}$$

In this way, the cardinal of the random fields included in the set ${\displaystyle {\widehat{\mathbf{I}}}_n^d}$ is given by the formula

$$\begin{array}{c}\hfill {\omega }_n^d=\sum _{l=1}^n\mathrm{Card}\left({\mathbf{S}}_l^d\right).\end{array}$$

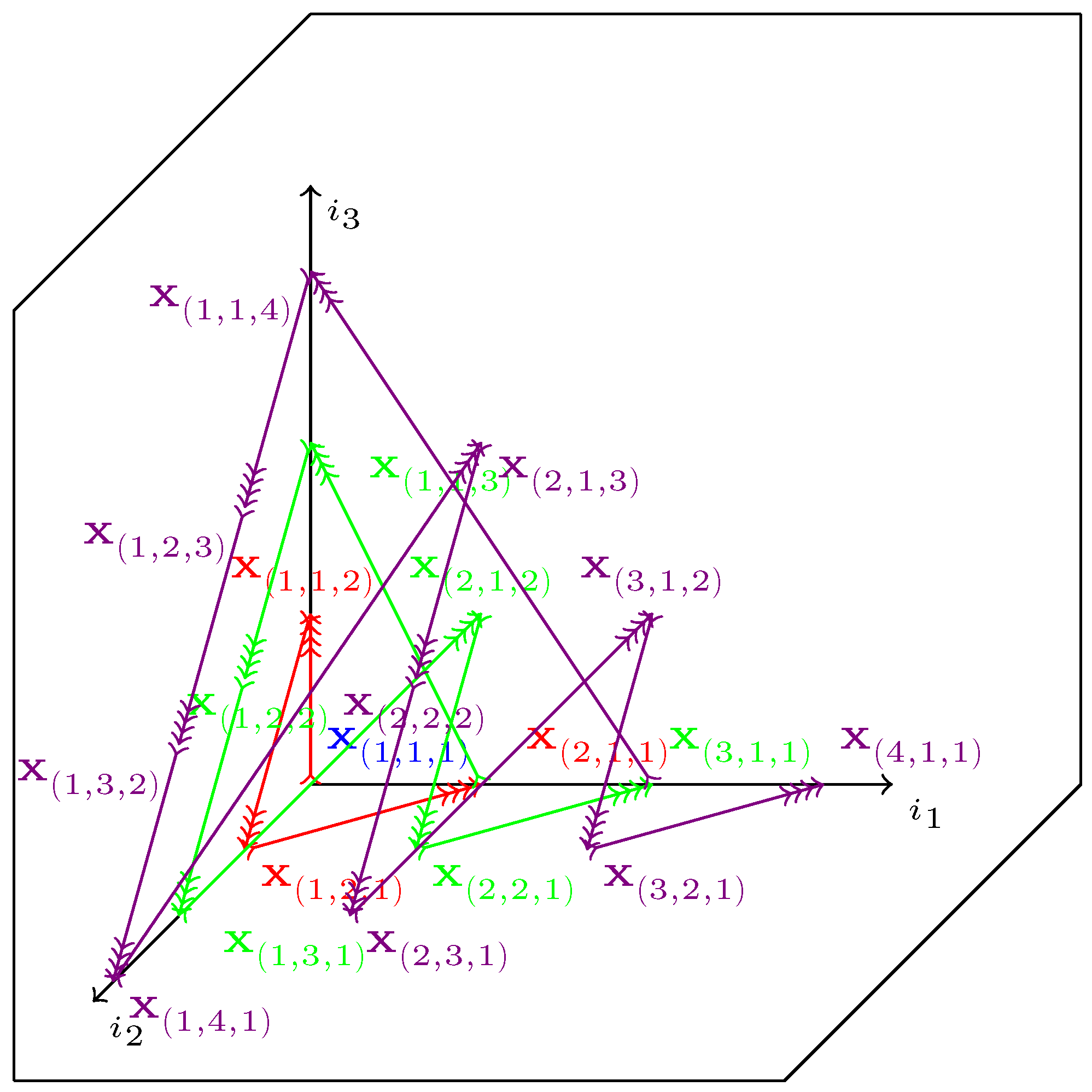
For illustration, let

$$\begin{array}{c}\hfill {\widehat{\mathbf{I}}}_n^3=\left\{(i_1,i_2,i_3)\mathrm{such}\mathrm{that}{i}_1+i_2+i_3\le n+2,i_1=1,\dots ,n;i_2=1,\dots ,n;i_3=1,\dots ,n\right\},\end{array}$$

$$\begin{array}{c}\hfill \left(i_1,i_2,i_3\right){\prec }_3\left(i_1^{\prime },i_2^{\prime },i_3^{\prime }\right)\iff \left\{\begin{array}{c}{i}_1+i_2+i_3=i_1^{\prime }+i_2^{\prime }+i_3^{\prime }\mathrm{and}\left\{\begin{array}{c}\{i_1=i_1^{\prime }\mathrm{and}{i}_2<i_2^{\prime }\}\hfill \\ \{i_1<i_1^{\prime }\}\hfill \end{array}\right.\hfill \\ i_1+i_2+i_3<i_1^{\prime }+i_2^{\prime }+i_3^{\prime }\hfill \end{array}\right.,\end{array}$$

and

$$\begin{array}{c}\hfill {\mathbf{S}}_l^3=\left\{{\mathbf{X}}_{(i_1,i_2,i_3)};i_1+i_2+i_3=l+2,\mathrm{for}l\in {\mathbb{N}}^{\ast }\right\}.\end{array}$$

For ${\displaystyle l=\{1,2,3\}}$, we have

$$\begin{array}{c}\hfill {\mathbf{S}}_1^3=\left\{{\mathbf{X}}_{(1,1,1)}\right\},\end{array}$$

$$\begin{array}{c}\hfill {\mathbf{S}}_1^{\ast 3}={\mathbf{X}}_{(1,1,1)},\end{array}$$

and

$$\begin{array}{c}\hfill \mathrm{Card}\left({\mathbf{S}}_1^3\right)=1.\end{array}$$

$$\begin{array}{c}\hfill {\mathbf{S}}_2^3=\{{\mathbf{X}}_{(1,1,2)},{\mathbf{X}}_{(1,2,1)},{\mathbf{X}}_{(2,1,1)}\},\end{array}$$

$$\begin{array}{c}\hfill {\mathbf{S}}_2^{\ast 3}={\mathbf{X}}_{(1,1,2)}+{\mathbf{X}}_{(1,2,1)}+{\mathbf{X}}_{(2,1,1)},\end{array}$$

and

$$\begin{array}{c}\hfill \mathrm{Card}\left({\mathbf{S}}_2^3\right)=3.\end{array}$$

$$\begin{array}{c}\hfill {\mathbf{S}}_3^3=\{{\mathbf{X}}_{(1,1,3)},{\mathbf{X}}_{(1,2,2)},{\mathbf{X}}_{(1,3,1)},{\mathbf{X}}_{(2,1,2)},{\mathbf{X}}_{(2,2,1)},{\mathbf{X}}_{(3,1,1)}\},\end{array}$$

$$\begin{array}{c}\hfill {\mathbf{S}}_3^{\ast 3}={\mathbf{X}}_{(1,1,3)}+{\mathbf{X}}_{(1,2,2)}+{\mathbf{X}}_{(1,3,1)}+{\mathbf{X}}_{(2,1,2)}+{\mathbf{X}}_{(2,2,1)}+{\mathbf{X}}_{(3,1,1)},\end{array}$$

and

$$\begin{array}{c}\hfill \mathrm{Card}\left({\mathbf{S}}_3^3\right)=6.\end{array}$$

From the iteration of this sequence, we deduce that

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_l^3\right)& =& \sum _{j=1}^{l}j\hfill \\ & =& \frac{l(l+1)}{2},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\omega }_n^3& =& \sum _{l=1}^n\mathrm{Card}\left({\mathbf{S}}_l^3\right)\hfill \\ & =& \sum _{l=1}^n\frac{l(l+1)}{2}\hfill \\ & =& \frac{n^3+3n^2+2n}{6}\hfill \\ & =& \mathcal{O}\left(n^3\right).\hfill \end{array}$$

We show the evolution of this concept through ${\displaystyle {\mathbf{S}}_j^{\ast 3}}$ for ${\displaystyle 1\le j\le 4}$, illustrated in Figure 1, Figure 2, Figure 3 and Figure 4.

To study the case for the four-dimensional random fields, put ${\displaystyle u_1=1,u_2=2,\dots ,u_j=j}$ and denote ${\displaystyle s_l\left(u\right)=\mathrm{Card}\left({\mathbf{S}}_l^3\right)}$ such that

$$\begin{array}{ccc}\hfill s_l\left(u\right)& =& \mathrm{Card}\left({\mathbf{S}}_l^3\right)\hfill \\ & =& \sum _{j=1}^l{u}_j\hfill \end{array}$$

Then, we obtain the following iteration:

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_2^4\right)& =& s_1\left(u\right)+s_2\left(u\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_3^4\right)& =& s_1\left(u\right)+s_2\left(u\right)+s_3\left(u\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_l^4\right)& =& s_1\left(u\right)+s_2\left(u\right)+\dots +s_l\left(u\right)\hfill \\ & =& \sum _{p=1}^l{s}_p\left(u\right)\hfill \\ & =& \sum _{p=1}^l\left(\sum _{j=1}^p\frac{j(j+1)}{2}\right)\hfill \\ & =& \sum _{j_2=1}^l\left(\sum _{j_1=1}^{j_2}\frac{j_1(j_1+1)}{2}\right)\hfill \\ & =& s\left(s_l\left(u\right)\right)\hfill \\ & =& s\circ s_l\left(u\right),\hfill \end{array}$$

where ${\displaystyle \circ }$ is the composition of the function.

Then,

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_l^4\right)& =& \frac{l^3+3l^2+2l}{6},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill {\omega }_n^4& =& \sum _{l=1}^n\frac{l^3+3l^2+2l}{6}\hfill \\ & =& \mathcal{O}\left(n^4\right).\hfill \end{array}$$

For five-dimensional random fields, we have

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_l^5\right)& =& \sum _{p=1}^l{s}_p\left(u\right)+\sum _{j=1}^{l-1}{s}_j\left(u\right)+\dots +\sum _{j=1}^3{s}_j\left(u\right)+\sum _{r=1}^2{s}_r\left(u\right)+s_1\left(u\right)\hfill \\ & =& \sum _{p=1}^l\left(\sum _{j=1}^p{s}_j\left(u\right)\right)\hfill \\ & =& \sum _{j_2=1}^l\left(\sum _{j_1=1}^{j_2}{s}_{j_1}\left(u\right)\right)\hfill \\ & =& s\left(s\left(s_l\left(u\right)\right)\right)\hfill \\ & =& s\circ s\circ s_l\left(u\right)\hfill \\ & =& s^{\left(2\right)}\circ s_l\left(u\right),\hfill \end{array}$$

where ${\displaystyle s^{\left(2\right)}\circ s_l\left(u\right)}$ is the second composition of ${\displaystyle s_l\left(u\right)}$.

For ${\displaystyle d}$-dimensional random fields, we deduce

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_l^d\right)& =& \sum _{j_{d-3}=1}^l\left(\sum _{j_{d-4}=1}^{j_{d-3}}...\left(\sum _{j_1=1}^{j_2}{s}_{j_1}\left(u\right)\right)\right)\hfill \\ & =& s^{(d-3)}\circ s_l\left(u\right).\hfill \end{array}$$

Then, the cardinal of the random fields in ${\displaystyle {\widehat{\mathbf{I}}}_n^d}$ is given by the formula

$$\begin{array}{ccc}\hfill {\omega }_n^d& =& \mathrm{Card}\left({\mathbf{S}}_1^d\right)+\mathrm{Card}\left({\mathbf{S}}_2^d\right)+\dots +\mathrm{Card}\left({\mathbf{S}}_n^d\right),\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill \mathrm{Card}\left({\mathbf{S}}_n^d\right)& =& \sum _{j_{d-3}=1}^n\left(\sum _{j_{d-4}=1}^{j_{d-3}}\dots \left(\sum _{j_1=1}^{j_2}{s}_{j_1}\left(u\right)\right)\right)\hfill \\ & =& \sum _{j_{d-3}=1}^n\left(\sum _{j_{d-4}=1}^{j_{d-3}}\dots \left(\sum _{j_1=1}^{j_2}\left(\sum _{p=1}^{j_1}\frac{p(p+1)}{2}\right)\right)\right)\hfill \\ & =& \sum _{j_{d-2}=1}^n\left(\sum _{j_{d-3}=1}^{j_{d-2}}\dots \left(\sum _{j_1=1}^{j_2}\left(\frac{j_1(j_1+1)}{2}\right)\right)\right)\hfill \\ & =& \sum _{j_{d-1}=1}^n\left(\sum _{j_{d-2}=1}^{j_{d-1}}\dots \left(\sum _{j_1=1}^{j_2}{j}_1\right)\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill =\mathcal{O}\left(\sum _{j_1=1}^n{j}_1^{d-1}\right).\end{array}$$

By using [24], we have

$$\begin{array}{ccc}\hfill \sum _{j=1}^n{j}^d& =& \frac{1}{d+1}\left({(n+1)}^{d+1}-1-\sum _{p=0}^{d-1}\left(\genfrac{}{}{0pt}{}{k+1}{p}\right)\sum _{p=1}^n{p}^d\right)\hfill \\ & =& \mathcal{O}\left({\left(n+1\right)}^{d+1}\right),\hfill \end{array}$$

then,

$$\begin{array}{c}\hfill {\omega }_n^d=\mathcal{O}\left(n^d\right).\end{array}$$

For the ${\displaystyle d}$-dimensional random fields, denote by ${\displaystyle {\mathbf{I}}_k^{†d}}$ the set of the ${\displaystyle k}$ first indices ${\displaystyle \{{\mathbf{i}}_1,{\mathbf{i}}_2,\dots ,{\mathbf{i}}_k\}}$ according to the order relation ${\displaystyle {\prec }_d}$. A sequence ${\displaystyle {\mathbf{I}}_k^d}$ of ${\displaystyle k}$ indices is called equivalent to ${\displaystyle {\mathbf{I}}_k^{†d}}$ if for each subset consisting of all indices which have the same first component, the next ${\displaystyle d-1}$ components starting from ${\displaystyle (1,1,\dots ,1)}$ are consecutive to the order: ${\displaystyle {\prec }_{d-1}}$.

Denote by ${\displaystyle {\mathcal{I}}_k^d=\{{\mathbf{I}}_k^d;{\mathbf{I}}_k^d\sim {\mathbf{I}}_k^{†d}\}}$ the set of ${\displaystyle k}$ indices equivalent to ${\displaystyle {\mathbf{I}}_k^{†d}}$. The random fields being ${\displaystyle i.i.d.}$, we deduce that

$$\begin{array}{c}\hfill P\left(\sum _{\mathbf{i}\in {\mathbf{I}}_k^d}{\mathbf{X}}_{\mathbf{i}}\le t\right)=P\left(\sum _{\mathbf{i}\in {\mathbf{I}}_k^{†d}}{\mathbf{X}}_{\mathbf{i}}\le t\right),\mathrm{for}\mathrm{any}{\mathbf{I}}_k^d\in {\mathcal{I}}_k^d.\end{array}$$

Let ${\displaystyle {\widehat{\mathbf{w}}}_n^d\left(k\right)}$ be the number defined by

$$\begin{array}{c}\hfill {\widehat{\mathbf{w}}}_n^d\left(k\right)=⌊\frac{{\omega }_n^d}{k}⌋,\end{array}$$

where ${\displaystyle ⌊x⌋}$ is the integer part of ${\displaystyle x}$.

A sequence of ${\displaystyle {\mathbf{i}}_{\mathbf{k}}=\{{\mathbf{i}}_1,\dots ,{\mathbf{i}}_k\}}$ of ${\displaystyle k}$ indices is called strictly ordered if, for each ${\displaystyle m}$, ${\displaystyle 1<m<k}$, it exists no index such that ${\displaystyle {\mathbf{i}}_m{\prec }_d\mathbf{i}{\prec }_d{\mathbf{i}}_{m+1}}$.

Two sequences of ${\displaystyle {\mathbf{i}}_{\mathbf{k}}}$ and ${\displaystyle {\mathbf{i}}_{\mathbf{k}}^{\prime }}$ of ${\displaystyle k}$ indices are called strictly consecutives if it exists no index ${\displaystyle \mathbf{i}}$ such that ${\displaystyle {\mathbf{i}}_k{\prec }_d\mathbf{i}{\prec }_d{\mathbf{i}}_{k+1}^{\prime }}$.

It exists ${\displaystyle {\widehat{\mathbf{w}}}_n^d\left(k\right)}$ sequences of ${\displaystyle k}$ strictly ordered indices which are strictly consecutives in the set ${\displaystyle {\widehat{\mathbf{I}}}_n^d}$ defined in (2) where ${\displaystyle \{1,\dots ,k\}}$ is the first index.

Denote by ${\displaystyle \{{\mathbf{I}}_{k,n}^{l,d},1\le l\le {\widehat{\mathbf{w}}}_n^d\left(k\right)\}}$ the set of these strictly consecutive sequences of ${\displaystyle k}$ indices in the set ${\displaystyle {\widehat{\mathbf{I}}}_n^d}$.

Now, put

$$\begin{array}{c}\hfill Y_{l,n}^{(k,d)}=\sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{(l,d)}}{\mathbf{X}}_{\mathbf{i}},\mathrm{for}1\le l\le {\widehat{\mathbf{w}}}_n^d\left(k\right).\end{array}$$

(3)

Note that the sequence ${\displaystyle \left\{Y_{l,n}^{(k,d)}\right\}}$ is a sequence of ${\displaystyle i.i.d.}$ random fields.

If we denote by ${\displaystyle S_n}$ the sum of ${\displaystyle n-}$first random fields according to the order relation ${\displaystyle {\prec }_d}$, define

$$N\left(t\right)=sup\{n,S_n\le t\}.$$

The process ${\displaystyle N\left(t\right)}$ is the number of events by time ${\displaystyle t}$ and called the counting process.

Let

$$\begin{array}{c}\hfill H\left(t\right)=E\left(N\left(t\right)\right),\end{array}$$

${\displaystyle H}$ is called renewal function.

Given a sequence of random fields ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}},}$${\displaystyle {\mathbf{X}}_{\mathbf{i}}}$ has a cumulative distribution function ${\displaystyle F_{\mathbf{i}}}$. Put ${\displaystyle F^{\left(k\right)}}$ the distribution function defined as follows:

$$\begin{array}{c}\hfill F^{\left(k\right)}\left(t\right)=P\left(S_k\le t\right).\end{array}$$

Since ${\displaystyle N\left(t\right)}$ is a process with integer value, then the renewal function can be also written by

$$\begin{array}{ccc}\hfill H\left(t\right)& =& \sum _{k=1}^{\infty }{F}^{\left(k\right)}\left(t\right).\hfill \end{array}$$

Let ${\displaystyle m=m\left(n\right)}$ be an integer sequence fulfilling ${\displaystyle m\left(n\right)\to \infty }$, as ${\displaystyle n\to \infty }$ and ${\displaystyle m\left(n\right)\le n}$, we estimate ${\displaystyle H}$ by an asymptotically unbiased estimator ${\displaystyle {\widehat{H}}_n}$ defined by

$$\begin{array}{c}\hfill {\widehat{H}}_n\left(t\right)=\sum _{k=1}^{m\left(n\right)}{\widehat{F}}_n^{\left(k\right)}\left(t\right),\end{array}$$

where ${\displaystyle {\widehat{F}}_n^{\left(k\right)}}$ is the unbiased estimator of the distribution function ${\displaystyle F^{\left(k\right)}}$ defined such as

$$\begin{array}{ccc}\hfill {\widehat{F}}_n^{\left(k\right)}\left(t\right)& =& \frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\mathbb{I}\left(\sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{(l,d)}}{\mathbf{X}}_{\mathbf{i}}\le t\right),\hfill \end{array}$$

and ${\displaystyle \mathbb{I}(.)}$ is the indicator function.

3. Concrete Application in Multidimensional Case

For application in the multidimensional case, we consider the propagation in France of a disease which is already spreading in another country and the penetration is between the departments. We suppose that the time to infect the individuals in France follows a law of a sequence of random fields ${\displaystyle {\mathbf{X}}_{(i_1,i_2,i_3)}}$. The index ${\displaystyle i_1}$ of the first component is the rank of an infected person. The second index ${\displaystyle i_2}$ is the sex of the infected person, ${\displaystyle i_2=1}$ for a male patient and ${\displaystyle i_2=2}$ for a female patient. The third index ${\displaystyle i_3}$ is the index of the department, ${\displaystyle i_3=1}$ for the department where a person is infected for the time in France. The first infected person in France follows the law ${\displaystyle {\mathbf{X}}_{(1,1,1)}}$ if this person is male and ${\displaystyle X_{(1,2,1)}}$ is this person is female. The law of ${\displaystyle X_{(1,1,1)}}$ or ${\displaystyle X_{(1,2,1)}}$ is the law of the time that it will take to this person to move from a validated healthy situation to an infected situation. Suppose that the first infected person is a male patient and the second infected person is a female person in another department, the time to be infected after the first infected person will follow the law of the random field ${\displaystyle X_{(1,2,2)}}$ and ${\displaystyle X_{(2,2,1)}}$ if this person is in the same department. The index of the infection time of the next infected individuals will be assigned to the same process. If we have two types of infections, such as flu and COVID-19, a person infected with one of the two types of infections becomes more susceptible to the other type of infection. In this case, we work with random fields for which ${\displaystyle d=4}$. The index ${\displaystyle i_4}$ is the index of the type of the infection, ${\displaystyle i_4=1}$ for the flu, and ${\displaystyle i_4=2}$ for COVID-19. For this type of application, the order of the path traveled by the contaminations will be random.

The contamination time of ${\displaystyle k}$ person follows a law of the sum of ${\displaystyle k}$ random fields such as ${\displaystyle \sum _{\mathbf{i}\in {\mathbf{I}}_k}{\mathbf{X}}_{\mathbf{i}}}$ where ${\displaystyle {\mathbf{I}}_k\in {\mathcal{I}}_k}$. ${\displaystyle N\left(t\right)}$, the number of infected individuals by time ${\displaystyle t}$ will be defined by

$$\begin{array}{c}\hfill N\left(t\right)=sup\left\{k,\sum _{\mathbf{i}\in {\mathbf{I}}_k}{\mathbf{X}}_{\mathbf{i}}\le t\right\}.\end{array}$$

The following results will make it possible to estimate the average time for ${\displaystyle k}$ people to be infected before a time ${\displaystyle t}$ and also to estimate the average number of people infected in the population before a time ${\displaystyle t.}$

There is another type of applications for which the path will be programmed. This could be the case in the telecommunications wherein the order of signals sent by or to different satellites must be programmed. In mining research or agriculture, the path order of the random fields can also be programmed.

4. Almost Sure Convergence of ${\displaystyle {\widehat{\mathit{F}}}_{\mathit{n}}^{\left(\mathit{k}\right)}\left(\mathit{t}\right)}$

In this section, we show the almost sure convergence of ${\displaystyle {\widehat{F}}_n^{\left(k\right)}}$, unbiaised estimator of ${\displaystyle F^{\left(k\right)}}$.

Theorem 1.

Let ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ be a sequence of ${\displaystyle i.i.d.}$ random fields and absolutely continuous positive. Suppose that the summation path of ${\displaystyle {\mathbf{X}}_{\mathbf{i}}}$ is ordered under Conditions (1) and (2); then, the process ${\displaystyle {\widehat{F}}_n^{\left(k\right)}\left(t\right)}$ converges almost surely to ${\displaystyle F^{\left(k\right)}\left(t\right)}$.

Proof. 

For ${\displaystyle n}$ sufficiently large, ${\displaystyle {\omega }_n^d\to \infty }$ implies that ${\displaystyle {\widehat{\mathbf{w}}}_n^d\left(k\right)\to \infty }$. Since ${\displaystyle {\left\{Y_{l,n}^{(k,d)}\right\}}_{1\le l\le {\widehat{\mathbf{w}}}_n^d\left(k\right)}}$ is a sequence of ${\displaystyle i.i.d.}$ random fields, by using the strong law of large number, we have

$$\begin{array}{c}\hfill \frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)\to E\left(\mathbb{I}\left(Y_{1,n}^{(k,d)}\le t\right)\right)\mathrm{almost}\mathrm{surely}.\end{array}$$

Then, ${\displaystyle \underset{n\to \infty }{lim}{\widehat{F}}_n^{\left(k\right)}\left(t\right)=F^{\left(k\right)}\left(t\right)}$ almost surely. ${\displaystyle \square }$

5. Almost Sure Convergence of ${\displaystyle {\widehat{\mathit{H}}}_{\mathit{n}}\left(\mathit{t}\right)}$

In this section, we investigate the almost sure convergence of the asymptotically unbiased estimator of the renewal function associated to the multidimensional random fields. The proofs are based on Lemma 1 stated below.

For a ${\displaystyle d}$-dimensional vector ${\displaystyle V=V^{\left(j\right)}(1\le j\le d)}$, we consider the norm defined by

$$\begin{array}{c}\hfill \left|\left|V\right|\right|=\underset{1\le j\le d}{max}\left|V^{\left(j\right)}\right|.\end{array}$$

Lemma 1

([25]). Let ${\displaystyle {\left(V_i\right)}_{i\ge 0}}$ be a sequence of ${\displaystyle d}$-dimensional centered absolutely regular and non-necessarily strictly stationary random vectors with rate satisfying

$$\begin{array}{c}\hfill \sum _{i\ge 0}{(i+1)}^{\frac{v}{2}}{\left(\beta \left(i\right)\right)}^{\frac{{\delta }_0}{{\delta }_0+2}}<\infty ,\end{array}$$

and

$$\begin{array}{c}\hfill \underset{i\ge 0}{sup}E\left({\left|\left|V_i\right|\right|}^{v+{\delta }_0}\right)<\infty ,\end{array}$$

(4)

for some ${\displaystyle v>0}$ and ${\displaystyle {\delta }_0>0}$.

Then,

$$\begin{array}{c}\hfill \frac{1}{n}\sum _{i=1}^n{V}_i\to 0withprobability1asn\to \infty .\end{array}$$

Since our random fields are ${\displaystyle i.i.d.}$, then the mixing coefficient ${\displaystyle \beta \left(i\right)}$ is equal to zero for all ${\displaystyle i\in {\mathbb{N}}^{\ast }}$.

For each ${\displaystyle k\ge 1}$, define

$$\begin{array}{c}\hfill m^{-1}\left(k\right)=inf\{n:m\left(n\right)\ge k\}.\end{array}$$

(5)

Theorem 2.

Let ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ be a sequence of ${\displaystyle i.i.d.}$ random fields and absolutely continuous positive. Suppose that the summation path of ${\displaystyle {\mathbf{X}}_{\mathbf{i}}}$ is ordered under Conditions (1) and (2). Suppose that either, for ${\displaystyle r>4}$

$$\begin{array}{c}\hfill n=\mathcal{O}\left(m^{r-4}\right).\end{array}$$

Then,

$$\begin{array}{c}\hfill \frac{1}{n}\left({\widehat{H}}_n\left(t\right)\to H\left(t\right)\right)almostsurely.\end{array}$$

Proof. 

We have

$$\begin{array}{ccc}\hfill \frac{1}{n}\left({\widehat{H}}_n\left(t\right)-H\left(t\right)\right)& =& \frac{1}{n}\left(\sum _{k=1}^m\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)-\sum _{k=1}^{\infty }{F}^{\left(k\right)}\left(t\right)\right)\hfill \\ & =& \frac{1}{n}\left(\sum _{k=1}^m\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)-\sum _{k=1}^m{F}^{\left(k\right)}\left(t\right)-\sum _{k>m}{F}^{\left(k\right)}\left(t\right)\right)\hfill \\ & =& \frac{1}{n}\left(\sum _{k=1}^m\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)-F^{\left(k\right)}\left(t\right)\right)-\sum _{k>m}{F}^{\left(k\right)}\left(t\right)\right)\hfill \\ & =& \frac{1}{n}\sum _{k=1}^m{V}_k-\frac{1}{n}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill V_k& =& \frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)-F^{\left(k\right)}\left(t\right)\right).\hfill \end{array}$$

We have to show that ${\displaystyle \frac{1}{n}\sum _{k=1}^m{V}_k}$ converges almost surely to zero by using Lemma 1 and ${\displaystyle \underset{n\to \infty }{lim}\frac{1}{n}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)=0}$ almost surely. To apply Lemma 1, we show only that the sequence ${\displaystyle V_k}$ satisfies Condition (4). Using the well-known inequality

$$\begin{array}{c}\hfill {\left|a+b\right|}^l\le 2^l\left({\left|a\right|}^l+{\left|b\right|}^l\right),\end{array}$$

(6)

we have

$$\begin{array}{ccc}\hfill \underset{k\ge 0}{sup}E{\left|V_k\right|}^{v+{\delta }_0}& \le & 2^{v+{\delta }_0}(E{\left|\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right|}^{v+{\delta }_0}\hfill \\ & +& {\left|\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{F}^{\left(k\right)}\left(t\right)\right|}^{v+{\delta }_0}),\hfill \end{array}$$

(7)

To continue the proofs, we need the following lemma. ${\displaystyle \square }$

Lemma 2.

Let ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ be a sequence of random fields such that ${\displaystyle E|{\mathbf{X}}_{\mathbf{i}}{|}^r<\infty }$, ${\displaystyle r>4}$, ${\displaystyle E\left({\mathbf{X}}_{\mathbf{i}}\right)>0}$ for each ${\displaystyle \mathbf{i}\in {\mathbb{N}}^{\ast d}}$,

$$\begin{array}{c}\hfill P\left(S_k\le t\right)\le \mathcal{O}\left(k^{-\frac{r}{2}}\right),fort>0.\end{array}$$

(8)

Proof. 

Put ${\displaystyle E\left({\mathbf{X}}_{\mathbf{i}}\right)=\mu }$ and choose ${\displaystyle \epsilon }$ sufficiently small such that ${\displaystyle \epsilon <\mu }$ and ${\displaystyle t\le (\mu -\epsilon )k}$, by using Markov’s inequality, we have

$$\begin{array}{ccc}\hfill P\left\{\left|S_k-k\mu \right|\ge k\epsilon \right\}& =& P\left\{{\left|S_k-k\mu \right|}^r\ge {\left(k\epsilon \right)}^r\right\}\hfill \\ & \le & \frac{1}{{\left(k\epsilon \right)}^r}E\left({\left|S_k-k\mu \right|}^r\right).\hfill \end{array}$$

Put ${\displaystyle {\check{\mathbf{X}}}_{\mathbf{i}}={\mathbf{X}}_{\mathbf{i}}-\mu }$, we have

$$\begin{array}{ccc}\hfill P\left\{\left|S_k-k\mu \right|\ge k\epsilon \right\}& \le & \frac{1}{{\left(k\epsilon \right)}^r}\left(E{\left|{\check{S}}_k\right|}^r\right).\hfill \end{array}$$

where ${\displaystyle {\check{S}}_k}$ is the sum of ${\displaystyle k}$-first of ${\displaystyle {\check{\mathbf{X}}}_{\mathbf{i}}}$.

Since ${\displaystyle {\left({\check{\mathbf{X}}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ is a sequence of centered random fields, from the moment inequality of Yokohama [26], we deduce that there exists a positive constant ${\displaystyle C}$ such that

$$\begin{array}{c}\hfill E{\left|{\check{S}}_k\right|}^r<{Ck}^{\frac{r}{2}}.\end{array}$$

(9)

Then,

$$\begin{array}{ccc}\hfill P\left\{\left|S_k-k\mu \right|\ge k\epsilon \right\}& \le & \frac{C}{{\left(k\epsilon \right)}^r}{k}^{\frac{r}{2}}\hfill \\ & =& \frac{C}{{\epsilon }^r}{k}^{-\frac{r}{2}}.\hfill \end{array}$$

As

$$\begin{array}{c}\hfill \left|S_k-k\mu \right|\ge k\epsilon \iff \left\{\begin{array}{cc}{S}_k-k\mu \ge k\epsilon \hfill & \hfill \\ S_k-k\mu \le -k\epsilon .\hfill & \hfill \end{array}\right.\end{array}$$

By using the particular inequality ${\displaystyle S_k-k\mu \le -k\epsilon }$, we have

$$P\left(S_k\le (\mu -\epsilon )k\right)\le \frac{C}{{\epsilon }^r}{k}^{-\frac{r}{2}}.$$

For ${\displaystyle k}$ sufficiently large,

$$\begin{array}{ccc}\hfill F^{\left(k\right)}\left(t\right)& =& P\left(S_k\le t\right)\hfill \\ & \le & P\left(S_k\le (\mu -\epsilon )k\right)\hfill \\ & \le & \mathcal{O}\left(k^{-\frac{r}{2}}\right).\hfill \end{array}$$

It achieves the proof of Lemma 2. ${\displaystyle \square }$

Now, we continue the proof Theorem 2. From (7) and (8), we have

$$\begin{array}{ccc}\hfill {\left|\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{F}^{\left(k\right)}\left(t\right)\right|}^{v+{\delta }_0}& =& {\left|k^{-\frac{r}{2}}\right|}^{v+{\delta }_0}\hfill \\ & <& \infty .\hfill \end{array}$$

(10)

From Inequality (6), we have

$$\begin{array}{c}\hfill {\left|\sum _{l=1}^{\mathbf{w}}{Y}_l\right|}^p\le 2^{(\mathbf{w}-1)p}{\left|Y_{\mathbf{w}-1}\right|}^p+2^{(\mathbf{w}-2)p}{\left|Y_{\mathbf{w}-2}\right|}^p+\dots +2^p{\left|Y_1\right|}^p.\end{array}$$

(11)

To apply this inequality, put ${\displaystyle p=v+{\delta }_0}$, ${\displaystyle \mathbf{w}={\widehat{\mathbf{w}}}_n^d\left(k\right)}$ and ${\displaystyle Y_l=\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)}$; then,

$$\begin{array}{ccc}\hfill E{\left|\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right|}^{v+{\delta }_0}& =& E{\left|\frac{1}{\mathbf{w}}\sum _{l=1}^{\mathbf{w}}\mathbb{I}\left(Y_l\le t\right)\right|}^p.\hfill \end{array}$$

Using (11), we have

$$\begin{array}{ccc}\hfill E{\left|\frac{1}{\mathbf{w}}\sum _{l=1}^{\mathbf{w}}\mathbb{I}\left(Y_l\le t\right)\right|}^p& \le & \frac{2^{\left(\mathbf{w}-1\right)p}}{{\mathbf{w}}^p}E{\left|\mathbb{I}\left(Y_{\mathbf{w}-1}\le t\right)\right|}^p+\frac{2^{(\mathbf{w}-2)p}}{{\mathbf{w}}^p}E{\left|\mathbb{I}\left(Y_{\mathbf{w}-2}\le t\right)\right|}^p\hfill \\ & +& \dots +\frac{2^p}{{\mathbf{w}}^p}E{\left|\mathbb{I}\left(Y_1\le t\right)\right|}^p\hfill \\ & =& \frac{2^{\left(\mathbf{w}-1\right)p}}{{\mathbf{w}}^p}E\left|\mathbb{I}\left(Y_{\mathbf{w}-1}\le t\right)\right|+\frac{2^{(\mathbf{w}-2)p}}{{\mathbf{w}}^p}E\left|\mathbb{I}\left(Y_{\mathbf{w}-2}\le t\right)\right|\hfill \\ & +& \dots +\frac{2^p}{{\mathbf{w}}^p}E\left|\mathbb{I}\left(Y_1\le t\right)\right|\hfill \\ & =& \frac{1}{{\mathbf{w}}^p}\sum _{l=1}^{\mathbf{w}}{2}^{kp}{F}^{\left(k\right)}\left(t\right)\hfill \\ & \le & \frac{1}{{\mathbf{w}}^{p-1}}{2}^{kp}{k}^{-\frac{r}{2}}.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill E{\left|\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right|}^{v+{\delta }_0}& \le & \frac{2^{k(v+{\delta }_0)}{k}^{-\frac{r}{2}}}{{\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}^{v+{\delta }_0-1}}\hfill \\ & =& 2^{k(v+{\delta }_0)}{k}^{-\frac{r}{2}}\mathcal{O}{\left(n^{-d}\right)}^{v+{\delta }_0-1}\hfill \\ & \to & 0\hfill \end{array}$$

(12)

Conditions (10) and (12) are sufficient to prove Condition (4) and ${\displaystyle \frac{1}{m}\sum _{k=1}^m{V}_k\to 0}$ almost surely. From Lemma 1, we deduce that ${\displaystyle \frac{1}{n}\sum _{k=1}^m{V}_k}$ converges almost surely to 0 as ${\displaystyle n\to \infty }$ because ${\displaystyle \frac{1}{n}\sum _{k=1}^m{V}_k\le \frac{1}{m}\sum _{k=1}^m{V}_k}$.

Finally, we show that ${\displaystyle \underset{n\to \infty }{lim}\frac{1}{n}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)=0}$ almost surely.

Since ${\displaystyle n=\mathcal{O}\left(m^{r-4}\right)}$ implies ${\displaystyle m^{-1}\left(n\right)=\mathcal{O}\left(n^{r-4}\right)}$

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}\frac{1}{n}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)& =& \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}{k}^{-r+4}{F}^{\left(k\right)}\left(t\right)\right)\hfill \\ & =& \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}{k}^{-r+4}{k}^{-\frac{r}{2}}\right)\hfill \\ & =& \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}{k}^{\frac{-3r+8}{2}}\right)\hfill \\ & =& 0,\mathrm{almost}\mathrm{surely}.\hfill \end{array}$$

This achieves the proof of Theorem 2.

6. Asymptotic Normality of ${\displaystyle {\widehat{\mathit{F}}}_{\mathit{n}}^{\left(\mathit{k}\right)}\left(\mathit{t}\right)}$

We establish the central limit theorem of the empirical estimator ${\displaystyle {\widehat{F}}_n^{\left(k\right)}}$ by using the convergence of the characteristic function, and we show that its second-order moments of Taylor expansion converge to a characteristic function of a Gaussian random variable and the order higher than the fourth order converges to zero.

Theorem 3.

Let ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ be a sequence of ${\displaystyle i.i.d.}$ random fields and absolutely continuous positive, ordered under Conditions (1) and (2), the process ${\displaystyle n^{\frac{d}{2}}\left({\widehat{F}}_n^{\left(k\right)}\left(t\right)-F^{\left(k\right)}\left(t\right)\right)}$, ${\displaystyle t>0}$, converges in distribution to ${\displaystyle \mathcal{N}(0,{\sigma }_k^2)}$ where ${\displaystyle \mathcal{N}}$ is the centered normal random variable with variance defined by ${\displaystyle {\sigma }_k^2=F^{\left(k\right)}\left(t\right)\left(1-F^{\left(k\right)}\left(t\right)\right)}$.

Proof. 

We have

$$\begin{array}{ccc}\hfill n^{\frac{d}{2}}\left({\widehat{F}}_n^{\left(k\right)}\left(t\right)-F^{\left(k\right)}\left(t\right)\right)& =& n^{\frac{d}{2}}\left(\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\mathbb{I}\left(\sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{(l,d)}}{\mathbf{X}}_{\mathbf{i}}\le t\right)-F^{\left(k\right)}\left(t\right)\right)\hfill \\ \\ & =& \frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(\sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{(l,d)}}{\mathbf{X}}_{\mathbf{i}}\le t\right)-F^{\left(k\right)}\left(t\right)\right)\hfill \\ \\ & =& \frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)-F^{\left(k\right)}\left(t\right)\right),\hfill \end{array}$$

where ${\displaystyle Y_{l,n}^{(k,d)}}$ is the ${\displaystyle i.i.d.}$ random fields defined in (3).

Now, put ${\displaystyle \left\{A_{l,n}^{(k,d)}\right\}}$ the sequence of ${\displaystyle i.i.d.}$ random fields defined as follows:

$$\begin{array}{ccc}\hfill A_{l,n}^{(k,d)}& =& \mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)-F^{\left(k\right)}\left(t\right),\mathrm{for}\mathrm{all}1\le l\le {\widehat{\mathbf{w}}}_n\left(k\right).\hfill \end{array}$$

(13)

Let ${\displaystyle {\varphi }_n}$ be the characteristic function of the process ${\displaystyle n^{\frac{d}{2}}\left({\widehat{F}}_n^{\left(k\right)}\left(t\right)-F^{\left(k\right)}\left(t\right)\right)}$ such that

$$\begin{array}{ccc}\hfill {\varphi }_n\left(u\right)& =& E\left(exp\left(iu{n}^{\frac{d}{2}}\left(\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\mathbb{I}\left(\sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{(l,d)}}{\mathbf{X}}_{\mathbf{i}}\le t\right)-F^{\left(k\right)}\left(t\right)\right)\right)\right),u\in \mathbb{R},\hfill \end{array}$$

where ${\displaystyle i}$ is the complex number unity. We have to show that ${\displaystyle {\varphi }_n}$ converges in distribution to a Gaussian characteristic function ${\displaystyle \varphi }$ of a centered random variable.

From the Taylor expansion neighborhood of zero,

$$\begin{array}{ccc}E\left(e^{iu{A}_{l,n}^{(k,d)}}\right)\hfill & =\hfill & 1+\left(iu\right)E\left(A_{l,n}^{(k,d)}\right)+\frac{{\left(iu\right)}^{2}E{\left(A_{l,n}^{(k,d)}\right)}^2}{2!}+\dots +\frac{{\left(iu\right)}^{n}E{\left(A_{l,n}^{(k,d)}\right)}^n}{n!}\hfill \\ \\ & +\hfill & o\left({\left|u\right|}^n\right),\hfill \end{array}$$

(14)

and

$$\begin{array}{c}\hfill ln(1-u)=-u-\frac{u^2}{2}+o\left({\left|u\right|}^2\right),\end{array}$$

(15)

we have

$$\begin{array}{ccc}\hfill exp\left[ln\left({\varphi }_n\left(u\right)\right)\right]& =& exp\left(ln\left(E\left(exp\left(\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(\mathbf{k}\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(\mathbb{I}\left(\sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{(l,d)}}{\mathbf{X}}_{\mathbf{i}}\le t\right)-F^{\left(k\right)}\left(t\right)\right)\right)\right)\right)\right)\hfill \\ & =& exp\left(ln\left(E\left(exp\left(\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{l,n}^{(k,d)}\right)\right)\right)\right)\hfill \\ & =& exp\left(ln{\left(E\left(exp\left(\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{l,n}^{(k,d)}\right)\right)\right)\right)}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right)\hfill \\ & =& exp\left({\widehat{\mathbf{w}}}_n^d\left(k\right)ln\left(E\left(exp\left(\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{l,n}^{(k,d)}\right)\right)\right)\right)\hfill \\ & =& exp\left({\widehat{\mathbf{w}}}_n^d\left(k\right)ln\left(1-\frac{u^2{n}^d}{2{\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}^2}E{\left(A_{l,n}^{(k,d)}\right)}^2\right)+o\left(\left|\frac{u^2}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|\right)\right)\hfill \\ & =& exp(-\frac{u^2{n}^d{\widehat{\mathbf{w}}}_n^d\left(k\right)}{2{\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}^2}E{\left(A_{l,n}^{(k,d)}\right)}^2-\frac{u^4{n}^{2d}\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}{8{\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}^4}{\left(E{\left(A_{l,n}^{(k,d)}\right)}^2\right)}^2\hfill \\ & +& o\left({\left|\frac{u}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|}^4\right)).\hfill \end{array}$$

We can easily show that the order higher than the term ${\displaystyle \frac{u^4{n}^{2d}\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}{8{\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)}^4}{\left(E{\left(A_{l,n}^{(k,d)}\right)}^2\right)}^2+o\left({\left|\frac{u}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|}^4\right)}$ converges to zero for ${\displaystyle n}$ sufficiently large because ${\displaystyle \mathcal{O}\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)=n^d}$.

From (13),

$$\begin{array}{ccc}\hfill E{\left(A_{l,n}^{(k,d)}\right)}^2& =& E{\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)-F^{\left(k\right)}\left(t\right)\right)}^2\hfill \\ \\ & =& E\left({\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)}^2-2\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)F^{\left(k\right)}\left(t\right)+{\left(F^{\left(k\right)}\left(t\right)\right)}^2\right)\hfill \\ \\ & =& E\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)-2E\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)\right)F^{\left(k\right)}\left(t\right)+{\left(F^{\left(k\right)}\left(t\right)\right)}^2\hfill \\ \\ & =& F^{\left(k\right)}\left(t\right)-{\left(F^{\left(k\right)}\left(t\right)\right)}^2\hfill \\ \\ & =& F^{\left(k\right)}\left(t\right)\left(1-F^{\left(k\right)}\left(t\right)\right)\hfill \\ \\ & =& {\sigma }_k^2.\hfill \end{array}$$

Then, for ${\displaystyle n}$ sufficiently large, ${\displaystyle \underset{n\to \infty }{lim}exp\left(ln\left({\varphi }_n\left(u\right)\right)\right)\to exp\left(-\frac{u^2}{2}{\sigma }_k^2\right)}$.

To conclude, the characteristic function of ${\displaystyle n^{\frac{d}{2}}\left({\widehat{F}}_n^{\left(k\right)}\left(t\right)-F^{\left(k\right)}\left(t\right)\right)}$ converges in distribution to the characteristic function of the Gaussian centered random variable with variance ${\displaystyle {\sigma }_k^2}$. This achieves the proof of Theorem 3. ${\displaystyle \square }$

7. Asymptotic Normality of ${\displaystyle {\widehat{\mathit{H}}}_{\mathit{n}}\left(\mathit{t}\right)}$

We study the central limit theorem of the empirical estimator ${\displaystyle {\widehat{H}}_n}$ associated to the multidimensional random fields.

For ${\displaystyle \{{\mathbf{i}}_1,{\mathbf{i}}_2,\dots ,{\mathbf{i}}_k\}}$ and ${\displaystyle \{{\mathbf{j}}_1,{\mathbf{j}}_2,\dots ,{\mathbf{j}}_{k^{\prime }}\}}$, two subsets of ${\displaystyle {{\mathbb{N}}^{\ast }}^d}$ that have ${\displaystyle u\le min(k,k^{\prime })}$ elements in common, we define

$$\begin{array}{c}\hfill F_u^{(k,k^{\prime })}\left(t\right)=P\left(({\mathbf{X}}_{{\mathbf{i}}_1}+{\mathbf{X}}_{{\mathbf{i}}_2}+\dots +{\mathbf{X}}_{{\mathbf{i}}_k}\le t)\cap ({\mathbf{X}}_{{\mathbf{j}}_1}+{\mathbf{X}}_{{\mathbf{j}}_2}+\dots +{\mathbf{X}}_{{\mathbf{j}}_{k^{\prime }}}\le t)\right)\end{array}$$

and

$$\begin{array}{c}\hfill {\xi }_{k{k}^{\prime }}\left(c\right)=\mathrm{Cov}\left(F^{(k-c)}\left(t-({\mathbf{X}}_{{\mathbf{i}}_1}+\dots +{\mathbf{X}}_{{\mathbf{i}}_c})\right),F^{(k^{\prime }-c)}\left(t-({\mathbf{X}}_{{\mathbf{j}}_1}+\dots +{\mathbf{X}}_{{\mathbf{j}}_c})\right)\right).\end{array}$$

We state the result after the following lemma.

Lemma 3.

If Condition (16) is satisfied, then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{n}^{\frac{d}{2}}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)=0.\end{array}$$

Proof. 

From Condition (5), ${\displaystyle n=\mathcal{O}\left(m^{\frac{r-4}{d}}\right)}$ implies ${\displaystyle m^{-1}\left(n\right)=\mathcal{O}\left(n^{\frac{r-4}{d}}\right)}$ and from Condition (16), we obtain

$$\begin{array}{ccc}\hfill n^{\frac{d}{2}}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)& =& \mathcal{O}\left(\sum _{k>m}{k}^{\frac{r-4}{2}}{F}^{\left(k\right)}\left(t\right)\right).\hfill \end{array}$$

Using Lemma 2, we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{n}^{\frac{d}{2}}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)& =& \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}{k}^{\frac{r-4}{2}}{F}^{\left(k\right)}\left(t\right)\right)\hfill \\ & \le & \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}{k}^{\frac{r-4}{2}-\frac{r}{2}}\right)\hfill \\ & \le & \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}{k}^{-2}\right)\hfill \\ & \le & \underset{n\to \infty }{lim}\mathcal{O}\left(\sum _{k>m}\frac{1}{k^2}\right)\hfill \\ & =& 0.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{n}^{\frac{d}{2}}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)=0.\end{array}$$

This achieves the proof of Lemma 3. ${\displaystyle \square }$

Theorem 4.

Let ${\displaystyle {\left({\mathbf{X}}_{\mathbf{i}}\right)}_{\mathbf{i}\in {\mathbb{N}}^{\ast d}}}$ be a sequence of ${\displaystyle i.i.d.}$ random fields and absolutely continuous positive, ordered under Conditions (1) and (2). Suppose that, for ${\displaystyle r>4}$,

$$\begin{array}{c}\hfill E{\left|{\mathbf{X}}_{\mathbf{i}}\right|}^r<\infty \mathrm{and}n=\mathcal{O}\left(m^{\frac{r-4}{d}}\right)\end{array}$$

(16)

then, the process ${\displaystyle n^{\frac{d}{2}}\left({\widehat{H}}_n\left(t\right)-H\left(t\right)\right)}$, ${\displaystyle t>0}$, converges in distribution to ${\displaystyle \mathcal{N}(0,{\varsigma }^2)}$, where ${\displaystyle \mathcal{N}}$ is the centered normal random variable with variance defined as

$$\begin{array}{c}\hfill {\varsigma }^2=\sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }{\xi }_{k{k}^{\prime }}\left(c\right).\end{array}$$

Proof. 

We use the ideas of the proof of Theorem 3, denote ${\displaystyle {\mathrm{\Psi }}_n}$ the characteristic function of the process ${\displaystyle n^{\frac{d}{2}}\left({\widehat{H}}_n\left(t\right)-H\left(t\right)\right)}$. We have

$$\begin{array}{ccc}{n}^{\frac{d}{2}}\left({\widehat{H}}_n\left(t\right)-H\left(t\right)\right)\hfill & =\hfill & n^{\frac{d}{2}}\left({\displaystyle \sum _{k=1}^m}\frac{1}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{\displaystyle \sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}}\mathbb{I}\left({\displaystyle \sum _{\mathbf{i}\in {\mathbf{I}}_{k,n}^{\left(l\right)}}}{\mathbf{X}}_{\mathbf{i}}\le t\right)-F^{\left(k\right)}\left(t\right)\right)-n^{\frac{d}{2}}{\displaystyle \sum _{k>m}}{F}^{\left(k\right)}\left(t\right)\hfill \\ & =\hfill & {\displaystyle \sum _{k=1}^m}\left(\frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{\displaystyle \sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}}\left(\mathbb{I}\left(Y_{l,n}^{(k,d)}\le t\right)-F^{\left(k\right)}\left(t\right)\right)\right)-n^{\frac{d}{2}}{\displaystyle \sum _{k>m}}{F}^{\left(k\right)}\left(t\right)\hfill \\ \\ & =\hfill & {\displaystyle \sum _{k=1}^m}\frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{\displaystyle \sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}}{A}_{l,n}^{(k,d)}-n^{\frac{d}{2}}{\displaystyle \sum _{k>m}}{F}^{\left(k\right)}\left(t\right),\hfill \end{array}$$

(17)

where ${\displaystyle {\left\{A_{l,n}^{(k,d)}\right\}}_{1\le l\le {\widehat{\mathbf{w}}}_n\left(k\right)}}$ is the sequence of random fields defined in (13).

We have showed that ${\displaystyle n^{\frac{d}{2}}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)}$ is negligible from Lemma 3.

From (17), since ${\displaystyle \underset{n\to \infty }{lim}{n}^{\frac{d}{2}}\sum _{k>m}{F}^{\left(k\right)}\left(t\right)=0}$, we have

$$\begin{array}{ccc}\hfill {\mathrm{\Psi }}_n\left(u\right)& =& exp\left(ln\left({\mathrm{\Psi }}_n\left(u\right)\right)\right)\hfill \\ & =& exp\left(ln\left(E\left(exp\left(iu{n}^{\frac{d}{2}}\left({\widehat{H}}_n\left(t\right)-H\left(t\right)\right)\right)\right)\right)\right)\hfill \\ & =& exp\left(ln\left(E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\sum _{l=1}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{l,n}^{(k,d)}\right)\right)\right)\right)\hfill \\ & =& exp\left(ln\left(E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{1,n}^{\left(k\right)}+\dots +\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{{\widehat{\mathbf{w}}}_n^d\left(k\right),n}^{\left(k\right)}\right)\right)\right)\right)\hfill \\ & =& exp(ln(E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{1,n}^{(k,d)}\right)\right)\times \dots \hfill \\ & \times & E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{{\widehat{\mathbf{w}}}_n^d\left(k\right),n}^{(k,d)}\right)\right)\left)\right)\hfill \\ & =& exp\left(ln{\left(E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{1,n}^{(k,d)}\right)\right)\right)}^{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right)\hfill \\ & =& exp\left({\widehat{\mathbf{w}}}_n^d\left(k\right)ln\left(E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{1,n}^{(k,d)}\right)\right)\right)\right).\hfill \end{array}$$

and by using successively the expansion formula in (14) and (15), we obtain

$$\begin{array}{ccc}\hfill E\left(exp\left(\sum _{k=1}^m\frac{iu{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}{A}_{1,n}^{(k,d)}\right)\right)& =& 1-\frac{1}{2}E{\left(\sum _{k=1}^m\frac{u{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{1,n}^{(k,d)}\right)\right)}^2+o\left({\left|\sum _{k=1}^m\frac{u}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|}^2\right).\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill exp\left(ln\left({\mathrm{\Psi }}_n\left(u\right)\right)\right)& =& exp({\widehat{\mathbf{w}}}_n^d\left(k\right)ln\left(1-\frac{1}{2}E{\left(\sum _{k=1}^m\frac{u{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{1,n}^{(k,d)}\right)\right)}^2\right)\hfill \\ & +& o\left({\left|\sum _{k=1}^m\frac{u}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|}^2\right))\hfill \\ & =& exp(-\frac{1}{2}{\widehat{\mathbf{w}}}_n^d\left(k\right)E{\left(\sum _{k=1}^m\frac{u{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{1,n}^{(k,d)}\right)\right)}^2\hfill \\ & -& \frac{1}{8}{\widehat{\mathbf{w}}}_n^d\left(k\right)E{\left(\sum _{k=1}^m\frac{u{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{1,n}^{(k,d)}\right)\right)}^4+{\widehat{\mathbf{w}}}_n^d\left(k\right)\times o\left({\left|\sum _{k=1}^m\frac{u{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|}^4\right))\hfill \\ & =& exp\left(-\frac{u^2}{2}{Q}_n\left(k\right)-\frac{u^4}{8}{K}_n\left(k\right)+o\left({\widehat{\mathbf{w}}}_n^d\left(k\right){\left|\sum _{k=1}^m\frac{u{n}^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\right|}^4\right)\right).\hfill \end{array}$$

where

$$\begin{array}{c}\hfill Q_n\left(k\right)={\widehat{\mathbf{w}}}_n^d\left(k\right)E{\left(\sum _{k=1}^m\frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{l,n}^{(k,d)}\right)\right)}^2,\end{array}$$

and

$$\begin{array}{c}\hfill K_n\left(k\right)={\widehat{\mathbf{w}}}_n^d\left(k\right)E{\left(\sum _{k=1}^m\frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{l,n}^{(k,d)}\right)\right)}^4.\end{array}$$

We have to show that ${\displaystyle \underset{n\to \infty }{lim}{Q}_n\left(k\right)}$ is finite and the quantity ${\displaystyle K_n\left(k\right)}$ converges to zero for ${\displaystyle n}$ sufficiently large.

Since

$$\begin{array}{c}\hfill \mathcal{O}\left({\widehat{\mathbf{w}}}_n^d\left(k\right)\right)\simeq n^d,\end{array}$$

(18)

then,

$$\begin{array}{c}\hfill \frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\simeq \frac{1}{n^{\frac{d}{2}}}.\end{array}$$

(19)

and

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{Q}_n\left(k\right)& =& \underset{n\to \infty }{lim}{\widehat{\mathbf{w}}}_n^d\left(k\right)E{\left(\sum _{k=1}^m\frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{l,n}^{(k,d)}\right)\right)}^2\hfill \\ & \simeq & \underset{n\to \infty }{lim}{n}^{d}E{\left(\sum _{k=1}^m\frac{1}{n^{\frac{d}{2}}}\left(A_{l,n}^{(k,d)}\right)\right)}^2\hfill \\ & =& \underset{n\to \infty }{lim}\frac{n^d}{n^d}E{\left(\sum _{k=1}^m\left(A_{l,n}^{(k,d)}\right)\right)}^2.\hfill \\ & =& \underset{n\to \infty }{lim}E{\left(\sum _{k=1}^m\left(A_{l,n}^{(k,d)}\right)\right)}^2\hfill \\ & =& \underset{n\to \infty }{lim}\mathrm{Cov}\left(\sum _{k=1}^m{A}_{l,n}^{(k,d)},\sum _{k^{\prime }=1}^m{A}_{l,n}^{(k^{\prime },d)}\right)\hfill \\ & =& \underset{n\to \infty }{lim}\sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }\left(E\right(\mathbb{I}({\mathbf{X}}_{{\mathbf{i}}_1}+{\mathbf{X}}_{{\mathbf{i}}_2}+\dots +{\mathbf{X}}_{{\mathbf{i}}_k}\le t)\hfill \\ & \times & \mathbb{I}({\mathbf{X}}_{{\mathbf{j}}_1}+{\mathbf{X}}_{{\mathbf{j}}_2}+\dots +{\mathbf{X}}_{{\mathbf{j}}_{k^{\prime }}}\le t))-F^{\left(k\right)}\left(t\right)F^{\left(k^{\prime }\right)}\left(t\right))\hfill \\ & =& \sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }\left(F_c^{(k,k^{\prime })}\left(t\right)-F^{\left(k\right)}\left(t\right)F^{\left(k^{\prime }\right)}\left(t\right)\right)\hfill \\ & =& \sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }{\xi }_{k{k}^{\prime }}\left(c\right).\hfill \end{array}$$

Then,

$$\begin{array}{c}\hfill E{\left(\sum _{k=1}^m\left(A_{l,n}^{(k,d)}\right)\right)}^2=\sum _{k=1}^m\sum _{k^{\prime }=1}^m{\xi }_{k{k}^{\prime }}\left(c\right).\end{array}$$

Thus,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{Q}_n\left(k\right)=\sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }{\xi }_{k{k}^{\prime }}\left(c\right).\end{array}$$

From the condition

$$\begin{array}{c}\hfill F_c^{(k,k^{\prime })}\left(t\right)\le min\left(F^{\left(k\right)}\left(t\right),F^{\left(k^{\prime }\right)}\left(t\right)\right),\end{array}$$

and

$$\begin{array}{ccc}\hfill \sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }{F}^{\left(k\right)}\left(t\right)F^{\left(k^{\prime }\right)}\left(t\right)& =& \sum _{k=1}^{\infty }\sum _{k=1}^{\infty }\mathcal{O}\left(k^{-\frac{r}{2}}{k^{\prime }}^{-\frac{r}{2}}\right)\hfill \\ & =& \sum _{k_1=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }\frac{1}{k^{\frac{r}{2}}}\frac{1}{{k^{\prime }}^{\frac{r}{2}}}\hfill \\ & <& \infty ,\hfill \end{array}$$

because ${\displaystyle \sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }\frac{1}{k^{\frac{r}{2}}}\frac{1}{{k^{\prime }}^{\frac{r}{2}}}}$ is a convergent Riemann’s series under the condition ${\displaystyle r>4}$, we deduce that the variance ${\displaystyle \sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }{\xi }_{k{k}^{\prime }}\left(c\right)}$ is finite.

To achieve the proof, we show that the quantity ${\displaystyle K_n\left(k\right)}$ converges to zero.

From Conditions (18) and (19), we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{K}_n\left(k\right)& =& \underset{n\to \infty }{lim}{\widehat{\mathbf{w}}}_n^d\left(k\right)E{\left(\sum _{k=1}^m\frac{n^{\frac{d}{2}}}{{\widehat{\mathbf{w}}}_n^d\left(k\right)}\left(A_{l,n}^{(k,d)}\right)\right)}^4\hfill \\ & \simeq & \underset{n\to \infty }{lim}{n}^{d}E{\left(\sum _{k=1}^m\frac{1}{n^{\frac{d}{2}}}\left(A_{l,n}^{\left(k\right)}\right)\right)}^4\hfill \\ & =& \underset{n\to \infty }{lim}\frac{n^d}{n^{2d}}E{\left(\sum _{k=1}^m\left(A_{l,n}^{\left(k\right)}\right)\right)}^4\hfill \\ & =& \underset{n\to \infty }{lim}\frac{1}{n^d}E{\left(\sum _{k=1}^m\left(A_{l,n}^{\left(k\right)}\right)\right)}^4\hfill \end{array}$$

Using Inequality (9), it exists a positive constant ${\displaystyle C}$ such that

$$\begin{array}{c}\hfill E{\left(\sum _{k=1}^m\left(A_{l,n}^{(k,d)}\right)\right)}^4\le C{m}^2.\end{array}$$

Then,

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{K}_n\left(k\right)& \le & \underset{n\to \infty }{lim}\frac{C{m}^2}{n^d}\hfill \\ & =& \underset{n\to \infty }{lim}\frac{C}{m^{r-4}}\hfill \\ & =& 0.\hfill \end{array}$$

Finally, we can conclude that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}exp\left(ln\left({\mathrm{\Psi }}_n\left(u\right)\right)\right)=exp\left(-\frac{u^2}{2}{\varsigma }^2\right).\end{array}$$

where ${\displaystyle {\varsigma }^2=\sum _{k=1}^{\infty }\sum _{k^{\prime }=1}^{\infty }{\xi }_{k{k}^{\prime }}\left(c\right)}$; then, the characteristic function of ${\displaystyle n^{\frac{d}{2}}\left({\widehat{H}}_n\left(t\right)-H\left(t\right)\right)}$ converges in distribution to the characteristic function of the Gaussian centered random variable with variance ${\displaystyle {\varsigma }^2}$. This achieves the proof of Theorem 4. ${\displaystyle \square }$

8. Discussion

Andriamampionona et al. [23] show the asymptotic normality of the renewal function estimator in two-dimensional case. In this paper, we extend these results from two-dimensions into ${\displaystyle d}$-dimension, ${\displaystyle d>2}$, by studying the almost sure convergence and asymptotic normality of the empirical function ${\displaystyle {\widehat{F}}_n^{\left(k\right)}\left(t\right)}$ and the renewal function estimator ${\displaystyle {\widehat{H}}_n\left(t\right)}$. The latter is an asymptotically unbiased estimator. We use appropriate conditions to prove the results. For the asymptotic normality, we note that the convergence speed increases rapidly when the dimension increases. It is ${\displaystyle n}$ for the dimension ${\displaystyle d=2}$ and ${\displaystyle n^{\frac{d}{2}}}$ for the dimension ${\displaystyle d>2}$.

9. Conclusions

We studied the asymptotic behavior of the estimator of the renewal function based on ${\displaystyle i.i.d.}$ and positive multidimensional random fields. The future research concerns the same studies based on mixing random fields and we may consider other perspectives. Indeed, we must define appropriate estimators and find associated convergence conditions. Then, we can use the strict order relation developed in this paper, or otherwise find other paths.