Constant Angle Ruled Surfaces with a Pointwise 1-Type Gauss Map

Abstract

In this study, constant angle ruled surfaces with a pointwise 1-type Gauss map, which is very useful in the classification of surfaces, are investigated in terms of the Frenet elements of the base curves of the ruled surfaces in Euclidean 3-space. In order to form a basis for our work, firstly, basic concepts related to the Gauss map of an oriented surface are given. Later, a classification is satisfied by determining the necessary conditions to be the first kind, the second kind, and the harmonic of the pointwise 1-type of the Gauss map for these surfaces. Finally, some examples of these surfaces are provided, and their graphical illustrations are displayed.

1. Introduction

The idea of a finite-type submanifold in Euclidean and semi-Euclidean spaces was first proposed by Chen [1,2]. The finite-type Gauss map notion, which is highly beneficial in surface classification, was later developed by extending this idea to differentiable maps formed on submanifolds [3]. During this process, the theory of submanifolds with a finite-type Gauss map was founded by Chen and Piccinni’s comprehensive examination of submanifolds of Euclidean spaces with a finite-type Gauss map, and the authors also classified compact surfaces with this type of map [4]. The ruled surfaces with a finite-type Gauss map have strongly attracted the attention of numerous researchers, and some studies have presented different aspects [5,6,7,8,9,10]. Furthermore, a specific type of ruled surface called the pointwise 1-type Gauss maps of the Darboux ruled surfaces and a new classification were provided by [11]. Moreover, the Gauss maps of framed developable surfaces formed by curves that do not need to be regular were investigated in [12]. On the other hand, the Gauss map is also related to vector bundles by providing a section of a surface’s normal bundle as well as mapping points to their associated normal vectors. The fact that the curvatures and normal directions are important components of the vector bundle structures shows us the crucial link between the Gauss map and the geometric properties of vector bundles. Recent research on vector bundles over surfaces and curves includes the vector bundle moduli spaces over Riemann surfaces [13], the moduli space of Higgs bundles [14,15], as well as vector bundles discussed in [16,17]. The Gauss map can also visualize vector bundles’ transition functions, sections, and moduli spaces, providing insights into the geometric structures of principal bundles over compact algebraic curves that were recently studied in [18].

A surface is termed a constant angle surface if the unit normal at each point on the surface forms a constant angle with a specified direction. Some authors also refer to these surfaces as helical surfaces. Ref. [19] derived the parametric equations for constant angle surfaces in Euclidean 3-space, where the velocity vectors of parameter curves are perpendicular to each other, and the characterizations related to the curvatures of these surfaces were provided. Moreover, the concepts of time-like constant angle surfaces with constant time-like and space-like directions separately in Minkowski 3-space were investigated in [20] and a study on space-like constant angle surfaces was presented by [21]. Furthermore, the general characterizations for constant angle surfaces were presented in Minkowski space [22]. Within this period, the criteria for the tangent, normal, and binormal ruled surfaces on curves to be constant angle surfaces were examined, and an extended study emerged from the perspective of the constant angle property [23]. Moreover, the characterizations for certain special curves on these constant angle surfaces, such as geodesic curves, asymptotic curves, and curvature lines were researched in [24], and the space-like constant angle surface family in Minkowski 3-space was researched in [25]. Additionally, the relationship between constant angle ruled surfaces and helical curves was considered by [26]. Constant angle ruled surfaces have continued to attract the interest of researchers. There are some recent investigations that are currently devoted to this subject, too. For instance, constant angle ruled surfaces were studied and classified based on the constant angle property of the surface in [27], and conchoidal surfaces in Euclidean 3-space satisfying $\Delta x_i={\lambda }_i{x}_i$ were investigated in [28].

It is known that a ruled surface can be completely determined by a function f and a vector C satisfying the relation $\Delta \Omega =f\left(\Omega +C\right)$ when their Gauss map is a pointwise 1-type. However, constant angle ruled surfaces with a pointwise 1-type Gauss map parallel to any Frenet vectors of the base curves have not been characterized with the curvature and torsion of base curves yet. In this context, this study focuses on constant angle ruled surfaces with pointwise 1-type Gauss maps, essential for surface classification in Euclidean 3-space. Each type of constant angle ruled surface is characterized separately by the existence of pointwise 1-type Gauss maps, with the base curve being a helix or planar curve, etc. Lastly, graphical illustrations of exemplified surfaces are plotted. The findings can be used in any field that requires information about surfaces due to the characterizations providing insights into surface theory.

2. Preliminaries

It is widely acknowledged that a continuous function from an oriented surface to the unit sphere mapping each point of the surface to its oriented unit normal vector serves as the Gauss map of the surface.

Let $M:\Phi =\Phi \left(s_1,s_2\right)$ be an oriented regular surface and $S^2$ denote the unit sphere in Euclidean 3-space. Denoting the Gauss map of M with $\Omega$, it is defined as

$$\begin{array}{c}\Omega :M\to S^2\subset R^3\hfill \\ p\to \Omega \left(p\right)=\frac{{\Phi }_{s_1}\times {\Phi }_{s_2}}{∥{\Phi }_{s_1}\times {\Phi }_{s_2}∥},\hfill \end{array}$$

where ${\Phi }_{s_1}=\frac{𝜕\Phi }{𝜕s_2}$ and ${\Phi }_{s_2}=\frac{𝜕\Phi }{𝜕s_2}$ are the first-order partial derivatives in terms of the local coordinates $s_1$ and $s_2$ and “×” indicates the two vectors’ cross-product. $\Omega \left(p\right)$ is the position vector of the point on the unit sphere corresponding to the direction of the normal vector at any point p on M.

Let $g_{ij}=〈\frac{𝜕\Phi }{𝜕s_i},\frac{𝜕\Phi }{𝜕s_j}〉$ be the induced metric on the surface M for $i,j\in \left\{1,2\right\}$; then, the Laplacian operator $\Delta$ with respect to the induced metric on M is defined as

$$\Delta =-\frac{1}{\sqrt{g}}\sum _{i,j=1}^2\frac{𝜕}{𝜕s_i}\left(\sqrt{g}{g}^{ij}\frac{𝜕}{𝜕s_j}\right).$$

Also, the matrix $\left(g_{ij}\right)$ of the first fundamental form of and its inverse matrix $\left(g^{ij}\right)$ can be written as

$$\left(g_{ij}\right)=\left(\begin{array}{cc}{g}_{11}& g_{12}\\ g_{21}& g_{22}\end{array}\right)\mathrm{and}\left(g^{ij}\right)=\frac{1}{det\left(g_{ij}\right)}\left(\begin{array}{cc}{g}_{22}& -g_{12}\\ -g_{21}& g_{11}\end{array}\right),$$

respectively. Furthermore, $g=det\left(g_{ij}\right)$ indicates the determinant of the matrix $\left(g_{ij}\right)$.

The Gauss map $\Omega$ of M is a 1–type Gauss map if, and only if, the Gauss map $\Omega$ satisfies the equation $\Delta \Omega =\lambda \left(\Omega +C\right)$ for a non-zero real constant $\lambda$ and constant vector C [4]. From the research carried out over time, it has been observed that the Gauss maps of some surfaces provide this equality for a regular function f, not for a constant $\lambda$. The conjugate of Enneper surfaces, catenoid surfaces, and helicoid surfaces can be given as examples in Euclidean space. Due to this circumstance, the notion of the pointwise 1-type Gauss map evolved. If the Gauss map $\Omega$ of a surface M in $R^3$ satisfies the equation $\Delta \Omega =f\left(\Omega +C\right)$ for a regular function f and a constant vector C then this Gauss map is called a pointwise 1-type Gauss map [7]. In particular, it is classified as follows:

i.

If the constant vector C vanishes and f is a regular function, the pointwise 1-type Gauss map of M is called the first kind.

ii.

If the constant vector C does not vanish and f is a regular function, the pointwise 1-type Gauss map of M is called the second kind.

iii.

If $\Delta \Omega =0$, the pointwise 1-type Gauss map of M is called harmonic [8].

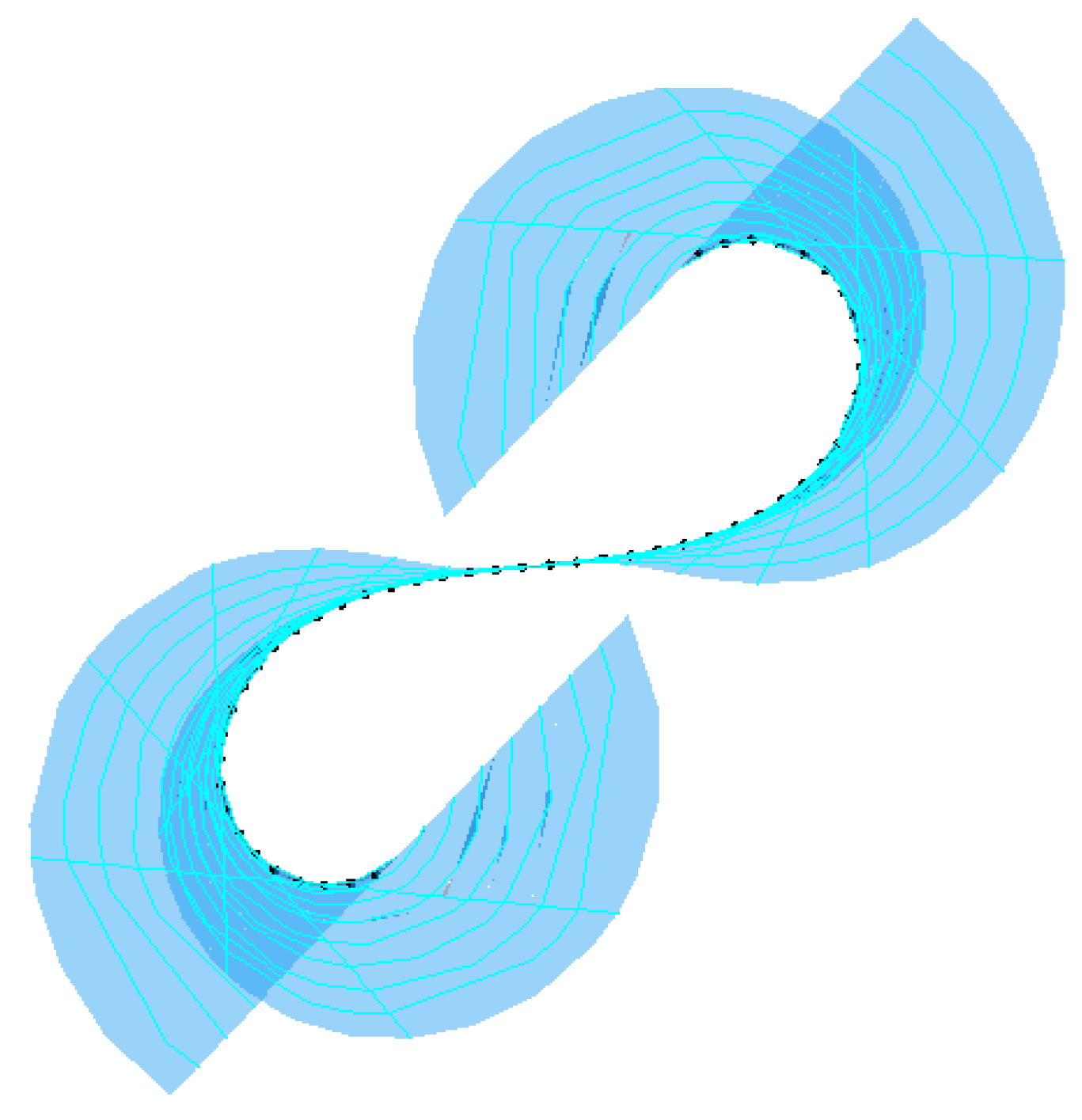
3. Constant Angle Ruled Surface with Pointwise 1-Type Gauss Map

In this section, the constant angle ruled surfaces parallel to the tangent vector, principal normal, and binormal vectors of a unit speed moving space curve with a pointwise 1-type Gauss map are investigated in Euclidean 3-space.

First, let us recall the Frenet–Serret formulae for use in the rest of the article. If $\alpha =\alpha \left(s\right)$ is a unit speed moving space curve, where s measures its arc length in Euclidean 3-space, then the derivatives of the tangent, principal normal, and binormal unit vectors T, N, and B satisfy the formulae

$$T_s=\kappa N,N_s=-\kappa T+\tau B,B_s=-\tau N,$$

(1)

at each point $\alpha \left(s\right)$, where $\kappa$ and $\tau$ are the curvature and the torsion functions of $\alpha$, respectively.

Now, let us consider a ruled surface $\Phi \left(s,v\right)$ generated by sweeping a moving generator ${\rm Y}=\epsilon T+\eta N+\mu B$ along a unit speed curve $\alpha$; then, it has a parametrization of the form

$$\Phi \left(s,v\right)=\alpha \left(s\right)+v{\rm Y}\left(s\right),$$

(2)

where $\epsilon$, $\eta$, and $\mu$ are the smooth functions of s. Here, the curve $\alpha \left(s\right)$ is called a base curve, and ${\rm Y}\left(s\right)$ is called a ruling. By considering the Frenet formulae (1), the partial derivatives of the equation of this surface $\Phi \left(s,v\right)$ are found as

$${\Phi }_s=\left(1-v\left(\eta \kappa -{\epsilon }_s\right)\right)T+v\left(\epsilon \kappa -\mu \tau +{\eta }_s\right)N+v\left(\eta \tau +{\mu }_s\right)B$$

and

$${\Phi }_v=\epsilon T+\eta N+\mu B.$$

Then, the cross-product of these tangent vectors is obtained as

$$\begin{array}{c}{\Phi }_s\times {\Phi }_v=v\left(\mu \left(\epsilon \kappa -\mu \tau +{\eta }_s\right)-\eta \left(\eta \tau +{\mu }_s\right)\right)T\hfill \\ +\left(\mu \left(-1+v\left(\eta \kappa -{\epsilon }_s\right)\right)+v\epsilon \left(\eta \tau +{\mu }_s\right)\right)N\hfill \\ +\left(\eta +v\left(-{\eta }^2\kappa +\eta {\epsilon }_s-\epsilon \left(\epsilon \kappa -\mu \tau +{\eta }_s\right)\right)\right)B.\hfill \end{array}$$

For the sake of brevity, the normal vector of the surface can be written as

$$u\left(s,v\right)=u_1\left(s,v\right)T\left(s\right)+u_2\left(s,v\right)N\left(s\right)+u_3\left(s,v\right)B\left(s\right).$$

with the notations of the coefficients

$$u_i\left(s,v\right)=u_{i1}\left(s\right)+v{u}_{i2}\left(s\right)$$

for all $i\in \left\{1,2,3\right\}$. By straightforward computation, the coefficient components of the normal vector are as follows:

$$\left\{\begin{array}{cc}{u}_{11}=0,\hfill & u_{12}=\mu \left(\epsilon \kappa -\mu \tau +{\eta }_s\right)-\eta \left(\eta \tau +{\mu }_s\right),\hfill \\ u_{21}=-\mu ,\hfill & u_{22}=\mu \left(\eta \kappa -{\epsilon }_s\right)+\epsilon \left(\eta \tau +{\mu }_s\right),\hfill \\ u_{31}=\eta , \hfill & u_{32}=-{\eta }^2\kappa +\eta {\epsilon }_s-\epsilon \left(\epsilon \kappa -\mu \tau +{\eta }_s\right).\hfill \end{array}\right.$$

(3)

3.1. Constant Angle Ruled Surface Parallel to Tangent Vector

Theorem 1.

There is not any constant angle ruled surface $\Phi \left(s,v\right)$ parallel to the tangent vector of its base curve.

Proof. 

Let the normal vector field u of an oriented ruled surface $\Phi \left(s,v\right)$ be parallel to the tangent vector T of the base curve $\alpha \left(s\right)$; then, we have the following criteria:

$$u_1\ne 0,u_2=u_3=0.$$

The criteria $u_2=u_3=0$ require $\epsilon =\eta =\mu =0$ from the solution of Equation (3). This situation contradicts the fact that ${\rm Y}\left(s\right)\ne 0$ and $u_1=u_{11}+v{u}_{12}\ne 0$. □

3.2. Constant Angle Ruled Surface Parallel to Principal Normal Vector with Pointwise 1-Type Gauss Map

Theorem 2.

Let the normal vector field u of an oriented ruled surface $\Phi \left(s,v\right)$ be parallel to the principal normal vector N of the base curve $\alpha \left(s\right)$; then, we have the criteria

i. 

$\eta =0$,

ii. 

$\mu \ne 0$,

iii. 

($\epsilon \kappa =\mu \tau$) or ($\epsilon =0$ and $\tau =0$).

Proof. 

If the normal vector field u of $\Phi \left(s,v\right)$ is assumed to be parallel to the principal normal vector N of the base curve $\alpha \left(s\right)$, then there must be $u_2\ne 0$, $u_1=u_3=0$ in the equality $u=u_{1}T+u_{2}N+u_{3}B$.

i.

$u_3=0$ requires $u_{31}=0$, that is, $\eta$ vanishes.

ii.

$u_2\ne 0$ requires $\mu \ne 0$.

iii.

Considering (i) and (ii), Equation (3) becomes

$$\left\{\begin{array}{c}{u}_{11}=0,u_{12}=\mu \left(\epsilon \kappa -\mu \tau \right),\hfill \\ u_{21}=-\mu ,u_{22}=-\mu {\epsilon }_s+\epsilon {\mu }_s,\hfill \\ u_{31}=0,u_{32}=-\epsilon \left(\epsilon \kappa -\mu \tau \right).\hfill \end{array}\right.$$

These equalities give us $\epsilon \kappa -\mu \tau =0$ or $\epsilon =0$; therefore, $\tau =0$ from the fact that $u_1=u_3=0$ implies that $u_{12}=u_{32}=0$.

□

Now, let us investigate the emergent two cases given in Theorem 2 (iii) separately.

Case 3.2.1. Let $\epsilon \kappa =\mu \tau$, $\eta =0$. Then, there has to be $\mu {\epsilon }_s-\epsilon {\mu }_s\ne 0$, i.e., $\frac{\epsilon }{\mu }$ is non-constant and $\mu \ne 0$. With these criteria, a ruled surface given by (2) becomes a constant angle ruled surface. So, this constant angle ruled surface takes the form:

$${\Phi }_1^N\left(s,v\right)=\alpha \left(s\right)+v\left(\epsilon T+\mu B\right),$$

where $\epsilon \kappa =\mu \tau$. Differentiating the equation of ${\Phi }_1^N\left(s,v\right)$ in terms of s and v, respectively, gives us the following partial differential equations:

$${\left({\Phi }_1^N\right)}_s=\left(1+v{\epsilon }_s\right)T+v{\mu }_{s}B\mathrm{and}{\left({\Phi }_1^N\right)}_v=\epsilon T+\mu B.$$

Using these partial differentiation equations, the Gauss map $\Omega$ of the constant angle ruled surface ${\Phi }_1^N\left(s,v\right)$ is found as

$$\Omega =-N.$$

The matrix $\left(g_{ij}\right)$ consisting of the components of the induced metric on ${\Phi }_1^N\left(s,v\right)$, its determinant g, and inverse matrix $\left(g^{ij}\right)$ are found as

$$\left(g_{ij}\right)=\left(\begin{array}{cc}{\left(1+v{\epsilon }_s\right)}^2+{\left(v{\mu }_s\right)}^2& \epsilon +v{\left(\epsilon \mu \right)}_s\\ \epsilon +v{\left(\epsilon \mu \right)}_s& {\epsilon }^2+{\mu }^2\end{array}\right),g={\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2,$$

and

$$\left(g^{ij}\right)=\left(\begin{array}{cc}\frac{{\epsilon }^2+{\mu }^2}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2}& -\frac{\epsilon +v{\left(\epsilon \mu \right)}_s}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2}\\ -\frac{\epsilon +v{\left(\epsilon \mu \right)}_s}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2}& \frac{{\left(1+v{\epsilon }_s\right)}^2+{\left(v{\mu }_s\right)}^2}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2}\end{array}\right),$$

respectively. Here, it is obvious that $\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\ne 0$, since $\mu {\epsilon }_s-\epsilon {\mu }_s\ne 0$ or $\mu \ne 0$. Therefore, the formula of the Laplacian $\Delta$ on the constant angle ruled surface ${\Phi }_1^N\left(s,v\right)$ is

$$\Delta ={\delta }_1\frac{{𝜕}^2}{𝜕s^2}+{\delta }_2\frac{{𝜕}^2}{𝜕v^2}+{\delta }_3\frac{𝜕}{𝜕s}+{\delta }_4\frac{𝜕}{𝜕v}+{\delta }_5\frac{{𝜕}^2}{𝜕s𝜕v}$$

(4)

such that

$$\begin{array}{c}{\delta }_1=-\frac{{\epsilon }^2+{\mu }^2}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2},\hfill \\ {\delta }_2=-\frac{{\left(1+v{\epsilon }_s\right)}^2+{\left(v{\mu }_s\right)}^2}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2},\hfill \\ {\delta }_3=\frac{{\mu }^2\left(-{\mu }_s+v\left({\epsilon }_s{\mu }_s-\mu {\epsilon }_{ss}\right)\right)-{\epsilon }^2\left(2{\mu }_s+v\left({\epsilon }_s{\mu }_s+\mu {\epsilon }_{ss}\right)\right)+v{\epsilon }^3{\mu }_{ss}+\epsilon \mu \left({\epsilon }_s+v\left({{\epsilon }_s}^2-{{\mu }_s}^2+\mu {\mu }_{ss}\right)\right)}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2},\hfill \\ {\delta }_4=-\frac{\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\left({\left(1+v{\epsilon }_s\right)}^2+{\left(v{\mu }_s\right)}^2\right)-\left(\epsilon +v\left(\epsilon {\epsilon }_s+\mu {\mu }_s\right)\right)\left({\mu }_s+v\left(\mu {\epsilon }_{ss}-\epsilon {\mu }_{ss}\right)\right)}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2},\hfill \\ {\delta }_5=\frac{2\left(\epsilon +v\left(\epsilon {\epsilon }_s+\mu {\mu }_s\right)\right)}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2}.\hfill \end{array}$$

Now, let us apply this Laplace operator $\Delta$ to the Gauss map $\Omega$. If the derivatives of the Gauss map ${\Omega }_s$, ${\Omega }_{ss}$, ${\Omega }_v$, ${\Omega }_{vv}$, and ${\Omega }_{sv}$ are substituted into Equation (4), then we can easily calculate that the Laplacian of the Gauss map $\Omega$ of M is

$$\Delta \Omega =-{\delta }_1\left({\kappa }^2+{\tau }^2\right)\Omega +\left({\delta }_1{\kappa }_s+{\delta }_3\kappa \right)T-\left({\delta }_1{\tau }_s+{\delta }_3\tau \right)B.$$

(5)

Theorem 3.

Let a constant angle ruled surface parallel to the principal normal vector be given by ${\Phi }_1^N\left(s,v\right)=\alpha \left(s\right)+v\left(\epsilon T+\mu B\right)$ such that $\epsilon \kappa =\mu \tau$, where $\epsilon \ne 0$ and $\mu \ne 0$. Then, ${\Phi }_1^N\left(s,v\right)$ has a pointwise 1-type Gauss map of the first kind if, and only if, the curve α is a helix.

Proof. 

$\left(\Rightarrow :\right)$ Let $\Omega$ be a pointwise 1-type Gauss map of the first kind. Then, Equation (5) can be written in the form $\Delta \Omega =f\left(\Omega +C\right)$ such that

$$f=-{\delta }_1\left({\kappa }^2+{\tau }^2\right),C=-\frac{{\delta }_1{\kappa }_s+{\delta }_3\kappa }{{\delta }_1\left({\kappa }^2+{\tau }^2\right)}T+\frac{{\delta }_1{\tau }_s+{\delta }_3\tau }{{\delta }_1\left({\kappa }^2+{\tau }^2\right)}B,$$

and it requires the following criteria:

$${\delta }_1\left({\kappa }^2+{\tau }^2\right)\ne 0,$$

which is obviously satisfied, and

$$-\frac{{\delta }_1{\kappa }_s+{\delta }_3\kappa }{{\delta }_1\left({\kappa }^2+{\tau }^2\right)}T+\frac{{\delta }_1{\tau }_s+{\delta }_3\tau }{{\delta }_1\left({\kappa }^2+{\tau }^2\right)}B=0.$$

Since T and B are linearly independent, we find that

$$\frac{{\delta }_1{\kappa }_s+{\delta }_3\kappa }{{\delta }_1\left({\kappa }^2+{\tau }^2\right)}=0\mathrm{and}\frac{{\delta }_1{\tau }_s+{\delta }_3\tau }{{\delta }_1\left({\kappa }^2+{\tau }^2\right)}=0.$$

Multiplication of the last first equation by $\tau$ and the second one by $-\kappa$ and addition of them give us

$${\delta }_1{\left(\frac{\kappa }{\tau }\right)}_s{\tau }^2=0.$$

Since ${\delta }_1\ne 0$ and $\tau \ne 0$, we obtain that $\frac{\kappa }{\tau }$ is a constant, which means the curve is a helix.

$\left(\Leftarrow :\right)$ Assume that the base curve of the ruled surface is a helix, then the ratio of curvature to torsion is a constant at each point of the curve, which requires ${\kappa }_s\tau -\kappa {\tau }_s=0$ and considering $\epsilon \kappa =\mu \tau$ gives us $C=0$. Since ${\delta }_1\left({\kappa }^2+{\tau }^2\right)\ne 0$, we can say that the Gauss map of the constant angle ruled surface ${\Phi }_1^N\left(s,v\right)$ is a pointwise 1-type map of the first kind. □

The following corollary is obvious.

Corollary 1.

Let ${\Phi }_1^N\left(s,v\right)$ be a constant angle ruled surface parallel to the principal normal vector with pointwise 1-type Gauss map of the first kind; then, the following equality

$$\Delta \Omega =\frac{\left({\epsilon }^2+{\mu }^2\right)\left({\kappa }^2+{\tau }^2\right)}{{\left(\mu +v\left(\mu {\epsilon }_s-\epsilon {\mu }_s\right)\right)}^2}\Omega ,$$

where $\epsilon \kappa =\mu \tau$ and $\mu \ne 0$.

Example 1.

Let us construct a constant angle ruled surface ${\Phi }_1^N:\left(-5\pi ,5\pi \right)\times \left(-5,5\right)\to R^3$ parallel to the principal normal vector associated with a unit speed base curve $\alpha :\left(-5\pi ,5\pi \right)\to R^3$ defined by the parametric equation

$$\alpha \left(s\right)=\left(3cos\left(\frac{s}{5}\right),3sin\left(\frac{s}{5}\right),\frac{4s}{5}\right).$$

The Frenet apparatus of this curve is the collection:

$$\begin{array}{c}T=\left(-\frac{3}{5}sin\left(\frac{s}{5}\right),\frac{3}{5}cos\left(\frac{s}{5}\right),\frac{4}{5}\right),N=\left(-cos\left(\frac{s}{5}\right),-sin\left(\frac{s}{5}\right),0\right)\hfill \\ B=\left(\frac{4}{5}sin\left(\frac{s}{5}\right),-\frac{4}{5}cos\left(\frac{s}{5}\right),\frac{3}{5}\right),\kappa =\frac{3}{25},\tau =\frac{4}{25}.\hfill \end{array}$$

Consequently, the constant angle ruled surface parallel to the principal normal vector associated with the base curve is parameterized as

$${\Phi }_1^N\left(s,v\right)=\left(3cos\left(\frac{s}{5}\right),3sin\left(\frac{s}{5}\right),v+\frac{4s}{5}\right)$$

for $\epsilon =\frac{4}{5}$ and $\mu =\frac{3}{5}$. Hence,

$$\Delta =-\frac{25}{9}\frac{{𝜕}^2}{𝜕s^2}-\frac{25}{9}\frac{{𝜕}^2}{𝜕v^2}+\frac{40}{9}\frac{{𝜕}^2}{𝜕s𝜕v}\mathrm{and}\Delta \Omega =-\frac{1}{9}\Omega .$$

Therefore, the Gauss map of the constant angle ruled surface ${\Phi }_1^N\left(s,v\right)$ is a pointwise 1-type of the first kind (see Figure 1).

Case 3.2.2. Let $\epsilon =0$, $\eta =0$, $\mu \ne 0$ and $\tau =0$. This condition satisfies that the ruled surface is a constant angle ruled surface. So, we have obtained the constant angle ruled surface in the parametric form:

$${\Phi }_2^N\left(s,v\right)=\alpha \left(s\right)+v\mu B$$

where $\alpha \left(s\right)$ is a planar curve. Differentiating the equation of ${\Phi }_2^N\left(s,v\right)$ in terms of s and v, respectively, gives the following partial differential equations:

$${\left({\Phi }_2^N\right)}_s=T+v{\mu }_{s}B\mathrm{and}{\left({\Phi }_2^N\right)}_v=\mu B.$$

Using these partial differentiation equations, the Gauss map $\Omega$ of the constant angle ruled surface ${\Phi }_2^N\left(s,v\right)$ is found as

$$\Omega =-N.$$

The matrix $\left(g_{ij}\right)$ with the components of the induced metric on ${\Phi }_2^N\left(s,v\right)$, its determinant g, and its inverse $\left(g^{ij}\right)$ are found as

$$g_{ij}=\left(\begin{array}{cc}1+{\left(v{\mu }_s\right)}^2& v\mu {\mu }_s\\ v\mu {\mu }_s& {\mu }^2\end{array}\right),g={\mu }^2,$$

and

$$g^{ij}=\left(\begin{array}{cc}1& -\frac{v{\mu }_s}{\mu }\\ -\frac{v{\mu }_s}{\mu }& \frac{1+{\left(v{\mu }_s\right)}^2}{{\mu }^2}\end{array}\right),$$

respectively. Therefore, the formula of the Laplacian $\Delta$ on the constant angle ruled surface is given as follows:

$$\Delta ={\delta }_1\frac{{𝜕}^2}{𝜕s^2}+{\delta }_2\frac{{𝜕}^2}{𝜕v^2}+{\delta }_3\frac{𝜕}{𝜕s}+{\delta }_4\frac{𝜕}{𝜕v}+{\delta }_5\frac{{𝜕}^2}{𝜕s𝜕v}$$

such that

$${\delta }_1=-1,{\delta }_2=-\frac{1+{\left(v\mu \right)}^2}{{\mu }^2},{\delta }_3=-\frac{{\mu }_s}{\mu },{\delta }_4=\frac{v{{\mu }_s}^2}{{\mu }^2},{\delta }_5=\frac{2v{\mu }_s}{\mu }.$$

From here, we can easily calculate that the Laplacian of the Gauss map $\Omega$ of M is

$$\Delta \Omega ={\kappa }^2\Omega -\frac{\left({\kappa }_s\mu +\kappa {\mu }_s\right)}{\mu }T.$$

(6)

Theorem 4.

Let ${\Phi }_2^N\left(s,v\right)$ be a constant angle ruled surface parallel to the principal normal vector; then, the surface ${\Phi }_2^N\left(s,v\right)$ has a pointwise 1-type Gauss map of the first kind if, and only if, $\alpha \left(s\right)$ is a planar curve and $\kappa \mu$ is constant.

Proof. 

$\left(\Rightarrow :\right)$ Let $\Omega$ be a pointwise 1-type Gauss map of the first kind; then, Equation (6) can be written in the form $\Delta \Omega =f\left(\Omega +C\right)$ such that

$$C=-\frac{\left({\kappa }_s\mu +\kappa {\mu }_s\right)}{{\kappa }^2\mu }T,$$

and it requires the following criteria:

$$\kappa \ne 0.$$

which is obviously satisfied, and

$$\frac{{\kappa }_s\mu +\kappa {\mu }_s}{{\kappa }^2\mu }=0.$$

Since $\kappa \ne 0$ and $\tau =0$, we obtain that $\kappa \mu$ is a constant.

$\left(\Leftarrow :\right)$ Assume that the base curve $\alpha \left(s\right)$ is planar and $\kappa \mu$ is a constant; then, ${\kappa }_s\mu +\kappa {\mu }_s=0$ is found and, therefore, $C=0$. Since $\kappa \ne 0$ is considered, we can say that the Gauss map of the constant angle ruled surface ${\Phi }_2^N\left(s,v\right)$ is the pointwise 1-type map of the first kind. □

We can give the following corollary:

Corollary 2.

Let ${\Phi }_2^N\left(s,v\right)$ be a constant angle ruled surface parallel to the principal normal vector with the pointwise 1-type Gauss map of the first kind; then, the relationship

$$\Delta \Omega ={\kappa }^2\Omega$$

exists, where $\tau =0$.

Example 2.

Let us construct a constant angle ruled surface ${\Phi }_2^N:\left(\frac{-\pi }{2},\frac{\pi }{2}\right)\times \left(-0.5,0.5\right)\to R^3$ parallel to the principal normal vector associated with a unit speed base curve $\alpha :\left(\frac{-\pi }{2},\frac{\pi }{2}\right)\to R^3$ defined by the parametric equation

$$\alpha \left(s\right)=\left(\underset{0}{\overset{s}{\int }}cos\left(\frac{\pi t^2}{2}\right)dt,\underset{0}{\overset{s}{\int }}sin\left(\frac{\pi t^2}{2}\right)dt,1\right).$$

The Frenet vectors and the curvatures of this curve are found as

$$\begin{array}{c}T=\left(cos\left(\frac{\pi s^2}{2}\right),sin\left(\frac{\pi s^2}{2}\right),0\right),N=\left(-sin\left(\frac{\pi s^2}{2}\right),cos\left(\frac{\pi s^2}{2}\right),0\right),\hfill \\ B=\left(0,0,1\right),\kappa =\pi s,\tau =0.\hfill \end{array}$$

Consequently, the constant angle ruled surface parallel to the principal normal vector associated with α is parameterized as

$${\Phi }_2^N\left(s,v\right)=\left(\underset{0}{\overset{s}{\int }}cos\left(\frac{\pi t^2}{2}\right)dt,\underset{0}{\overset{s}{\int }}sin\left(\frac{\pi t^2}{2}\right)dt,1+\frac{v}{\pi s}\right)$$

for $\mu =\frac{1}{\pi s}.$ Hence,

$$\Delta =-\frac{{𝜕}^2}{𝜕s^2}-\frac{{\pi }^2{s}^4+v^2}{s^2}\frac{{𝜕}^2}{𝜕v^2}+\frac{1}{s}\frac{𝜕}{𝜕s}+\frac{v}{s^2}\frac{𝜕}{𝜕v}-\frac{2v}{s}\frac{{𝜕}^2}{𝜕s𝜕v}$$

and

$$\Delta \Omega ={\pi }^2{s}^2\Omega .$$

Therefore, the Gauss map is a pointwise 1-type of the first kind (see Figure 2).

3.3. Constant Angle Ruled Surface Parallel to Binormal Vector with Pointwise 1-Type Gauss Map

Theorem 5.

Let the normal vector field u of an oriented ruled surface $\Phi \left(s,v\right)$ be parallel to the binormal vector B of the base curve $\alpha \left(s\right)$; then, we have the criteria

i. 

$\mu =0$,

ii. 

$\epsilon \ne 0$ provided that $\eta =0$,

iii. 

$\tau =0$ provided that $\eta \ne 0$.

Proof. 

If the normal vector field u of $\Phi \left(s,v\right)$ is assumed to be parallel to the binormal vector B of the base curve $\alpha \left(s\right)$, then there must be $u_3\ne 0$, $u_1=u_2=0$ in the equality $u=u_{1}T+u_{2}N+u_{3}B$. By considering Equation (3), we give the proof as follows:

i.

$u_2=0$ requires $u_{21}=0$, that is, $\mu$ vanishes.

Then, we obtain the following coefficient components for u:

$$\left\{\begin{array}{c}{u}_{11}=0,u_{12}=-{\eta }^2\tau ,\hfill \\ u_{21}=0,u_{22}=\epsilon \eta \tau ,\hfill \\ u_{31}=\eta ,u_{32}=-\kappa \left({\epsilon }^2+{\eta }^2\right)+{\epsilon }_s\eta -\epsilon {\eta }_s.\hfill \end{array}\right.$$

ii.

If $\eta =0$, then $\epsilon \ne 0$ by the fact that $u_3\ne 0$.

iii.

If $\eta \ne 0$, then $\tau =0$ from $u_1=0$. In this case, $\epsilon$ can be zero or non-zero.

□

Consequently, three cases occur from Theorem 5. Let us investigate them separately.

Case 3.3.1. Let $\epsilon \ne 0$, $\eta =0$, and $\mu =0$. Under these criteria, the ruled surface becomes a constant angle ruled surface. So, we give the parametric form of this constant angle ruled surface as:

$${\Phi }_1^B\left(s,v\right)=\alpha \left(s\right)+v\epsilon T,$$

where $\kappa \ne 0$. The partial differentiations of ${\Phi }_1^B\left(s,v\right)$ in terms of s and v are

$${\left({\Phi }_1^B\right)}_s=\left(1+v{\epsilon }_s\right)T+v\epsilon \kappa N\mathrm{and}{\left({\Phi }_1^B\right)}_v=\epsilon T.$$

Based on these last equations, the Gauss map $\Omega$ of the constant angle ruled surface ${\Phi }_1^B\left(s,v\right)$ is found as

$$\Omega =\frac{{\left({\Phi }_1^B\right)}_s\times {\left({\Phi }_1^B\right)}_v}{∥{\left({\Phi }_1^B\right)}_s\times {\left({\Phi }_1^B\right)}_v∥}=-B.$$

The matrix of the first fundamental form of ${\Phi }_1^B\left(s,v\right)$, its determinant and inverse matrix are, respectively,

$$g_{ij}=\left(\begin{array}{cc}{\left(1+v{\epsilon }_s\right)}^2+{\left(v\epsilon \kappa \right)}^2& \epsilon \left(1+v{\epsilon }_s\right)\\ \epsilon \left(1+v{\epsilon }_s\right)& {\epsilon }^2\end{array}\right),g={\left(v{\epsilon }^2\kappa \right)}^2,$$

and

$$g^{ij}=\left(\begin{array}{cc}\frac{1}{{\left(v\epsilon \kappa \right)}^2}& -\frac{\epsilon \left(1+v{\epsilon }_s\right)}{{\left(v{\epsilon }^2\kappa \right)}^2}\\ -\frac{\epsilon \left(1+v{\epsilon }_s\right)}{{\left(v{\epsilon }^2\kappa \right)}^2}& \frac{{\left(v\epsilon \kappa \right)}^2+{\left(1+v{\epsilon }_s\right)}^2}{{\left(v{\epsilon }^2\kappa \right)}^2}\end{array}\right),$$

where $\kappa \ne 0$. Therefore, the formula of the Laplacian $\Delta$ on the constant angle ruled surface is given as follows:

$$\Delta ={\delta }_1\frac{{𝜕}^2}{𝜕s^2}+{\delta }_2\frac{{𝜕}^2}{𝜕v^2}+{\delta }_3\frac{𝜕}{𝜕s}+{\delta }_4\frac{𝜕}{𝜕v}+{\delta }_5\frac{{𝜕}^2}{𝜕s𝜕v}$$

(7)

such that

$$\begin{array}{c}{\delta }_1=-\frac{1}{{\left(v\epsilon \kappa \right)}^2},{\delta }_2=-\frac{{\left(v\epsilon \kappa \right)}^2+{\left(1+v{\epsilon }_s\right)}^2}{{\left(v{\epsilon }^2\kappa \right)}^2},{\delta }_3=\frac{\kappa -v{\left(\kappa \epsilon \right)}_s}{{\left(v\epsilon \kappa \right)}^3},\hfill \\ {\delta }_4=\frac{-v^2{\epsilon }^2{\kappa }^3-\kappa \left(1-v^2{{\epsilon }_s}^2\right)+v\epsilon {\kappa }_s\left(1+v{\epsilon }_s\right)}{v^3{\epsilon }^4{\kappa }^3},{\delta }_5=\frac{2+2v{\epsilon }_s}{v^2{\epsilon }^3{\kappa }^2}.\hfill \end{array}$$

Now, let us apply the Laplace operator $\Delta$ to the Gauss map $\Omega$. If the derivatives of the Gauss map ${\Omega }_s$, ${\Omega }_{ss}$, ${\Omega }_v$, ${\Omega }_{vv}$, and ${\Omega }_{sv}$ are substituted into Equation (7), then we can easily calculate that the Laplacian of the Gauss map $\Omega$ of ${\Phi }_1^B\left(s,v\right)$ is

$$\Delta \Omega =-{\delta }_1{\tau }^2\Omega -{\delta }_1\kappa \tau T+\left({\delta }_1{\tau }_s+{\delta }_3\tau \right)N.$$

(8)

Theorem 6.

Let ${\Phi }_1^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector; then, the Gauss map of the constant angle surface ${\Phi }_1^B\left(s,v\right)$ is harmonic if, and only if, the curve $\alpha \left(s\right)$ is a planar curve.

Proof. 

Let ${\Phi }_1^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector, and the Gauss map of the constant angle surface ${\Phi }_1^B\left(s,v\right)$ is harmonic; then, Equation (8) can be written in the form

$$\Delta \Omega =0$$

for $\tau =0$. So, we can say that the Gauss map of the surface is harmonic. The sufficient condition is obvious. □

Corollary 3.

Let ${\Phi }_1^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector; then, the Gauss map of ${\Phi }_1^B\left(s,v\right)$ cannot be the pointwise 1-type map of the first kind.

Proof. 

Let ${\Phi }_1^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector; then, Equation (8) can be written in the form $\Delta \Omega =f\left(\Omega +C\right)$ such that

$$f=-{\delta }_1{\tau }^2,C=\frac{\kappa }{\tau }T-\frac{{\delta }_1{\tau }_s+{\delta }_3\tau }{{\delta }_1{\tau }^2}N,$$

where $\tau \ne 0.$ Since $\kappa \ne 0$, C never vanishes, the Gauss map of ${\Phi }_1^B\left(s,v\right)$ cannot be the pointwise 1-type map of the first kind. □

Example 3.

Let us consider the planar curve in Example 2. The constant angle ruled surface parallel to the binormal vector ${\Phi }_1^B\left(s,v\right)$ is parameterized as

$${\Phi }_1^B\left(s,v\right)=\left(\underset{0}{\overset{s}{\int }}cos\left(\frac{\pi t^2}{2}\right)dt+vscos\left(\frac{\pi s^2}{2}\right),\underset{0}{\overset{s}{\int }}sin\left(\frac{\pi t^2}{2}\right)dt+vssin\left(\frac{\pi s^2}{2}\right),1\right)$$

for $\epsilon =s$. Hence,

$$\begin{array}{c}\Delta =-\frac{1}{{\pi }^2{s}^4{v}^2}\frac{{𝜕}^2}{𝜕s^2}-\frac{1+v\left(2+v+{\pi }^2{s}^{4}v\right)}{{\pi }^2{s}^6{v}^2}\frac{{𝜕}^2}{𝜕v^2}+\frac{1-2v}{{\pi }^2{s}^5{v}^3}\frac{𝜕}{𝜕s}\hfill \\ +\frac{v-1+\left(2-{\pi }^2{s}^4\right)v^2}{{\pi }^2{s}^6{v}^3}\frac{𝜕}{𝜕v}+\frac{2\left(1+v\right)}{{\pi }^2{s}^5{v}^2}\frac{{𝜕}^2}{𝜕s𝜕v}\hfill \end{array}$$

and

$$\Delta \Omega =0.$$

Therefore, the Gauss map of ${\Phi }_1^B\left(s,v\right)$ is harmonic (see Figure 3).

Case 3.3.2. Let $\epsilon \ne 0$, $\eta \ne 0$, $\mu =0$, and $\tau =0.$ So, the constant angle ruled surface constructed with these criteria has the parametric form:

$${\Phi }_2^B\left(s,v\right)=\alpha \left(s\right)+v\left(\epsilon T+\eta N\right)$$

where $\alpha \left(s\right)$ is a planar curve. The partial differentials of ${\Phi }_2^B\left(s,v\right)$ with respect to s and v are

$${\left({\Phi }_2^B\right)}_s=\left(1-v\eta \kappa +v{\epsilon }_s\right)T+v\left(\epsilon \kappa +{\eta }_s\right)N\mathrm{and}{\left({\Phi }_2^B\right)}_v=\epsilon T+\eta N.$$

These give us the Gauss map $\Omega$ of the constant angle ruled surface ${\Phi }_2^B\left(s,v\right)$ as

$$\Omega =\frac{{\left({\Phi }_2^B\right)}_s\times {\left({\Phi }_2^B\right)}_v}{∥{\left({\Phi }_2^B\right)}_s\times {\left({\Phi }_2^B\right)}_v∥}=B.$$

There are the following relationships:

$$\begin{array}{c}{g}_{ij}=\left(\begin{array}{cc}{\left(1-v\eta \kappa +v{\epsilon }_s\right)}^2+v^2{\left(\epsilon \kappa +{\eta }_s\right)}^2& \epsilon +v\left(\epsilon {\epsilon }_s+\eta {\eta }_s\right)\\ \epsilon +v\left(\epsilon {\epsilon }_s+\eta {\eta }_s\right)& {\epsilon }^2+{\eta }^2\end{array}\right),\hfill \\ g={\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2,\hfill \end{array}$$

and

$$g^{ij}=\left(\begin{array}{cc}\frac{{\epsilon }^2+{\eta }^2}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2}& -\frac{\epsilon +v\left(\epsilon {\epsilon }_s+\eta {\eta }_s\right)}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2}\\ -\frac{\epsilon +v\left(\epsilon {\epsilon }_s+\eta {\eta }_s\right)}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2}& \frac{{\left(1-v\eta \kappa +v{\epsilon }_s\right)}^2+v^2{\left(\epsilon \kappa +{\eta }_s\right)}^2}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2}\end{array}\right).$$

Therefore, the formula of the Laplacian $\Delta$ on the constant angle ruled surface is given as follows:

$$\Delta ={\delta }_1\frac{{𝜕}^2}{𝜕s^2}+{\delta }_2\frac{{𝜕}^2}{𝜕v^2}+{\delta }_3\frac{𝜕}{𝜕s}+{\delta }_4\frac{𝜕}{𝜕v}+{\delta }_5\frac{{𝜕}^2}{𝜕s𝜕v}$$

such that

$$\begin{array}{c}{\delta }_1=-\frac{{\epsilon }^2+{\eta }^2}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2},{\delta }_2=-\frac{{\left(1-v\eta \kappa +v{\epsilon }_s\right)}^2+v^2{\left(\epsilon \kappa +{\eta }_s\right)}^2}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2},\hfill \\ \hfill \\ {\delta }_3=\frac{\begin{array}{c}{\epsilon }^2\left({\eta }_s\left(2-v\eta \kappa +v{\epsilon }_s\right)+v\eta \left(-2\eta {\kappa }_s+{\epsilon }_{ss}\right)\right)+{\eta }^2\left(-\left(-1+v\eta \kappa +v{\epsilon }_s\right){\eta }_s+v\eta \left(-\eta {\kappa }_s+{\epsilon }_{ss}\right)\right)\hfill \\ +{\epsilon }^3\left(\kappa -v\kappa {\epsilon }_s-v{\eta }_{ss}\right)-\epsilon \eta \left({\epsilon }_s+v{{\epsilon }_s}^2-v{{\eta }_s}^2+\eta \left(\kappa \left(-1+v{\epsilon }_s\right)+v{\eta }_{ss}\right)\right)-v{\epsilon }^4{\kappa }_s\hfill \end{array}}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^3},\hfill \\ \hfill \\ {\delta }_4=-\frac{\begin{array}{c}\left({\eta }^2\kappa -\eta {\epsilon }_s+\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)\left({\left(1-v\eta \kappa +v{\epsilon }_s\right)}^2+v^2{\left(\epsilon \kappa +{\eta }_s\right)}^2\right)-\hfill \\ \left(\epsilon +v\left(\epsilon {\epsilon }_s+\eta {\eta }_s\right)\right)\left(\left(-1+2v\eta \kappa \right){\eta }_s+v{\epsilon }^2{\kappa }_s+v\eta \left(\eta {\kappa }_s-{\epsilon }_{ss}\right)+v\epsilon \left(2\kappa {\epsilon }_s+{\eta }_{ss}\right)\right)\hfill \end{array}}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^3},\hfill \\ {\delta }_5=\frac{2\left(\epsilon +v\left(\epsilon {\epsilon }_s+\eta {\eta }_s\right)\right)}{{\left(v{\eta }^2\kappa -\eta \left(1+v{\epsilon }_s\right)+v\epsilon \left(\epsilon \kappa +{\eta }_s\right)\right)}^2}.\hfill \end{array}$$

From here, we can easily calculate that the Laplacian of the Gauss map $\Omega$ of ${\Phi }_2^B\left(s,v\right)$ is

$$\Delta \Omega =0.$$

(9)

Theorem 7.

Let ${\Phi }_2^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector. Then, the Gauss map of the constant angle surface ${\Phi }_2^B\left(s,v\right)$ is harmonic if, and only if, the curve $\alpha \left(s\right)$ is a planar curve.

Proof. 

Let ${\Phi }_2^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector. From the facts that $\tau =0$ and Equation (9), we conclude that the Gauss map of the constant angle surface ${\Phi }_2^B\left(s,v\right)$ is harmonic. □

Example 4.

Let us consider the planar curve in Example 2. The constant angle ruled surface parallel to the binormal vector ${\Phi }_2^B\left(s,v\right)$ is parameterized as

$${\Phi }_2^B\left(s,v\right)=\left(\begin{array}{c}\underset{0}{\overset{s}{\int }}cos\left(\frac{\pi t^2}{2}\right)dt+vs\left(cos\left(\frac{\pi s^2}{2}\right)-ssin\left(\frac{\pi s^2}{2}\right)\right),\hfill \\ \underset{0}{\overset{s}{\int }}sin\left(\frac{\pi t^2}{2}\right)dt+vs\left(scos\left(\frac{\pi s^2}{2}\right)+sin\left(\frac{\pi s^2}{2}\right)\right),1\hfill \end{array}\right)$$

for $\epsilon ,\eta =s$. Hence,

$$\begin{array}{c}\Delta =-\frac{1+s^2}{s^2{\left(-1+\left(1+\pi \left(s+s^3\right)\right)v\right)}^2}\frac{{𝜕}^2}{𝜕s^2}\hfill \\ -\frac{1+v\left(2+v+s^2\left(4v+\pi s\left(-2+\left(2+\pi \left(s+s^3\right)\right)v\right)\right)\right)}{s^4{\left(-1+\left(1+\pi \left(s+s^3\right)\right)v\right)}^2}\frac{{𝜕}^2}{𝜕v^2}\hfill \\ -\frac{-3-2s^2+v+\pi \left(s+s^3\right)\left(-1+\left(2+3s^2\right)v\right)}{s^3{\left(-1+\left(1+\pi \left(s+s^3\right)\right)v\right)}^3}\frac{𝜕}{𝜕s}\hfill \\ -\frac{\begin{array}{c}3+\pi \left(s+s^3\right)+2v-s\left(-4s+\pi \left(1+s^2\left(5+2\pi \left(s+s^3\right)\right)\right)\right)v\hfill \\ +\left(-1+\pi s\left(-2+s^2\left(-4+s\left(-6s+\pi \left(1+s^2\right)\left(3+\pi \left(s+s^3\right)\right)\right)\right)\right)\right)v^2\hfill \end{array}}{s^4{\left(-1+\left(1+\pi \left(s+s^3\right)\right)v\right)}^3}\frac{𝜕}{𝜕v}\hfill \\ +\frac{2\left(1+v+2s^{2}v\right)}{s^3{\left(-1+\left(1+\pi \left(s+s^3\right)\right)v\right)}^2}\frac{{𝜕}^2}{𝜕s𝜕v}\hfill \end{array}$$

and

$$\Delta \Omega =0.$$

Therefore, it is seen that the Gauss map of ${\Phi }_2^B\left(s,v\right)$ is harmonic (see Figure 4).

Similarly, if $\epsilon =0$ the following special case is obtained:

Case 3.3.3. Let $\epsilon =0$, $\eta \ne 0$, $\mu =0$, and $\tau =0$. Then, the constant angle ruled surface given with these criteria is represented by

$${\Phi }_3^B\left(s,v\right)=\alpha \left(s\right)+v\eta N$$

where $\alpha \left(s\right)$ is a planar curve. If the operations in Case 3.3.2 in Section 3.3 are carried out similarly, the following equations are obtained:

The Gauss map of ${\Phi }_3^B\left(s,v\right)$ is

$$\Omega =B.$$

The coefficients of the Laplacian $\Delta$ on the constant angle ruled surface are found as

$$\begin{array}{c}{\delta }_1=-\frac{1}{{\left(-1+v\eta \kappa \right)}^2},{\delta }_2=-\frac{{\left(-1+v\eta \kappa \right)}^2+{\left(v{\eta }_s\right)}^2}{{\eta }^2{\left(-1+v\eta \kappa \right)}^2},{\delta }_3=\frac{\left(1-v\eta \kappa \right){\eta }_s-v{\eta }^2{\kappa }_s}{\eta {\left(-1+v\eta \kappa \right)}^3},\hfill \\ \hfill \\ {\delta }_4=\frac{-v^2{\eta }^3{\kappa }^3-v{{\eta }_s}^2+\eta \kappa \left(-1+v^2{{\eta }_s}^2\right)+v{\eta }^2\left(2{\kappa }^2+v{\eta }_s{\kappa }_s\right)}{{\eta }^2{\left(-1+v\eta \kappa \right)}^3},{\delta }_5=\frac{2v{\eta }_s}{\eta {\left(-1+v\eta \kappa \right)}^2}.\hfill \end{array}$$

Consequently, the Laplacian of the Gauss map of ${\Phi }_3^B\left(s,v\right)$ is

$$\Delta \Omega =0.$$

(10)

Theorem 8.

Let ${\Phi }_3^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector. The Gauss map of the constant angle surface ${\Phi }_3^B\left(s,v\right)$ is harmonic if, and only if, the base curve $\alpha \left(s\right)$ is a planar curve.

Proof. 

Let ${\Phi }_3^B\left(s,v\right)$ be a constant angle ruled surface parallel to the binormal vector. Here, $\tau =0$ and Equation (10) gives us the necessary and sufficient condition for the Gauss map of the constant angle surface ${\Phi }_3^B\left(s,v\right)$ to be harmonic. □

Example 5.

Let us consider the planar curve in Example 2. The constant angle ruled surface parallel to the binormal vector ${\Phi }_3^B\left(s,v\right)$ is represented by

$${\Phi }_3^B\left(s,v\right)=\left(\underset{0}{\overset{s}{\int }}cos\left(\frac{\pi t^2}{2}\right)dt-vssin\left(\frac{\pi s^2}{2}\right),\underset{0}{\overset{s}{\int }}sin\left(\frac{\pi t^2}{2}\right)dt+vscos\left(\frac{\pi s^2}{2}\right),1\right)$$

for $\eta =s$. Hence,

$$\begin{array}{c}\Delta =-\frac{1}{{\left(-1+\pi s^{2}v\right)}^2}\frac{{𝜕}^2}{𝜕s^2}-\frac{1+v\left(v+\pi s^2\left(-2+\pi s^{2}v\right)\right)}{s^2{\left(-1+\pi s^{2}v\right)}^2}\frac{{𝜕}^2}{𝜕v^2}+\frac{1-2\pi s^{2}v}{s{\left(-1+\pi s^{2}v\right)}^3}\frac{𝜕}{𝜕s}\hfill \\ +\frac{-v+\pi s^2\left(-1+v\left(2v+\pi s^2\left(2-\pi s^{2}v\right)\right)\right)}{s^2{\left(-1+\pi s^{2}v\right)}^3}\frac{𝜕}{𝜕v}+\frac{2v}{s{\left(-1+\pi s^{2}v\right)}^2}\frac{{𝜕}^2}{𝜕s𝜕v}\hfill \end{array}$$

and

$$\Delta \Omega =0.$$

Therefore, the Gauss map of ${\Phi }_3^B\left(s,v\right)$ is harmonic (see Figure 5).

4. Conclusions

In conclusion, this study involved the exploration of constant angle ruled surfaces featuring a pointwise 1-type Gauss map, one of the key approaches in surface classification. The novelty of this study is establishing a foundational understanding of the Gauss map for oriented surfaces based on the analysis of the Frenet elements of the base curves within Euclidean 3-space. After a thorough examination, we determined the essential criteria distinguishing the ruled surfaces with the pointwise 1-type of the Gauss map of the first and second kinds and the harmonic. Additionally, we provided illustrative examples of each class of these surfaces, which improve conceptual understanding by using graphical representations. This research provides knowledge that may have applications in computer-aided design, engineering, or architecture by providing important insights into the geometric features and classifications of ruled surfaces. One of the most attractive fields of study is curve and surface theory in Minkowski space, which has been taken into consideration from various aspects. In addition, there exists the classification of ruled surfaces with a pointwise 1-type Gauss map in Minkowski space too. This implies that the results of this research can be verified for space-like ruled surfaces with constant angles and pointwise 1-type Gauss maps, provided that the limitations on coordinate singularities resulting from the Lorentzian metric are thoroughly examined.