A Parallel Multi-Party Privacy-Preserving Record Linkage Method Based on a Consortium Blockchain
Abstract
1. Introduction
- We utilize a consortium blockchain to validate the trustworthiness of third parties and all involved parties, controlling data access and introducing a consensus algorithm to enhance the efficiency and security of the consortium blockchain;
- Using a homomorphic encryption technique for encoding the Bloom filter, the encryption process incorporates the MapReduce model for parallel encryption. This not only enhances computational efficiency but also strengthens the security of the encoding process;
- Using the binary storage tree to store the data to be linked and employing the Jaccard similarity function to calculate the similarity among the splitting Bloom filter encoding effectively reduces the number of comparisons among records.
- The experimental results show that our method can effectively ensure data security while also exhibiting relatively high linkage quality and scalability.
2. Related Works
3. Preliminaries and Background
3.1. PPRL
3.2. Bloom Filter
3.3. Jaccard Similarity Function
3.4. Splitting Bloom Filter
3.5. Homomorphic Encryption
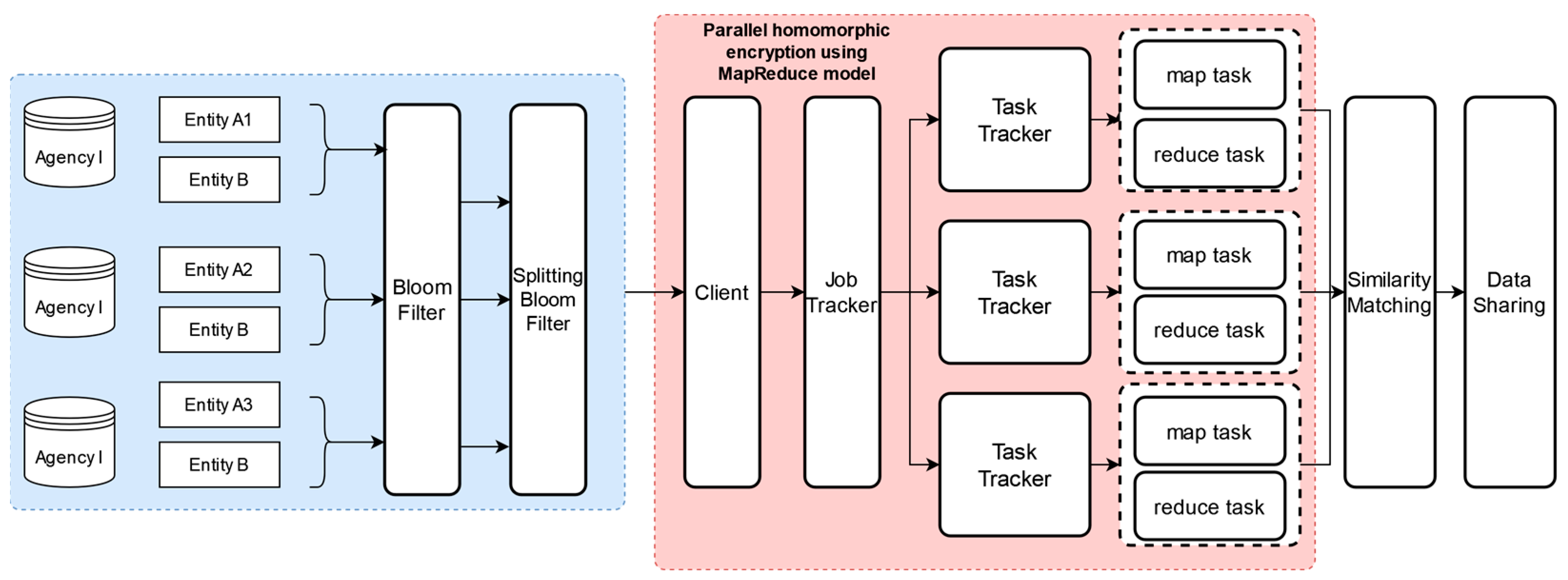
3.6. MapReduce Model
3.7. Consortium Blockchain
3.8. Consensus Algorithm
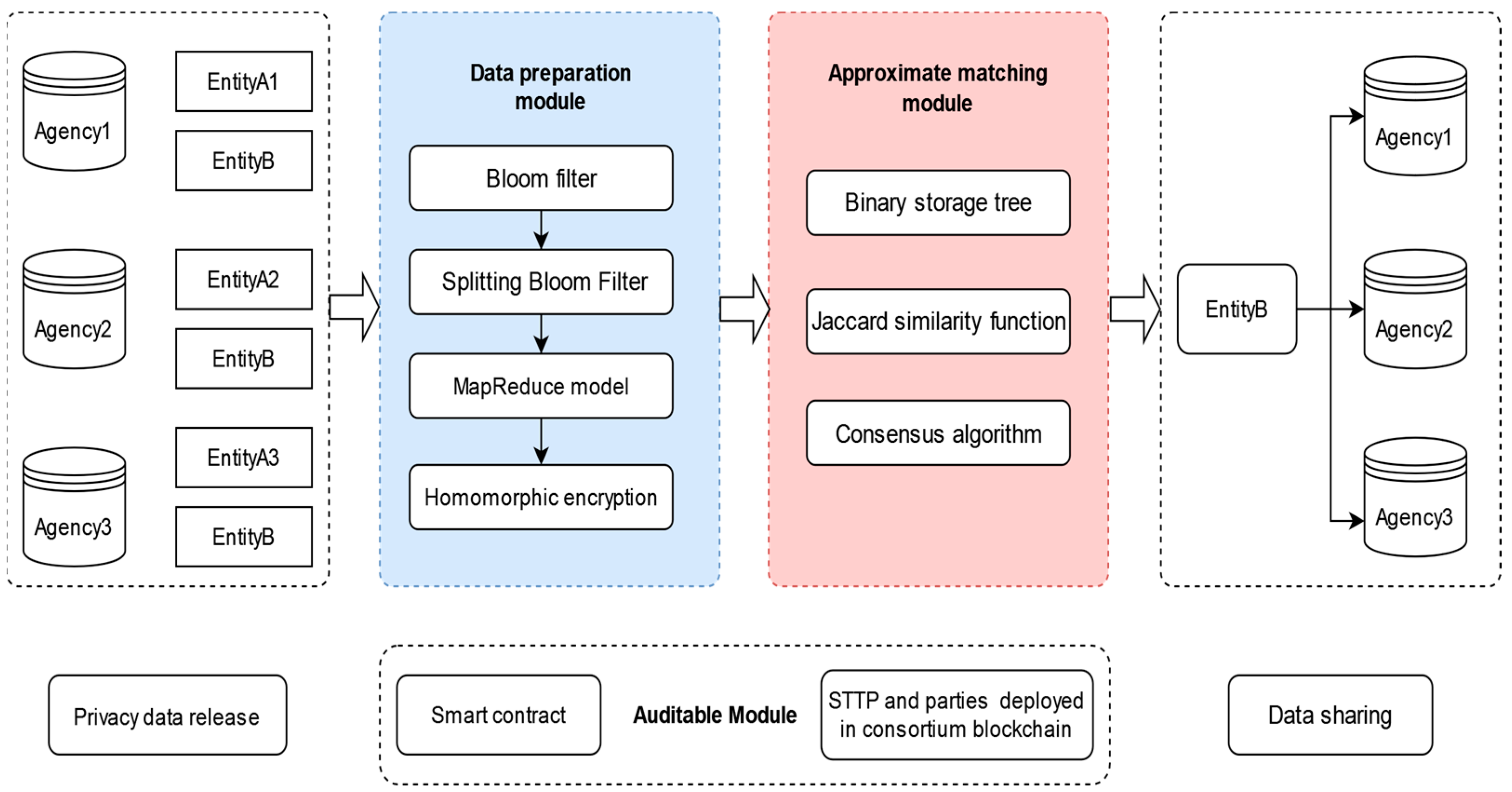
4. Methods
4.1. Data Preparation and Generation Module
4.1.1. Generate Key
4.1.2. Encryption Process
4.1.3. Decryption Process
| Algorithm 1 Parallel Homomorphic Encryption Algorithm |
| Input: Part of the SBF for Participants Output: The encrypted SBF for Participants 1: for each sets of SBF in do 2: public key , private key generate_key 3: Set the plaintext as (MB), divide it into groups of 256 bits long packets 4: The number of packets is 5: for each sets of SBF in do 6: Convert each packet plaintext into a large integer type, set the value to 7: if is an even number then 8: 9: else if 10: 11: end if 12: integer 13: , 14: |
4.2. Approximate Matching Module
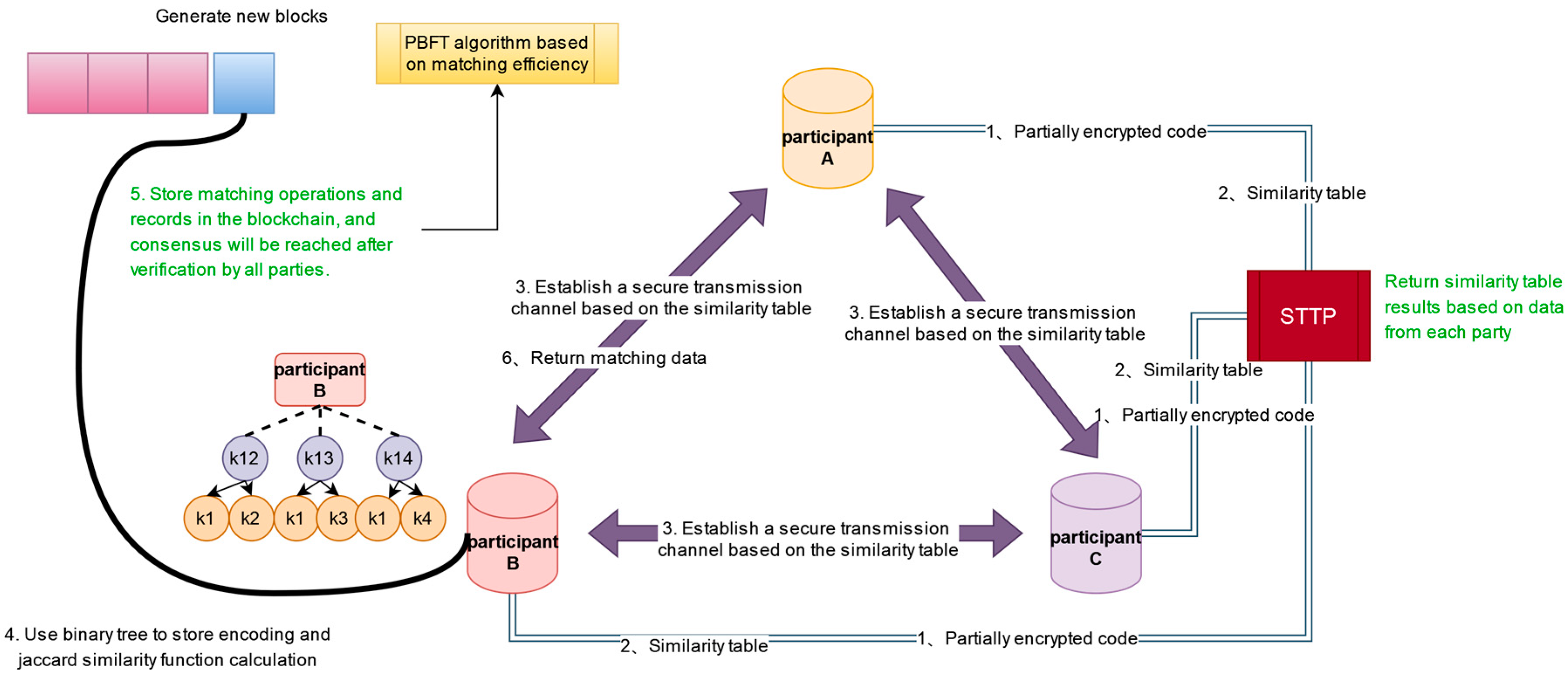
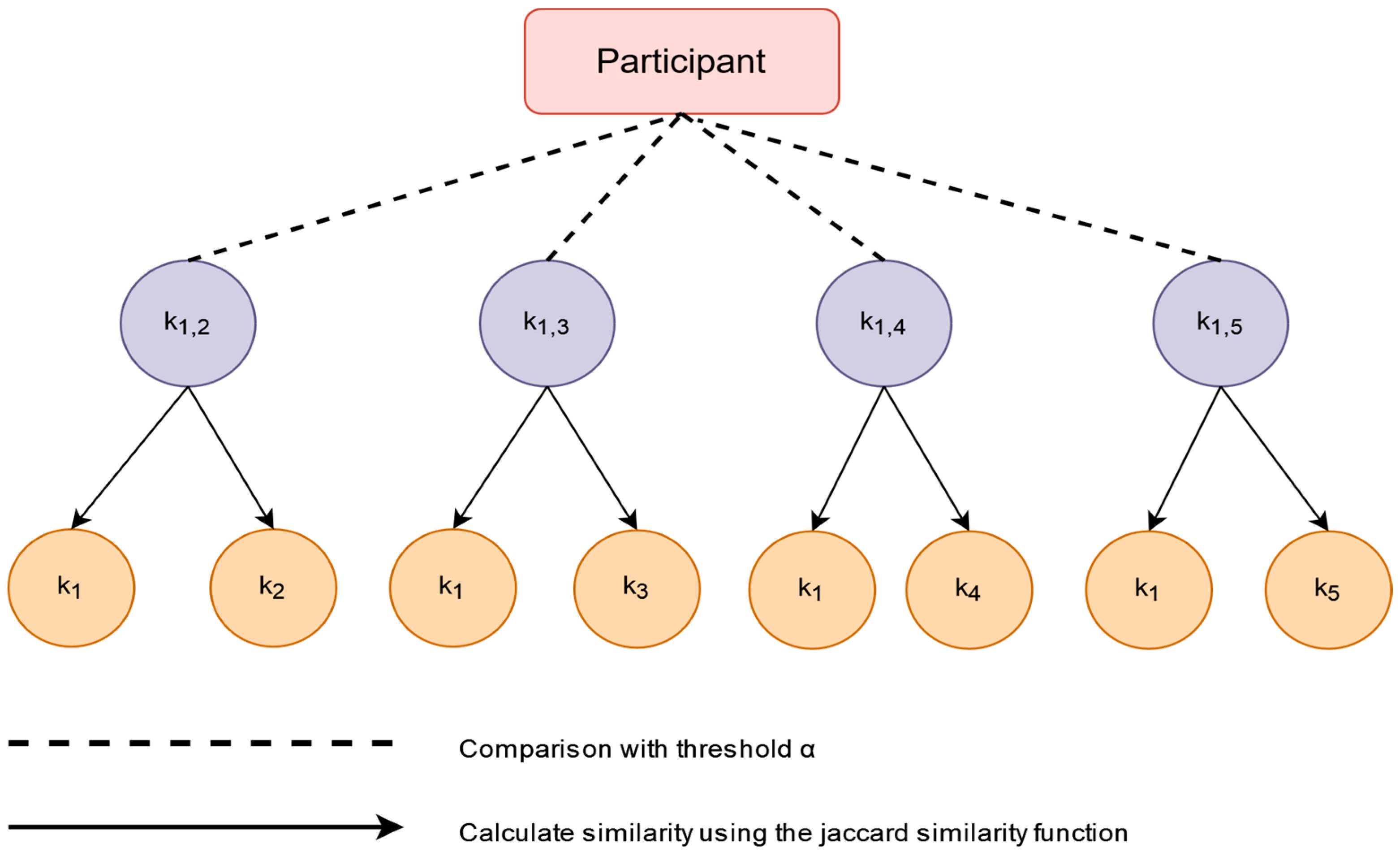
4.2.1. Binary Storage Tree
| Algorithm 2 Similarity Calculation Algorithm |
| Input: Part of the SBF encrypted by the participants Output: The record group successfully matched by each participant 1: Build the binary storage tree to store the SBF of participants 2: for each fixed encrypted value in do 3: for others fixed encrypted value in do 4: 5: 6: Calculate the Jaccard similarity value between left and right subtree SBF 7: 8: Compared with the similarity in the table , is the error value 9: if then 10: Indicates that two splitting bloom filter match 11: end if 12: end for 13: end for |
4.2.2. Consensus Algorithm
| Algorithm 3 Node voting algorithm |
| Input: The number of pending votes for all nodes Output: Number of votes cast on all nodes 1: for i = 1:nodenumber 2: for j = 1:nodenumber/2 3: selected_node = randi(nodenumber/2) 4: nodes_getticket(selected_node) = nodes_getticket(selected_node) + 1 5: end 6: for k = 1:ticket-nodenumber/2 7: 8: selected_node = randi([t, nodenumber]) 9: nodes_getticket(selected_node) = nodes_getticket(selected_node) + 1 10: end 11: end |
4.3. Auditable Module
| Algorithm 4 Auditable algorithm |
| Input: Encryption value threshold a table consisting of approximately matching candidate record groups Output: The set composed of the true matching candidate record groups 1: The input of each participant is SBF , STTP verifies the input of each participant 2: STTP performs the similarity calculation and stores entity pairs with high similarity probability in table 3: Send the table to all participants 4: The participants exchange the rest of the entities in the table 5: 6: Compared with the similarity in the table , is the error value 7: if then 8: Indicates that STTP is trusted 9: end if 10: The participants exchange the similarity calculated in the previous step and au dited whether the participant were trustworthy 11: 12: if then 13: Add it to 14: end if |
5. Security Analysis
6. Experimental Results
6.1. Experiment Preparation
6.2. Experimental Results and Analysis
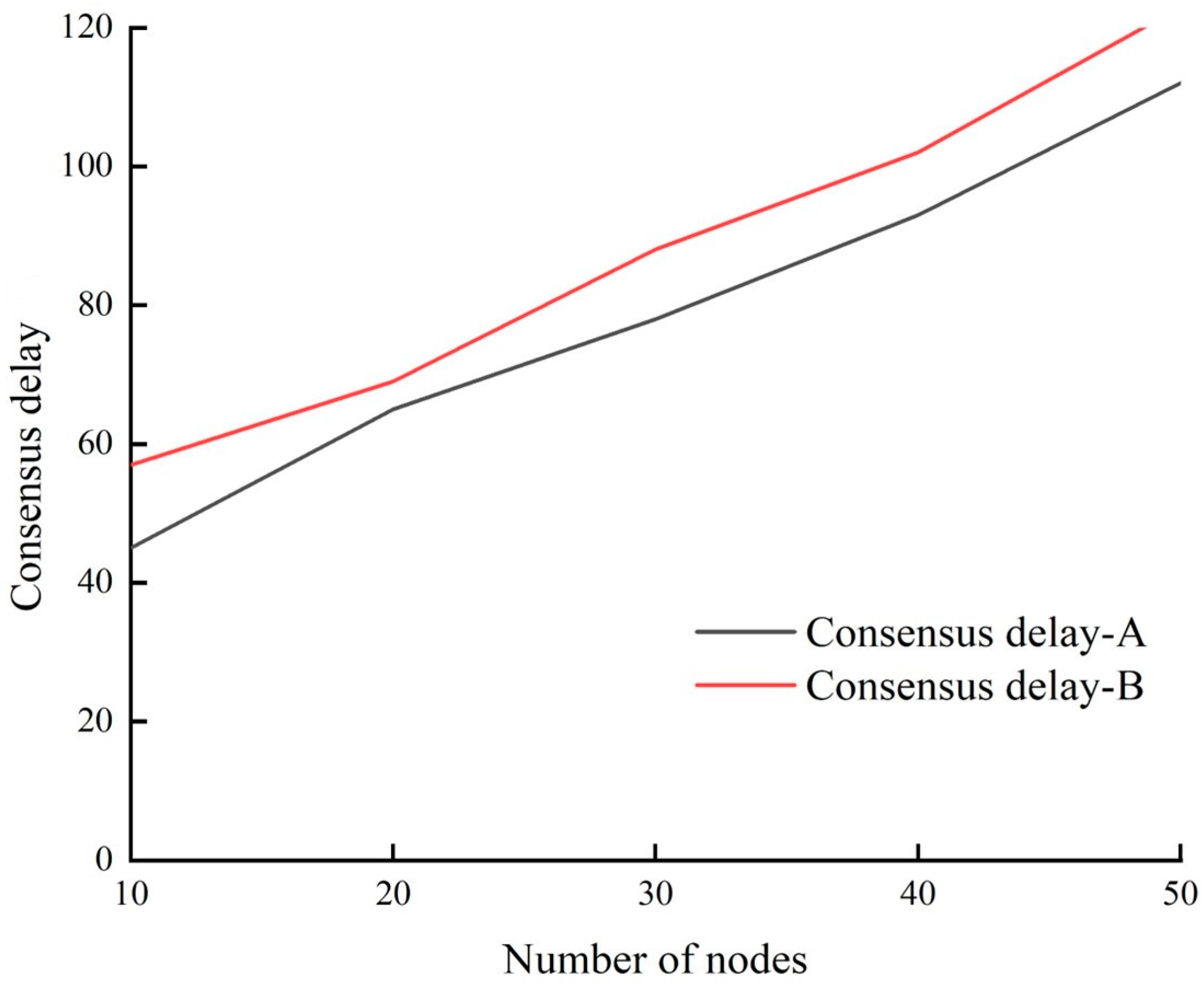
6.2.1. Scalability Assessment
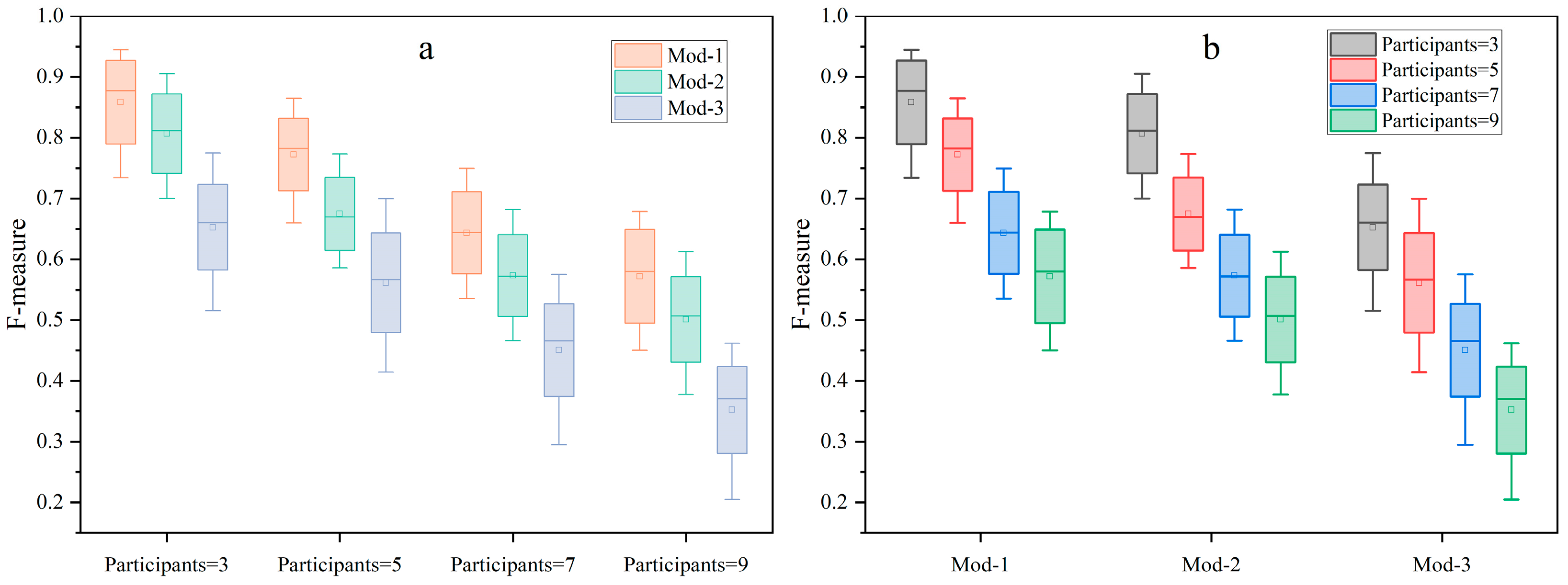
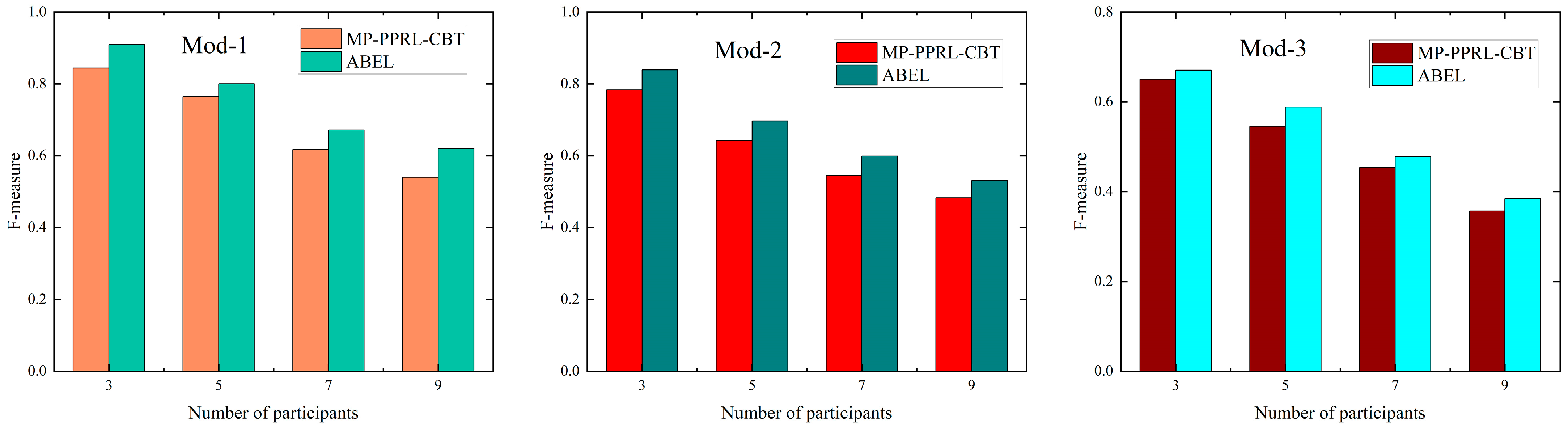
6.2.2. Method Performance Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, T.; Gu, Y.; Zhou, X.; Ma, Q.; Yu, G. An effective and efficient truth discovery framework over data streams. In Proceedings of the EDBT, Venice, Italy, 21–24 March 2017; pp. 180–191. [Google Scholar]
- Wang, J.; Li, T.; Wang, A.; Liu, X.; Chen, L.; Chen, J.; Liu, J.; Wu, J.; Li, F.; Gao, Y. Real-time Workload Pattern Analysis for Large-scale Cloud Databases. arXiv 2023, arXiv:2307.02626. [Google Scholar] [CrossRef]
- Vatsalan, D.; Christen, P.; Verykios, V.S. A taxonomy of privacy-preserving record linkage techniques. Inf. Syst. 2013, 38, 946–969. [Google Scholar] [CrossRef]
- Christen, P.; Vatsalan, D. A Flexible Data Generator for Privacy-Preserving Data Mining and Record Linkage; The Australian National University: Canberra, Australia, 2012. [Google Scholar]
- Christen, P.; Vatsalan, D.; Verykios, V.S. Challenges for privacy preservation in data integration. J. Data Inf. Qual. (JDIQ) 2014, 5, 1–3. [Google Scholar] [CrossRef]
- Vatsalan, D.; Karapiperis, D.; Gkoulalas-Divanis, A. An Overview of Big Data Issues in Privacy-Preserving Record Linkage. In Proceedings of the Algorithmic Aspects of Cloud Computing: 4th International Symposium, ALGOCLOUD 2018, Helsinki, Finland, 20–21 August 2018; Revised Selected Papers 4. 2019; pp. 118–136. [Google Scholar]
- Pita, R.; Pinto, C.; Melo, P.; Silva, M.; Barreto, M.; Rasella, D. A Spark-based Workflow for Probabilistic Record Linkage of Healthcare Data. In Proceedings of the EDBT/ICDT Workshops, Brussels, Belgium, 27 March 2015; pp. 17–26. [Google Scholar]
- Papadakis, G.; Skoutas, D.; Thanos, E.; Palpanas, T. A survey of blocking and filtering techniques for entity resolution. arXiv 2019, arXiv:1905.06167. [Google Scholar]
- El-Hindi, M.; Heyden, M.; Binnig, C.; Ramamurthy, R.; Arasu, A.; Kossmann, D. Blockchaindb-towards a shared database on blockchains. In Proceedings of the 2019 International Conference on Management of Data, Amsterdam, The Netherlands, 30 June–5 July 2019; pp. 1905–1908. [Google Scholar]
- Karapiperis, D.; Gkoulalas-Divanis, A.; Verykios, V.S. FEDERAL: A framework for distance-aware privacy-preserving record linkage. IEEE Trans. Knowl. Data Eng. 2017, 30, 292–304. [Google Scholar] [CrossRef]
- Karapiperis, D.; Gkoulalas-Divanis, A.; Verykios, V.S. Distance-aware encoding of numerical values for privacy-preserving record linkage. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017; pp. 135–138. [Google Scholar]
- Durham, E.A.; Kantarcioglu, M.; Xue, Y.; Toth, C.; Kuzu, M.; Malin, B. Composite bloom filters for secure record linkage. IEEE Trans. Knowl. Data Eng. 2013, 26, 2956–2968. [Google Scholar] [CrossRef] [PubMed]
- Nóbrega, T.; Pires, C.E.S.; Nascimento, D.C. Blockchain-based privacy-preserving record linkage: Enhancing data privacy in an untrusted environment. Inf. Syst. 2021, 102, 101826. [Google Scholar] [CrossRef]
- Vatsalan, D.; Christen, P. Multi-party privacy-preserving record linkage using bloom filters. arXiv 2016, arXiv:1612.08835. [Google Scholar]
- Han, S.; Shen, D.; Nie, T.; Kou, Y.; Yu, G. An enhanced privacy-preserving record linkage approach for multiple databases. Clust. Comput. 2022, 25, 3641–3652. [Google Scholar] [CrossRef]
- Yao, S.; Ren, Y.; Wang, D.; Wang, Y.; Yin, W.; Yuan, L. SNN-PPRL: A secure record matching scheme based on siamese neural network. J. Inf. Secur. Appl. 2023, 76, 103529. [Google Scholar] [CrossRef]
- Randall, S.M.; Brown, A.P.; Ferrante, A.M.; Boyd, J.H.; Semmens, J.B. Privacy preserving record linkage using homomorphic encryption. In Proceedings of the First International Workshop on Population Informatics for Big Data (PopInfo’15), Sydney, Australia, 10 August 2015. [Google Scholar]
- Christen, P.; Schnell, R.; Ranbaduge, T.; Vidanage, A. A critique and attack on “Blockchain-based privacy-preserving record linkage”. Inf. Syst. 2022, 108, 101930. [Google Scholar] [CrossRef]
- Yao, H.; Wei, H.; Han, S.; Shen, D. Efficient multi-party privacy-preserving record linkage based on blockchain. In Proceedings of the International Conference on Web Information Systems and Applications, Dalian, China, 16–18 September 2022; pp. 649–660. [Google Scholar]
- Christen, P.; Ranbaduge, T.; Vatsalan, D.; Schnell, R. Precise and fast cryptanalysis for Bloom filter based privacy-preserving record linkage. IEEE Trans. Knowl. Data Eng. 2018, 31, 2164–2177. [Google Scholar] [CrossRef]
- Vidanage, A.; Ranbaduge, T.; Christen, P.; Schnell, R. Efficient pattern mining based cryptanalysis for privacy-preserving record linkage. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 1698–1701. [Google Scholar]
- Li, T.; Huang, R.; Chen, L.; Jensen, C.S.; Pedersen, T.B. Compression of uncertain trajectories in road networks. Proc. VLDB Endow. 2020, 13, 1050–1063. [Google Scholar] [CrossRef]
- Di Matteo, S.; Gerfo, M.L.; Saponara, S. VLSI Design and FPGA implementation of an NTT hardware accelerator for Homomorphic seal-embedded library. IEEE Access 2023, 11, 72498–72508. [Google Scholar] [CrossRef]
- Doröz, Y.; Öztürk, E.; Sunar, B. Accelerating fully homomorphic encryption in hardware. IEEE Trans. Comput. 2014, 64, 1509–1521. [Google Scholar] [CrossRef]
- Jung, W.; Lee, E.; Kim, S.; Kim, J.; Kim, N.; Lee, K.; Min, C.; Cheon, J.H.; Ahn, J.H. Accelerating fully homomorphic encryption through architecture-centric analysis and optimization. IEEE Access 2021, 9, 98772–98789. [Google Scholar] [CrossRef]
- Tien Tuan Anh, D.; Ji, W.; Gang, C.; Rui, L.; Blockbench, A. Framework for Analyzing Private Blockchains. In Proceedings of the 2017 ACM International Conference on Management of Data, Chicago, IL, USA, 14–19 May 2017; pp. 14–19. [Google Scholar]
- Boussis, D.; Dritsas, E.; Kanavos, A.; Sioutas, S.; Tzimas, G.; Verykios, V.S. MapReduce Implementations for Privacy Preserving Record Linkage. In Proceedings of the 10th Hellenic Conference on Artificial Intelligence, Athens, Greece, 9–12 July 2018; pp. 1–4. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; pp. 223–238. [Google Scholar]
- Nóbrega, T.; Pires, C.E.S.; Nascimento, D.C. Explanation and answers to critiques on: Blockchain-based Privacy-Preserving Record Linkage. Inf. Syst. 2022, 108, 101935. [Google Scholar] [CrossRef]
- Li, T.; Chen, L.; Jensen, C.S.; Pedersen, T.B. TRACE: Real-time compression of streaming trajectories in road networks. Proc. VLDB Endow. 2021, 14, 1175–1187. [Google Scholar] [CrossRef]
- Li, T.; Chen, L.; Jensen, C.S.; Pedersen, T.B.; Gao, Y.; Hu, J. Evolutionary clustering of moving objects. In Proceedings of the 2022 IEEE 38th International Conference on Data Engineering (ICDE), Kuala Lumpur, Malaysia, 9–12 May 2022; pp. 2399–2411. [Google Scholar]




| Method | Advantages | Disadvantages | Solutions |
|---|---|---|---|
| The PPRL methods based on the honest but curious model | Linkage quality is high and efficiency is fast | Typically, the linkage needs to be entrusted to STTPs | Consortium blockchain |
| The PPRL methods based on the malicious adversary model | The security of linkage is high | The efficiency is slow and it cannot verify which malicious party deviated from the protocol | Consortium blockchain and MapReduce model |
| The PPRL methods based on blockchain | Auditing all parties involved in the PPRL process for potential malicious tampering or attacks | The efficiency is slow and still has security issues | Homomorphic encryption, consensus algorithm, and binary storage tree |
| Parameters | Description |
|---|---|
| Participant of PPRL | |
| Entity | |
| Anonymized entity | |
| Dataset of participant | |
| Anonymized dataset of participant | |
| Bloom filter length | |
| Collection of q-grams to be added to Bloom filter | |
| hash functions | |
| Number of splits | |
| Splitting Bloom filter (SBF) | |
| Homomorphic encryption value of SBF | |
| Threshold α | |
| Threshold β (β = α − error) | |
| List of entity (id) pairs with their similarity values | |
| A set of SBF () | |
| Error |
| Method | Dataset Size = 5 K | Dataset Size = 50 K | Dataset Size = 500 K |
|---|---|---|---|
| MP-PPRL-CBT | 12 | 90 | 1300 |
| MP-PPRL-CBT (Binary Storage Tree) | 70 | 600 | 8800 |
| MP-PPRL-CBT (MapReduce) | 18 | 130 | 2100 |
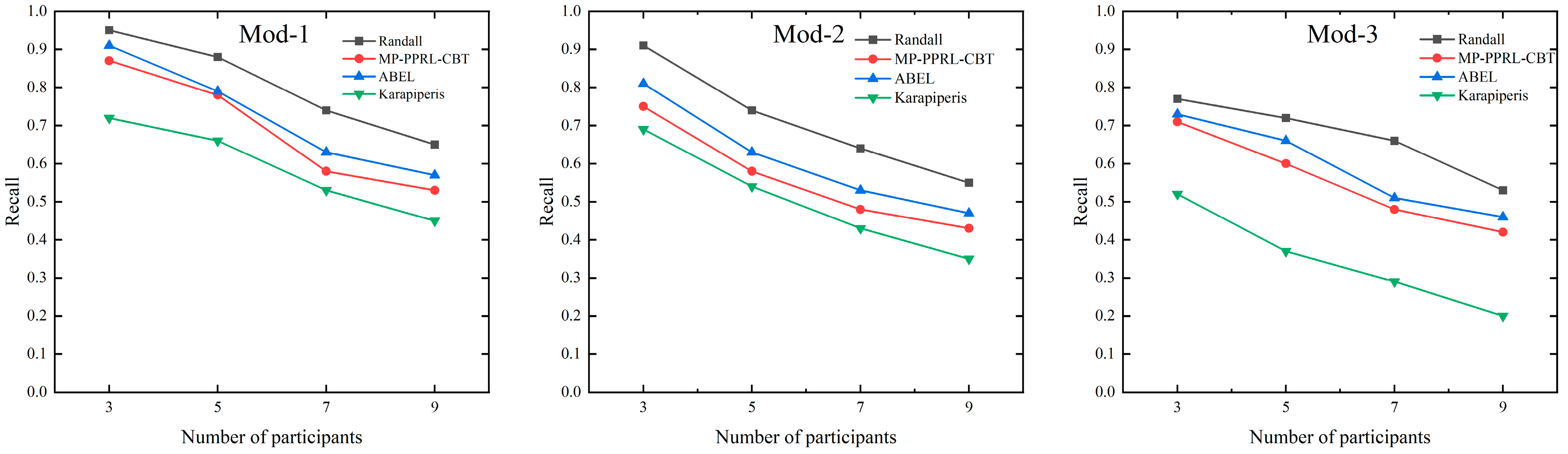
| Method | Participants = 3 | Participants = 5 | Participants = 7 | Participants = 9 |
|---|---|---|---|---|
| Randall | 0.95 (Mod-1) | 0.88 (Mod-1) | 0.74 (Mod-1) | 0.65 (Mod-1) |
| 0.91 (Mod-2) | 0.74 (Mod-2) | 0.64 (Mod-2) | 0.55 (Mod-2) | |
| 0.77 (Mod-3) | 0.72 (Mod-3) | 0.66 (Mod-3) | 0.53 (Mod-3) | |
| MP-PPRL-CBT | 0.87 (Mod-1) | 0.78(Mod-1) | 0.58 (Mod-1) | 0.53 (Mod-1) |
| 0.75 (Mod-2) | 0.58 (Mod-2) | 0.48 (Mod-2) | 0.43 (Mod-2) | |
| 0.71 (Mod-3) | 0.61 (Mod-3) | 0.48 (Mod-3) | 0.42 (Mod-3) | |
| ABEL | 0.91 (Mod-1) | 0.79 (Mod-1) | 0.63 (Mod-1) | 0.57 (Mod-1) |
| 0.81 (Mod-2) | 0.63 (Mod-2) | 0.53 (Mod-2) | 0.47 (Mod-2) | |
| 0.73 (Mod-3) | 0.66 (Mod-3) | 0.51 (Mod-3) | 0.46 (Mod-3) | |
| Karapiperis | 0.72 (Mod-1) | 0.66 (Mod-1) | 0.53 (Mod-1) | 0.45 (Mod-1) |
| 0.69 (Mod-2) | 0.54 (Mod-2) | 0.43 (Mod-2) | 0.35 (Mod-2) | |
| 0.52 (Mod-3) | 0.37 (Mod-3) | 0.29 (Mod-3) | 0.20 (Mod-3) |
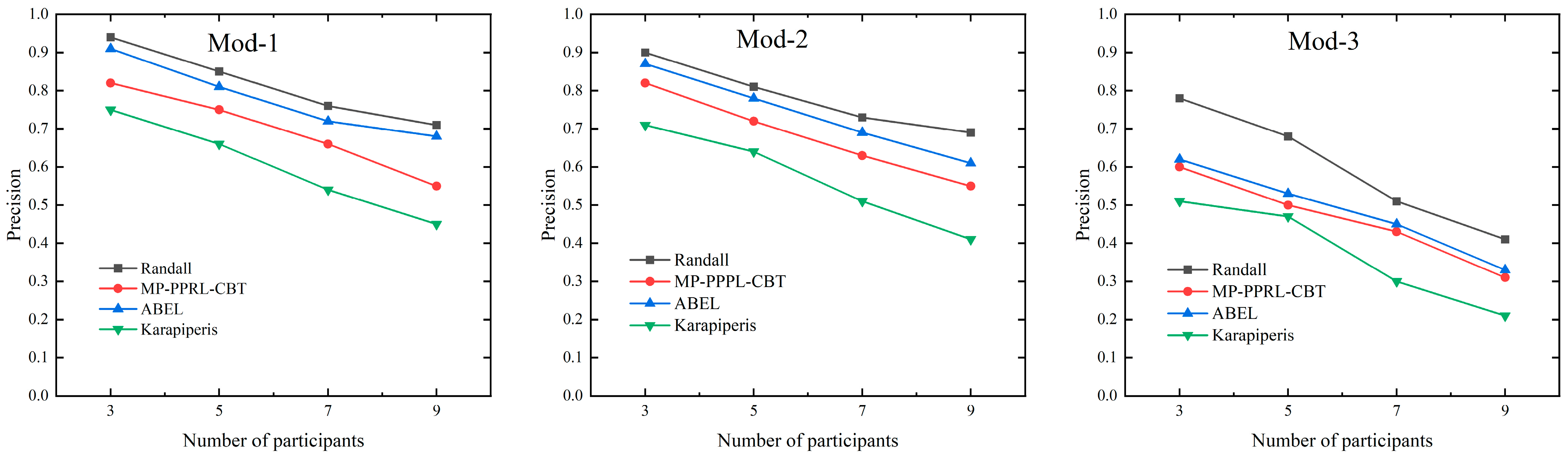
| Method | Participants = 3 | Participants = 5 | Participants = 7 | Participants = 9 |
|---|---|---|---|---|
| Randall | 0.94 (Mod-1) | 0.85 (Mod-1) | 0.76 (Mod-1) | 0.71 (Mod-1) |
| 0.90 (Mod-2) | 0.81 (Mod-2) | 0.73 (Mod-2) | 0.69 (Mod-2) | |
| 0.78 (Mod-3) | 0.68 (Mod-3) | 0.51 (Mod-3) | 0.41 (Mod-3) | |
| MP-PPRL-CBT | 0.82 (Mod-1) | 0.75(Mod-1) | 0.66 (Mod-1) | 0.55 (Mod-1) |
| 0.82 (Mod-2) | 0.72 (Mod-2) | 0.63 (Mod-2) | 0.55 (Mod-2) | |
| 0.60 (Mod-3) | 0.50 (Mod-3) | 0.43 (Mod-3) | 0.31 (Mod-3) | |
| ABEL | 0.91 (Mod-1) | 0.81 (Mod-1) | 0.72 (Mod-1) | 0.68 (Mod-1) |
| 0.87 (Mod-2) | 0.78 (Mod-2) | 0.69 (Mod-2) | 0.61 (Mod-2) | |
| 0.62 (Mod-3) | 0.53 (Mod-3) | 0.45 (Mod-3) | 0.33 (Mod-3) | |
| Karapiperis | 0.75 (Mod-1) | 0.66 (Mod-1) | 0.54 (Mod-1) | 0.45 (Mod-1) |
| 0.71 (Mod-2) | 0.64 (Mod-2) | 0.51 (Mod-2) | 0.41 (Mod-2) | |
| 0.51 (Mod-3) | 0.47 (Mod-3) | 0.30 (Mod-3) | 0.21 (Mod-3) |
| Method | Participants = 3 | Participants = 5 | Participants = 7 | Participants = 9 |
|---|---|---|---|---|
| Randall | 0.94 (Mod-1) | 0.86 (Mod-1) | 0.74 (Mod-1) | 0.67 (Mod-1) |
| 0.90 (Mod-2) | 0.77 (Mod-2) | 0.68 (Mod-2) | 0.61 (Mod-2) | |
| 0.77 (Mod-3) | 0.69 (Mod-3) | 0.57 (Mod-3) | 0.46 (Mod-3) | |
| MP-PPRL-CBT | 0.84 (Mod-1) | 0.76(Mod-1) | 0.61 (Mod-1) | 0.53 (Mod-1) |
| 0.78 (Mod-2) | 0.64 (Mod-2) | 0.54 (Mod-2) | 0.48 (Mod-2) | |
| 0.65 (Mod-3) | 0.54 (Mod-3) | 0.45 (Mod-3) | 0.35 (Mod-3) | |
| ABEL | 0.91 (Mod-1) | 0.80 (Mod-1) | 0.67 (Mod-1) | 0.62 (Mod-1) |
| 0.83 (Mod-2) | 0.69 (Mod-2) | 0.59 (Mod-2) | 0.53 (Mod-2) | |
| 0.67 (Mod-3) | 0.58 (Mod-3) | 0.48 (Mod-3) | 0.38 (Mod-3) | |
| Karapiperis | 0.73 (Mod-1) | 0.66 (Mod-1) | 0.53 (Mod-1) | 0.45 (Mod-1) |
| 0.69 (Mod-2) | 0.58 (Mod-2) | 0.46 (Mod-2) | 0.37 (Mod-2) | |
| 0.51 (Mod-3) | 0.41 (Mod-3) | 0.29 (Mod-3) | 0.20 (Mod-3) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Wang, Z.; Shen, D.; Wang, C. A Parallel Multi-Party Privacy-Preserving Record Linkage Method Based on a Consortium Blockchain. Mathematics 2024, 12, 1854. https://doi.org/10.3390/math12121854
Han S, Wang Z, Shen D, Wang C. A Parallel Multi-Party Privacy-Preserving Record Linkage Method Based on a Consortium Blockchain. Mathematics. 2024; 12(12):1854. https://doi.org/10.3390/math12121854
Chicago/Turabian StyleHan, Shumin, Zikang Wang, Dengrong Shen, and Chuang Wang. 2024. "A Parallel Multi-Party Privacy-Preserving Record Linkage Method Based on a Consortium Blockchain" Mathematics 12, no. 12: 1854. https://doi.org/10.3390/math12121854
APA StyleHan, S., Wang, Z., Shen, D., & Wang, C. (2024). A Parallel Multi-Party Privacy-Preserving Record Linkage Method Based on a Consortium Blockchain. Mathematics, 12(12), 1854. https://doi.org/10.3390/math12121854





