A Multi-Party Privacy-Preserving Record Linkage Method Based on Secondary Encoding

Abstract

With the advent of the big data era, data security and sharing have become the core elements of new-era data processing. Privacy-preserving record linkage (PPRL), as a method capable of accurately and securely matching and sharing the same entity across multiple data sources, is receiving increasing attention. Among the existing research methods, although PPRL methods based on Bloom Filter encoding excel in computational efficiency, they are susceptible to privacy attacks, and the security risks they face cannot be ignored. To balance the contradiction between security and computational efficiency, we propose a multi-party PPRL method based on secondary encoding. This method, based on Bloom Filter encoding, generates secondary encoding according to well-designed encoding rules and utilizes the proposed linking rules for secure matching. Owing to its excellent encoding and linking rules, this method successfully addresses the balance between security and computational efficiency. The experimental results clearly show that, in comparison to the original Bloom Filter encoding, this method has nearly equivalent computational efficiency and linkage quality. The proposed rules can effectively prevent the re-identification problem in Bloom Filter encoding (proven). Compared to existing privacy-preserving record linkage methods, this method shows higher security, making it more suitable for various practical application scenarios. The introduction of this method is of great significance for promoting the widespread application of privacy-preserving record linkage technology.

1. Introduction

As the Internet continues to evolve, big data has become a critically important strategic resource, with its profound impact spanning various fields such as hospitals, enterprises, and governments. The linking and integration of data not only help various industries gain value but also drive continuous progress in human society. Record linkage [1], as a core technology, can accurately match entities from different data sources to the same real-world entity [2], thereby facilitating data integration and sharing. However, record linkage faces significant challenges [3,4,5], with the most prominent being privacy and security concerns. In the process of linking data, given that the data contain sensitive information such as personal details, medical data, etc., we must carefully consider and properly address privacy protection issues to ensure the security of the data. To address this challenge, PPRL technology [6,7] has emerged. PPRL aims to achieve accurate linkage of records between multiple data sources while ensuring no additional data source information is disclosed, thereby guaranteeing the security. Here is an example from the medical field. When patients receive treatment at different healthcare institutions, it is crucial for their medical information to be mutually identifiable and shareable. The key to this process is how to achieve sharing only the user’s medical condition information without compromising the patient’s privacy. Through PPRL technology, this information can be shared while protecting patient privacy, allowing for more accurate analysis of patient conditions and enhancing medical quality and efficiency. The application of this technology is not only beneficial to the healthcare sector but also provides feasible solutions for other industries to achieve data sharing while protecting privacy [8,9,10].

Although PPRL demonstrates significant potential in theory, such as its wide applicability in deidentified records within a public health surveillance system [11], PPRL for the context of a national statistical institute [12], privacy protection in medical data [13], and as a privacy-preserving tool for clinical research network [14], as well as achieving efficient record linkage in large datasets [15], its practical application has encountered certain limitations and challenges [16]. This is mainly due to the challenge of striking an ideal balance between computational efficiency and security. In PPRL technology, data encoding and data encryption are two commonly used data protection measures. While encryption-based PPRL methods can provide high security [17], they often come with high computational costs, making them difficult to apply to large datasets. However, encoding-based PPRL methods often employ Bloom Filter encoding (BFS). For instance, Randall, S.M. et al. used encrypted personal identifying information in a probability-based linkage framework [18]. Similarly, Karapiperis, D et al. proposed a fast scheme for online record linkage based on Bloom Filters [19], further demonstrating the practicality and efficiency of Bloom Filters in PPRL methods. Although BFS excels in improving computational efficiency, in the process of linking different data sources, BFS is susceptible to attacks. These attacks include brute-force collision attacks on hash algorithms or frequency attacks and password attacks on BFS. [20], thereby increasing the risk of privacy leakage. In PPRL, attackers may exploit the characteristics of these technologies like BFS, employing precise password analysis and other methods to reveal personal identity information, thereby increasing the risk of privacy leakage [21,22]. Therefore, finding ways to enhance the security of PPRL technology while ensuring computational efficiency has become an urgent problem to solve. This not only requires innovation and optimization at the technical level but also necessitates a deeper understanding of the inherent requirements of data privacy protection [23], thus developing more secure and efficient PPRL methods.

To address the challenge of balancing computational efficiency and security in PPRL technology, we propose a multi-party PPRL method based on secondary encoding. This method aims to ensure data privacy while minimizing computational resource consumption as much as possible, making PPRL methods more efficient and practical in real-world applications. By employing secondary encoding technology, we are able to enhance data security while still maintaining high scalability, thereby laying a solid foundation for the widespread application of PPRL technology.

The contributions are as follows:

(1)

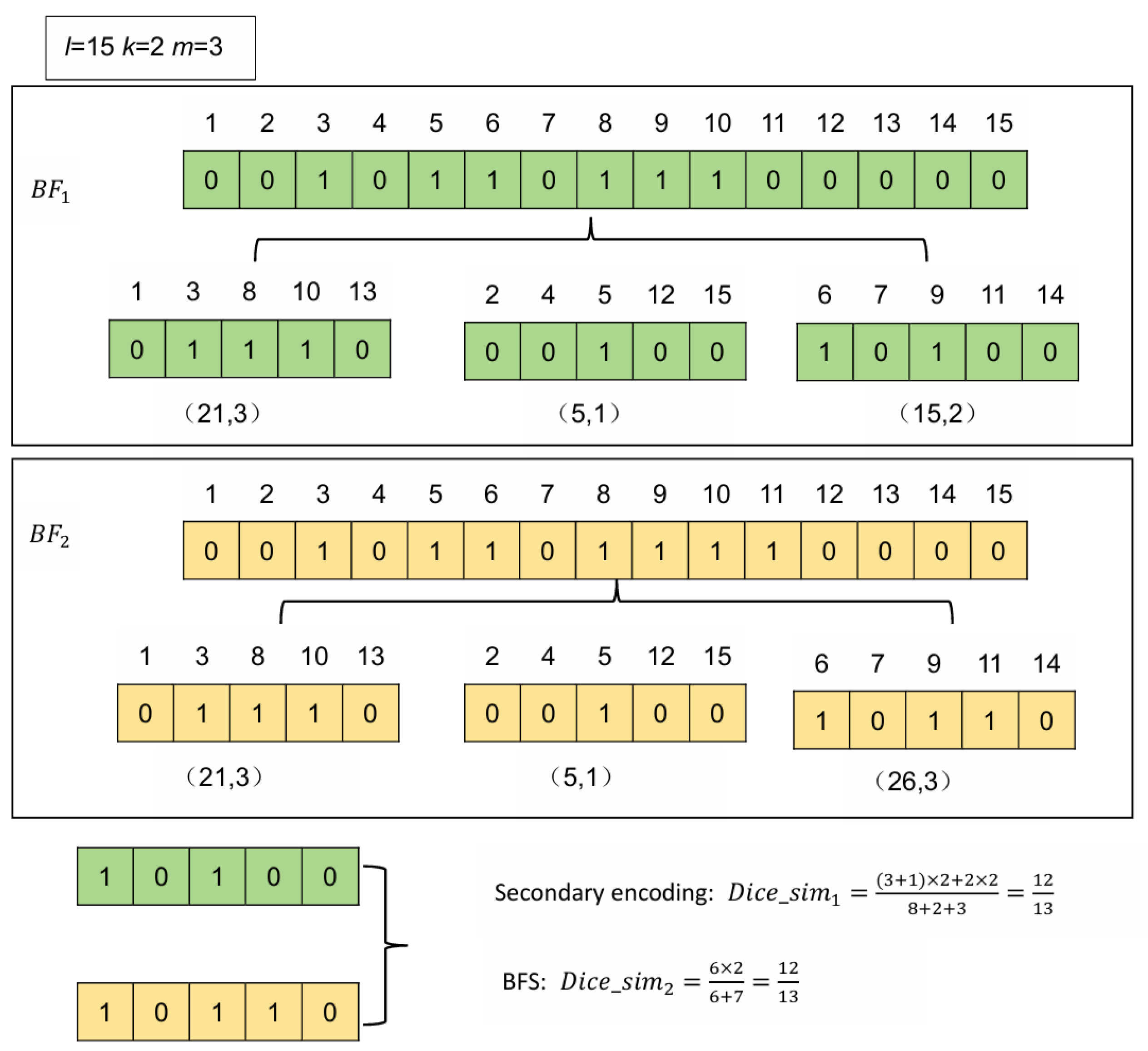
By introducing secondary encoding, security is enhanced. The BFS is divided into multiple splits, and by setting certain rules, secondary encoding is generated for each split. Moreover, each secondary encoding corresponds to multiple BFS combinations, making it impossible to deduce a unique corresponding BFS. Therefore, our method has higher security.

(2)

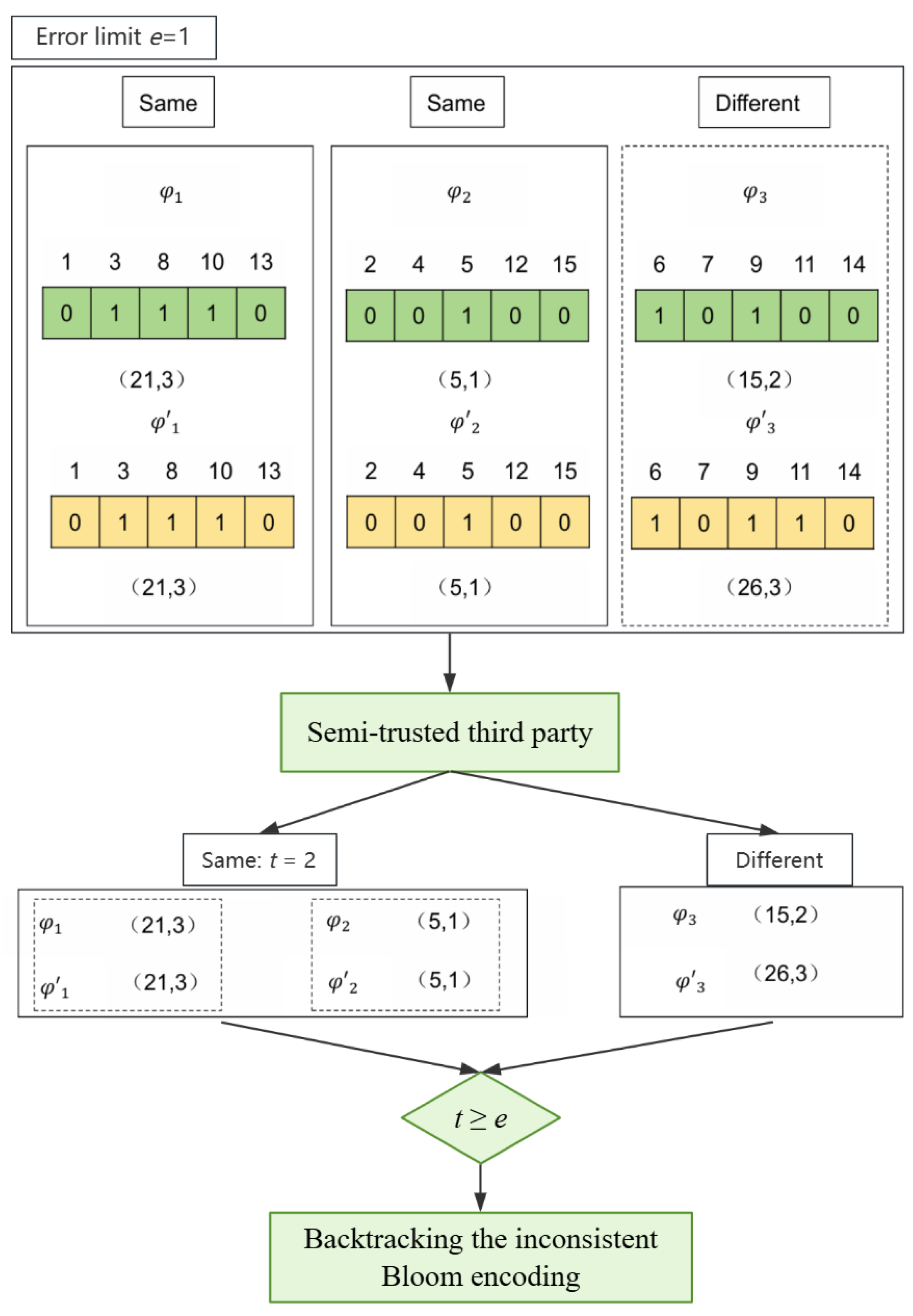
Introducing error limits has improved efficiency. By setting an error limit, the degree of fault tolerance can be controlled. When the error limit is larger, the pass rate is smaller, thus filtering out unnecessary computations. Only when the number of identical splits is greater than or equal to the error limit will inconsistent splits be backtracked and similarity calculations performed, thus achieving efficiency improvement.

(3)

Experimental verification has demonstrated that the introduction of secondary encoding provides higher security compared to BFS, with minimal impact on matching quality. Our method exhibits equivalent computational efficiency and linkage quality to BFS. Therefore, our approach enables efficient PPRL with good matching quality and higher security compared to the existing methods.

In this section, we introduce the risks and challenges faced by the current record link, and we discuss the application of PPRL in the Internet era. We introduce the relevant work in Section 2 and the definition of theoretical issues in Section 3. Furthermore, in Section 4, the specific process and algorithm of the multi-party PPRL method based on secondary encoding are elaborated in detail. The experimental results are described and analyzed in Section 5. Section 6 summarizes the content of this article and points out future work directions.

2. Related Work

In PPRL methods, the security assurance mainly relies on the encryption or encoding techniques employed. Encryption-based PPRL methods, such as secure multi-party computation (SMC)-based PPRL and multi-party PPRL methods using homomorphic encryption principles, ensure data security but also face significant time costs and have low computational efficiency. In comparison, encoding-based PPRL methods, such as approximate matching-based multi-party PPRL methods, methods utilizing BFS for exact matching, and the method proposed in this paper, hold an advantage in efficiency. However, they are more susceptible to privacy attacks when dealing with sensitive information. This necessitates a careful balance between efficiency and security in practical applications.

PPRL technology holds significant importance in practical applications. In recent years, PPRL technology has made some achievements, but balancing the relationship between linkage quality, computational efficiency, and security is a current concern. In 2006, Lai et al. proposed an efficient multi-party PPRL method [24], which achieves high computational efficiency by performing exact matches on records encoded using the Bloom Filter. However, the drawback of this method is that it only performs exact matching and lacks fault tolerance. To overcome this issue, Lai et al. subsequently transformed the comparison method to calculate the Dice coefficient similarity through secure summation of Bloom Filter code fragments from different parties. In 2016, Vatsalan et al. proposed an improved method [25,26], which calculates similarity by vertically summing each bit position and finding the number of positions equal to the number of BFS.

Currently, most existing PPRL methods can only partially ensure the security of records or defend against certain attacks, rather than guaranteeing the overall security of records and effectively resisting privacy attacks. Although BFS demonstrates excellent computational efficiency, it is prone to being reversed back to the original plaintext. Hence, many methods have been proposed to enhance BFS. In 2015, D Vatsalan proposed multi-party PPRL (MP-PPRL) based on incremental clustering techniques [27]. This method effectively addresses the lack of support for linkage of large databases and subset linkage in current technologies, significantly enhancing the accuracy of linkage and computational efficiency. In 2016, Schnell et al. proposed a solution involving approximate mean values [28], where a BFS of length l is flipped to obtain another encoding BFS′, and they are concatenated to form a bit array S of length 2l (S = BFS − BFS′). While this method reduces the susceptibility to frequency attacks, it requires additional space compared to the original BFS and increases the probability of matching errors, thereby reducing linkage quality. Additionally, due to [28], Schnell and Borgs also proposed a scheme involving random bit flipping, where bit values are flipped at certain positions in the Bloom Filter according to differential privacy mechanisms to enhance security. However, due to the noise mechanism of differential privacy, data quality is compromised, leading to a decrease in linkage quality. In 2020, BK Mohanta proposed a multi-party computation review for secure data processing in an IoT-fog computing environment [29]. This was aimed at addressing some of the issues in that centralized system, which include malicious behavior, node capture, and failure. In 2020, T Ranbaduge proposed a PPRL that introduces two-step hash encoding [30]. Through this innovation, they significantly enhanced the quality and security of data linkage. However, compared to other PPRL methods, the introduction of two-step hash encoding functions also resulted in an increase in memory usage. In 2020, Vijay Maruti Shelake proposed a dual-factor encoding PPRL method based on phonetic and BFS [31]. This introduction significantly enhanced the security of data, providing users with a more robust protection barrier. However, due to the possibility of false positives in the processing of voice filters, there may be a certain degree of decrease in the quality of data linkage. In 2022, an enhanced approximate MP-PPRL approach [32] was introduced by S Han, aiming to enhance privacy protection, scalability, and linkage quality. While this method effectively enhances security, it comes with a higher time cost. In 2022, S Stammler proposed a secure multi-party computation that does not require third-party involvement while ensuring the confidentiality of information, avoiding the leakage of any unexpected sensitive data [33]. This method demonstrates excellent performance when handling large datasets, efficiently coping even with incomplete and noisy data. However, its application may be somewhat limited in small-scale databases or high-latency environments. In 2022, X He proposed a method that integrates a trusted execution environment (TEE) into the system, significantly reducing the necessary decryption operations and optimizing runtime [34]. However, it is worth noting that despite the numerous advantages brought by this method, TEE technology itself has some inherent limitations.

Overall, while encryption-based PPRL techniques offer robust security, they come with significant time costs. On the other hand, while encoding-based PPRL techniques can obscure the original meaning of data, the encoding process may lead to the loss of some details, rendering data irrecoverable, and they lack resilience against attacks. Finally, hardware-based PPRL techniques also have limitations when used in conjunction with hardware. Therefore, we propose a multi-party PPRL method based on secondary encoding technology. Building upon the initial BFS, this method constructs secondary encoding according to specific encoding and linkage rules. It ensures the metric relationship between secondary encoding and BFS as well as the efficiency of secondary encoding, preventing a decline in linkage quality and computational efficiency. Through experiments, we have also demonstrated that each secondary encoding does not uniquely correspond to a BFS, significantly reducing the possibility of deducing the original data and enhancing security. Based on these rules, approximate linkage between records can be achieved, while an error limit is set to control the fault tolerance of the method, filtering out unnecessary computations to improve efficiency. This innovative approach aims to better balance the security and computational efficiency of PPRL methods, making them more suitable for various practical application scenarios.

3. Problem Definition

Problem Formulation

Definition 1 

(Privacy-Preserving Record Linkage). Privacy-preserving record linkage [35] (PPRL) refers to a process of identifying records representing the same real-world entity from multiple data sources under privacy protection. Suppose there are p participants $(p_1,\dots ,p_p)$, each with their respective data sources $(D_1,\dots ,D_p)$. The goal is to identify and match the same entity across different data sources while ensuring that during the record linkage process, only successfully matched entities are shared among the parties. This ensures that the remaining data are not leaked.

Definition 2 

(Bloom Filter). The Bloom Filter [36] (BF) is an efficient space-efficient probabilistic data structure used for efficient set membership testing. It utilizes a bit array and hash functions to achieve efficient detection of set membership. The BF uses an n-bit array, typically initialized to all zeros. For a set of m inputs and using k independent hash functions $h_1,\dots ,h_k$, each input undergoes hashing calculations, and the input is mapped to one position in the bit array $\left\{1,\dots ,n\right\}$. The values at these positions are then set to “1”.

Definition 3 

(Dice Coefficient Similarity). The Dice similarity function [37] is a measure used to calculate similarity between multiple sets. If we are calculating the similarity between the P sets ${BF}_1,{BF}_2,\dots ,{BF}_P$, it is computed using the following Formula (1):

$$Dic{e}_{\_}sim\left({BF}_1,\dots ,B_{FP}\right)=\frac{c\times P}{\sum _{i=1}^P{x}_i}$$

(1)

where c is the number of positions, the result of the $\left|{BF}_1\cap {BF}_2\dots \cap {BF}_P\right|$ operation is 1, and x is the number of encoding positions set to 1 in ${BF}_i$

4. A Multi-Party PPRL Method Based on Secondary Encoding

The multi-party PPRL method based on secondary encoding proposed in our paper mainly consists of three modules: the data preparation and generation module, the approximate linkage module, and the similarity matching module. The process is illustrated in Figure 1.

The function of the data preparation and generation module is to set various parameters and encode data from multiple sources using BF. The design of secondary encoding rules encodes the initial BFS to maintain the metric relationship between original data, preventing a decline in linkage quality and further reducing the likelihood of decoding the encodings.

The function of the approximate linkage module among records involves integrating the secondary encoding of each split of the previous module, designing linkage rules, setting parameter e as the error limit, t as the number of consistent splits, and m as the number of splits, and determining whether it matches based on this error limit. These linkage rules ensure the efficiency of secondary encoding and prevent a decrease in computational efficiency.

The function of the similarity matching module is to compute the similarity among different splits and determine whether the match is successful based on a threshold.

4.1. Data Preparation and Generation

At this stage, to maintain the metric relationship between the primary encoding and the secondary encoding, and prevent a decrease in linkage quality, the following encoding rules are formulated: Firstly, it is crucial for all involved parties to ensure consistency in input parameters. This is because inconsistencies in input parameters may lead to linkage errors or privacy breaches, significantly impacting the accuracy and reliability of the research.

Table 1. Parameter table for multi-party PPRL method based on secondary encoding.

Parameter	Description
P	Participant of PPRL
$D_i$	Dataset
${BF}_i$	$\mathrm{Bloom} \mathrm{Filter} \mathrm{encoding} \mathrm{of} D_i$
k	Bloom Filter hash functions h1, …, hk
$N_i$	$\mathrm{Size} \mathrm{of} \mathrm{the} \mathrm{data} \mathrm{source} D_i$
i	i-th participant (1 ≤ i ≤ P)
${\phi }_u$	u-th split (1 ≤ u ≤ m)
n	Bloom Filter length
m	Number of splits
X	Sum of positions encoded as 1
Y	Number of positions encoded as 1
A	Common attribute set among all participants
α	Threshold
e	Error limit (e = m − ak)
a	Tolerance level
l	Encoding length
t	Number of consistent splits

illustrates the parameters used in this method and their meanings. Secondly, generating BFS, the dataset is mapped to a bit array of length n using k hash functions (Algorithm 1, line 1). Then, each dataset is divided into m splits (${\phi }_1,{\phi }_2,\dots ,{\phi }_m$) (Algorithm 1, line 2), and the secondary encoding of each split is calculated (Algorithm 1, lines 3–5) in the format (X, Y), where X represents the sum of positions encoded as 1, and Y represents the number of positions encoded as 1. Finally, the secondary encoding generated from each split is integrated. An example of secondary encoding is shown in Figure 2, where ${\mathrm{B}\mathrm{F}}_1$ is 001011011100000 and ${\mathrm{B}\mathrm{F}}_2$ is 001011011110010. Here, the encoding length(l) is 15, the number of hash functions(k) is 2, and the number of splits(m) is 3. They are divided into three splits according to the positions of the BFS: (1,3,8,10,13), (2,4,5,12,15), and (6,7,9,11,14). The calculated secondary encoding results for ${\mathrm{B}\mathrm{F}}_1$ are (21,3), (5,1), and (15,2), and for ${\mathrm{B}\mathrm{F}}_2,$ they are (21,3), (5,1), and (26,3).

As shown in Algorithm 1, secondary encoding only involves simple addition operations. Therefore, the novel method using secondary encoding has a minimal impact on computational efficiency and maintains a high level of matching quality. At the same time, existing privacy attack methods cannot decode secondary encoding, thus enhancing security. Its security is proven in Section 4.4 later in the article.

Algorithm 1 Data preparation and generation algorithm
$\mathbf{Input}: \mathrm{Data} \mathrm{sources} \mathrm{of} P\mathrm{participants} {BF}_i$
Output: Secondary encoding of P participants
1:	FOR (int i = 1; i <= P; i++){
2:	$N_i$$=\mathrm{genetateBloomfilters}(D_i$, A);
3:	$\mathrm{divide}(N_i$$)=\{{\phi }_{i1},\dots ,{\phi }_{im}$};
4:	$\mathbf{IF} {\phi }_{im}\left[j\right]==1$ THEN:
5:	$X_i=X_i+j;$
6:	$Y_i++;$
7:	RETURN$(X_i$$,Y_i$);}
8:	}

4.2. Approximate Record Linkage

In the approximate record linkage module, each split ${\phi }_j$ generates secondary encoding according to the designed encoding rules, and then transmits its secondary encoding to the semi-trusted third party. However, BFS may be vulnerable to most current privacy attacks. Therefore, using secondary encoding technology ensures the security of data, thereby ensuring linkage quality.

To ensure the linkage quality between records, we formulated corresponding linkage rules: ① If the secondary encodings of each split are consistent, then the linkage is deemed successful (Algorithm 2, lines 1–2). ② If there are at least e splits that are the same in the secondary encoding (Algorithm 2, lines 4–5), then the BFS of the inconsistent splits is traced back, and further calculation of the Dice similarity is performed to determine whether the match is successful. ③ If there are fewer than e splits that are the same in the secondary encoding (Algorithm 2, lines 6–7), then the linkage is deemed unsuccessful. Here, a represents the fault tolerance level, and the setting of e can control the fault tolerance level of the method, referred to as the error limit. Only when the number of consistent splits is greater than e are the record linkage and similarity calculation performed for the different splits. Assuming a characters are allowed to be erroneous, there could be up to ak erroneous positions in the BFS, and hence, e = m − ak. As a decreases, e increases, indicating that fewer inconsistent splits need to be addressed. As shown in Figure 3, in this example, the BFS results of ${\phi }_1$ and ${\phi \prime }_1$ and those of ${\phi }_2$ and ${{\phi }_2}^{\prime }$ are the same, and so is their secondary encoding. However, the BFS results of ${\phi }_3$ and ${{\phi }_3}^{\prime }$ are not the same, and thus their secondary encoding is also different, where ${\phi }_3$ is (15,2) and ${{\phi }_3}^{\prime }$ is (26,3). If we assume one character error is allowed, then e = m − ak = 3 − 2 = 1 < 2, which satisfies linkage rule ②. Therefore, we backtrack the inconsistent splits of the BFS and calculate the similarity. If we assume zero character errors are allowed, then e = m − ak = 3 − 0 = 3 > 2, which satisfies linkage rule ③. Therefore, it does not match, as shown in Algorithm 2.

Algorithm 2 Approximate record linkage algorithm
Input: Secondary encoding of P participants
Output: Match or Non-Match
1:	FOR(int i = 1; i <= P; i++){
2:	$\mathbf{IF} {\phi }_i={{\phi }^{\prime }}_i$ THEN:
3:	Return TRUE;
4:	ELSE IF ${\phi }_i!={{\phi }^{\prime }}_i$ THEN:
5:	IF e = m − ak ≤ t THEN:
6:	Backtrack the inconsistent splits of the BFS;
7:	ELSE IF e = m − ak > t THEN:
8:	RETURN FALSE;
9:	}

4.3. Similarity Matching Module

The similarity calculation formula used in this method is shown in Formula (2):

$${Dic{e}_{\_}sim}_1\left({BF}_1,\dots ,{BF}_P\right)=\frac{\sum _{i=1}^n{Y}_i\times P+Y^{\prime }\times P}{\sum _{i=1}^P{x}_i}=\frac{\left(\sum _{i=1}^n{Y}_i+Y^{\prime }\right)\times P}{\sum _{i=1}^P{x}_i}$$

(2)

where $Y_i$ is the number of encoding positions set to 1 in ${BF}_i$ that are completely consistent in the secondary encoding, n is the number of splits in secondary encoding that are completely consistent with secondary encoding, $Y^{\prime }$ is the number of positions in ${BF}_i$ where the inconsistent splits of the secondary encoding have a sum of 1, and $x_i$ is the total number of positions encoded as 1 in ${BF}_i$.

According to Formula (2), we calculate the Dice similarity coefficient between different encodings (Algorithm 3, line 1). If the similarity coefficient is greater than the threshold, then it matches; otherwise, it does not match (Algorithm 3, lines 2–5), as shown in Figure 4. In the approximate matching process, the BFS of ${\phi }_3$ is not the same as that of ${{\phi }_3}^{\prime }$, so the Dice coefficient similarity between ${BF}_1$ and ${BF}_2$ is $\frac{12}{13}$. Therefore, based on the threshold, we determine whether it matches, as shown in Algorithm 3.

Algorithm 3 Similarity calculation algorithm
Input: Secondary encoding of the inconsistent splits
Output: Dice coefficient similarity and whether it matches
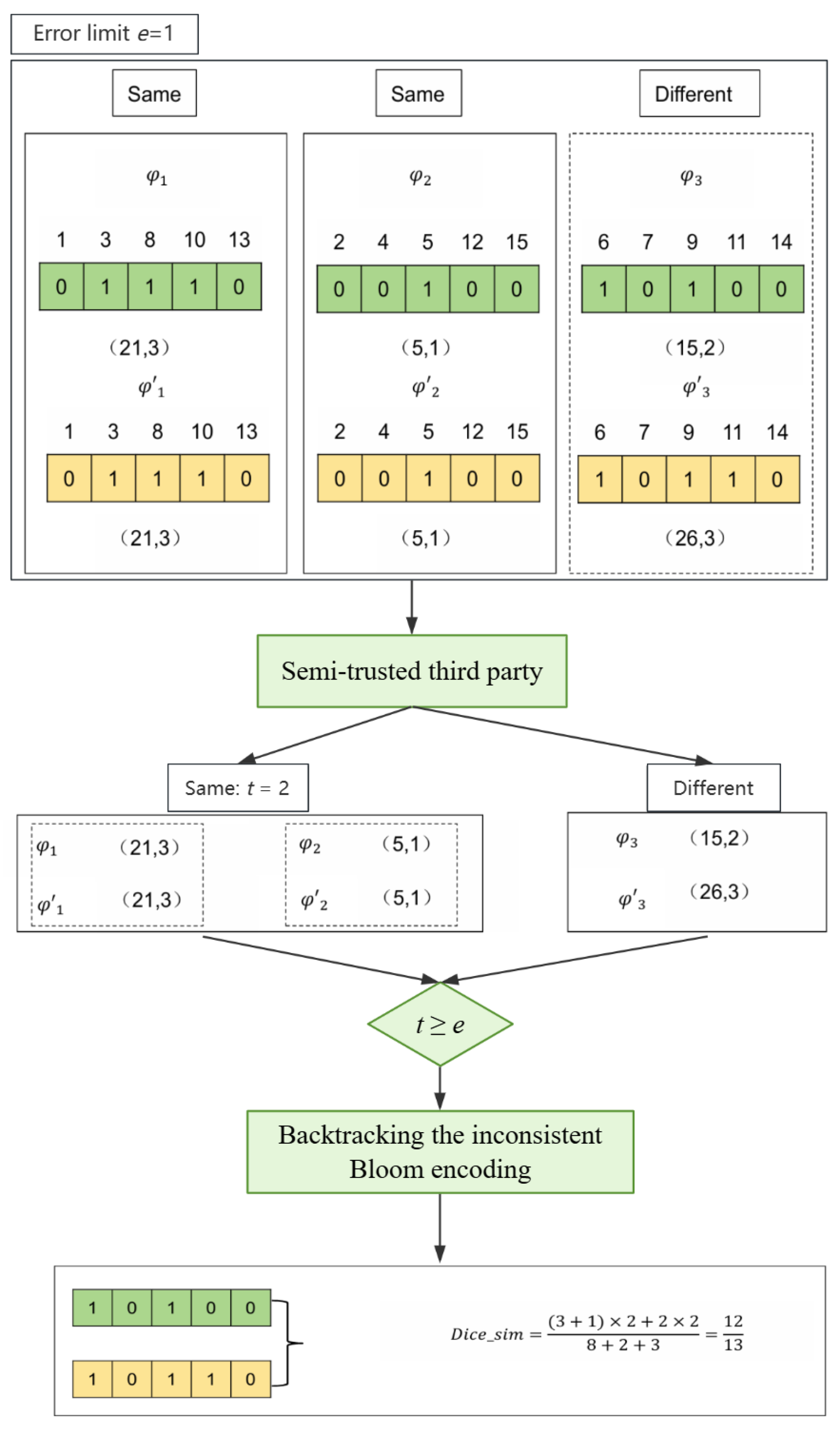
1:	$Dice\_sim({BF}_1,\dots ,{BF}_P)=\frac{\sum _{i=1}^n{Y}_i\times P+Y^{\prime }\times P}{\sum _{i=1}^P{x}_i}$
2:	IF Dice_sim ≥ α THEN:
3:	RETURN Dice_sim;
4:	ELSE
5:	RETURN FALSE;

4.4. Analysis of Linkage Quality and Security

In the secondary encoding rules we have adopted, the prior considerations are computational efficiency and linkage quality. Our encoding method is based on simple summation operations, making it more cost-effective compared to other encryption algorithms. Moreover, through similarity calculation analysis, we have demonstrated that our method maintains a good linkage quality. Given the prevalence of attack strategies against BFS, our encoding design places a special emphasis on security. Consequently, our encoding method generates diverse combinations of 0 s and 1 s, making it extremely difficult for anyone to accurately reconstruct the unique corresponding BFS through guessing. This innovation not only effectively mitigates the potential weaknesses of BFS but also achieves a delicate balance between computational efficiency and security.

Theorem 1. 

The similarity calculation formula (Formula (2)) used in this method is equivalent to the Dice similarity calculation formula (Formula (3)) for BFS.

Proof of Theorem 1. 

Let’s assume that Formula (2) is not equivalent to Formula (3).

The Dice similarity calculation formula for BFS is shown in Formula (3):

$${Dic{e}_{\_}sim}_2\left({BF}_1,\dots ,{BF}_P\right)=\frac{c\times P}{\sum _{i=1}^P{x}_i}$$

(3)

where c is the number of positions where the operation $\left|{BF}_1\cap {BF}_2\dots \cap {BF}_P\right|$ results in a value of 1, and $x_i$ is the total number of positions encoded as 1 in ${BF}_i$.

In Formula (2), $\sum _{i=1}^n{Y}_i$ is the sum of the number of encoding positions in ${BF}_i$ where the completely consistent splits of the secondary encoding are set to 1, and $Y^{\prime }$ is the number of positions in ${BF}_i$ where the inconsistent splits of the secondary encoding have a sum of 1. Therefore, the result of $\sum _{i=1}^n{Y}_i+Y^{\prime }$ is the number of positions where the result of the $\left|{BF}_1\cap {BF}_2\dots \cap {BF}_P\right|$ operation is 1, equivalent to the parameter c in Formula 3. Thus, it can be concluded that the similarity calculation formula used in this method is equivalent to the Dice coefficient similarity calculation formula for BFS.

As a consequence, the assumption is false, and we prove Theorem 1. □

According to the above Formulas (2) and (3), let’s calculate the Dice coefficient similarity for the example shown in Figure 5. Since ${Dice\_sim}_1=\frac{(3 + 1) \times 2 + 2 \times 2}{8 + 2 + 3}=\frac{12}{13}$ and ${Dice\_sim}_2=\frac{6 \times 2}{8 + 2 + 3}=\frac{12}{13}$ yield the same result, Formula (2) is equivalent to Formula (3) for calculating the Dice similarity coefficient for BFS.

From the above content, it can be inferred that for secondary encoding that passes the error limit, the similarity with BFS is completely consistent. There may be a few matches that are filtered out, but the majority are retained. Therefore, the secondary encoding and BFS maintain a similar linkage quality, and the introduction of secondary encoding does not lead to a decrease in linkage quality. In terms of computational efficiency, secondary encoding does not involve computationally expensive encoding techniques. Instead, it only utilizes basic addition operations. Therefore, it has minimal interference with computational efficiency.

In terms of security, most existing privacy attacks rely on partially or completely known BFS. However, the uniqueness of secondary encoding lies in the fact that it is constructed from the sum of positions encoded as 1 and the number of positions encoded as 1. This design allows secondary encoding to generate multiple possible combinations of 0 s and 1 s, making it impossible to accurately infer the unique corresponding BFS.

Theorem 2. 

For each secondary encoding, there are multiple corresponding BFS.

Proof of Theorem 2. 

Let’s assume that the secondary encoding is (21,3), (5,1), (15,2) and there exists a unique corresponding BFS for it.

Now, let’s consider the possible combinations of BFS corresponding to these secondary encoding values. Since the secondary encoding is based on the sum of positions encoded as 1 and the number of positions encoded as 1, we can have different arrangements of 1 s and 0 s in the BFS while maintaining the same sum and count of 1 s.

When the BFS positions are (1,2,6,9,14), (4,5,8,13,15), and (3,7,10,11,12), the secondary encoding is (21,3), (5,1), (15,2) and the BFS is 101011000001010. When the BFS positions are (1,3,8,10,13), (2,4,5,12,15), and (6,7,9,11,14), the BFS is 001011011100000. Therefore, the BFS for the secondary encoding—(21,3), (5,1), (15,2)—is not unique. This conclusion demonstrates that for each secondary encoding, there is not a unique corresponding BFS.

As a consequence, the assumption is false, and we prove Theorem 2. □

Based on the above proof, we can draw the conclusion that there can indeed be multiple corresponding BFS results for a given secondary encoding. Therefore, the proposition is proven. Regardless of whether facing internal or external attackers, they can only access secondary encoding. Since attackers cannot directly access the unique and accurate original BFS, this secondary encoding mechanism can significantly enhance the defense capabilities against privacy attacks on the BFS, thereby greatly improving overall security and privacy.

5. Experimental Preparation

5.1. Experimental Preparation

We implemented the methods described using Python (version 3.7) on an Intel(R) Core(TM) i7-8565U processor with a clock speed of 1.80 GHz, 8 GB of RAM, and operating system Windows 10, 64-bit.

The experiments conducted for this measure utilized the North Carolina Voter Registration list (NCVR), accessible for direct download from https://www.ncsbe.gov/results-data (accessed on 8 June 2024). All data used in these experiments originate from genuine public voter registration records, guaranteeing the authenticity and reliability of the dataset.

For the multi-party PPRL on secondary encoding (SE_PPRL) that we employed, four metrics were used to evaluate its effectiveness and scalability: runtime, recall, precision, and the F-measure. Precision measures the ratio of correctly matched records to all records matched by the method. It reflects the ability of this method to identify truly matching records. As precision increases, the matching results become more precise. Recall measures the ratio of truly matching records found by the method to all truly matching records that exist. It assesses the ability of this method to cover all truly matching records. As recall increases, the method identifies more truly matching records. Runtime serves as a measure of the scalability of this method. The F-measure, which comprehensively considers both recall and precision, is employed to evaluate the performance of this method. It is calculated using Formula (4):

$$\mathrm{F}=2\times \frac{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}\times \mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}+\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}$$

(4)

In this experiment, the proposed multi-party PPRL method based on secondary encoding is compared with the methods proposed by Vatsalan [25] and Lai [24]. These two methods are chosen for comparison because they are considered relatively classic approaches in the field compared to other methods. The evaluation involves varying the data source size, the number of participants, and the error limit and observing the changes in the aforementioned metrics. The data source sizes considered are 5000, 10,000, 50,000, 100,000, 500,000, and 1,000,000 records. The numbers of participants are 3, 5, 7, and 10, respectively. The error limits are 1, 2, 3, 4, and 5, respectively.

5.2. Experimental Analysis and Results

5.2.1. Scalability Evaluation

Firstly, the evaluation focuses on how the runtime of the proposed method varies with the increase in data source size. During the evaluation process, the number of participating parties is set as P = 3, the error limit as e = 1, and the number of splits as m = 5. By comparing the results presented in Figure 6, that is, the runtime with the size of the data source, we found that the runtime of our method is longer compared to the methods of Vatsalan and Lai, and the runtime of all three methods increases as the size of the data source increases. This is primarily because our measure proposes the use of a quadratic encoding technique for re-encoding Bloom Filters. As a result, compared to Lai’s and Vatsalan’s methods, our approach adds time for data partitioning and secondary encoding. Although this step increases the runtime, it ensures that the scalability of the method remains excellent.

Next, it was necessary to further evaluate how the runtime of our method changes with the increase in the number of participating parties. In this evaluation, we kept the dataset size $\left|N_i\right|$ = 10,000, the error limit e = 1, and the number of splits m = 5. From Figure 7, on the runtime with the number of parties, it can be seen that the runtime of our method proposed is still slightly higher than those of Vatsalan’s and Lai’s methods. Specifically, the runtime of both our method and Vatsalan’s method increases significantly with the number of parties involved, whereas Lai’s method experiences only a minor increase. This result once again demonstrates that employing a secondary encoding technique for re-encoding Bloom Filters has a certain impact on the runtime. However, considering its good scalability, this impact is acceptable.

Next, we further evaluated how the runtime of our method changes with the increase in error limit. In this assessment, we maintained the dataset size $\left|N_i\right|$= 10,000, the number of participants P = 3, and the split count m = 5. From Figure 8, it can be observed that when e < 3, the runtime of our method is slightly higher than the other two methods. However, when e ≥ 3, the runtime of our method is lower than the other two algorithms. This phenomenon occurs because in our proposed method, only the remaining inconsistent splits are subjected to similarity calculation and approximate linkage when the number of consistent splits exceeds the error limit. Other splits that are completely consistent are not processed because they are fully matched. Therefore, for Vatsalan’s and Lai’s methods, their runtime does not vary with changes in the error threshold. However, in our method, as the error threshold increases, fewer inconsistent splits need to be processed, resulting in a decrease in runtime.

5.2.2. Method Performance Evaluation

We conducted a performance analysis of our method from three aspects: precision, recall, and F-measure, comparing it with the methods proposed by Vatsalan and Lai.

First, we evaluated the three methods based on the three evaluation metrics as the number of participants varied. Here, we set the number of splits m = 5, the dataset size $\left|N_i\right|$ = 10,000, and the error limit e = 1. From Figure 9, it can be observed that the recall of our method, Vatsalan’s method, and Lai’s method all decrease as the number of participants P increases, with similar trends and closely aligned results. This decrease in recall is consistent and can be attributed to the increased likelihood of losing true matches as the number of participants grows, particularly in the presence of data quality issues. Similarly, as shown in Figure 10, the precision of all three methods decreases as P increases, with similar trends and closely aligned results. Therefore, it can be inferred that the introduction of the secondary encoding technique in our method ensures a high linkage quality while minimally affecting computational efficiency.

As depicted in Figure 11, by observing the changes in the F-measure, it can be seen that the F-scores of all three methods decrease as the number of parties increases. However, it is evident that all three evaluated methods demonstrate excellent performance. This result fully demonstrates the stability and reliability of these methods in practical applications.

When the number of parties is seven, we can clearly observe a trend from Figure 12: as the precision increases, the recall gradually decreases for all three methods. Notably, when the precision reaches a critical point, that is, at the threshold where precision and recall are relatively balanced, the recall rate declines significantly faster. This turning point is the balance point between precision and recall. Although the area under the precision–recall curve for Vatsalan’s and Lai’s methods is larger than that of our method, the overall trends remain consistent among the three methods.

Next, we evaluated the three evaluation metrics of the two methods as the error limit varied. We did so with the number of splits set to m = 5, dataset size $\left|N_i\right|$ = 10,000, and the number of participants P = 5. As shown in Figure 13 and Figure 14, both the Vatsalan method and the Lai method maintain stable recall and precision rates regardless of changes in the error limit. However, in the proposed method of ours, as the error limit increases, both recall and precision show a decreasing trend. This is because with a higher error limit, the number of inconsistent backtrack splits decreases, reducing the workload of similarity calculations. However, this may also lead to the erroneous filtering out of suspiciously similar duplicate records that are truly matches, or mistakenly classifying non-match records as matches. Consequently, both recall and precision decrease with an increasing error limit, with recall being more sensitive to changes in the error limit, showing a more significant decline. From Figure 15, it can be observed that the F-measure remains constant for the Vatsalan and Lai methods as the error limit change, while in our proposed method, the F-measure decreases with the decline in recall and precision. Despite this, even with an increased error limit and a decrease in the F-measure, the F-measure of our proposed method still remains within a relatively good range.

Therefore, we can observe that, despite some impact on the three evaluation metrics as the error limit changes, the overall performance remains satisfactory. Properly setting the error limit can significantly reduce the workload of similarity calculations for the same splits, thereby reducing runtime and maintaining computational efficiency. Although there may be risks of filtering out true matching records or mistakenly classifying non-matching records as matches when dealing with large datasets, our proposed method can still maintain a high computational efficiency while preserving linkage quality. This indicates that our method exhibits a certain degree of stability and practicality when handling large-scale data.

Under the condition of an error limit of 3, we can clearly observe a distinct trend from Figure 16: the area under the precision–recall curve for Vatsalan’s and Lai’s methods is larger than that of our method. All three methods exhibit the phenomenon where recall gradually decreases as precision increases.

5.2.3. Security Analysis

First, let’s delve into the leakage risk level with the number of participants. Here, we set the number of splits m = 5, data source size $\left|N_i\right|$ = 10,000, and the error limit e = 1. As shown in Figure 17, it is clear that both the leakage risks of the method proposed in our measure and the Vatsalan method decrease as the number of parties increases. Compared to the method of Vatsalan, the method proposed in our measure exhibits a superior performance in terms of leakage risk, thus fully demonstrating the effective enhancement of record linkage security by our proposed method.

In order to ensure the security of records for all participants during the record linkage process, we introduced the technique of secondary encoding and formulated specific encoding rules, significantly reducing the risk of privacy attacks. Given that most current privacy attacks rely on partially or fully known BFS, the encoding rules proposed in this measure combine the summation of positions with encoding as 1 and the count of positions with encoding as 1, thereby generating multiple different combinations of 0 s and 1 s. This diversification of outputs makes it difficult for attackers to deduce a unique corresponding BFS, thereby greatly reducing the likelihood of inferring the original data. Therefore, our method enhances security by leveraging secondary encoding techniques, effectively thwarting privacy attacks and protecting sensitive data.

5.2.4. Experimental Results

The experiments conducted in this study demonstrate that the proposed method achieves high precision and recall rates in approximating record linkage. Despite taking longer in terms of runtime compared to other methods, the approach presented in this article incurs a relatively low time cost compared to some other cumbersome encoding techniques, demonstrating good scalability. Overall, the proposed method sacrifices a small amount of time to ensure the linkage quality and computational efficiency, thereby enhancing security.

6. Conclusions

In summary, we have successfully proposed a multi-party PPRL method based on secondary encoding. This method ensures data privacy and security while maintaining computational efficiency, demonstrating excellent precision and recall rates and achieving a balance between computational efficiency and privacy protection. By innovatively integrating secondary encoding technology, this method effectively avoids the re-identification issues that may arise from BFS, greatly enhancing data security and reducing the runtime for processing consistent part encoding. While maintaining high-quality linkage results, this method significantly reduces the risk of privacy leakage, fully ensuring the security of sensitive data during the record linkage process. Looking ahead, we will continue to explore optimization strategies for this method to further reduce time costs and seek a better balance between efficiency and privacy protection. We will conduct testing and analysis closely aligned with real-world application scenarios. Based on the specific requirements of these scenarios, we will continuously optimize the PPRL method to ensure its optimal performance in practical applications, meeting various needs for data sharing and privacy protection.