Dynamic Responses of U-Shaped Caverns under Transient Stress Waves in Deep Rock Engineering
Abstract
1. Introduction
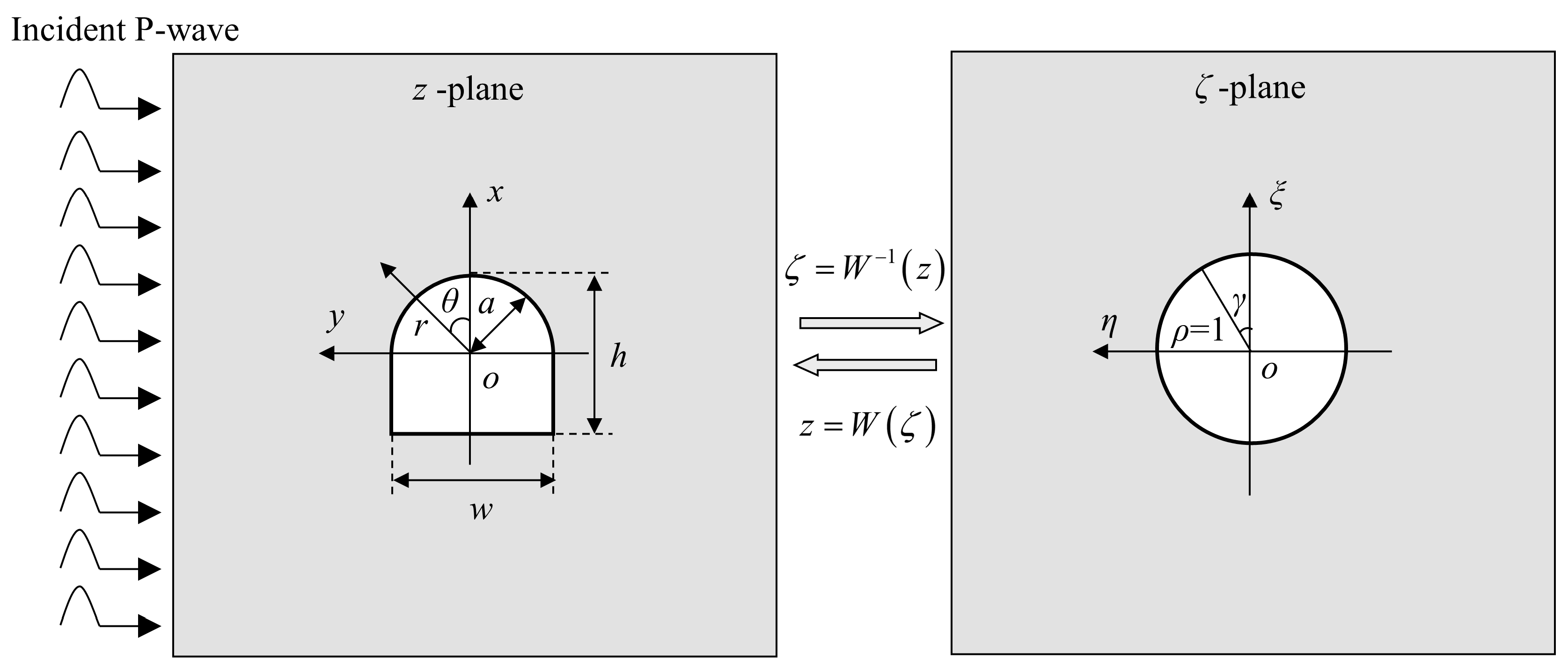
2. Theoretical Analyses for the Dynamic Responses of U-Shaped Caverns
2.1. Dynamic Responses of U-Shaped Cavern under the Harmonic Wave
2.2. Dynamic Responses of U-Shaped Cavern under the Transient Wave
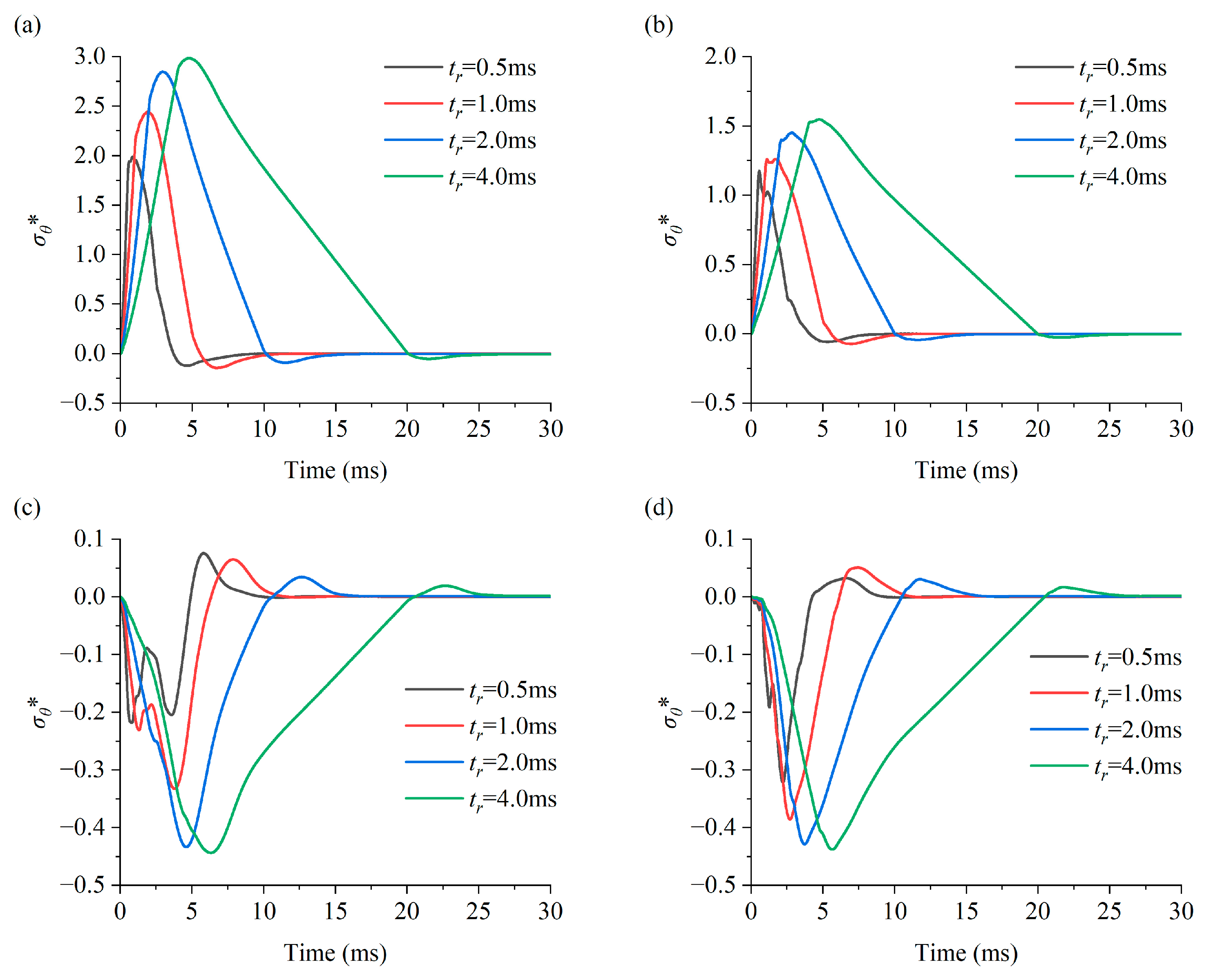
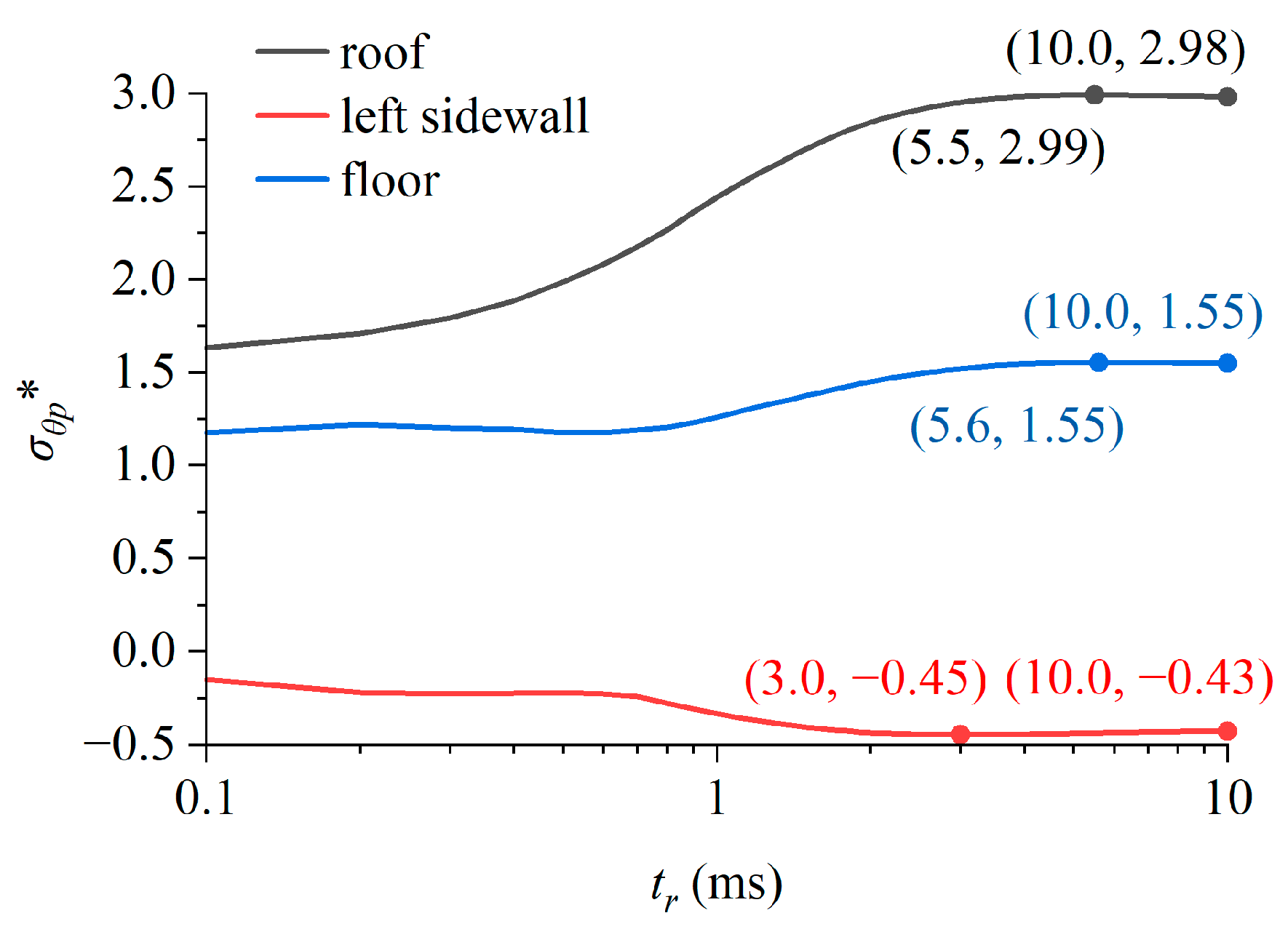
3. Theoretical Solutions and Analysis
4. Failure Behaviors of Deep U-Shaped Caverns under Dynamic Disturbances
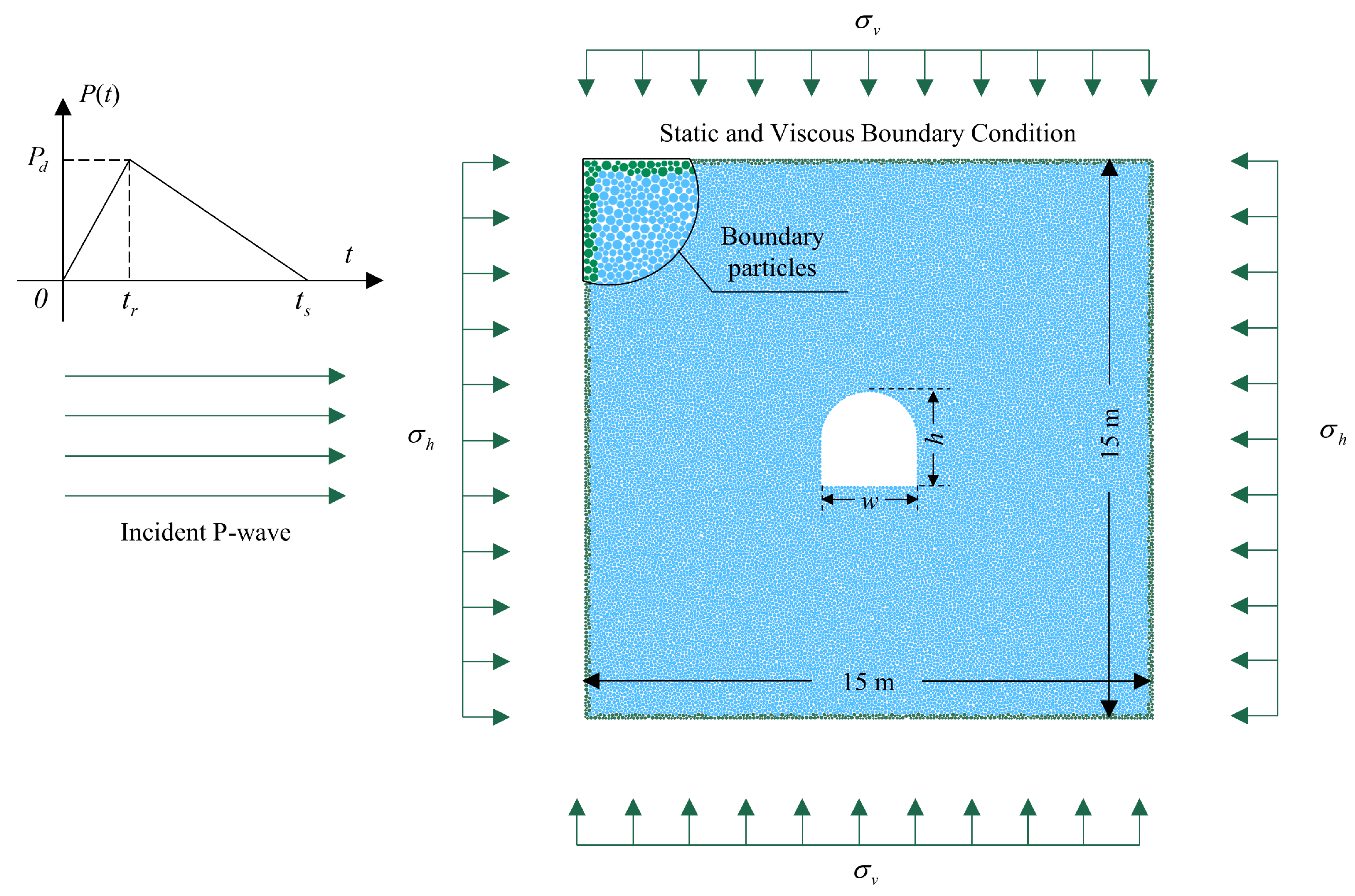
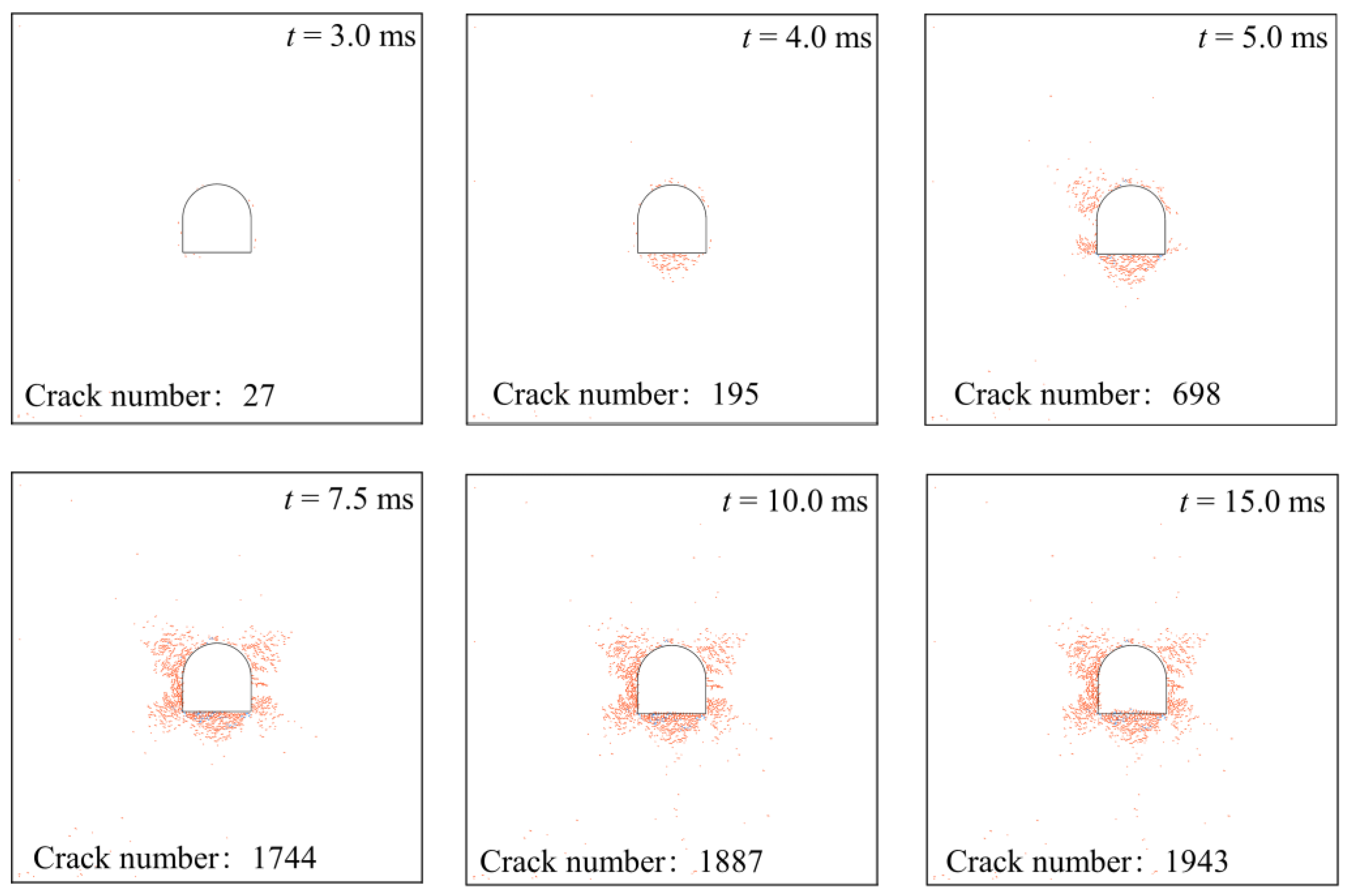
4.1. Numerical Model
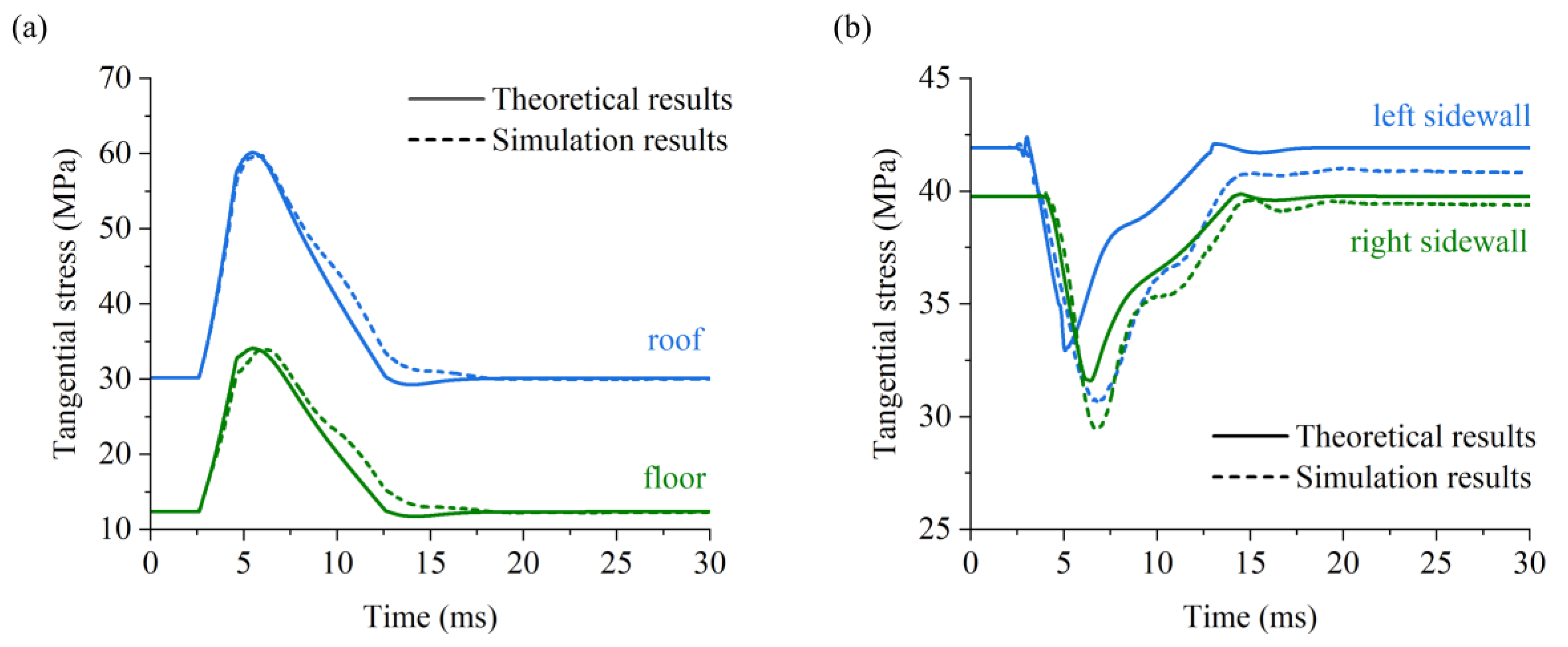
4.2. Evolution Processes of Dynamic Responses of Deep U-Shaped Caverns under Coupled Static–Dynamic Loading
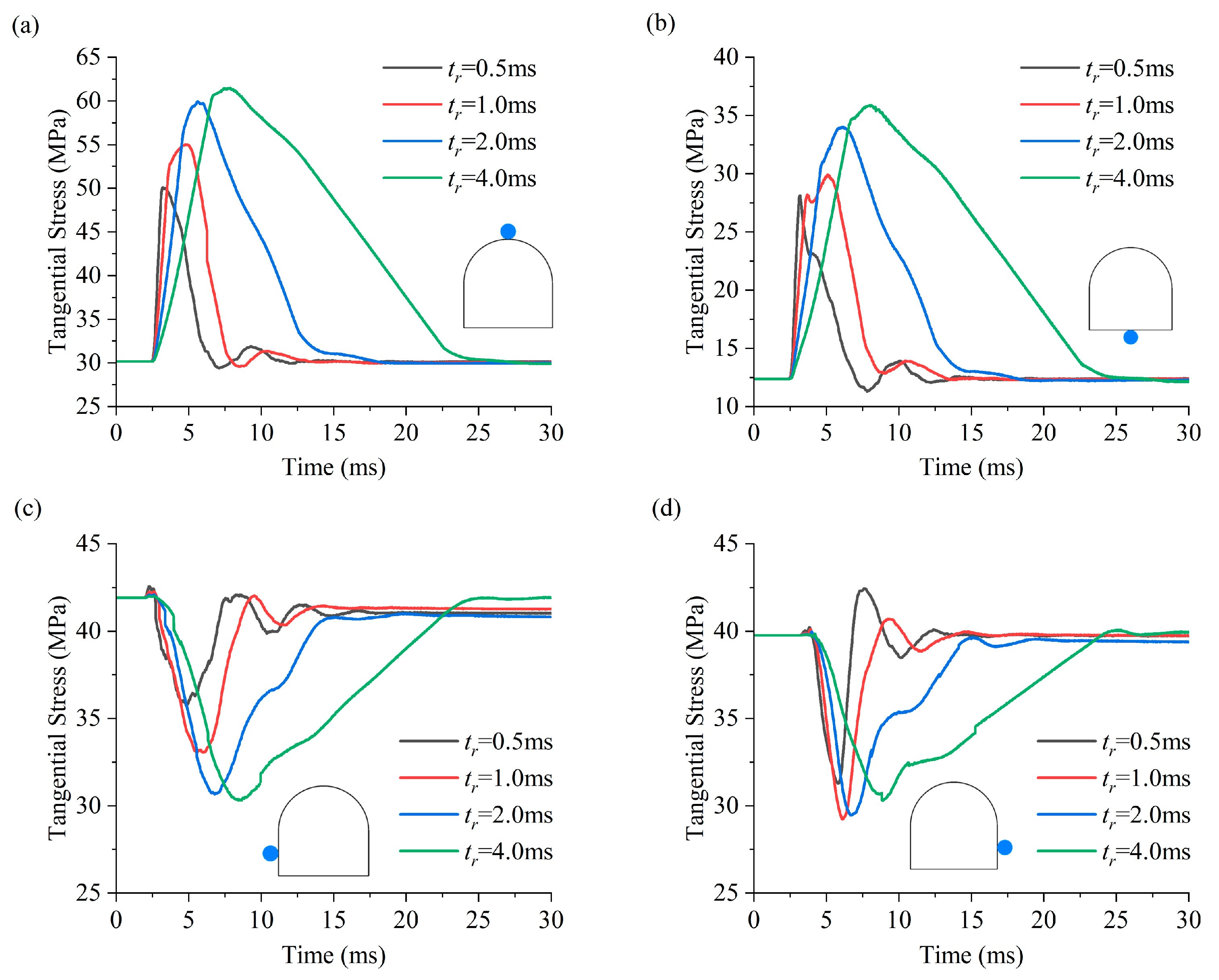
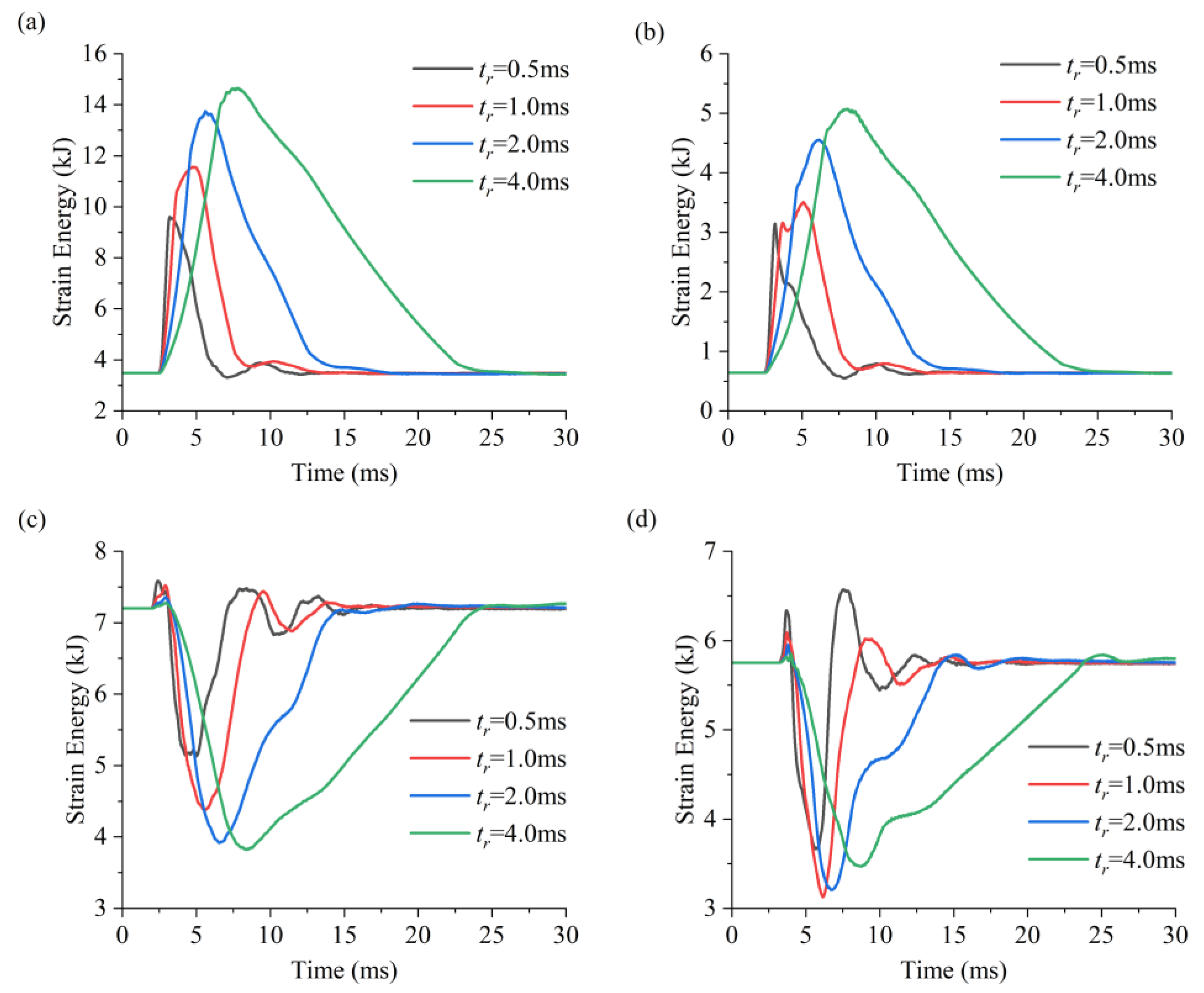
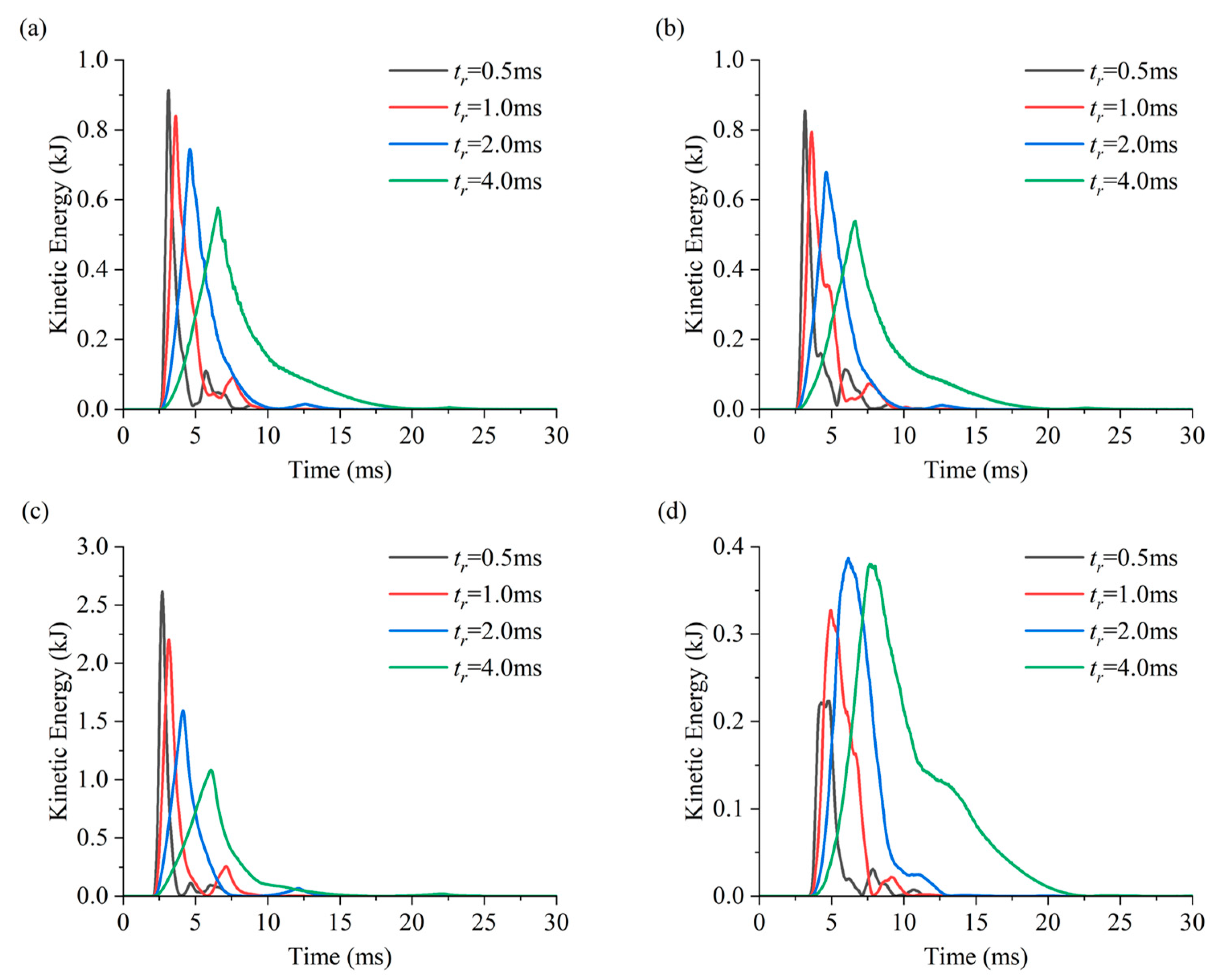
| Position | Tangential Stress (MPa) | Strain Energy (kJ) | Kinetic Energy (kJ) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| tr (ms) | 0.5 | 1.0 | 2.0 | 4.0 | 0.5 | 1.0 | 2.0 | 4.0 | 0.5 | 1.0 | 2.0 | 4.0 | |
| Roof | 50.10 | 55.01 | 59.93 | 61.48 | 9.60 | 11.56 | 13.74 | 14.65 | 0.91 | 0.84 | 0.74 | 0.58 | |
| Floor | 28.13 | 29.92 | 34.00 | 35.88 | 3.15 | 3.50 | 4.56 | 5.07 | 0.85 | 0.79 | 0.68 | 0.54 | |
| Left sidewall | 35.73 | 33.06 | 30.67 | 30.31 | 4.82 | 4.18 | 3.74 | 3.67 | 2.61 | 2.20 | 1.59 | 1.08 | |
| Right sidewall | 31.27 | 29.24 | 29.44 | 30.31 | 4.20 | 3.73 | 3.80 | 4.11 | 0.22 | 0.33 | 0.39 | 0.38 | |
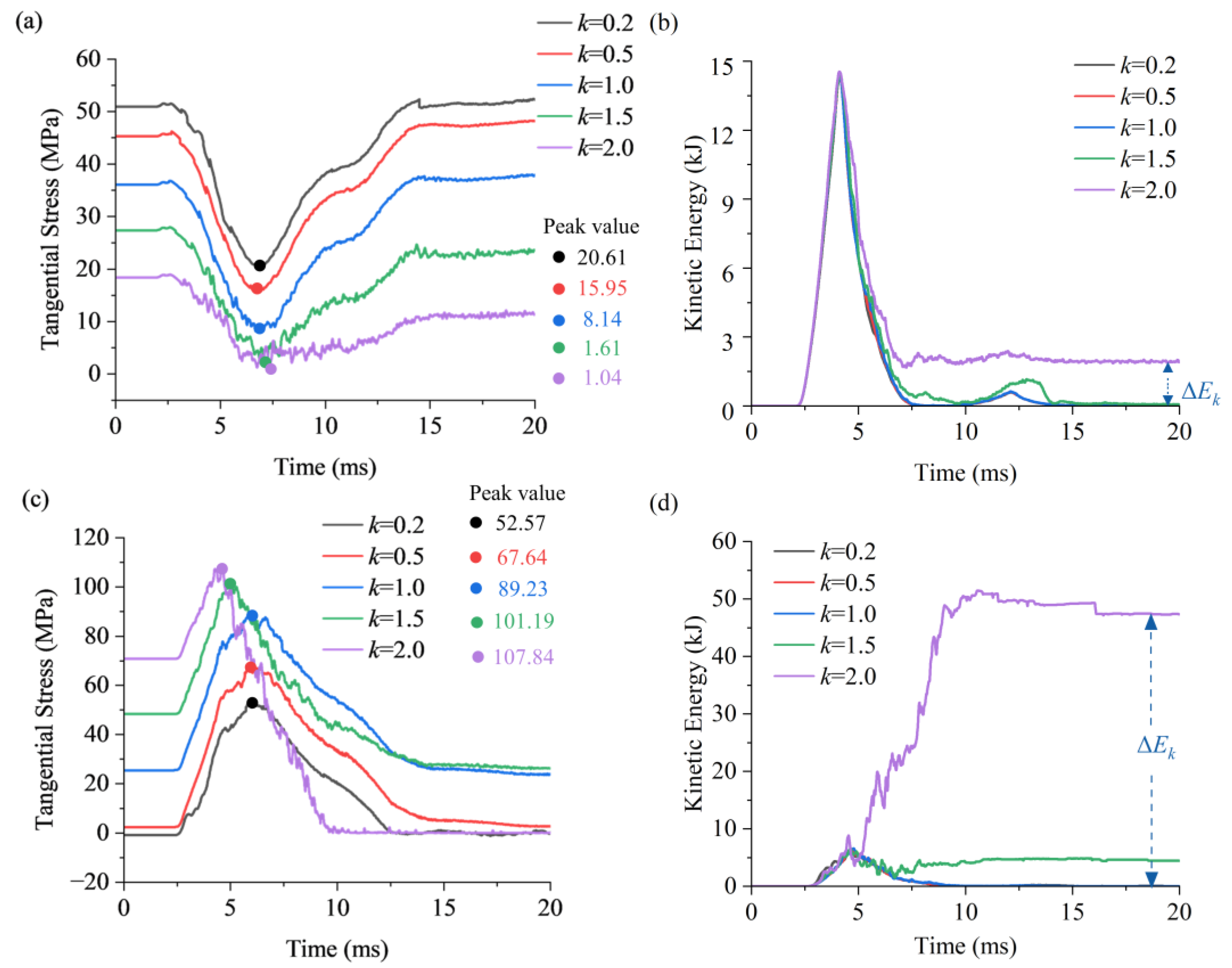
4.3. Lateral Pressure Coefficient Effect on Failure Behaviors of Deep U-Shaped Caverns under Coupled Static–Dynamic Loading
5. Conclusions
- (1)
- The scattering of stress waves induces the dynamic compressive stress concentration in the roof and floor and dynamic tensile stress concentrations in the sidewalls when the stress wave is horizontally incident. When the rising time of the stress wave is greater than 6.0 ms, the peak dynamic stress concentration factor converges to a stable value, and the stress condition of the surrounding rock can be considered as a quasi-static state.
- (2)
- When the stress wave is horizontally incident, the strain energy accumulates in the roof and floor, and dynamic compressive shear failure is more likely to occur in the cavern floor. The maximum peak kinetic energy occurs in the incident sidewall, which is prone to producing dynamic tensile failure. The incident sidewall and the floor are considered potential hazard areas, and the presence of a supporting structure is essential.
- (3)
- Rockburst tends to occur at the cavern boundary that is perpendicular to the incident direction, especially when the incident direction of the stress wave is parallel to the maximum principal stress. The higher the lateral pressure coefficient, the higher the amount of residual kinetic energy that is released. In practical engineering, the dynamic disturbances that come from the direction of the maximum principal stress should be minimized as much as possible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Complex variables in z-plane | |
| Complex variables in ζ-plane | |
| Polar radius in the ζ-plane | |
| Polar angle in the ζ-plane | |
| Mapping function that transforms the exterior of the cavern section in the z-plane into the exterior of a unit circle in the ζ-plane | |
| Conjugate of the mapping function | |
| Amplitude of incident wave | |
| Potential function of the incident P-wave | |
| Potential function of the reflected P-wave | |
| Potential function of the reflected SV-wave | |
| Circular frequency of incident stress wave | |
| P-wave number | |
| S-wave number | |
| Time | |
| Total time of the incident wave | |
| Rising time of the incident wave | |
| P-wave velocity | |
| S-wave velocity | |
| Hankel function of the first kind | |
| , | Undetermined coefficients |
| Radial stress components | |
| Tangential stress components | |
| Shear stress components | |
| , | Lame constants |
| Stress amplitude of the incident wave | |
| Dynamic stress concentration factor | |
| Transient response | |
| Transient response caused by the unit pulse function | |
| Fourier transform of the incident wave | |
| Admittance function of the steady-state response | |
| Real part of the admittance function | |
| Incident stress wave of blasting disturbance | |
| Amplitude of the incident wave |
References
- Yan, P.; Zhao, Z.G.; Lu, W.B.; Fan, Y.; Chen, X.R.; Shan, Z.G. Mitigation of rock burst events by blasting techniques during deep-tunnel excavation. Eng. Geol. 2015, 188, 126–136. [Google Scholar] [CrossRef]
- He, B.; Armaghani, D.J.; Lai, S.H.; He, X.Z.; Asteris, P.G.; Sheng, D.C. A deep dive into tunnel blasting studies between 2000 and 2023—A systematic review. Tunn. Undergr. Space Technol. 2024, 147, 105727. [Google Scholar] [CrossRef]
- Guo, Y.D.; Dyskin, A.; Pasternak, E. Thermal spallation of dry rocks induced by flame parallel or normal to layering: Effect of anisotropy. Energy 2024, 288, 129697. [Google Scholar] [CrossRef]
- Li, X.B.; Gong, F.Q.; Tao, M.; Dong, L.J.; Du, K.; Ma, C.D.; Zhou, Z.L.; Yin, T.B. Failure mechanism and coupled static-dynamic loading theory in deep hard rock mining: A review. J. Rock Mech. Geotech. Eng. 2017, 9, 767–782. [Google Scholar] [CrossRef]
- Ortlepp, W.D. The behaviour of tunnels at great depth under large static and dynamic pressures. Tunn. Undergr. Space Technol. 2001, 16, 41–48. [Google Scholar] [CrossRef]
- Pao, Y.H.; Mow, C.C. Diffraction of Elastic Waves and Dynamic Stress Concentrations; Crane Russak & Co.: New York, NY, USA, 1973. [Google Scholar]
- Liu, D.K.; Gai, B.Z.; Tao, G.Y. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion 1982, 4, 293–304. [Google Scholar] [CrossRef]
- Bouaré, H.; Mesgouez, A.; Lefeuve-Mesgouez, G. Stress and displacement fields around an arbitrary shape tunnel surrounded by a multilayered elastic medium subjected to harmonic waves under plane strain conditions. Soil Dyn. Earthq. Eng. 2022, 154, 107158. [Google Scholar] [CrossRef]
- Liu, D.K. Dynamic stress concentration around a circular hole due to SH-wave in anisotropic media. Acta Mech. Sin. 1988, 4, 146–155. [Google Scholar]
- Zhang, X.P.; Jiang, Y.J.; Sugimoto, S. Anti-plane dynamic response of a non-circular tunnel with imperfect interface in anisotropic rock mass. Tunn. Undergr. Space Technol. 2019, 87, 134–144. [Google Scholar] [CrossRef]
- Yi, C.P.; Zhang, P.; Johansson, D.; Nyberg, U. Dynamic response of a circular lined tunnel with an imperfect interface subjected to cylindrical P-waves. Comput. Geotech. 2014, 55, 165–171. [Google Scholar] [CrossRef]
- Fang, X.Q.; Jin, H.X. Visco-elastic imperfect bonding effect on dynamic response of a non-circular lined tunnel subjected to P and SV waves. Soil Dyn. Earthq. Eng. 2016, 88, 1–7. [Google Scholar] [CrossRef]
- Fang, X.Q.; Jin, H.X.; Liu, J.X.; Huang, M.J. Imperfect bonding effect on dynamic response of a non-circular lined tunnel subjected to shear waves. Tunn. Undergr. Space Technol. 2016, 56, 226–231. [Google Scholar] [CrossRef]
- Li, X.B.; Li, C.J.; Cao, W.Z.; Tao, M. Dynamic stress concentration and energy evolution of deep-buried tunnels under blasting loads. Int. J. Rock Mech. Min. Sci. 2018, 104, 131–146. [Google Scholar] [CrossRef]
- Mei, W.Q.; Xia, Y.Y.; Han, G.S.; Pan, P.Z.; Li, M.; Wang, Z.D. Theoretical responses of shallow-buried circular cavity subjected to transient P wave. Comput. Geotech. 2021, 139, 104411. [Google Scholar] [CrossRef]
- Mei, W.Q.; Xia, Y.Y.; Pan, P.Z.; Li, M.; Tan, S.R.; Zhang, Y.H. Transient responses of deep-buried unlined tunnels subjected to blasting P wave. Comput. Geotech. 2022, 146, 104729. [Google Scholar] [CrossRef]
- Tao, M.; Zhao, H.T.; Li, Z.W.; Zhu, J.B. Analytical and numerical study of a circular cavity subjected to plane and cylindrical P-wave scattering. Tunn. Undergr. Space Technol. 2020, 95, 103143. [Google Scholar] [CrossRef]
- Lu, S.W.; Zhou, C.B.; Zhang, Z.; Jiang, N. Particle velocity response of surrounding rock of a circular tunnel subjected to cylindrical P-waves. Tunn. Undergr. Space Technol. 2019, 83, 393–400. [Google Scholar] [CrossRef]
- Wu, H.; Fan, A.Q.; Zheng, Z.; Wang, M.L.; Li, S.J.; Zhang, B.; Liu, Y.H. Dynamic mechanical properties and failure behaviors of brittle rock materials with a tunnel-shaped opening subjected to impact loads. J. Mater. Res. Technol. 2023, 25, 3285–3297. [Google Scholar] [CrossRef]
- Wang, X.; Cai, M. Numerical modeling of seismic wave propagation and ground motion in underground mines. Tunn. Undergr. Space Technol. 2017, 68, 211–230. [Google Scholar] [CrossRef]
- Zhu, W.C.; Li, Z.H.; Zhu, L.; Tang, C.A. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance. Tunn. Undergr. Space Technol. 2010, 25, 587–599. [Google Scholar] [CrossRef]
- Li, X.; Li, X.F.; Zhang, Q.B.; Zhao, J. A numerical study of spalling and related rockburst under dynamic disturbance using a particle-based numerical manifold method (PNMM). Tunn. Undergr. Space Technol. 2018, 81, 438–449. [Google Scholar] [CrossRef]
- Wei, P.C.; Lin, P.; Peng, H.Y.; Yang, Z.L.; Qiao, Y. Analysis of cracking mechanism of concrete galleries in a super high arch dam. Eng. Struct. 2021, 248, 113227. [Google Scholar] [CrossRef]
- Liu, G.F.; Feng, X.T.; Jiang, Q.; Yao, Z.B.; Li, S.J. In situ observation of spalling process of intact rock mass at large cavern excavation. Eng. Geol. 2017, 226, 52–69. [Google Scholar] [CrossRef]
- Zeng, G.S.; Cai, H.; Lu, A.Z. An Analytical Solution for an Arbitrary Cavity in an Elastic Half-Plane. Rock Mech. Rock Eng. 2019, 52, 4509–4526. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, C.; Zhou, T.; Zhu, J.; Xie, H. Experimental study on strain evolution and failure behavior of sandstone containing a single pre-existing flaw under compressive-shear loading. Chin. J. Rock Mech. Eng. 2023, 42, 1743–1758. (In Chinese) [Google Scholar]
- Yilmaz, O.; Unlu, T. Three dimensional numerical rock damage analysis under blasting load. Tunn. Undergr. Space Technol. 2013, 38, 266–278. [Google Scholar] [CrossRef]
- Manouchehrian, A.; Cai, M. Analysis of rockburst in tunnels subjected to static and dynamic loads. J. Rock Mech. Geotech. Eng. 2017, 9, 1031–1040. [Google Scholar] [CrossRef]
- Hu, X.D.; Zhao, G.F.; Deng, X.F.; Hao, Y.F.; Fan, L.F.; Ma, G.W.; Zhao, J. Application of the four-dimensional lattice spring model for blasting wave propagation around the underground rock cavern. Tunn. Undergr. Space Technol. 2018, 82, 135–147. [Google Scholar] [CrossRef]
- Liang, L.S.; Li, X.B.; Zhu, Q.Q.; Peng, S.Y.; Si, X.F. Stress distribution and failure characteristics around U-shaped caverns with different height-to-width ratios under biaxial compression. Eng. Fail. Anal. 2024, 156, 107800. [Google Scholar] [CrossRef]
- Wang, X.; Cai, M. Influence of wavelength-to-excavation span ratio on ground motion around deep underground excavations. Tunn. Undergr. Space Technol. 2015, 49, 438–453. [Google Scholar] [CrossRef]
- Li, C.; Li, X. Influence of wavelength-to-tunnel-diameter ratio on dynamic response of underground tunnels subjected to blasting loads. Int. J. Rock Mech. Min. Sci. 2018, 112, 323–338. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Sun, Y.; Tan, C.X. An analysis of present day regional tectonic stress field and crustal movement trend in China. J. Geomech. 1995, 1, 1–12. (In Chinese) [Google Scholar]
- Chen, H.L.; Xia, Z.C.; Zhou, J.N.; Fan, H.L.; Jin, F.N. Dynamic responses of underground arch structures subjected to conventional blast loads: Curvature effects. Arch. Civ. Mech. Eng. 2013, 13, 322–333. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, Z.; Zhou, L.; Wang, M.; Ma, L.; Nie, F.; Shi, T. Dynamic mechanical properties and failure characteristics of layered composite rock containing a tunnel-shaped hole. Theor. Appl. Fract. Mech. 2024, 129, 104217. [Google Scholar] [CrossRef]
| Microscopic Parameters | Values | Microscopic Parameters | Values |
|---|---|---|---|
| Particle density, ρ (kg/m3) | 2711 | Elastic modulus, Ec (GPa) | 18.34 |
| Particle minimum radius, rmin (m) | 2 × 10−4 | Stiffness ratio, kn/ks | 2.0 |
| Particle radius ratio, rmax/rmin | 2.0 | Tensile Strength, σc (MPa) | 8.25 ± 0.83 |
| Number of elements | 2 | Bonding strength, c (MPa) | 45.60 ± 4.56 |
| Porosity | 0.1 | Friction angle, φ (°) | 46 |
| Local damping coefficient | 0.0 | Friction coefficient, μ | 0.50 |
| Mechanical Parameters | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Uniaxial Compressive Strength (MPa) | Brazilian Tensile Strength (MPa) |
|---|---|---|---|---|---|
| Laboratory results | 2440 | 18.60 | 0.21 | 97.60 | 4.87 |
| Numerical results | 2440 | 18.74 | 0.21 | 97.38 | 4.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Li, X.; Liu, Z.; Peng, S. Dynamic Responses of U-Shaped Caverns under Transient Stress Waves in Deep Rock Engineering. Mathematics 2024, 12, 1836. https://doi.org/10.3390/math12121836
Liang L, Li X, Liu Z, Peng S. Dynamic Responses of U-Shaped Caverns under Transient Stress Waves in Deep Rock Engineering. Mathematics. 2024; 12(12):1836. https://doi.org/10.3390/math12121836
Chicago/Turabian StyleLiang, Lisha, Xibing Li, Zhixiang Liu, and Siyu Peng. 2024. "Dynamic Responses of U-Shaped Caverns under Transient Stress Waves in Deep Rock Engineering" Mathematics 12, no. 12: 1836. https://doi.org/10.3390/math12121836
APA StyleLiang, L., Li, X., Liu, Z., & Peng, S. (2024). Dynamic Responses of U-Shaped Caverns under Transient Stress Waves in Deep Rock Engineering. Mathematics, 12(12), 1836. https://doi.org/10.3390/math12121836







