A Block Triple-Relaxation-Time Lattice Boltzmann Method for Solid–Liquid Phase Change Problem
Abstract
:1. Introduction
2. The Block Triple-Relaxation-Time Lattice Boltzmann Model
3. Numerical Diffusion Analysis of the B-TriRT LB Model for Solid–Liquid Phase Transition
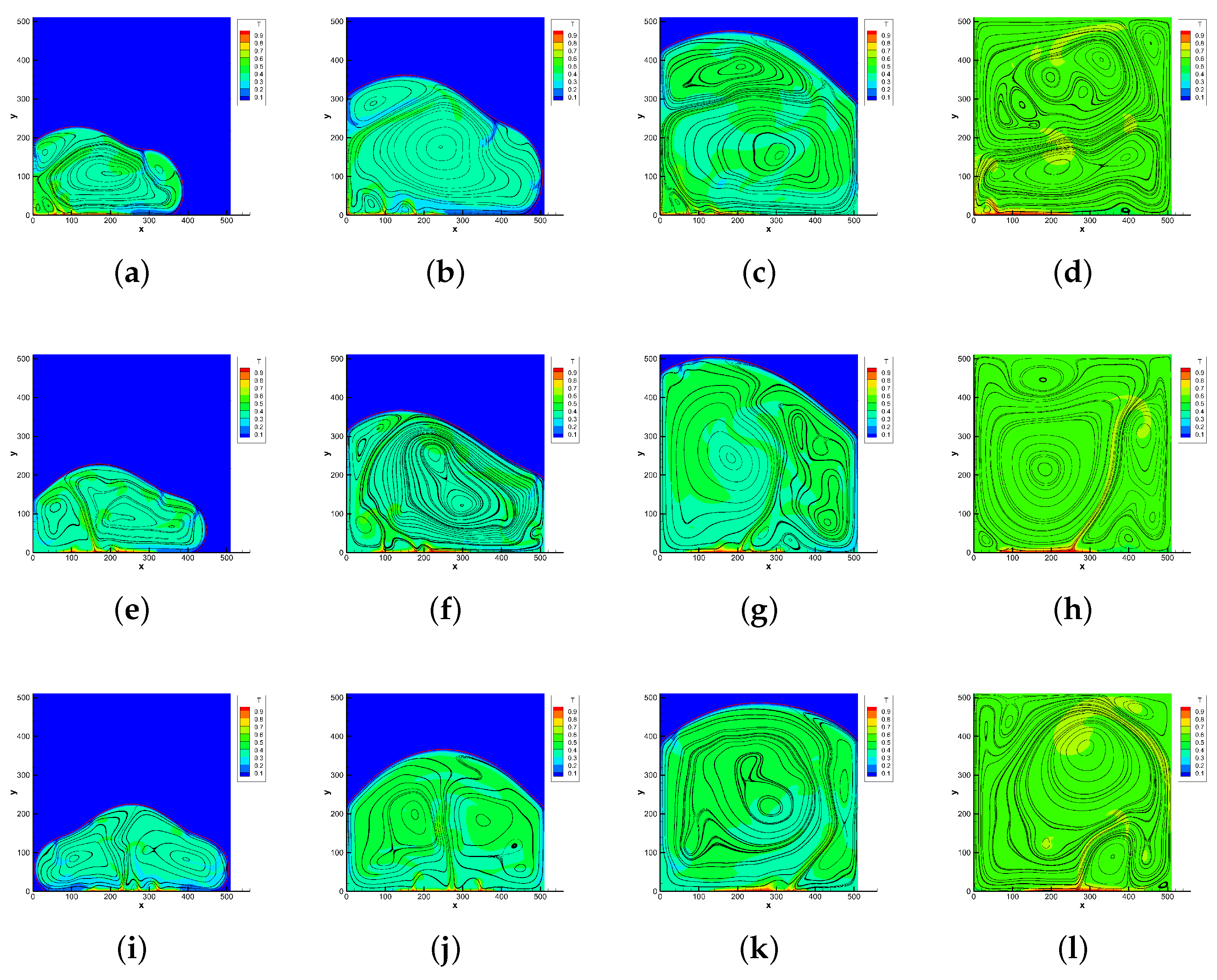
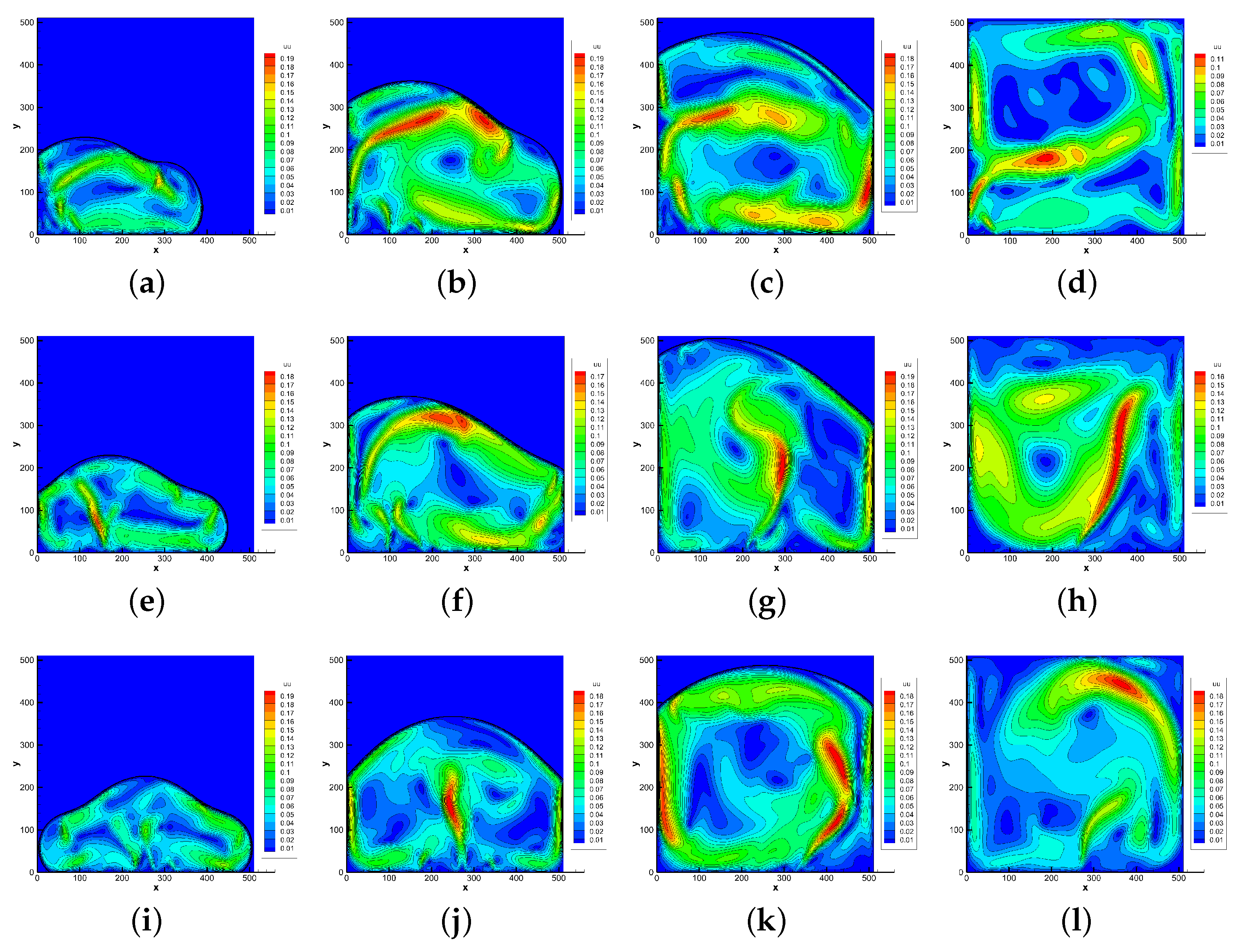
4. Numerical Results
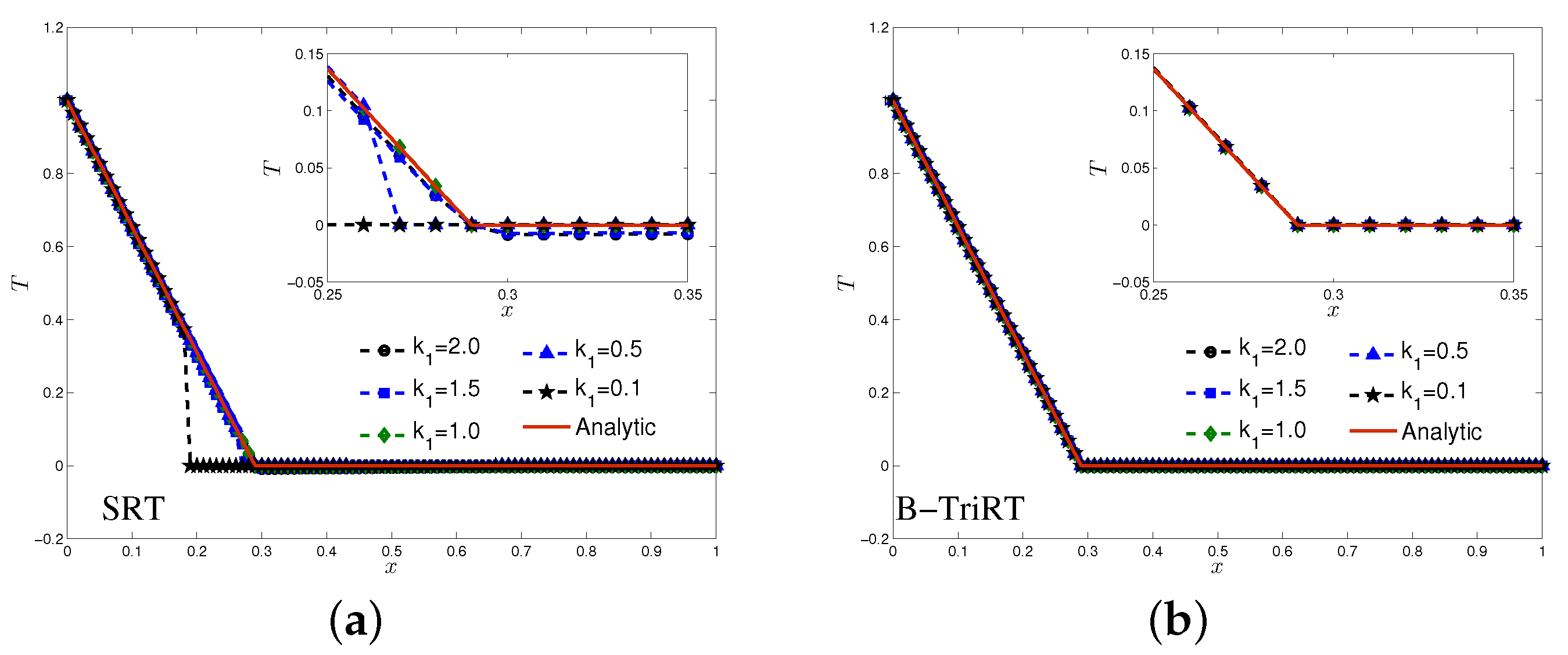
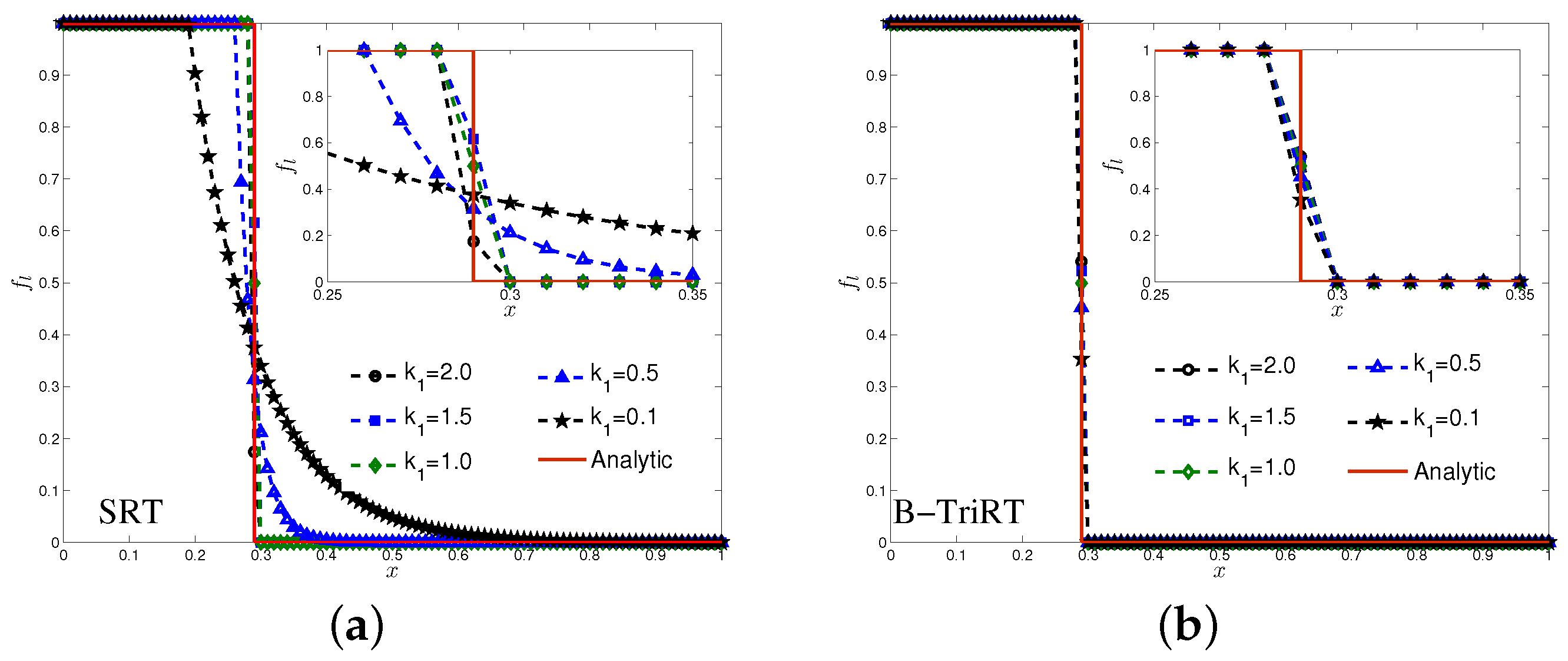
4.1. One-Phase Melting by Conduction
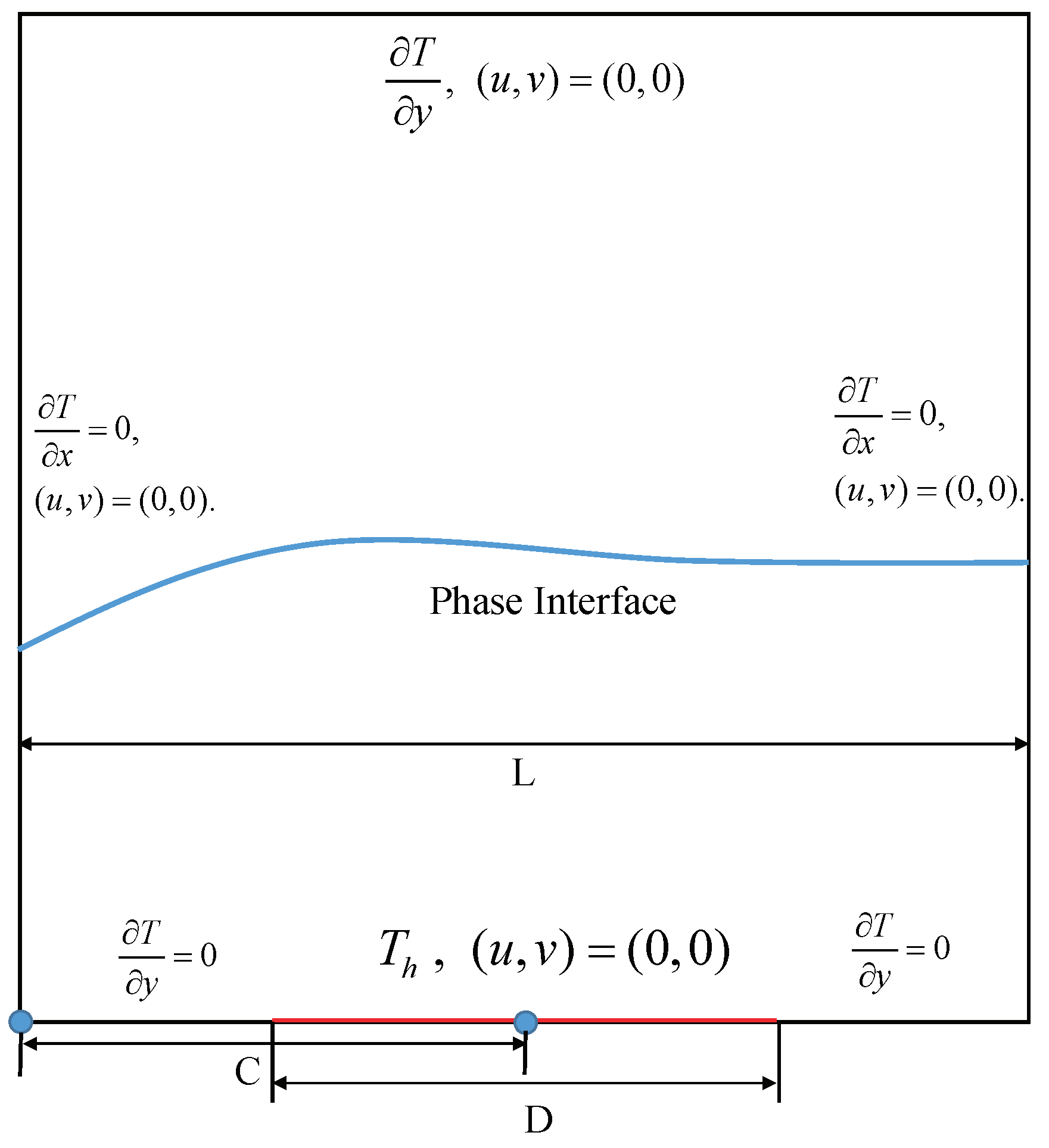
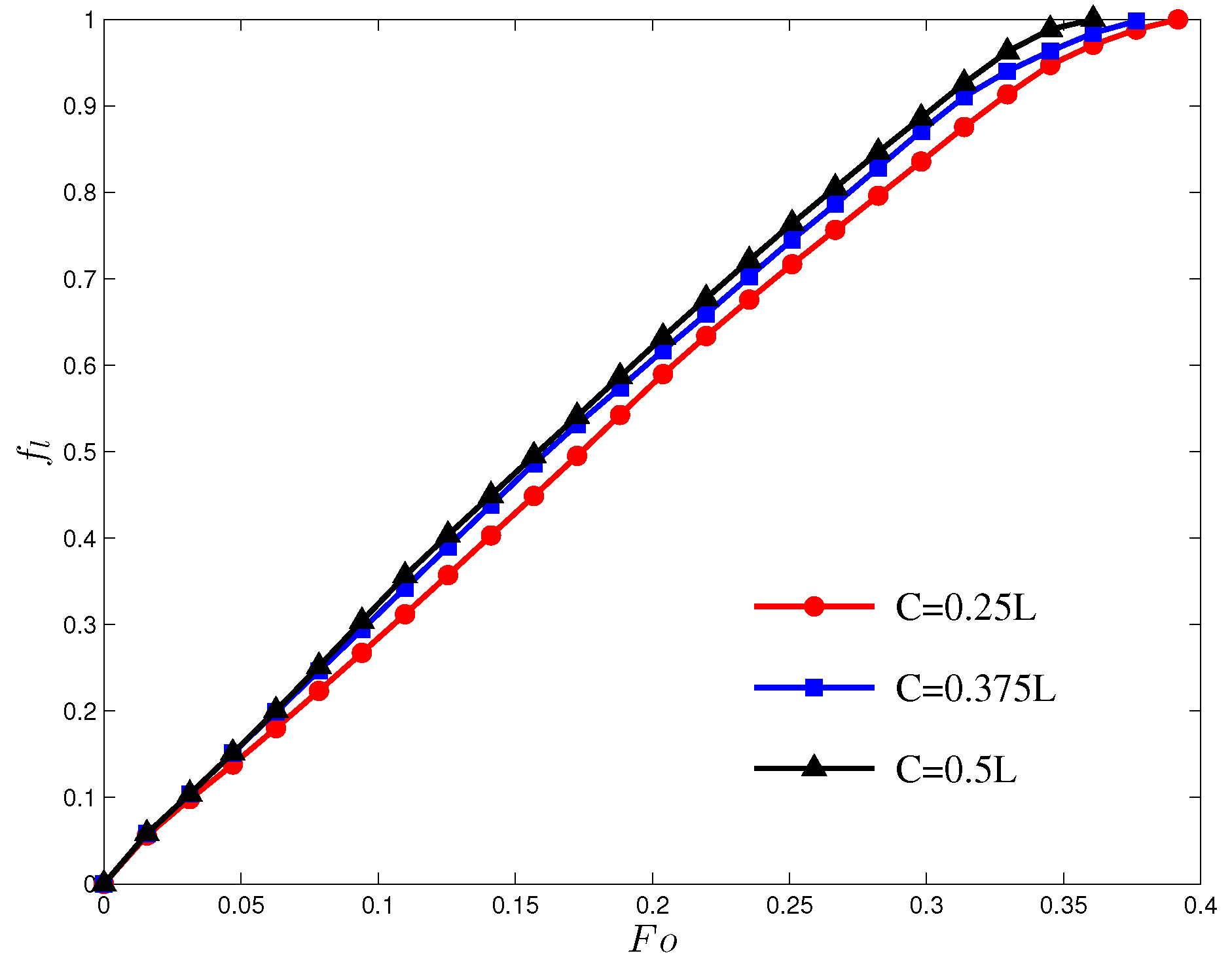
4.2. Melting in a Cavity Heated Locally from Below
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, N.; Yuan, Y.; Cao, X.; Du, Y.; Zhang, Z.; Gui, Y. Latent heat thermal energy storage systems with solid–liquid phase change materials: A review. Adv. Eng. Mater. 2018, 20, 1700753. [Google Scholar] [CrossRef]
- Tomita, S.; Celik, H.; Mobedi, M. Thermal analysis of solid/liquid phase change in a cavity with one wall at periodic temperature. Energies 2021, 14, 5957. [Google Scholar] [CrossRef]
- Malik, M.; Dincer, I.; Rosen, M. Review on use of phase change materials in battery thermal management for electric and hybrid electric vehicles. Int. J. Energy Res. 2016, 40, 1011–1031. [Google Scholar] [CrossRef]
- Konuklu, Y.; Ostry, M.; Paksoy, H.; Charvat, P. Review on using microencapsulated phase change materials (PCM) in building applications. Energy Build. 2015, 106, 134–155. [Google Scholar] [CrossRef]
- Shirbani, M.; Siavashi, M.; Bidabadi, M. Phase Change Materials Energy Storage Enhancement Schemes and Implementing the Lattice Boltzmann Method for Simulations: A Review. Energies 2023, 16, 1059. [Google Scholar] [CrossRef]
- Chen, D.; Riaz, A.; Aute, V.; Radermacher, R. A solid-liquid model based on lattice Boltzmann method for phase change material melting with porous media in cylindrical heat exchangers. Appl. Therm. Eng. 2022, 207, 118080. [Google Scholar] [CrossRef]
- Chiappini, D. A coupled lattice Boltzmann-finite volume method for phase change material analysis. Int. J. Therm. Sci. 2021, 164, 106893. [Google Scholar] [CrossRef]
- Rui, Z.; Li, J.; Ma, J.; Cai, H.; Nie, B.; Peng, H. Comparative study on natural convection melting in square cavity using lattice Boltzmann method. Results Phys. 2020, 18, 103274. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C.; Yang, L.; Zhao, X.; Liu, N. Phase-field-simplified lattice Boltzmann method for modeling solid-liquid phase change. Phys. Rev. E 2021, 103, 023308. [Google Scholar] [CrossRef]
- Han, Q.; Wang, H.; Yu, C.; Zhang, C. Lattice Boltzmann simulation of melting heat transfer in a composite phase change material. Appl. Therm. Eng. 2020, 176, 115423. [Google Scholar] [CrossRef]
- Feng, Y.; Li, H.; Li, L.; Bu, L.; Wang, T. Numerical investigation on the melting of nanoparticle-enhanced phase change materials (NEPCM) in a bottom-heated rectangular cavity using lattice Boltzmann method. Int. J. Heat Mass Transf. 2015, 81, 415–425. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Qian, Y.; Succi, S.; Orszag, S. Recent advances in lattice Boltzmann computing. Annu. Rev. Comput. Phys. 1995, 3, 195–242. [Google Scholar]
- d’Humières, D. Generalized lattice-Boltzmann equations, in: Rarefied gas dynamics: Theory and simulations. Progress Astronaut. Aeronaut. 1992, 159, 450–458. [Google Scholar]
- Lallemand, P.; Luo, L. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applicatons in Engineering; World Scientific Publishing: Singapore, 2013. [Google Scholar]
- Isfahani, A.H.; Tasdighi, I.; Karimipour, A.; Shirani, E.; Afrand, M. A joint lattice Boltzmann and molecular dynamics investigation for thermohydraulical simulation of nano flows through porous media. Eur. J. Mech. B-Fluids 2016, 55, 15–23. [Google Scholar] [CrossRef]
- Chai, Z.; He, N.; Guo, Z.; Shi, B. Lattice Boltzmann model for high-order nonlinear partial differential equations. Phys. Rev. E 2018, 97, 013304. [Google Scholar] [CrossRef]
- Chai, Z.; Shi, B. Multiple-relaxation-time lattice Boltzmann method for the Navier-Stokes and nonlinear convection-diffusion equations: Modeling, analysis, and elements. Phys. Rev. E 2020, 102, 023306. [Google Scholar] [CrossRef]
- Shi, B.; Guo, Z. Lattice Boltzmann model for nonlinear convection-diffusion equations. Phys. Rev. E 2009, 79, 016701. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Z.; Yang, X.; Zhang, Y. Mass conservative lattice Boltzmann scheme for a three-dimensional diffuse interface model with Peng-Robinson equation of state. Phys. Rev. E 2018, 98, 023306. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Shi, B.; Chai, Z.; Guo, Z. A Coupled Lattice Boltzmann Method to Solve Nernst-Planck Model for Simulating Electro-osmotic Flows. J. Sci. Comput. 2014, 61, 222–238. [Google Scholar] [CrossRef]
- Wang, L.; He, K.; Wang, H. Phase-field-based lattice Boltzmann model for simulating thermocapillary flows. Phys. Rev. E 2023, 108, 055306. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Pereira, G.; Kuang, S.; Chai, Z.; Shi, B. A generalized lattice Boltzmann model for solid-liquid phase change with variable density and thermophysical properties. Appl. Math. Lett. 2020, 104, 106250. [Google Scholar] [CrossRef]
- Huang, R.; Wu, H. Phase interface effects in the total enthalpy-based lattice Boltzmann model for solid-liquid phase change. J. Comput. Phys. 2015, 294, 346–362. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, X.; Feng, X.; Liu, F. An enthalpy-based cascaded lattice Boltzmann method for solid-liquid phase-change heat transfer. Appl. Therm. Eng. 2022, 209, 118283. [Google Scholar] [CrossRef]
- Liu, X.; Tong, Z.; He, Y. Enthalpy-based immersed boundary-lattice Boltzmann model for solid-liquid phase change in porous media under local thermal non-equilibrium condition. Int. J. Therm. Sci. 2022, 182, 107786. [Google Scholar] [CrossRef]
- Xu, X.; He, Y.; Han, J.; Zhu, J. Multiple-relaxation-time lattice Boltzmann model for anisotropic liquid-solid phase change. Appl. Math. Lett. 2022, 134, 108358. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Y.; Chai, Z.; Shi, B. A block triple-relaxation-time lattice Boltzmann model for nonlinear anisotropic convection-diffusion equations. Comput. Math. Appl. 2020, 79, 2550–2573. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Y.; Chai, Z.; Shi, B. Lattice Boltzmann simulations of melting in a rectangular cavity heated locally from below at high Rayleigh number. arXiv 2019, arXiv:1909.13086. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Chen, Z.; Zhao, Y. A Block Triple-Relaxation-Time Lattice Boltzmann Method for Solid–Liquid Phase Change Problem. Mathematics 2024, 12, 1815. https://doi.org/10.3390/math12121815
Yang X, Chen Z, Zhao Y. A Block Triple-Relaxation-Time Lattice Boltzmann Method for Solid–Liquid Phase Change Problem. Mathematics. 2024; 12(12):1815. https://doi.org/10.3390/math12121815
Chicago/Turabian StyleYang, Xuguang, Zhenyu Chen, and Yong Zhao. 2024. "A Block Triple-Relaxation-Time Lattice Boltzmann Method for Solid–Liquid Phase Change Problem" Mathematics 12, no. 12: 1815. https://doi.org/10.3390/math12121815
APA StyleYang, X., Chen, Z., & Zhao, Y. (2024). A Block Triple-Relaxation-Time Lattice Boltzmann Method for Solid–Liquid Phase Change Problem. Mathematics, 12(12), 1815. https://doi.org/10.3390/math12121815





