Appendix A
This section presents the code generated in this research.
#Estimation with Maximum Likelihood Method (MLM)
#EstimatorML: estimates the parameters of the DPB by the MLM
#X=((X_{1i},X_{2i})), i=1,2,…,n
EstimatorML = function(X){
n = dim(X)[2]
t1 = mean(X[1,])
t2 = mean(X[2,])
t3 = min(t1,t2)/2 # initial value of parameter t3
x_min = min(X[1,])
x_max = max(X[1,])
y_min = min(X[2,])
y_max = max(X[2,])
frec = matrix(0,x_max-x_min+1,y_max-y_min+1)
for(i in x_min:x_max){
p = i - x_min + 1
for(j in y_min:y_max){
q = j - y_min + 1
for (k in 1:n){
if(X[1,k]==i && X[2,k]==j) frec[p,q] = frec[p,q]+1
}
}
}
# Newton-Raphson Method
# prev_t3 saves the previous value of t3
# RMyDerRM_t3 calculates RM and the derivative of RM with respect to t3
num = 1
difm = 0.001
diff = 100
dif_min = 100
t3_min <- t3
while (diff>=difm && num<=200){
prev_t3 = t3
RM_Der = RMyDerRM_t3(n,x_min,x_max,y_min,y_max,frec,t1,t2,t3)
t3 = t3 - (RM_Der[1] - 1)/RM_Der[2]
diff = abs(prev_t3 - t3)
if(is.na(diff)){
diff = difm/10
num = 250
t3 = t3_min
} else if(diff<dif_min){
dif_min <- diff
t3_min <- t3
}
}
num = num + 1
}
return(c(t1,t2,t3))
}
# probPB calculates the probability function of a PB(t1,t2,t3)
probPB = function(x,y,t1,t2,t3){
s = 0
if(x>=0 && y>=0){
m = min(x,y)
tt1 = t1 - t3
tt2 = t2 - t3
for(i in 0:m){
s = s + tt1^(x-i)*tt2^(y-i)*t3^i/(gamma(x-i+1)*gamma(y-i+1)*gamma(i+1))
}
s = s*exp(-tt1 - tt2 - t3)
}
return(s)
}
RMyDerRM_t3 = function(n,x_min,x_max,y_min,y_max,frec,t1,t2,t3){
der = rm = 0
for(i in x_min:x_max){
p = i - x_min + 1
for(j in y_min:y_max){
q = j - y_min + 1
if(frec[p,q]>0){
prob_ij = probPB(i,j,t1,t2,t3)
prob_im1jm1 = probPB(i-1,j-1,t1,t2,t3)
prob_im2jm2 = probPB(i-2,j-2,t1,t2,t3)
prob_im2jm1 = probPB(i-2,j-1,t1,t2,t3)
prob_im1jm2 = probPB(i-1,j-2,t1,t2,t3)
prob_im1j = probPB(i-1,j,t1,t2,t3)
prob_ijm1 = probPB(i,j-1,t1,t2,t3)
rm = rm + frec[p,q]*prob_im1jm1/prob_ij
sum1 = (prob_im2jm2 - prob_im2jm1 - prob_im1jm2)/prob_ij
sum2 = prob_im1jm1*(prob_im1j + prob_ijm1 - prob_im1jm1)/(prob_ij^2)
der = der + frec[p,q]*(sum1 + sum2)
}
}
}
return(c(rm/n,der/n))
}
f_n = function(i,j,n,X){
ind1 = ind2 = rep(0,n)
ind1[X[1,]==i] = ind2[X[2,]==j] = 1
ss = sum(ind1*ind2)
return(ss/n)
}
# Bivariate Poisson Sample Generation
gmpb = function(n,t1,t2,t3){
if (t1>t3 && t2>t3 && t3>0){
a = rpois(n,t1-t3)
b = rpois(n,t2-t3)
c = rpois(n,t3)
return(rbind(a+c,b+c))
} else { stop("The parameters do not meet the requirements"); on.exit}
}
# Calculation of the statistic R_n,a # n is the sample size
R = function(X,t1,t2,t3){
m = 10
inf = max(max(X[1,]),max(X[2,])) + m
fp = Prob <- matrix(0,inf+1,inf+1)
for(i in 0:inf){
for(j in 0:inf){
Prob[i+1,j+1] = probPB(i,j,t1,t2,t3)
fp[i+1,j+1] = f_n(i,j,n,X) - probPB(i,j,t1,t2,t3)
}
}
k = l = 0:inf
f = function(k,l){1/((ii + k + a1 + 1)*(jj + l + a2 + 1))}
sa = 0
for(ii in 0:inf){
for(jj in 0:inf){
s = s + fp[ii+1,jj+1]*sum(fp*outer(k,l,FUN=f))
}
}
return(n*s)
}
# A function is defined to be introduced as an argument in parRapply
# Must be a function of a column
full_function = function(X){
X = data.frame(matrix(unlist(X), ncol = 2, byrow = F))
X = t(X)
th_estim = EstimatorML(X)
t1 = th_estim[1]
t2 = th_estim[2]
t3 = th_estim[3]
r_obs = R(X,t1,t2,t3)
r_boot = rep(0,B)
for (b in 1:B){
next = "F"
while(next=="F"){ # B bootstrap samples (Mboot) are generated
X_PBboot = gmpb(n,th_estim[1],th_estim[2],th_estim[3])
th_est_boot = EstimadorML(X_PBboot) # bootstrap theta estimator
th_dif1 = th_est_boot[1] - th_est_boot[3]
th_dif2 = th_est_boot[2] - th_est_boot[3]
if(th_dif1 > 0 && th_dif2 > 0 && th_est_boot[3] > 0) next = "T"
}
# Statistics are evaluated in each bootstrap sample
r_boot[b] = R(X_PBboot,th_est_boot[1],th_est_boot[2],th_est_boot[3])
}
# An approximation of the p-value is accumulated for each statistic
ind_r = rep(0,B)
ind_r[r_boot >= r_obs] = 1
vp_b = sum(ind_r)/B
}
M = 1000 # Monte Carlo iterations B = 500 # Bootstrap iterations
va1 = c(0,0,1,1); va2 = c(0,1,0,1) # vector (a1,a2)
library(parallel) nc = detectCores()
tm = c(30,50,70,100,150,200,250,300,500) # Sample sizes
Theta = matrix(0,6,3)
Theta[1,] = c(1.5,1,0.31); Theta[2,] = c(1.5,1,0.62)
Theta[3,] = c(1.5,1,0.92); Theta[4,] = c(1,1,0.5)
Theta[5,] = c(1,1,0.25); Theta[6,] = c(1,1,0.75) for(i in 1:6){
th = Theta[i,]
even = odd = c()
for(i in 1:(2*M)){
if(i%%2==0){
even = c(even,i)
} else {odd<-c(odd,i)}
}
for(t in 1:length(tm)){
n = tm[t]
X = Y = matrix(0,M,n)
carpet = "folder where the samples are saved"
file_L = paste0(carpet,"/Theta_",th[1],"_",th[2],"_",th[3],"_n",n,".txt")
XY = matrix(scan(file_L,sep=","),nrow=2*M,byrow=TRUE)
X = XY[odd,]
Y = XY[even,]
XY_col = matrix(0,2*n,M)
for (m in 1:M){
XY_col[,m] = c(X[m,],Y[m,])
}
# parallelize with parRapply with nc processors
carp_file = "folder where the outputs will be saved"
file = paste0(carp_file,th[1],"_",th[2],"_",th[3],"_n",n,".txt")
for (a_12 in 1:4){
a1 = va1[a_12]
a2 = va2[a_12]
for(nn in 1:nc){
cl = parallel::makeCluster(nn)
clusterExport(cl, "EstimatorML")
clusterExport(cl, "RMyDerRM_t3")
clusterExport(cl, "probPB")
clusterExport(cl, "f_n")
clusterExport(cl, "n")
clusterExport(cl, "a1")
clusterExport(cl, "a2")
clusterExport(cl, "B")
clusterExport(cl, "M")
clusterExport(cl, "R")
clusterExport(cl, "gmpb")
SS = paste0("Outings with ",nn," processors", "a1=",a1, "a2=",a2)
write(SS,file=file,append=TRUE)
a = proc.time()
res = parRapply(cl, t(XY_col), full_function)
parallel::stopCluster(cl)
execution_time = proc.time()-a
write("",file=file,append=TRUE)
write(c("vp : ",res),ncolumns=length(res)+1,file=file,append=TRUE)
ind1_r = ind2_r = ind3_r = rep(0,M)
ind1_r[res <= .01] = 1
error1_r = sum(ind1_r)/M
ind2_r[res <= .05] = 1
error5_r = sum(ind2_r)/M
ind3_r[res <= .1] = 1
error10_r = sum(ind3_r)/M
write("",file=file,append=TRUE)
write(c(error1_r,error5_r,error10_r),file=file,ncolumns=4,append=TRUE)
write("",file=file,append=TRUE)
write("Execution time",file=arch,append=TRUE)
write(execution_time,file=file,append=TRUE)
}
}
}
}
Appendix B
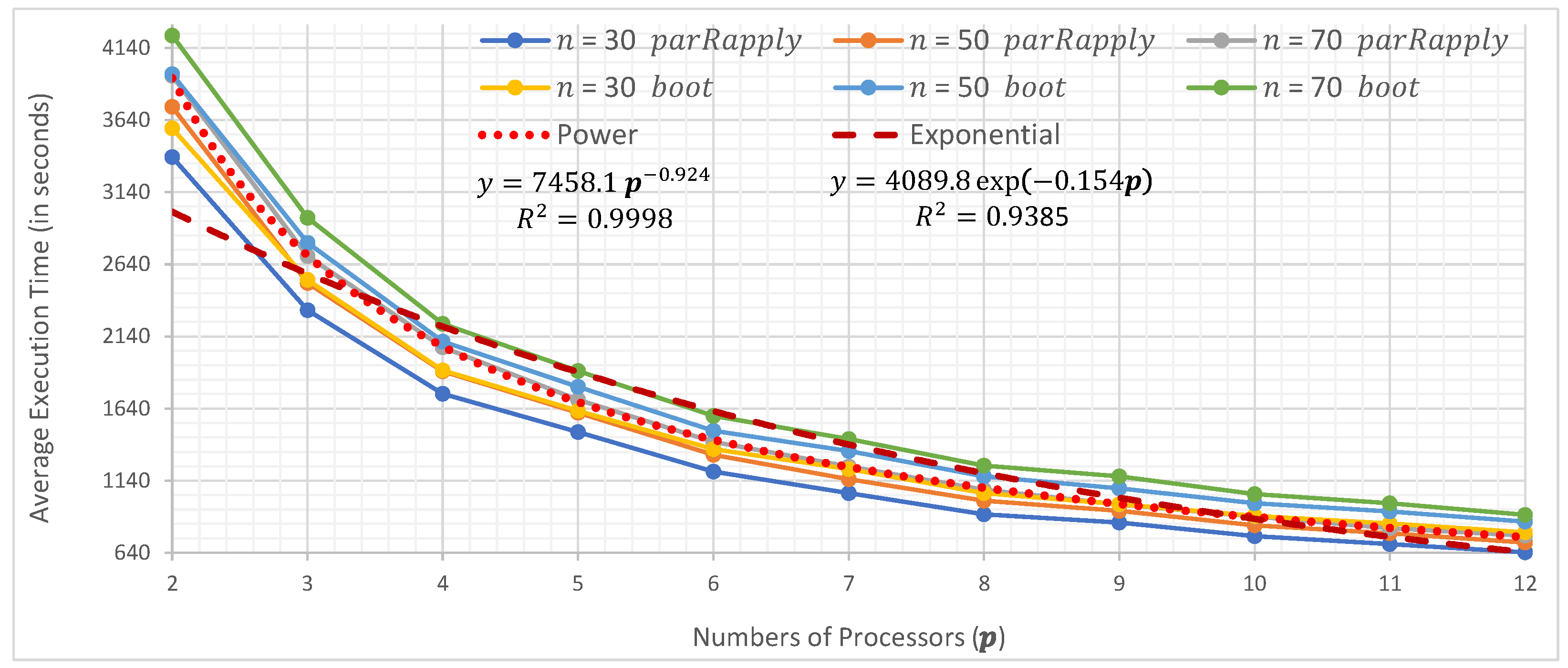
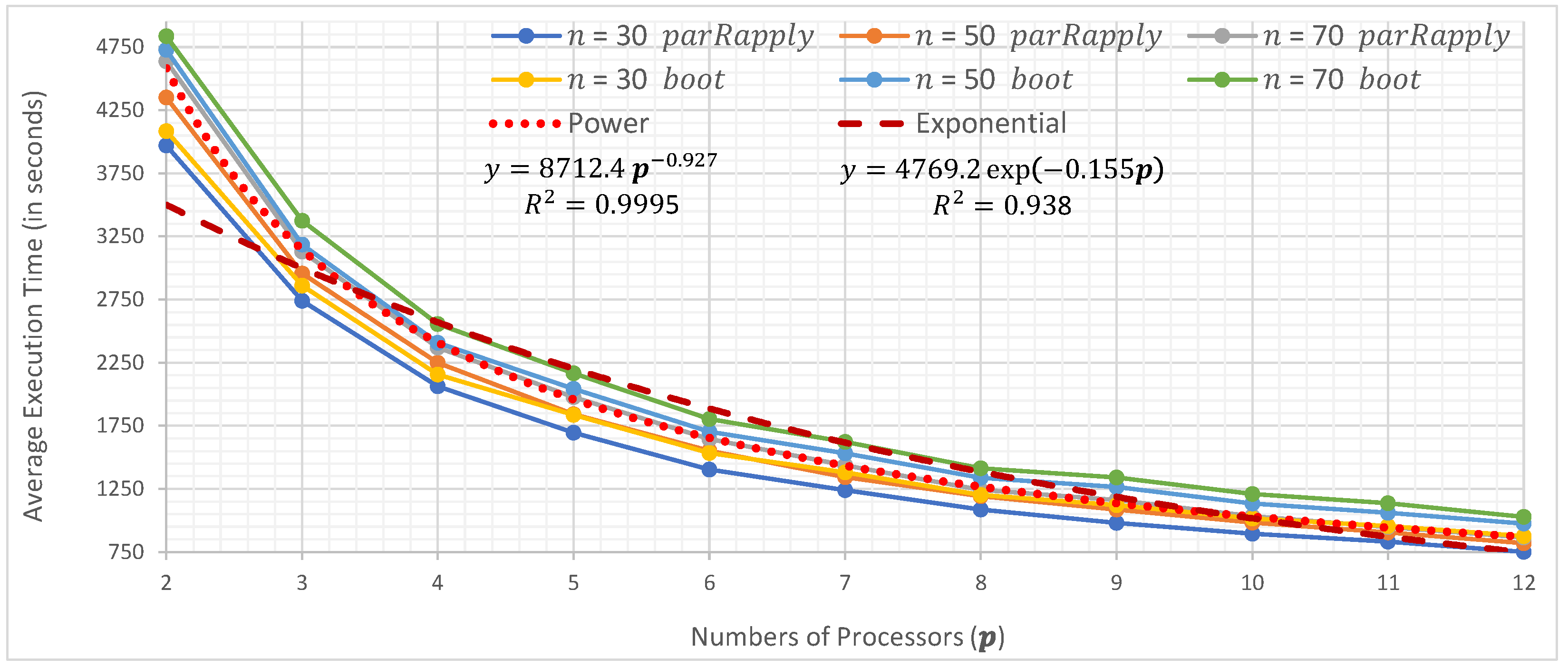
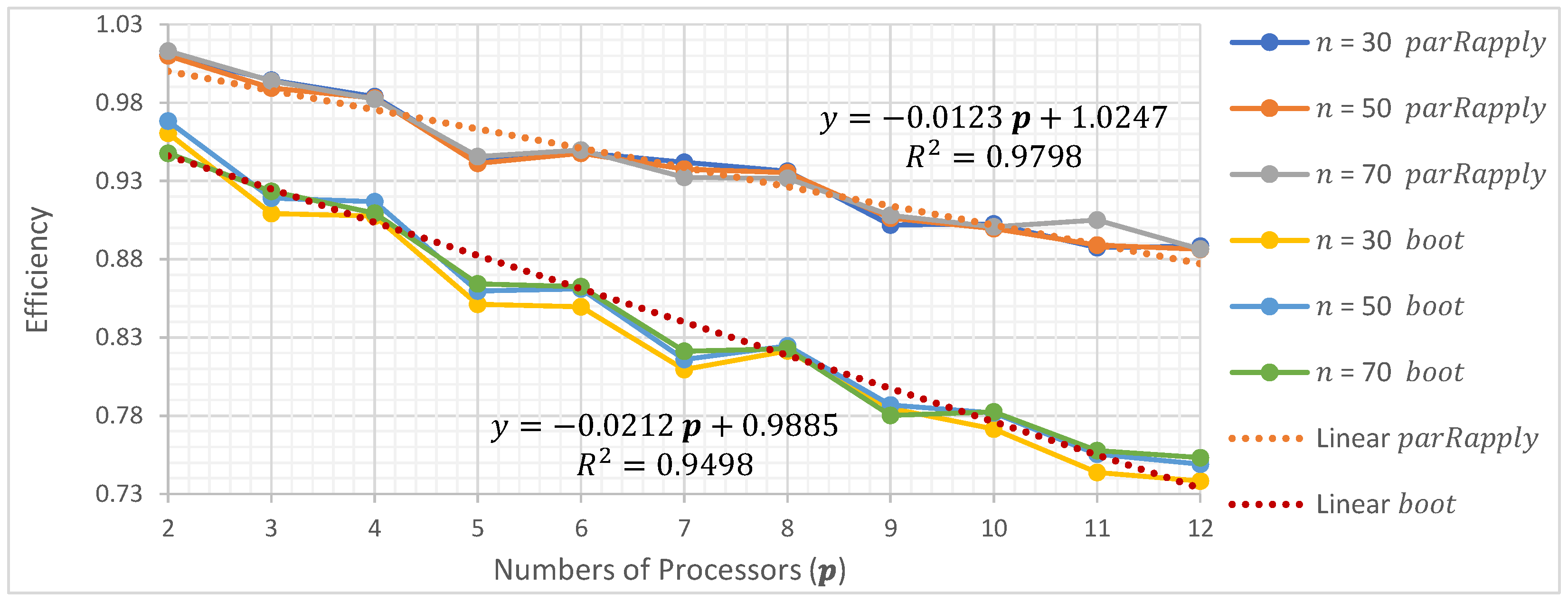
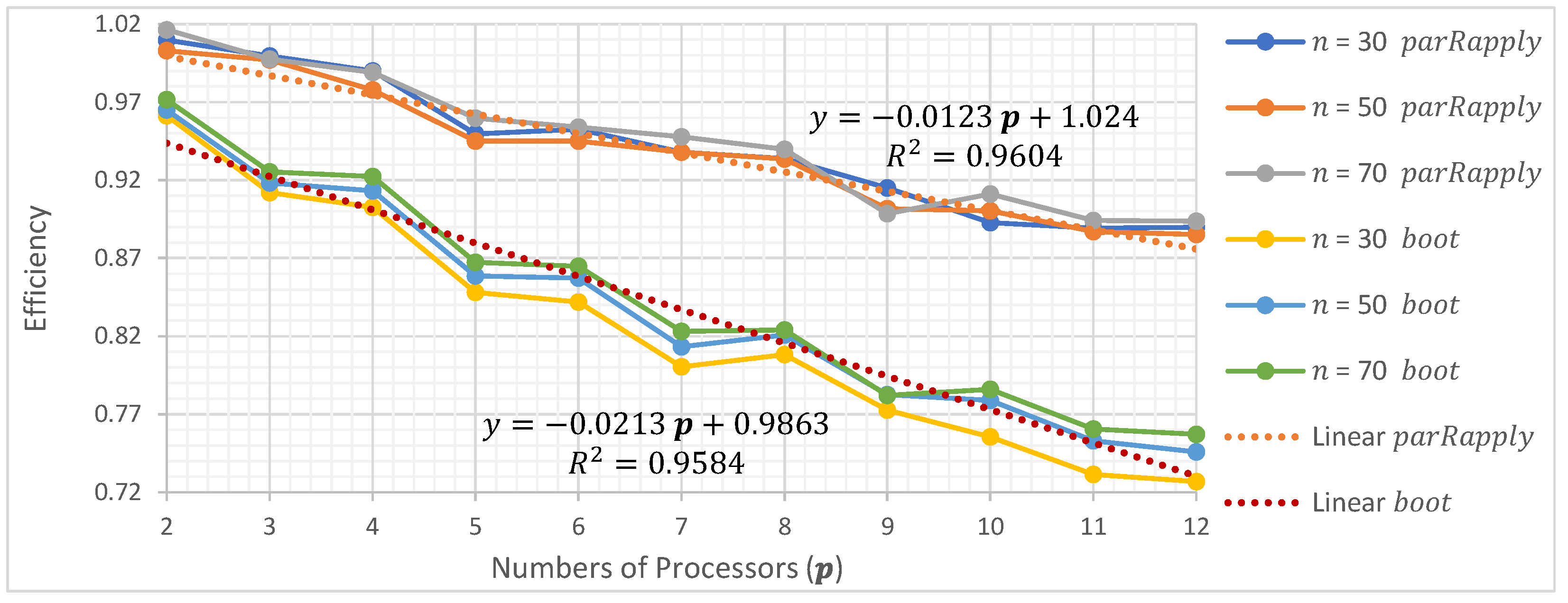
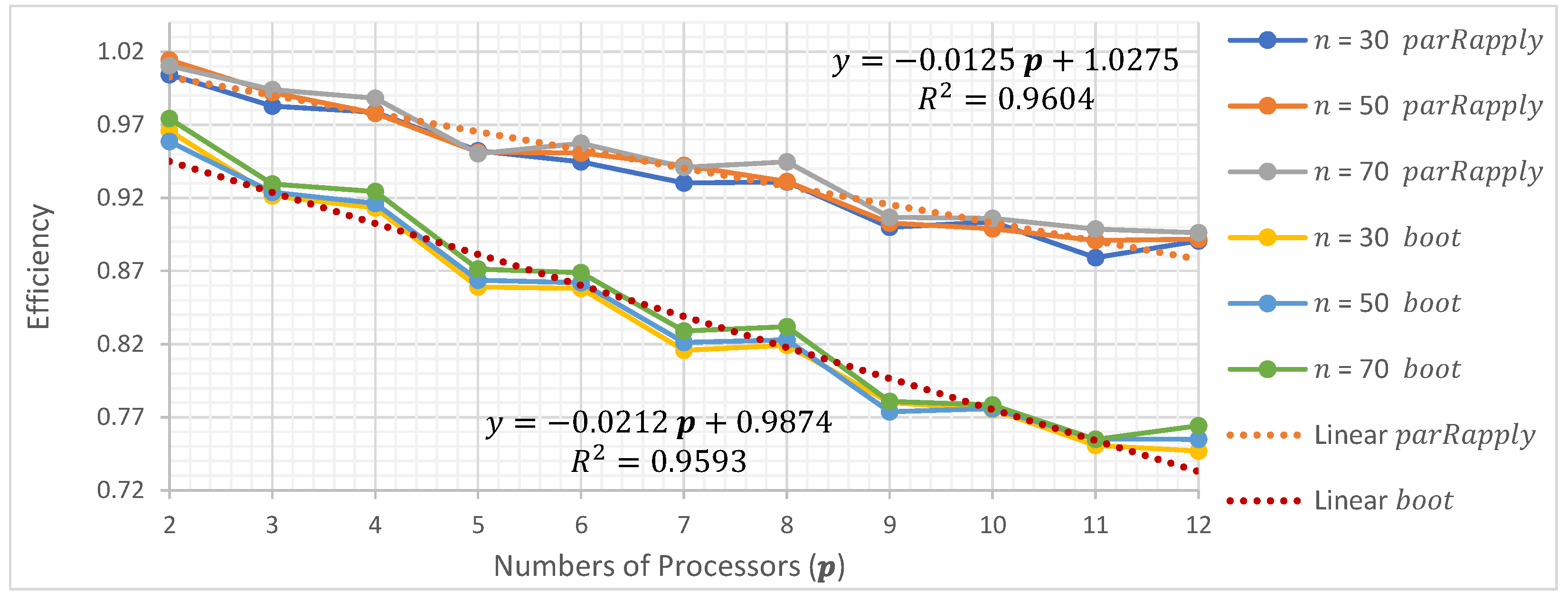
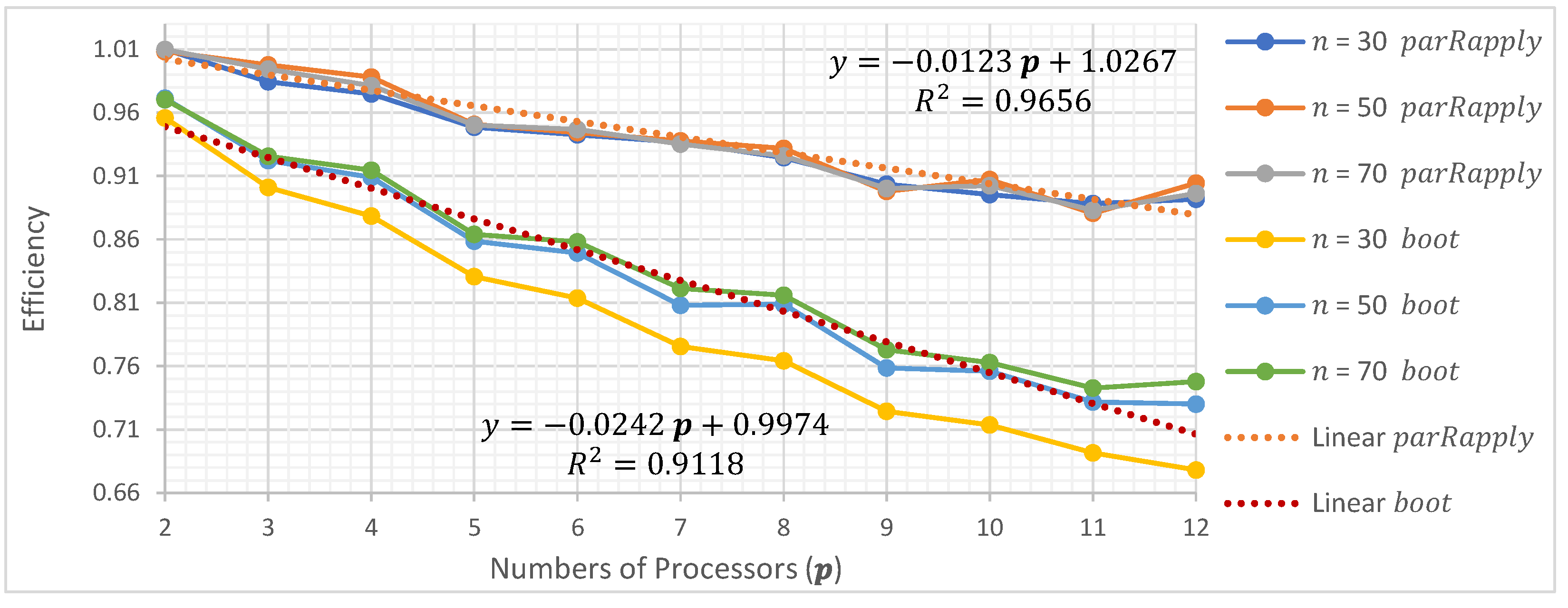
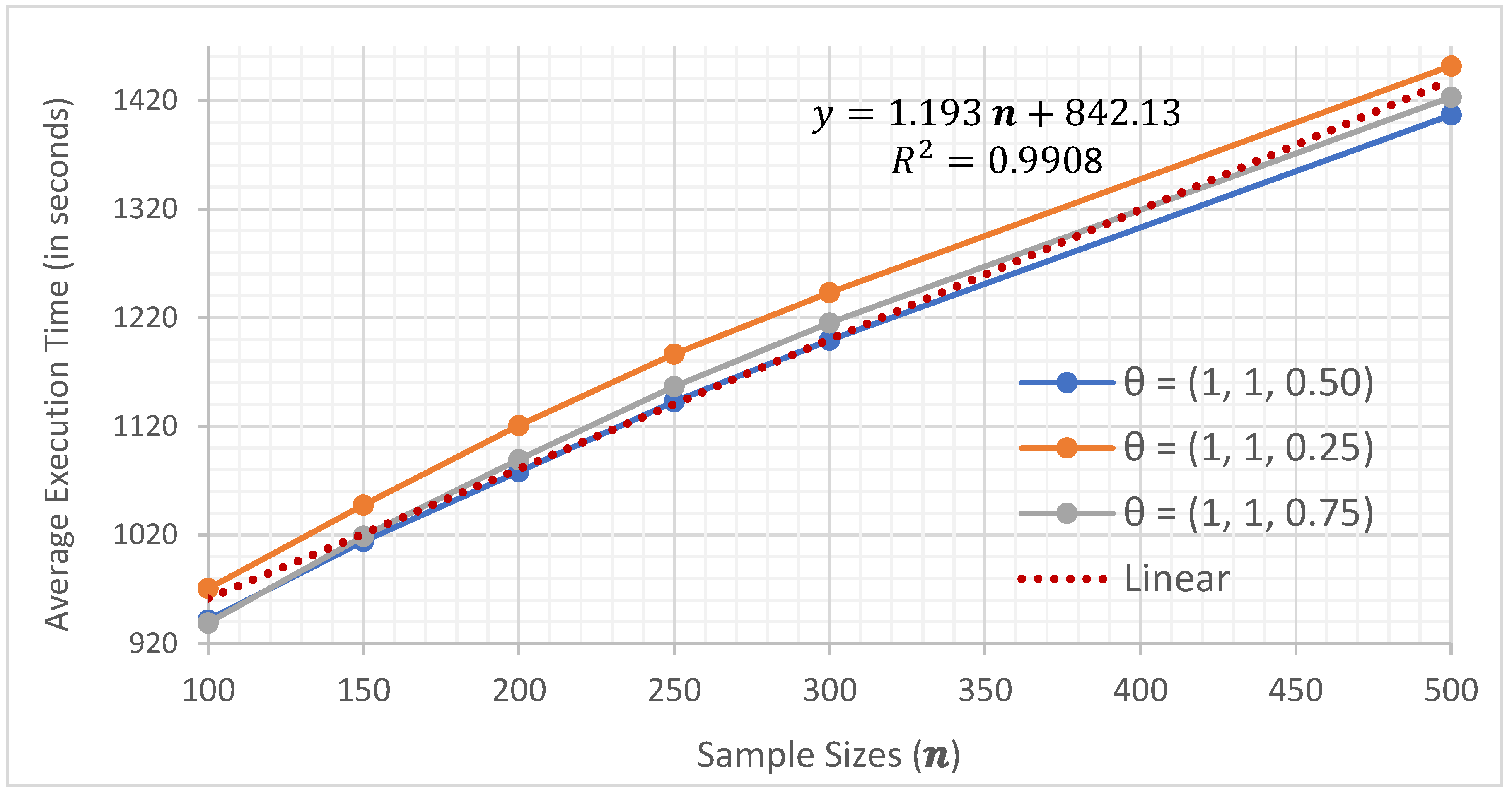
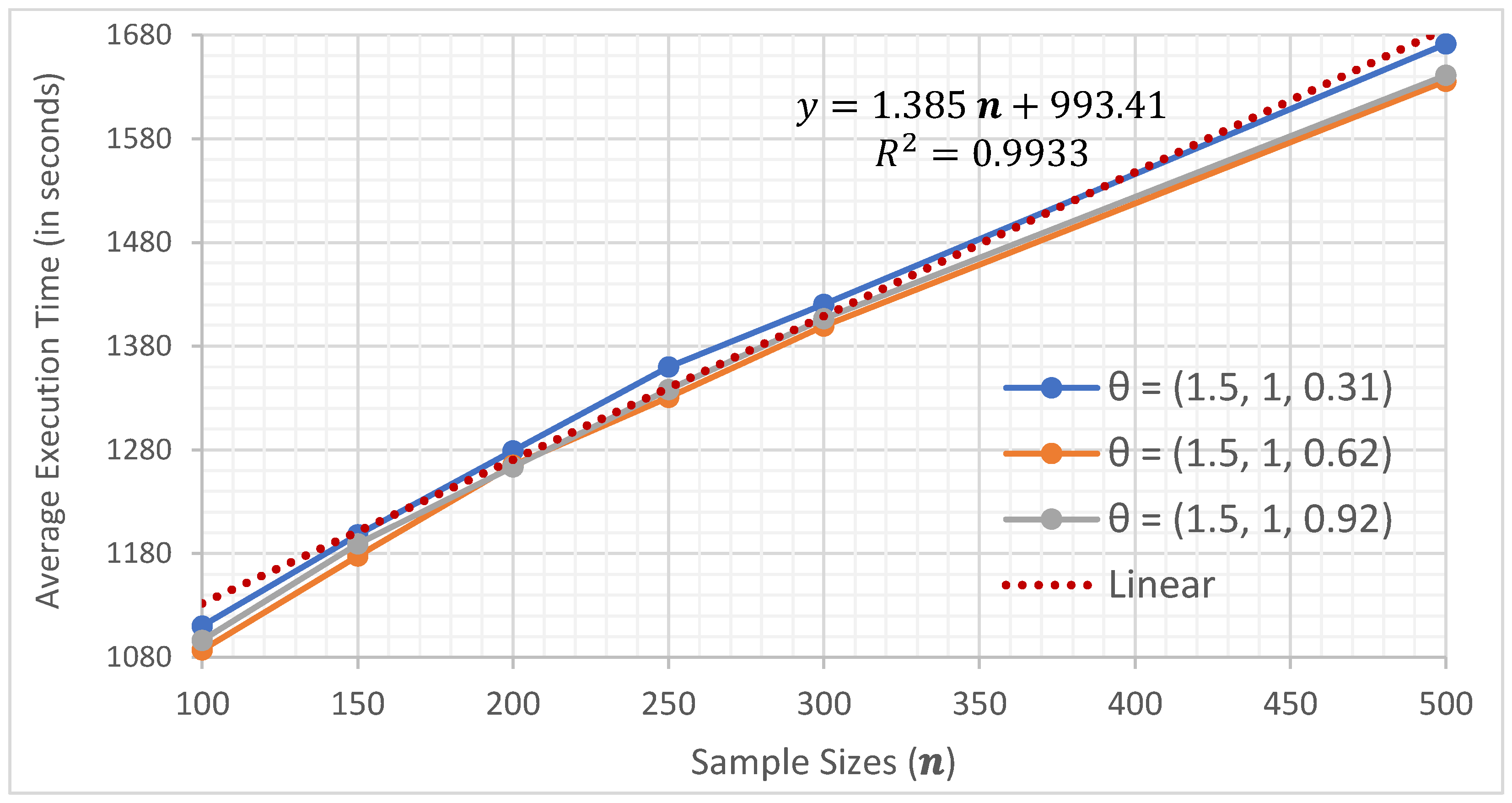
In this section, the average execution times are presented as a function of the number of processors used when running the two parallel implementations (parRapply and boot) analyzed in this research.
Table A1.
Average execution time (in seconds) using parRapply, (1.5, 1, 0.31), weight vectors , sample size n, for different numbers of processors p.
Table A1.
Average execution time (in seconds) using parRapply, (1.5, 1, 0.31), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 4049 | 4058 | 4063 | 4088 | 4402 | 4428 | 4413 | 4440 | 4657 | 4662 | 4663 | 4,674 |
| 3 | 2764 | 2762 | 2801 | 2793 | 2959 | 2979 | 2970 | 3006 | 3164 | 3142 | 3164 | 3162 |
| 4 | 2118 | 2100 | 2092 | 2112 | 2261 | 2259 | 2255 | 2248 | 2406 | 2399 | 2389 | 2404 |
| 5 | 1726 | 1761 | 1713 | 1724 | 1868 | 1888 | 1874 | 1870 | 2004 | 1970 | 1988 | 1,969 |
| 6 | 1445 | 1457 | 1444 | 1461 | 1575 | 1551 | 1601 | 1567 | 1679 | 1658 | 1640 | 1655 |
| 7 | 1242 | 1246 | 1257 | 1263 | 1365 | 1350 | 1361 | 1356 | 1432 | 1457 | 1420 | 1447 |
| 8 | 1102 | 1125 | 1123 | 1090 | 1203 | 1193 | 1191 | 1196 | 1288 | 1261 | 1274 | 1264 |
| 9 | 1007 | 1007 | 1012 | 1012 | 1105 | 1099 | 1112 | 1097 | 1158 | 1162 | 1160 | 1171 |
| 10 | 919 | 916 | 914 | 918 | 988 | 981 | 976 | 986 | 1044 | 1039 | 1055 | 1037 |
| 11 | 841 | 840 | 835 | 845 | 905 | 931 | 913 | 933 | 963 | 975 | 960 | 981 |
| 12 | 764 | 765 | 764 | 776 | 823 | 820 | 820 | 823 | 869 | 875 | 882 | 877 |
Table A2.
Average execution time (in seconds) using boot, (1.5, 1, 0.31), weight vectors , sample size n, for different numbers of processors p.
Table A2.
Average execution time (in seconds) using boot, (1.5, 1, 0.31), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 4359 | 4377 | 4338 | 4351 | 4645 | 4660 | 4672 | 4650 | 4936 | 4943 | 4941 | 4,948 |
| 3 | 3089 | 3078 | 3078 | 3079 | 3271 | 3280 | 3269 | 3258 | 3453 | 3454 | 3465 | 3,443 |
| 4 | 2368 | 2368 | 2367 | 2380 | 2496 | 2489 | 2489 | 2478 | 2631 | 2626 | 2626 | 2605 |
| 5 | 2003 | 2010 | 1998 | 2010 | 2110 | 2114 | 2098 | 2107 | 2229 | 2225 | 2219 | 2,209 |
| 6 | 1701 | 1707 | 1710 | 1706 | 1775 | 1772 | 1783 | 1771 | 1875 | 1852 | 1861 | 1,863 |
| 7 | 1543 | 1533 | 1532 | 1530 | 1598 | 1602 | 1600 | 1598 | 1670 | 1670 | 1666 | 1666 |
| 8 | 1366 | 1360 | 1362 | 1362 | 1395 | 1400 | 1403 | 1393 | 1465 | 1471 | 1465 | 1476 |
| 9 | 1280 | 1270 | 1281 | 1280 | 1322 | 1322 | 1328 | 1328 | 1376 | 1379 | 1377 | 1382 |
| 10 | 1161 | 1177 | 1162 | 1169 | 1194 | 1193 | 1203 | 1196 | 1260 | 1255 | 1261 | 1254 |
| 11 | 1098 | 1088 | 1095 | 1099 | 1126 | 1125 | 1119 | 1126 | 1173 | 1175 | 1170 | 1178 |
| 12 | 1025 | 1020 | 1022 | 1027 | 1027 | 1029 | 1040 | 1034 | 1074 | 1072 | 1058 | 1071 |
Table A3.
Average execution time (in seconds) using parRapply, (1.5, 1, 0.62), weight vectors , sample size n, for different numbers of processors p.
Table A3.
Average execution time (in seconds) using parRapply, (1.5, 1, 0.62), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3897 | 3879 | 3969 | 3890 | 4257 | 4316 | 4291 | 4261 | 4529 | 4544 | 4530 | 4,564 |
| 3 | 2658 | 2632 | 2626 | 2646 | 2889 | 2886 | 2915 | 2909 | 3107 | 3109 | 3091 | 3,093 |
| 4 | 2037 | 2011 | 2015 | 2005 | 2178 | 2208 | 2195 | 2186 | 2330 | 2322 | 2343 | 2,344 |
| 5 | 1669 | 1638 | 1672 | 1673 | 1797 | 1819 | 1823 | 1809 | 1925 | 1934 | 1949 | 1,927 |
| 6 | 1391 | 1392 | 1375 | 1392 | 1495 | 1514 | 1524 | 1516 | 1609 | 1610 | 1610 | 1,615 |
| 7 | 1200 | 1195 | 1205 | 1201 | 1311 | 1307 | 1317 | 1326 | 1388 | 1396 | 1380 | 1399 |
| 8 | 1064 | 1046 | 1053 | 1001 | 1149 | 1156 | 1149 | 1151 | 1218 | 1236 | 1212 | 1224 |
| 9 | 974 | 976 | 970 | 970 | 1058 | 1066 | 1059 | 1071 | 1117 | 1135 | 1124 | 1131 |
| 10 | 867 | 873 | 877 | 874 | 973 | 948 | 972 | 950 | 1021 | 1004 | 1016 | 1023 |
| 11 | 819 | 806 | 807 | 815 | 873 | 886 | 876 | 886 | 929 | 959 | 959 | 948 |
| 12 | 728 | 737 | 730 | 738 | 820 | 807 | 806 | 810 | 859 | 861 | 853 | 858 |
Table A4.
Average execution time (in seconds) using boot, (1.5, 1, 0.62), weight vectors , sample size n, for different numbers of processors p.
Table A4.
Average execution time (in seconds) using boot, (1.5, 1, 0.62), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 4133 | 4111 | 4110 | 4110 | 4542 | 4552 | 4529 | 4530 | 4840 | 4836 | 4844 | 4833 |
| 3 | 2883 | 2874 | 2891 | 2875 | 3169 | 3175 | 3162 | 3160 | 3381 | 3372 | 3395 | 3373 |
| 4 | 2184 | 2184 | 2188 | 2181 | 2394 | 2396 | 2388 | 2394 | 2549 | 2547 | 2564 | 2550 |
| 5 | 1857 | 1854 | 1853 | 1854 | 2034 | 2031 | 2027 | 2033 | 2163 | 2155 | 2174 | 2158 |
| 6 | 1555 | 1559 | 1554 | 1553 | 1697 | 1696 | 1697 | 1696 | 1810 | 1798 | 1810 | 1801 |
| 7 | 1403 | 1397 | 1401 | 1399 | 1528 | 1526 | 1524 | 1525 | 1621 | 1619 | 1622 | 1622 |
| 8 | 1223 | 1226 | 1223 | 1225 | 1335 | 1333 | 1335 | 1333 | 1420 | 1411 | 1419 | 1410 |
| 9 | 1147 | 1144 | 1145 | 1145 | 1259 | 1258 | 1256 | 1256 | 1340 | 1338 | 1341 | 1,339 |
| 10 | 1037 | 1036 | 1036 | 1037 | 1132 | 1131 | 1132 | 1132 | 1211 | 1208 | 1212 | 1209 |
| 11 | 972 | 973 | 968 | 972 | 1058 | 1056 | 1055 | 1056 | 1133 | 1132 | 1133 | 1129 |
| 12 | 892 | 893 | 895 | 898 | 973 | 971 | 962 | 973 | 1035 | 1024 | 1032 | 1024 |
Table A5.
Average execution time (in seconds) using parRapply, (1.5, 1, 0.92), weight vectors , sample size n, for different numbers of processors p.
Table A5.
Average execution time (in seconds) using parRapply, (1.5, 1, 0.92), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3970 | 3971 | 4000 | 4004 | 4351 | 4331 | 4355 | 4326 | 4639 | 4619 | 4654 | 4599 |
| 3 | 2740 | 2713 | 2701 | 2708 | 2956 | 2963 | 2969 | 2947 | 3130 | 3178 | 3106 | 3130 |
| 4 | 2064 | 2049 | 2028 | 2042 | 2250 | 2251 | 2253 | 2251 | 2369 | 2391 | 2349 | 2354 |
| 5 | 1696 | 1677 | 1668 | 1686 | 1841 | 1865 | 1855 | 1845 | 1978 | 1962 | 1959 | 1973 |
| 6 | 1403 | 1411 | 1399 | 1438 | 1551 | 1549 | 1538 | 1537 | 1645 | 1630 | 1620 | 1617 |
| 7 | 1239 | 1221 | 1235 | 1224 | 1344 | 1339 | 1329 | 1328 | 1436 | 1414 | 1419 | 1409 |
| 8 | 1087 | 1059 | 1079 | 1076 | 1191 | 1172 | 1174 | 1192 | 1243 | 1238 | 1234 | 1234 |
| 9 | 981 | 986 | 998 | 989 | 1086 | 1080 | 1083 | 1086 | 1162 | 1144 | 1139 | 1138 |
| 10 | 896 | 881 | 886 | 882 | 983 | 975 | 972 | 989 | 1034 | 1037 | 1027 | 1030 |
| 11 | 832 | 819 | 841 | 820 | 906 | 893 | 884 | 912 | 948 | 943 | 944 | 948 |
| 12 | 751 | 742 | 753 | 751 | 820 | 823 | 825 | 823 | 866 | 868 | 873 | 871 |
Table A6.
Average execution time (in seconds) using boot, (1.5, 1, 0.92), weight vectors , sample size n, for different numbers of processors p.
Table A6.
Average execution time (in seconds) using boot, (1.5, 1, 0.92), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 4085 | 4083 | 4083 | 4082 | 4728 | 4551 | 4539 | 4535 | 4836 | 4839 | 4839 | 4830 |
| 3 | 2860 | 2850 | 2847 | 2856 | 3185 | 3175 | 3165 | 3166 | 3374 | 3372 | 3396 | 3376 |
| 4 | 2155 | 2159 | 2169 | 2155 | 2407 | 2396 | 2391 | 2401 | 2556 | 2543 | 2547 | 2547 |
| 5 | 1836 | 1838 | 1837 | 1835 | 2044 | 2034 | 2032 | 2035 | 2166 | 2156 | 2164 | 2164 |
| 6 | 1534 | 1530 | 1536 | 1527 | 1704 | 1700 | 1698 | 1698 | 1804 | 1806 | 1808 | 1,811 |
| 7 | 1381 | 1382 | 1380 | 1381 | 1533 | 1531 | 1526 | 1528 | 1622 | 1622 | 1625 | 1,626 |
| 8 | 1202 | 1203 | 1203 | 1206 | 1339 | 1337 | 1333 | 1333 | 1414 | 1417 | 1418 | 1413 |
| 9 | 1121 | 1125 | 1122 | 1126 | 1264 | 1264 | 1262 | 1260 | 1341 | 1341 | 1342 | 1339 |
| 10 | 1016 | 1018 | 1018 | 1018 | 1133 | 1132 | 1133 | 1135 | 1210 | 1210 | 1214 | 1208 |
| 11 | 956 | 955 | 955 | 954 | 1060 | 1059 | 1058 | 1058 | 1136 | 1134 | 1135 | 1134 |
| 12 | 876 | 881 | 886 | 877 | 975 | 976 | 965 | 966 | 1028 | 1028 | 1027 | 1027 |
Table A7.
Average execution time (in seconds) using parRapply, (1, 1, 0.5), weight vectors , sample size n, for different numbers of processors p.
Table A7.
Average execution time (in seconds) using parRapply, (1, 1, 0.5), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3457 | 3439 | 3509 | 3475 | 3727 | 3759 | 3767 | 3771 | 3960 | 3978 | 3952 | 3979 |
| 3 | 2341 | 2330 | 2326 | 2350 | 2498 | 2522 | 2539 | 2517 | 2679 | 2721 | 2676 | 2704 |
| 4 | 1782 | 1769 | 1769 | 1758 | 1929 | 1931 | 1914 | 1930 | 2053 | 2037 | 2031 | 2034 |
| 5 | 1466 | 1479 | 1468 | 1491 | 1591 | 1595 | 1602 | 1590 | 1679 | 1673 | 1690 | 1680 |
| 6 | 1222 | 1228 | 1222 | 1232 | 1326 | 1335 | 1325 | 1329 | 1415 | 1399 | 1413 | 1409 |
| 7 | 1070 | 1075 | 1063 | 1061 | 1150 | 1156 | 1138 | 1146 | 1229 | 1211 | 1210 | 1213 |
| 8 | 941 | 938 | 942 | 931 | 1003 | 1004 | 1015 | 1013 | 1075 | 1070 | 1072 | 1074 |
| 9 | 848 | 849 | 849 | 858 | 936 | 924 | 923 | 930 | 976 | 1011 | 987 | 1016 |
| 10 | 777 | 808 | 781 | 774 | 839 | 834 | 835 | 839 | 888 | 877 | 877 | 899 |
| 11 | 715 | 703 | 725 | 723 | 773 | 768 | 773 | 774 | 813 | 821 | 823 | 823 |
| 12 | 656 | 654 | 655 | 660 | 709 | 706 | 710 | 712 | 755 | 761 | 743 | 749 |
Table A8.
Average execution time (in seconds) using boot, (1, 1, 0.5), weight vectors , sample size n, for different numbers of processors p.
Table A8.
Average execution time (in seconds) using boot, (1, 1, 0.5), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3665 | 3673 | 3670 | 3682 | 4000 | 3983 | 3988 | 3992 | 4249 | 4255 | 4238 | 4241 |
| 3 | 2577 | 2572 | 2589 | 2586 | 2792 | 2786 | 2799 | 2806 | 2971 | 2984 | 2966 | 2967 |
| 4 | 1955 | 1947 | 1959 | 1961 | 2109 | 2103 | 2113 | 2110 | 2233 | 2247 | 2229 | 2235 |
| 5 | 1668 | 1663 | 1662 | 1667 | 1794 | 1790 | 1797 | 1795 | 1901 | 1908 | 1898 | 1903 |
| 6 | 1399 | 1400 | 1394 | 1399 | 1497 | 1498 | 1497 | 1498 | 1584 | 1591 | 1590 | 1594 |
| 7 | 1263 | 1260 | 1262 | 1256 | 1351 | 1353 | 1355 | 1352 | 1431 | 1432 | 1431 | 1433 |
| 8 | 1091 | 1092 | 1093 | 1092 | 1175 | 1170 | 1172 | 1174 | 1254 | 1250 | 1250 | 1252 |
| 9 | 1014 | 1014 | 1019 | 1015 | 1093 | 1091 | 1095 | 1095 | 1172 | 1172 | 1175 | 1169 |
| 10 | 938 | 935 | 933 | 932 | 989 | 989 | 988 | 989 | 1049 | 1048 | 1052 | 1050 |
| 11 | 875 | 878 | 880 | 877 | 931 | 929 | 929 | 930 | 985 | 986 | 988 | 986 |
| 12 | 809 | 810 | 809 | 810 | 859 | 862 | 861 | 860 | 904 | 904 | 913 | 911 |
Table A9.
Average execution time (in seconds) using parRapply, (1, 1, 0.25), weight vectors , sample size n, for different numbers of processors p.
Table A9.
Average execution time (in seconds) using parRapply, (1, 1, 0.25), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3589 | 3605 | 3583 | 3587 | 3925 | 3975 | 3867 | 3904 | 4113 | 4063 | 4154 | 4105 |
| 3 | 2436 | 2452 | 2442 | 2458 | 2660 | 2628 | 2630 | 2667 | 2792 | 2837 | 2796 | 2803 |
| 4 | 1844 | 1851 | 1859 | 1879 | 1998 | 1991 | 2018 | 1993 | 2105 | 2103 | 2139 | 2106 |
| 5 | 1528 | 1563 | 1545 | 1537 | 1667 | 1669 | 1652 | 1648 | 1760 | 1762 | 1748 | 1745 |
| 6 | 1280 | 1296 | 1277 | 1289 | 1375 | 1384 | 1382 | 1379 | 1445 | 1468 | 1449 | 1465 |
| 7 | 1125 | 1114 | 1111 | 1136 | 1200 | 1194 | 1203 | 1223 | 1260 | 1267 | 1253 | 1260 |
| 8 | 988 | 972 | 980 | 974 | 1062 | 1043 | 1049 | 1059 | 1108 | 1100 | 1109 | 1111 |
| 9 | 890 | 892 | 897 | 892 | 960 | 957 | 968 | 958 | 1054 | 1014 | 1038 | 1017 |
| 10 | 811 | 812 | 810 | 799 | 874 | 880 | 870 | 872 | 914 | 925 | 910 | 921 |
| 11 | 748 | 746 | 751 | 742 | 797 | 821 | 799 | 794 | 846 | 850 | 855 | 846 |
| 12 | 689 | 678 | 687 | 685 | 745 | 736 | 738 | 739 | 771 | 786 | 773 | 779 |
Table A10.
Average execution time (in seconds) using boot, (1, 1, 0.25), weight vectors , sample size n, for different numbers of processors p.
Table A10.
Average execution time (in seconds) using boot, (1, 1, 0.25), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3968 | 3950 | 3972 | 3954 | 4136 | 4150 | 4142 | 4141 | 4368 | 4354 | 4384 | 4386 |
| 3 | 2830 | 2809 | 2812 | 2813 | 2923 | 2913 | 2922 | 2907 | 3069 | 3086 | 3058 | 3065 |
| 4 | 2175 | 2166 | 2169 | 2164 | 2215 | 2222 | 2229 | 2222 | 2319 | 2328 | 2333 | 2323 |
| 5 | 1848 | 1845 | 1853 | 1856 | 1892 | 1892 | 1893 | 1888 | 1972 | 1980 | 1972 | 1972 |
| 6 | 1586 | 1570 | 1570 | 1580 | 1590 | 1590 | 1595 | 1586 | 1663 | 1659 | 1651 | 1664 |
| 7 | 1416 | 1421 | 1419 | 1424 | 1430 | 1438 | 1443 | 1434 | 1487 | 1484 | 1480 | 1483 |
| 8 | 1255 | 1251 | 1252 | 1256 | 1255 | 1261 | 1260 | 1255 | 1303 | 1299 | 1302 | 1310 |
| 9 | 1171 | 1180 | 1181 | 1178 | 1169 | 1174 | 1176 | 1176 | 1222 | 1224 | 1226 | 1219 |
| 10 | 1082 | 1086 | 1087 | 1084 | 1069 | 1070 | 1068 | 1074 | 1100 | 1096 | 1099 | 1102 |
| 11 | 1028 | 1020 | 1019 | 1025 | 1003 | 1008 | 1007 | 1002 | 1028 | 1031 | 1032 | 1027 |
| 12 | 954 | 952 | 959 | 952 | 931 | 935 | 925 | 927 | 950 | 952 | 946 | 953 |
Table A11.
Average execution time (in seconds) using parRapply, (1, 1, 0.75), weight vectors , sample size n, for different numbers of processors p.
Table A11.
Average execution time (in seconds) using parRapply, (1, 1, 0.75), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3383 | 3426 | 3400 | 3418 | 3731 | 3716 | 3725 | 3733 | 3946 | 3970 | 3981 | 3963 |
| 3 | 2321 | 2293 | 2321 | 2296 | 2511 | 2543 | 2525 | 2566 | 2697 | 2690 | 2705 | 2683 |
| 4 | 1742 | 1755 | 1752 | 1747 | 1899 | 1910 | 1931 | 1918 | 2064 | 2021 | 2031 | 2063 |
| 5 | 1478 | 1451 | 1462 | 1444 | 1610 | 1585 | 1599 | 1603 | 1701 | 1693 | 1702 | 1700 |
| 6 | 1204 | 1205 | 1214 | 1217 | 1320 | 1315 | 1338 | 1322 | 1410 | 1405 | 1416 | 1408 |
| 7 | 1053 | 1040 | 1036 | 1047 | 1150 | 1146 | 1145 | 1147 | 1238 | 1234 | 1225 | 1227 |
| 8 | 907 | 927 | 916 | 927 | 1002 | 1009 | 1009 | 1004 | 1077 | 1083 | 1090 | 1062 |
| 9 | 850 | 844 | 847 | 852 | 931 | 921 | 920 | 920 | 974 | 988 | 978 | 992 |
| 10 | 755 | 767 | 762 | 767 | 831 | 831 | 843 | 842 | 892 | 897 | 894 | 885 |
| 11 | 701 | 708 | 713 | 699 | 775 | 762 | 770 | 772 | 810 | 801 | 805 | 812 |
| 12 | 643 | 647 | 648 | 645 | 711 | 713 | 700 | 707 | 759 | 750 | 759 | 753 |
Table A12.
Average execution time (in seconds) using boot, (1, 1, 0.75), weight vectors , sample size n, for different numbers of processors p.
Table A12.
Average execution time (in seconds) using boot, (1, 1, 0.75), weight vectors , sample size n, for different numbers of processors p.
| | | n = 30 | n = 50 | n = 70 |
|---|
| | | | | | | | | | | | | | |
|---|
| p | |
|---|
| 2 | 3582 | 3601 | 3601 | 3596 | 3957 | 3978 | 3983 | 3966 | 4226 | 4631 | 4244 | 4254 |
| 3 | 2533 | 2524 | 2539 | 2532 | 2789 | 2790 | 2795 | 2783 | 2963 | 2957 | 2966 | 2972 |
| 4 | 1904 | 1900 | 1905 | 1900 | 2105 | 2099 | 2095 | 2088 | 2228 | 2335 | 2229 | 2241 |
| 5 | 1625 | 1623 | 1621 | 1622 | 1791 | 1791 | 1789 | 1785 | 1901 | 1904 | 1898 | 1897 |
| 6 | 1358 | 1356 | 1353 | 1351 | 1486 | 1492 | 1491 | 1484 | 1588 | 1589 | 1585 | 1585 |
| 7 | 1220 | 1219 | 1218 | 1218 | 1346 | 1347 | 1345 | 1347 | 1428 | 1432 | 1427 | 1427 |
| 8 | 1053 | 1050 | 1049 | 1052 | 1169 | 1166 | 1166 | 1161 | 1245 | 1249 | 1249 | 1247 |
| 9 | 976 | 978 | 978 | 979 | 1086 | 1087 | 1087 | 1084 | 1169 | 1170 | 1170 | 1169 |
| 10 | 895 | 895 | 894 | 896 | 983 | 984 | 985 | 982 | 1048 | 1050 | 1049 | 1051 |
| 11 | 843 | 844 | 843 | 846 | 927 | 925 | 925 | 924 | 984 | 986 | 986 | 985 |
| 12 | 782 | 777 | 775 | 784 | 856 | 849 | 860 | 857 | 903 | 911 | 914 | 906 |