Deterministic and Stochastic Nonlinear Model for Transmission Dynamics of COVID-19 with Vaccinations Following Bayesian-Type Procedure

Abstract

We develop a mathematical model for the SARAS-CoV-2 double variant transmission characteristics with variant 1 vaccination to address this novel aspect of the disease. The model is theoretically examined, and adequate requirements are derived for the stability of its equilibrium points. The model includes the single variant 1 and variant 2 endemic equilibria in addition to the endemic and disease-free equilibria. Various approaches are used for the global and local stability of the model. For both strains, we determine the basic reproductive numbers ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$. To investigate the occurrence of the layers (waves), we expand the model to include some analysis based on the second-order derivative. The model is then expanded to its stochastic form, and numerical outcomes are computed. For numerical purposes, we use the nonstandard finite difference method. Some error analysis is also recorded.

1. Introduction

COVID-19 is a viral infectious disease which was discovered in Wuhan, China, at the end of 2019. The disease then became an outbreak and spread all over the world in next few months [1]. The Severe Acute Respiratory Syndrome (SARS) virus, which causes COVID-19, has been responsible for persistent human-to-human transmission. As we mentioned, in Wuhan city, the first case of the new virus was reported in December 2019 [2]. The general death rate for COVID-19 is below 5 percent, with an average of 2.3 percent [3], while mortality rates for those over 80 years of age are 14.8 percent and 8 percent, respectively; older populations are more at risk [4]. Hospitalization rates are quite high, placing a heavy global strain on health-care systems everywhere [5], despite the mortality rate appearing to be low. COVID-19 is transmitted from one person to another by personal interaction with infected surfaces or objects and also via the inhaling of droplets from the air from both asymptomatic and infected individuals [6]. The continuous COVID-19 outbreak poses a huge threat to communities around the world, risking millions of people’s health, and causing serious social and economic problems as a result of the procedures of isolation. Further, it is indicated that when the recruitment rate of immigrants is below a specific threshold value, restricting the stream of emigrants could have a substantial influence in decreasing the rate of infected people. Researchers [7,8,9,10,11] have conducted a detailed survey about the physical activity in specific regions before and after the COVID-19 pandemic.

Compartmental models have been essentials tools for understanding the transmission dynamics of various infectious diseases. Researchers in this regard have formulated various mathematical models; we refer to [12]. In the same way, the author of [8] developed a SIRD-type model to investigate the transmission of COVID-19 in different countries. Vaccines are an essential pharmaceutical tool in the fight against the COVID-19 pandemic. We currently face an epidemiological environment that is considered different from that of the early pandemic. This makes it possible to examine real-world situations that combine the impacts of both therapeutic measures like therapy and mass vaccination campaigns. Additionally, nontherapeutic public health interventions like face masks, hand washing, and social distancing have also been considered as precautionary measures. The COVID-19 outbreak has given rise to a number of research projects using compartmental epidemic models which address various key aspects of the disease’s management, transmission, and reduction [9]. There are several mathematical models that have been formulated for double variant diseases. The authors studied a two-strain malaria model in [10]. In the same way, the authors investigated two-strain influenza model with cross-immunity in [11,13]. Also, the authors of [14,15,16] studied two-strain mathematical models for dengue disease, suffering from infection, and the flu. Cross-immunity and co-infection have been taken into consideration in research on the structure between two viral infections [17]. Also, other studies have reported the consequences of double competing variants that are characterized by cross-immunization [18]. It has since been noted that the maximum rate of infected persons and the average fatality rate grow logarithmically with the number of strains. Multiple virus strains and reinfection (perhaps brought on by diminishing immunity) are a couple of the biggest problems with the present COVID-19 pandemic [19]. SARS-CoV-2 variations were very rapidly spreading in the initial stage, so it is important to account for variations and changing growth in the mathematical models. Therefore, researchers have used multi-strains mathematical models to investigate the transmission dynamics of COVID-19 [20,21].

Researchers have used a multi-strain SEIR epidemic model to investigate the global dynamics of COVID-19 (see [22]). In addition, the authors of [23] developed some control strategies using a multi-strain epidemic model for the said infectious disease. Moreover, researchers have investigated the co-circulation of two infectious diseases and the impact of vaccination against one of them [24]. The SIR model for the temporal evolution of the said disease was studied in [25]. Additionally, the authors of [26] estimated the COVID-19 outbreak size in Harbin. Investigation of the procedure of vaccination and treatment were analyzed for influenza disease [27,28]. Keeping in mind the importance of the reproductive number in mathematical modeling, researchers performed fundamental analysis of the said quantity in [29]. Also, the authors of [30,31] established a detailed numerical scheme for the classical as well as fractional-order COVID-19 mathematical model called the nonstandard finite difference (NSFD) scheme. The said numerical scheme is utilized in this work to simulate our results. We determine basic reproductive numbers in cases of both variants. The results show that both strains will remain active when ${\mathcal{R}}_1>1$ and ${\mathcal{R}}_2>1$. However, due to the new herd immunity brought on by the effectiveness of the strain 1 immunity and given that the initially stain 2 reproduction number ${\mathcal{R}}_2$ is maintained below one, variant 2 will not become established or carry on in society.

Model Formulation

It is assumed that the population is homogeneously mixed and that each member has an equal chance of contracting the infection. The only way to transmit an infection of COVID-19 is from person to person.The whole population of the human community at time t, represented by $\mathcal{N}\left(t\right)$, is divided into sub-population compartments of susceptible individuals $\mathcal{S}\left(t\right)$, vaccinated individuals $\mathcal{V}\left(t\right)$, individuals infected with variant 1 $\mathcal{A}\left(t\right)$, individuals infected with variant two $\mathcal{B}\left(t\right)$, and recovered individuals $\mathcal{R}\left(t\right)$ based on the disease status of each individual. Here, we also structure our investigation via using Bayesian-type flow Figure 1 as.

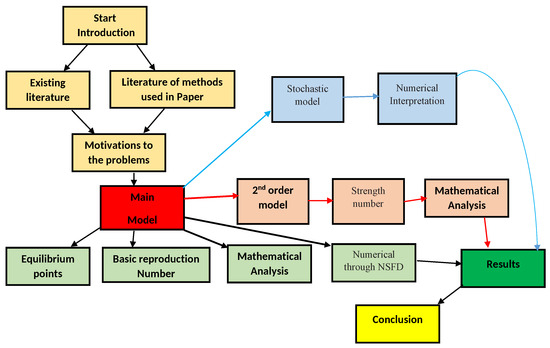
Figure 1. The flow chart of the procedure to conduct this research work for model (1).

The total number of people is provided by $\mathcal{N}\left(t\right)$:

$$\mathcal{N}\left(t\right)=\mathcal{S}\left(t\right)+\mathcal{V}\left(t\right)+\mathcal{A}\left(t\right)+\mathcal{B}\left(t\right)+\mathcal{R}\left(t\right).$$

For the standard rate (the rate of strain 1 infection per unit time) to be $\frac{{\mu }_1\mathcal{A}\left(t\right)}{\mathcal{N}\left(t\right)}$, it is supposed that individuals are homogeneously mixed within the population. As a result, the possibility that an individual will take the variant 1 infection at any given time t is $\frac{\mathcal{A}\left(t\right)}{\mathcal{N}\left(t\right)}$. With strain 1, infected people either have a constant incidence of natural death $d_0$ or a constant rate of disease-related death $d_A$. The fraction $\frac{1}{d_0+d_A}$ represents the infectious average life expectancy of people infected with strain 1 while $d_A$. Also, $\frac{1}{d_0}$ represents the death-adjusted per capita life expectancy.

Even though at the start time of the COVID-19 pandemic, the transmission of infection was more rapid than that of new recruitment and death because of the pandemic’s small duration at the time [25], ignoring these types of demographic parameters was fully verified in the variety of mathematical models in the study [26]. However, at this time, it is crucial to take into account the essential model dynamics while explaining the progression of the COVID-19 pandemic because the illness has been around for a long (since December 2019). As a result, both spontaneous death and the disease-specific death rate $(d_A,d_B$, respectively, for strains 1 and 2) are taken into account. In our model, we employ both ongoing vaccination (where a fraction of susceptible individuals are immunized per unit of time) and cohort vaccination, which involves immunizing a part of the recently recruited community members. Although COVID-19 immunization is not yet administered at birth, we should remark that its inclusion in our theoretical investigation has no bearing on the conclusions because it has been demonstrated that various numerical/analytical modeling outcomes are independent of the types of vaccination program used [26,27].

This result is demonstrated graphically by examining the potential impact of the model variables on the initial transmission rates ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$. Due to the re-emergence of SARS-CoV-2 following its several waves and various strains, as well as the fact that SARS-CoV-2 vaccination is still in development with younger age groups being taken into consideration, our recommended strategy is preemptive in case the manufacturing of the vaccine includes immunizations in the new recruitment. We formulate the following deterministic model of nonlinear differential equations as

$$\begin{array}{cc}\hfill \frac{d\mathcal{S}}{dt}& =(1-\beta )\alpha -(a+b+\eta +d_0)\mathcal{S}+\gamma \mathcal{R},\hfill \\ \hfill \frac{d\mathcal{V}}{dt}& =\beta \alpha +\eta \mathcal{S}-(b+(1-\delta )a+d_0)\mathcal{V},\hfill \\ \hfill \frac{d\mathcal{A}}{dt}& =a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A},\hfill \\ \hfill \frac{d\mathcal{B}}{dt}& =b(\mathcal{S}+\mathcal{V})-(r_2+d_0+d_B)\mathcal{B},\hfill \\ \hfill \frac{d\mathcal{R}}{dt}& =r_1\mathcal{A}+r_2\mathcal{B}-(\gamma +d_0)\mathcal{R}.\hfill \end{array}$$

(1)

where $a=\frac{k{\mu }_1\mathcal{A}}{\mathcal{N}}$ is the infection rate of the delta virus, and $b=\frac{k{\mu }_2\mathcal{B}}{\mathcal{N}}$ is the infection rate of the omicron virus (Table 1).

Table 1. Parameters and biological description (1).

Parameters	Physical Meaning and Representation
$\mathcal{S}$	Susceptible compartment
$\mathcal{V}$	Vaccinated compartment
$\mathcal{A}$	Delta virus infected compartment
$\mathcal{B}$	Omicron virus infected compartment
$\mathcal{R}$	Recovered compartment
$\alpha$	Birth rate
$d_A$	Disease death rate of delta virus
$d_0$	Natural death rate
$d_B$	Disease death rate of omicron virus
$\eta$	Vaccination rate
k	Contact rate
${\mu }_1$	Transmission of delta virus
${\mu }_2$	Transmission of omicron virus
$\delta$	Delta virus vaccine efficacy
$\gamma$	Loss of immunity
$\beta$	Vaccination rate
$r_1$	Recovery from delta virus
$r_2$	Recovery of omicron virus

With the initial condition

$$\mathcal{S}\ge 0,$$

$$\mathcal{V}\ge 0,$$

$$\mathcal{A}\ge 0,$$

$$\mathcal{B}\ge 0,$$

and

$$\mathcal{R}\ge 0.$$

The parameters used in the above sysytem is describe in the following (Table 1),

In Figure 2, the schematic diagram is presented.

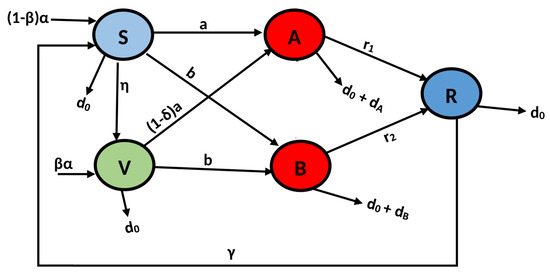
Figure 2. Diagrammatical presentation of the model (1).

The outline of this paper is as follows: In Section 1, we write the introduction and formulation of our deterministic model. Section 2, we provide the fundamental analysis about the equilibrium points and reproductive number for the deterministic model. In Section 3, the stability analysis is given. In Section 4, we perform an analysis based on the second derivative test. In Section 5, a numerical scheme based on the NSFD method is formulated. In Section 6, the stochastic model is analyzed. In Section 7, the numerical results for the stochastic model is given. Finally, a brief conclusion is given in Section 8.

2. Fundamental Analysis

The total population $\mathcal{N}$ can be expressed in any time t as

$$\mathcal{N}\left(t\right)=\mathcal{S}\left(t\right)+\mathcal{V}\left(t\right)+\mathcal{A}\left(t\right)+\mathcal{B}\left(t\right)+\mathcal{R}\left(t\right),$$

and taking derivative $N\left(t\right)$ with respect to t, one has

$$\frac{d\mathcal{N}}{dt}=\alpha -d_A\mathcal{A}-d_B\mathcal{B}-d_0\mathcal{N}\le \alpha -d_0\mathcal{N}.$$

(2)

Hence,

$$\mathcal{N}\to \frac{\alpha }{d_0}\mathrm{as}t\to \infty .$$

It demonstrates that the model positivity, and feasible region for the deterministic model is

$$\chi =(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}{+}^5):\mathcal{N}\le \frac{\alpha }{d_0}.$$

In feasible region $\chi$, we checked the solution of model (1) with the initial condition, for which the existence, uniqueness and results hold.

The solutions of system (1) are always bounded and non-negative, provided that the initial numerical values are positive. Next, we demonstrate that the model system (1) solutions enter a confined region $\chi$.

3. Uniqueness and Existence

We look to find the uniqueness and existence of system (1). To accomplish this, we provide the model (1) in the manner specified by

$$\begin{array}{cc}\hfill {\mathcal{S}}^{\prime }& =h_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right),\hfill \\ \hfill {\mathcal{V}}^{\prime }& =h_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right),\hfill \\ \hfill {\mathcal{X}}_3^{\prime }& =h_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right),\hfill \\ \hfill {\mathcal{X}}_4^{\prime }& =h_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right),\hfill \\ \hfill {\mathcal{R}}^{\prime }& =h_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right).\hfill \end{array}$$

(3)

Norm is defined as

$${\left|\right|\chi \left|\right|}_{\infty }=\underset{t\in x}{sup}.$$

(4)

where $x\in [0,\mathcal{T}]$. We supposed that $\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},$ and $\mathcal{R}$ are bounded in $[0,\mathcal{T}]$ and there exist $l_1,l_2,l_3,l_4,$ and $l_5$ for any t which belong to $[0,\mathcal{T}]$ such that

$${\left|\right|\mathcal{S}\left|\right|}_{\infty }<l_1,$$

$${\left|\right|\mathcal{V}\left|\right|}_{\infty }<l_2,$$

$${\left|\right|\mathcal{A}\left|\right|}_{\infty }<l_3,$$

$${\left|\right|\mathcal{B}\left|\right|}_{\infty }<l_4,$$

$${\left|\right|\mathcal{R}\left|\right|}_{\infty }<l_5.$$

Now, we have to prove (1) is bonded

$$\begin{array}{c}\begin{array}{lll}|h_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)|& =& |(1-\beta )\alpha -(a+b+\eta +d_0)\mathcal{S}+\gamma \mathcal{R}|\\ & \le & (1-\beta )\alpha +(a+b+\eta +d_0)\left|\mathcal{S}\right|+\gamma \left|\mathcal{R}\right|\\ & \le & (1-\beta )\alpha +(a+b+\eta +d_0)\underset{M}{sup}\left|\mathcal{S}\right|+\gamma \underset{M}{sup}\left|\mathcal{R}\right|\\ & \le & (1-\beta )\alpha +(a+b+\eta +d_0){\left|\right|\mathcal{S}\left|\right|}_{\infty }+{\gamma \left|\right|\mathcal{R}\left|\right|}_{\infty }\\ & \le & (1-\beta )\alpha +(a+b+\eta +d_0)l_1+\gamma l_5<\infty .\end{array}\end{array}$$

(5)

where $M=t\in [0,\mathcal{T}]$. Similarly, with the same procedure, we have

$$\begin{array}{c}\begin{array}{lll}|h_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)|& =& |\beta \alpha +\eta \mathcal{S}-(b+(1-\delta )a+d_0\left)\mathcal{V}\right|\\ & \le & \beta \alpha +\eta l_1+(b+(1-\delta )a+d_0)l_2<\infty .\end{array}\end{array}$$

(6)

$$\begin{array}{c}\begin{array}{lll}|h_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)|& =& |a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A}|\\ & \le & a{l}_1+(1-\delta )a{l}_2+(r_1+d_0+d_A)l_3<\infty .\end{array}\end{array}$$

(7)

$$\begin{array}{c}\begin{array}{lll}|h_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)|& =& |b(\mathcal{S}+\mathcal{V})-(r_2+d_0+d_B)\mathcal{B}|\\ & \le & b(l_1+l_2)+(r_2+d_0+d_B)l_4<\infty .\end{array}\end{array}$$

(8)

$$\begin{array}{c}\begin{array}{lll}|h_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)|& =& |r_1\mathcal{A}+r_2\mathcal{B}-(\gamma +d_0)\mathcal{R}|\\ & \le & r_1{l}_3+r_2{l}_4+(\gamma +d_0)l_5<\infty .\end{array}\end{array}$$

(9)

Thus, $\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}$ and $\mathcal{C}$ are bounded, and there exist $K_1,K_2,K_3,K_4,K_5$ and $K_6$ such that

$$\underset{M}{sup}\left|h_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)\right|<K_1,$$

$$\underset{M}{sup}\left|h_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)\right|<K_2,$$

$$\underset{M}{sup}\left|h_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)\right|<K_3,$$

$$\underset{M}{sup}\left|h_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)\right|<K_4,$$

$$\underset{M}{sup}\left|h_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)\right|<K_5,$$

$$\underset{M}{sup}\left|h_6\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)\right|<K_6.$$

Next, we have to prove

$$\begin{array}{c}\begin{array}{lll}|h_1\left(t,{\mathcal{S}}_1,\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)-h_1\left(t,{\mathcal{S}}_2,\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)|& =& |(1-\beta )\alpha -(a+b+\eta +d_0){\mathcal{S}}_1+\gamma \mathcal{R}\\ -(1-\beta )\alpha -((a+b+\eta +d_0){\mathcal{S}}_2+\gamma \mathcal{R})|\hfill \\ & <& (a+b+\eta +d_0)|{\mathcal{S}}_1-{\mathcal{S}}_2|\\ & <& c_1|{\mathcal{S}}_1-{\mathcal{S}}_2|.\end{array}\end{array}$$

(10)

where $c_1=(a+b+\eta +d_0)$. Similarly, with the same method, we have

$$|h_2\left(t,\mathcal{S},{\mathcal{V}}_1,\mathcal{A},\mathcal{B},\mathcal{R}\right)-h_2\left(t,\mathcal{S},{\mathcal{V}}_2,\mathcal{A},\mathcal{B},\mathcal{R},\right)|<c_2|{\mathcal{V}}_1-{\mathcal{V}}_2|,$$

$$|h_3\left(t,\mathcal{S},\mathcal{V},{\mathcal{A}}_1,\mathcal{B},\mathcal{R}\right)-h_3\left(t,\mathcal{S},\mathcal{V},{\mathcal{A}}_2,\mathcal{B},\mathcal{R},\right)|<c_3|{\mathcal{A}}_1-{\mathcal{A}}_2|,$$

$$|h_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},{\mathcal{B}}_1,\mathcal{R}\right)-h_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},{\mathcal{B}}_2,\mathcal{R},\right)|<c_4|{\mathcal{B}}_1-{\mathcal{B}}_2|,$$

$$|h_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},{\mathcal{R}}_1\right)-h_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},{\mathcal{R}}_2,\right)|<c_5|{\mathcal{R}}_1-{\mathcal{R}}_2|.$$

where

$$\begin{array}{c}\hfill \begin{array}{c}{c}_2=b+(1-\delta )a+d_0,\hfill \\ c_3=r_1+d_A+d_0,\hfill \\ c_4=r_2+d_B+d_0,\hfill \\ c_5=\gamma +d_0.\hfill \end{array}\end{array}$$

(11)

Thus, model (1) has a unique set of solutions as indicated by the uniqueness and existence.

4. Mathematical Analysis of Deterministic Model

In the next part of the paper, we study some basic results regarding the local as well as global stability of equilibrium points. We also study the formulation and derivation of ${\mathcal{R}}_0$.

4.1. Disease-Free Equilibrium Points

${\mathcal{P}}^0=({\mathcal{S}}^0,0,0,0,0)$ represents the equilibrium of disease-free state of model (1). Therefore, we analyzed the model in equilibrium:

$$\begin{array}{c}{\mathcal{S}}^0=\frac{(1-\beta )\alpha }{\eta +d_0}\hfill \\ {\mathcal{N}}^0=\frac{\alpha }{d_0}.\hfill \end{array}$$

4.2. Endemic Equilibrium

Endemic equilibrium of (1) is calculated as follows:

$$\begin{array}{c}{\mathcal{S}}^{*}=\frac{(1-\beta )\alpha -\gamma {\mathcal{R}}^{*}}{a+b+\eta +d_0}\hfill \\ {\mathcal{V}}^{*}=\frac{\beta \alpha +\eta {\mathcal{S}}^{*}}{b+(1-\delta )a+d_0}\hfill \\ {\mathcal{A}}^{*}=\frac{a{\mathcal{S}}^{*}+(1-\delta )a{\mathcal{V}}^{*}}{r_1+d_A+d_0}\hfill \\ {\mathcal{B}}^{*}=\frac{b({\mathcal{S}}^{*}+{\mathcal{V}}^{*})}{r_2+d_B+d_0}\hfill \\ {\mathcal{R}}^{*}=\frac{r_1{\mathcal{A}}^{*}+r_2{\mathcal{B}}^{*}}{\gamma +d_0}.\hfill \end{array}$$

4.3. Expression for ${\mathcal{R}}_0$

In mathematical modeling or epidemic modeling, there is a term ${\mathcal{R}}_0$, which is called the basic reproduction rate, from which we describe the spreading of disease or how to manage disease. We examined the infection rate and separated the COVID-19 populations from ${\mathcal{R}}_0$. The following is how we determined ${\mathcal{R}}_0$ using the next generation matrix.

Assume $\chi =(\mathcal{A},\mathcal{B})$.

Then, form model (1),

$$\frac{d\succ }{dt}=\mathcal{F}-\mathcal{V},$$

where

$$\begin{array}{c}\hfill \mathcal{F}=\left(\begin{array}{c}\frac{{\mu }_{1}k\mathcal{A}}{\mathcal{N}}\left(\mathcal{S}+(1-\delta )\mathcal{V}\right)\\ \frac{{\mu }_{2}k\mathcal{B}}{\mathcal{N}}\left(\mathcal{S}+\mathcal{V}\right)\end{array}\right).\end{array}$$

and

$$\begin{array}{c}\hfill \mathbf{V}=\left(\begin{array}{c}(r_1+d_0+d_A)\mathcal{A}\\ (r_2+d_0+d_B)\mathcal{B}\end{array}\right).\end{array}$$

For the disease-free equilibrium, the Jacobian of $\mathcal{F}$ is

$$\begin{array}{c}\hfill \mathcal{D}\mathcal{F}\left(P^0\right)=\left(\begin{array}{cc}\frac{{\mu }_{1}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& 0\\ 0& \frac{{\mu }_{2}k{\mathcal{S}}^0}{{\mathcal{N}}^0}\end{array}\right).\end{array}$$

For the disease-fee equilibrium, the Jacobian of $\mathcal{V}$ is

$$\begin{array}{c}\hfill \mathcal{D}\mathbf{V}\left(P^0\right)=\left(\begin{array}{cc}{r}_1+d_0+d_A& 0\\ 0& r_2+d_0+d_B\end{array}\right).\end{array}$$

We have

$$\begin{array}{c}\hfill {\mathbf{V}}^{-1}=\frac{1}{(r_1+d_0+d_A)(r_2+d_0+d_B)}\left(\begin{array}{cc}{r}_2+d_0+d_B& 0\\ 0& r_A+d_0+d_A\end{array}\right).\end{array}$$

Now,

$$\begin{array}{c}\hfill \mathcal{F}{\mathbf{V}}^{-1}=\frac{1}{(r_1+d_0+d_A)(r_2+d_0+d_B)}\left(\begin{array}{cc}\frac{k{\mu }_1{d}_0(1-\beta )(r_2+d_0+d_B)}{\eta +d_0}& 0\\ 0& \frac{k{\mu }_2{d}_0(1-\beta )(r_1+d_0+d_A)}{\eta +d_0}\end{array}\right).\end{array}$$

(12)

Our constructed model behaves like [28] the two-strain compartment model. Here, the two strains are the delta virus and omicron virus. We have two different values for ${\mathcal{R}}_0$:

$${\mathcal{R}}_1=\frac{k{\mu }_1{d}_0(1-\beta )}{(\eta +d_0)(r_1+d_0+d_A)}.$$

This is also called the infection rate of the delta virus. Also,

$${\mathcal{R}}_2=\frac{k{\mu }_2{d}_0(1-\beta )}{(\eta +d_0)(r_2+d_0+d_B)}.$$

${\mathcal{R}}_2$ represents the infection rate of omicron infection:

$${\mathcal{R}}_0=max\left({\mathcal{R}}_1,{\mathcal{R}}_2\right).$$

On the basis of basic reproduction rate ${\mathcal{R}}_0$, we present the following theorem.

Theorem 1. 

(i) 

If ${\mathcal{R}}_1<1$ or/and ${\mathcal{R}}_2<1$, then there is no positive equilibrium.

(ii) 

If ${\mathcal{R}}_1>1$ or/and ${\mathcal{R}}_2>1$ There exists a unique positive equilibrium ${\mathcal{E}}^{*}=({\mathcal{S}}^{*},{\mathcal{V}}^{*},{\mathcal{A}}^{*},{\mathcal{B}}^{*},{\mathcal{R}}^{*})$ called the endemic equilibrium.

5. Stability Analysis

This part of our study is further divided into two sections: local stability and global stability of the model (1). We checked first the local stability through the Jacobian matrix and the global stability through a function known as the Lyapnuov function.

5.1. Local Stability

Here, we study the local stability of disease-free equilibrium state ${\mathcal{E}}^0$ of model (1). In the very next theorem, we utilize the Jacobian matrix to investigate the required goal.

Theorem 2.

The disease-free equilibrium ${\mathcal{E}}^0$ of model (1) is locally asymptotically stable, if and only if ${\mathcal{R}}_1<1$ or/and ${\mathcal{R}}_2<1$.

Proof. 

We calculate the Jacobian matrix of model (1) at ${\mathcal{E}}^0$. Here, we use the Laypunov direct method:

${\mathcal{M}}^0=\left[\begin{array}{ccccc}-(\eta +d_0)& 0& \frac{-{\mu }_{1}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& \frac{-{\mu }_{2}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& \gamma \\ \eta & -d_0& \frac{-{\mu }_{1}k(1-\delta )}{{\mathcal{N}}^0}& \frac{-{\mu }_{2}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& 0\\ 0& 0& ({\mathcal{R}}_1-1)(r_1+d_0+d_A)& 0& 0\\ 0& 0& 0& ({\mathcal{R}}_2-1)(r_2+d_0+d_B)& 0\\ 0& 0& r_1& r_2& -(\gamma +d_0)\end{array}\right].$

By simple calculation,

${\mathcal{M}}^0=\left[\begin{array}{ccccc}-(\eta +d_0)& 0& \frac{-{\mu }_{1}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& \frac{-{\mu }_{2}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& \gamma \\ \eta & -d_0& \frac{-{\mu }_{1}k(1-\delta )}{{\mathcal{N}}^0}& \frac{-{\mu }_{2}k{\mathcal{S}}^0}{{\mathcal{N}}^0}& 0\\ 0& 0& \frac{-{\mu }_{1}k({\mathcal{S}}^0+(1-\delta ))}{{\mathcal{N}}^0}-(r_1+d_0+d_A)& 0& 0\\ 0& 0& 0& \frac{-{\mu }_{2}k{\mathcal{S}}^0}{{\mathcal{N}}^0}-(r_2+d_0+d_B)& 0\\ 0& 0& r_1& r_2& -(\gamma +d_0)\end{array}\right].$

Eigenvalues of ${\mathcal{M}}^0$ are

$$\begin{array}{c}{\lambda }_1=-(\eta +d_0)\hfill \\ {\lambda }_2=-d_0\hfill \\ {\lambda }_3=-(\gamma +d_0)\hfill \\ {\lambda }_4=-(r_1+d_0+d_A)(1-{\mathcal{R}}_1)\hfill \\ {\lambda }_5=-(r_2+d_0+d_B)(1-{\mathcal{R}}_2).\hfill \end{array}$$

${\mathcal{R}}_1$ is a subset of ${\mathcal{R}}_0$, and also ${\mathcal{R}}_2$ is a subset of ${\mathcal{R}}_0$. ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are strictly negative. The sign of ${\lambda }_4$ and ${\lambda }_5$ depend on $(1-{\mathcal{R}}_1)$ and $(1-{\mathcal{R}}_2)$. The disease-free equilibrium, DFE, indicates the dynamics of (1) whenever a small amount of emigrants are add to the population. □

Note: If ${\mathcal{R}}_1<1$ and ${\mathcal{R}}_2<1$, then ${\lambda }_4$ and ${\lambda }_5$ are strictly negative. Hence, the system is locally and asymptotically stable.

5.2. Global Stability

Here in this section, we investigate the global stability of model (1) for which we use a Lyapnuov function.

Theorem 3.

The disease-free equilibrium ${\mathcal{E}}^0$ of the system (1) is globally and asymptotically stable in χ whenever ${\mathcal{R}}_1<\frac{N}{k}$ and ${\mathcal{R}}_2<\frac{N}{k}$.

Proof. 

Let

$$\mathcal{L}(\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R})=\frac{(\mathcal{A}+\mathcal{B})N}{k}.$$

(13)

Here, $\mathcal{A},\mathcal{B}>0$. Now, with respect to t, we take the derivative of the above equation:

$$\dot{\mathcal{L}}=\frac{(\dot{\mathcal{A}}+\dot{\mathcal{B}})N}{k}.$$

(14)

Putting values from (1), we obtain

$$\dot{\mathcal{L}}=\mathcal{A}\mathcal{S}{\mu }_1+(1-\delta )\mathcal{A}\mathcal{V}{\mu }_1-\frac{(r_1+d_0+d_A)\mathcal{A}N{\mu }_2\mathcal{B}}{k}(\mathcal{S}+\mathcal{V})-\frac{(r_2+d_0+d_B)\mathcal{B}N}{k}.$$

After some basic calculation,

$$\begin{array}{cc}& \dot{L}=\frac{(r_1+d_0+d_A)\mathcal{A}k}{N}\left(\frac{k{\mu }_1(\mathcal{S}+(1-\delta )\mathcal{V})}{\mathcal{N}(r_1+d_0+d_A)}-\frac{N}{k}\right)\hfill \\ \hfill +\frac{(r_2+d_0+d_B)\mathcal{B}k}{N}\left(\frac{k{\mu }_2(\mathcal{S}+\mathcal{V})}{\mathcal{N}(r_2+d_0+d_B)}-\frac{N}{k}\right).\end{array}$$

Since $\mathcal{S}\left(t\right)$ declines at any time $t\ge 0$ because of disease and also $\mathcal{V}\left(t\right)$ declines due to defective immunization, suppose $\mathcal{S}\left(t\right)\le {\mathcal{S}}^0$ and $\mathcal{V}\left(t\right)\le {\mathcal{V}}^0$

$$\begin{array}{cc}& \dot{L}\le (r_1+d_0+d_A)\mathcal{A}\frac{k}{N}({\mathcal{R}}_1-\frac{N}{k})+(r_2+d_0+d_B)\mathcal{B}\frac{k}{N}({\mathcal{R}}_2-\frac{N}{k}).\hfill \end{array}$$

If ${\mathcal{R}}_1<\frac{N}{k}$ or/and ${\mathcal{R}}_2<\frac{N}{k}$, the system is globally asymptotically stable. □

Theorem 4.

System (1) has the following:

1.

A unique single variant of the delta infection equilibrium ${\mathcal{E}}_1=({\mathcal{S}}^{*},{\mathcal{V}}^{*},{\mathcal{A}}^{*},0,{\mathcal{R}}^{*})$ if and only if ${\mathcal{R}}_1>1$.

2.

A unique single variant of the omicron infection equilibrium ${\mathcal{E}}_2=({\mathcal{S}}^{*},{\mathcal{V}}^{*},0,{\mathcal{B}}^{*},{\mathcal{R}}^{*})$ if and only if ${\mathcal{R}}_2>1$.

3.

A double infection equilibrium ${\mathcal{E}}_3=({\mathcal{S}}^{*},{\mathcal{V}}^{*},{\mathcal{A}}^{*},0,{\mathcal{R}}^{*})$ when ${\mathcal{R}}_0=max\left({\mathcal{R}}_1,{\mathcal{R}}_2\right)>1$.

Proof. 

For the method used to prove this, we look for the endemic equilibrium whenever the single variant of the delta infection equilibrium is present and in case 2, when the single variant of the omicron infection equilibrium is present. In case 3, it is when the double infection equilibrium is present.

Case 1. The single variant of delta infection is dominant.

${\mathcal{E}}_1\left(t\right)$ is the solution of system (1):

$$\begin{array}{cc}\hfill (1-\beta )\alpha -(a^{*}+\eta +d_0){\mathcal{S}}^{*}+\gamma {\mathcal{R}}^{*}& =0\hfill \\ \hfill \beta \alpha +\eta {\mathcal{S}}^{*}-((1-\delta )a^{*}+d_0){\mathcal{V}}^{*}& =0\hfill \\ \hfill a^{*}{\mathcal{S}}^{*}+(1-\delta )a^{*}{\mathcal{V}}^{*}-(r_1+d_0+d_A){\mathcal{A}}^{*}& =0\hfill \\ \hfill r_1{\mathcal{A}}^{*}+r_2{\mathcal{B}}^{*}-(\gamma +d_0){\mathcal{R}}^{*}& =0.\hfill \end{array}$$

(15)

From the above Equation (15), we have the values for ${\mathcal{S}}^{*},{\mathcal{V}}^{*},{\mathcal{A}}^{*}$ and ${\mathcal{R}}^{*}$ as

$$\begin{array}{c}{\mathcal{S}}^{*}=\frac{(1-\beta )\alpha -\gamma {\mathcal{R}}^{*}}{a+b+\eta +d_0}\hfill \\ {\mathcal{V}}^{*}=\frac{\beta \alpha +\eta {\mathcal{S}}^{*}}{b+(1-\delta )a+d_0}\hfill \\ {\mathcal{A}}^{*}=\frac{a{\mathcal{S}}^{*}+(1-\delta )a{\mathcal{V}}^{*}}{r_1+d_A+d_0}.\hfill \end{array}$$

Putting the values of ${\mathcal{S}}^{*},{\mathcal{V}}^{*},$ and ${\mathcal{A}}^{*}$, we obtain ${\mathcal{R}}^{*}$ as

$${\mathcal{R}}^{*}=\frac{a^{*}\gamma \alpha [(1-\delta )(a^{*}+\eta )+d_0(1-\delta \beta )]}{P_2{a}^{*2}+P_1{a}^{*}+P_0},$$

where

$$\begin{array}{c}{P}_0=d_0(d_0+\gamma )(d_0+\eta )(d_0+d_A+r_1)\hfill \\ P_1=d_0(2-\delta )(d_0+d_A)(d_0+\gamma )+r_1{d}_0((1-\delta )(d_0+\gamma )+d_0)\hfill \\ +\eta (1-\delta )((d_A+d_0)(d_0+\gamma )+r_1{d}_0)\hfill \\ P_2=(1-\delta )\left[d_0(d_0+\gamma +d_A+r_1)\right].\hfill \end{array}$$

So, we can therefore have $\mathcal{S}\left(t\right),\mathcal{V}\left(t\right),$ and $\mathcal{A}\left(t\right)$ according to $a^{*}=\frac{{\mu }_{1}k{\mathcal{A}}^{*}}{{\mathcal{N}}^{*}}$, replacing ${\mathcal{A}}^{*}$ and ${\mathcal{N}}^{*}=\frac{\alpha -d_A\mathcal{A}}{d_0}$ with equations, then by some simple algebraic calculations, we obtain $a^{*}$ as the solution:

$$a^{*}(n_2{a}^{*2}+n_1{a}^{*}+n_0)=0,$$

(16)

where

$$\begin{array}{c}{n}_0=(d_0+\gamma )(d_0+\eta )(d_0+d_A+r_1)(1-{\mathcal{R}}_1)\hfill \\ n_1=(d_0+\gamma +r_1)(d_0+(1-\delta )\eta )+(d_0+\gamma )[d_A\beta +(1-\delta )(d_0+r_1+d_A(1-\beta )-{\mu }_{1}k)]\hfill \\ n_2=(1-\delta )(d_0+\gamma +r_1)>0.\hfill \end{array}$$

When ${\mathcal{R}}_1>1,n_0<0,$ then, we obtain the discriminant of Equation (16) as $T=n_1^2-4n_0{n}_2$ which is positive (because $n_1$ and $n_2$ have different signs), so Equation (16) has two solutions which are real. Furthermore, the multiplication of those solutions is $q=\frac{n_0}{n_2}<0$, which implies that both solutions have opposite signs. Therefore, we can see that whenever ${\mathcal{R}}_1>1$, then the model has a unique variant 1 delta infected equilibrium.

Case 2. The single variant of omicron infection is dominant.

The scientific proof applies the same strategy and procedures as in Case 1 mentioned above.

Case 3. Double infection is present.

We consider the system for ${\mathcal{E}}_3\left(t\right)$ as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill (1-\beta )\alpha -(a^{*}+b^{*}+\eta +d_0){\mathcal{S}}^{*}+\gamma {\mathcal{R}}^{*}& =0\hfill \\ \hfill \beta \alpha +\eta {\mathcal{S}}^{*}-(b^{*}+(1-\delta )a^{*}+d_0){\mathcal{V}}^{*}& =0\hfill \\ \hfill a^{*}{\mathcal{S}}^{*}+(1-\delta )a^{*}{\mathcal{V}}^{*}-(r_1+d_0+d_A){\mathcal{A}}^{*}& =0\hfill \\ \hfill b({\mathcal{S}}^{*}+{\mathcal{V}}^{*})-(r_2+d_0+d_B){\mathcal{B}}^{*}& =0\hfill \\ \hfill r_1{\mathcal{A}}^{*}+r_2{\mathcal{B}}^{*}-(\gamma +d_0){\mathcal{R}}^{*}& =0,\hfill \end{array}\end{array}$$

where $a^{*}=\frac{{\mu }_{1}k{\mathcal{A}}^{*}}{{\mathcal{N}}^{*}},b^{*}=\frac{{\mu }_{2}k{\mathcal{B}}^{*}}{{\mathcal{N}}^{*}},$ and ${\mathcal{N}}^{*}=\frac{\alpha +d_A{\mathcal{A}}^{*}+d_B{\mathcal{B}}^{*}}{d_0}.$ After some calculation,

$$\begin{array}{c}\hfill \begin{array}{c}{\mathcal{R}}^{*}=\frac{r_1{\mathcal{A}}^{*}+r_2{\mathcal{B}}^{*}}{(\gamma +d_0)}\hfill \\ {\mathcal{S}}^{*}=\frac{(1-\beta )\alpha -\gamma {\mathcal{R}}^{*}}{a+b+\eta +d_0}\hfill \\ {\mathcal{V}}^{*}=\frac{\beta \alpha +\eta {\mathcal{S}}^{*}}{b+(1-\delta )a+d_0}.\hfill \end{array}\end{array}$$

Putting values of ${\mathcal{S}}^{*}$, ${\mathcal{V}}^{*}$ and ${\mathcal{R}}^{*},$ we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill g({\mathcal{A}}^{*},{\mathcal{B}}^{*})& =0\hfill \\ \hfill h({\mathcal{A}}^{*},{\mathcal{B}}^{*})& =0,\hfill \end{array}\end{array}$$

where $g({\mathcal{A}}^{*},{\mathcal{B}}^{*})$ and $h({\mathcal{A}}^{*},{\mathcal{B}}^{*})$ are monotone functions defined by

$$\begin{array}{c}\hfill \begin{array}{c}g({\mathcal{A}}^{*},{\mathcal{B}}^{*})=\frac{\mathcal{A}k{\mu }_1(1-\delta )(\alpha (d_0+\gamma )(k\beta ({\mu }_1\mathcal{A}+{\mu }_2\mathcal{B})+\mathcal{N}(d_0\beta +\eta ))+\mathcal{N}\gamma \eta (r_1\mathcal{A}+r_2\mathcal{B}))}{(d_0+\gamma )(k({\mu }_1\mathcal{A}+{\mu }_2\mathcal{B})+\mathcal{N}(d_0+\eta ))(\mathcal{A}k{\mu }_1(1-\delta )+\mathcal{B}k{\mu }_2+\mathcal{N}{d}_0)}\hfill \\ +\frac{\mathcal{A}k{\mu }_1(\gamma (r_1\mathcal{A}+r_2\mathcal{B})+\alpha (1-\beta )(d_0+\gamma ))}{(d_0+\gamma )(k({\mu }_1\mathcal{A}+{\mu }_2\mathcal{B})+\mathcal{N}(d_0+\eta ))}-\mathcal{A}(r_1+d_0+d_A)\hfill \\ h({\mathcal{A}}^{*},{\mathcal{B}}^{*})=\frac{\mathcal{A}k{\mu }_2\left(\gamma (d_0+\gamma )(k\beta ({\mu }_1\mathcal{A}+{\mu }_2\mathcal{B})+\mathcal{N}(d_0\beta +\eta ))\right)+\mathcal{N}\gamma \eta (r_1\mathcal{A}+r_2\mathcal{B})}{(d_0+\gamma )(k({\mu }_1\mathcal{A}+{\mu }_2\mathcal{B})+\mathcal{N}(d_0+\eta ))(\mathcal{A}k{\mu }_1(1-\delta )+\mathcal{B}k{\mu }_2+\mathcal{N}{d}_0)}\hfill \\ +\frac{\mathcal{B}k{\mu }_2(\gamma (r_1\mathcal{A}+r_2\mathcal{B})+\alpha (1-\beta )(d_0+\gamma ))}{(d_0+\gamma )(k({\mu }_1\mathcal{A}+{\mu }_2\mathcal{B})+\mathcal{N}(d_0+\eta ))}-\mathcal{A}(r_1+d_0+d_A).\hfill \end{array}\end{array}$$

This follow the conclusion. □

6. Second-Order Derivative Model

The graph’s concavity or curvature is represented by the second-order derivative. The parts of the graph of the function that are concave down and up are determined using the second-order derivative. If the second derivative of a function is non-negative, it will be up concave; if it is negative, it will be down concave; and if it is equal to zero, it may be the stationary point. If the sign of the second derivative is changing from positive to negative, then the graph of the function will also change from concave up to concave down. This idea can also be applied to epidemic models with multiple layers or waves of illness cases. The down and up concavities for an infected curve may be determined by this second-order model under the aforementioned conditions because it is typically challenging to create a model with the first order for better match cases with many waves. This results in a proper undersetting for the data to the proposed model. We analyze the following model to provide the required results by using the second-order derivative with respect to time t of model (1) as

$$\begin{array}{c}\hfill \begin{array}{c}\frac{d^2\mathcal{S}}{d{t}^2}=-[\left(\frac{\mathcal{N}({\mu }_{1}k\dot{\mathcal{A}}-{\mu }_{1}k\mathcal{A}\dot{\mathcal{N}})}{{\mathcal{N}}^2}+\frac{\mathcal{N}({\mu }_{2}k\dot{\mathcal{B}}-{\mu }_{2}k\mathcal{B}\dot{\mathcal{N}})}{{\mathcal{N}}^2}\right)\mathcal{S}\hfill \\ +\left(\frac{k{\mu }_1\mathcal{A}}{\mathcal{N}}+\frac{k{\mu }_2\mathcal{B}}{\mathcal{N}}+\eta +d_0\right)\dot{\mathcal{S}}]+\gamma \dot{\mathcal{R}},\hfill \\ \frac{d^2\mathcal{V}}{d{t}^2}=\eta \dot{\mathcal{S}}-[\left(\frac{\mathcal{N}({\mu }_{2}k\dot{\mathcal{B}}-{\mu }_{2}k\mathcal{B}\dot{\mathcal{N}})}{{\mathcal{N}}^2}+(1-\delta )\frac{\mathcal{N}({\mu }_{1}k\dot{\mathcal{A}}-{\mu }_{1}k\mathcal{A}\dot{\mathcal{N}})}{{\mathcal{N}}^2}\right)\mathcal{V}\hfill \\ +\left(\frac{k{\mu }_2\mathcal{B}}{\mathcal{N}}+\frac{k(1-\delta ){\mu }_1\mathcal{A}}{\mathcal{N}}+d_0\right)\dot{\mathcal{V}}],\hfill \\ \frac{d^2\mathcal{A}}{d{t}^2}=\frac{k{\mu }_1\mathcal{A}\dot{\mathcal{S}}}{\mathcal{N}}+\frac{k{\mu }_1(\mathcal{N}\dot{\mathcal{A}}-\dot{\mathcal{N}}\mathcal{A})\mathcal{S}}{{\mathcal{N}}^2}+(1-\delta )k{\mu }_1\left(\frac{\mathcal{A}\dot{\mathcal{V}}}{\mathcal{N}}+\mathcal{V}\left(\frac{\mathcal{N}\dot{\mathcal{A}}-\dot{\mathcal{N}}\mathcal{A}}{{\mathcal{N}}^2}\right)\right)\hfill \\ -(r_1+d_0+d_A)\dot{\mathcal{A}},\hfill \\ \frac{d^2\mathcal{B}}{d{t}^2}=\frac{k{\mu }_2\mathcal{B}(\dot{\mathcal{S}}+\dot{\mathcal{V}})}{\mathcal{N}}+k{\mu }_2(\mathcal{S}+\mathcal{V})\left(\frac{\mathcal{N}\dot{\mathcal{B}}-\dot{\mathcal{N}}\mathcal{B}}{{\mathcal{N}}^2}\right)-(r_2+d_0+d_B)\dot{\mathcal{B}},\hfill \\ \frac{d^2\mathcal{R}}{d{t}^2}=r_1\dot{\mathcal{A}}+r_2\dot{\mathcal{B}}-(\gamma +d_0)\dot{\mathcal{R}}.\hfill \end{array}\end{array}$$

(17)

This above system (17) is used further to obtain the strength number ${\mathcal{R}}_{st}$.

6.1. Strength Number

For the first-order model, we find ${\mathcal{R}}_0$ to study the flow of disease and for the second-order model, ${\mathcal{R}}_{st}$ is used.

To calculate the strength number, we find the second-order derivative of the above matrix F (12) and then compute ${\mathcal{R}}_{st}$ by the simple next generation matrix as

$${\mathcal{R}}_{st}=\frac{-2k{\mu }_1\left[(1-\delta )(d_0\beta +\eta )+d_0(1-\beta )\right]d^3}{{\alpha }^3(d_0+\eta )(r_1+d_0+dA)}.$$

(18)

6.2. Mathematical Analysis

Considering the equilibrium points, which represent the endemic and disease-free cases, demonstrates the potential concavity of the system (17). To demonstrate this, we must show that each second-order equations of the system (17), which is the second-order derivative with larger time t, will be concave up, and if it is negative, it will appear to concave down; on the other hand, if it is zero, it is simply a stationary point. We initially begin with the disease-free ${\mathcal{E}}_0$ case and, using the model (17), we obtain the following.

The model’s equations all describe the stationary point for the disease-free scenario when the change in temporal rate is zero, and we utilize the system’s disease-free equilibrium (17). As a result, we may conclude that there is no chance that ${\mathcal{E}}_0$ will concave up or down. Additionally, we verify and explain the following to see if up concavity, down concavity, or merely the inflection points for endemic equilibrium $Q_1$ are possible:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{d^2\mathcal{S}}{d{t}^2}& =0\hfill \\ \hfill \frac{d^2\mathcal{V}}{d{t}^2}& =0\hfill \\ \hfill \frac{d^2\mathcal{A}}{d{t}^2}& =0\hfill \\ \hfill \frac{d^2\mathcal{B}}{d{t}^2}& =0\hfill \\ \hfill \frac{d^2\mathcal{R}}{d{t}^2}& =0.\hfill \end{array}\end{array}$$

(19)

From (19), it is clear that we only have the situation for the inflection or stationary points when employing all second-order time derivatives to compute concavity. In conclusion, the model (17) only provides the infection or stationary points for the second-order model (17) at the disease-free and endemic equilibrium ${\mathcal{E}}_0$ and $Q_1$ instead of the up concavity and down concavity.

7. Numerical Results and Discussion for Deterministic Model

We present the fundamental procedure of our model and support the analytical results through some graphical representations of the model (1) whenever the basic reproduction rate ${\mathcal{R}}_0$ is less or greater than one.

The current simulation provides general information and results that can be used for any type of region. It has five compartments: susceptible, vaccinated, delta infected, omicron infected, and recovered. It is also affected by such important measures as lockdown, quarantine and emergence from infected places. Here, we use the numerical scheme established in [30] for COVID-19 mathematical model. From model (1), we first take it and rewrite it in difference form as

$$\frac{d\mathcal{S}}{dt}=(1-\beta )\alpha -(a+b+\eta +d_0)\mathcal{S}+\gamma \mathcal{R}.$$

(20)

This is decomposed in the nonstandard finite difference scheme as

$$\begin{array}{c}\hfill \frac{{\mathcal{S}}_{j+1}-{\mathcal{S}}_j}{h}=(1-\beta )\alpha -(a+b+\eta +d_0){\mathcal{S}}_k+\gamma {\mathcal{R}}_k.\end{array}$$

(21)

Like (21), using the NSFD scheme, we decompose the system (1) as follows:

$$\begin{array}{ccc}\hfill {\mathcal{S}}_{j+1}& =& {\mathcal{S}}_j+h\left((1-\beta )\alpha -(a+b+\eta +d_0){\mathcal{S}}_k+\gamma {\mathcal{R}}_k\right),\hfill \\ \hfill {\mathcal{V}}_{j+1}& =& {\mathcal{V}}_j+h\left(\beta \alpha +\eta {\mathcal{S}}_k-(b+(1-\delta )a+d_0){\mathcal{V}}_k\right),\hfill \\ \hfill {\mathcal{A}}_{j+1}& =& {\mathcal{A}}_j+h\left(a{\mathcal{S}}_k+(1-\delta )a{\mathcal{V}}_k-(r_1+d_0+d_A){\mathcal{A}}_k\right),\hfill \\ \hfill {\mathcal{B}}_{j+1}& =& {\mathcal{B}}_j+h\left(b({\mathcal{S}}_k+{\mathcal{V}}_k)-(r_2+d_0+d_B){\mathcal{B}}_k\right),\hfill \\ \hfill {\mathcal{R}}_{j+1}& =& {\mathcal{R}}_j+h\left(r_1{\mathcal{A}}_K+r_2{\mathcal{B}}_K-(\gamma +d_0){\mathcal{R}}_K\right).\hfill \end{array}$$

(22)

We present graphically the results of the model (1) by using the numerical values of Table 2 through the scheme (22). We take real data to support our numerical results of model (1).

Table 2. Numerical values of parameters used in (1).

Parameters	Approximate Values [31,32]
$\mathcal{S}$	$200,150,120,180$
$\mathcal{V}$	$100,65,80,130$
$\mathcal{A}$	$70,40,30,45$
$\mathcal{B}$	$30,20,40,35$
$\mathcal{R}$	$20,10,25,30$
$\alpha$	0.0016
$d_A$	0.0000683
$d_0$	0.0032
$d_B$	0.0032
$\eta$	0.011
k	0.024
${\mu }_1$	0.127
${\mu }_2$	0.127
$\delta$	0.16
$\gamma$	0.01111
$\beta$	0.09
$r_1$	0.09
$r_2$	0.09

Here, the dynamical behaviors corresponding to different initial data of each compartment of the proposed model are presented in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. The decline in susceptible class is shown in Figure 3. Further, the increase in the vaccinated class and dynamical behaviors of the first and second variants are shown in Figure 4, Figure 5, and Figure 6, respectively. In addition, the dynamical growth in the recovered class is shown in Figure 7.

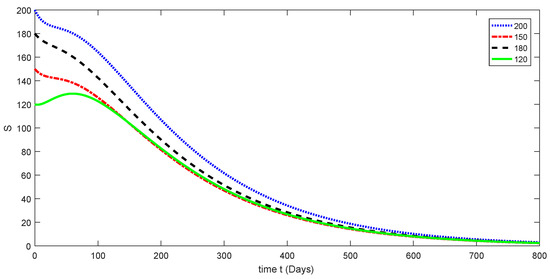
Figure 3. Dynamical behavior for different values of ${\mathcal{S}}_0$ of model (1).

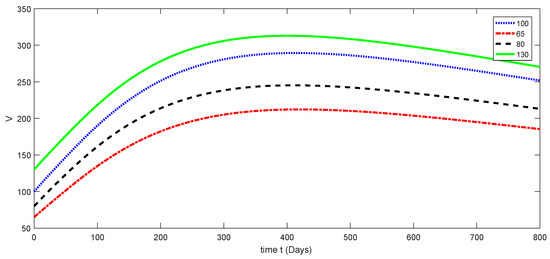
Figure 4. Dynamical behavior for different values of ${\mathcal{V}}_0$ of model (1).

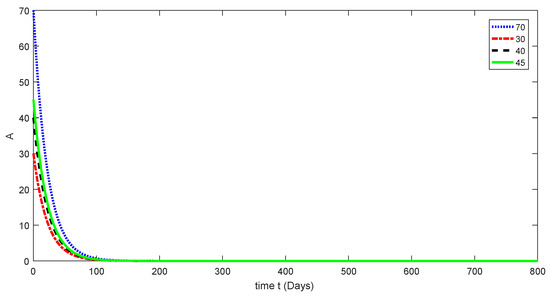
Figure 5. Dynamical behavior for different values of ${\mathcal{A}}_0$ of model (1).

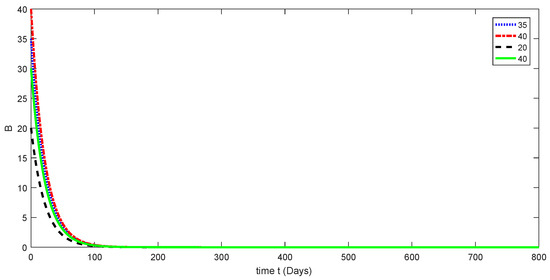
Figure 6. Dynamical behavior for different values of ${\mathcal{B}}_0$ of model (1).

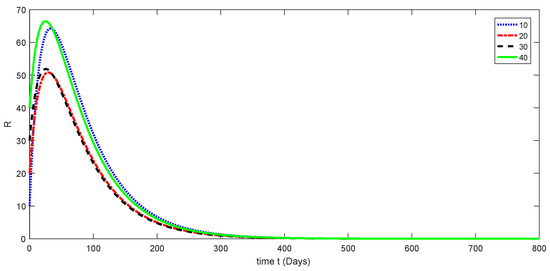
Figure 7. Dynamical behavior for different values of ${\mathcal{R}}_0$ of model (1).

8. Stochastic form of the Proposed Model

The dynamics of disease transmission can be understood using a stochastic epidemic model. Determining the persistence or extinction of a disease in the population is one of the most important roles of stochastic epidemic models. Random occurrences and inherent uncertainty frequently impact real-world systems. These unpredictabilities are taken into consideration by stochastic models, which provide complex systems with a better representation. In epidemiology, for instance, random occurrences like individual migrations, contact patterns, and environmental factors, which deterministic models might not properly represent, may have an impact on the spread of a viral disease. The authors in [33] used an SVITR deterministic model and extended it to a stochastic model by introducing the intensity of stochastic factors and Brownian motion. They took the vaccination and treatment compartments in the study to understand the dynamics of the model. Here, we convert our proposed deterministic two-variant model (1) into a stochastic model. To do this, nonlinear perturbations are introduced into each system equation. As shown for each class below, we only change the rate of each class with $i=1,2$ as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{S}& :-{\mu }_i\to -{\mu }_i+({\mathsf{\Delta }}_{11}\mathcal{S}+{\mathsf{\Delta }}_{12}){\mathcal{C}}_1\left(t\right),\hfill \\ \hfill \mathcal{V}& :-\eta \to -\eta +({\mathsf{\Delta }}_{21}\mathcal{S}+{\mathsf{\Delta }}_{22}){\mathcal{C}}_2\left(t\right),\hfill \\ \hfill \mathcal{A}& :-r_1\to -r_2+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32}){\mathcal{C}}_3\left(t\right),\hfill \\ \hfill \mathcal{B}& :-r_1\to -r_2+({\mathsf{\Delta }}_{41}\mathcal{S}+{\mathsf{\Delta }}_{42}){\mathcal{C}}_4\left(t\right),\hfill \\ \hfill \mathcal{R}& :-d_0\to -d_0+({\mathsf{\Delta }}_{51}\mathcal{S}+{\mathsf{\Delta }}_{52}){\mathcal{C}}_5\left(t\right).\hfill \end{array}\end{array}$$

As a result, we have the following system of Equation (1) that shows the stochastic model version:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill d\mathcal{S}& =((1-\beta )\alpha -(a+b+\eta +d_0)\mathcal{S}+\gamma \mathcal{R})dt+({\mathsf{\Delta }}_{11}\mathcal{S}+{\mathsf{\Delta }}_{12})\mathcal{S}d{\mathcal{C}}_1\left(t\right),\hfill \\ \hfill d\mathcal{V}& =(\beta \alpha +\eta \mathcal{S}-(b+(1-\delta )a+d_0)\mathcal{V})dt+({\mathsf{\Delta }}_{21}\mathcal{S}+{\mathsf{\Delta }}_{22})\mathcal{V}d{\mathcal{C}}_2\left(t\right),\hfill \\ \hfill d\mathcal{A}& =(a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A})dt+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})\mathcal{A}d{\mathcal{C}}_3\left(t\right),\hfill \\ \hfill d\mathcal{B}& =(b(\mathcal{S}+\mathcal{V})-(r_2+d_0+d_B)\mathcal{B})dt+({\mathsf{\Delta }}_{41}\mathcal{S}+{\mathsf{\Delta }}_{42})\mathcal{B}d{\mathcal{C}}_4\left(t\right),\hfill \\ \hfill d\mathcal{R}& =(r_1\mathcal{A}+r_2\mathcal{B}-(\gamma +d_0)\mathcal{R})dt+({\mathsf{\Delta }}_{51}\mathcal{S}+{\mathsf{\Delta }}_{52})\mathcal{R}d{\mathcal{C}}_5\left(t\right).\hfill \end{array}\end{array}$$

(23)

Existence and Uniqueness of (23)

Here, we investigate the stochastic system (23) solution and proof for the existence and uniqueness of the model. We set as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill d\mathcal{S}& =P_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_1(t,\mathcal{S})d{\mathcal{C}}_1\left(t\right),\hfill \\ \hfill d\mathcal{V}& =P_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_2(t,\mathcal{S})d{\mathcal{C}}_2\left(t\right),\hfill \\ \hfill d\mathcal{A}& =P_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_3(t,\mathcal{S})d{\mathcal{C}}_3\left(t\right),\hfill \\ \hfill d\mathcal{B}& =P_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_4(t,\mathcal{S})d{\mathcal{C}}_4\left(t\right),\hfill \\ \hfill d\mathcal{R}& =P_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_5(t,\mathcal{S})d{\mathcal{C}}_5\left(t\right).\hfill \end{array}\end{array}$$

(24)

In following method, we convert system (24) into the Volterra integral operator (25) as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathcal{S}\left(t\right)=\mathcal{S}\left(0\right)+{\int }_0^t{P}_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_1(t,\mathcal{S})d{\mathcal{C}}_1\left(t\right),\\ \hfill \mathcal{V}\left(t\right)=\mathcal{V}\left(0\right)+{\int }_0^t{P}_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_2(t,\mathcal{V})d{\mathcal{C}}_2\left(t\right),\\ \hfill \mathcal{A}\left(t\right)=\mathcal{A}\left(0\right)+{\int }_0^t{P}_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_3(t,\mathcal{A})d{\mathcal{C}}_3\left(t\right),\\ \hfill \mathcal{B}\left(t\right)=\mathcal{B}\left(0\right)+{\int }_0^t{P}_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_4(t,\mathcal{B})d{\mathcal{C}}_4\left(t\right),\\ \hfill \mathcal{R}\left(t\right)=\mathcal{R}\left(0\right)+{\int }_0^t{P}_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_5(t,\mathcal{R})d{\mathcal{C}}_5\left(t\right).\end{array}\end{array}$$

(25)

We use the next theorem for the existence and uniqueness of model (23).

Theorem 5.

Suppose the following conditions hold such that there exist ${\mathcal{C}}_j,{\widehat{\mathcal{C}}}_j$:

(i) 

$|P_j(y,t)-P_j(y_i,t){|}^2<{\mathcal{C}}_j{|y-y_i|}^2,$  $|Q_j(y,t)-V_i(y_j,t){|}^2<{\widehat{\mathcal{C}}}_j{|y-y_j|}^2;$

(ii) 

$\forall (y,t)\in {\mathbb{R}}^5\times [0,\mathcal{T}],$ then $|P_j{(y,t)|}^2,|Q_j{(y,t)|}^2{<\mathcal{C}\left(\right|y|}^2+1).$

These are satisfied for $i=1,\cdots ,5.$

Proof. 

Let

$${\displaystyle |P_1(t,\mathcal{S})-P_1(t,{\mathcal{S}}_1){|}^2={\left|(a+b+\eta +d_0)(\mathcal{S}-{\mathcal{S}}_1)\right|}^2.}$$

(26)

Define the norm as,

$${\left|\right|\chi \left|\right|}_{\infty }=\underset{t\in [0,\mathcal{T}]}{sup}{\left|\chi \right|}^2$$

Equation (26) is transformed into

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |P_1(t,S)-P_1(t,S_1){|}^2\le }& {\displaystyle \underset{t\in [0,\mathcal{T}]}{sup}{\left|(a+b+\eta +d_0)(\mathcal{S}-{\mathcal{S}}_1)\right|}^2,}\hfill \\ \hfill \le & \left|\right|(a+b+\eta +d_0){\left|\right|}_{\infty }^2{|\mathcal{S}-{\mathcal{S}}_1|}^2,\hfill \\ \hfill \le & {\mathcal{C}}_1{|\mathcal{S}-{\mathcal{S}}_1|}^2,\hfill \end{array}\end{array}$$

and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |Q_1(\mathcal{S},t)-Q_1({\mathcal{S}}_1,t){|}^2=}& {\displaystyle |({\mathsf{\Delta }}_{11}\mathcal{S}+{\mathsf{\Delta }}_{12})\mathcal{S}-({\mathsf{\Delta }}_{11}{\mathcal{S}}_1+{\mathsf{\Delta }}_{12}){\mathcal{S}}_1{|}^2,}\hfill \\ \hfill \le & {\displaystyle \left|\right({\mathsf{\Delta }}_{11}({\mathcal{S}}^2-{\mathcal{S}}_1^2)-{\mathsf{\Delta }}_{12}(\mathcal{S}-{\mathcal{S}}_1){|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left({\mathsf{\Delta }}_{11}(\mathcal{S}+{\mathcal{S}}_1)+{\mathsf{\Delta }}_{12}\right)}^2{|\mathcal{S}-{\mathcal{S}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle \left({\mathsf{\Delta }}_{11}^2{(\mathcal{S}+{\mathcal{S}}_1)}^2+2{\mathsf{\Delta }}_{11}{\mathsf{\Delta }}_{12}(\mathcal{S}+{\mathcal{S}}_1)+{\mathsf{\Delta }}_{12}^2\right){|\mathcal{S}-{\mathcal{S}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle \left({\mathsf{\Delta }}_{11}^2({\mathcal{S}}^2+2\mathcal{S}{\mathcal{S}}_1+{\mathcal{S}}_1^2)+2{\mathsf{\Delta }}_{11}{\mathsf{\Delta }}_{12}(\mathcal{S}+{\mathcal{S}}_1)+{\mathsf{\Delta }}_{12}^2\right){|\mathcal{S}-{\mathcal{S}}_1|}^2,}\hfill \\ \hfill \le & (\underset{t\in [0,\mathcal{T}]}{sup}\left|{\mathcal{S}}^2\left(t\right)\right|+2\underset{t\in [0,\mathcal{T}]}{sup}\left|\mathcal{S}\left(t\right)\right|\underset{t\in [0,\mathcal{T}]}{sup}\left|{\mathcal{S}}_1\left(t\right)\right|+\underset{t\in [0,T]}{sup}\left|{\mathcal{S}}_1^t\left(t\right)\right|\hfill \\ & +2{\mathsf{\Delta }}_{11}{\mathsf{\Delta }}_{12}(\underset{t\in [0,\mathcal{T}]}{sup}|\mathcal{S}\left(t\right)|+\underset{t\in [0,\mathcal{T}]}{sup}|{\mathcal{S}}_1\left(t\right)|)+{\mathsf{\Delta }}_{12}^2){|\mathcal{S}-{\mathcal{S}}_1|}^2,\hfill \\ \hfill \le & {\displaystyle \left({\mathsf{\Delta }}_{11}^2\left(\left|\right|{\mathcal{S}}^2{\left|\right|}_{\infty }+{2\left|\right|\mathcal{S}\left|\right|}_{\infty }\left|\right|{\mathcal{S}}_1{\left|\right|}_{\infty }+\left|\right|{\mathcal{S}}_1^2{\left|\right|}_{\infty }\right)+2{\mathsf{\Delta }}_{11}{\mathsf{\Delta }}_{12}{\left|\right|\mathcal{S}\left|\right|}_{\infty }\left|\right|{\mathcal{S}}_1{\left|\right|}_{\infty }+{\mathsf{\Delta }}_{12}^2\right){|\mathcal{S}-{\mathcal{S}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle {\tilde{\mathcal{C}}}_1{|\mathcal{S}-{\mathcal{S}}_1|}^2,}\hfill \end{array}\end{array}$$

(27)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle {\tilde{\mathcal{C}}}_1=}& {\displaystyle {\mathsf{\Delta }}_{11}^2\left(\left|\right|{\mathcal{S}}^2{\left|\right|}_{\infty }+{2\left|\right|\mathcal{S}\left|\right|}_{\infty }\left|\right|{\mathcal{S}}_1{\left|\right|}_{\infty }+\left|\right|{\mathcal{S}}_1^2{\left|\right|}_{\infty }\right)+2{\mathsf{\Delta }}_{11}{\mathsf{\Delta }}_{12}{\left|\right|\mathcal{S}\left|\right|}_{\infty }\left|\right|{\mathcal{S}}_1{\left|\right|}_{\infty }+{\mathsf{\Delta }}_{12}^2,}\hfill \\ \hfill =& {\displaystyle {\mathsf{\Delta }}_{11}^2{\left({\left|\right|\mathcal{S}\left|\right|}_{\infty }+\left|\right|{\mathcal{S}}_1{\left|\right|}_{\infty }\left|\right|\right)}^2+2{\mathsf{\Delta }}_{11}{\mathsf{\Delta }}_{12}{\left|\right|\mathcal{S}\left|\right|}_{\infty }\left|\right|{\mathcal{S}}_1{\left|\right|}_{\infty }\left|\right|+{\mathsf{\Delta }}_{12}^2.}\hfill \end{array}\end{array}$$

Similarly, we can demonstrate that condition (i) is satisfied by the remaining equations in the model (23). Consequently,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle {\widehat{\mathcal{C}}}_2=}& {\displaystyle {\mathsf{\Delta }}_{21}^2{\left({\left|\right|\mathcal{V}\left|\right|}_{\infty }+\left|\right|{\mathcal{V}}_1{\left|\right|}_{\infty }\left|\right|\right)}^2+2{\mathsf{\Delta }}_{21}{\mathsf{\Delta }}_{22}{\left|\right|\mathcal{V}\left|\right|}_{\infty }\left|\right|{\mathcal{V}}_1{\left|\right|}_{\infty }+{\mathsf{\Delta }}_{22}^2,}\hfill \\ \hfill {\displaystyle {\widehat{\mathcal{C}}}_3=}& {\displaystyle {\mathsf{\Delta }}_{31}^2{\left({\left|\right|\mathcal{A}\left|\right|}_{\infty }+\left|\right|{\mathcal{A}}_1{\left|\right|}_{\infty }\left|\right|\right)}^2+2{\mathsf{\Delta }}_{31}{\mathsf{\Delta }}_{32}{\left|\right|\mathcal{A}\left|\right|}_{\infty }\left|\right|{\mathcal{A}}_1{\left|\right|}_{\infty }+{\mathsf{\Delta }}_{32}^2,}\hfill \\ \hfill {\displaystyle {\widehat{\mathcal{C}}}_4=}& {\displaystyle {\mathsf{\Delta }}_{41}^2{\left({\left|\right|\mathcal{B}\left|\right|}_{\infty }+\left|\right|{\mathcal{B}}_1{\left|\right|}_{\infty }\left|\right|\right)}^2+2{\mathsf{\Delta }}_{41}{\mathsf{\Delta }}_{42}{\left|\right|\mathcal{B}\left|\right|}_{\infty }\left|\right|{\mathcal{B}}_1{\left|\right|}_{\infty }+{\mathsf{\Delta }}_{42}^2,}\hfill \\ \hfill {\displaystyle {\widehat{\mathcal{C}}}_5=}& {\displaystyle {\mathsf{\Delta }}_{51}^2{\left({\left|\right|\mathcal{R}\left|\right|}_{\infty }+\left|\right|{\mathcal{R}}_1{\left|\right|}_{\infty }\left|\right|\right)}^2+2{\mathsf{\Delta }}_{51}{\mathsf{\Delta }}_{52}{\left|\right|\mathcal{R}\left|\right|}_{\infty }\left|\right|{\mathcal{R}}_1{\left|\right|}_{\infty }+{\mathsf{\Delta }}_{52}^2.}\hfill \end{array}\end{array}$$

Furthermore, taking $\mathcal{V}$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |P_2(\mathcal{V},t)-P_2({\mathcal{V}}_1,t){|}^2=}& {\displaystyle |-(b+(1-\delta )a+d_0)(\mathcal{V}-{\mathcal{V}}_1){|}^2,}\hfill \\ \hfill \le & {\displaystyle 2|(b+(1-\delta )a+d_0){|}^2{|\mathcal{V}-{\mathcal{V}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_2{|\mathcal{V}-{\mathcal{V}}_1|}^2}\hfill \end{array}\end{array}$$

where ${\displaystyle {\mathcal{C}}_2=2{\left|(b+(1-\delta )a+d_0)\right|}^2.}$ Similarly for $\mathcal{A}$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |P_3(\mathcal{A},t)-P_3({\mathcal{A}}_1,t){|}^2=}& {\displaystyle |-(r_1+d_0+d_A)(\mathcal{A}-{\mathcal{A}}_1){|}^2,}\hfill \\ \hfill \le & {\displaystyle 2|(r_1+d_0+d_A){|}^2{|\mathcal{A}-{\mathcal{A}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_3{|\mathcal{A}-{\mathcal{A}}_1|}^2,}\hfill \end{array}\end{array}$$

where ${\displaystyle {\mathcal{C}}_3=2{\left|(r_1+d_0+d_A)\right|}^2.}$ Also for $\mathcal{B}$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |P_4(\mathcal{B},t)-P_4({\mathcal{B}}_1,t){|}^2=}& {\displaystyle |-(r_2+d_0+d_B)(\mathcal{B}-{\mathcal{B}}_1){|}^2,}\hfill \\ \hfill \le & {\displaystyle 2|(r_1+d_0+d_A){|}^2{|\mathcal{B}-{\mathcal{B}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_4{|\mathcal{B}-{\mathcal{B}}_1|}^2,}\hfill \end{array}\end{array}$$

where ${\displaystyle {\mathcal{C}}_4=2{\left|(r_2+d_0+d_B)\right|}^2.}$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |P_5(\mathcal{R},t)-P_5({\mathcal{R}}_1,t){|}^2=}& {\displaystyle |-(\gamma +d_0)(\mathcal{R}-{\mathcal{R}}_1){|}^2,}\hfill \\ \hfill \le & {\displaystyle {2\left|\chi \right|}^3{|\mathcal{R}-{\mathcal{R}}_1|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_5{|\mathcal{R}-{\mathcal{R}}_1|}^2}\hfill \end{array}\end{array}$$

where ${\displaystyle {\mathcal{C}}_5=2{\left|(\gamma +d_0)\right|}^2.}$

Then, for our model (23), we check that condition (ii) is met.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |P_1{(S,t)|}^2=}& {\displaystyle |(1-\beta )\alpha -(a+b+\eta +d_0){\mathcal{S}+\gamma \mathcal{R}|}^2,}\hfill \\ \hfill \le & {\displaystyle |(1-\beta )\alpha \mathcal{S}-(a+b+\eta +d_0){\mathcal{S}+\gamma \mathcal{R}|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left|\mathcal{S}\right|}^2{|\mathsf{\Lambda }-(\lambda +\mu )|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left(\right|\mathcal{S}|}^2+1\left)\right|(1-\beta )\alpha -(a+b+\eta +d_0)+\gamma \mathcal{R}{{|}^2|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left(\right|\mathcal{S}|}^2+1)\underset{t\in [0,\mathcal{T}]}{sup}{|(1-\beta )\alpha -(a+b+\eta +d_0)+\gamma \mathcal{R}|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}^1{\left(\right|\mathcal{S}|}^2+1)}\hfill \end{array}\end{array}$$

for ${\displaystyle {\mathcal{C}}^1=\underset{t\in [0,\mathcal{T}]}{sup}{|(1-\beta )\alpha -(a+b+\eta +d_0)+\gamma \mathcal{R}|}^2.}$

Also, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle |Q_1(\mathcal{S},t)-Q_1({\mathcal{S}}_1,t){|}^2=}& {\displaystyle |({\mathsf{\Delta }}_{11}\mathcal{S}+{\mathsf{\Delta }}_{12}){\mathcal{S}|}^2,}\hfill \\ \hfill \le & {\displaystyle |{\mathsf{\Delta }}_{11}{\mathcal{S}}^2+{\mathsf{\Delta }}_{12}{\mathcal{S}}^2{|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left({\mathsf{\Delta }}_{11}+{\mathsf{\Delta }}_{12}\right)}^2{\left|{\mathcal{S}}^2\right|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left({\mathsf{\Delta }}_{11}+{\mathsf{\Delta }}_{12}\right)}^2\underset{t\in [0,\mathcal{T}]}{sup}\left|{\mathcal{S}}^2\right|{\left|\mathcal{S}\right|}^2,}\hfill \\ \hfill \le & {\displaystyle {\left({\mathsf{\Delta }}_{11}+{\mathsf{\Delta }}_{12}\right)}^2\left|\right|{\mathcal{S}}^2{\left|\right|}_{\infty }{\left(\right|\mathcal{S}|}^2+1),}\hfill \\ \hfill \le & {\displaystyle {\tilde{\mathcal{C}}}^1{\left(\right|\mathcal{S}|}^2+1),}\hfill \end{array}\end{array}$$

(28)

where ${\displaystyle {\widehat{\mathcal{C}}}_1={\left({\mathsf{\Delta }}_{11}+{\mathsf{\Delta }}_{12}\right)}^2\left|\right|{\mathcal{S}}^2{\left|\right|}_{\infty }.}$ In a comparable manner

$${\displaystyle {\widehat{\mathcal{C}}}_2={\left({\mathsf{\Delta }}_{21}+{\mathsf{\Delta }}_{22}\right)}^2\left|\right|{\mathcal{V}}^2{\left|\right|}_{\infty },}$$

$${\displaystyle {\widehat{\mathcal{C}}}_3={\left({\mathsf{\Delta }}_{31}+{\mathsf{\Delta }}_{32}\right)}^2\left|\right|{\mathcal{A}}^2{\left|\right|}_{\infty },}$$

and

$${\displaystyle {\widehat{\mathcal{C}}}_4={\left({\mathsf{\Delta }}_{41}+{\mathsf{\Delta }}_{42}\right)}^2\left|\right|{\mathcal{B}}^2{\left|\right|}_{\infty },}$$

$${\displaystyle {\widehat{\mathcal{C}}}_5={\left({\mathsf{\Delta }}_{51}+{\mathsf{\Delta }}_{52}\right)}^2\left|\right|{\mathcal{R}}^2{\left|\right|}_{\infty }}$$

In similar fashion, for $\mathcal{V}$, $\mathcal{A}$, $\mathcal{B}$, and $\mathcal{R}$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle {\left|Q_2(\mathcal{V},t)\right|}^2=}& {\displaystyle |\beta \alpha +\eta \mathcal{S}-(b+(1-\delta )a+d_0){\mathcal{V}|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_2{\left(\right|\mathcal{V}|}^2+1),}\hfill \\ \\ \hfill {\displaystyle {\left|Q_3(\mathcal{A},t)\right|}^2=}& {\displaystyle |a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A){\mathcal{A}|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_3{\left(\right|\mathcal{A}|}^2+1),}\hfill \\ \\ \hfill {\displaystyle {\left|Q_4(\mathcal{B},t)\right|}^2=}& {\displaystyle |b(\mathcal{S}+\mathcal{V})-(r_2+d_0+d_B){\mathcal{B}|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_4{\left(\right|\mathcal{B}|}^2+1),}\hfill \\ \\ \hfill {\displaystyle |Q_5{(\mathcal{R},t)|}^2=}& {\displaystyle |r_1\mathcal{A}+r_2\mathcal{B}-(\gamma +d_0){\mathcal{R}|}^2,}\hfill \\ \hfill \le & {\displaystyle {\mathcal{C}}_5{\left(\right|\mathcal{R}|}^2+1).}\hfill \end{array}\end{array}$$

where

$${\displaystyle {\widehat{\mathcal{C}}}_2=\underset{t\in [0,\mathcal{T}]}{sup}\left|\right|\beta \alpha +\eta \mathcal{S}-(b+(1-\delta )a+d_0){|}^2,}$$

$${\displaystyle {\widehat{\mathcal{C}}}_3=\underset{t\in [0,\mathcal{T}]}{sup}{|a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)|}^2,}$$

$${\displaystyle {\widehat{\mathcal{C}}}_4=\underset{t\in [0,\mathcal{T}]}{sup}\left|\right|b(\mathcal{S}+\mathcal{V})-(r_2+d_0+d_B){|}^2,}$$

and

$${\displaystyle {\widehat{\mathcal{C}}}_5=\underset{t\in [0,\mathcal{T}]}{sup}\left|\right|r_1\mathcal{A}+r_2\mathcal{B}-(\gamma +d_0){|}^2.}$$

There, model (23) exists and has a unique solution since both $P_i$ and $Q_i$ for $i=1,2,\cdots ,5$ satisfy all the conditions stated in the theorem. This completes the proof. □

9. Basic Reproduction Number for Stochastic Model

We take into consideration the infected class $\mathcal{A}$ of stochastic model (23) in order to derive the stochastic basic reproduction number:

$$d\mathcal{A}=(a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A})dt+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32}){\mathcal{C}}_3\left(t\right).$$

We now determine our fundamental reproduction number in the stochastic manner using Ito’s formula. Now let us examine the Taylor series representation of $h(t,\mathcal{A}(t\left)\right)=In\left(\mathcal{A}\right(t\left)\right)$;

$$dh(t,\mathcal{A}\left(t\right))=\frac{\partial h}{\partial t}dt+\frac{\partial h}{\partial \mathcal{A}\left(t\right)}d\mathcal{A}\left(t\right)+\frac{1}{2}\frac{{\partial }^{2}h}{\partial {\mathcal{A}}^2\left(t\right)}{\left(d\mathcal{A}\left(t\right)\right)}^2+\frac{{\partial }^{2}h}{\partial \mathcal{A}\left(t\right)\partial t}d\mathcal{A}\left(t\right)dt+\frac{1}{2}\frac{{\partial }^{2}h}{\partial t^2}{\left(dt\right)}^2.$$

where $\frac{\partial h}{\partial t}=0$, $\frac{\partial h}{\partial \mathcal{A}\left(t\right)}=\frac{1}{\mathcal{A}\left(t\right)}$, $\frac{{\partial }^{2}h}{\partial {\mathcal{A}}^2\left(t\right)}=\frac{1}{{\mathcal{A}}^2\left(t\right)}$, $\frac{{\partial }^{2}h}{\partial \mathcal{A}\partial t}=0$ and $\frac{{\partial }^{2}h}{\partial t^2}=0$

$$dh(t,\mathcal{A}\left(t\right))=\frac{1}{\mathcal{A}\left(t\right)}d\mathcal{A}\left(t\right)-\frac{1}{2{\mathcal{A}}^2\left(t\right)}d{\mathcal{A}}^2\left(t\right).$$

This implies

$$\begin{array}{c}\hfill dh(t,\mathcal{A}\left(t\right))=\frac{1}{\mathcal{A}\left(t\right)}(a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A})dt+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32}){\mathcal{C}}_3\left(t\right)\\ \hfill -\frac{1}{2{\mathcal{A}}^2\left(t\right)}{((a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A})dt+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32}){\mathcal{C}}_3\left(t\right))}^2\left(t\right).\end{array}$$

Next, using the chain rule, we obtain

$$dh(t,\mathcal{A}\left(t\right))=\left[a\mathcal{S}\left(t\right)+(1-\delta )a\mathcal{V}\left(t\right)-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right]dt+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})d{\mathcal{C}}_3\left(t\right).$$

Let $\mathcal{F}$ represent the new infection introduction rate and $\mathcal{V}$ represent the new infection transfer rate. After that, at the disease-free equilibrium point, $\mathcal{F}$ and $\mathcal{F}$ become

$$\mathcal{F}=\left[\frac{k{\mu }_1\alpha (1-\beta )d_0}{\eta +d_0}-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right]$$

$$\mathcal{V}=(r_1+d_0+d_A)$$

$${\mathcal{V}}^{-1}=\frac{1}{(r_1+d_0+d_A)}.$$

This implies

$$\mathcal{F}{\mathcal{V}}^{-1}=\left[\frac{k{\mu }_1\alpha (1-\beta )d_0}{(\eta +d_0)(r_1+d_0+d_A)}-\frac{{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2}{2(r_1+d_0+d_A)}\right]$$

where, ${\mathcal{R}}_1=\frac{k{\mu }_1{d}_0(1-\beta )}{(\eta +d_0)(r_1+d_0+d_A)}$

Thus, under the stochastic model, our basic reproduction number of the delta virus is

$${\mathcal{R}}_1^S={\mathcal{R}}_1-\frac{{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2}{2(r_1+d_0+d_A)}.$$

Similarly, we have

$${\mathcal{R}}_2^S={\mathcal{R}}_2-\frac{{({\mathsf{\Delta }}_{41}\mathcal{S}+{\mathsf{\Delta }}_{42})}^2}{2(r_2+d_0+d_B)}.$$

10. Stability Analysis of Stochastic Model

In this section, we discuss the stability of the stochastic model based on the stochastic basic reproduction number. If ${\mathcal{R}}_1^S<1$ or ${\mathcal{R}}_2^S<1$, then the stochastic model (23) will be locally asymptotically stable as follows in the next theorem.

Theorem 6.

If ${\mathcal{R}}_1^S<1$ or ${\mathcal{R}}_2^S<1$, then DFE point ${\mathcal{P}}^0$ is stable, locally and asymptotically.

Proof. 

Let $F(t,\mathcal{A}(t\left)\right)=ln\mathcal{A}\left(t\right)$ be a Taylor expansion, then using the $it\widehat{0}$ formula, one has

$$\begin{array}{ccc}\hfill dE(t,\mathcal{A}(t\left)\right)& =& \left[a\mathcal{S}\left(t\right)+(1-\delta )a\mathcal{V}\left(t\right)-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right]dt\hfill \\ & +& ({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})d{\mathcal{C}}_3\left(t\right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill dln\mathcal{A}\left(t\right)& =& \left[a\mathcal{S}\left(t\right)+(1-\delta )a\mathcal{V}\left(t\right)-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right]dt\hfill \\ & +& ({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})d{\mathcal{C}}_3\left(t\right)\hfill \end{array}$$

(29)

Applying integration on (29), we obtain

$$\begin{array}{ccc}\hfill ln\mathcal{A}\left(t\right)-ln\mathcal{A}\left(0\right)& =& {\int }_0^t{P}_1\left(a\mathcal{S}\left(t\right)+(1-\delta )a\mathcal{V}\left(t\right)-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right)dt\hfill \\ & +& {\int }_0^t{P}_1({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})d{\mathcal{C}}_3\left(t\right).\hfill \end{array}$$

(30)

Now, solving at DFE equilibrium point (30), we obtain

$$\begin{array}{ccc}\hfill ln\mathcal{A}\left(t\right)& =& ln\mathcal{A}\left(0\right)+{\int }_0^t{P}_1\left(\frac{k{\mu }_1\alpha (1-\beta )d_0}{\eta +d_0}-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right)dt\hfill \\ & +& {\int }_0^t{P}_1({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})d{\mathcal{C}}_3\left(t\right).\hfill \end{array}$$

$$\begin{array}{c}\hfill ln\mathcal{A}\left(t\right)\le ln\mathcal{A}\left(0\right)+\left(\frac{k{\mu }_1\alpha (1-\beta )d_0}{\eta +d_0}-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right)t+H\left(t\right).\end{array}$$

(31)

where $H\left(t\right)={\int }_0^t{P}_1({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})d{\mathcal{C}}_3\left(t\right)$.

We know that ${lim}_{t\to \infty }\sup \frac{H\left(t\right)}{t}=0$, using martingales. Furthermore, we divide (31) by t and apply ${lim}_{t\to \infty }\sup$, and we obtain

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim}sup\frac{ln\mathcal{A}\left(t\right)}{t}& \le & \underset{t\to \infty }{lim}sup\frac{ln\mathcal{A}\left(0\right)}{t}+\left(\frac{k{\mu }_1\alpha (1-\beta )d_0}{\eta +d_0}-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right)\hfill \\ & +& \underset{t\to \infty }{lim}sup\frac{H\left(t\right)}{t}.\hfill \end{array}$$

(32)

This implies,

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim}sup\frac{ln\mathcal{A}\left(t\right)}{t}& \le & \left(\frac{k{\mu }_1\alpha (1-\beta )d_0}{\eta +d_0}-(r_1+d_0+d_A)-\frac{1}{2}{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2\right)<0.\hfill \\ & =& (r_1+d_0+d_A)\left(\frac{k{\mu }_1\alpha (1-\beta )d_0}{\eta +d_0}-\frac{{({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32})}^2}{r_1+d_0+d_0}-1\right)<0.\hfill \\ & =& (r_1+d_0+d_A)({\mathcal{R}}_1^S-1).\hfill \end{array}$$

We know $(r_1+d_0+d_A)>0$; therefore,

$$({\mathcal{R}}_1^S-1)<0,$$

implies

$${\mathcal{R}}_1^S<1.$$

Similarly, we can obtain ${\mathcal{R}}_2^S<1.$ Hence, the DFE point ${\mathcal{P}}^0$ is stable locally and asymptotically, if ${\mathcal{R}}_1^S<1$ or ${\mathcal{R}}_2^S<1.$ □

11. Stochastic Model and Numerical Interpretation

Here, we convert the proposed deterministic two-variant model (1) into a stochastic model. That is, we investigate the stochastic system (23) for the numerical solution. We set

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill d\mathcal{S}& =P_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_1(t,\mathcal{S})d{\mathcal{C}}_1\left(t\right)\hfill \\ \hfill d\mathcal{V}& =P_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_2(t,\mathcal{S})d{\mathcal{C}}_2\left(t\right)\hfill \\ \hfill d\mathcal{A}& =P_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_3(t,\mathcal{S})d{\mathcal{C}}_3\left(t\right)\hfill \\ \hfill d\mathcal{B}& =P_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_4(t,\mathcal{S})d{\mathcal{C}}_4\left(t\right)\hfill \\ \hfill d\mathcal{R}& =P_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+Q_5(t,\mathcal{S})d{\mathcal{C}}_5\left(t\right).\hfill \end{array}\end{array}$$

We can convert the (23) system into a Volterra integral system of equations as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathcal{S}\left(t\right)=\mathcal{S}\left(0\right)+{\int }_0^t{P}_1\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_1(t,\mathcal{S})d{\mathcal{C}}_1\left(t\right)\\ \hfill \mathcal{V}\left(t\right)=\mathcal{V}\left(0\right)+{\int }_0^t{P}_2\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_2(t,\mathcal{V})d{\mathcal{C}}_2\left(t\right)\\ \hfill \mathcal{S}\left(t\right)=\mathcal{A}\left(0\right)+{\int }_0^t{P}_3\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_3(t,\mathcal{A})d{\mathcal{C}}_3\left(t\right)\\ \hfill \mathcal{S}\left(t\right)=\mathcal{B}\left(0\right)+{\int }_0^t{P}_4\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_4(t,\mathcal{B})d{\mathcal{C}}_4\left(t\right)\\ \hfill \mathcal{S}\left(t\right)=\mathcal{R}\left(0\right)+{\int }_0^t{P}_5\left(t,\mathcal{S},\mathcal{V},\mathcal{A},\mathcal{B},\mathcal{R}\right)dt+{\int }_0^t{Q}_5(t,\mathcal{R})d{\mathcal{C}}_5\left(t\right).\end{array}\end{array}$$

Obviously, the solution of (23) exists and is unique. To do this, nonlinear perturbations are introduced into each system equation. As shown for each class below, we only change the rate of each class:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{S}& :-{\mu }_i\to -{\mu }_i+({\mathsf{\Delta }}_{11}\mathcal{S}+{\mathsf{\Delta }}_{12}){\mathcal{C}}_1\left(t\right),\mathrm{where}i=1,2,\hfill \\ \hfill \mathcal{V}& :-\eta \to -\eta +({\mathsf{\Delta }}_{21}\mathcal{S}+{\mathsf{\Delta }}_{22}){\mathcal{C}}_2\left(t\right)\hfill \\ \hfill \mathcal{A}& :-r_1\to -r_2+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32}){\mathcal{C}}_3\left(t\right)\hfill \\ \hfill \mathcal{B}& :-r_1\to -r_2+({\mathsf{\Delta }}_{41}\mathcal{S}+{\mathsf{\Delta }}_{42}){\mathcal{C}}_4\left(t\right)\hfill \\ \hfill \mathcal{R}& :-d_0\to -d_0+({\mathsf{\Delta }}_{51}\mathcal{S}+{\mathsf{\Delta }}_{52}){\mathcal{C}}_5\left(t\right).\hfill \end{array}\end{array}$$

As a result, we have the following system of Equation (1) that shows the stochastic model version:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill d\mathcal{S}& =((1-\beta )\alpha -(a+b+\eta +d_0)\mathcal{S}+\gamma \mathcal{R})dt+({\mathsf{\Delta }}_{11}\mathcal{S}+{\mathsf{\Delta }}_{12}){\mathcal{C}}_1\left(t\right)\hfill \\ \hfill d\mathcal{V}& =(\beta \alpha +\eta \mathcal{S}-(b+(1-\delta )a+d_0)\mathcal{V})dt+({\mathsf{\Delta }}_{21}\mathcal{S}+{\mathsf{\Delta }}_{22}){\mathcal{C}}_2\left(t\right)\hfill \\ \hfill d\mathcal{A}& =(a\mathcal{S}+(1-\delta )a\mathcal{V}-(r_1+d_0+d_A)\mathcal{A})dt+({\mathsf{\Delta }}_{31}\mathcal{S}+{\mathsf{\Delta }}_{32}){\mathcal{C}}_3\left(t\right)\hfill \\ \hfill d\mathcal{B}& =(b(\mathcal{S}+\mathcal{V})-(r_2+d_0+d_B)\mathcal{B})dt+({\mathsf{\Delta }}_{41}\mathcal{S}+{\mathsf{\Delta }}_{42}){\mathcal{C}}_4\left(t\right)\hfill \\ \hfill d\mathcal{R}& =(r_1\mathcal{A}+r_2\mathcal{B}-(\gamma +d_0)\mathcal{R})dt+({\mathsf{\Delta }}_{51}\mathcal{S}+{\mathsf{\Delta }}_{52}){\mathcal{C}}_5\left(t\right).\hfill \end{array}\end{array}$$

(33)

Using the same numerical data of Table 2, we simulate the model (23). We take ${\mathcal{C}}_1=0.02,{\mathcal{C}}_2=0.01;{\mathcal{C}}_3=0.01;{\mathcal{C}}_4=0.001;{\mathcal{C}}_5=0.01.$ The concerned dynamics of the different classes under the stochastic concept is given in Figure 8, Figure 9, Figure 10, Figure 11, and Figure 12, respectively. We take ${\mathcal{S}}_0=3000,{\mathcal{V}}_0=1000,{\mathcal{A}}_0=500,{\mathcal{B}}_0=450,{\mathcal{R}}_0=0.$

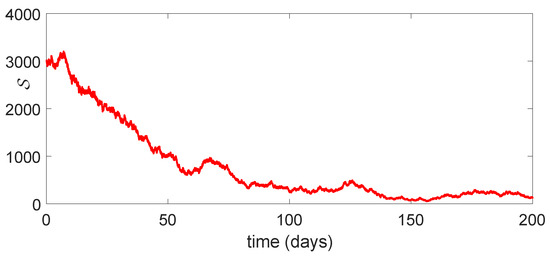
Figure 8. Dynamical behavior of $\mathcal{S}$ of model (23).

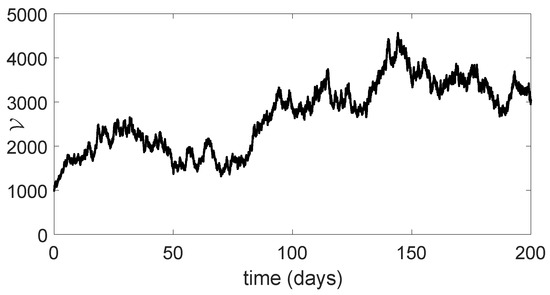
Figure 9. Dynamical behavior of $\mathcal{V}$ of model (23).

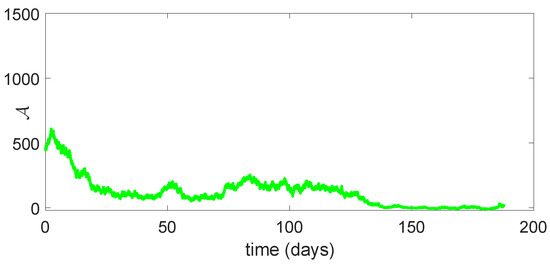
Figure 10. Dynamical behavior of $\mathcal{A}$ of model (23).

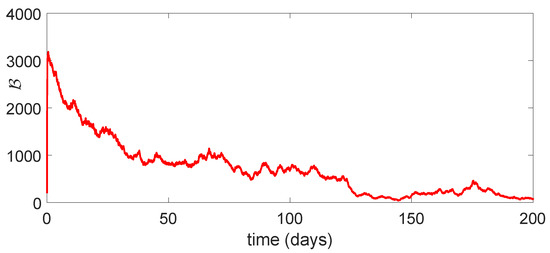
Figure 11. Dynamical behavior of $\mathcal{B}$ of model (23).

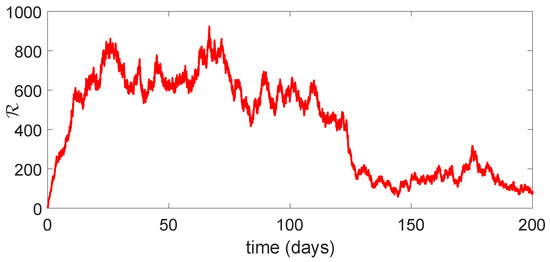
Figure 12. Dynamical behavior of $\mathcal{R}$ of model (23).

Onward in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, we compare the deterministic and stochastic model.

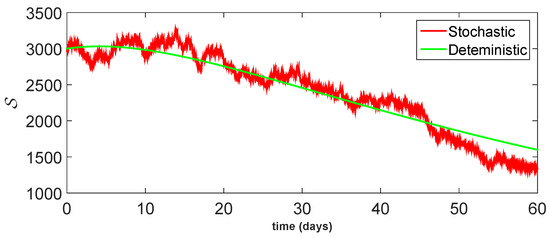
Figure 13. Comparison between dynamical behavior of stochastic and deterministic results for $\mathcal{S}$ of model (23).

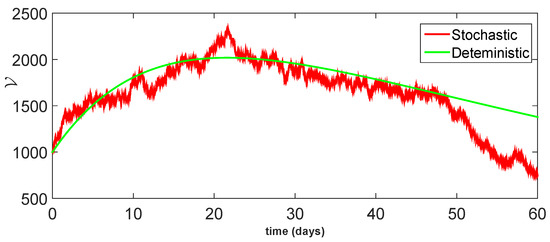
Figure 14. Comparison between dynamical behavior of stochastic and deterministic results for $\mathcal{V}$ of model (23).

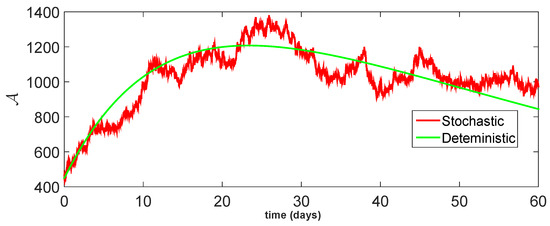
Figure 15. Comparison between dynamical behavior of stochastic and deterministic results for $\mathcal{A}$ of model (23).

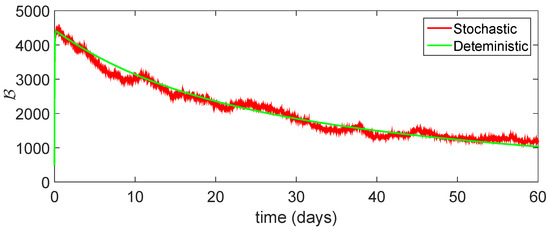
Figure 16. Comparison between dynamical behavior of stochastic and deterministic results for $\mathcal{B}$ of model (23).

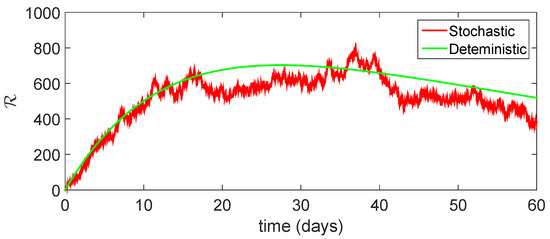
Figure 17. Comparison between dynamical behavior of stochastic and deterministic results for $\mathcal{R}$ of model (23).

From the given Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, we observe that both behaviors have close resemblance in the proposed model, which demonstrates the accuracy of our results. Here, in Table 3, we give the error analysis of stochastic and deterministic model compartments with the initial data given as ${\mathcal{S}}_0=3000,{\mathcal{V}}_0=1000,{\mathcal{A}}_0=500,{\mathcal{B}}_0=450,{\mathcal{R}}_0=0.$ We see that the errors of approximation for $t=2$ are much smaller when we use the stochastic model as compared to the deterministic model. Hence, dealing with population dynamical systems, the stochastic-type models are more realistic as compared to the deterministic model.

Table 3. Comparison of errors of approximation for deterministic and stochastic forms of the proposed model (1).

Error Analysis
Compartment	Error of Approximation for Deterministic Model	Error of Approximation for Stochastic Model
$\mathcal{S}$	0.05432	0.00345
$\mathcal{V}$	0.03214	0.008765
$\mathcal{A}$	0.01236	0.001129
$\mathcal{B}$	0.06754	0.003214
$\mathcal{R}$	0.00769	0.000341

12. Conclusions

One of the most efficient methods for examining the critical elements of disease outbreaks and assessing intervention tactics is through the use of infectious disease dynamics models. Here, we remark that the transmission dynamics model of infectious diseases like COVID-19 can forecast the trajectory of disease development and assess the efficacy of control measures based on the spread of diseases. The basic reproduction number serves as a threshold for determining whether a disease is widespread and can also be used to determine the peak and ultimate size of an epidemic, offering statistics and a theoretical foundation for disease prevention and control. There are now several SARS-CoV-2 strains that have emerged and are working together to shape the course of the COVID-19 pandemic. But the dynamics of several strains, their varying rates of transmission, and their reactions to vaccinations are rarely taken into consideration by the models in use today. We provide a novel mathematical model that takes into consideration the introduction of a vaccination program and two virus types. This research has examined a compartmental dynamical system for COVID-19 using a two-strain deterministic and stochastic model. The model’s fundamental results, equilibria, and reproductive numbers have been computed for both deterministic and stochastic models. Global and local stability analyses have been deduced. Numerical simulations using the NSFD method for the deterministic form of the proposed model have been performed. Additionally, the stochastic form has also been studied. The existence, uniqueness, basic reproduction number, and stability analysis have been discussed. Furthermore, a necessary condition has also been provided for the unique ergodic stationary distribution to exist for any positive solution. Also, a numerical interpretation of the theoretical results has been given by the stochastic numerical method. We have investigated the effects of both strains in a population where vaccination against strains is in progress. The model can be expanded to cover the latent class and people infected with strains 1 and 2, including hospitalized and quarantined individuals, in future.