Convolutional Neural Networks for Local Component Number Estimation from Time–Frequency Distributions of Multicomponent Nonstationary Signals
Abstract
1. Introduction
- Development of a novel CNN-based framework for accurate local component counting in TFDs, overcoming the limitations of traditional LRE methods.
- Introduction of a comprehensive training dataset comprising synthetic signals with LFM and QFM components, facilitating the robust generalization of the CNN across a wide range of synthetic and real-world signal types and complexities.
- Incorporation of AWGN into the training process, improving the CNN’s robustness to noise.
- Simplification of the local component counting process by eliminating the need for additional parameter tuning within the LRE method and the use of additional iterative LRE and NBRE approaches, streamlining the application for end-users.
2. Materials and Methods
2.1. Adaptive Time–Frequency Distributions
2.2. The Localized Rényi Entropy
Limitations
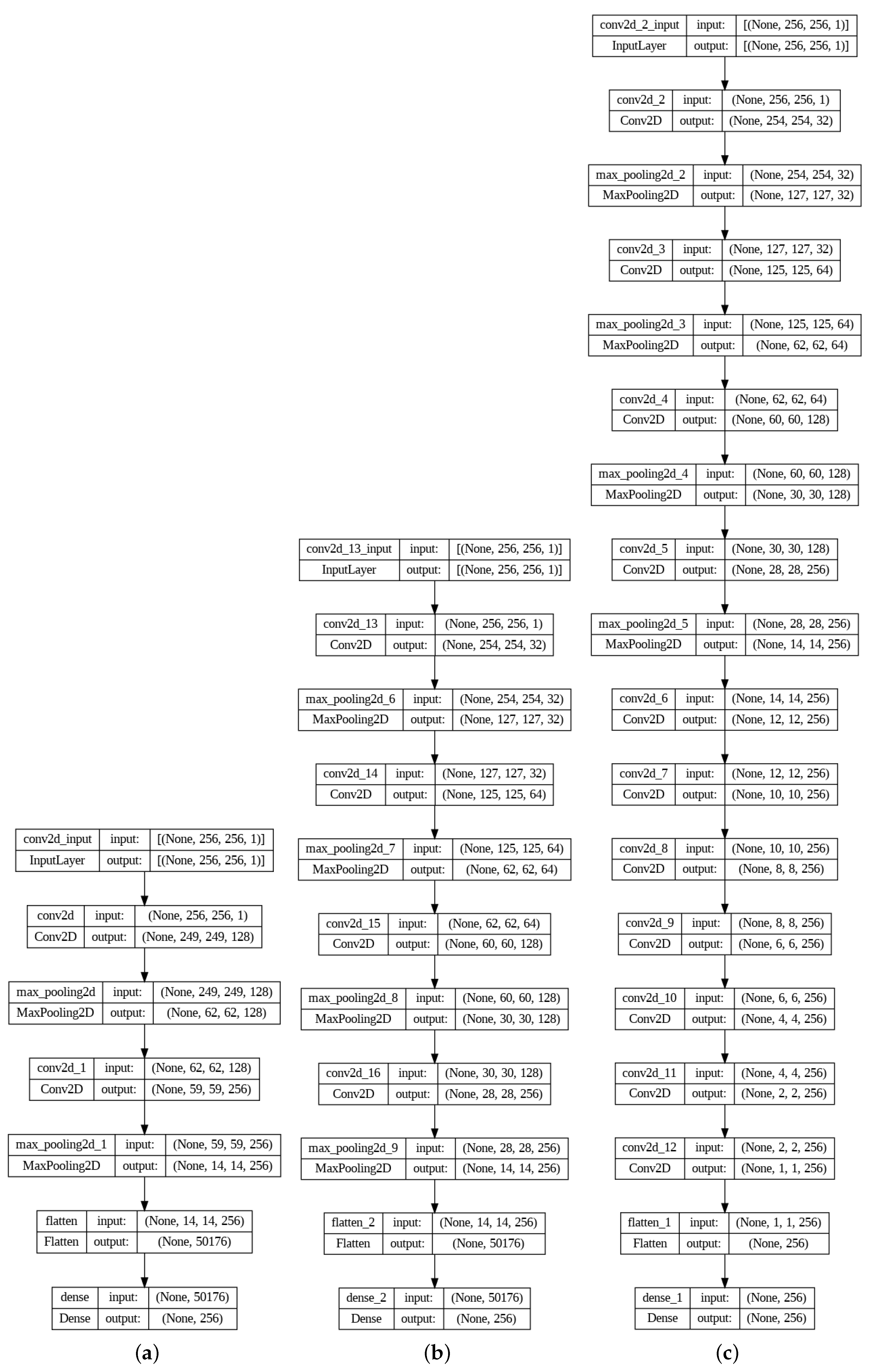
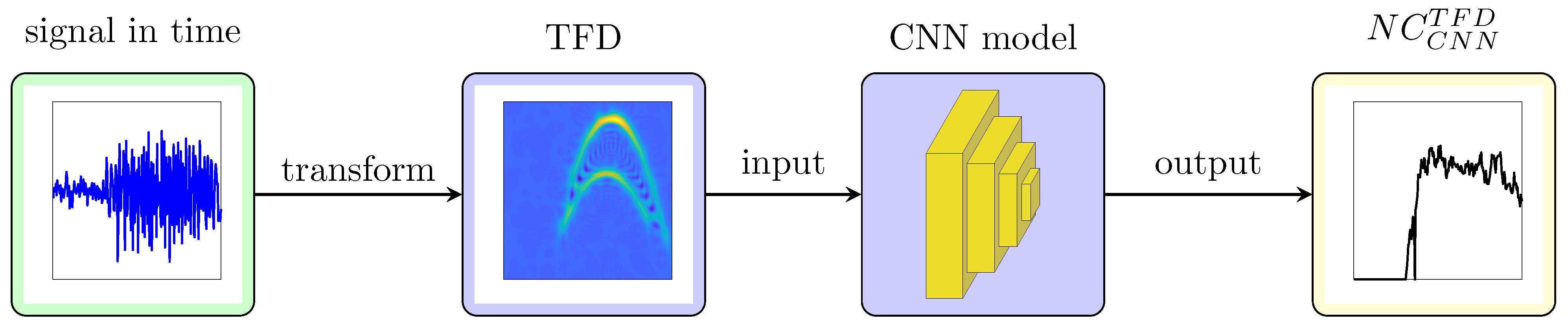
2.3. The Proposed CNN-Based Approach
Training Set
2.4. Summary of the Proposed Approach
3. Results and Discussion
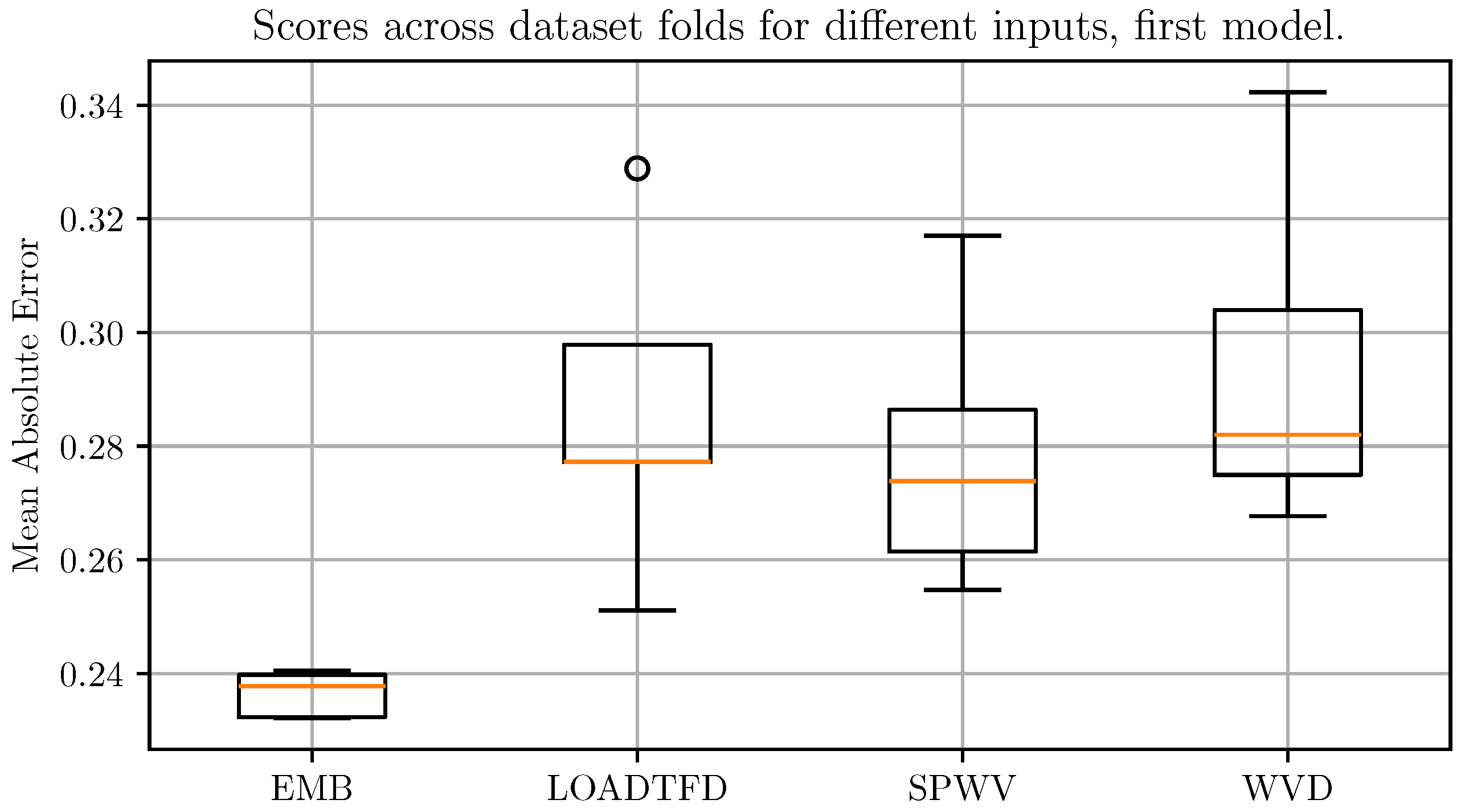
3.1. Model Evaluation
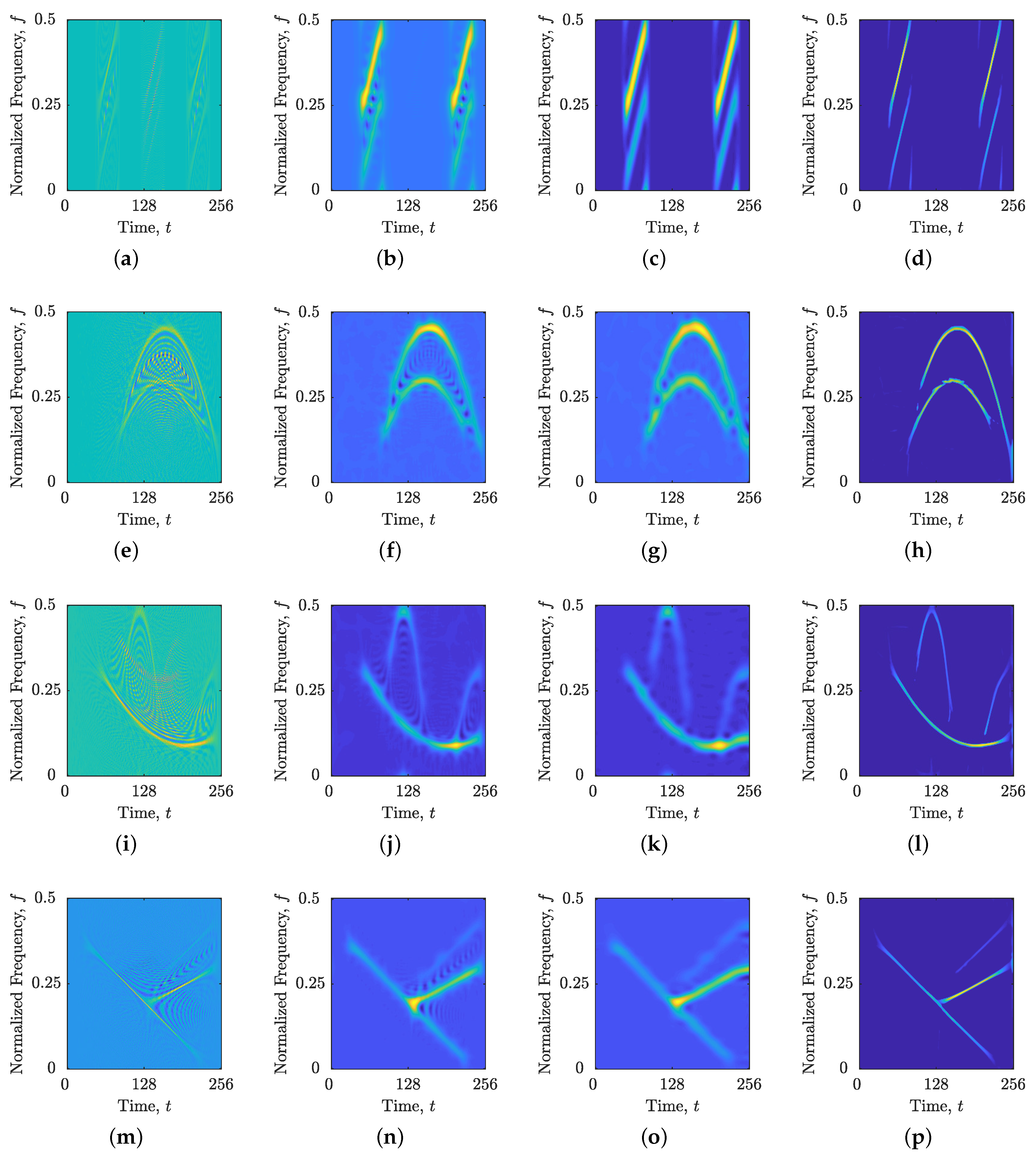
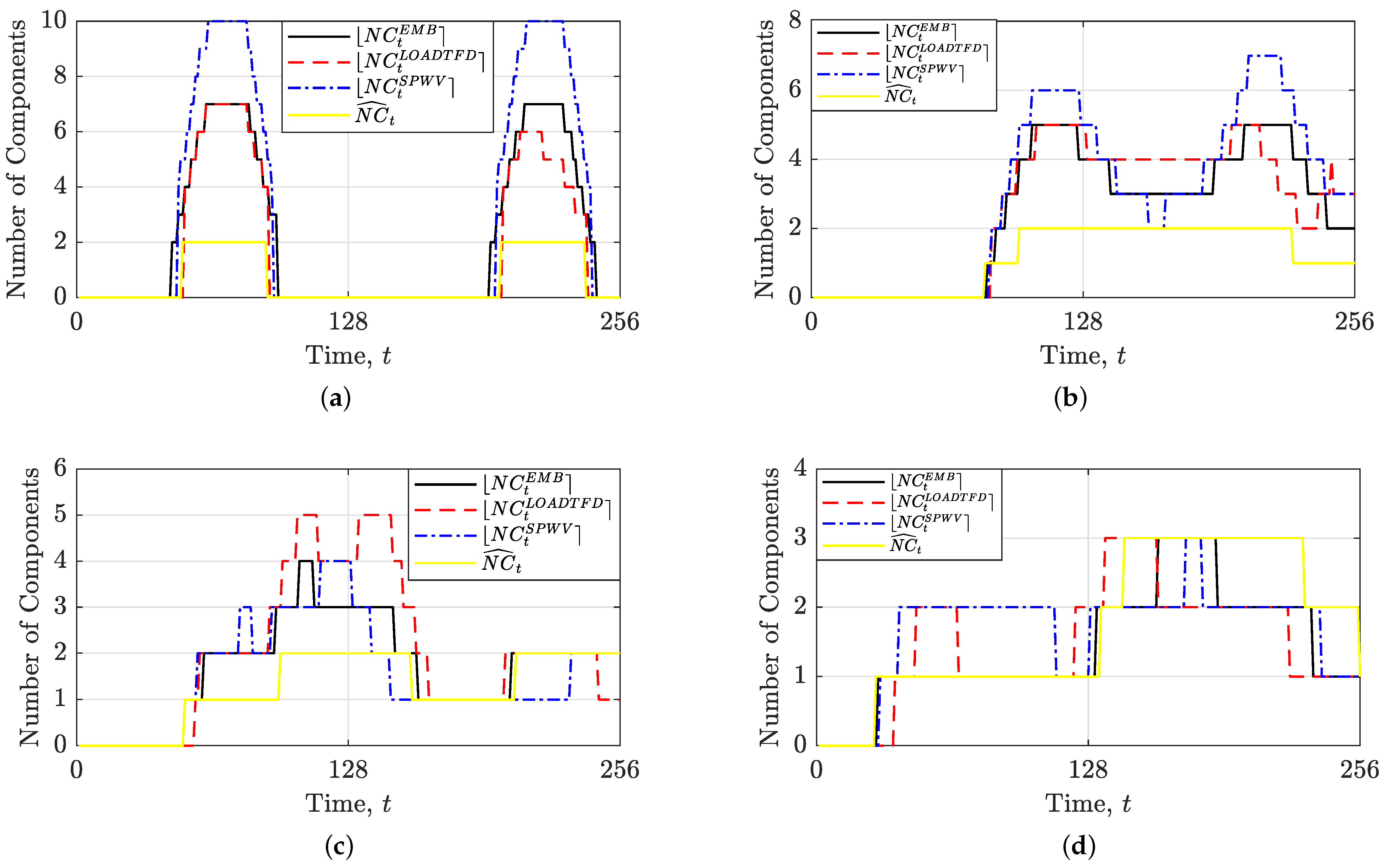
3.2. Results: Synthetic Signals
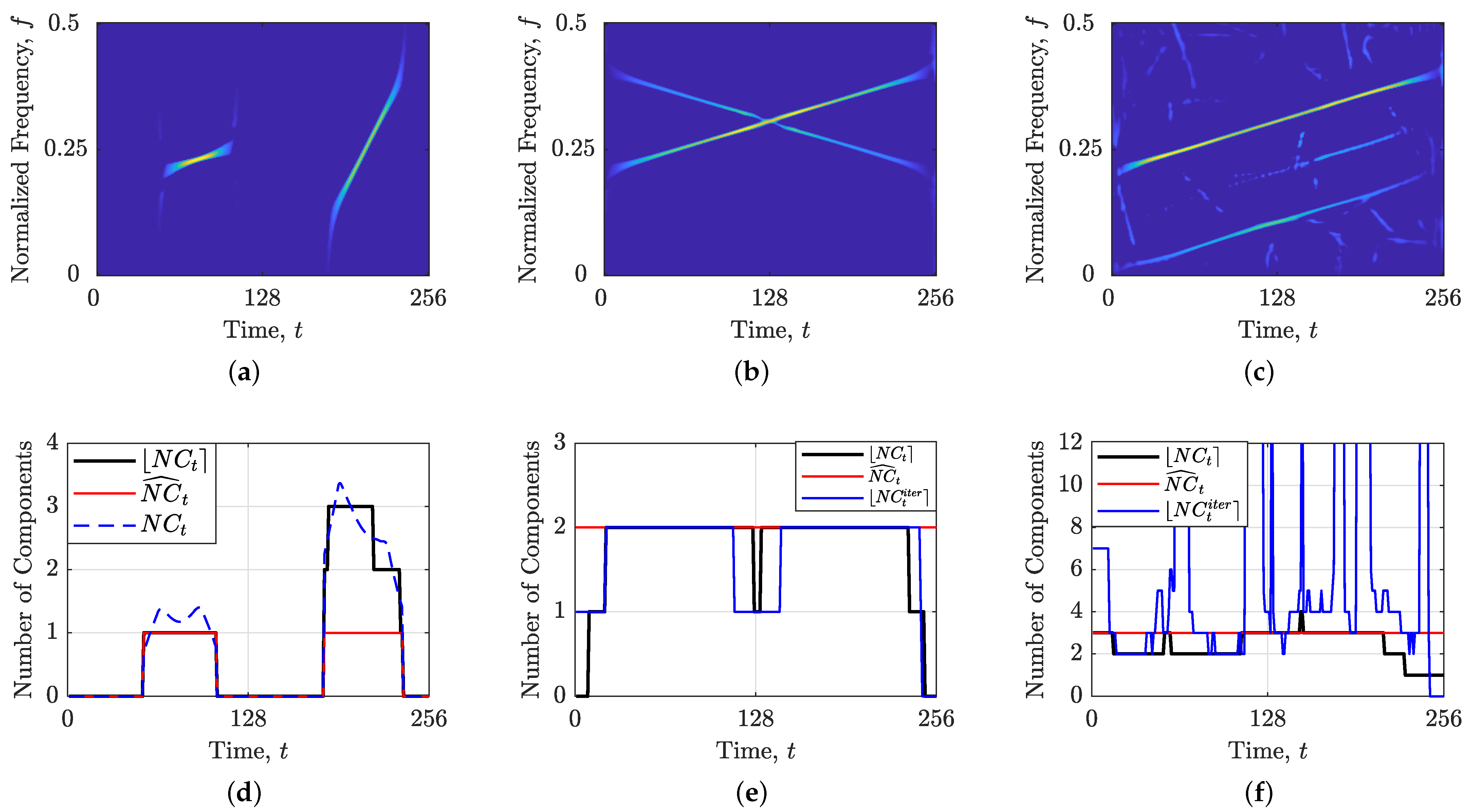
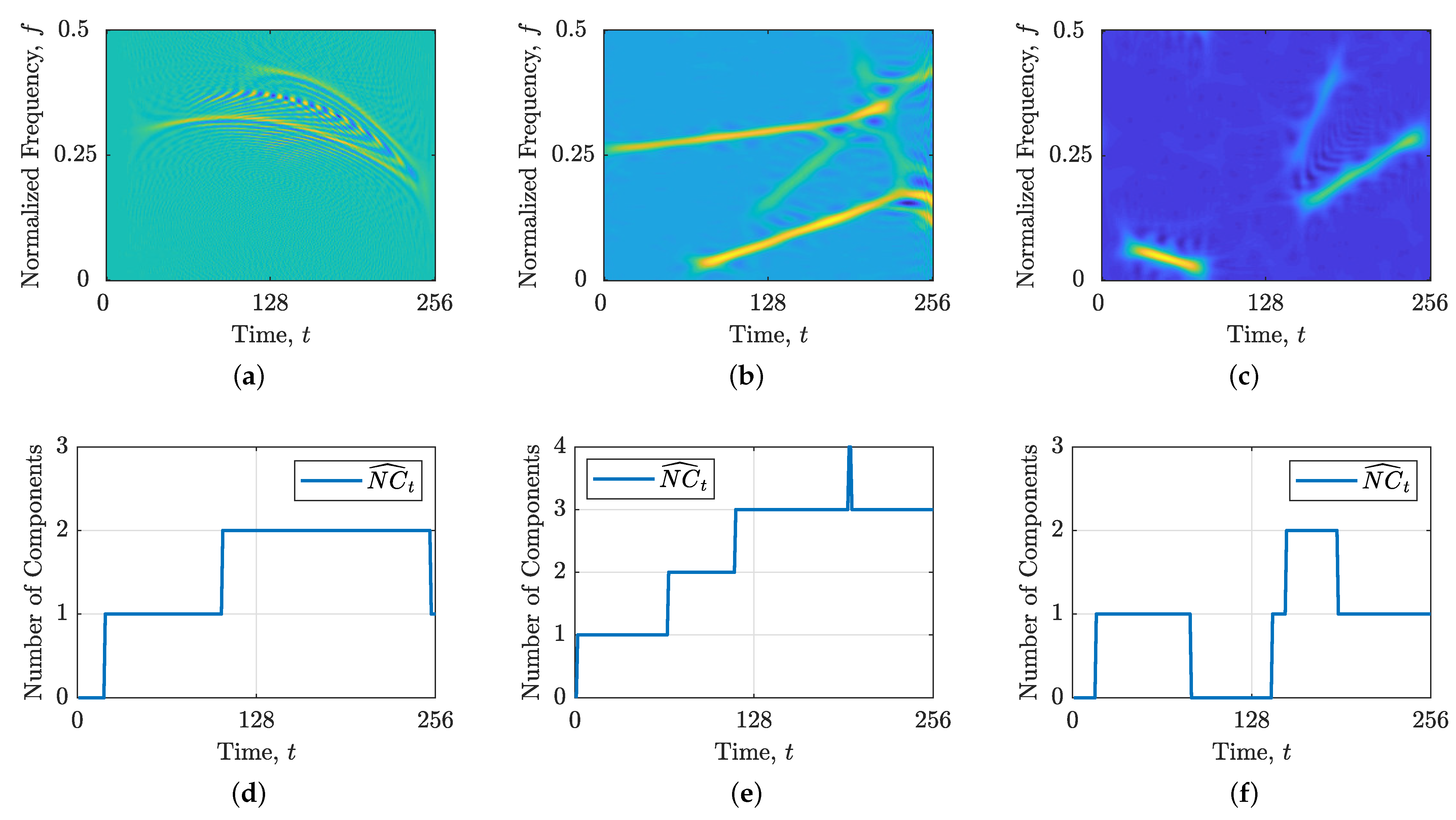
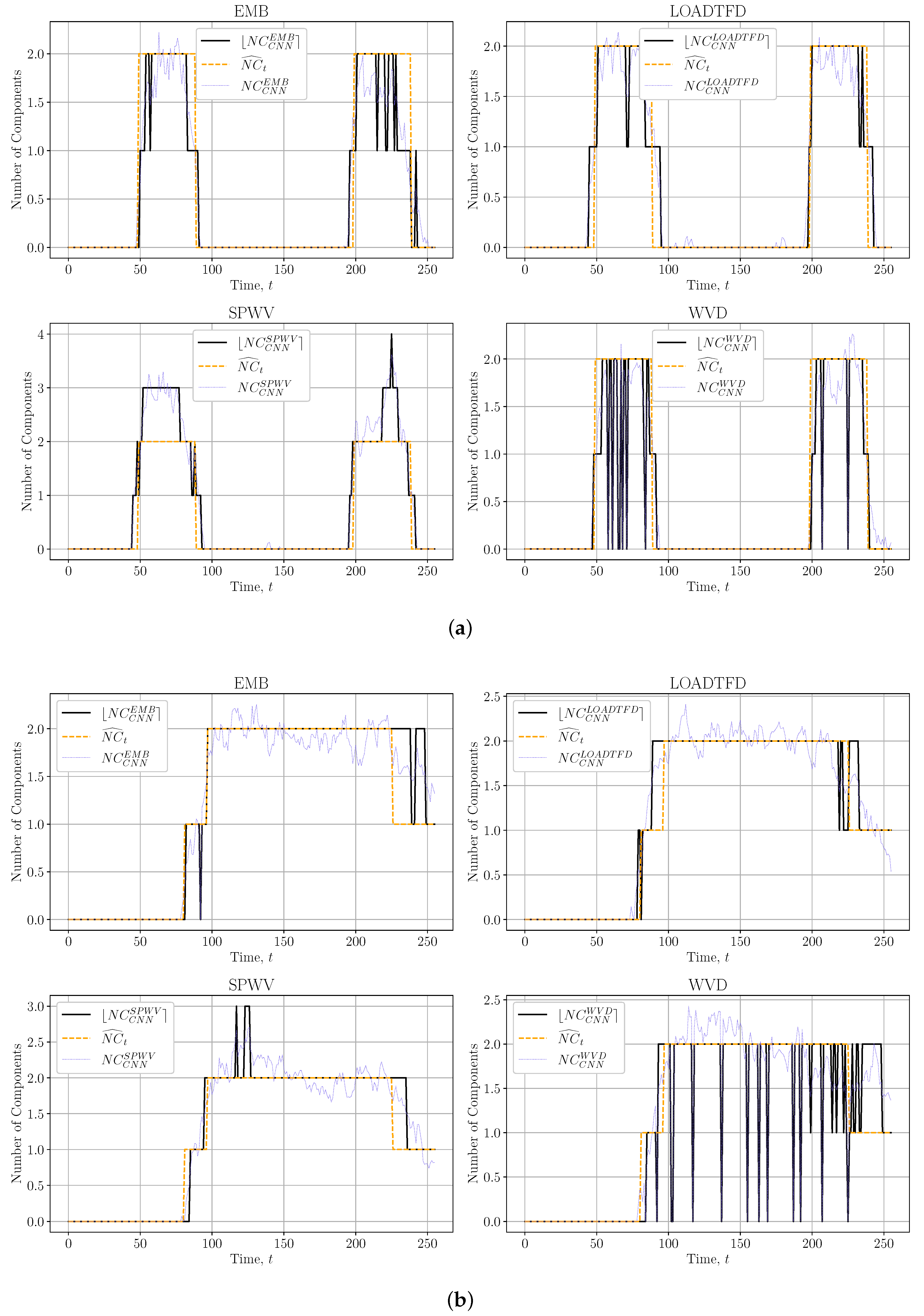
3.3. Results: Real-World Signals
Noise Sensitivity Analysis
3.4. Interpretation of the Results
Limitations of the Proposed Approach
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADTFD | Adaptive directional time–frequency distribution |
| AF | Ambiguity function |
| ANN | Artificial neural network |
| AWGN | Additive white Gaussian noise |
| CNN | Convolutional neural network |
| DGF | Double-derivative directional Gaussian filter |
| EEG | Electroencephalogram |
| EMB | Extended modified B distribution |
| FM | Frequency modulation |
| FT | Fourier transform |
| IACF | Instantaneous auto-correlation function |
| IF | Instantaneous frequency |
| LFM | Linear frequency-modulation |
| LOADTFD | Locally adaptive directional time-frequency distribution |
| LRE | Localized Renyi entropy |
| MAE | Mean absolute error |
| MAX | Maximum absolute error |
| MSE | Mean squared error |
| NBRE | Narrow-band Renyi entropy |
| QFM | Quadratic frequency-modulation |
| QTFD | Quadratic time-frequency distribution |
| SNR | Signal-to-noise ratio |
| SPWV | Smoothed-pseudo Wigner–Ville distribution |
| STRE | Short-term Renyi entropy |
| TF | Time–frequency |
| TFD | Time–frequency distribution |
| WVD | Wigner–Ville distribution |
References
- Lopac, N. Detection of Gravitational-Wave Signals from Time-Frequency Distributions Using Deep Learning. Ph.D. Thesis, University of Rijeka, Faculty of Engineering, Rijeka, Croatia, 2022. [Google Scholar]
- Milczarek, H.; Leśnik, C.; Djurović, I.; Kawalec, A. Estimating the Instantaneous Frequency of Linear and Nonlinear Frequency Modulated Radar Signals—A Comparative Study. Sensors 2021, 21, 2840. [Google Scholar] [CrossRef] [PubMed]
- Swiercz, E.; Janczak, D.; Konopko, K. Detection of LFM Radar Signals and Chirp Rate Estimation Based on Time-Frequency Rate Distribution. Sensors 2021, 21, 5415. [Google Scholar] [CrossRef]
- Dózsa, T.; Jurdana, V.; Šegota, S.B.; Volk, J.; Radó, J.; Soumelidis, A.; Kovács, P. Road Type Classification Using Time-Frequency Representations of Tire Sensor Signals. IEEE Access 2024, 12, 53361–53372. [Google Scholar] [CrossRef]
- Lerga, J.; Saulig, N.; Lerga, R.; Štajduhar, I. TFD thresholding in estimating the number of EEG components and the dominant if using the short-term Rényi entropy. In Proceedings of the 10th International Symposium on Image and Signal Processing and Analysis, Ljubljana, Slovenia, 18–20 September 2017; pp. 80–85. [Google Scholar]
- Lerga, J.; Saulig, N.; Stanković, L.; Seršić, D. Rule-based EEG classifier utilizing local entropy of time–frequency distributions. Mathematics 2021, 9, 451. [Google Scholar] [CrossRef]
- Boashash, B. Time-Frequency Signal Analysis and Processing, A Comprehensive Reference, 2nd ed.; EURASIP and Academic Press Series in Signal and Image Processing; Elsevier: London, UK, 2016. [Google Scholar]
- Stankovic, L.; Dakovic, M.; Thayaparan, T. Time-Frequency Signal Analysis with Applications; Artech House Publishers: Boston, MA, USA, 2013. [Google Scholar]
- Pachori, R.B. Time-Frequency Analysis Techniques and Their Applications; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Akan, A.; Karabiber Cura, O. Time–frequency signal processing: Today and future. Digit. Signal Process. 2021, 119, 103216. [Google Scholar] [CrossRef]
- Jurdana, V. A Multi-Objective Optimization Procedure for Locally Adaptive Time-Frequency Analysis with Application in EEG Signal Processing. Ph.D. Thesis, University of Rijeka, Faculty of Engineering, Rijeka, Croatia, 2023. [Google Scholar]
- Lerga, J.; Sucic, V.; Boashash, B. An efficient algorithm for instantaneous frequency estimation of nonstationary multicomponent signals in low SNR. EURASIP J. Adv. Signal Process. 2011, 2011, 725189. [Google Scholar] [CrossRef]
- Khan, N.A.; Mohammadi, M.; Djurović, I. A modified viterbi algorithm-based IF estimation algorithm for adaptive directional time-frequency distributions. Circuits Syst. Signal Process. 2019, 38, 2227–2244. [Google Scholar] [CrossRef]
- Khan, N.A.; Ali, S. Classification of EEG signals using adaptive time-frequency distributions. Metrol. Meas. Syst. 2016, 23, 251–260. [Google Scholar] [CrossRef]
- Sucic, V.; Saulig, N.; Boashash, B. Estimating the number of components of a multicomponent nonstationary signal using the short-term time-frequency Rényi entropy. EURASIP J. Adv. Signal Process. 2011, 2011, 125. [Google Scholar] [CrossRef]
- Sucic, V.; Saulig, N.; Boashash, B. Analysis of local time-frequency entropy features for nonstationary signal components time supports detection. Digit. Signal Process. 2014, 34, 56–66. [Google Scholar] [CrossRef]
- Saulig, N.; Orović, I.; Sucic, V. Optimization of quadratic time–frequency distributions using the local Rényi entropy information. Signal Process. 2016, 129, 17–24. [Google Scholar] [CrossRef]
- Jurdana, V.; Volaric, I.; Sucic, V. The local Rényi entropy based shrinkage algorithm for sparse TFD reconstruction. In Proceedings of the 2020 International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications (CoBCom), Graz, Austria, 7–9 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Jurdana, V.; Volaric, I.; Sucic, V. Sparse time-frequency distribution reconstruction based on the 2D Rényi entropy shrinkage algorithm. Digit. Signal Process. 2021, 118, 103225. [Google Scholar] [CrossRef]
- Jurdana, V.; Volaric, I.; Sucic, V. A sparse TFD reconstruction approach using the S-method and local entropies information. In Proceedings of the 2021 12th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 13–15 September 2021; pp. 4–9. [Google Scholar] [CrossRef]
- Jurdana, V.; Volaric, I.; Sucic, V. Application of the 2D local entropy information in sparse TFD reconstruction. In Proceedings of the 2022 International Conference on Broadband Communications for Next Generation Networks and Multimedia Applications (CoBCom), Graz, Austria, 12–14 July 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Jurdana, V.; Vrankic, M.; Lopac, N.; Jadav, G.M. Method for automatic estimation of instantaneous frequency and group delay in time-frequency distributions with application in EEG seizure signals analysis. Sensors 2023, 23, 4680. [Google Scholar] [CrossRef] [PubMed]
- Jurdana, V. Local Rényi entropy-based Gini index for measuring and optimizing sparse time-frequency distributions. Digit. Signal Process. 2024, 147, 104401. [Google Scholar] [CrossRef]
- Saulig, N.; Lerga, J.; Miličić, S.; Tomasović, Z. Block-adaptive Rényi entropy-based denoising for non-stationary signals. Sensors 2022, 22, 8251. [Google Scholar] [CrossRef]
- Saulig, N.; Lerga, J.; Milanović, Z.; Ioana, C. Extraction of useful information content from noisy signals based on structural affinity of clustered TFDs’ coefficients. IEEE Trans. Signal Process. 2019, 67, 3154–3167. [Google Scholar] [CrossRef]
- Bruni, V.; Tartaglione, M.; Vitulano, D. A Signal Complexity-Based Approach for AM–FM Signal Modes Counting. Mathematics 2020, 8, 2170. [Google Scholar] [CrossRef]
- Saulig, N.; Pustelnik, N.; Borgnat, P.; Flandrin, P.; Sucic, V. Instantaneous counting of components in nonstationary signals. In Proceedings of the 21st European Signal Processing Conference (EUSIPCO 2013), Marrakech, Morocco, 9–13 September 2013; pp. 1–5. [Google Scholar]
- Shang, L.; Zhang, Z.; Tang, F.; Cao, Q.; Pan, H.; Lin, Z. CNN-LSTM hybrid model to promote signal processing of ultrasonic guided lamb waves for damage detection in metallic pipelines. Sensors 2023, 23, 7059. [Google Scholar] [CrossRef]
- Zaman, W.; Ahmad, Z.; Siddique, M.F.; Ullah, N.; Kim, J.M. Centrifugal Pump Fault Diagnosis Based on a Novel SobelEdge Scalogram and CNN. Sensors 2023, 23, 5255. [Google Scholar] [CrossRef]
- Patil, S.S.; Pardeshi, S.S.; Patange, A.D. Health Monitoring of Milling Tool Inserts Using CNN Architectures Trained by Vibration Spectrograms. CMES-Comput. Model. Eng. Sci. 2023, 136, 177–199. [Google Scholar] [CrossRef]
- Jung, H.; Choi, S.; Lee, B. Rotor fault diagnosis method using CNN-Based transfer learning with 2D sound spectrogram analysis. Electronics 2023, 12, 480. [Google Scholar] [CrossRef]
- Khan, N.A.; Boashash, B. Multi-component instantaneous frequency estimation using locally adaptive directional time frequency distributions. Int. J. Adapt. Control. Signal Process. 2016, 30, 429–442. [Google Scholar] [CrossRef]
- Mohammadi, M.; Pouyan, A.A.; Khan, N.A.; Abolghasemi, V. Locally Optimized Adaptive Directional Time-Frequency Distributions. Circuits Syst. Signal Process. 2018, 37, 3154–3174. [Google Scholar] [CrossRef]
- Mohammadi, M.; Ali Khan, N.; Hassanpour, H.; Hussien Mohammed, A. Spike Detection Based on the Adaptive Time-Frequency Analysis. Circuits Syst. Signal Process. 2020, 39, 5656–5680. [Google Scholar] [CrossRef]
- Stanković, L. A measure of some time–frequency distributions concentration. Signal Process. 2001, 81, 621–631. [Google Scholar] [CrossRef]
- Baraniuk, R.G.; Flandrin, P.; Janssen, A.J.E.M.; Michel, O.J.J. Measuring time-frequency information content using the Rényi entropies. IEEE Trans. Inf. Theory 2001, 47, 1391–1409. [Google Scholar] [CrossRef]
- Aviyente, S.; Williams, W.J. Minimum entropy time-frequency distributions. IEEE Signal Process. Lett. 2005, 12, 37–40. [Google Scholar] [CrossRef]
- Principe, J. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Jurdana, V.; Lopac, N.; Vrankic, M. Sparse Time-Frequency Distribution Reconstruction Using the Adaptive Compressed Sensed Area Optimized with the Multi-Objective Approach. Sensors 2023, 23, 4148. [Google Scholar] [CrossRef] [PubMed]
- Taye, M.M. Theoretical understanding of convolutional neural network: Concepts, architectures, applications, future directions. Computation 2023, 11, 52. [Google Scholar] [CrossRef]
- Bartlett, P.L.; Montanari, A.; Rakhlin, A. Deep Learning: A Statistical Viewpoint; Cambridge University Press: Cambridge, UK, 2021; Volume 30, pp. 87–201. [Google Scholar]
- Boashash, B.; Khan, N.A.; Ben-Jabeur, T. Time–frequency features for pattern recognition using high-resolution TFDs: A tutorial review. Digit. Signal Process. 2015, 40, 1–30. [Google Scholar] [CrossRef]
- Ai, D.; Cheng, J. A deep learning approach for electromechanical impedance based concrete structural damage quantification using two-dimensional convolutional neural network. Mech. Syst. Signal Process. 2023, 183, 109634. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, K.P.; Kumar, S.; Vetrivendan, L. Image classification in python using Keras. In Proceedings of the Data Analytics and Management: ICDAM 2021; Springer: Berlin/Heidelberg, Germany, 2022; Volume 1, pp. 541–556. [Google Scholar]
- Singh, R.; Agarwal, B.B. An automated brain tumor classification in MR images using an enhanced convolutional neural network. Int. J. Inf. Technol. 2023, 15, 665–674. [Google Scholar] [CrossRef]
- Boashash, B.; Jawad, B.K.; Ouelha, S. Refining the ambiguity domain characteristics of non-stationary signals for improved time–frequency analysis: Test case of multidirectional and multicomponent piecewise LFM and HFM signals. Digit. Signal Process. 2018, 83, 367–382. [Google Scholar] [CrossRef]
- Lopac, N.; Hržić, F.; Vuksanović, I.P.; Lerga, J. Detection of non-stationary GW signals in high noise from Cohen’s class of time-frequency representations using deep learning. IEEE Access 2021, 10, 2408–2428. [Google Scholar] [CrossRef]
- Boashash, B.; Azemi, G.; Ali Khan, N. Principles of time–frequency feature extraction for change detection in non-stationary signals: Applications to newborn EEG abnormality detection. Pattern Recognit. 2015, 48, 616–627. [Google Scholar] [CrossRef]
- Khan, N.A.; Ali, S.; Choi, K. An instantaneous frequency and group delay based feature for classifying EEG signals. Biomed. Signal Process. Control. 2021, 67, 102562. [Google Scholar] [CrossRef]
- Khan, N.A.; Ali, S. A new feature for the classification of non-stationary signals based on the direction of signal energy in the time–frequency domain. Comput. Biol. Med. 2018, 100, 10–16. [Google Scholar] [CrossRef]
- Majumdar, K. Differential operator in seizure detection. Comput. Biol. Med. 2012, 42, 70–74. [Google Scholar] [CrossRef]
- Stevenson, N.; O’Toole, J.; Rankine, L.; Boylan, G.; Boashash, B. A nonparametric feature for neonatal EEG seizure detection based on a representation of pseudo-periodicity. Med. Eng. Phys. 2012, 34, 437–446. [Google Scholar] [CrossRef]
- Rankine, L.; Mesbah, M.; Boashash, B. IF estimation for multicomponent signals using image processing techniques in the time–frequency domain. Signal Process. 2007, 87, 1234–1250. [Google Scholar] [CrossRef]
- Volaric, I.; Sucic, V.; Stankovic, S. A Data Driven Compressive Sensing Approach for Time-Frequency Signal Enhancement. Signal Process. 2017, 141, 229–239. [Google Scholar] [CrossRef]



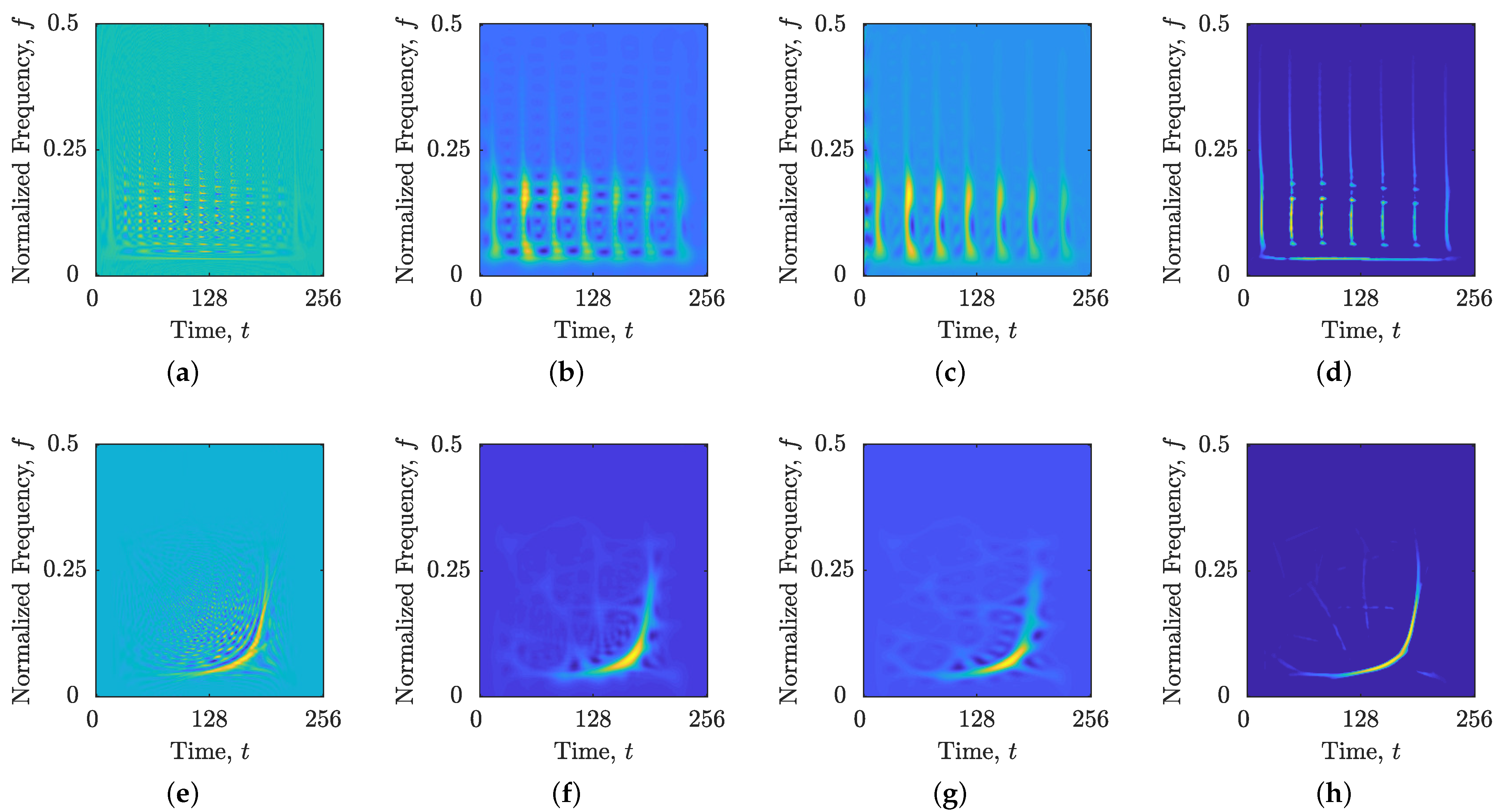
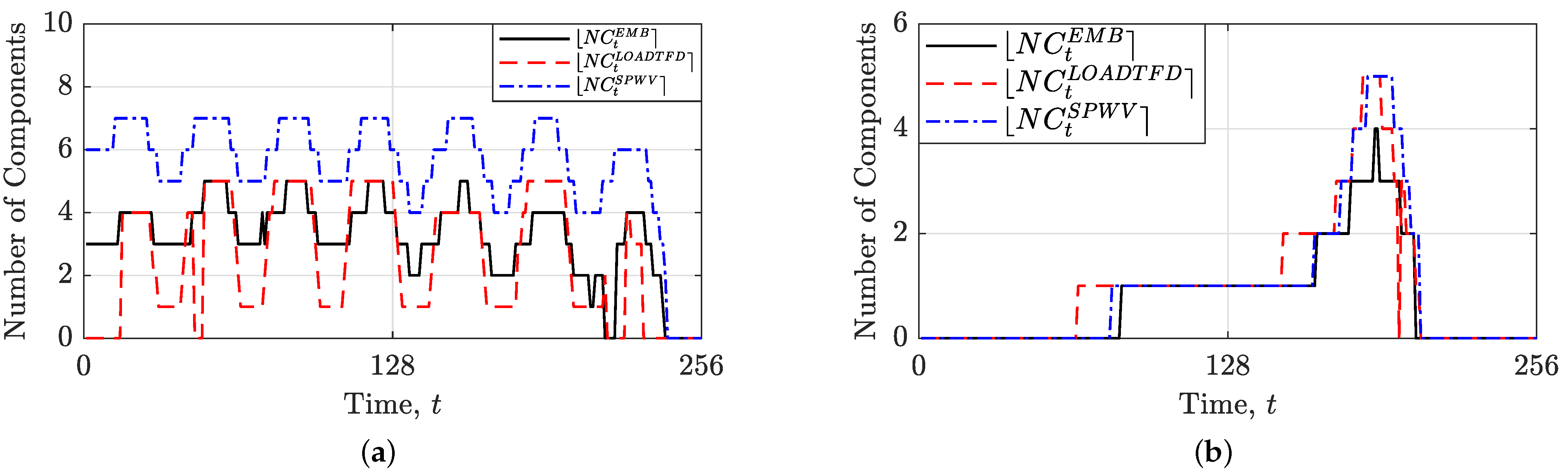
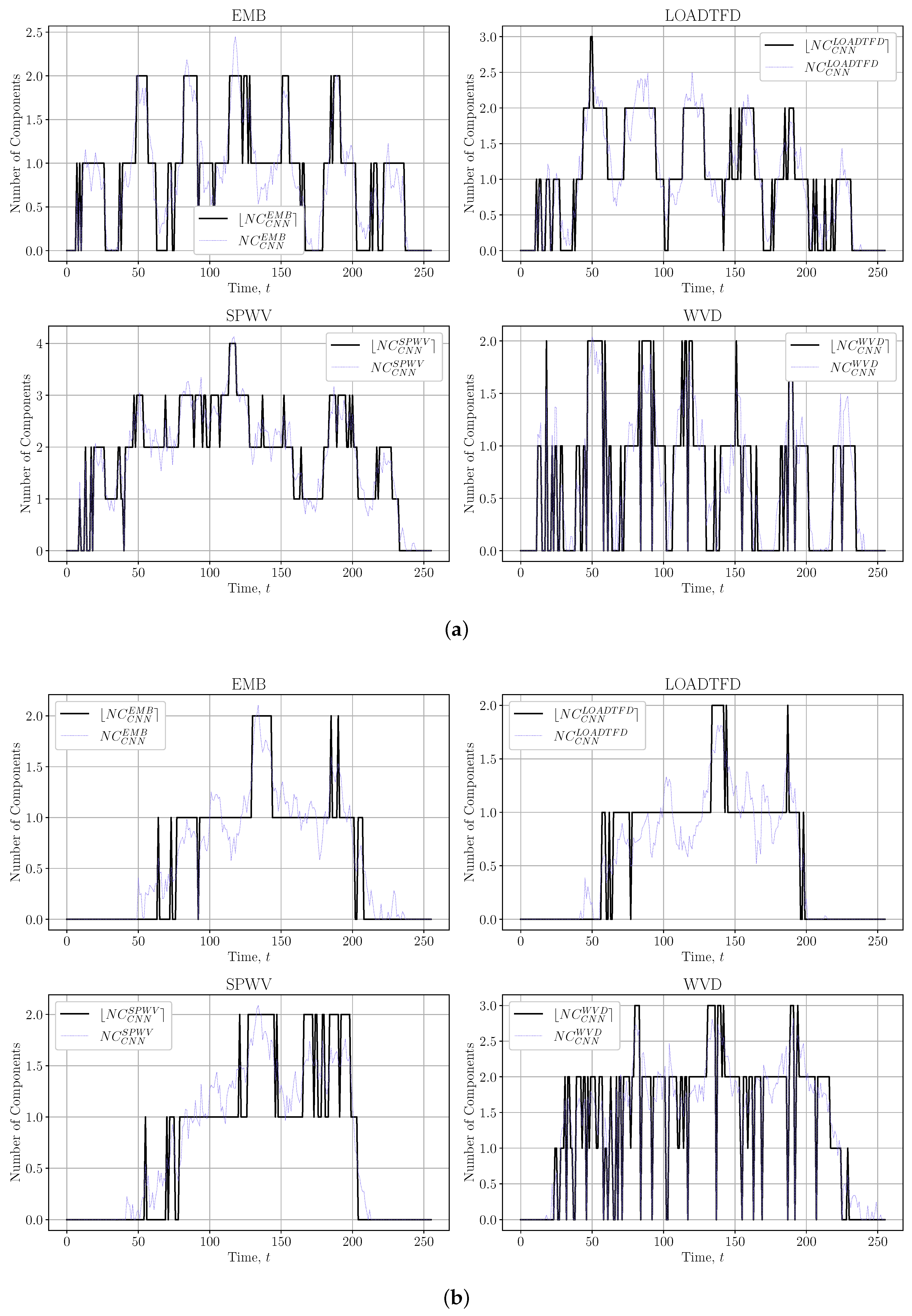
| LRE Version | Advantages | Disadvantages |
|---|---|---|
| Original (STRE) [15,16] | 1. Used in many applications 2. Robust against noise | 1. Limited by overlapping components 2. Struggles with low amplitudes 3. Constant reference signal unsuitable for certain signal components |
| Iterative LRE [27] | Detects components with lower amplitudes | 1. Sensitive to noise 2. Less effective for close or intersecting components 3. Emphasizes unresolved interference terms |
| NBRE [18,19] | 1. Provides number of local components in frequency slices 2. More suitable than STRE for certain signal components | Same limitations as STRE |
| Signal | Preprocessing Steps |
|---|---|
| gravitational, | initially consisted of 3441 samples downsampled by a factor of 14, samples duration of s, frequency range of Hz |
| EEG, | prefiltered using a 0.5 to 70 Hz analog bandpass filter downsampled to 256 Hz and further to 32 Hz, samples enhanced spike signatures using a differentiator filter [49,50,51,52] |
| Model | EMB | SPVW | WVD | LOADTFD | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.23651 | 0.00361 | 0.27869 | 0.02202 | 0.29417 | 0.02963 | 0.28645 | 0.02588 |
| 2 | 0.17033 | 0.00215 | 0.18934 | 0.00192 | 0.23495 | 0.00293 | 0.18671 | 0.00526 |
| 3 | 0.22810 | 0.00559 | 0.22227 | 0.00522 | 0.26483 | 0.02865 | 0.22360 | 0.00600 |
| Method | LRE | CNN | |||||
|---|---|---|---|---|---|---|---|
| EMB | SPWV | LOADTFD | WVD | EMB | SPWV | LOADTFD | |
| 6.0395 | 15.3992 | 4.2530 | 0.2332 | 0.1462 | 0.2569 | 0.1186 | |
| 1.5880 | 2.4549 | 1.2017 | 0.1674 | 0.1502 | 0.2532 | 0.1288 | |
| 5.0 | 8.0 | 5.0 | 2.0 | 2.0 | 2.0 | 1.0 | |
| 2.9051 | 6.0316 | 3.2292 | 0.2964 | 0.0870 | 0.0830 | 0.0909 | |
| 1.3433 | 1.8455 | 1.4592 | 0.2060 | 0.0730 | 0.0901 | 0.0987 | |
| 3.0 | 5.0 | 3.0 | 2.0 | 1.0 | 1.0 | 1.0 | |
| 0.4822 | 0.7628 | 1.7747 | 0.2055 | 0.0277 | 0.0435 | 0.0356 | |
| 0.4464 | 0.6137 | 0.8927 | 0.1631 | 0.0300 | 0.0472 | 0.0343 | |
| 2.0 | 2.0 | 3.0 | 2.0 | 1.0 | 1.0 | 1.0 | |
| 0.3202 | 0.6917 | 0.6522 | 0.3834 | 0.1423 | 0.1265 | 0.1818 | |
| 0.3047 | 0.7082 | 0.6052 | 0.2232 | 0.1502 | 0.1373 | 0.1545 | |
| 1.0 | 1.0 | 2.0 | 3.0 | 1.0 | 1.0 | 1.0 | |
| Method | LRE | CNN | |||||
|---|---|---|---|---|---|---|---|
| EMB | SPWV | LOADTFD | WVD | EMB | SPWV | LOADTFD | |
| 0.0087 | 0.0574 | 0.0804 | 11.5030 | 3.5436 | 5.1649 | 2.8838 | |
| 0.0165 | 0.0251 | 0.3095 | 12.6532 | 4.3124 | 3.6477 | 3.3645 | |
| 0.0406 | 0.0815 | 0.1659 | 21.1449 | 6.9535 | 5.2687 | 5.3525 | |
| 0.0263 | 0.0376 | 0.1002 | 27.4028 | 8.2332 | 8.3377 | 7.0315 | |
| SNR | LRE | CNN | |||||
|---|---|---|---|---|---|---|---|
| EMB | SPWV | LOADTFD | WVD | EMB | SPWV | LOADTFD | |
| 0 dB | 7.0717 | 8.9815 | 1.2492 | −7.3362 | −10.1252 | −2.5303 | −3.4793 |
| 3 dB | −0.0602 | 1.2639 | −2.5805 | −9.1106 | −13.2208 | −4.3948 | −7.9652 |
| 6 dB | −4.3212 | −2.3822 | −4.7755 | −10.8443 | −15.5875 | −8.0980 | −11.3878 |
| 9 dB | −7.4027 | −4.6578 | −6.0891 | −13.0621 | −16.8464 | −11.1452 | −13.6729 |
| 0 dB | 6.1719 | 7.1244 | 2.9371 | −6.8008 | −2.2093 | −2.8176 | −0.6299 |
| 3 dB | −2.3075 | −0.8763 | −1.9152 | −7.9310 | −6.2736 | −6.2562 | −4.5125 |
| 6 dB | −8.2379 | −5.0221 | −5.4218 | −9.2890 | −9.7337 | −8.9689 | −7.4425 |
| 9 dB | −10.3168 | −7.5535 | −7.7290 | −10.4291 | −12.3286 | −10.7149 | −11.0231 |
| 0 dB | 3.5811 | 4.5762 | 0.1177 | −6.9751 | −4.1474 | −3.8873 | −3.8927 |
| 3 dB | −2.8621 | −0.9289 | −2.3439 | −9.2096 | −7.2424 | −6.3909 | −7.0320 |
| 6 dB | −6.5891 | −4.9981 | −5.0144 | −11.2254 | −10.2509 | −8.8513 | −9.9522 |
| 9 dB | −8.6492 | −7.6334 | −7.6453 | −13.8818 | −13.1040 | −10.5345 | −12.6545 |
| 0 dB | 2.1689 | 2.3456 | −1.4015 | −5.0527 | −3.3821 | −2.8123 | −3.2841 |
| 3 dB | −3.9897 | −3.4443 | −5.2725 | −7.1899 | −4.7324 | −4.1367 | −5.1539 |
| 6 dB | −6.9598 | −5.1053 | −7.3501 | −10.0241 | −7.5194 | −6.8762 | −8.2932 |
| 9 dB | −9.7742 | −6.5977 | −9.5550 | −12.8951 | −9.8615 | −9.2832 | −10.7190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jurdana, V.; Baressi Šegota, S. Convolutional Neural Networks for Local Component Number Estimation from Time–Frequency Distributions of Multicomponent Nonstationary Signals. Mathematics 2024, 12, 1661. https://doi.org/10.3390/math12111661
Jurdana V, Baressi Šegota S. Convolutional Neural Networks for Local Component Number Estimation from Time–Frequency Distributions of Multicomponent Nonstationary Signals. Mathematics. 2024; 12(11):1661. https://doi.org/10.3390/math12111661
Chicago/Turabian StyleJurdana, Vedran, and Sandi Baressi Šegota. 2024. "Convolutional Neural Networks for Local Component Number Estimation from Time–Frequency Distributions of Multicomponent Nonstationary Signals" Mathematics 12, no. 11: 1661. https://doi.org/10.3390/math12111661
APA StyleJurdana, V., & Baressi Šegota, S. (2024). Convolutional Neural Networks for Local Component Number Estimation from Time–Frequency Distributions of Multicomponent Nonstationary Signals. Mathematics, 12(11), 1661. https://doi.org/10.3390/math12111661







