A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via
Abstract
1. Introduction, Definitions, and Motivation
2. Definition and Examples
- Analytically (see [30]): The function defined byis univalent due to being the extremal functions of the class of univalent functions. To show , we proceed as follows.By putting in (9), we have:On the other hand, the Maclaurin series expansion of on the LHS of (11) is as follows:This means that andNow, we check if satisfies the second part of the definition.which impliesNow, substitute (16) into (15), which givesSubstituting and into (16), we havefor the left-hand side of (10). The inverse of follows the same solving process as the L.H.S of (10), since (13) and (14) are equal. That is,Comparing (18) and (19), we deduce that both sides are equal. We conclude that they also satisfy both equations in Definition 5.Now, we can conclude that the extremal function given in (12) shows that our defined class of analytic and bi-univalent function is not empty.
- Geometrically: (see [31]) Let denote the functions given by:To establish the univalence of the function , we commence by assuming that . Our objective is to demonstrate that this assumption implies . We initiate the proof by considering the given condition:Now, let us correct the second equation:This simplifies to:So, indeed, we have shown that , thus proving that is univalent; moreover, with its inverse:By utilizing the notations provided in Equations (9) and (10), we can easily demonstrate through a straightforward calculation thatFurthermore, for every , it follows that , thereby implying that . Hence, we can conclude that , and there exist certain values for the parameters χ and for the identity function such that
- Letting , the expression is reduced to , representing the bi-univalent class of functions , provided the following subordination conditions hold:
- If , then the class is reduced to , representing the bi-univalent class of functions , provided the following subordination conditions hold:
- Let and . Then, the class is reduced to , representing the bi-univalent class of functions , provided the following subordination conditions hold:
3. The Bounds of the Coefficients within the Class
4. The Fekete–Szegö Functional
5. Corollaries
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, S.S. Differential inequalities and Carathéodory functions. Bull. Am. Math. Soc. 1975, 81, 79–81. [Google Scholar] [CrossRef]
- Duren, P.L. Univalent Functions; Grundlehren der Mathematischen Wissenschaften, Band 259; Springer: New York, NY, USA; Berlin/Heidelberg, Germany; Tokyo, Japan, 1983. [Google Scholar]
- Ma, W.; Minda, D. A unified treatment of some special classes of univalent functions. In Proceedings of the Complex Analysis, Tianjin, China, 16–20 March 1992; pp. 157–169. [Google Scholar]
- Sokół, J.; Stankiewicz, J. Radius of convexity of some subclasses of strongly starlike functions. Zeszyty Nauk. Politech. Rzeszowskiej Mat. 1996, 19, 101–105. [Google Scholar]
- Raina, R.K.; Sokól, R.K. On Coefficient estimates for a certain class of starlike functions. Hacettepe J. Math. Statist. 2015, 44, 1427–1433. [Google Scholar] [CrossRef]
- Priya, M.H.; Sharma, R.B. On a class of bounded turning functions subordinate to a leaf-like domain. J. Phys. Conf. Ser. 2018, 1000, 012056. [Google Scholar] [CrossRef]
- Rath, B.; Kumar, K.S.; Krishna, D.V.; Lecko, A. The sharp bound of the third Hankel determinant for starlike functions of order 1/2. Complex Anal. Oper. Theory 2022, 16, 1–8. [Google Scholar] [CrossRef]
- Mahmood, S.; Srivastava, H.M.; Khan, N.; Ahmad, Q.Z.; Khan, B.; Ali, I. Upper bound of the third Hankel determinant for a subclass of q-starlike functions. Symmetry 2019, 11, 347. [Google Scholar] [CrossRef]
- Ullah, K.; Srivastava, H.M.; Rafiq, A.; Arif, M.; Arjika, S. A study of sharp coefficient bounds for a new subfamily of starlike functions. J. Inequal. Appl. 2021, 2021, 194. [Google Scholar] [CrossRef]
- Shi, L.; Shutaywi, M.; Alreshidi, N.; Arif, M.; Ghufran, S.M. The sharp bounds of the third-order Hankel determinant for certain analytic functions associated with an eight-shaped domain. Fractal Fract. 2022, 6, 223. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, 2nd ed.; Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, MA, USA, 2004; Volume 96. [Google Scholar]
- Alsoboh, A.; Amourah, A.; Sakar, F.M.; Breaz, D. New Subfamily of Bi-starlike and Bi-convex Functions Defined by the q-Janowski Function. Preprints 2023, 2023061002. [Google Scholar] [CrossRef]
- Ismail, M.E.; Merkes, E.; Styer, D. A generalization of starlike functions. Complex Var. Theory Appl. 1990, 14, 77–84. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Khan, B.; Khan, N.; Ahmad, Q.Z.; Tahir, M. A generalized conic domain and its applications to certain subclasses of analytic functions. Rocky Mt. J. Math. 2019, 49, 2325–2346. [Google Scholar] [CrossRef]
- Srivastava, H.M. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Al-Salam, W.A. Some fractional q-integrals and q-derivatives. Proc. Edinburgh Math. Soc. 1966, 15, 135–140. [Google Scholar] [CrossRef]
- Agarwal, R.P. Certain fractional q-integrals and q-derivatives. Proc. Cambridge Philos. 1969, 66, 365–370. [Google Scholar] [CrossRef]
- Uçar, H.E.Ö. Coefficient inequality for q-starlike functions. App. Math. Comput. 2016, 276, 122–126. [Google Scholar] [CrossRef]
- Aldweby, H.; Darus, M. Some subordination results on q-analogue of Ruscheweyh differential operator. Abstr. Appl. Anal. 2014, 2014, 958563. [Google Scholar] [CrossRef]
- Aldweby, H.; Darus, M. On a subclass of bi-univalent functions associated with the q-derivative operator. J. Math. Comput. Sci. 2019, 19, 58–64. [Google Scholar] [CrossRef]
- Ahuja, O.; Bohra, N.; Cetinkaya, A.; Kumar, S. Univalent functions associated with the symmetric points and cardioid-shaped domain involving (p,q)-calculus. Kyungpook Math. J. 2021, 61, 75–98. [Google Scholar]
- Alb Lupaş, A.; Oros, G.I. Sandwich-type results regarding Riemann-Liouville fractional integral of q-hypergeometric function. Demonstr. Math. 2023, 56, 20220186. [Google Scholar] [CrossRef]
- Ali, E.E.; Oros, G.I.; Albalahi, A.M. Differential subordination and superordination studies involving symmetric functions using a q-analogue multiplier operator. AIMS Math. 2023, 8, 27924–27946. [Google Scholar] [CrossRef]
- Andrei, L.; Căuș, V.A. Subordinations Results on a q-Derivative Differential Operator. Mathematics 2024, 12, 208. [Google Scholar] [CrossRef]
- Khan, M.F.; AbaOud, M. New Applications of Fractional q-Calculus Operator for a New Subclass of q-Starlike Functions Related with the Cardioid Domain. Fractal Fract. 2024, 8, 71. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Darus, M.; Rudder, C.A. Studying the Harmonic Functions Associated with Quantum Calculus. Mathematics 2023, 11, 2220. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Darus, M.; Rudder, C.A. Investigating New Subclasses of Bi-Univalent Functions Associated with q-Pascal Distribution Series Using the Subordination Principle. Symmetry 2023, 15, 1109. [Google Scholar] [CrossRef]
- Alsoboh, A.; Amourah, A.; Sakar, F.M.; Ogilat, O.; Gharib, G.M.; Zomot, N. Coefficient Estimation Utilizing the Faber Polynomial for a Subfamily of Bi-Univalent Functions. Axioms 2023, 12, 512. [Google Scholar] [CrossRef]
- Khan, B.; Srivastava, H.M.; Khan, N.; Darus, M.; Tahir, M.; Ahmad, Q.Z. Coefficient Estimates for a Subclass of Analytic Functions Associated with a Certain Leaf-Like Domain. Mathematics 2020, 8, 1334. [Google Scholar] [CrossRef]
- Shaba, T.G.; Araci, S.; Ro, J.-S.; Tchier, F.; Adebesin, B.O.; Zainab, S. Coefficient Inequalities of q-Bi-Univalent Mappings Associated with q-Hyperbolic Tangent Function. Fractal Fract. 2023, 7, 675. [Google Scholar] [CrossRef]
- Analouei Adegani, E.; Jafari, M.; Bulboacă, T.; Zaprawa, P. Coefficient Bounds for Some Families of Bi-Univalent Functions with Missing Coefficients. Axioms 2023, 12, 1071. [Google Scholar] [CrossRef]
- Fekete, M.; Szegö, G. Eine Bemerkung über ungerade schlichte Funktionen. J. Lond. Math. Soc. 1933, 1, 85–89. [Google Scholar] [CrossRef]
- Zaprawa, P. On the Fekete-Szegö problem for classes of bi-univalent functions. Bull. Belg. Math. Soc. Simon Stevin 2014, 21, 169–178. [Google Scholar] [CrossRef]

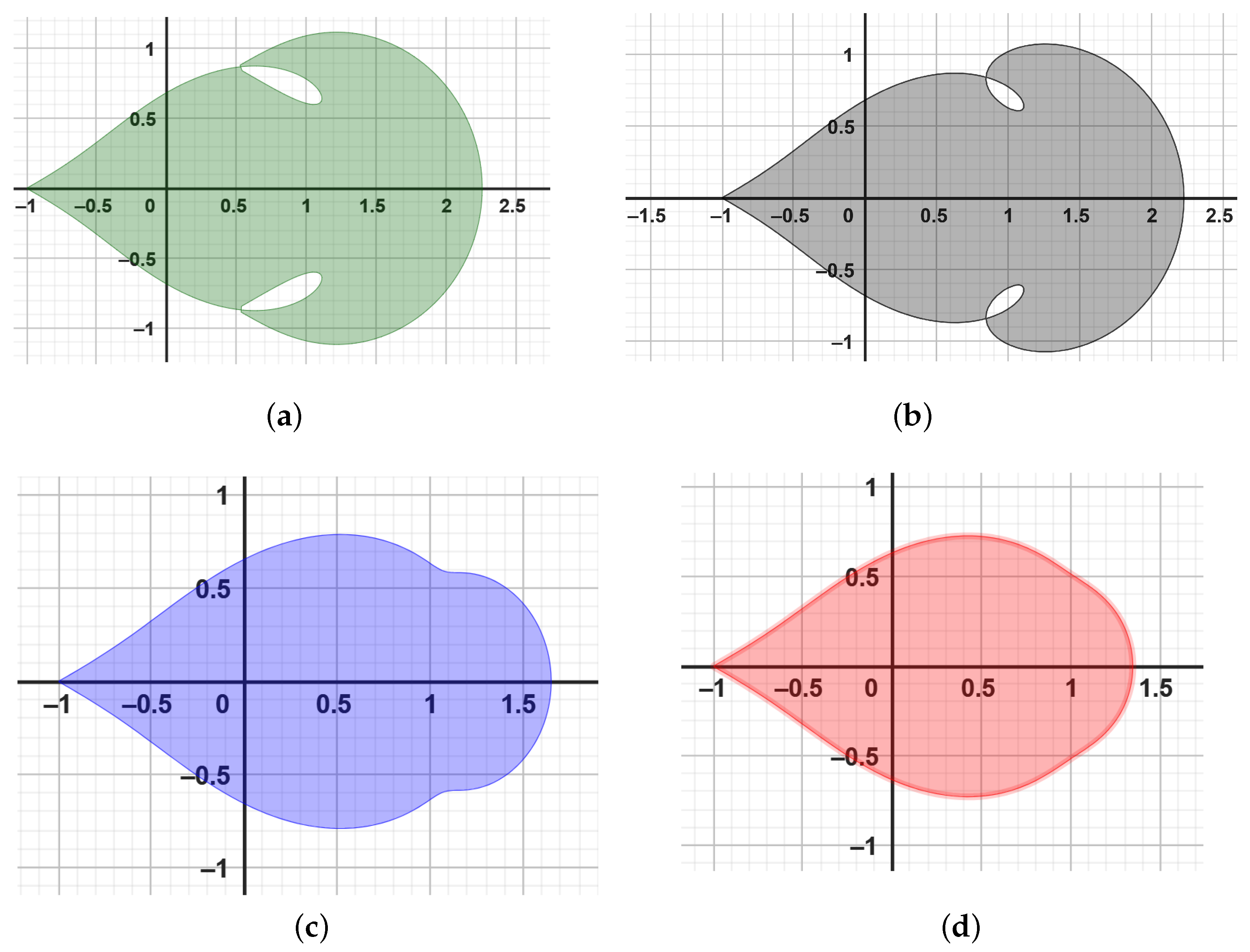

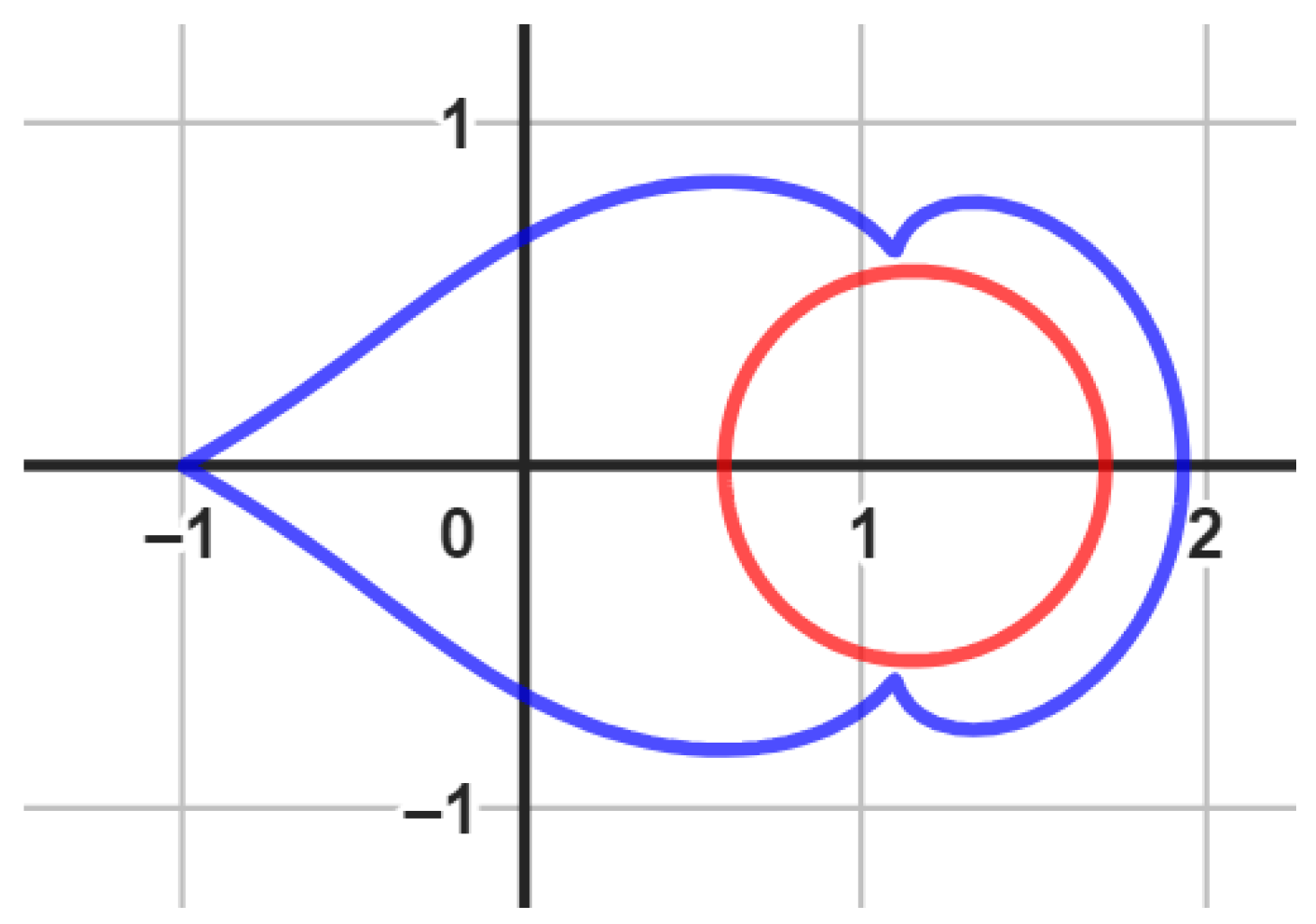
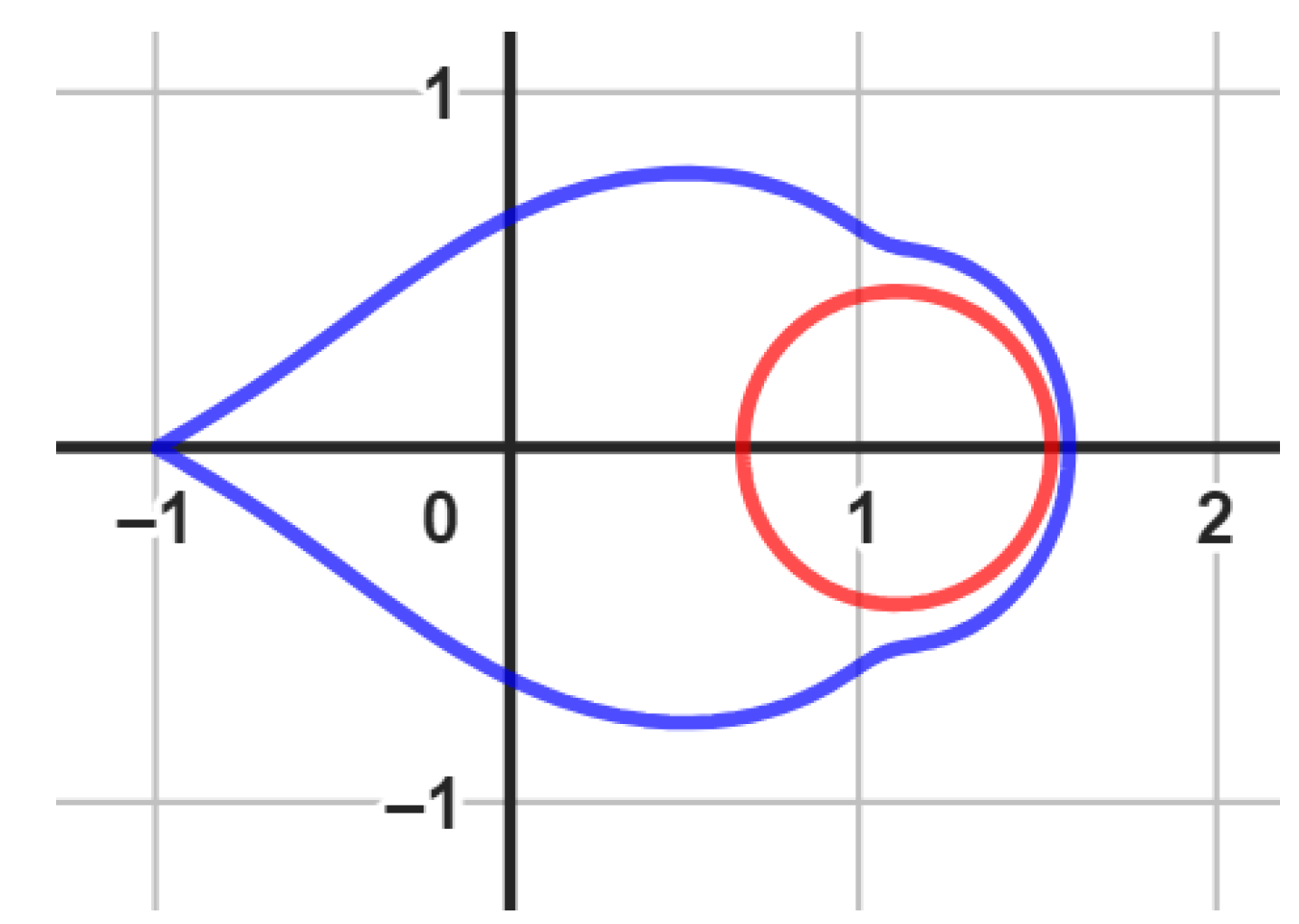
| The Function | The Corresponding Inverse |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsoboh, A.; Oros, G.I.
A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via
Alsoboh A, Oros GI.
A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via
Alsoboh, Abdullah, and Georgia Irina Oros.
2024. "A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via
Alsoboh, A., & Oros, G. I.
(2024). A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via







