Abstract
Modern challenges such as the liberalization of the railway sector and growing demands for sustainability, high-quality services, and user satisfaction set new standards in railway operations. In this context, railway infrastructure managers (RIMs) play a crucial role in ensuring innovative approaches that will strengthen the position of railways in the market by enhancing efficiency and competitiveness. Evaluating their performance is essential for assessing the achieved objectives, and it is conducted through a wide range of key performance indicators (KPIs), which encompass various dimensions of operations. Monitoring and analyzing KPIs are crucial for improving service quality, achieving sustainability, and establishing a foundation for research and development of new strategies in the railway sector. This paper provides a detailed overview and evaluation of KPIs for RIMs. This paper creates a framework for RIM evaluation using various scientific methods, from identifying KPIs to applying complex analysis methods. A novel hybrid model, which integrates the fuzzy Delphi method for aggregating expert opinions on the KPIs’ importance, the extended fuzzy analytic hierarchy process (AHP) method for determining the relative weights of these KPIs, and the ADAM method for ranking RIMs, has been developed in this paper. This approach enables a detailed analysis and comparison of RIMs and their performances, providing the basis for informed decision-making and the development of new strategies within the railway sector. The analysis results provide insight into the current state of railway infrastructure and encourage further efforts to improve the railway sector by identifying key areas for enhancement. The main contributions of the research include a detailed overview of KPIs for RIMs and the development of a hybrid multi-criteria decision making (MCDM) model. The hybrid model represents a significant step in RIM performance analysis, providing a basis for future research in this area. The model is universal and, as such, represents a valuable contribution to MCDM theory.
Keywords:
key performance indicators; evaluation; railway infrastructure managers; MCDM model; fuzzy Delphi; extended fuzzy AHP; ADAM method MSC:
03B52; 90B50
1. Introduction
In the modern context of sustainability and environmental responsibility, railways play a crucial role in promoting environmentally friendly forms of transportation. Despite its significance, the railway sector faces challenges of decreasing market share regarding the other modes of transportation. Initiatives for liberalization and market competitiveness in the railway sector began with implementing Directive 91/440 [1]. Since the 1990s, the revitalizing railways has become a key goal of EU transport policy. As stated in the European Commission’s White Paper of 2001, rail transport is a strategic sector, upon which the success of efforts to shift the balance between modes of transportation will depend [2]. The White Paper published in 2011 set a target whereby 30% of road freight over 300 km should shift to other modes, such as rail or waterborne, by 2030, and more than 50% should transition to green freight corridors by 2050 [3]. To enhance the competitiveness of the railway sector, improving performance is essential, with a particular focus on the key stakeholders—railway infrastructure managers (RIMs). In this context, RIMs emerge as pivotal figures in attaining sustainability objectives and bolstering competitiveness. Numerous countries have chosen to restructure the railway sector and achieve greater efficiency and service quality by delineating the responsibilities of infrastructure managers and operators. This transformation aims to establish a more transparent division of duties, fostering increased transparency and stimulating market competition [4]. Therefore, analyzing the operational efficiency of RIMs and operators becomes necessary.
Effective management of railway infrastructure is crucial to ensure safe and reliable traffic, optimal capacity utilization, reduced delays, and improved passenger experience. In this context, analyzing RIM performance becomes imperative to understanding their effectiveness in achieving set goals. Assessing RIMs’ performance requires considering the diversity of managers’ operations in different countries, which results from factors such as the size of the railway network, restructuring models, and the number of operators. The European Commission launched the Platform for European Railway Infrastructure Managers (PRIME) in 2013 to create a standardized platform for performance monitoring. Through PRIME, a catalog of key performance indicators (KPIs) has been developed to systematize KPIs to cover all dimensions of infrastructure managers’ operations: the contextual framework, safety and environment, performance, delivery, finance, and growth [5]. This study focuses on selecting the most important KPIs of RIMs to identify best practices and analyze results to gain a deeper understanding of RIM efficiency. A novel hybrid multi-criteria decision-making (MCDM) model has been developed in this study. The first part of the model determines the relative importance and weights of RIMs’ KPIs using the fuzzy Delphi method and the extended fuzzy analytic hierarchy process (AHP) method. The second part employs the axial distance-based aggregated measurement (ADAM) method for ranking RIMs. Expert opinions from the field of railway infrastructure management played a crucial role in determining the relative importance and weight of KPIs. This approach aims to enhance the understanding of RIM performances, providing a concrete model for selecting and weighting KPIs, and analyzing RIM performances. The ultimate goal of the research is to identify the RIM with the highest potential, providing a foundation for further improvement and development strategies in the sector. This research contributes to the growing area of performance monitoring in the railway sector and provides a basis for further development in this important domain.
The rest of the paper is structured as follows. Section 2 provides an overview of the relevant literature, examining issues of efficiency and performance assessment in the railway sector, including the role of RIMs. A literature review of the methods used is also provided, contributing to a deeper understanding of the topics addressed in the research on efficiency in the railway sector. Section 3 presents an overview of the dimensions of KPIs to be covered in the study. Section 4 describes the hybrid model developed for evaluating RIMs. Section 5 presents the results of applying the developed model to rank nine selected European RIMs according to defined KPIs. It also provides sensitivity analysis and validation of the obtained results and developed methodology. Section 6 discusses the findings, explores their practical and theoretical implications, and highlights their limitations. The final section, Section 7, concludes the paper and suggests directions for future research.
2. The Literature Review
For the railway industry, which is a capital-intensive sector, business performance analysis is vital for prosperity. Assuming that high levels of economic efficiency and productivity and high productivity growth are desirable goals, it is important to define and measure business performance in ways that adhere to economic theory and thus provide useful information to managers and policymakers. The benchmarking of railway networks and companies has been prompted by the European policy of deregulating transport markets, opening national railway networks and markets to new participants, and separating infrastructure and railway transport [6]. When developing strategies to enhance performance in the railway sector, a crucial step is adopting an efficiency assessment methodology. This involves selecting appropriate measurement and evaluation methods to identify areas requiring improvement. Accordingly, various efficiency assessment methods have been applied in the railway sector. The following is a literature review on efficiency and performance in the railway sector, with a particular emphasis on the methods used and the role of RIMs, contributing to a better understanding of approaches to evaluating efficiency in this sector.
2.1. Efficiency and Performance Measurement in the Railway Sector
Over the past two decades, performance measurement and analysis in the railway sector have gained prominence. The primary aim is to combine diverse methods and techniques to define performance, establish priorities, and devise future actions for enhancing performance to meet strategic and operational objectives. In the study [7], the authors analyzed the distribution of existing studies of the railway system efficiency analysis. They summarized that out of 100 reviewed studies, 70 studies analyzed the efficiency of railway operators at the company level, 24 studies focused on large-scale comparisons at the national or regional level, 5 studies examined the efficiency of urban systems or transit agencies, and 1 study concentrated on local business units. Various parametric and non-parametric approaches have been utilized in scientific papers for measuring and comparing the efficiency of railway companies. The most commonly used methods in the analysis of railway system efficiency and effectiveness in recent years include the index number approach [8], the data envelopment analysis (DEA) method [9], bootstrap–DEA [10], network data envelopment analysis (NDEA) [11], stochastic frontier analysis (SFA) [12], the efficiency analysis with target setting (EATWOS) technique [13], and benchmarking analysis [14]. Table 1 provides an overview of selected recent studies investigating efficiency and performance in the railway sector. They are presented according to the methodologies and indicators used. Table 1 offers a systematic insight into diverse approaches and research focusing on efficiency in the railway sector. These studies encompass various scientific and analytical approaches including statistical analysis, multi-criteria methods, cost–benefit analysis, and modeling. Additionally, such a review of works aids in identifying the diversity of research in the field of railway sector efficiency, providing a foundation for understanding the methodologies and key indicators that have been the subject of study in the relevant literature.

Table 1.
Literature review on efficiency in the railway sector.
Although the existing literature has provided diverse insights into the efficiency of the railway sector, there is a clear need for specific research focusing on the performance of RIMs. Previous studies have primarily focused on railway operators, so this gap in research presents both a challenge and an opportunity for assessing the performance of RIMs.
2.2. Efficiency and Performance Measurement of RIMs
Infrastructure managers play a crucial role in enhancing performance in the railway industry by providing access to open networks and striving to strengthen collaboration and information exchange to facilitate safe, sustainable, and highly efficient rail transport. Emphasizing collaboration and information exchange is crucial for improving the performance and business development of RIMs. A comprehensive performance analysis is necessary to identify areas for improvement and optimize operational efficiency, safety, and sustainability. The Platform of Rail Infrastructure Managers in Europe (PRIME), created in 2013, provides a framework for intensified collaboration among RIMs and facilitates the exchange of information and best practices for improving rail transport [32]. The main goal of PRIME is to improve the railway infrastructure sector by promoting the exchange of best practices among infrastructure managers. In March 2014, a comprehensive catalog of KPIs for RIMs was adopted [5]. Prokić and Bugarinović [33] proposed defining unified indicators for the operation and network performance of RIMs, and the structure of the KPI catalog. They presented the network operation and business indicators of a RIM from the Slovak Republic, along with an assessment of the potential monitoring and application of similar network operation and business indicators of a RIM in the Republic of Serbia. The efficiency evaluation, productivity, and effectiveness assessment of railway networks and operators in the paper [14] encompassed both technical and economic indicators. Utilizing the DEA method, they analyzed empirical technical and commercial data to ascertain the network’s productivity and the business efficiency of 11 European infrastructure managers and companies operating in passenger and freight transport in 2009. Furthermore, in the paper [34], researchers investigated the feasibility of evaluating and ranking different infrastructure manager strategies using a combined AHP/DEA method. The outcomes derived from this research can facilitate evaluating the concurrent efficient utilization of infrastructure capacities and the financial efficiency of infrastructure managers.
Analyzing the literature on RIM performance, a lack of a comprehensive approach to encompassing KPIs, which would include the contextual framework, safety and the environment, performance, delivery, finance, and growth, has been noticed. Previous research has failed to adequately address this issue, resulting in a gap in the holistic understanding of RIM performance. This gap in the literature presents both a challenge and an opportunity to create a comprehensive framework for assessing the performance of RIMs.
2.3. An Overview of the Methods in the Proposed MCDM Model
The issue discussed in this research could potentially be resolved through different methods. These may involve using simulations of diverse scenarios (e.g., [35]), optimization models offering mathematical frameworks to systematically identify the best possible solutions given specific constraints and objectives (e.g., [36]), metaheuristic algorithms to effectively explore solution spaces (e.g., [37]), and artificial intelligence methods like neural networks to analyze intricate datasets (e.g., [38]). Each method presents distinct advantages, from offering insights into potential results to utilizing large data sets for predictive analysis. However, MCDM techniques serve as a thorough approach to simultaneously consider various factors, guaranteeing a comprehensive assessment of infrastructure manager performance. Moreover, combining various MCDM methods is useful because it allows for a more comprehensive analysis by leveraging the strengths of different models to mitigate individual biases and uncertainties, thereby enhancing the robustness and reliability of the decision-making process [39].
Therefore, a hybrid model for evaluating RIMs has been developed in this study. This model utilizes MCDM methods and fuzzy logic to comprehensively analyze the managers’ performances. The proposed hybrid model integrates the fuzzy Delphi method for assessing and selecting KPIs, the extended fuzzy AHP method for determining the weighting of KPIs, and the ADAM method for ranking RIMs. The methods combination within the hybrid model enables a comprehensive evaluation of performance, the ranking of managers, and the identification of the best RIM according to defined KPIs.
The fuzzy Delphi method combines fuzzy theory with the traditional Delphi method to overcome uncertainty in expert evaluations, enable consensus among experts, and reduce research time [40]. The classical Delphi method has its drawbacks, including imperfect interpretation of expert opinions due to a lack of consideration of uncertainty, a lack of clear rules for achieving desired results, the loss of interest and data on behalf of experts due to the lengthy process that may result in re-surveys, and the increased research costs [41]. Dalkey and Helmer [42], developed the classical Delphi method, while Ishikawa et al. [43] originally introduced the fuzzy Delphi method, which is widely utilized for gathering expert opinions through questionnaires and surveys. This method converts qualitative information into robust and reliable statistical conclusions. In contrast to some statistical methods, the Delphi method relies on the dynamics of expert groups. The typical sample size for this method ranges from 5 to 20 experts [44], with criteria for expert selection including education, expertise, experience, and willingness to participate in the research. Determining the number of experts for applying the fuzzy Delphi method can be guided by previous studies, guidelines, or recommendations, and it can vary according to the context and specific project requirements. Yussof et al. [45], suggest that the number of experts for the Delphi method should range between 10 and 15 individuals, provided that the experts can reach a consensus. Gene et al. recommend 5 to 20 experts [44], with criteria for expert selection including education, expertise, experience, and willingness to participate in the research. Okol and Pawlowski recommend involving 10–18 experts in the study [46]. Authors in papers [47,48,49] use the fuzzy Delphi method with a range of 10–15 experts.
The basic process of the fuzzy Delphi method consists of three main phases: preparation of input data, data analysis, and final decision-making [50]. Preparation of input data involves gathering information, creating questionnaires, and selecting experts to participate. Data analysis comprises three steps: transforming the Likert scale into fuzzy levels, determining threshold values and the percentage of expert consensus, and the defuzzification process. The decision is ultimately made based on the results of the data analysis phase. In this phase, the following prerequisites are required: threshold values (d) of 0.2 or less, an expert consensus percentage of 75% or more, and a defuzzification value of 0.5 or more. The fuzzy Delphi method has been widely applied in previous research addressing various topics. Its scope of application extends across different contexts, and recent examples in the past few years include its use in many fields. This methodology has proven successful in addressing diverse issues, including identifying significant barriers in sustainable solid waste management [51], developing e-portfolio factors for competency certification [52], validating questionnaire content used for pesticide research [47], constructing indicators for sustainable campus environments, evaluating the HyTEE model [49], determining KPIs for hospital emergency departments [53], evaluating factors and indicators in a model [54], assessing strategies for using drones in last-mile logistics [55], selecting the most reliable scenario for developing a smart reverse logistics system [56], road freight transport firm selection [57], and so on.
The fuzzy analytic hierarchy process (FAHP) method for multi-criteria decision-making integrates the AHP method and fuzzy theory [58]. The classical AHP method has its drawbacks, including its failure to account for the uncertainty arising from converting subjective judgments into numerical values, and the significant influence of decision-makers’ subjective judgments, choices, and preferences in the process. Due to these limitations, fuzzy theory is often employed to compensate for the shortcomings of the classical AHP method. The FAHP method has been widely applied across various sectors due to its ability to address uncertainty in decision-making. Some examples include its use in the construction industry [59], aviation industry [60], management [61], manufacturing [62], renewable energy [63], supplier selection [64], urban logistics sustainability initiatives [65], road traffic safety analysis [66], and so on. Kubler et al. [67] explored the applications of the FAHP method through an extensive review and analysis of 190 papers. Their analysis indicates that FAHP is predominantly utilized in the manufacturing, industrial, and governmental sectors. FAHP is commonly combined with other tools such as fuzzy DEMATEL, MOORA, fuzzy MOORA, TOPSIS, fuzzy TOPSIS, VIKOR, and DEA. The authors of papers [68,69] employed the fuzzy AHP method for criterion weighting, and the VIKOR and fuzzy TOPSIS methods for ranking scenarios for the development of the Belgrade central business district logistics system [68].
In the context of questionnaire analysis within the scope of this study, an extended fuzzy AHP method (E-FAHP) was utilized to quantify and interpret human preferences and responses to questions. Chang’s extended fuzzy AHP method has been applied in various contexts. For instance, in the study [70], the E-FAHP method was employed to conduct a multi-criteria analysis and evaluation of catering services. In [71], the authors utilized the E-FAHP method to select the ideal vessel for officers monitoring open seas. Furthermore, research [72] focused on analyzing the impact of different stages of product development through SECI (socialization–externalization–combination–internalization) modes. In [73], Chang’s E-F-AHP method was applied to prioritize key indicators for measuring human capital. In the study [74], the E-FAHP method was utilized for supplier evaluation and selection, whereas in [75], it was employed for selecting the optimal logistics software solution. Through this approach, researchers effectively addressed diverse issues and derived pertinent conclusions in their respective domains. This paper integrates Delphi and AHP methods within a fuzzy framework, aiming to amalgamate their strengths into a unified method for determining the weights of KPIs for RIMs.
The axial distance-based aggregated measurement (ADAM) method presents an innovative MCDM approach within multi-criteria analysis theory, particularly among geometric multi-criteria analysis methods. This method requires the direct input of criterion weights, making it suitable for integration within this hybrid model. Developed by Krstić et al. [76], the ADAM method was initially employed in combination with the best worst method (BWM) to evaluate business models grounded in circular economy principles within the agroindustry sector. Criterion weights were derived using the BWM method, while the ADAM method was utilized to establish the final ranking of business models. In the paper [77], the authors implemented a hybrid model for multi-criteria decision-making, integrating the fuzzy FARE and ADAM methods. The study aimed to identify the primary drivers of e-tracking within the agrifood supply chain. Through analysis, they determined that the most crucial drivers included supply chain efficiency, technological development, and sustainability. The ADAM method was utilized to assess and rank these drivers, providing a clearer understanding of their importance and contribution to the successful implementation of e-tracking. In [78], a hybrid multi-criteria decision-making model was proposed, integrating the fuzzy FARE method to ascertain criterion weights and the fuzzy ADAM method for ranking cold chain service providers. These methodologies were employed to conduct a comprehensive analysis and evaluation of service providers, offering a structured approach to selecting cold chain service providers, with a focus on efficiency, reliability, as well as factors such as temperature control and infrastructural robustness. Kovač et al. [79] developed the concept of potentially sustainable urban logistics, including the establishment of urban consolidation centers on riverbanks and micro-consolidation centers within cities, known as dry ports. By utilizing a methodology that combines mathematical programming and the ADAM method, they identified and evaluated the most sustainable variants of the concept. Through the combined use of the SWOT–ANP and ADAM methodologies, the authors in [80] addressed the issue of identifying key digitization strategies that support circularity in the agrifood industry. SWOT analysis enables the assessment of internal strengths and weaknesses, as well as external opportunities and threats posed by digitization in the agrifood industry, while ANP facilitates the evaluation of the impact of these factors. The ADAM method ranks the best alternative for achieving circularity through digitization in the agrifood supply chain.
The proposed model integrating the fuzzy Delphi, expanded fuzzy AHP, and ADAM methods offers an unprecedented and unique methodology, yet to be explored in both traditional and fuzzy domains. This innovative approach represents a noteworthy contribution to the study of railway infrastructure manager performance, facilitating a comprehensive examination and deeper comprehension of their efficiency.
3. Key Performance Indicators for RIMs
In today’s dynamic environment of the European railway sector, performance evaluation has become a key determinant of success. The introduction of European sustainable and smart mobility strategies, such as the European Green Deal, sets ambitious goals for the railway sector by 2050. In this context, the performance evaluation of railway operators and infrastructure managers becomes essential to ensure the achievement of these goals, enhance sector efficiency, and lay the foundations for developing a sustainable, safe, and innovative railway system in Europe. Infrastructure managers are responsible for developing, maintaining, and managing all aspects of railway infrastructure. Their ability to achieve high performance is essential for sustainability and innovation in the European railway sector.
Performance is integrated into European railway regulation, encompassing various technical and market regulation aspects. According to the Fourth Railway Package [81], RIMs are committed to collaborating in monitoring and comparing performance and participating in railway market monitoring. Evaluating the performance of IMs is essential for several reasons. First, it provides insight into the efficiency of their operations, which is crucial for ensuring the proper functioning of railway traffic. Through these evaluations, any potential shortcomings or areas for improvement can be identified [32]. Second, performance research helps maintain high service standards for railway users. Timely problem resolution and improvement can be ensured by monitoring performance and addressing aspects such as schedule accuracy, infrastructure maintenance, and safety. Performance assessments also contribute significantly to the transparency of railway infrastructure managers’ operations, ensuring accountability to users, regulatory bodies, and the public. This transparency fosters trust within the railway sector. Furthermore, regular performance evaluations form the foundation for making well-informed decisions within the organizations of infrastructure managers and at regulatory and community levels. This is indispensable for maintaining safe, efficient, and sustainable railway systems.
Effective management of railway infrastructure and collaboration among infrastructure managers are pivotal for advancing the railway sector in Europe. These efforts aim to attract new operators and users and ensure the seamless functioning of the Single European Railway Area. The PRIME project, launched upon the European Commission’s recommendation, seeks to bolster collaboration among infrastructure managers, enhance the implementation of ERTMS, and achieve harmonization. PRIME has released a comprehensive catalog of KPIs, categorized into six dimensions, each delineating specific characteristics and objectives [5]:
Dimension C: Contextual Framework encompasses a range of indicators aimed at providing a deeper understanding of the specific characteristics of each IM. This dimension comprises KPIs that shape each infrastructure manager and facilitate comparisons between different railways. The objective is to enhance comprehension of the specific attributes of each IM.
Dimension S: Safety and Environment focuses on ensuring safety in railway traffic and environmental protection. This involves monitoring and managing safety behavior and standards. The goal is to ensure that railway traffic is safe for passengers, freight, and the environment.
Dimension P: Performance analyzes the performance of assets and the railway network. This includes assessing speed, reliability, and the quality of services provided by IMs. The goal is to ensure that the railway system is efficient and meets the needs of operators and users.
Dimension D: Delivery assesses the effectiveness of internal processes within IMs, encompassing asset management, infrastructure maintenance, and enhancement, as well as service provision to contractors and suppliers. The objective is to guarantee efficient resource utilization and high-quality services.
Dimension F: Finance analyzes the financial performance of IMs, including cost tracking, revenue, and access charge collection for infrastructure. The aim is to ensure economic sustainability and efficient financial management.
Dimension G: Growth pertains to increasing the utilization of existing railway networks, improving infrastructure, expanding the network, and integrating with other modes of transportation. This dimension also promotes the use of new technologies to enhance service delivery. The goal is to stimulate the growth and development of the railway sector.
Each of these dimensions has its specific performance indicators and goals, and monitoring them enables a comprehensive understanding of the work of RIMs, a better grasp of their position in the railway industry, and the identification of areas requiring improvement. This study encompasses all the mentioned dimensions to gain insight into the overall efficiency of railway infrastructure management. The indicators selected are those characterized as high-priority by PRIME and those used for benchmarking RIM analyses. Table A1 provides a list of selected performance indicators, offering a detailed overview of various aspects of RIM performance evaluation.
4. Proposed Hybrid MCDM Model
The hybrid model for evaluating RIMs is based on the integration of multicriteria decision-making methods, fuzzy Delphi, E-FAHP, and the ADAM method. Structurally, the model consists of three key parts. In the first part of the model, the fuzzy Delphi method is used to assess the importance of KPIs. This method engages a panel of experts to reach a consensus on the importance of indicators, using a fuzzy approach to account for uncertainty and ambiguity in expert assessments. The aim is to obtain a shared view of the importance of indicators and identify key indicators contributing to the success of RIMs. The second part of the model utilizes the extended fuzzy AHP method to determine the weights of KPIs. This method enables hierarchical evaluation and allocation of weights to different dimensions and KPIs within the hierarchy. It integrates a fuzzy approach to account for uncertainty in expert assessments, providing a more precise determination of the impact of different indicators on performance evaluation. The third part of the model uses the ADAM method to rank RIMs. The ADAM method uses the weights of indicators obtained from the extended fuzzy AHP method to assess and rank RIMs. This approach provides a final assessment and ranking based on defined indicators and their weights. Figure 1 provides an overview of the hybrid model for evaluating RIMs, and the steps to implement this model are detailed in the following section.
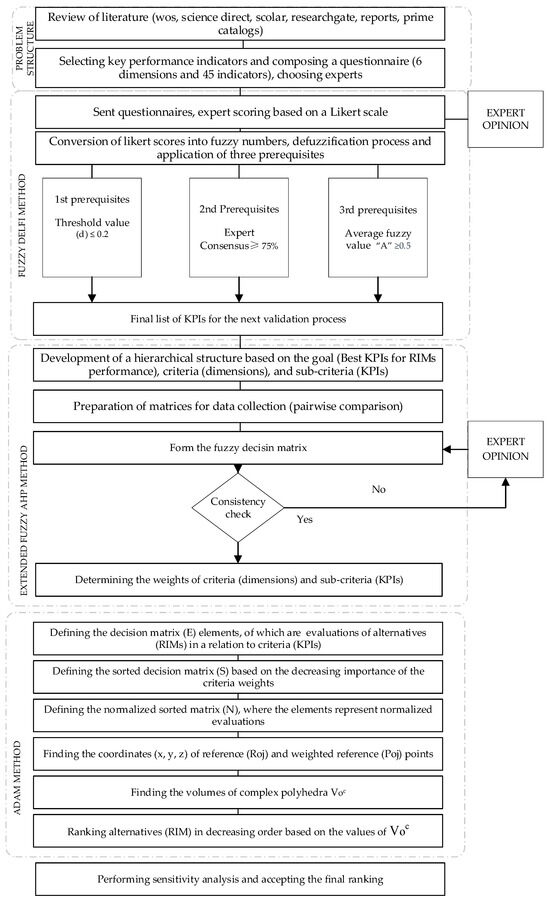
Figure 1.
The hybrid model for evaluating RIMs (adapted from [55,82]).
Step 1: The initial phase includes forming a list of KPIs, with the selection of experts possessing relevant experience and knowledge to participate in the decision-making process.
Step 2: With the finalized list of KPIs and the chosen experts, surveys are distributed to the experts to assess the importance of each indicator. This assessment employs a five-point Likert scale, as depicted in Table 2.

Table 2.
Fuzzy scale for evaluation [83].
Step 3: Subsequently, the importance of KPIs is evaluated using the fuzzy Delphi method. This process involves the following sub-steps:
Step 3.1: Determination of the threshold value ‘d’. The threshold value is crucial in determining the degree of consensus among experts. To achieve consensus among experts for each item, the threshold value () must not exceed 0.2 [84]. The equation used to determine the threshold (d) is:
where are the minimum, reasonable, and maximum values of the fuzzy assessment grade , and represent the minimum, reasonable, and maximum values of the fuzzy number , which signifies the average value of all grades from Table 2.
Step 3.2: Verification of Expert Consensus. In this stage of the fuzzy Delphi method, we assess the fulfillment of the second prerequisite, which pertains to expert consensus, specifically whether it is ≥75% for each item. If the percentage of expert consensus is ≥75% for each item, then the item is regarded as having achieved expert consensus [84]. The percentage of expert consensus can be calculated using the following equation:
Step 3.3: Defuzzification Process and Final Decision Making. In the fuzzy Delphi method, the defuzzification process involves assessing the third prerequisite, known as the α-cut threshold, which should be greater than or equal to 0.5. This threshold indicates the minimum level of agreement among experts required for accepting an item [84]. To ascertain the acceptability of an item, the equation for calculating the fuzzy value is used:
If the value is greater than or equal to the α-cut value, set at 0.5, then the item is considered acceptable. Based on meeting the three prerequisites, an assessment is made regarding whether the items will be retained or discarded. The prerequisites for retaining items based on expert consensus are [85]: threshold value , percentage of expert consensus ≥75%, average fuzzy value (“” value) ≥ 0.5. All three prerequisites must be met for the items to be retained.
Step 4. The next step involves obtaining indicator weights using the extended fuzzy AHP method, which includes the following sub-steps:
Step 4.1: Indicator Evaluation Matrices. After creating the hierarchical structure, an n × n comparison matrix is formed (Equation (4)). Experts compare one indicator to another using linguistic values, considering the overall goal. The linguistic values are transformed into triangular fuzzy numbers (TFNs) by applying the relationships in Table 3.
where is the number of indicators to be evaluated and is the importance of indicator i compared to indicator . If in the comparison matrix, then the value will be (1, 1, 1).

Table 3.
Evaluation Scale.
Step 4.2: Geometric Mean of the Weights of Experts. After converting linguistic into fuzzy values, the method proposed by Buckley [86] is used to aggregate responses from multiple experts. If we have a matrix of fuzzy numbers expressed using parameters (smallest possible value), (most promising value), and i (largest possible value), the geometric mean is calculated as follows:
where krepresents the total number of decision-makers, .
Step 4.3. Consistency Check. The consistency index () and consistency ratio () are used to assess measurable consistency within the AHP method [87].
is the largest eigenvalue of the comparison matrix, is the dimension of the matrix, and is a random index depending on . To calculate , a transformation of comparison matrices, represented as triangular fuzzy numbers, into crisp matrices is performed [88]. A triangular fuzzy number, denoted as can be defuzzified into a crisp number using Equation (9), thereby obtaining a crisp matrix:
If the calculated of the comparison matrix for is less than 10%, the consistency of pairwise assessments can be considered acceptable. Otherwise, the assessments provided by the experts are considered inconsistent, and it is necessary to repeat the pairwise comparison matrix.
Step 4.4. Calculate Fuzzy Synthetic Extent Value. The extended method is utilized to evaluate the performance of each object concerning the established goal. The set of objects is denoted as while the set of goals is denoted as . Each object from set is individually analyzed concerning each goal from set . Once the analysis is completed, “” values of extended analysis are obtained for each object. These values are denoted as , , where () are triangular fuzzy numbers.
Let be the values of extended analysis for the -th object concerning goals. Then, the value of the fuzzy synthetic range regarding the -th object is defined as:
The value is estimated by adding the fuzzy values for range analysis using the addition operation (Equations (11) and (12)).
After calculating the values of extended analysis and performing certain fuzzy operations with these values, the mathematical expression for calculating the inverse vector is used according to Equation (13):
Step 4.5. Determine the Comparative Superiority. In this step, the degree of possibility () is introduced, which measures the probability that one fuzzy number is greater than another fuzzy number
When there exists a pair (x, y) such that and , then Since and are convex fuzzy numbers, therefore
where is the ordinate, the highest point of intersection between and (Figure 2).
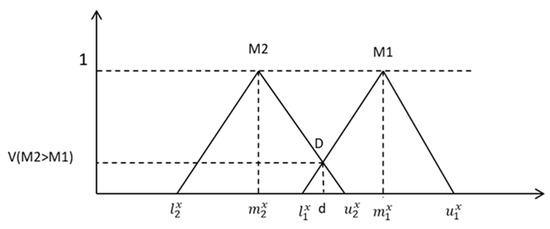
Figure 2.
Intersection point between and .
When and , the ordinate of the point is determined by the following equation:
For comparing and , both values of the expressions and are needed.
Step 4.6. Select the Minimum Value of Superiority. In this step, the degree of possibility for a convex fuzzy number to be greater than k other convex fuzzy numbers Mi, where i varies from 1 to k, is determined. The degree of possibility is determined by the minimum values of the degree of possibility for each condition . In other words, the expression signifies the minimum probability that the convex fuzzy number is greater than each of the .
Step 4.7. Calculate the Weight Vector and Normalize it for Each Criterion. This procedure aims to determine the weight vector for each criterion, which is used in the analysis. Firstly, the relative superiority between every two fuzzy numbers is determined, and then the minimum superiority is selected for each criterion.
The weight vector is calculated using the following equation:
represents the number of elements.
The obtained weight vector is normalized to the final normalized weight vector W, which is utilized in further analysis.
where W is a nonfuzzy number.
Step 5. In this step, the ADAM method is used for ranking alternatives after obtaining the relative weights of indicators using the E-FAHP method.
Step 5.1: Define the decision matrix E, whose elements are evaluations of alternative according to criterion , i.e., the magnitude of vectors corresponding to evaluations of alternatives according to the criterion.
where is the total number of alternatives, and is the total number of criteria.
Step 5.2: Define the sorted decision matrix elements, which are , indicating the sorted evaluations eoj in descending order of importance (weight) of the criteria:
Each element represents the sorted evaluation in descending order of importance (weight) of a specific criterion.
Step 5.3: Define the elements of the normalized sorted matrix , which are normalized evaluations obtained as:
where is the set of benefits, and is the set of cost criteria.
Step 5.4: Find the coordinates of reference points and weighted reference points () defining the complex polyhedron as follows:
where is the angle determining the direction of the vector defining the value of the alternative, obtained as:
Step 5.5: Find the volumes of complex polyhedra as the sum of volumes of pyramids it is composed of, using the following equation:
where is the volume of the pyramid obtained by applying the following equation:
where is the surface of the base of the pyramid defined by the reference and weighted reference points of two consecutive criteria, obtained by applying the following equation:
where is the Euclidean distance between the reference points of two consecutive criteria, obtained by applying the following equation:
where and are the magnitudes of vectors corresponding to the weights of two consecutive criteria:
where is the height of the pyramid from the defined base to the apex located at the origin (), obtained by applying the following equation:
where is the semi-circumference of the triangle defined by the and coordinates of two consecutive criteria and the origin, obtained as:
where and are the Euclidean distances of the reference points of two consecutive criteria from the origin, obtained as:
Step 5.6: Ranking alternatives according to decreasing values of volumes of complex polyhedra (o = 1,…, m). The best alternative is the one with the highest volume value.
5. Application of a Hybrid MCDM Model for Evaluating RIMs
In this section, a hybrid MCDM model for the evaluation and ranking of RIMs is applied. An analysis of the research results, including sensitivity analysis, is presented. To evaluate KPIs, the process began with the definition of an initial list of indicators and the selection of experts to participate in the research (Step 1). Experts were chosen based on their specialization in railway infrastructure management, deep understanding of working conditions in the railway sector, significant authority in the field, and a minimum of five years of experience. Table A2 provides an overview of the data on experts included in the research. The panel included representatives from the railway infrastructure management sector of the Republic of Serbia, Albania, Montenegro, and Bosnia and Herzegovina, as well as academic experts in railway infrastructure. Overall, fourteen experts were selected for this phase of the research.
The questionnaire with KPIs (Table S1) and their explanations was distributed to the experts via email, accompanied by a request to rate the importance of the indicators using a five-point Likert scale from Table 2 (Step 2). To boost response rates, targeted respondents were contacted through telephone calls and messages containing explanations, allowing ample time for their responses. Subsequent analyses were conducted based on the received feedback (Table S2).
In the next step (Step 3), the fuzzy Delphi method was applied to assess the significance of KPIs. Linguistic expressions were converted into fuzzy numbers using the relationships outlined in Table 2. The threshold value () was determined using Equation (1) (Step 3.1), while the percentage of expert consensus was calculated using Equation (2) (Step 3.2). Additionally, the average fuzzy value “” was computed using Equation (3) (Step 3.3). All three prerequisites must be satisfied for the indicators to be retained. The results of the fuzzy Delphi method and the final decisions regarding the retained indicators are presented in Table 4.

Table 4.
The results of expert consensus regarding the list of KPIs.
The expert ratings indicate the high importance of 45 KPIs in the context of railway infrastructure management, thus they were selected for analysis. The fuzzy Delphi method demonstrated satisfactory and good overall results in this research. The first condition of the fuzzy Delphi method, the threshold value , was satisfied by 95.56% of the indicators. The second condition, the percentage of expert consensus ≥ 75%, was met by 77.78%. The third condition, the average fuzzy value A ≥ 0.5, was fulfilled by all indicators. Finally, a framework for evaluating the performance of RIMs was defined, consisting of 35 KPIs as shown in Figure 3.
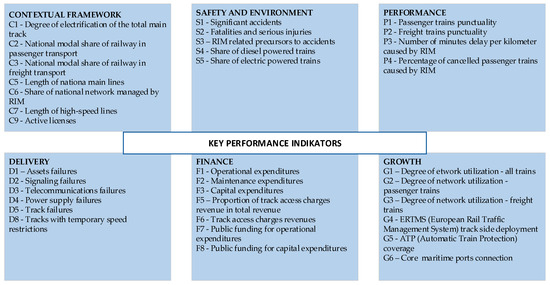
Figure 3.
The final list of KPIs for evaluating RIMs.
In the next step (Step 4), the E-FAHP method is applied to obtain the weights of the indicators. A hierarchical structure is defined, representing the relationships within the structure and enabling comparisons between each pair at each level within the hierarchy. The hierarchy consists of three levels: at the top is the level representing the research objective, which in the context of modeling involves determining the KPIs for evaluating the performance of RIMs; the second level consists of six performance dimensions; the third level encompasses the final KPIs within each dimension. After forming the hierarchical problem structure, a questionnaire for pairwise comparisons of KPIs within each dimension was composed (Table S3). The same experts as in the first part of the model made the evaluations.
Linguistic expressions are transformed using relationships from Table 3. to create a matrix for evaluating dimensions and KPIs, using Equations (4) and (5) (Step 4.1) (Table S4). The geometric mean of fuzzy expert ratings is calculated using Equation (6) (Step 4.2), followed by checking the consistency of comparison matrices using Equations (7)–(9) (Step 4.3). Subsequently, the calculation of the fuzzy synthetic value range is performed using Equations (10)–(13) (Step 4.4), identification of comparative superiority using Equations (14)–(16) (Step 4.5), determination of the minimum value of superiority using Equations (17) (Step 4.6), and finally, calculation of weight vectors and their normalization for each criterion using Equations (18)–(20) (Step 4.7). The final weights of the KPIs are obtained through an iterative process where the described procedure is repeated for each group of KPI dimensions and the KPIs within them. After calculating the weights of all KPI dimensions and KPIs, the final values are obtained by multiplying the weights of KPI dimensions by the weights of KPIs within their respective dimensions. The results of the E-FAHP method are presented in Table 5.

Table 5.
The results of dimensions and KPI weights obtained through the application of E-FAHP.
The indicator P4—Percentage of canceled passenger trains caused by RIM is ranked first. Its exceptionally high weight suggests that the reliability of passenger services is crucial, and cancellations represent the most significant challenge to address. The indicator P3—Number of minutes delay per kilometer caused by RIM is also highly ranked, indicating the importance of reducing delays caused by infrastructure issues. The indicators P1—Passenger train punctuality and P2—Freight trains punctuality hold high positions as well, emphasizing the importance of precision in adhering to schedules. S2—Fatalities and serious injuries and S1—Significant accidents are also highly ranked indicators, highlighting the necessity of improving safety standards and reducing injuries.
In the next step (Step 5), the ADAM method is applied to evaluate and rank RIMs by assigning weights to selected indicators. A dataset has been compiled for nine European RIMs based on data extracted from PRIME reports for the year 2021 [89]. These RIMs include Bane NOR from Norway, DB Netz AG from Germany, Infraestruturas de Portugal S.A. from Portugal, PKP PLK from Poland, ProRail from the Netherlands, SBB CFF FFS from Switzerland, SNCF RÉSEAU from France, Správa železnic, s.o. from the Czech Republic, and Trafikverket from Sweden. For confidentiality purposes, the identities of the railway infrastructure managers are anonymized and referred to as RIMs in the presentation of results. The ranking of RIMs was conducted using the ADAM 1.2-beta software package developed by Krstić et al. [76], which relies on the values of corresponding polyhedron volumes. The acquired volumes are presented in Table 6. The top-ranked RIM according to the ADAM method is RIM2.

Table 6.
The results of ranking RIMs using the ADAM method.
The ADAM method also allows for visual representation, namely a graphical depiction of the polyhedron surfaces defined by reference and weighted reference points (Figure 4). The polyhedron volume of RIM2, obtained using the ADAM 1.2-beta software package, was the highest compared to other RIMs. On the other hand, RIM3 was the lowest ranked based on the values and weights of the selected KPIs. The ADAM method also enables visual representation or graphical depiction of polyhedron surfaces.
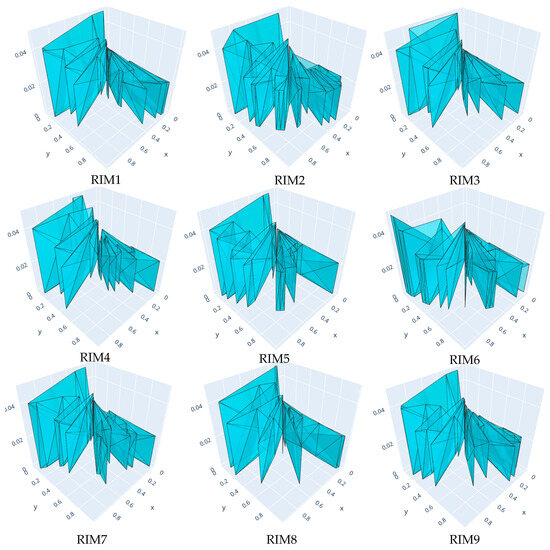
Figure 4.
Complex polyhedra for the RIMs ranking.
5.1. Sensitivity Analysis
The sensitivity analysis aims to evaluate the stability of the obtained solution by adjusting the weights of the KPIs. Twelve scenarios were defined for this purpose. In the initial four scenarios, the weight of the most crucial indicator (P4) was gradually decreased by specific percentages: 50%, 70%, 90%, and 100%, respectively. In these scenarios, the weights of the remaining KPIs were adjusted to ensure that their total sum remained constant at 1, despite any alterations in the weight of the primary indicator [76]. Similarly, the eight subsequent scenarios adopted a comparable approach, where the weights of the second and third most important indicators (P3 and P1) were decreased by identical percentages, with proportional adjustments made to the remaining weights. Subsequently, these scenarios were compared against the rankings obtained in the baseline scenario (SC0).
Based on the results of the sensitivity analysis (Table 7), it is observed that the rankings remained unchanged in all scenarios except for SC5. In this scenario, RIM3 and RIM4 changed positions, as did RIM9 and RIM7. Upon analyzing the rankings of RIMs in the defined scenarios, as shown in Figure 5, it is evident that there are no significant variations in the results. Therefore, it can be concluded that the ranking obtained in the baseline scenario demonstrates satisfactory stability.

Table 7.
The rankings of RIMs in the defined scenarios.
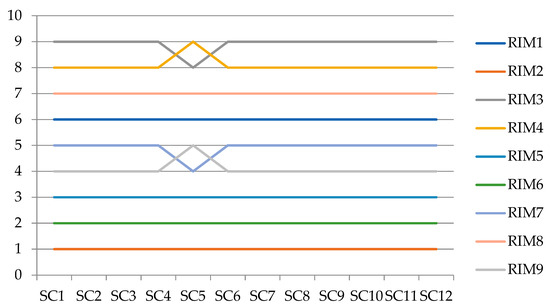
Figure 5.
Sensitivity analysis.
5.2. Validation of Results
The validation of the obtained results and the methodology used was performed by comparing them with the results obtained using other widely used MCDM methods such as TOPSIS, VIKOR, COBRA, SAW, COPRAS, and AHP. The final ranks of RIMs obtained by these methods are shown in Table 8. The Spearman correlation coefficient (SCC) was used to assess the similarity of the obtained results. These values for each method are also shown in Table 8. The mean SCC value of 0.908 indicates that the ranking obtained by the ADAM method has a very high degree of correlation with the results of other methods, which additionally emphasizes the stability and quality of the obtained solution. Compared to the TOPSIS, VIKOR, and COBRA methods, the ADAM method simplifies decision-making by visually highlighting the best alternative, making it easily identifiable. In contrast to methods such as SAW, COPRAS, and AHP, ADAM stands out for its efficiency, requiring significantly fewer resources, particularly time and human effort, for evaluation and implementation. A comparative view of the obtained results is shown in Figure 6.

Table 8.
Validation of the model and the obtained results.
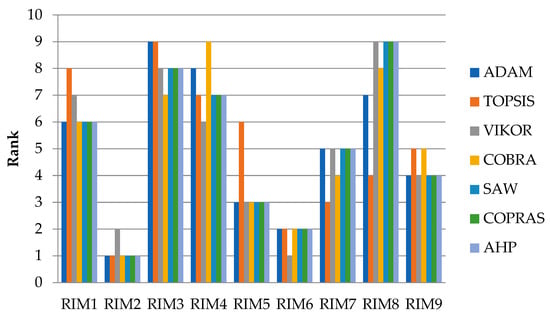
Figure 6.
Ranking comparison obtained by different methods.
6. Discussion
The research results indicate the impressive performance of RIM2 across various dimensions of railway infrastructure management, reaffirming their high position in the ranking encompassing 35 KPIs. Through the analysis of six dimensions, including the contextual framework, safety and environment, performance, delivery, finances, and growth, RIM2 stands out as an outstanding example of excellence in the sector. Their commitment to quality and efficiency in service provision is reflected in the results, providing stakeholders and decision-makers with a comprehensive view of their leadership. Additionally, RIM2 can serve as an inspiration to other RIMs, offering a model for achieving high standards in this industry. Furthermore, these results not only provide insights into current performance but also prompt consideration of practices that could serve as a model for achieving high standards in the industry. The inspiration provided by RIM2 to others can stimulate performance improvement and the pursuit of excellence. Through an objective assessment of KPIs, this analysis aids decision-makers in informed planning, encouraging fact-based decision-making. Additionally, the results can foster competition within the industry, prompting other organizations to enhance their operations to remain competitive in the railway infrastructure market. This analysis provides a crucial framework for decision-makers to better understand the state of the railway industry and identify opportunities for improvement. The proposed hybrid MCDM model enables a comprehensive evaluation of RIMs, encompassing the assessment of KPIs’ importance, defining the weighted values of KPIs, and ranking RIMs. This approach represents a significant advancement compared to previous research, which primarily relied on benchmarking analyses of individual indicators across RIMs [14], analysis of KPIs for two RIMs [33], or benchmarking analyses of RIMs using KPIs [89].
Using the fuzzy Delphi method for assessing the importance of indicators instead of the classical Delphi method brings advantages in situations where we face uncertainty, subjectivity, or different interpretations among experts. The classical Delphi method has its drawbacks, including imperfect interpretation of expert opinions due to a lack of consideration for uncertainty, lack of clear rules for achieving desired results, and loss of interest and data from experts due to the lengthy process that can result in re-surveys [40]. The fuzzy Delphi method brings significant benefits, including reducing the time for evaluation in questionnaires/surveys and reducing the number of survey rounds. It allows experts to anonymously express their opinions without fear of ambiguity or bias, resulting in greater completeness and consistency of opinions. It also facilitates consensus among experts without compromising their initial views, allowing them to freely express their genuine reactions to questions or assessments of criteria, factors, and the like. The final decision is based on satisfying three prerequisites: the threshold value “”, expert consensus, and defuzzification value “”.
The ADAM method, used for ranking RIMs in this study, represents an innovative approach in this specific field. It is important to note that this method, utilized to achieve final results and rankings, has not been previously applied in the realm of railway infrastructure. This original application of the ADAM method contributes to new insights and expands the range of methodologies used in research related to the performance evaluation of RIMs. This approach further confirms the innovation of the research, standing out as a contribution to the development and application of new methods in this specific domain.
The proposed MCDM model represents another significant contribution of this study. The fuzzy Delphi method confirmed the importance of indicators and was used as a tool for pre-validation to select appropriate indicators before undergoing the validation process. The combination of the fuzzy Delphi, extended fuzzy AHP, and ADAM methods adds further value to the decision-making process as it covers different phases of analysis, from gathering expert opinions, and determining indicator weights, to final alternative ranking. This integrated approach enables decision-makers to better understand and quantify uncertainties and complexities in the decision-making process, thereby contributing to a more precise and comprehensive analytical framework.
Despite its significant advantages, the developed model for analyzing the performance of RMIs faces several challenges and limitations that require careful analysis. Firstly, reliance on subjective expert opinions implies that the quality of the results directly depends on the experience, expertise, and interpretations of individual experts. This can lead to potential variations in the final results and interpretations, which may affect the reliability and validity of the analysis. Secondly, the availability of experts and their willingness to participate in the analysis process, as well as the time required to collect their responses, pose challenges. Finally, the availability of relevant data, including the values of KPIs for RIMs, is also crucial. Therefore, it is necessary to carefully consider these limitations when applying the model and to develop strategies to overcome or mitigate them.
This study provides a wide range of potential applications. The theoretical contribution of the study lies in the fact that the results can benefit researchers and the academic community in further understanding the complexity of RIM performance, providing new insights into integrated analysis models. Additionally, this study can serve as a foundation for further research in the optimization and enhancement of performance in the railway sector. On a practical level, the results of this research can be valuable for policymakers, RIMs, and other relevant stakeholders in the industry in shaping policies and strategies for the development of the railway sector, as well as in identifying priorities for investments and improvements. Ultimately, this research can contribute to more efficient and sustainable functioning of railway infrastructure, which can have a positive impact on society as a whole through improved connectivity, economic development, and environmental protection. The developed MCDM model is not only a practical tool for addressing specific issues in the railway sector but also provides a basis for broader application in other industries and domains facing complex decision-making. Its flexibility and adaptability enable its use in various contexts, making it a contribution not only to MCDM theory but also to the broader field of decision-making.
7. Conclusions
Directive 91/440/EC initiated the reform of European railways, resulting in the creation of a new key player, the RIM, whose role is essential for the performance of the railway sector. As the sole provider of railway capacity to train operators, RIMs provide a crucial input to operators. In the conditions of an open market, high standards become imperative, requiring continuous alignment and improvement of performance in this sector. Infrastructure managers are faced with the need to meet high demands for transparency, efficiency, and service quality. Performance evaluation becomes a crucial activity in this context, providing deeper insights into efficiency, identifying areas for improvement, and supporting ongoing compliance with evolving standards.
The proposed hybrid MCDM model evaluates the performance of RIMs according to KPIs. A significant contribution of this research is the creation of a hybrid model that combines the ADAM method with the fuzzy Delphi and extended fuzzy AHP methods, thereby developing a universal decision-making tool in various fields. Other important contributions of this research focus on the analysis and resolution of the identification of KPIs of RIMs, assessing their importance, and assigning weight values. Finally, a significant contribution is the identification of the most efficient RIM. So far, there has been no research in the literature dealing with performance analysis based on performance indicators, or studies systematically analyzing, evaluating, and ranking different RIMs. Ultimately, the contribution of the proposed model lies in its comprehensiveness, innovativeness, and applicability in real-world conditions, providing a valuable tool for evaluating RIMs.
The proposed model for analyzing RIMs faces several challenges and limitations, including reliance on subjective expert opinions, the availability of experts, and response time, as well as the availability of relevant data on the values of KPIs of RIMs. The research has identified guidelines for future research in the context of evaluating the performance of RIMs. Future research in the field of evaluating RIMs could explore different methodologies to enrich the analysis and make comparisons between models. Additionally, future research could assess the effectiveness of the model on a larger sample of RIMs, providing a deeper understanding of its applicability and results. The analysis should also compare the results with other relevant studies in this area to confirm the consistency and generalization of the conclusions. Future research could deepen the analysis of the impact of external factors on the performance of RIMs. Research should also carefully consider changes in legislation, technological advancements, and the organizational model of the railway sector. A deeper understanding of these factors could contribute to the context of performance analysis, allowing for a better understanding of the impact of these elements on evaluation results. Additionally, research could analyze how the organizational model of the railway sector influences the performance of RIMs, contributing to a broader understanding of the complexity of factors shaping success in this industry.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math12101590/s1, Table S1. Questionnaire for identification of KPIs for RIMs; Table S2: Expert KPI evaluation; Table S3: Questionnaire for KPIs’ pair-wise comparison; Table S4. Experts’ evaluations of dimensions and KPIs; Table S5. Dataset for RIMs.
Author Contributions
Conceptualization, A.K., S.T., and M.K.; methodology, M.K.; software, M.K.; validation, S.T. and M.K.; formal analysis, A.K., S.T., N.Č., and N.B.; investigation, A.K. and S.T.; data curation, A.K. and S.T.; writing—original draft preparation, A.K., S.T., and M.K.; writing—review and editing, S.T. and M.K.; visualization, A.K.; supervision, S.T., N.Č., and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All relevant data are presented within the paper or in the Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
List of key performance indicators.
Table A1.
List of key performance indicators.
| KPI Dimensions | KPI Name | KPI Definition | KPI Unit |
| Contextual Framework C: entails the characteristics of each infrastructure manager (RIM), illustrates their significance, and the market of railway services in each of the RIM’s respective countries, enabling the observation of differences between railways | C1—Degree of electrification of total main track | Percentage of the main track km which are electrified | % of main track km |
| C2—National modal share of railways in passenger transport | The proportion of national rail passenger km compared to total passenger km of passenger cars, buses/coaches, aviation, and railways (Source: European Commission, Eurostat) | % of passenger km | |
| C3—National modal share of railways in freight transport | Proportion of national rail tonne km compared to total tonne km of road, inland waterways, and rail freight (Source: European Commission, Eurostat). | % of tonne km | |
| C4—Proportion of high- speed main track km (≥200 km/h and <250 km/h) | High-speed main track kilometers (≥200 km/h and <250 km/h) as a percentage of total main track kilometers. | % of main track km | |
| C5—Length of national main lines | Refers to the total extent of the primary railway lines or routes that exist within a specific country or national territory. | km | |
| C6—Share of national network managed % by RIM | Refers to the percentage of a country’s entire railway infrastructure that is under the direct management or operation of an infrastructure manager. | % | |
| C7—Length of high-speed lines | Refers to the total extent of the primary railway tracks or routes within a specific railway network or system that is managed by the infrastructure manager. | km | |
| C8—Full time employees | Refers to individuals who are employed by an organization or company on a full-time basis, typically defined by working a standard or customary number of hours per week, such as 35 to 40 h or more. | fte | |
| C9—Active licenses | The number of currently valid licenses or permits issued to railway operators for conducting their activities within the railway market. | number | |
| Safety and Environment S: encompass the management of behaviors and standards in railway traffic safety and ecology | S1—Significant accidents | The relative number of significant accidents including sidings, excluding accidents in workshops, warehouses, and depots, based on the following types of accidents (collisions, derailment of train, level crossing accident, and others). | Number per million train km |
| S2—Fatalities and weighted serious injuries | The sum of the number of persons killed (i.e., killed immediately or dying within 30 days, excluding any suicide) and of the weighted number of persons seriously injured (i.e., hospitalized for more than 24 h, excluding any attempted suicide). | Number per million train km | |
| S3—RIM related precursors to accidents | The relative number of accidents with the following types of precursors (broken rail, track buckle, signaling failure). | Number per million train km | |
| S4—Share of diesel-powered trains | Train kilometers of diesel-powered trains compared to total train kilometers (both for passenger and freight trains). | % of total train km | |
| S5—Share of electricity-powered trains | Train kilometers of electricity-powered trains com- pared to total train kilometers (both for passenger and freight trains). | % of total train km | |
| S6—CO2 emission produced from maintenance rolling stock | Tonnes of carbon dioxide emission produced from the activity of maintenance rolling stock compared to the main track km. | tCO2 per main track km | |
| S7—Share of renewable traction energy | Share of renewable electric traction energy of total traction energy in % of kWh. Renewable energy is energy that is derived from natural processes that are replenished constantly, such as energy generated from solar, wind, biomass, geothermal, hydropower and ocean resources, solid biomass, biogas, and liquid bio-fuels. Only electric energy is included. | % of total kWh | |
| Performance P: refers to the performance of the assets and network of the RIM, and their impact on operators and users; it pertains to accuracy and reliability | P1—Passenger trains punctuality | Percentage of actually operating (i.e., not canceled) national and international passenger trains (excluding work trains) that arrive at each strategic measuring point with a delay of less than or equal to 5:29 min. | % of actually oper- ating trains |
| P2—Freight trains punctuality | Percentage of actually operating (i.e., not canceled) national and international freight trains (excluding work trains) that arrive at each strategic measuring point with a delay of less than or equal to 15:29 min. | % of actually oper- ating trains | |
| P3—Number of minutes delay per kilometer caused by RIM | Delay minutes caused by incidents that are regarded as RIM’s responsibility divided by total train- km operated (revenue service + shunting operations to and from depots + RIM’s work traffic). | Minutes per train- km | |
| P4—Percentage of passenger train cancellations caused by the RIM | Percentage of fully or partially canceled national and international passenger trains that were caused by incidents that are regarded as RIM’s responsibility. | % of scheduled and cancelled passenger trains | |
| P5—Average delay minutes per asset failure | The average delay minutes per asset failure caused by all asset failures on the main track. | Minutes per failure | |
| Delivery D: encompasses the efficiency of RIM’s internal processes, and asset management, ensuring a high-quality infrastructure network, and delivering to contractors and suppliers | D1—Assets failures in relation to network size | The average number of all asset failures on the main track. | Number per thousand main track km |
| D2—Signaling failures in relation to network size | The average number of all asset failures of signaling. | Number per thou- sand main track km | |
| D3—Telecommunication failures in relation to network size | The average number of all asset failures of telecommunication installations (GSM-R, radio failure, and more) on the main track. | Number per thou- sand main track km | |
| D4—Power supply failures in relation to network size | The average number of all asset failures of power supply equipment (power supply for electric traction, variation and drops of voltage, and others) on the main track. | Number per thou- sand main track km | |
| D5—Track failures in relation to network size | The average number of all track failures (rail breakage, lateral distortion, and other track failures) on the main track. | Number per thou- sand main track km | |
| D6—Other infrastructure failures in relation to network size | The average number of all asset failures due to the managing and planning of staff and other causes related to infrastructure installations on the main track. | Number per thou- sand main track km | |
| D7—Tracks with permanent speed restrictions | Percentage of main tracks with permanent speed restriction due to deteriorating asset condition weighted by the time the restrictions are in place (included in the yearly timetable) related to total main track km; restrictions are counted whenever criterion is met regardless of whether RIM reports permanent speed restrictions as such or if they are included in the timetable. | % of main track km | |
| D8—Tracks with temporary speed restrictions | Percentage of main tracks with temporary speed restriction due to deteriorating asset condition weighted by the time the restrictions are in place (not included in the yearly timetable) related to total main track km. | % of main track km | |
| Finances F: encompass the financial operations of the RIM including cost and revenue efficiency and track access charges | F1—Operational expenditures (OPEX) in relation to network size | RIM’s total annual operational expenditures (net values, excluding value-added tax) per main track km. | Euro per main track km |
| F2—Maintenance expenditures in relation to network size | RIM’s total annual maintenance expenditures (net values, excluding value-added tax) per main track- km. | Euro per main track km | |
| F3—Capital expenditures (CAPEX) in relation to network size | RIM’s total annual capital expenditures (net values, excluding value-added tax) per main track km. | Euro per main track km | |
| F4—Maintenance and renewal in relation to network size | RIM’s total annual renewal and maintenance expenditures (sum of total RIM’s annual renewal expenditures and total RIM’s annual maintenance expenditures, both net values, excluding value added tax) per main track km. | Euro per main track km | |
| F5—Proportion of Track Access Charges (TAC) in total revenue | Percentage of RIM’s annual TAC revenues (including freight, passenger, and touristic trains) compared to total revenues. | % of monetary value | |
| F6—Track Access Charges (TAC) revenue in relation to network size | RIM’s total annual TAC revenues (including freight, passenger, and touristic trains) compared to total main track km. | Euro per main track km | |
| F7—Public funding for operational expenditures (OPEX) | Total public funding for operational expenditures (OPEX) related to network size. | Euro per main track km | |
| F8—Public funding for capital expenditures (CAPEX) | Total public funding for capital expenditures (CAPEX) related to network size. | Euro per main track km | |
| Growth G: encompasses the level of utilization of the existing rail network, improvement and expansion of the network, integration with other modes of transportation, and the use of new technologies to enhance delivery | G1—Degree of network utilization all trains | The average daily train km on the main track (passenger and freight revenue service only, no shunting, no work trains) related to the main track km. | Daily train km per main track km |
| G2—Degree of network utilization—passenger trains | The average daily passenger train km on the main track (revenue service only, no shunting, no work trains) related to the main track km. | Daily passenger train–km per main track km | |
| G3—Degree of network utilization—freight trains | The average daily freight train km on the main track (revenue service only, no shunting, no work trains) related to the main track km. | Daily freight train– km per main track- km | |
| G4—ERTMS track-side deployment | The main tracks with ERTMS in operation in proportion to total main tracks (measured in track km). | % of main track km | |
| G5—ATP (automatic train protect) coverage | Share of the main track km equipped with ATP. ATP is a train protection system providing warning and automatic stop and continuous supervision of speed, protection of danger points, and continuous supervision of the speed limits of the line, where “continuous supervision of speed” means continuous indication and enforcement of the maximal allowed target speed on all sections of the line. Including, e.g., ETCS, ATB, LZB, CBTC, and similar systems. | % of main track km | |
| G6—Core maritime ports connection | Percentage of core maritime ports linked to the TEN-T network connected. | % of core maritime ports | |
| G7—Core inland waterways connection | Percentage of core inland waterways linked to the TEN-T network. | % of core inland waterways | |
| G8—Core airports connection | Percentage of core airports linked to the TEN-T network. | % of core airports |

Table A2.
Demographic characteristics of experts who participated in the research.
Table A2.
Demographic characteristics of experts who participated in the research.
| Variables | A Sample | Percentage | |
|---|---|---|---|
| Sex | M | 12 | 85.71% |
| F | 2 | 14.29% | |
| Age (years) | 30–35 | 3 | 21.43% |
| 35–40 | 1 | 7.14% | |
| 40–45 | 7 | 50% | |
| 50–55 | 1 | 7.14% | |
| 60–70 | 2 | 14.29% | |
| Years of experience | 5–10 | 4 | 28.57% |
| 10–15 | 6 | 42.86% | |
| 15–20 | 1 | 7.14% | |
| 20–30 | 2 | 14.29% | |
| 30- | 1 | 7.14% | |
References
- Nash, C.; Smith, A.; Crozet, Y.; Link, H.; Nilsson, J.-E. How to liberalise rail passenger services? Lessons from European experience. Transp. Policy 2019, 79, 11–20. [Google Scholar] [CrossRef]
- European Commission. WHITE PAPER: European Transport Policy for 2010: Time to Decide; Commission of the European Communities: Brussels, Belgium, 2001; Volume 124. [Google Scholar]
- European Court of Auditors. Rail Freight Transport in the EU: Still not on the Right Track; European Court of Auditors: Luxembourg, 2016; ISBN 9789287246103. [Google Scholar]
- Esposito, G.; Cicatiello, L.; Ercolano, S. Reforming railways in the EU: An empirical assessment of liberalisation policies in the European rail freight market. Transp. Res. Part A Policy Pract. 2019, 132, 606–613. [Google Scholar] [CrossRef]
- Platform of Rail Infrastructure Managers in Europe. Key Performance Indicators for Performance Benchmarking; Rail Infrastructure Managers: Brussels, Belgium, 2022. [Google Scholar]
- Crozet, Y. Introducing Competition in the European Rail Sector: Insights for a Holistic Regulatory Assessment; International Transport Forum Discussion Papers, No. 2019/08; OECD Publishing: Paris, France, 2019. [Google Scholar] [CrossRef]
- Catalano, G.; Daraio, C.; Diana, M.; Gregori, M.; Matteucci, G. Efficiency, effectiveness, and impacts assessment in the rail transport sector: A state-of-the-art critical analysis of current research. Int. Trans. Oper. Res. 2018, 26, 1–36. [Google Scholar] [CrossRef]
- Growitsch, C.; Wetzel, H. Testing for Economies of Scope in European Railways An Efficiency Analysis. J. Transp. Econ. Policy 2009, 43, 1–24. [Google Scholar]
- Doomernik, J.E. Performance and efficiency of high-speed rail systems. Proc. Transp. Res. Procedia 2015, 8, 136–144. [Google Scholar] [CrossRef]
- Niu, Y.; Xiao, F.; Zhang, N.; Sadeghi, M. Transportation Efficiency of Railway Operation Enterprises. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Yu, M.M. Assessing the technical efficiency, service effectiveness, and technical effectiveness of the world’s railways through NDEA analysis. Transp. Res. Part A Policy Pract. 2008, 42, 1283–1294. [Google Scholar] [CrossRef]
- Lan, L.W.; Lin, E.T.J. Performance measurement for railway transport: Stochastic distance functions with inefficiency and ineffectiveness effects. J. Transp. Econ. Policy 2015, 40, 383–408. [Google Scholar]
- Iyigun, I. Evaluation of Efficiency of Rail Transportation of Black Sea Countries by Using An Integrated Mcdm Approach. Econ. Bus. 2019, 13, 305–323. [Google Scholar]
- Hansen, I.A.; Wiggenraad, P.B.L.; Wolff, J.W. Benchmark Analysis of Railway Networks and Undertakings. In Proceedings of the RailCopenhagen2013: 5th International Conference on Railway Operations Modelling and Analysis, Copenhagen, Denmark, 13–15 May 2013. [Google Scholar]
- Blagojević, A.; Vesković, S.; Kasalica, S.; Gojić, A.; Allamani, A. The Application of the Fuzzy AHP and DEA for Measuring the Efficiency of Freight Transport Railway Undertakings. Oper. Res. Eng. Sci. Theory Appl. 2020, 3. [Google Scholar] [CrossRef]
- Kapetanovic, M.; Milenkovic, M.; Bojovic, N.; Avramovic, Z. Evaluation of European railway companies efficiency: Application of a two-stage analysis. Tehnika 2017, 72, 403–410. [Google Scholar] [CrossRef]
- Moreno, J.; Suarez, C. Has the efficiency of European railway companies been improved? Eur. Bus. Rev. 2003, 15, 213–220. [Google Scholar]
- Soumai, A.H.; Benazai, Y. Measuring the Technical Efficiency of Railways in Developing Countries: A Two Stage-Bootstrap Data Envelopment Analysis. Dirassat J. Econ. Issue 2021, 12, 661–679. [Google Scholar] [CrossRef]
- Li, W.; Hilmola, O.-P. Belt and Road Initiative and Railway Sector Efficiency—Application of Networked Benchmarking Analysis. Sustainability 2019, 11, 2070. [Google Scholar] [CrossRef]
- Bojovic, N.; Milenkovic, M.; Kapetanovic, M.; Knezevic, N. Innovations Impact on Efficiency of European Railway Companies. Manag. Sustain. Bus. Manag. Solut. Emerg. Econ. 2016, 21, 13–26. [Google Scholar] [CrossRef]
- Ghanem, O.; Xuemei, L.L. Decision-Making Support in Evaluating Gaps and Efficiencies of the Railway Industry Performance: Using Non-Radial of Data Envelopment Analysis. Int. J. Decis. Support Syst. Technol. 2020, 12, 65–79. [Google Scholar] [CrossRef]
- Maltseva, V.; Na, J.; Kim, G.; Ha, H.K. Efficiency analysis of Russian rail freight transportation companies with super slack-based measurement data envelopment analysis. J. Int. Logist. Trade 2020, 18, 77–89. [Google Scholar] [CrossRef]
- Marchetti, D.; Wanke, P. Brazil’s rail freight transport: Efficiency analysis using two-stage DEA and cluster-driven public policies. Socio-Econ. Plan. Sci. 2017, 59, 26–42. [Google Scholar] [CrossRef]
- Kabasakal, A.; Kutlar, A.; Sarikaya, M. Efficiency determinations of the worldwide railway companies via DEA and contributions of the outputs to the efficiency and TFP by panel regression. Cent. Eur. J. Oper. Res. 2013, 23, 69–88. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Alam Khalid, M. Measuring technical efficiency of Chinese railway administrations by DEA method. J. Interdiscip. Math. 2018, 21, 825–836. [Google Scholar] [CrossRef]
- Alam, K.M.; Xuemei, L.; Baig, S.; Yadong, L.; Shah, A.A. Analysis of Technical, Pure Technical and Scale Efficiencies of Pakistan Railways Using Data Envelopment Analysis and Tobit Regression Model. Netw. Spat. Econ. 2020, 20, 989–1014. [Google Scholar] [CrossRef]
- Alam, K.M.; Ghanem, O.; Li, X. An efficiency analysis of Turkish railways using data envelopment analysis: Comparison study. Int. J. Technol. Policy Manag. 2020, 20, 21. [Google Scholar] [CrossRef]
- Ünver, M.; Tekez, E.K.; Dİzdar, E.N. The assessment of turkish railway transportation system at the first decade of the 21th century by applying multi-criteria decision making methods. In Proceedings of the 2. Uluslararası Raylı Sistemler Mühendisliği Sempozyumu Başladı (ISERSE’13), Karabük, Türkiye, 9–11 October 2013; pp. 9–11. [Google Scholar]
- Sabri, K.; Colson, G.E.; Mbangala, A.M.; Dubois, D.M. Multiple Criteria and Multiple Periods Performance Analysis: The Comparison of North African Railways. In Proceedings of the Computing Anticipatory Systems: Casys’07—Eighth International Conference, Liège, Belgium, 6–11 August 2007; pp. 351–365. [Google Scholar]
- Dodgson, J. New, disaggregated, British railway total factor productivity growth estimates, 1875 to 19121. Econ. Hist. Rev. 2011, 64, 621–643. [Google Scholar] [CrossRef]
- Le, Y.; Oka, M.; Kato, H. Efficiencies of the urban railway lines incorporating financial performance and in-vehicle congestion in the Tokyo Metropolitan Area. Transp. Policy 2021, 116, 343–354. [Google Scholar] [CrossRef]
- Platform of Rail Infrastructure Managers in Europe. Good Practice Benchmarking of the Rail Infrastructure Managers; Rail Infrastructure Managers: Brussels, Belgium, 2018. [Google Scholar]
- Prokic, M.; Bugarinovic, M. Unique Performances Indicators for Railway Infrastructure. In Proceedings of the VI International Symposium. New Horizons 2017 of Transport and Communications, Doboj, Bosnia and Herzegovina, 17–18 November 2017. [Google Scholar]
- Kecman, P.; Jovanovic, P.; Bugarinovic, M. Evaluating and Ranking Infrastructure Manager Strategies Using the Combined Ahp/Dea Method. In Proceedings of the 5th International Scientific Conference Theoretical and Practical Issues in Transport, Bombay, India, 16–19 December 2014. [Google Scholar]
- Samha, A.K. Strategies for Efficient Resource Management in Federated Cloud Environments Supporting Infrastructure as a Service (IaaS). J. Eng. Res. 2023; in press. [Google Scholar] [CrossRef]
- Sawik, B. Optimizing Last-Mile Delivery: A Multi-Criteria Approach with Automated Smart Lockers, Capillary Distribution and Crowdshipping. Logistics 2024, 8, 52. [Google Scholar] [CrossRef]
- K․, N.K.; S․, J.N.; Jadoun, V. Risk-based dynamic pricing by metaheuristic optimization approach for electric vehicle charging infrastructure powered by grid integrated microgrid system. Electr. Power Syst. Res. 2024, 230, 110250. [Google Scholar] [CrossRef]
- Yang, J.; Xu, X.; Xu, Q.; Yang, H.; Yu, M. Stability and Synchronization of Delayed Quaternion-Valued Neural Networks under Multi-Disturbances. Mathematics 2024, 12, 917. [Google Scholar] [CrossRef]
- Vatan, E.; Ardali, G.A.R.; Shahin, A. Selecting information systems development models based on organizational culture: An integrated approach of DEMATEL and ANP. VINE J. Inf. Knowl. Manag. Syst. 2022, 54, 531–560. [Google Scholar] [CrossRef]
- Saffie, N.A.M.; Shukor, N.M.; Rasmani, K.A. Fuzzy delphi method: Issues and challenges. In Proceedings of the 2016 International Conference on Logistics, Informatics and Service Sciences (LISS), Sydney, Australia, 24–27 July 2016; pp. 1–7. [Google Scholar]
- Leire, S.-J.; Retolaza, J.L. Is the Delphi method valid for business ethics? A survey analysis. Eur. J. Futures Res. 2016, 4, 19. [Google Scholar]
- Dalkey, N.; Helmer, O. An Experimental Application of the DELPHI Method to the Use of Experts. Manag. Sci. 1963, 9, 458–467. [Google Scholar] [CrossRef]
- Ishikawa, A.; Amagasa, M.; Shiga, T.; Tomizawa, G.; Tatsuta, R.; Mieno, H. The max-min Delphi method and fuzzy Delphi method via fuzzy integration. Fuzzy Sets Syst. 1993, 55, 241–253. [Google Scholar] [CrossRef]
- Rowe, G.; Wright, G. Expert Opinions in Forecasting: The Role of the Delphi Technique. Armstrong, J.S. Princ. Forecast. Int. Ser. Oper. Res. Manag. Sci. 2001, 30, 125–144. [Google Scholar]
- Yusoff, A.F.M.; Hashim, A.; Muhamad, N.; Hamat, W.N.W. Application of Fuzzy Delphi Technique to Identify the Elements for Designing and Developing the e-PBM PI-Poli Module. Asian J. Univ. Educ. 2021, 17, 292–304. [Google Scholar] [CrossRef]
- Okoli, C.; Pawlowski, S.D. The Delphi method as a research tool: An example, design considerations and applications. Inf. Manag. 2004, 42, 15–29. [Google Scholar] [CrossRef]
- Manakandan, S.K.; Rosnah, I.; Mohd, R.; Ragunath, P. Pesticide applicators questionnaire content validation: A fuzzy delphi method. Med. J. Malays. 2017, 72, 228–235. [Google Scholar]
- Rahman, N.; Yaacob, N.; Noh, A.Y.M.; Bakar, M.A.A.; Rahman, A. Determination of service key performance indicators for emergency departments of teaching hospitals in Malaysia: A fuzzy delphi method. Med. J. Malays. 2021, 76, 792–798. [Google Scholar]
- Rejab, M.M.; Firdaus, N.; Chuprat, S. Fuzzy Delphi Method for Evaluating HyTEE Model (Hybrid Software Change Management Tool with Test Effort Estimation). Int. J. Adv. Comput. Sci. Appl. 2019, 10, 529–535. [Google Scholar] [CrossRef][Green Version]
- Dawood, K.A.; Sharif, K.Y.; Ghani, A.A.; Zulzalil, H.; Zaidan, A.; Zaidan, B. Towards a unified criteria model for usability evaluation in the context of open source software based on a fuzzy Delphi method. Inf. Softw. Technol. 2020, 130, 106453. [Google Scholar] [CrossRef]
- Bui, T.D.; Tsai, F.M.; Tseng, M.-L.; Ali, M.H. Identifying sustainable solid waste management barriers in practice using the fuzzy Delphi method. Resour. Conserv. Recycl. 2019, 154, 104625. [Google Scholar] [CrossRef]
- Rahayu, P.; Wulandari, I.A. Defining e-portfolio factor for competency certification using fuzzy delphi method. Procedia Comput. Sci. 2022, 197, 566–575. [Google Scholar] [CrossRef]
- Rahman, N.H.; Hairulnizam, T. Developing Key Performance Indicators for Emergency Department of Teaching Hospitals: A Mixed Fuzzy Delphi and Nominal Group Technique Approach. Malays. J. Med. Sci. 2022, 29, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Marlina, E.; Hidayanto, A.N.; Purwandari, B. Towards a model of research data management readiness in Indonesian context: An investigation of factors and indicators through the fuzzy delphi method. Libr. Inf. Sci. Res. 2022, 44, 101141. [Google Scholar] [CrossRef]
- Tadić, S.; Krstić, M.; Radovanović, L. Assessing Strategies to Overcome Barriers for Drone Usage in Last-Mile Logistics: A Novel Hybrid Fuzzy MCDM Model. Mathematics 2024, 12, 367. [Google Scholar] [CrossRef]
- Krstić, M.; Agnusdei, G.P.; Miglietta, P.P.; Tadić, S. Evaluation of the smart reverse logistics development scenarios using a novel MCDM model. Clean. Environ. Syst. 2022, 7, 100099. [Google Scholar] [CrossRef]
- Görçün, Ö.F.; Chatterjee, P.; Stević, Ž.; Küçükönder, H. An integrated model for road freight transport firm selection in third-party logistics using T-spherical Fuzzy sets. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103542. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Tofan, A.S.; Breesam, H.K. Using the Fuzzy-AHP technique for determining the key performance indicators of public construction companies in Iraq. Int. J. Civ. Eng. Technol. 2018, 9, 1431–1445. [Google Scholar]
- Garg, C.P.; Agrawal, V. Evaluation of key performance indicators of Indian airlines using fuzzy AHP method. Int. J. Bus. Perform. Manag. 2022, 24, 1–21. [Google Scholar] [CrossRef]
- Ali, R.; Nikolic, M.; Zahra, A. Personnel selection using group fuzzy AHP and SAW methods. J. Eng. Manag. Compet. 2017, 7, 3–10. [Google Scholar] [CrossRef]
- Stevic, Z.; Tanackov, I. Fuzzy Multicriteria Model for Ranking Suppliers in Manufacturing Company. SSRN Electron. J. 2018, 2, 196–203. [Google Scholar] [CrossRef]
- Gundogdu, F.K.; Kahraman, C. A novel spherical fuzzy analytic hierarchy process and its renewable energy application. Soft Comput. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Kilincci, O.; Onal, S.A. Fuzzy AHP approach for supplier selection in a washing machine company. Expert Syst. Appl. 2011, 38, 9656–9664. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. Assessment of the political city logistics initiatives sustainability. Transp. Res. Procedia 2018, 30, 285–294. [Google Scholar] [CrossRef]
- Moslem, S.; Farooq, D.; Jamal, A.; Almarhabi, Y.; Almoshaogeh, M. An Integrated Fuzzy Analytic Hierarchy Process (AHP) Model. Entropy 2022, 24, 367. [Google Scholar] [CrossRef] [PubMed]
- Kubler, S.; Robert, J.; Derigent, W.; Voisin, A.; Le Traon, Y. A state-of the-art survey & testbed of fuzzy AHP (FAHP) applications. Expert Syst. Appl. 2016, 65, 398–422. [Google Scholar] [CrossRef]
- Tadić, S.R.; Zečević, S.M.; Krstić, M.D. Ranking of Logistics System Scenarios for Central Business District. Promet Traffic Transp. 2014, 26, 159–167. [Google Scholar] [CrossRef]
- Tadić, S.; Zečević, S.; Krstić, M. Ranking of logistics system scenarios using combined fuzzy AHP-VIKOR model. Int. J. Traffic Transp. Eng. 2015, 5, 54–63. [Google Scholar] [CrossRef]
- Kahraman, C.; Cebeci, U.; Ruan, D. Multi-attribute comparison of catering service companies using fuzzy AHP: The case of Turkey. Int. J. Prod. Econ. 2004, 87, 171–184. [Google Scholar] [CrossRef]
- Uğurlu, Ö. Application of Fuzzy Extended AHP methodology for selection of ideal ship for oceangoing watchkeeping officers. Int. J. Ind. Ergon. 2015, 47, 132–140. [Google Scholar] [CrossRef]
- Tyagi, S.; Agrawal, S.; Yang, K.; Ying, H. An extended Fuzzy-AHP approach to rank the influences of socialization-externalization-combination-internalization modes on the development phase. Appl. Soft Comput. 2016, 52, 505–518. [Google Scholar] [CrossRef]
- Bozbura, F.T.; Beskese, A.; Kahraman, C. Prioritization of human capital measurement indicators using fuzzy AHP. Expert Syst. Appl. 2007, 32, 1100–1112. [Google Scholar] [CrossRef]
- Chan, F.T.; Kumar, N. Global supplier development considering risk factors using fuzzy extended AHP-based approach. Omega 2007, 35, 417–431. [Google Scholar] [CrossRef]
- Cortes, Z.; Andrés, J.; Arango, S.; Martín, D.; Wilson, A.J. Applying fuzzy extended analytical hierarchy (FEAHP) for selecting logistics software. Ing. Investig. 2012, 32, 94–99. [Google Scholar] [CrossRef]
- Krstić, M.; Agnusdei, G.P.; Tadić, S.; Kovač, M.; Miglietta, P.P. A Novel Axial-Distance-Based Aggregated Measurement (ADAM) Method for the Evaluation of Agri-Food Circular-Economy-Based Business Models. Mathematics 2023, 11, 1334. [Google Scholar] [CrossRef]
- Krstić, M.; Agnusdei, G.P.; Tadić, S.; Miglietta, P.P. Prioritization of e-traceability drivers in the agri-food supply chains. Agric. Food Econ. 2023, 11, 42. [Google Scholar] [CrossRef]
- Krstić, M.; Tadić, S. Hybrid Multi-Criteria Decision-Making Model for Optimal Selection of Cold Chain Logistics Service Providers. J. Organ. Technol. Entrep. 2023, 1, 77–87. [Google Scholar] [CrossRef]
- Kovač, M.; Tadić, S.; Krstić, M.; Veljović, M. A Methodology for Planning City Logistics Concepts Based on City-Dry Port Micro-Consolidation Centres. Mathematics 2023, 11, 3347. [Google Scholar] [CrossRef]
- Agnusdei, L.; Krstić, M.; Palmi, P.; Miglietta, P.P. Digitalization as driver to achieve circularity in the agroindustry: A SWOT-ANP-ADAM approach. Sci. Total Environ. 2023, 882, 163441. [Google Scholar] [CrossRef]
- Scordamaglia, D.; Katsarova, I. The Fourth Railway Package: Another Step towards a Single European Railway Area, In-Depth Analysis; European Parliamentary Research Service (EPRS): Brussels, Belgium, 2016. [Google Scholar]
- Krstić, M.; Tadić, S.; Kovač, M.; Roso, V.; Zečević, S. A Novel Hybrid MCDM Model for the Evaluation of Sustainable Last Mile Solutions. Math. Probl. Eng. 2021, 2021, 5969788. [Google Scholar] [CrossRef]
- Wan Ab Kadir, W.N.H.; Yap Abdullah, N.S.; Roshawaty Mustapha, I. The Application of The Fuzzy Delphi Technique on A Component of Development of Form Four STEM-Based Physics Interactive Laboratory (I-Lab). Int. J. Sci. Technol. Res. 2019, 8, 2908–2912. [Google Scholar]
- Sulaiman, H.F.; Ismail, R.; Yusoff, H.M.; Anuar, N.; Jamil, M.R.M.; Daud, F. Validation of Occupational Zoonotic Disease Questionnaire Using Fuzzy Delphi Method. J. Agromed. 2019, 25, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Al-Rikabi, Y.K.; Montazer, G.A. Designing an E-learning Readiness Assessment Model for Iraqi Universities Employing Fuzzy Delphi Method. Educ. Inf. Technol. 2023, 29, 2217–2257. [Google Scholar] [CrossRef] [PubMed]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- van Laarhoven, P.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Kwong, C.K.; Bai, H. Determining the importance weights for the customer requirements in QFD using a fuzzy AHF with an extent analysis approach. IIE Trans. (Inst. Ind. Eng.) 2003, 35, 619–626. [Google Scholar]
- Platform of Rail Infrastructure Managers in Europe. 2021 PRIME Benchmarking Report; Rail Infrastructure Managers: Brussels, Belgium, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).