Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization
Abstract
1. Introduction
2. A Short Overview of (, )-Expansion Technique
3. Implementation of Nonlinearities Laws
3.1. Ker Law
3.2. Power Law
4. Method’s Application with Nonlinearities Laws
4.1. Application for Kerr Law
4.2. Application for Power Law
5. Graphs and Meanings
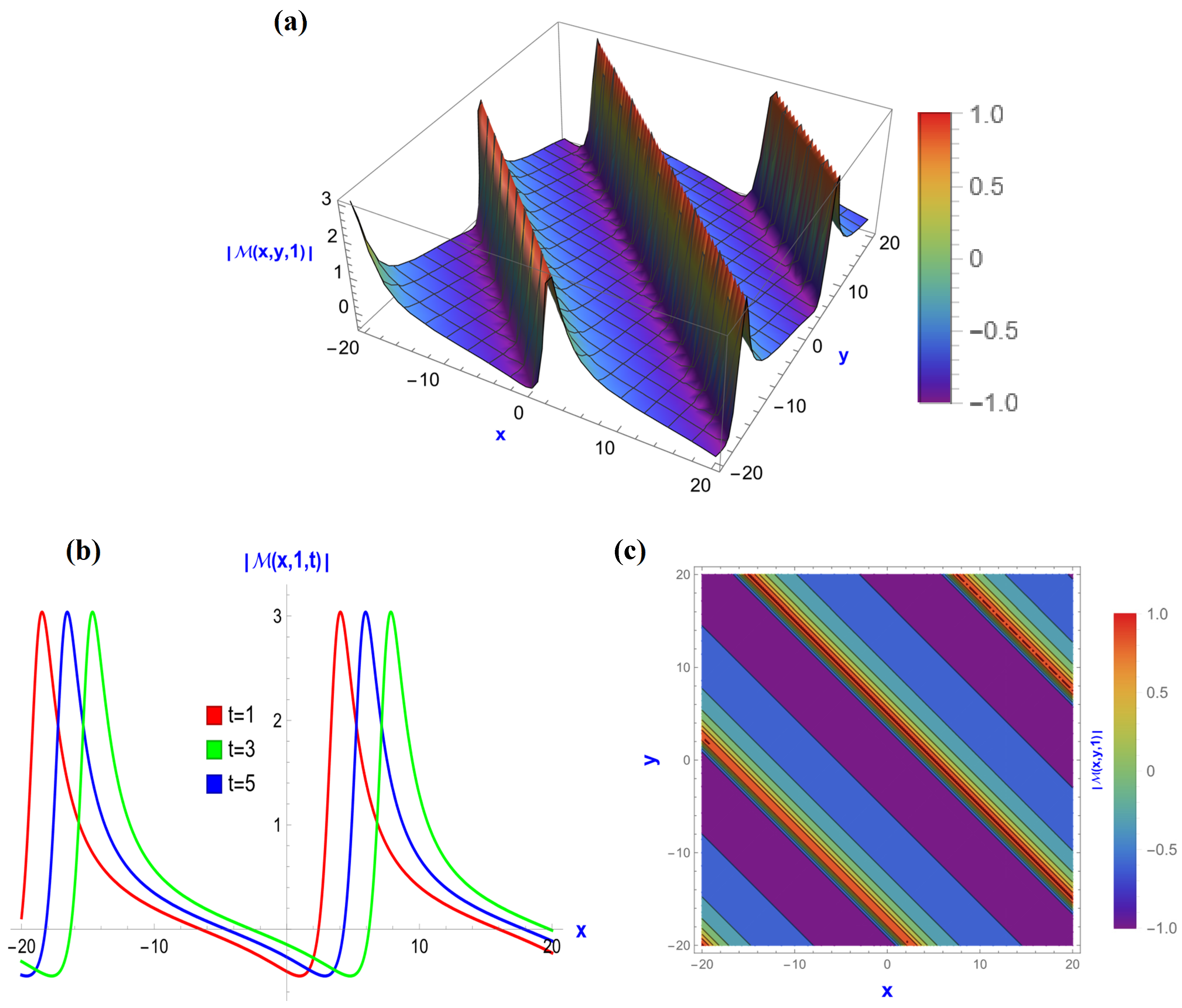
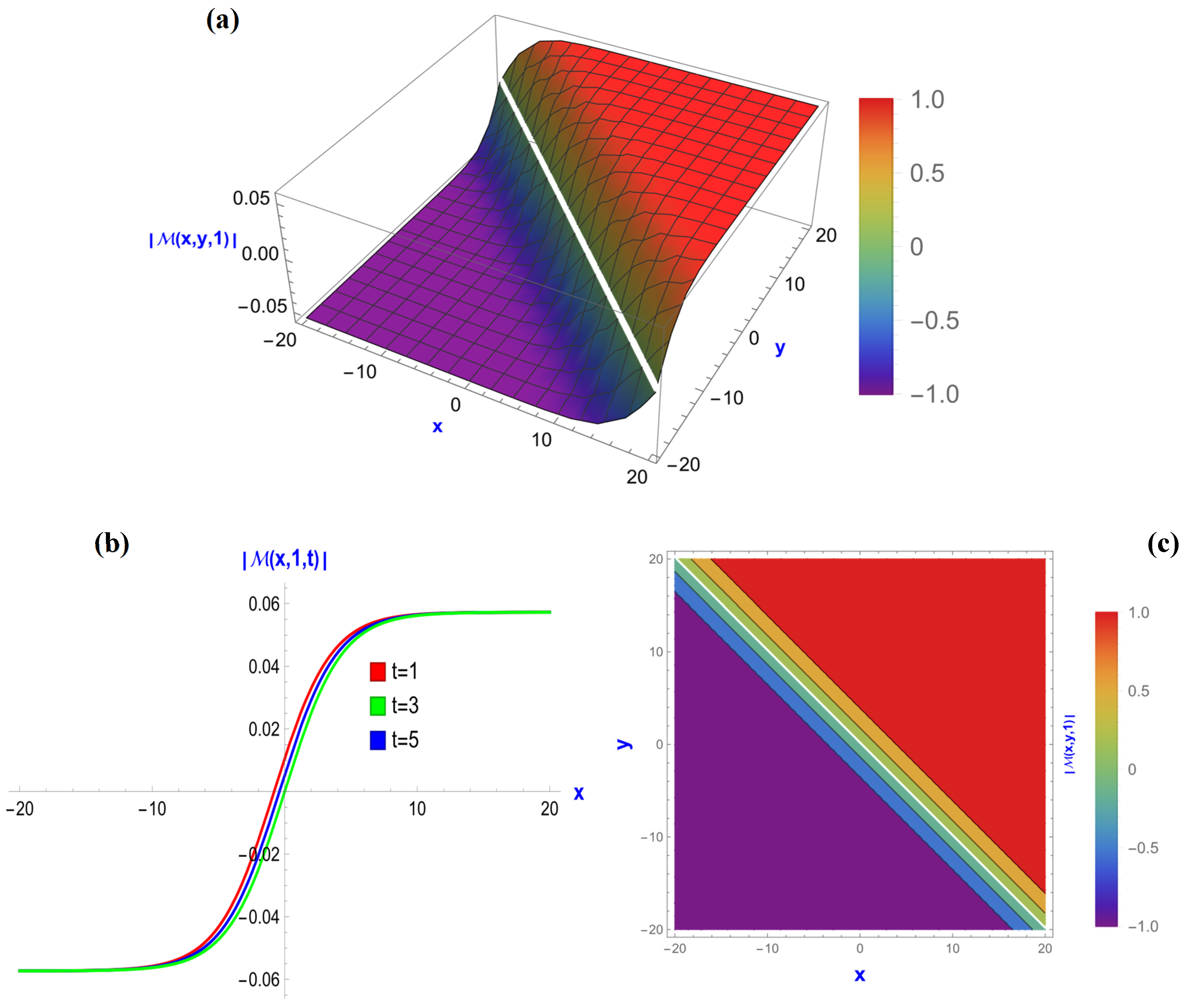
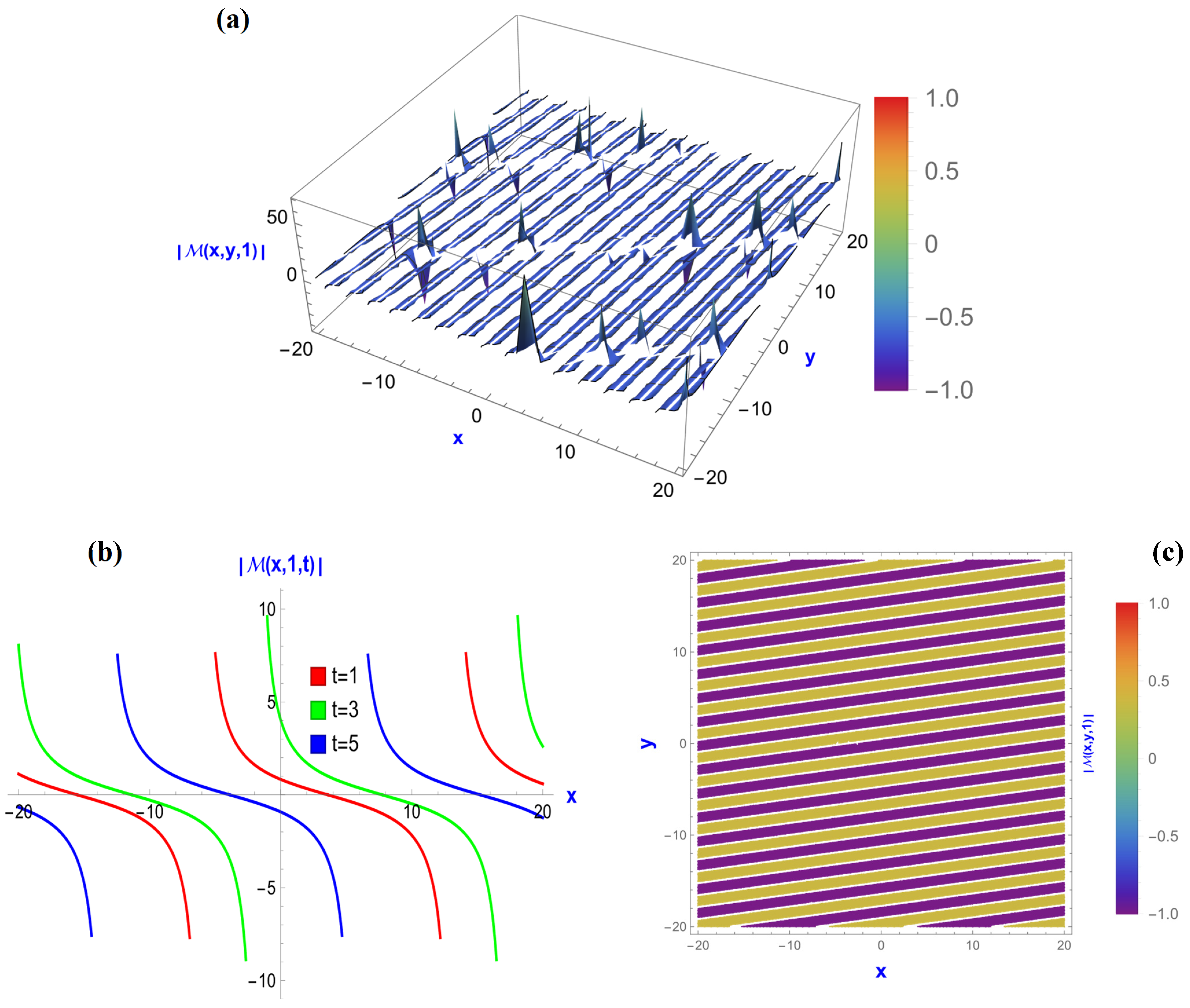
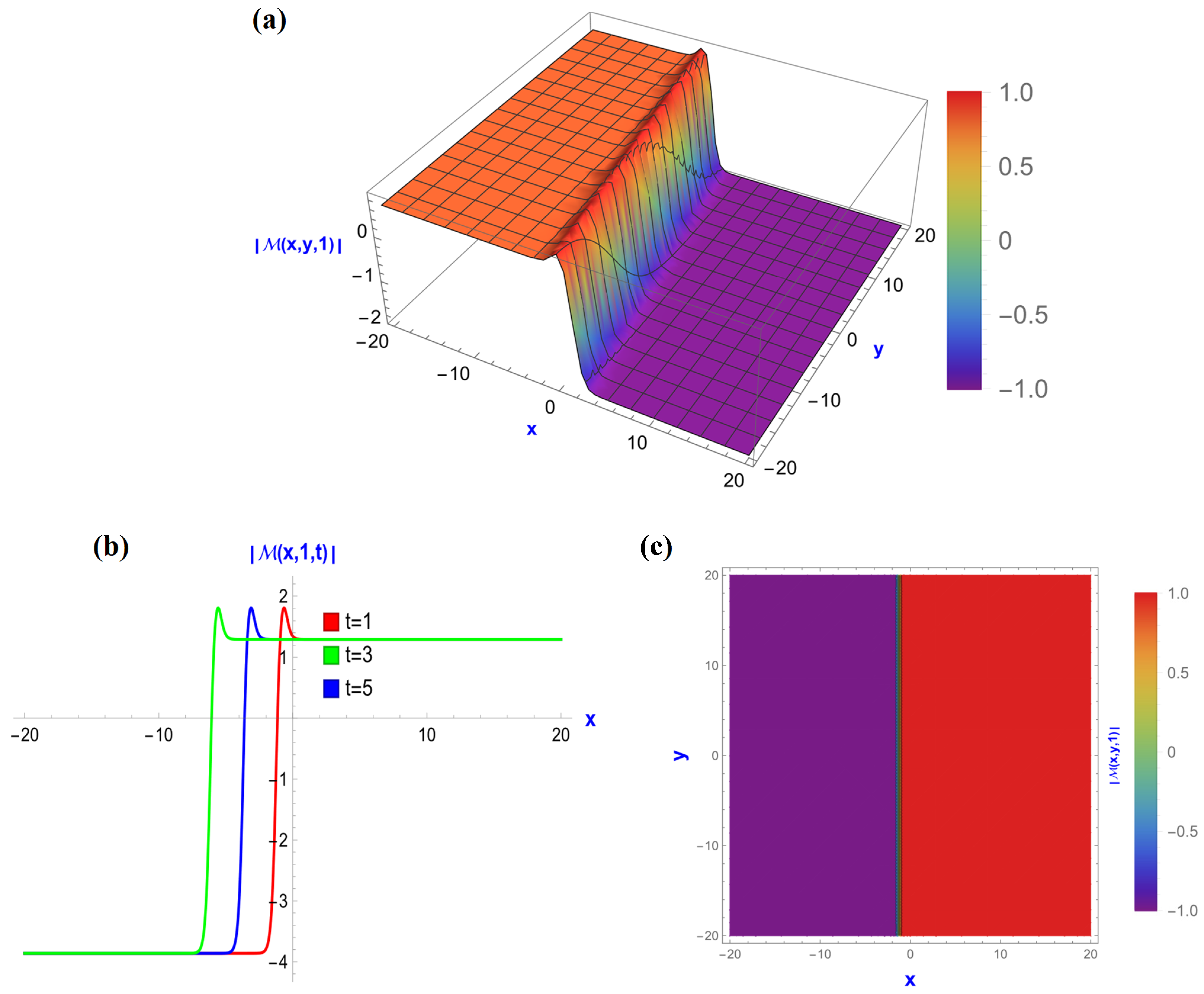
5.1. Visualization of the BME with Kerr Law Nonlinearity
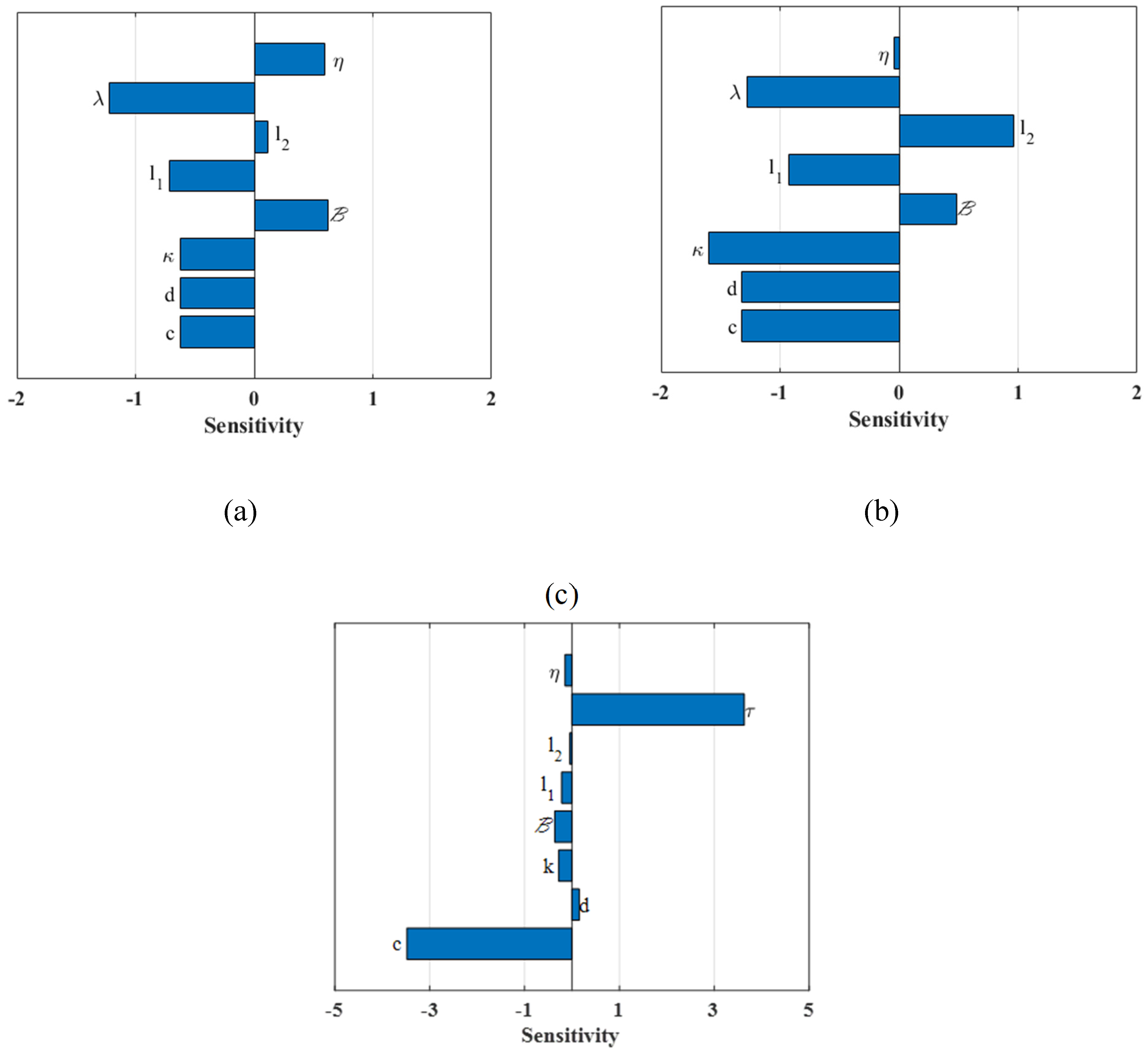
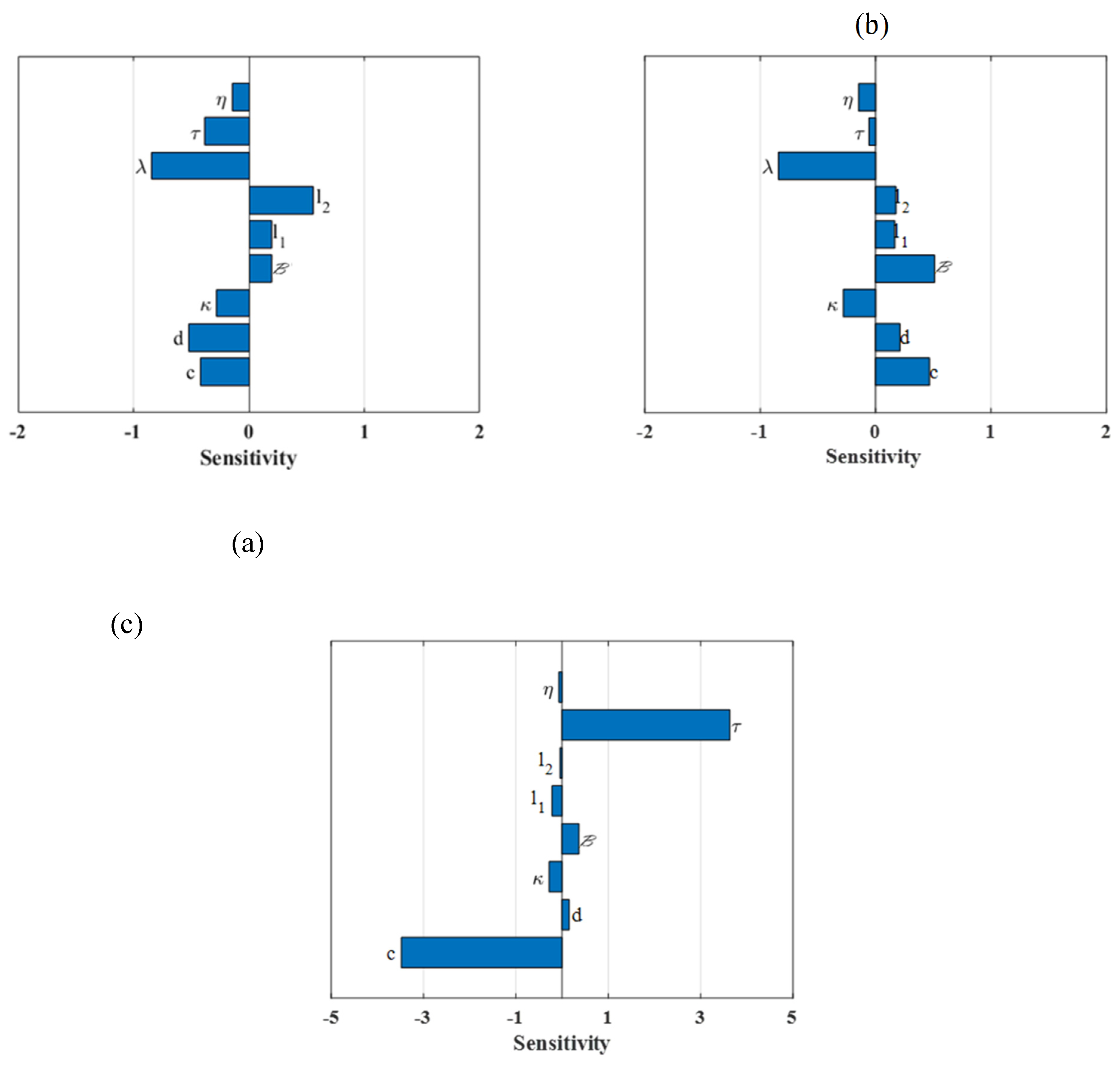
5.2. Sensitivity Analysis
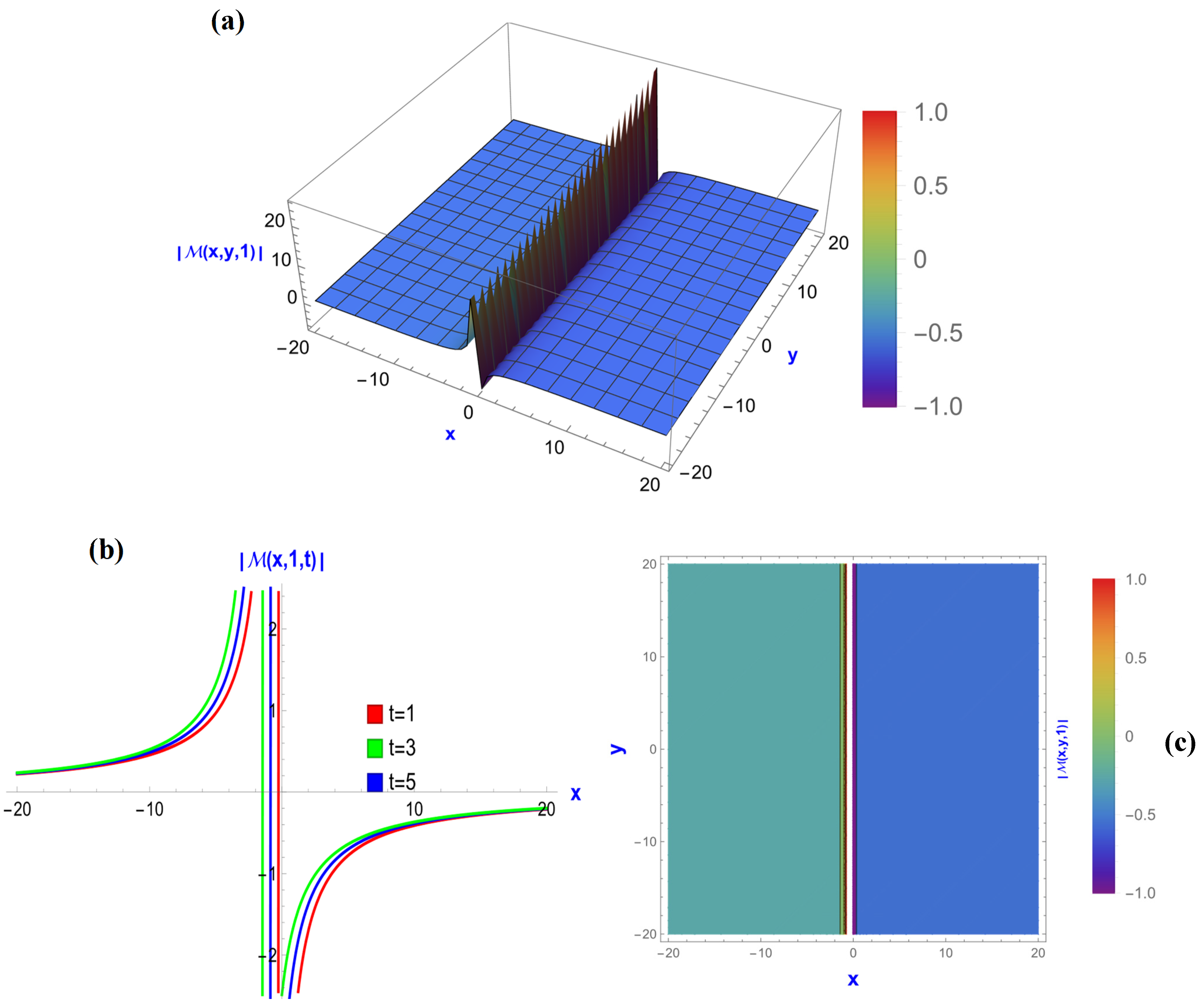
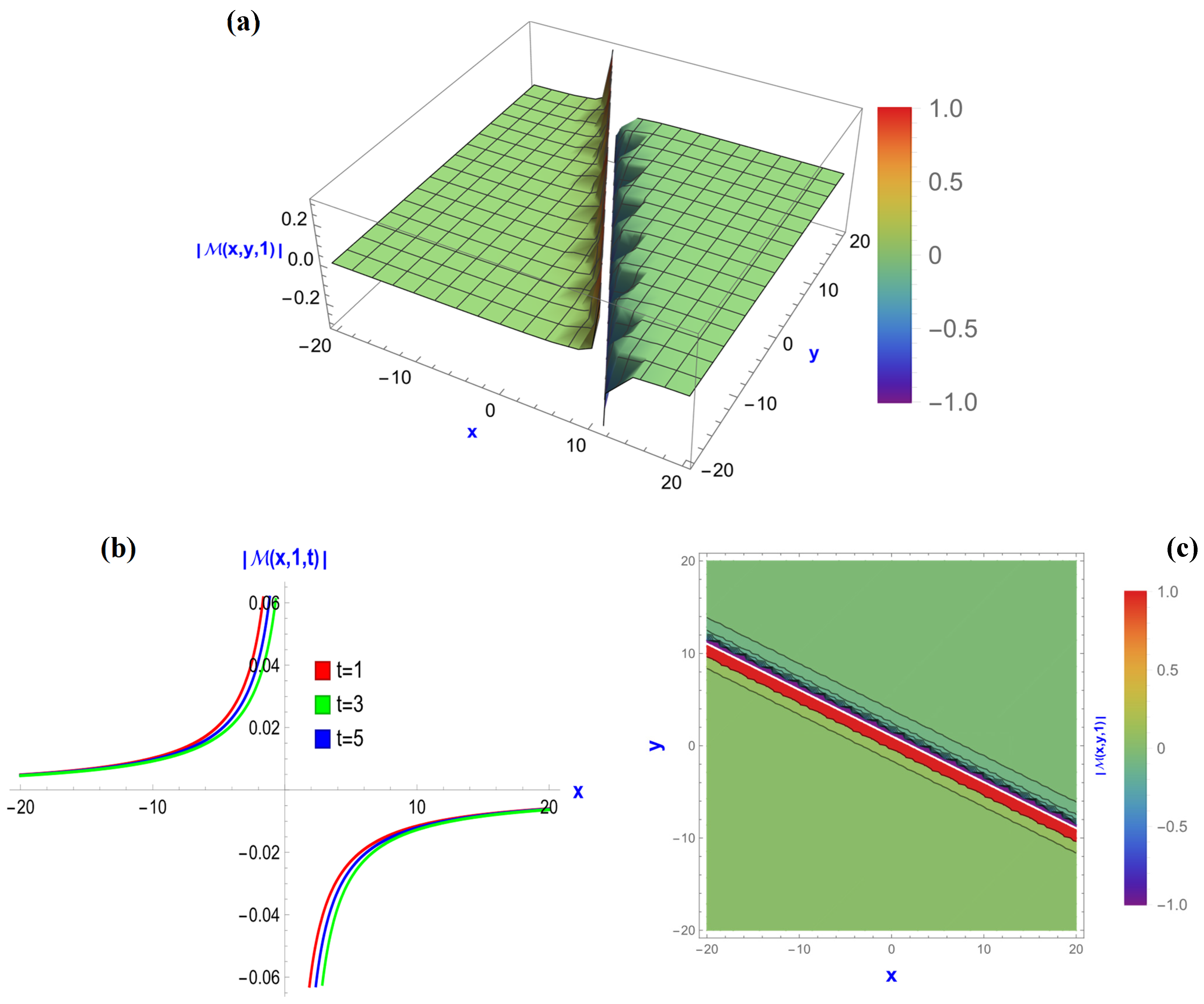
5.3. The Graphical Representation of the BME with Power Law Nonlinearity
5.4. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Verma, P.; Pandit, S.; Kumar, M.; Kumar, V.; Poonam, P. Time-fractional (2 + 1)-dimensional navier-stokes equations: Similarity reduction and exact solutions for one-parameter lie group of rotations. Phys. Scr. 2023, 98, 075233. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Hamid, A.; Osman, G.M.S. Discovering new abundant optical solutions for the resonant nonlinear Schrödinger equation using an analytical technique. Opt. Quantum Electron. 2024, 56, 847. [Google Scholar] [CrossRef]
- Kumar, V.; Jiwari, R.; Djurayevich, A.R.; Khudoyberganov, M.U. Hyperbolic (2+1)-dimensional Schrödinger equation: Similarity analysis, Optimal system and complexitons for the one-parameter group of rotations. Commun. Nonlinear Sci. Numer. Simul. 2022, 115, 106784. [Google Scholar] [CrossRef]
- Borhan, J.R.M.; Ganie, A.H.; Miah, M.M.; Iqbal, M.A.; Seadawy, A.R.; Mishra, N.K. A highly effective analytical approach to innovate the novel closed form soliton solutions of the Kadomtsev–Petviashivili equations with applications. Opt. Quantum Electron. 2024, 56, 938. [Google Scholar] [CrossRef]
- Altun, S.; Ozisik, M.; Secer, A.; Bayram, M. Optical solitons for Biswas–Milovic equation using the new Kudryashov’s scheme. Opt.-Int. J. Light Electron Opt. 2022, 270. [Google Scholar] [CrossRef]
- Ozdemir, N. Optical solitons for the Biswas-Milovic equation with anti-cubic law nonlinearity in the presence of spatio-temporal dispersion. Phys. Scr. 2023, 98, 085229. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Miah, M.M.; Rasid, M.M.; Alshehri, H.M.; Osman, M.S. An investigation of two integro-differential KP hierarchy equations to find out closed form solitons in mathematical physics. Arab J. Basic Appl. Sci. 2023, 30, 535–545. [Google Scholar] [CrossRef]
- Mia, R.; Mamun Miah, M.; Osman, M.S. A new implementation of a novel analytical method for finding the analytical solutions of the (2+1)-dimensional KP-BBM equation. Heliyon 2023, 9, e15690. [Google Scholar] [CrossRef]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New exact solutions of (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation by Sardar-subequation method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Rehman, H.U.; Iqbal, I.; Subhi Aiadi, S.; Mlaiki, N.; Saleem, M.S. Soliton Solutions of Klein–Fock–Gordon Equation Using Sardar Subequation Method. Mathematics 2022, 10, 3377. [Google Scholar] [CrossRef]
- Yomba, E. The general projective riccati equations method and exact solutions for a class of nonlinear partial differential equations. Chin. J. Phys. 2005, 43, 991–1003. [Google Scholar]
- Elsayed, M.E.Z.; Khaled, A.E.A. The generalized projective Riccati equations method and its applications for solving two nonlinear PDEs describing microtubules. Int. J. Phys. Sci. 2015, 10, 391–402. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Y.; Tian, L. Lump solution and interaction solutions to the fourth-order extended (2+1)-dimensional Boiti–Leon–Manna–Pempinelli equation. Commun. Theor. Phys. 2023, 75, 105003. [Google Scholar] [CrossRef]
- Kumar, D.; Nuruzzaman, M.; Paul, G.C.; Hoque, A. Novel localized waves and interaction solutions for a dimensionally reduced (2+1)-dimensional Boussinesq equation from N-soliton solutions. Nonlinear Dyn. 2022, 107, 2717–2743. [Google Scholar] [CrossRef]
- Jafari, H.; Kadkhoda, N.; Baleanu, D. Fractional Lie group method of the time-fractional Boussinesq equation. Nonlinear Dyn. 2015, 81, 1569–1574. [Google Scholar] [CrossRef]
- Buckwar, E.; Luchko, Y. Invariance of a Partial Differential Equation of Fractional Order under the Lie Group of Scaling Transformations. J. Math. Anal. Appl. 1998, 227, 81–97. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Kravchenko, O.V.; Deka, M.K.; Dev, A.N.; Churikov, D.V. The exact solutions of the 2+1–dimensional Kadomtsev–Petviashvili equation with variable coefficients by extended generalized [Formula presented]-expansion method. J. King Saud Univ.-Sci. 2023, 35, 102358. [Google Scholar] [CrossRef]
- Naher, H.; Abdullah, F.A. The Basic (G’/G)-Expansion Method for the Fourth Order Boussinesq Equation. Appl. Math. 2012, 03, 1144–1152. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Ali, K.K.; Razzaq, W. On optical soliton solutions of new Hamiltonian amplitude equation via Jacobi elliptic functions. Eur. Phys. J. Plus 2020, 135, 674. [Google Scholar] [CrossRef]
- Wen, X.; Lü, D. Extended Jacobi elliptic function expansion method and its application to nonlinear evolution equation. Chaos Solitons Fractals 2009, 41, 1454–1458. [Google Scholar] [CrossRef]
- Babajanov, B.; Abdikarimov, F. The Application of the Functional Variable Method for Solving the Loaded Non-linear Evaluation Equations. Front. Appl. Math. Stat. 2022, 8, 912674. [Google Scholar] [CrossRef]
- Bekir, A.; San, S. The Functional Variable Method to Some Complex Nonlinear Evolution Equations. J. Mod. Math. Front. Sept 2012, 1, 5–9. [Google Scholar]
- Wang, M.; Zhou, Y.; Li, Z. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics. Phys. Lett. Sect. A Gen. At. Solid State Phys. 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Fan, E.; Zhang, H. A note on the homogeneous balance method. Phys. Lett. Sect. A Gen. At. Solid State Phys. 1998, 246, 403–406. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solutions and the Hirota conditions in (1+1)-dimensions. De Gruyter 2021, 1–11. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solutions and the Hirota conditions in (2+1)-dimensions. Opt. Quantum Electron. 2020, 52, 511. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Arafat, S.M.Y.; Wang, H. Abundant closed-form wave solutions to the simplified modified Camassa-Holm equation. J. Ocean Eng. Sci. 2023, 8, 238–245. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Exact traveling wave solutions of the perturbed Klein-Gordon equation with quadratic nonlinearity in (1+1)-dimension, Part I: Without local inductance and dissipation effect. Turk. J. Phys. 2013, 37, 259–267. [Google Scholar] [CrossRef]
- Kumar, D.; Paul, G.C.; Seadawy, A.R.; Darvishi, M.T.J. A variety of novel closed-form soliton solutions to the family of Boussinesq-like equations with different types. Ocean Eng. Sci. 2022, 7, 543–554. [Google Scholar] [CrossRef]
- Parkes, E.J.; Duffy, B.R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations. Comput. Phys. Commun. 1996, 98, 288–300. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Kumar, A.; Pankaj, R.D. Tanh–coth scheme for traveling wave solutions for Nonlinear Wave Interaction model. J. Egypt. Math. Soc. 2015, 23, 282–285. [Google Scholar] [CrossRef]
- Mamun, A.-A.-; Ananna, S.N.; An, T.; Asaduzzaman, M.; Miah, M.M. Solitary wave structures of a family of 3D fractional WBBM equation via the tanh–coth approach. Partial Differ. Equ. Appl. Math. 2022, 5, 100237. [Google Scholar] [CrossRef]
- Habib, M.A.; Ali, H.M.S.; Miah, M.M.; Akbar, M.A. The generalized Kudryashov method for new closed form traveling wave solutions to some NLEEs. AIMS Math. 2019, 4, 896–909. [Google Scholar] [CrossRef]
- Islam, S.; Khan, K.; Arnous, A.H. Generalized Kudryashov method for solving some. New Trends Math. Sci. 2015, 57, 46–57. [Google Scholar]
- Raza, N.; Aslam, M.R.; Rezazadeh, H. Analytical study of resonant optical solitons with variable coefficients in Kerr and non-Kerr law media. Opt. Quantum Electron. 2019, 51, 59. [Google Scholar] [CrossRef]
- Roshid, H.O.; Kabir, M.R.; Bhowmik, R.C.; Datta, B.K. Investigation of Solitary wave solutions for Vakhnenko-Parkes equation via exp-function and Exp(−ϕ(ξ))-expansion method. Springerplus 2014, 3, 692. [Google Scholar] [CrossRef]
- Fokas, A.S.; Lenells, J. The unified method: I. Nonlinearizable problems on the half-line. J. Phys. A Math. Theor. 2012, 45, 195201. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Osman, M. On shallow water waves in a medium with time-dependent dispersion and nonlinearity coefficients. J. Adv. Res. 2015, 6, 593–599. [Google Scholar] [CrossRef]
- Ma, W.X.; Huang, T.; Zhang, Y. A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 2010, 82, 065003. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhu, Z. Solving the (3 + 1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 2012, 218, 11871–11879. [Google Scholar] [CrossRef]
- Sadaf, M.; Arshed, S.; Ghazala Akram, I. Exact soliton and solitary wave solutions to the Fokas system using two variables (G′/G,1/G )-expansion technique and generalized projective Riccati equation method. Opt.-Int. J. Light Electron. Opt. 2022, 268, 169713. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.M.S.; Akbar, M.A.; Wazwaz, A.M. Some applications of the (G’/G, 1/G)-expansion method to find new exact solutions of NLEEs. Eur. Phys. J. Plus 2017, 132, 252. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Akram, G.; Sadaf, M.; Arshed, S.; Rehan, K.; Farooq, K. Traveling wave behavior of new (2+1)-dimensional combined KdV–mKdV equation. Results Phys. 2023, 45, 106244. [Google Scholar] [CrossRef]
- Inan, I.E.; Ugurlu, Y. New Applications of the (G’/G, 1/G)-Expansion Method. Acta Phys. Pol. A 2015, 128, 245–251. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alurrfi, K.A.E. The (G’/G, 1/G)-Expansion Method and Its Applications for Solving Two Higher Order Nonlinear Evolution Equations. Math. Probl. Eng. 2014, 2014, 746538. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. Some applications of the (G’/G, 1/G)-expansion method for finding exact traveling wave solutions of nonlinear fractional evolution equations. Symmetry 2019, 11, 952. [Google Scholar] [CrossRef]
- Miah, M.M.; Seadawy, A.R.; Ali, H.M.S.; Akbar, M.A. Abundant closed form wave solutions to some nonlinear evolution equations in mathematical physics. J. Ocean Eng. Sci. 2020, 5, 269–278. [Google Scholar] [CrossRef]
- Rasid, M.M.; Miah, M.M.; Ganie, A.H.; Alshehri, H.M.; Osman, M.S.; Ma, W.X. Further advanced investigation of the complex Hirota-dynamical model to extract soliton solutions. Mod. Phys. Lett. B 2023, 38, 2450074. [Google Scholar] [CrossRef]
- Li, L.X.; Li, E.Q.; Wang, M.L. The (G′/G, 1/G)-expansion method and its application to travelling wave solutions of the Zakharov equations. Appl. Math. 2010, 25, 454–462. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Duraihem, F.Z.; Rehman, S. Stability, modulation instability, and analytical study of the confirmable time fractional Westervelt equation and the Wazwaz Kaur Boussinesq equation. Opt. Quantum Electron. 2024, 56, 948. [Google Scholar] [CrossRef]
- Biswas, A. Quasi-stationary optical solitons with dual-power law nonlinearity. Opt. Commun. 2004, 235, 183–194. [Google Scholar] [CrossRef]
- Zhou, Q.; Ekici, M.; Sonmezoglu, A.; Mirzazadeh, M.; Eslami, M. Optical solitons with Biswas–Milovic equation by extended trial equation method. Nonlinear Dyn. 2016, 84, 1883–1900. [Google Scholar] [CrossRef]
- Ali, A.; Ahmad, J.; Javed, S. Exploring the dynamic nature of soliton solutions to the fractional coupled nonlinear Schrödinger model with their sensitivity analysis. Opt. Quantum Electron. 2023, 55, 810. [Google Scholar] [CrossRef]
- Chahlaoui, Y.; Ali, A.; Ahmad, J.; Hussain, R.; Javed, S. Dynamical behavior of optical soliton solutions, time series and sensitivity analysis to the Schrödinger model with eta fractional derivative. Opt. Quantum Electron. 2024, 56, 704. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.N.; Alsharif, F.; Miah, M.M.; Kanan, M. Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization. Mathematics 2024, 12, 1585. https://doi.org/10.3390/math12101585
Hossain MN, Alsharif F, Miah MM, Kanan M. Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization. Mathematics. 2024; 12(10):1585. https://doi.org/10.3390/math12101585
Chicago/Turabian StyleHossain, Md Nur, Faisal Alsharif, M. Mamun Miah, and Mohammad Kanan. 2024. "Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization" Mathematics 12, no. 10: 1585. https://doi.org/10.3390/math12101585
APA StyleHossain, M. N., Alsharif, F., Miah, M. M., & Kanan, M. (2024). Abundant New Optical Soliton Solutions to the Biswas–Milovic Equation with Sensitivity Analysis for Optimization. Mathematics, 12(10), 1585. https://doi.org/10.3390/math12101585




