Streamlining Ocean Dynamics Modeling with Fourier Neural Operators: A Multiobjective Hyperparameter and Architecture Optimization Approach
Abstract
1. Introduction
2. Related Work
2.1. Fourier Neural Opearator
2.2. Hyperparameter Optimization with DeepHyper
2.2.1. Centralized Bayesian Optimization
2.2.2. Multiobjective Optimization
2.3. Data-Driven Ocean Modeling
3. Method
3.1. Problem Formulation
3.2. Bayesian Optimization and Multipoint Acquisition
4. Numerical Experiments
4.1. Dataset
4.2. Hyperparameter Search Space
4.3. Objectives
4.4. Implementation
5. Results and Discussion
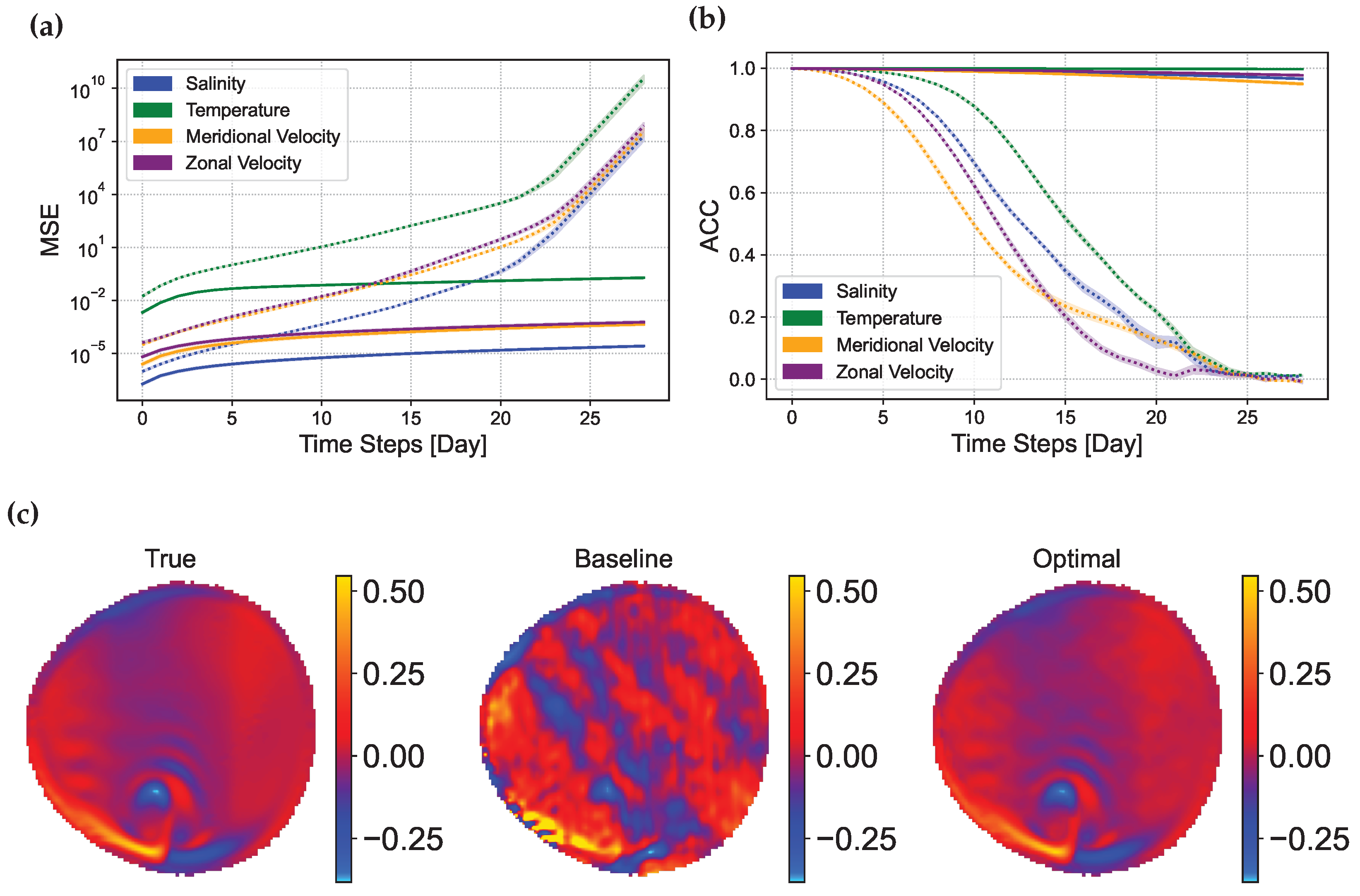
5.1. First Objective: Validation Mean Square Error
5.2. Second Objective: Validation Anomaly Coefficient Correlation
5.3. Relationship between MSE and ACC
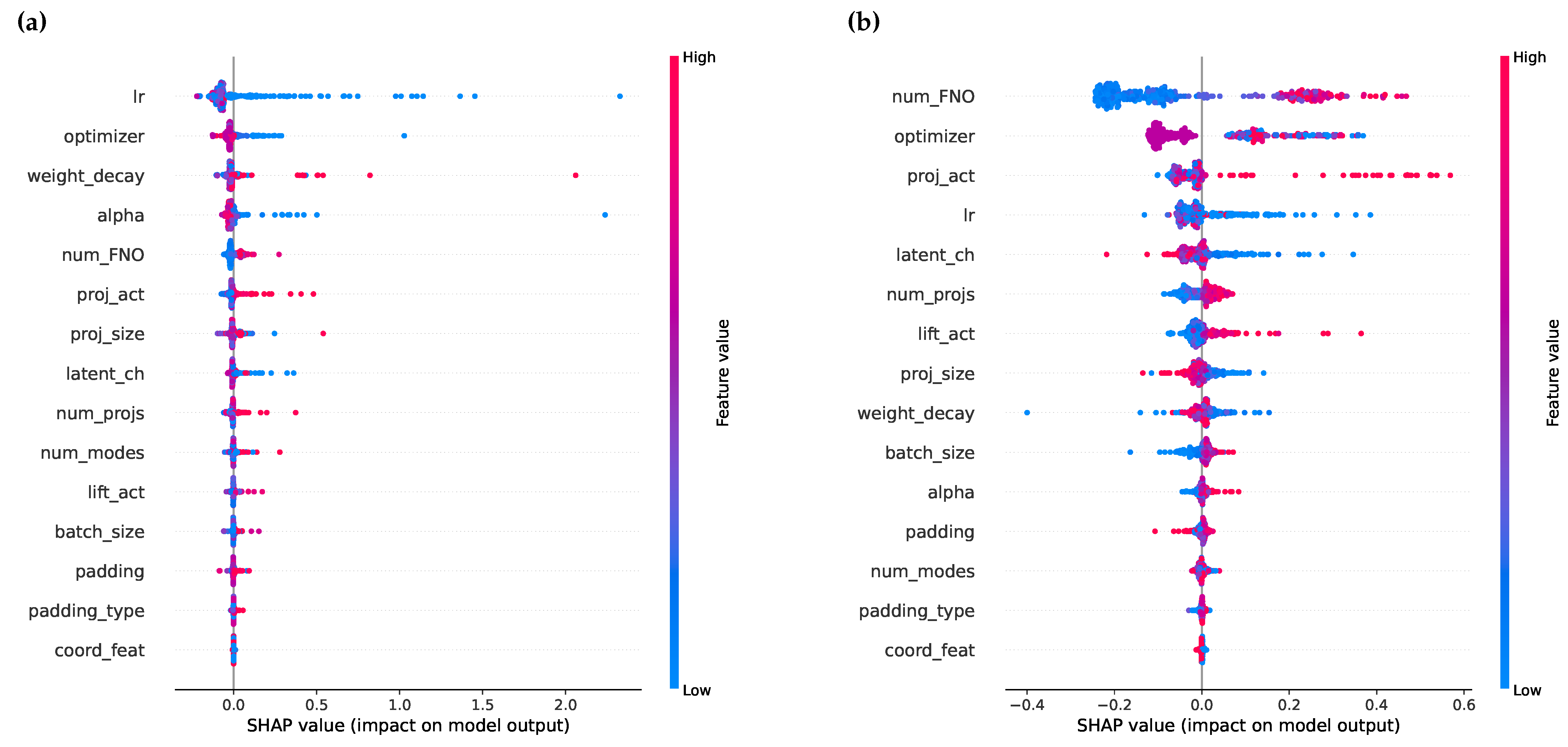
5.4. Sensitivity Analysis
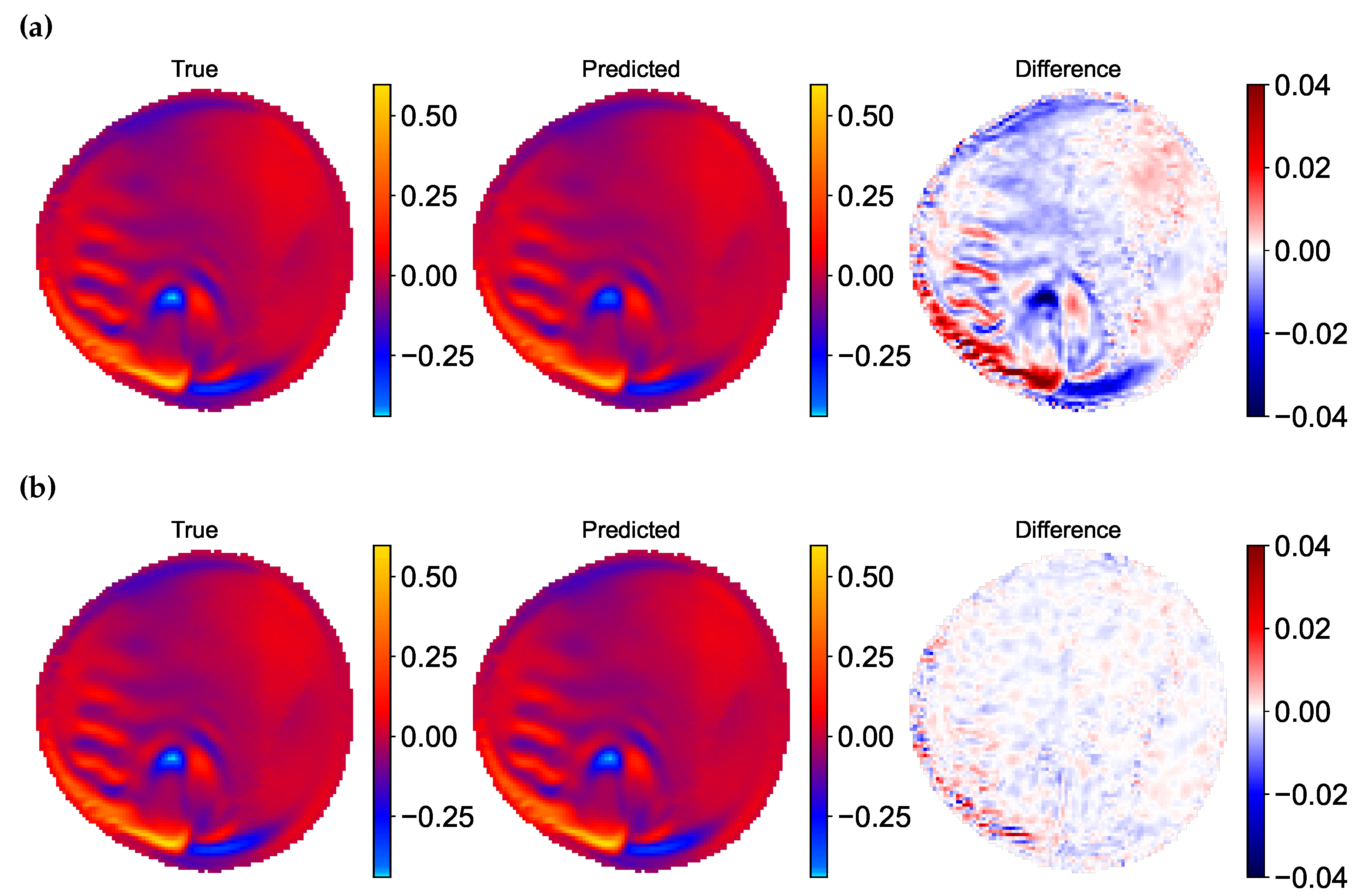
5.5. Train with Optimal Configuration
6. Conlusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kurth, T.; Treichler, S.; Romero, J.; Mudigonda, M.; Luehr, N.; Phillips, E.; Mahesh, A.; Matheson, M.; Deslippe, J.; Fatica, M.; et al. Exascale deep learning for climate analytics. In Proceedings of the SC18: International Conference for High Performance Computing, Computing, Networking, Storage and Analysis, Dallas, TX, USA, 11–16 November 2018; pp. 649–660. [Google Scholar]
- Rasp, S.; Pritchard, M.S.; Gentine, P. Deep learning to represent subgrid processes in climate models. Proc. Natl. Acad. Sci. USA 2018, 115, 9684–9689. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Brandstetter, J.; Kapoor, A.; Gupta, J.K.; Grover, A. ClimaX: A foundation model for weather and climate. arXiv 2023, arXiv:2301.10343. [Google Scholar]
- Gibson, P.B.; Chapman, W.E.; Altinok, A.; Delle Monache, L.; DeFlorio, M.J.; Waliser, D.E. Training machine learning models on climate model output yields skillful interpretable seasonal precipitation forecasts. Commun. Earth Environ. 2021, 2, 159. [Google Scholar] [CrossRef]
- Pathak, J.; Subramanian, S.; Harrington, P.; Raja, S.; Chattopadhyay, A.; Mardani, M.; Kurth, T.; Hall, D.; Li, Z.; Azizzadenesheli, K.; et al. FourCastNet: A global data-driven high-resolution weather model using adaptive Fourier neural operators. arXiv 2022, arXiv:2202.11214. [Google Scholar]
- Cheng, L.; Trenberth, K.E.; Fasullo, J.; Boyer, T.; Abraham, J.; Zhu, J. Improved estimates of ocean heat content from 1960 to 2015. Sci. Adv. 2017, 3, e1601545. [Google Scholar] [CrossRef] [PubMed]
- Gou, Y.; Zhang, T.; Liu, J.; Wei, L.; Cui, J.H. DeepOcean: A general deep learning framework for spatio-temporal ocean sensing data prediction. IEEE Access 2020, 8, 79192–79202. [Google Scholar] [CrossRef]
- Choi, Y.; Park, Y.; Hwang, J.; Jeong, K.; Kim, E. Improving ocean forecasting using deep learning and numerical model integration. J. Mar. Sci. Eng. 2022, 10, 450. [Google Scholar] [CrossRef]
- Partee, S.; Ellis, M.; Rigazzi, A.; Shao, A.E.; Bachman, S.; Marques, G.; Robbins, B. Using machine learning at scale in numerical simulations with SmartSim: An application to ocean climate modeling. J. Comput. Sci. 2022, 62, 101707. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, R.H.; Moum, J.N.; Wang, F.; Li, X.; Li, D. Physics-informed deep-learning parameterization of ocean vertical mixing improves climate simulations. Natl. Sci. Rev. 2022, 9, nwac044. [Google Scholar] [CrossRef]
- Guillaumin, A.P.; Zanna, L. Stochastic-deep learning parameterization of ocean momentum forcing. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002534. [Google Scholar] [CrossRef]
- Zanna, L.; Bolton, T. Data-driven equation discovery of ocean mesoscale closures. Geophys. Res. Lett. 2020, 47, e2020GL088376. [Google Scholar] [CrossRef]
- Liao, L.; Li, H.; Shang, W.; Ma, L. An empirical study of the impact of hyperparameter tuning and model optimization on the performance properties of deep neural networks. ACM Trans. Softw. Eng. Methodol. (TOSEM) 2022, 31, 1–40. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Pangu-Weather: A 3D High-Resolution Model for Fast and Accurate Global Weather Forecast. arXiv 2022, arXiv:2211.02556. [Google Scholar]
- Mustafa, A.; Mikhailiuk, A.; Iliescu, D.A.; Babbar, V.; Mantiuk, R.K. Training a Task-Specific Image Reconstruction Loss. arXiv 2021, arXiv:2103.14616. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss functions for image restoration with neural networks. IEEE Trans. Comput. Imaging 2016, 3, 47–57. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 694–711. [Google Scholar]
- Murphy, A.H.; Epstein, E.S. Skill scores and correlation coefficients in model verification. Mon. Weather Rev. 1989, 117, 572–582. [Google Scholar] [CrossRef]
- Li, Z.; Kovachki, N.; Azizzadenesheli, K.; Liu, B.; Bhattacharya, K.; Stuart, A.; Anandkumar, A. Fourier neural operator for parametric partial differential equations. arXiv 2020, arXiv:2010.08895. [Google Scholar]
- Balaprakash, P.; Salim, M.; Uram, T.D.; Vishwanath, V.; Wild, S.M. DeepHyper: Asynchronous hyperparameter search for deep neural networks. In Proceedings of the 2018 IEEE 25th International Conference on High Performance Computing (HiPC), Bengaluru, India, 17–20 December 2018; pp. 42–51. [Google Scholar]
- Balaprakash, P.; Egele, R.; Salim, M.; Maulik, R.; Vishwanath, V.; Wild, S. DeepHyper: A Python Package for Scalable Neural Architecture and Hyperparameter Search. 2018. [Google Scholar]
- Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.; et al. Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. [Google Scholar] [CrossRef]
- Guibas, J.; Mardani, M.; Li, Z.; Tao, A.; Anandkumar, A.; Catanzaro, B. Adaptive Fourier neural operators: Efficient token mixers for transformers. arXiv 2021, arXiv:2111.13587. [Google Scholar]
- Li, Z.; Zheng, H.; Kovachki, N.; Jin, D.; Chen, H.; Liu, B.; Azizzadenesheli, K.; Anandkumar, A. Physics-Informed Neural Operator for Learning Partial Differential Equations. arXiv 2023, arXiv:2111.03794. [Google Scholar] [CrossRef]
- Fanaskov, V.; Oseledets, I. Spectral Neural Operators. arXiv 2022, arXiv:2205.10573. [Google Scholar] [CrossRef]
- Grady, T.J.; Khan, R.; Louboutin, M.; Yin, Z.; Witte, P.A.; Chandra, R.; Hewett, R.J.; Herrmann, F. Towards Large-Scale Learned Solvers for Parametric PDEs with Model-Parallel Fourier Neural Operators. arXiv 2022, arXiv:abs/2204.01205. [Google Scholar]
- Zhang, T.; Trad, D.O.; Innanen, K.A. Learning to solve the elastic wave equation with Fourier neural operators. Geophysics 2023, 88, T101–T119. [Google Scholar] [CrossRef]
- Bire, S.; Lütjens, B.; Azizzadenesheli, K.; Anandkumar, A.; Hill, C.N. Ocean emulation with Fourier neural operators: Double gyre. Authorea Prepr. 2023. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-Based Optimization for General Algorithm Configuration. In Learning and Intelligent Optimization; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Egelé, R.; Guyon, I.; Vishwanath, V.; Balaprakash, P. Asynchronous Decentralized Bayesian Optimization for Large Scale Hyperparameter Optimization. In Proceedings of the 2023 IEEE 19th International Conference on e-Science (e-Science), Limassol, Cyprus, 9–13 October 2023; pp. 1–10. [Google Scholar]
- Wilson, J.T.; Moriconi, R.; Hutter, F.; Deisenroth, M.P. The reparameterization trick for acquisition functions. arXiv 2017, arXiv:1712.00424. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
- Ginsbourger, D.; Riche, R.L.; Carraro, L. Kriging is well-suited to parallelize optimization. In Computational Intelligence in Expensive Optimization Problems; Springe: Berlin/Heidelberg, Germany, 2010; pp. 131–162. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kadlec, P.; Raida, Z. Multi-objective self-organizing migrating algorithm. Self-Organizing Migrating Algorithm: Methodology and Implementation; Springer: Berlin/Heidelberg, Germany, 2016; pp. 83–103. [Google Scholar]
- Ehrgott, M. Multicriteria Optimization; Springer Science & Business Media: Berlin, Germany, 2005; Volume 491. [Google Scholar]
- Égelé, R.; Chang, T.; Sun, Y.; Vishwanath, V.; Balaprakash, P. Parallel Multi-Objective Hyperparameter Optimization with Uniform Normalization and Bounded Objectives. arXiv 2023, arXiv:2309.14936. [Google Scholar]
- Radeta, M.; Zuniga, A.; Motlagh, N.H.; Liyanage, M.; Freitas, R.; Youssef, M.A.; Tarkoma, S.; Flores, H.; Nurmi, P. Deep Learning and the Oceans. Computer 2022, 55, 39–50. [Google Scholar] [CrossRef]
- Er, M.J.; Chen, J.; Zhang, Y.; Gao, W. Research Challenges, Recent Advances, and Popular Datasets in Deep Learning-Based Underwater Marine Object Detection: A Review. Sensors 2023, 23, 1990. [Google Scholar] [CrossRef] [PubMed]
- Zrira, N.; Kamal-Idrissi, A.; Farssi, R.; Khan, H.A. Time series prediction of sea surface temperature based on BiLSTM model with attention mechanism. J. Sea Res. 2024, 198, 102472. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep-learning-based information mining from ocean remote-sensing imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef] [PubMed]
- Colin, A.; Tandeo, P.; Peureux, C.; Husson, R.; Longépé, N.; Fablet, R. Rain regime segmentation of Sentinel-1 observation learning from NEXRAD collocations with Convolution Neural Networks. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4202914. [Google Scholar] [CrossRef]
- Sun, Y.; Cucuzzella, E.; Brus, S.; Narayanan, S.H.K.; Nadiga, B.; Van Roekel, L.; Hückelheim, J.; Madireddy, S. Surrogate Neural Networks to Estimate Parametric Sensitivity of Ocean Models. arXiv 2023, arXiv:2311.08421. [Google Scholar]
- Wolfram, P.J.; Ringler, T.D.; Maltrud, M.E.; Jacobsen, D.W.; Petersen, M.R. Diagnosing isopycnal diffusivity in an eddying, idealized midlatitude ocean basin via Lagrangian, in situ, global, high-performance particle tracking (LIGHT). J. Phys. Oceanogr. 2015, 45, 2114–2133. [Google Scholar] [CrossRef]
- Alrasheedi, F.; Zhong, X.; Huang, P.C. Padding Module: Learning the Padding in Deep Neural Networks. IEEE Access 2023, 11, 7348–7357. [Google Scholar] [CrossRef]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. arXiv 2012, arXiv:1206.5533. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]


| (a) | |||
|---|---|---|---|
| Variable Names | Type | Range/Choice | Explanation |
| padding | bool | [True, False] | If zero-pad the data. |
| padding_type | str | [‘constant’, ‘reflect’, ‘replicate’, ‘circular’] | Types of padding. |
| coord_feat | bool | [True, False] | If use domain coordinates as additional features. |
| (b) | |||
| Variable Names | Type | Range/Choice | Explanation |
| lift_act | str | [‘relu’, ‘leaky_relu’, ‘prelu’, ‘relu6’, ‘elu’, ‘selu’, ‘silu’, ‘gelu’, ‘sigmoid’, ‘logsigmoid’, ‘softplus’, ‘softshrink’, ‘softsign’, ‘tanh’, ‘tanhshrink’, ‘threshold’, ‘hardtanh’, ‘identity’, ‘squareplus’] | Activation function for lifting layers. The choices include common activation functions implemented in PyTorch. |
| num_FNO | int | [2, 16] | The number of FNO blocks. |
| num_latent_feat | int | [2, 64] | The number of latent features in FNO blocks. This is equivalent to the number of channels in an image representation. |
| num_modes | int | [2, 32] | The number of Fourier modes to keep. |
| num_proj_layers | int | [2, 16] | The number of projection layers. |
| proj_size | int | [2, 16] | Projection layer size. |
| proj_act | str | [‘relu’, ‘leaky_relu’, ‘prelu’, ‘relu6’, ‘elu’, ‘selu’, ‘silu’, ‘gelu’, ‘sigmoid’, ‘logsigmoid’, ‘softplus’, ‘softshrink’, ‘softsign’, ‘tanh’, ‘tanhshrink’, ‘threshold’, ‘hardtanh’, ‘identity’, ‘squareplus’] | Activation function for projection layers. The choices include common activation functions implemented in PyTorch. |
| (c) | |||
| Variable Names | Type | Range/Choice | Explanation |
| alpha | float | (0, 1) | Weight associated with MSE and negative ACC in the loss function. |
| optimizer | str | [‘Adadelta’, ‘Adagrad’, ‘Adam’, ‘AdamW’, ‘RMSprop’, ‘SGD’] | Types of optimizers. |
| lr | float | (10−6, 10−2) | Learning rate |
| weight_decay | float | (0, 0.1) | The weighting factor of the regularization. |
| batch_size | int | (2, 64) | The batch size of training data during training. |
| log(RSE)↓ | log(1 −ACC)↓ | |||
|---|---|---|---|---|
| MSE Loss | MSE + NegACC Loss | MSE Loss | MSE + NegACC Loss | |
| Salinity | ||||
| Temperature | ||||
| Meridional V. | ||||
| Zonal V. | ||||
| Baseline | Optimal | |||
|---|---|---|---|---|
| log(RSE)↓ | log(1 − ACC)↓ | log(RSE)↓ | log(1 − ACC)↓ | |
| Salinity | ||||
| Temperature | ||||
| Meridional V. | ||||
| Zonal V. | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Sowunmi, O.; Egele, R.; Narayanan, S.H.K.; Van Roekel, L.; Balaprakash, P. Streamlining Ocean Dynamics Modeling with Fourier Neural Operators: A Multiobjective Hyperparameter and Architecture Optimization Approach. Mathematics 2024, 12, 1483. https://doi.org/10.3390/math12101483
Sun Y, Sowunmi O, Egele R, Narayanan SHK, Van Roekel L, Balaprakash P. Streamlining Ocean Dynamics Modeling with Fourier Neural Operators: A Multiobjective Hyperparameter and Architecture Optimization Approach. Mathematics. 2024; 12(10):1483. https://doi.org/10.3390/math12101483
Chicago/Turabian StyleSun, Yixuan, Ololade Sowunmi, Romain Egele, Sri Hari Krishna Narayanan, Luke Van Roekel, and Prasanna Balaprakash. 2024. "Streamlining Ocean Dynamics Modeling with Fourier Neural Operators: A Multiobjective Hyperparameter and Architecture Optimization Approach" Mathematics 12, no. 10: 1483. https://doi.org/10.3390/math12101483
APA StyleSun, Y., Sowunmi, O., Egele, R., Narayanan, S. H. K., Van Roekel, L., & Balaprakash, P. (2024). Streamlining Ocean Dynamics Modeling with Fourier Neural Operators: A Multiobjective Hyperparameter and Architecture Optimization Approach. Mathematics, 12(10), 1483. https://doi.org/10.3390/math12101483






