1. Introduction
Transportation infrastructure stands as the most pivotal component of a nation’s core infrastructure, often representing its largest subcomponent and serving as a critical foundation for economic prosperity and societal welfare. The allocation of resources towards this sector is perceived as a direct contribution to a nation’s economic and social growth, evidenced by leading institutions such as the World Bank allocating substantial financial support to transportation infrastructure, surpassing contributions towards health or education [
1]. This strategic emphasis highlights transportation infrastructure’s crucial role in catalyzing societal progression. Amidst an increasingly marked transition towards sustainable development, the investment strategy in transportation infrastructure now necessitates a holistic life cycle evaluation [
2]. This approach ensures that fiscal commitments address immediate needs and champion enduring, sustainable solutions that protect future generations’ interests. It integrates environmental sustainability and global interconnectivity into the essence of infrastructure development, fostering a paradigm that balances immediate benefits with long-term viability.
Within the crucial role of transportation infrastructure, the construction sector stands as a dynamic catalyst, essential for the fruition of these projects. The construction industry is poised for substantial growth, with forecasts indicating a surge beyond 14 trillion dollars globally in the ensuing year, significantly influencing the global economic landscape [
3]. This expansion illustrates the industry’s immense scale and its vital role in propelling economic advancement through the generation of employment opportunities, both during the design and construction phases and in the ongoing maintenance of infrastructure. Its operation strengthens job prospects within the sector and related fields, underscoring the construction industry’s contribution to broad-based economic development.
However, positioned as one of the most resource-intensive and environmentally impacting sectors, the construction industry is under increasing scrutiny to reform antiquated practices in favor of more sustainable approaches [
4]. This juxtaposition of the industry’s considerable economic contributions against its environmental and social implications has sparked a critical examination. Acknowledging this challenge has prompted a realignment of capital investment strategies, prioritizing incorporating life cycle sustainability—encompassing economic, environmental, and social considerations—right from the conceptual stages of transportation infrastructure projects [
5]. This shift is not merely a nod to ethical standards but emerges as a strategic necessity to secure investment and champion the cause of sustainable development. The construction sector is compelled to embrace a comprehensive strategy that transcends traditional methodologies. Adopting an integrated approach in designing highly efficient infrastructure is instrumental in realizing economically sound, environmentally sustainable, and socially equitable projects, marking a significant stride towards a balanced development paradigm.
Adopting an integrated framework incorporating sustainable design strategies from the outset is essential for aligning transportation infrastructure construction with overarching sustainable development objectives [
6]. This strategy ensures that efforts in construction engineering are developed with a comprehensive outlook, evaluating aspects such as economic viability, environmental preservation, and social responsibility. Embracing this broader framework, which considers the project’s entire life cycle, can stimulate innovation and foster more profound collaboration among all stakeholders. Moreover, it sets a foundational standard for integrating life cycle sustainability considerations, facilitating more enlightened decision-making throughout the critical phases of conception, design, and funding acquisition of transportation infrastructure projects. This refined approach ensures the immediate project needs are met while incorporating a shift towards more responsible and forward-thinking infrastructure development practices.
Embracing a life cycle standpoint necessitates the evaluation and objective quantification of environmental, social, and economic impacts spanning from a project’s inception to its decommissioning. This perspective fosters sensitive material and energy use, emphasizing long-term benefits for communities and the environment. Applying advanced life cycle and structural mathematical modeling signifies a pivotal transition from traditional to innovative design strategies. This shift promotes the early integration of optimization and decision-making techniques, significantly enhancing the alignment of infrastructure projects with sustainable development goals. Such an approach underlines the importance of a holistic view in infrastructure development, ensuring that projects are not only designed for immediate functionality under economic viability constraints but also for their long-term sustainability, operational efficiency, and positive societal impact throughout their entire life cycle.
The transition from single-objective optimization (SOO) to MOO in the context of structural design optimization signifies a substantial advancement [
7,
8,
9]. MOO enables the simultaneous evaluation of multiple critical factors, including economic efficiency, environmental sustainability, and social impact. This holistic approach broadens the scope of design considerations and ensures a deeper congruence between infrastructure design and overarching sustainable development purposes. The advancement of MOO strategies represents a paradigmatic evolution, enriching the design process with a multifaceted perspective that better captures the complexity of real-world engineering challenges.
In Ruiz-Velez et al. [
10], a novel design strategy is presented and applied to a real-world challenge in construction engineering. The study specifically focuses on the life cycle design optimization of reinforced concrete precast modular frames (RCPMF). Building on previous SOO results for the precast and cast-in-place typologies [
11,
12], the study introduces a customized non-dominated sorting genetic algorithm II (NSGA-II), enhanced with three novel repair operators, to navigate the complex handling of the mixed integer programming (MIP) during the optimization process [
13]. Furthermore, the framework proposed in the study is particularly relevant for its integration with MCDM techniques, computing the criteria weights via an entropy-based approach and applying the simple additive weighting (SAW) and faire un choix adéquat (FUCA) methods for assessing the optimization results [
14].
The statistical-based repair operator was identified as the preeminent algorithm for navigating the hurdles intrinsic to the MIP nature of the RCPMF optimization problem. Despite the inherent differences in the strategies for scoring and evaluating decision-making alternatives, the SAW and FUCA techniques ranked the optimal solutions similarly. This consistency attests to the capabilities of the proposed structural design framework and the potential of integrating MOO and MCDM. As a result, the study introduced and demonstrated a pioneering framework that leverages the strengths of MOO and MCDM to elevate the sustainability and efficacy of structural engineering projects. The research strongly supports deploying this integrative strategy in practical structural engineering scenarios, particularly those aimed at enhancing the sustainability of transportation infrastructure projects.
Integrating MOO with MCDM techniques presents a forward-looking strategy for refining structural design frameworks considering the life cycle implications of construction projects. The case study on optimizing the structural design of RCPMF sets a reliable standard for assessing the effectiveness of sophisticated design strategies in transportation infrastructure development. The results of exploring the NSGA-II algorithm alongside SAW and FUCA techniques underscored the potential benefits of integrating MOO and MCDM for addressing the complex task of embedding sustainability into structural design engineering, representing an important stride towards further analytical advancements. Consequently, this initiates a pivotal conversation about exploring and evaluating the performance of additional MOO algorithms and MCDM approaches. This scrutiny seeks to assess the framework’s efficacy and broaden its relevance throughout the structural design domain.
This paper focuses on the development stage of precast modular frames, adopting a comprehensive perspective on life cycle sustainability. By integrating optimization processes early in the foundational phase, the framework is conceived to significantly influence the entire life cycle—from inception to decommissioning—ensuring that every design decision upholds long-term sustainability objectives [
15]. The research builds substantially upon previous efforts by incorporating a broad spectrum of MOO algorithms and MCDM techniques, enhancing the framework’s ability to navigate the complex and multifaceted challenges common to diverse modern engineering projects and boosting its applicability and robustness.
Furthermore, by embedding life cycle sustainability objectives directly into the optimization process, aligning these objectives with decision-making criteria, and utilizing an entropy theory-based weighting method, the framework ensures robustness and impartiality. This holistic approach deepens the understanding of life cycle sustainability and improves the replicability and reliability of outcomes across various engineering domains, fostering real-world scalability for these advanced practices. The research showcases the practical implementation of the MOO and MCDM integrated framework, closely aligning with established best practices for sustainable infrastructure development.
Within this context, the present research implements and critically evaluates the performance of novel MOO algorithms and MCDM techniques for enhancing structural design efforts. Three optimization algorithms and five decision-making techniques are implemented within the integrated design framework and then employed to solve the RCPMF problem. This paper aims to comprehensively characterize and enhance the integrated design strategy’s capabilities for solving practical engineering challenges. This paper introduces and evaluates the performance of three novel MOO algorithms, NSGA-II, non-dominated sorting genetic algorithm III (NSGA-III), and reference vector guided evolutionary algorithm (RVEA), for solving the MOO RCPMF problem [
16,
17,
18,
19]. The statistical-based repair operator, previously identified as the best-performing repair algorithm, is implemented in all of them. This paper further innovates by substantially extending the scope of the MCDM problem by comparing five different decision-making techniques: SAW, FUCA, technique for order of preference by similarity to ideal solution (TOPSIS), preference ranking organization method for enrichment evaluation (PROMETHEE), and “visekriterijumska optimizacija i kompromisno resenje” (VIKOR), Serbian for multi-criteria optimization and compromise solution [
20,
21]. This exhaustive examination improves the understanding of the MOO and MCDM integrated life cycle design strategy’s suitability and efficiency in promoting sustainable development within transportation infrastructure.
The NSGA-III algorithm is identified as the best-performing MOO strategy across all objective functions. While differing in scoring and evaluation procedures, the decision-making strategies continue to rank the MCDM problem alternatives similarly. These findings are congruent with what was described in previous research, displaying a robust array of decision-making techniques to be considered when assessing transportation infrastructure development. The results of this study further validate the design framework combining advanced MOO algorithms with MCDM techniques and provide new insights into its application and performance.
The subsequent sections detail and thoroughly explain the methodologies utilized in this study.
Section 2.1 provides an overview of the RCPMF problem which serves as a standard for evaluating the effectiveness of the optimization algorithms.
Section 2.2 elaborates on the operation and tailored adjustments of the optimization algorithms, while
Section 2.3 offers similar clarification for the decision-making techniques. The analysis and interpretation of the results are presented in
Section 3, enabling the formulation of relevant conclusions highlighted in
Section 4.
3. Results
This section presents the outcomes of deploying optimization algorithms on the RCPMF problem and the subsequent decision-making approach.
Section 3.1 analyzes each MOO algorithm’s effectiveness in generating non-dominated solutions equivalent to highly efficient, sustainable designs. Subsequently,
Section 3.3 delves into evaluating the MCDM problem concerning ranking optimal solutions derived from the MOO.
3.1. Algorithm Comparisons
The tuning process for the crossover and mutation operators within the NSGA-II algorithm was conducted methodically in two phases, with the hypervolume metric serving as the primary evaluation criterion. For the calculation of the hypervolume, each configuration was executed five times. In the initial exploratory phase, a range of values—0.2, 0.5, and 0.9—were examined to assess their impact on offspring distribution relative to their parent solutions, applied to both the SBX and PM operators. Furthermore, the probabilities for these operators were tested across a range of values—0.01, 0.1, 0.2, and 0.3—to find a wide variety of potential settings aimed at improving the optimization efforts. This was followed by an exploitation phase considering values 0.1, 0.08, 0.06, 0.04, and 0.02. This stage aimed to find an initial setup that could support a balanced approach to exploration and exploitation in the multi-objective optimization environment.
Following the same structured approach, the tuning process was extended to the NSGA-III algorithm, adhering to the established and probability values to ensure consistency in the evaluation. For NSGA-III, the final value was settled at 0.5 after a comprehensive assessment, mirroring the decision-making process in NSGA-II. In the probability tuning phase, an expanded range of values—0.01, 0.03, 0.04, 0.05, 0.06, and 0.07—was investigated, ultimately selecting 0.05 as the optimal setting. Additionally, the partitioning count for determining reference directions was fixed at 12, aiming to capture a broad diversity of solution directions and thus enriching the algorithm’s ability to uniformly cover the Pareto front.
The tuning methodology was applied to the RVEA algorithm, with an emphasis on the conceptual underpinnings of the parameters being adjusted. Initially, the process focused on the probability of mating between neighboring solutions, exploring values of 0.2, 0.5, and 0.8, before refining the search to 0.15, 0.2, 0.25, and 0.3 in a subsequent phase. The optimal value was determined to be 0.2, highlighting the algorithm’s preference for exploiting local solution neighborhoods to enhance diversity and exploration. Similarly, the adaptation of the algorithm’s convergence rate, guided by the conceptually defined adaptation parameter, was explored through initial values of 1.0, 1.5, and 2.0, with further refinement to 2.1, 2.0, and 1.9. A final value of 2.0 was selected, underscoring the balance achieved between fast convergence and the maintenance of solution diversity over generations. The setting for the number of partitions used to determine the distribution of reference directions was maintained at 12, mirroring the approach in NSGA-III and ensuring a consistent framework for analysis. In the table shown in
Table 4, the different configurations tested, along with the optimal values identified for each parameter, are presented.
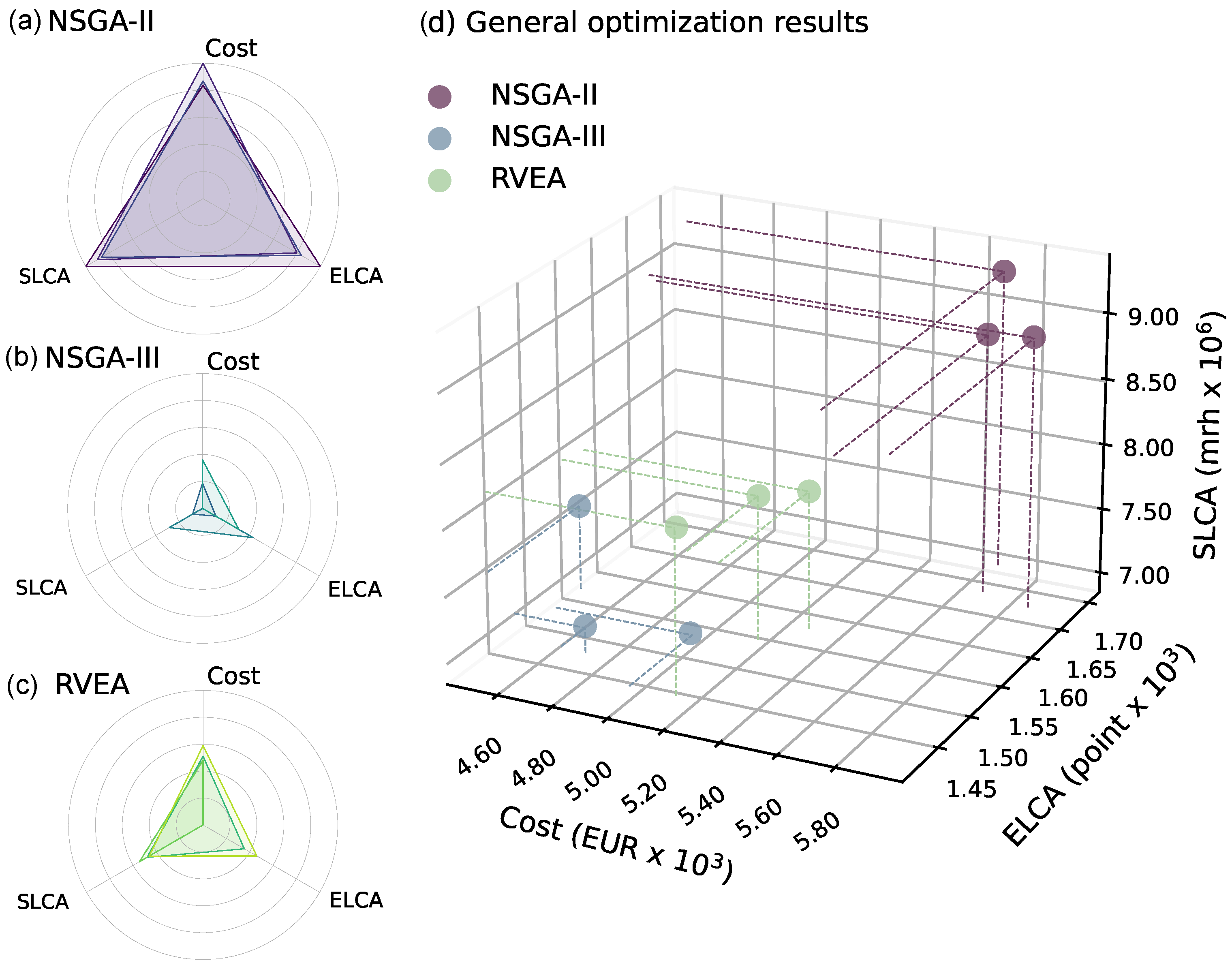
Table 5 showcases the quantitative analysis of the non-dominated solutions generated by the NSGA-II, NSGA-III, and RVEA optimization algorithms for the MOO problem. It includes the specific values of the objective functions for each design, facilitating an objective assessment of each algorithm’s performance based on three criteria: cost, ELCA, and SLCA.
This study utilizes an adapted min–max normalization technique to address the disparities in measurement units and magnitude scales across the evaluation criteria. In this framework, the radar charts depicted in
Figure 3 illustrate the performance of each algorithm against the three evaluation metrics, applying this normalized approach. The adjusted normalization method sets a baseline of 0.5 for the lowest value and a cap of 1 for the highest value in the dataset. In this setup, radar charts with smaller areas indicate superior performance by the algorithms. This superior performance is indicative of RCPMF designs that exhibit enhanced sustainability throughout their life cycle.
The analysis of the multi-objective optimization results, presented in
Table 5 and
Figure 3, underscores the performance of the NSGA-II, NSGA-III, and RVEA algorithms across three critical objectives: cost, environmental life cycle analysis (ELCA), and social life cycle analysis (SLCA). The findings are instrumental in elucidating the algorithms’ efficiencies and shortcomings in navigating the complex multi-objective landscape of sustainable infrastructure projects.
It was observed that NSGA-II consistently yielded the least favorable outcomes across all three objectives, indicating a relative underperformance in integrating cost efficiency with environmental and social sustainability metrics. In contrast, NSGA-III emerged as the most adept in minimizing costs and achieving superior SLCA outcomes compared to RVEA, suggesting a robust capability in optimizing for economic and social dimensions simultaneously. The distinction in performance between NSGA-III and RVEA became particularly pronounced when examining their ability to balance cost reduction with social sustainability, with NSGA-III demonstrating a more effective optimization pathway. Meanwhile, RVEA displayed good performance in the ELCA domain, albeit with outcomes closely rivaled by NSGA-III, highlighting its effectiveness in environmental sustainability optimization with marginally superior ELCA values. This nuanced performance profile underscores RVEA’s potential in addressing environmental aspects of sustainability, albeit within a competitive margin when juxtaposed with NSGA-III.
3.2. Performance Indicator Analysis
This study conducted a systematic experiment to assess the performance of three multi-objective optimization algorithms: NSGA-II, NSGA-III, and RVEA. The experiment consisted of 30 separate runs, during which five points were generated for each algorithm using the same predefined parameters. This methodology allowed for the direct comparison of the algorithms’ performance under fixed parameter settings. A min–max normalization procedure was applied to each function separately to ensure comparability among the results from different objective functions. This method involved standardizing the units of the variables for all data points, including those on the Pareto frontier. For each experiment, points from each algorithm were normalized by adjusting their values from the minimum to the maximum observed across the dataset. This process facilitated a consistent comparison across different optimization landscapes by transforming the varied scales into a uniform metric.
Two performance metrics were introduced to evaluate further the effectiveness of the optimization algorithms: generational distance (GD) and inverted generational distance (IGD). Both metrics quantify the quality of the solutions generated by the algorithms in terms of their convergence and diversity concerning a known Pareto frontier.
Generational distance (GD) quantifies the average Euclidean distance from each solution in a set to the nearest point in the Pareto front, reflecting the convergence of the algorithm-generated solutions. For this paper’s experiment, the size of set
A was 5, representing the five points obtained in each run. The GD is calculated using the following equation:
where
is the Euclidean distance from the
i-th solution
in set
A to its nearest point in the Pareto front
Z. Here,
A and
Z are defined as follows:
This measure is pivotal for assessing the proximity of the obtained solutions to the ideal solutions on the Pareto front.
Inverted generational distance (IGD) inverts the generational distance and measures the distance from any point in
Z, the Pareto front, to the closest point in
A. For this paper’s experiment, set
A contained five points generated in each run. The IGD is calculated using the following equation:
where
is the Euclidean distance (with
) from a point
in the Pareto front to its nearest reference point in set
A. The set
A is defined as
, representing the solutions obtained from each run. This metric is crucial for evaluating how well the generated set of solutions covers the Pareto front.
Advantages of Each Metric:
GD is particularly useful for assessing the convergence of the generated solutions to the Pareto front. A lower GD value indicates that the algorithm-generated solutions are closer to the optimal set of solutions, suggesting better performance in terms of convergence.
IGD offers insight into the convergence and diversity of the generated solutions. It shows how close the solutions are to the Pareto front and how well the solutions are distributed across the entire front. A lower IGD value signifies that the generated solutions uniformly cover the Pareto front, indicating a good spread in addition to proximity.
By incorporating both GD and IGD, this study evaluates the algorithms’ ability to generate solutions that are close to and well-distributed across the ideal solution set, capturing the nuanced performance differences between the algorithms in multi-objective optimization tasks.
Descriptive statistics were computed, providing basic insights into the distribution of results for each algorithm to evaluate the performance of the optimization algorithms. These included the mean, standard deviation, maximum, minimum, and median values, essential for summarizing the central tendency and dispersion of the data. Furthermore, the non-parametric Kruskal–Wallis test was employed to ascertain statistically significant differences between the algorithms. This test was chosen due to its robustness in handling non-normally distributed data and its ability to compare more than two groups without assuming equal variances, making it well-suited for the ordinal data generated in this experiment.
In
Table 6, the descriptive statistics reveal patterns in the performance of the MOO algorithms NSGA-II, NSGA-III, and RVEA. Regarding generational distance (GD), NSGA-III and RVEA display similar mean values, indicating comparable proficiency in converging to the Pareto front. This similarity is also reflected in the median and standard deviation values, suggesting consistent performance across the 30 experiments. On the other hand, a pronounced difference is observed for inverted generational distance (IGD). NSGA-III presents a substantially lower mean and median compared to RVEA, highlighting its enhanced capability to generate a diverse set of solutions that effectively span the entire Pareto front.
The non-parametric Kruskal–Wallis test was conducted to statistically affirm the differences in performance observed between the algorithms, as detailed in
Table 6. This test is ideal for data that do not follow a normal distribution, which often happens in the case of multi-objective optimization because it compares the median values across groups without assuming data normality. The resulting
p-values for both average generational distance (Avg GD) (
) and inverted generational distance (IGD) (
) were significantly low, leading to the rejection of the null hypothesis and confirming differences in algorithm performance. The results indicate that NSGA-III may be more effective in generating a diverse set of solutions, as demonstrated by its IGD results.
3.3. Multi-Criteria Decision Analysis for Structural Design Optimization
This paper comprehensively evaluates the efficacy of the NSGA-II, NSGA-III, and RVEA optimization algorithms within a structural design context. This section presents the analysis of the non-dominated solutions produced by each optimization algorithm in addressing the RCPMF challenge. Additionally, the results of deploying a comprehensive range of decision-making methods are examined to gauge the applicability of these techniques within the structural design framework and the robustness and replicability of its results, considering both optimization and MCDM perspectives.
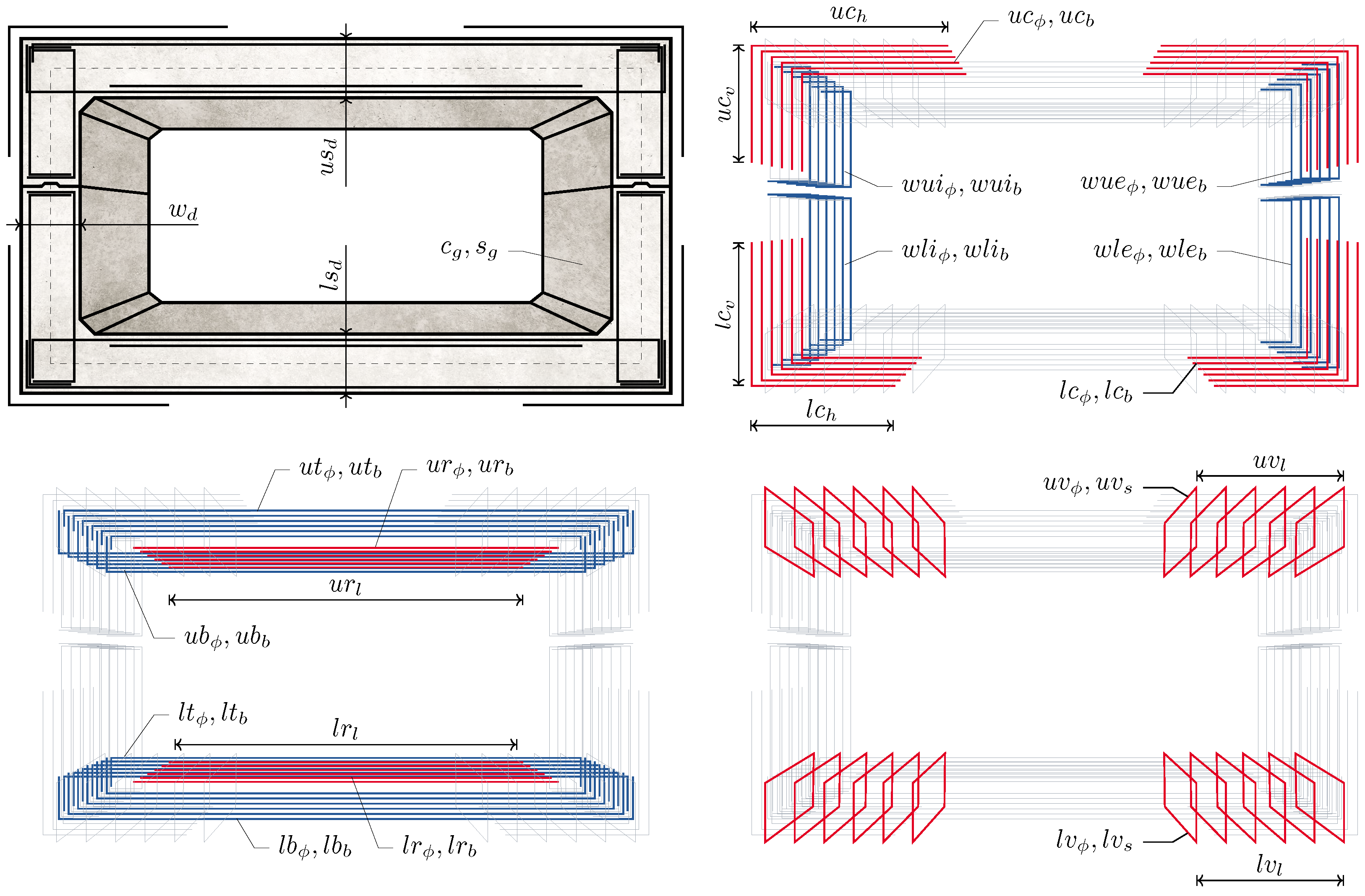
Within this context,
Table 7 presents the collection of optimization variables that delineate the non-dominated solutions. The configuration of passive reinforcement—encompassing aspects like diameter, the amount of bars, and separation of shear branches—is combined into an effective area
parameter. This method facilitates its interpretation, offering direct insight into the sectional properties and streamlining the comprehension of these elements.
Figure 4 showcases the primary geometric features of the upper and bottom slabs and the lateral walls for the structures yielded by each optimization algorithm. Across all the alternatives, optimal designs feature upper slab depths ranging between 0.75 and 1.07 m, with the RVEA algorithm exhibiting the most significant variability in its results. The NSGA-II algorithm, in particular, favors designs that incorporate wider lower slabs, reaching up to 0.93 m. This tendency towards increased lower slab depths is not as pronounced in the non-dominated solutions produced by NSGA-III and RVEA, which tend towards more moderate section depths, averaging 0.65 and 0.71 m, respectively. Despite the distinct variability observed in the designs of the upper and lower slabs, a consistent pattern emerges among all three optimization algorithms, converging on solutions with specified lateral wall depths, thereby narrowing the variability across these sections of the RCPMF.
Figure 5 portrays the analysis of the use of material resources for each non-dominated solution derived from the NSGA-II, NSGA-III, and RVEA optimization algorithms. Notably, the NSGA-III and RVEA algorithms lead to designs that consume less concrete. This trend correlates with the more pronounced sectional depths in solutions from NSGA-III for the RCPMF. Moreover, NSGA-III tends to converge towards designs that make more efficient use of passive reinforcement, thereby reducing the required mass of steel. In contrast, the NSGA-II algorithm exhibits less favorable outcomes in this regard, with its solutions generally demanding higher quantities of concrete and steel resources. Despite these differences, all solutions maintain passive reinforcement densities exceeding 100 kg/m
3. Within this spectrum, the NSGA-III algorithm trends towards solutions with somewhat lower reinforcement densities, whereas NSGA-II and RVEA display closely aligned results in terms of structural material usage.
This manuscript comprehensively evaluates the NSGA-II, NSGA-III, and RVEA algorithms, focusing on their proficiency in generating non-dominated optimal solutions within a MOO for the RCPMF design challenge.
Section 3.1 meticulously explored how these optimization algorithms perform against three sustainability metrics pertinent to the life cycle of the RCPMF. Previous paragraphs detailed the primary attributes of the RCPMF designs. This paper now critically assesses the design framework integrating MOO algorithms with MCDM approaches.
Table 8 analyzes the results of deploying the SAW, FUCA, TOPSIS, PROMETHEE, and VIKOR decision-making algorithms on the MCDM problem, explicitly focusing on ranking the non-dominated solutions generated from the MOO process.
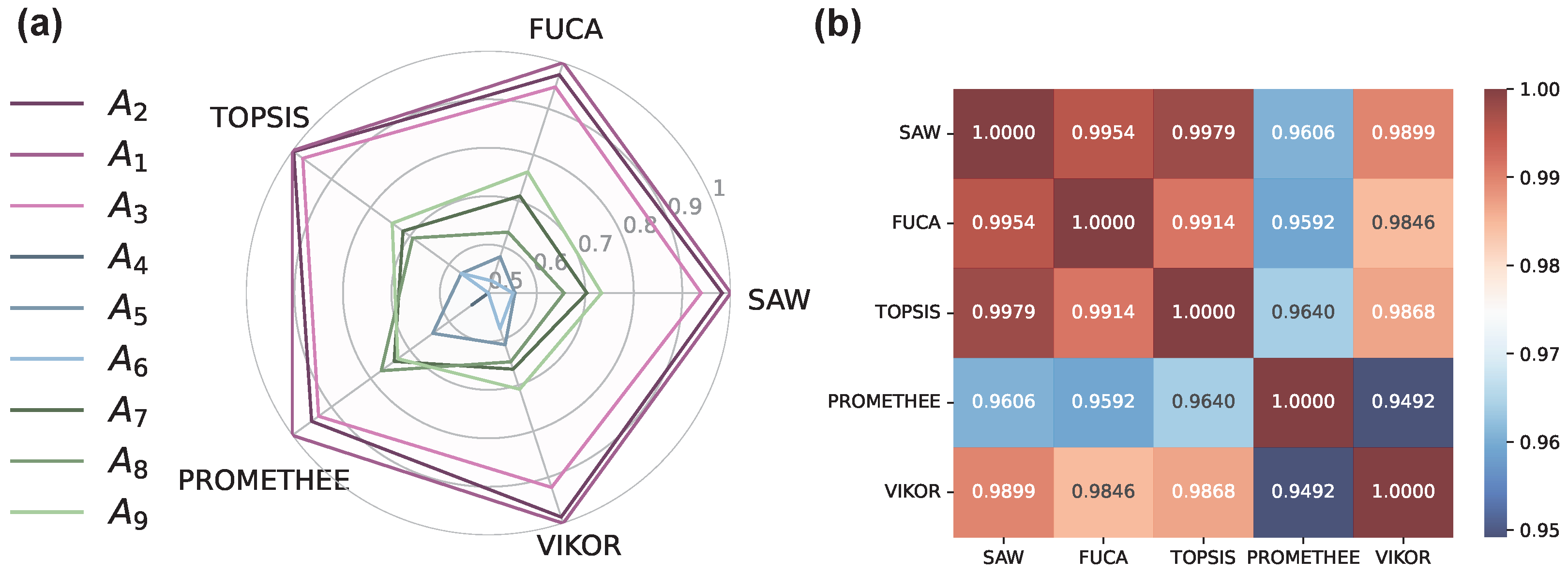
The radar plot featured in
Figure 6 employs the modified min–max normalization technique to represent the scoring outcomes of the nine alternatives utilizing the five distinct decision-making techniques. This methodology bypasses the scoring disparities inherent to the varied algorithmic structures of these techniques. Despite their operational discrepancies, the scoring outcomes from the five decision-making approaches exhibit remarkable uniformity across all alternatives. This consistency is further observed in the correlation heatmap, which effectively highlights the strong correlation among the five decision-making techniques.
The entropy-based weighting showcases a commendable equilibrium among the three life cycle assessment metrics, underscoring the importance of cost, ELCA, and SLCA in informing the decision-making process. The scoring outcomes reveal significant similarity in how the five decision-making techniques score and rank the alternatives, with correlation coefficients exceeding 0.94. This high correlation denotes a substantial uniformity in evaluation outcomes despite the inherent differences in each algorithm’s methodology. Interestingly, this consensus is particularly pronounced among the highest and lowest-ranked alternatives, whereas the most noticeable discrepancies in ranking occur among those in the middle. This pattern suggests a decision-making framework that effectively differentiates between the most and least sustainable options, with slight variations observed among the moderately performing alternatives.
Alternatives to , representing the non-dominated solutions produced by the NSGA-III algorithm, consistently emerge as the top three selections for the MCDM problem. Notably, alternative is deemed the highest-ranked RCPMF design by four decision-making techniques, with only PROMETHEE favoring as the leading option. On the other end of the spectrum, alternatives to , derived from the NSGA-II algorithm, are identified as the least favorable options. Each technique unambiguously categorizes these RCPMF designs as offering minimal life cycle sustainability benefits within highly efficient structures. This observation does not detract from their efficiency but underscores the NSGA-III’s superior compatibility with the RCPMF within the outlined MOO framework. Meanwhile, the alternatives to , generated by the RVEA algorithm, occupy the intermediate positions in the ranking.
The high correlation among the outcomes derived from the five decision-making algorithms highlights the replicability and reliability of the methodology that combines MOO and MCDM within the design framework for the RCPMF challenge. This section provided an in-depth assessment of the performance of various MOO algorithms in developing RCPMF designs that prioritize life cycle sustainability. Further, by applying a range of decision-making techniques, this analysis scrutinized the efficacy of the NSGA-II, NSGA-III, and RVEA algorithms, endorsing their incorporation into a cohesive structural design framework combining MOO and MCDM. This holistic strategy demonstrates the decision-making process’s integrity, validates the integrated design framework capabilities, and extends the range of techniques available to advance sustainable structural design methodologies.
4. Conclusions
This paper critically evaluates the life cycle optimization performance of three optimization algorithms within a cohesive design framework that integrates for advancing sustainable transportation infrastructure. Combining MOO techniques with MCDM methodologies, this work expands upon and substantiates a systematic approach to addressing the intricate challenges in efficient structural engineering design. The investigation employs the RCPMF design problem, leveraging an array of MOO algorithms: NSGA-II, NSGA-III, and RVEA. These algorithms are enhanced with specialized crossover, mutation, and statistical-based repair operators to address the MIP nature of the MOO problem. The algorithms’ performance is evaluated against life cycle sustainability metrics—economic cost, ELCA, and SLCA—across every non-dominated solution. The analysis highlights the NSGA-III as the best-performing algorithm, offering a nuanced understanding of its potential to facilitate sustainable design approaches.
Following the optimization phase, the MCDM problem is rigorously evaluated, addressing nine non-dominated solutions generated by the optimization algorithms. This study utilizes a comprehensive set of decision-making techniques, including SAW, FUCA, TOPSIS, PROMETHEE, and VIKOR, coupled with an entropy theory-based methodology for unbiased criteria weighting. This combination further enhances the framework’s capabilities in identifying efficient designs. The results corroborate and expand the methods available for a cohesive MOO and MCDM design framework, demonstrating the strategy’s efficiency and reliability. Such findings advocate for a transformative approach to infrastructure development, steering towards more advanced and sustainable engineering solutions.
NSGA-III is highlighted as the most effective algorithm, with its non-dominated solutions for the RCPMF designs consistently ranked as the top three choices by all applied decision-making techniques. RVEA positions next, with its solutions ranked in the mid-range, yet exhibiting some of the best scores for life cycle sustainability metrics.
On the other end, NSGA-II shows less favorable outcomes for RCPMF optimization within the defined framework of this study, pointing towards its limited applicability under the examined conditions. This evaluation outlines the relative performance of each algorithm, contributing valuable insights into their suitability for addressing the specific characteristics of the RCPMF problem within sustainable transportation infrastructure design.
The analysis of performance indicators has offered insights into the potential efficacy of the NSGA-II, NSGA-III, and RVEA algorithms. Descriptive statistics, based on 30 experimental runs, suggest that NSGA-III is relatively consistent in its approach towards the Pareto front, as reflected by its similar mean and GD values when compared to RVEA. In the case of IGD, NSGA-III appears to have an edge, hinting at its capability to produce a more varied set of solutions. The Kruskal–Wallis test lends statistical support to these observations, suggesting significant differences in performance among the algorithms.
In addressing the MCDM problem, a significant alignment is observed in the ranking of alternatives by the five decision-making algorithms despite the intrinsic differences in their algorithmic structure and scoring methodologies. This concurrence, represented by correlation coefficients from 0.94 to 0.99, underscores the robustness of the decision-making process within the integrated MOO and MCDM frameworks, demonstrating a cohesive understanding and evaluation of the alternatives’ sustainability performances.
Four out of five decision-making algorithms identified the alternative as the most sustainable design for the RCPMF over its life cycle. This design utilizes 35 MPa structural concrete to construct slender lateral walls and features restrained section depths for both the upper and lower slabs. Although it does not secure the lowest values in cost, ELCA, or SLCA, the design effectively leverages B500S steel for passive reinforcement, conforming to a well-rounded design. This outcome emphasizes the necessity of an integrated approach that employs MOO to address multiple aspects of sustainability simultaneously.
By applying and critically evaluating the design framework for the RCPMF optimization problem, this study aims to validate and expand upon a practical method for incorporating life cycle considerations right from the design phase. The findings underscore the effectiveness and reliability of combining MOO and MCDM techniques. This integrated approach aims to produce economically viable designs that excel in environmental and social sustainability across their life cycle. These solutions signify a significant stride towards embedding holistic sustainability criteria in structural design processes.
While the outcomes align with previous research and further underscore the efficacy and robustness of integrating MOO with MCDM, the authors recognize the limitations arising from the assumptions and premises articulated throughout this study. These constraints were essential to develop a comprehensive mathematical model capable of facilitating the design process, including structural calculation, constraint verification, objective function assessment, and exploration of the optimization landscape. Additionally, considering the modular nature of the structural solution, integrating factors related to supply chain and transportation challenges could lay the groundwork for further evaluating the scalability of the specific case study discussed in this paper. Given the focus on sustainable infrastructure development, the authors consider these additions a crucial direction for future research efforts. Nonetheless, these factors delineate the scope of the present investigation. Future work that delves into varied scenarios, optimization benchmarks, and data variability holds promise for refining this approach, potentially broadening its applicability and enhancing its precision in structural design optimization.
Given the observed variances in the convergence and diversity metrics among the NSGA-II, NSGA-III, and RVEA algorithms, future studies should thoroughly investigate the underlying mechanisms contributing to these differences. A detailed examination of algorithmic parameters, such as selection pressure, mutation rates, and crossover strategies, could provide insights into their impact on convergence behaviors. Additionally, exploring the interaction between these parameters and the specific problem characteristics of the RCPMF designs might reveal why certain algorithms outperform others in specific contexts. Pursuing these inquiries could lead to more tailored algorithmic adjustments that enhance performance across a broader range of optimization scenarios, optimizing the algorithms for specific types of multi-objective problems.