Abstract
Positive and unlabeled learning (PU learning) is a significant binary classification task in machine learning; it focuses on training accurate classifiers using positive data and unlabeled data. Most of the works in this area are based on a two-step strategy: the first step is to identify reliable negative examples from unlabeled examples, and the second step is to construct the classifiers based on the positive examples and the identified reliable negative examples using supervised learning methods. However, these methods always underutilize the remaining unlabeled data, which limits the performance of PU learning. Furthermore, many methods require the iterative solution of the formulated quadratic programming problems to obtain the final classifier, resulting in a large computational cost. In this paper, we propose a new method called the absolute value inequality support vector machine, which applies the concept of eccentricity to select reliable negative examples from unlabeled data and then constructs a classifier based on the positive examples, the selected negative examples, and the remaining unlabeled data. In addition, we apply a hyperparameter optimization technique to automatically search and select the optimal parameter values in the proposed algorithm. Numerical experimental results on ten real-world datasets demonstrate that our method is better than the other three benchmark algorithms.
Keywords:
PU learning; absolute value inequality; support vector machine; eccentricity; hyperparameter optimization MSC:
90C90
1. Introduction
In machine learning, the general classification task is to construct a classifier based on a labeled dataset. However, in various real-world applications, obtaining a large number of labeled examples is difficult or impractical. For instance, in text classification, it is challenging to identify a type of text from an enormous number of texts. As another example, in medical diagnosis, finding patients with a specific disease (positive examples) may be straightforward, while collecting a comprehensive group of healthy patients (negative examples) can be challenging. Therefore, solving semi-supervised classification problems with few labeled examples and a large number of unlabeled examples is of practical importance.
Positive and unlabeled learning (PU learning) is a unique semi-supervised classification task that performs binary classification on a set consisting of a small number of positive examples and a large number of unlabeled examples. To date, PU learning has been used to successfully solve various problems, such as gene identification [1], text classification [2,3], fraud detection [4,5], and recommendation [6].
The scarcity of negative examples necessitates the learning of information from unlabeled examples. Based on the means of processing the unlabeled examples, existing PU learning methods can be classified into three categories. The first category is related to one-class classification [7,8,9]. It estimates the distribution of the positive class only from positive examples, without using information from unlabeled examples. These methods often underperform when positive samples are scarce [10]. The second category is the one-step method [11,12,13,14]. It treats the PU learning problem as a supervised problem with noise; specifically, all unlabeled examples are assumed to be negative examples. This assumption may introduce label noise, degrading the performance due to misclassified unlabeled positives [15]. The third and most widely used category is the two-step method. This method selects potential negative examples from the unlabeled set and then constructs a classifier using both positive and identified negative examples [16,17,18,19,20]. Many algorithms of this category underutilize the remaining unlabeled data, resulting in limited classification performance. In addition, many approaches require the iterative solution of the quadratic programming problem to obtain the final classifier, resulting in a large computational cost.
As an excellent state-of-the-art tool for classical binary classification in machine learning, support vector machine (SVM) has already shown its superiority in comparison with other learning algorithms. Therefore, many methods based on SVM to solve semi-supervised problems have been proposed. For example, Mangasarian [21] proposed a novel method that utilizes convex absolute value inequality (AVI) to minimize the overlap of boundary hyperplanes to divide unlabeled data into two classes. The method is easy to implement, and the experimental results show that it can achieve good classification accuracy.
In this paper, we also follow the two-step strategy and propose a new algorithm for PU learning named AVI-SVM. First, negative examples are selected based on the concept of Typicality and Eccentricity Data Analytics (TEDA), introduced in [22]. In the next step, the convex absolute value inequality SVM is utilized to solve the resulting semi-supervised problem. Furthermore, to reduce the amount of resources spent in manually adjusting the parameters, we adopt the hyperparameter optimization method HORD, proposed in [23], to set the optimal values of the parameters in the algorithm. The main contributions of our work can be summarized as follows.
- (1)
- Our approach employs TEDA for the extraction of reliable negative examples from the unlabeled dataset. Unlike alternative methods for negative example selection, TEDA operates without predefined assumptions, relying solely on the spatial distribution of the data. Furthermore, this method is not only computationally straightforward but also remains effective even with a limited number of positive examples.
- (2)
- Our approach is the first to use the convex absolute value inequality technique to solve PU problems. This technique enables the successive linearization algorithm to resolve the optimization model, thus reducing the computational costs.
- (3)
- Our approach adopts the hyperparameter optimization method HORD to set the optimal values of the parameters in the algorithm, thus reducing the amount of resources spent in manually adjusting the parameters.
The rest of this paper is organized as follows. Section 2 provides a brief review of related research works. Section 3 introduces the concept of TEDA, convex absolute value inequality for semi-supervised algorithms, and the HORD algorithm. In Section 3, we propose the AVI-SVM algorithm for PU problems. The numerical results are reported in Section 4 and the conclusions are presented in Section 5.
2. Related Work
Various methods have been proposed to solve PU learning problems and most of them can be divided into three types.
The first type of approach is related to one-class classification, where the distribution of positive classes is estimated from known positive examples, such as the one-class support vector machine (OSVM) [7,8]. The Laplacian unit hyperplane classifier (LUHC) [9] places predicted labels and initial labels close to each other at the labeled points by adding a regularity factor. Only positive examples are used in this approach to discover the discriminant structure of the dataset.
Another type of method is the biased support vector method (B-SVM) [11]. It treats the PU learning problem as a supervised problem with noise, i.e., all unlabeled examples are assumed to be negative examples, and different classes are assigned different weights in the loss function. -BSVM [12] adopts the Chebyshev distance ( norm) instead of the norm in B-SVM to measure the empirical risk, which allows all examples to participate in the learning to improve the classification performance. Then, it uses an improved Sequential Minimal Optimization (SMO) algorithm with low time complexity to solve the classifier. In the last decade or so, nonparallel hyperplane support vector machines (NPSVM) [24,25] have attracted much attention. Some researchers have combined NPSVM and B-SVM to solve the PU problem, such as B-NPSVM [13] and B-NPSVM [14].
The third type of method is based on the two-step strategy. This type of method consists of two steps: (1) identifying reliable negative examples from the unlabeled examples, and (2) learning based on the labeled positive examples and the identified reliable negative examples. The representative methods in this category include S-EM [16], PEBL [17], Roc-SVM [18], SPUPIL [19], and KNN-SVM [20]. S-EM [16] uses the Spy technique to obtain some reliable negative examples from the unlabeled set and then runs the Expectation-Maximization (EM) algorithm to construct the final classifier. PEBL [17] is an SVM-based technique used to classify web pages given positive and unlabeled pages. It defines documents that do not contain any characteristics of positive data as strong negative documents. After identifying a set of strong negative documents, it iteratively applies an SVM to build a classifier. Roc-SVM [18] builds prototypes for labeled and unlabeled examples based on Rocchio classification, counts unlabeled examples closer to the unlabeled prototypes as reliable negative examples, and then applies the SVM algorithm to learn the classifier. SPUPIL [19] first takes the intersection of reliable negative examples extracted by the Spy [16] and Rocchio [18] methods as the final reliable negative examples, and then incorporates similarity weights and privileged information into the learning to extend the standard ranking SVM [26] to obtain a more accurate classifier. KNN-SVM [20] sorts the unlabeled examples by calculating the sum of the cosine similarities with the nearest k positive examples to select reliable negative examples in the first step. Then, the iterative SVM is used to train the classifiers, and the last classifier is chosen as the final classifier.
3. Preliminaries
In this section, we briefly introduce the convex absolute value inequality for semi-supervised problems, the concept of TEDA, and the HORD algorithm.
Throughout this paper, the training dataset is represented as
where is a positive input, and is an unlabeled datum known to belong to one of the two classes. The objective of PU learning is to find a function in such that the class of any input x can be predicted by the sign function of as
3.1. Convex Absolute Value Inequality with SVM
Consider the following absolute value inequality (AVI)
where the vector represents any data point, is the normal vector to the classification plane , and b denotes the distance from the plane to the origin. The inequality (3) divides the space into two overlapping half spaces via the following inequalities:
Ref. [21] applies AVI to the semi-supervised classification problem. The main idea is that if AVI (3) is imposed on an unlabeled dataset, the dataset will be classified into two classes to best fit the requirements of either AVI (3) or the two linear inequalities (4). Therefore, the objective of the method proposed in [21] is to minimize the overlap between the bounding planes To achieve this objective, it is necessary to find two planes in that designate the feasible region resulting from the two inequalities of (4) and that satisfy, with a minimal error vector , the following inequalities:
where is a vector of ones, is the matrix of unlabeled examples, is the matrix of p positive examples and m negative examples, and the matrix is the diagonal matrix formed by the labels corresponding to the labeled dataset. The second inequality means that the labeled dataset needs to be distributed on different sides of the hyperplane.
Then, the formulation of the SVM with the AVI for a semi-supervised problem is given as follows (see [21]):
where is the -norm of , is a penalty parameter, and is a slack variable. For this model, the purpose of maximizing and is to minimize the distance between the two hyperplanes (4).
3.2. Typicality and Eccentricity Data Analytics
TEDA [22,27] is an evolving method for outlier detection. It performs recursive computation on data samples and is very computationally efficient. The concept of typicality relates to the similarity of an example to the given examples. Eccentricity indicates how different a data example is from the data distribution, which means that a data example with high eccentricity is more likely to be an outlier. Here, we only briefly introduce eccentricity. Consider the dataset , which consists of a sequence of n-dimensional examples . The cumulative proximity from a data example to all remaining data samples up to the one is calculated as
where is any type of distance function (the Euclidean distance in this paper) between and . The eccentricity of the example is defined as
It has been shown in [22] that the eccentricity can be calculated recursively as
where is the eccentricity of the example in relation to all previous samples in the dataset, while and are the mean and the variance, respectively. Both and can be recursively updated as
The normalized eccentricity can be acquired as follows:
where is used to determine a threshold for Chebyshev inequality-based outlier detection [28]. The main idea of the Chebyshev inequality is that, under any distribution, no more than of the data samples are more than away from the mean, where l is a constant value and is the standard deviation of the dataset [28]. Thus, an example is considered to be an outlier if the condition
is satisfied. In Section 3, we will demonstrate how the eccentricity is used to determine reliable negative examples.
3.3. HORD Algorithm
The hyperparameter optimization using an RBF-based surrogate and DYCORS (HORD) algorithm is a hyperparameter optimization method based on a deterministic surrogate that requires relatively fewer function evaluations for optimization [23]. The advantages of HORD are that it is not only computationally fast but also performs well in both high- and low-dimensional parameter spaces. The main idea of the HORD algorithm is to use the radial basis function (RBF) as a surrogate to approximate the error function of the hyperparameters and to search for the near-optimal hyperparameter configuration through a dynamic coordinate search. After inputting the initial number of sampling points , the number of candidate points , and the maximum number of iterations , the algorithm first samples points using Latin hypercubic sampling and then evaluates the objective function values of these initial points to obtain the optimal point . The objective function values at these points are utilized to fit or update the surrogate model. Subsequently, the algorithm selects the next most promising point through coordinate perturbation. This new point is then incorporated into the initial point set, and the above operation is repeated. After reaching iterations, the algorithm finalizes and returns the hyperparameter configuration corresponding to , which results in the lowest validation error (for more details, please refer to [23]).
4. Proposed Approach
The proposed AVI-SVM algorithm follows the two-step strategy. The first step is to select reliable negative data samples. In this step, we select suitable examples as reliable negative examples based on the concept of eccentricity. The second step is to classify this dataset containing unlabeled data examples, in which the AVI integrated with the SVM will be applied. All three parameters in the proposed algorithm will be set automatically by the HORD algorithm, i.e., the constant l that affects the selection of reliable negative samples in the first step (see (17)) and the weights in the objective function of the classification model in the second step (see (20)).
4.1. Reliable Negative Samples
For the binary classification problem, if an example is an outlier to the positive dataset, then the probability of this example not belonging to the positive class is high. As mentioned in Section 2, an example with high eccentricity is usually considered an outlier. The eccentricity of any unlabeled example to the positive dataset is calculated as follows:
where is the number of samples in the set composed of dataset and sample , and and can be obtained using the following formulas:
where and are the mean and variance of the positive set P.
According to the concept of eccentricity, the threshold used to determine whether the unlabeled datum is an outlier is
where ; l represents the sensitivity of the threshold, and it will be set by using the HORD algorithm.
If the condition (17) holds, it implies that does not belong to the positive dataset , and we place it in the reliable negative dataset . The specific steps followed to generate the set of reliable negative examples are given in Algorithm 1.
| Algorithm 1 Generation of reliable negative samples |
|
It should be noted that when the number of examples in is larger than , we only take examples with the largest eccentricity to form (Lines 10–12) in order to ensure that the negative examples selected are reliable.
4.2. AVI-SVM Formulation for the Resulting Semi-Supervised Problem
After the set of reliable negative examples is obtained, the training set (1) is transformed into
where is the index of the examples selected as negative examples, and is the index of the remaining unlabeled examples. The PU problem then is converted into a normal semi-supervised one, which will be solved using the SVM formulation with the AVI given in Section 3.1.
We will make some changes to (6) to establish the SVM formulation. First, for the first constraint, we add a non-negative slack variable to it and minimize the slack variable in the objective function to relax this constraint appropriately. Second, we maximize in the objective function of model (6) while ignoring . The reason for this change is that, according to [21], maximizing both and aims to minimize the distance between the two overlapping feasible regions of the first constraint. However, maximizing only can also achieve this goal, and, in this way, the computational effort can be reduced. Therefore, the final optimization model for this problem is as follows:
where is the -norm of , are the penalty parameters, and are the slack variables, is the matrix of unlabeled examples, is the matrix of positive examples () and reliable negative examples , and the diagonal matrix with entries of denotes which class of or each row of belongs to.
It is clear that the formulation (19) can be rewritten as
where is a vector with each component being the absolute value of the corresponding component of . For this linearly constrained concave minimization problem with absolute value functions in the objective, we also use the successive linearization algorithm [29], as in [21]. Finally, the decision function is obtained. The specific steps are given in Algorithm 2.
In this framework, we select unlabeled data examples with high eccentricity for the positive dataset as reliable negative examples. Based on the positive examples, reliable negative examples, and remaining unlabeled examples, we construct the model (20) and obtain its solution via Algorithm 2, and we then build the decision function . Finally, for any input example, we can use this decision function to predict its class.
| Algorithm 2 Successive linearization algorithm for (20) |
|
4.3. Performance Metric
We use the metrics of the F-score and accuracy () for comprehensive comparisons. Note that the F-score takes into account both recall and precision :
where and . , , , and are the numbers of true positive, true negative, false positive, and false negative examples, respectively. However, the F-score cannot be directly calculated on the validation set during the training process due to the absence of labeled negative examples. An approximate measure to the F-score proposed in [30] is used instead to evaluate the performance:
where is the recall for the positive set in the validation set, is the random variable representing the input vector, and is the probability of an input example in the validation set being classified as a positive example.
Accuracy is the proportion of correct predictions (both true positives and true negatives) among the total number of examples. The formula for accuracy is
4.4. Parameter Tuning
The HORD algorithm [23] is employed to set the optimal parameters. The details are given in Algorithm 3.
In Lines 2 to 12, the black-box objective function handled by the HORD algorithm is defined via the N-fold cross-validation method. N-fold cross-validation divides the dataset into N equally sized folds. For each training iteration, a different fold is used as the validation set, with the remaining N-1 folds serving as the training set. Once the training and validation steps are completed for all N folds, the F values are averaged over all iterations. The solution with the highest average value is the optimal solution that we seek.
In the numerical experiments, the ranges of parameters l, , and are set as [1, 3], (0, 26), and (0, 26), respectively; the number of initial sampling points, the number of candidate points, and the maximum number of iterations in the HORD algorithm (Line 1) are set as 20, 300, and 200, respectively.
| Algorithm 3 Parameter tuning by HORD |
|
4.5. AVI-SVM Algorithm
The complete AVI-SVM algorithm for the PU learning problem is given as Algorithm 4. Its flowchart is shown in Figure 1. For the input positive dataset and the unlabeled dataset , AVI-SVM first uses Algorithm 3 to obtain the optimal parameters , , and and then applies Algorithm 1 to obtain the reliable negative examples and the remaining unlabeled examples , followed by generating the and b required for the decision function by Algorithm 2. Finally, for any input example , it uses decision function to predict and return its class.
| Algorithm 4 AVI-SVM algorithm for the PU learning problem |
|
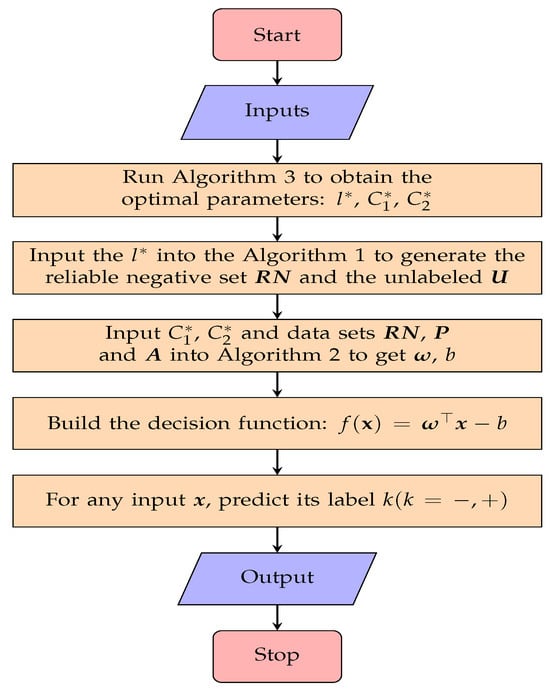
Figure 1.
Flowchart of the AVI-SVM algorithm.
5. Numerical Experiments
We evaluate and compare the performance of the proposed AVI-SVM algorithm with that of three well-known PU learning algorithms using ten UCI benchmark datasets.
5.1. Algorithms for Comparison
In our experiments, we evaluate the performance of the AVI-SVM algorithm compared with the following algorithms.
- LUHC [9]: It exploits both the geometrical and the discriminant properties of the examples; thus, it can improve the classification performance. This algorithm follows the one-class classification scheme.
- B-NPSVM [14]: It replaces the norm in NPSVM with an regularization term to address the PU learning problem, achieving satisfactory results in both classification and feature selection aspects. This algorithm follows the biased support vector method.
- kNN-SVM [20]: It sorts the unlabeled examples based on the sum of their distances to the k-nearest positive examples; it then selects the examples at the largest distance as reliable negative examples. The iterative SVM is used to train the classifier. This algorithm is one of the representative algorithms using the two-step strategy.
5.2. Experimental Results
We present the experimental results obtained by the algorithms in this subsection. All experiments are implemented in MATLAB 2020a on a PC with an Intel(R) Core(TM) i7-8700 CPU (3.20GHz) and 16.0GB RAM. The corresponding AVI-SVM MATLAB codes are available at https://github.com/Yongjia2/AVI-SVM (accessed 6 March 2024).
5.2.1. Illustration on the Iris Dataset
First, we apply our algorithm on the Iris dataset, which is a well-known dataset used to demonstrate the performance of classification algorithms. It contains three classes, Setosa, Versicolor, and Virginica, with each instance characterized by four features. For our PU learning task, we focus exclusively on two classes—Versicolor and Virginica—and two features—the petal length and petal width. Figure 2 presents the classification result of our algorithm on this dataset. We randomly select of the Versicolor examples and designate them as positive examples, represented by black circles in the figure. The remaining Versicolor and all Virginica examples are treated as unlabeled examples. In Figure 2b, the examples within diamond-shaped boxes are the selected reliable negative examples; the red solid line is the separating hyperplane ; and the two red dashed lines are hyperplanes . From this figure, we can see that the AVI-SVM algorithm can select some true negative samples that are far from the labeled positive examples as reliable negative examples, and it can identify all positive examples. Note that the direction of the separating line is appropriate for the distribution of the two classes of examples.
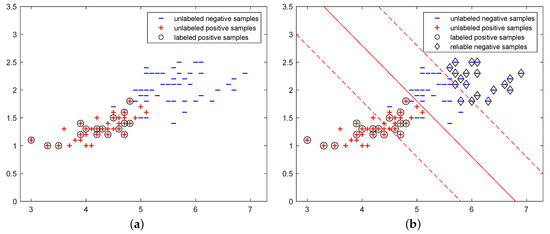
Figure 2.
Classification result obtained by AVI-SVM on the modified Iris dataset. (a) Modified Iris dataset with labeled positive examples; (b) the reliable negative examples identified and the separating line.
5.2.2. Results on Other UCI Datasets
To further demonstrate the effectiveness of our algorithm, numerical experiments on the three benchmark algorithms and the AVI-SVM algorithm on ten other real-world datasets from the UCI machine learning repository [31] have been undertaken. Table 1 gives detailed information about the ten UCI datasets.

Table 1.
Details of the ten UCI datasets.
The experiments are set up in the following way. Firstly, each dataset is randomly divided into two portions: of examples are for training and of examples are for testing. Then, we choose or of the positive data examples from the training set randomly as the positive set , and we use the remainder as the unlabeled dataset to generate the PU learning problems. Algorithm 3 determines the optimal parameters for both the AVI-SVM and kNN-SVM algorithms. Specifically, for AVI-SVM, the parameters l, , and are defined within the ranges of [1, 3], (0, 26), and (0, 26), respectively. Meanwhile, in kNN-SVM, parameters k and T are set within the ranges of and [0, 5], respectively. The parameters in the LUHC and the B-NPSVM algorithms are set as per the instructions in the experiments section in the references [9] and [14], respectively.
Each algorithm is run 10 times on every dataset, and the accuracy () and average F-score obtained by AVI-SVM and the three benchmark algorithms on these test sets are recorded in Table 2 and Table 3.

Table 2.
Accuracy and F-score comparison for four algorithms on datasets with of positive examples labeled. The best results are indicated by bold font in the table.

Table 3.
Accuracy and F-score comparison for four algorithms on datasets with of positive examples labeled. The best results are indicated by bold font in the table.
From Table 2, we can observe that our AVI-SVM algorithm demonstrates superior performance in terms of accuracy across five distinct datasets, Hearts, Australian, German, Banknote, and Spambase, surpassing the results achieved by the LUHC, NPSVM, and KNN-SVM algorithms. Meanwhile, on Twonorm, our AVI-SVM obtains accuracy of 97.39%, which is slightly lower than the highest of 97.84%. Moreover, when evaluating the F-score, our algorithm emerges as the top performer on six datasets: Hearts, Haberman, Australian, Banknote, Spambase, and HTRU2.
Compared with Table 2, Table 3 indicates that the and F-score values of all algorithms tend to increase with the increasing percentage of labeled positive examples. Table 3 also shows that our AVI-SVM algorithm has the best performance with respect to accuracy on six datasets (Hearts, Haberman, Australian, Banknote, Spambase, HTRU2) and second best on the BUPA, German, and Twonorm datasets. Meanwhile, as the ratio of positives increases, AVI-SVM still maintains the best F-score on Sonar, Hearts, Haberman, Australian, Banknote, and Spambase. Overall, it can be seen from the experimental results that the proposed AVI-SVM algorithm always performs efficiently on most of the datasets.
The experimental results clearly demonstrate that the AVI-SVM algorithm performs well on most of the test datasets. Furthermore, its ability to sustain the classification performance despite variations in the number of positive examples underscores the algorithm’s robustness and effectiveness.
6. Conclusions
The key to solving the PU problem via the two-step strategy lies in how to select reliable negative examples from the unlabeled examples. In this paper, the concept of eccentricity is used to perform the selection. After transforming the PU problem into a normal semi-supervised problem, the absolute value inequality SVM is employed to find the decision function. The procedures involved are easy to implement. Moreover, a hyperparameter optimization method is used to tune the parameters in order to obtain better classification results. The experimental results show the effectiveness of the proposed algorithm in dealing with the PU learning problem.
Note that the presented AVI-SVM strategy currently focuses on solving linear classification problems within PU learning. In the future, we plan to extend it with kernel methods to handle nonlinear classification situations in real-world scenarios.
Author Contributions
Conceptualization, F.B.; methodology, Y.Y. and F.B.; coding, Y.Y.; writing—original draft preparation, Y.Y.; writing—review and editing, F.B.; visualization, Y.Y.; supervision, F.B.; funding acquisition, F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Key Project of the Chongqing Municipality Education Commission Scientific and Technological Research Program (KJZD-K202114801) and the Innovation and Development Joint Project of the Chongqing Natural Science Foundation (2022NSCQ-LZX0301).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Stolfi, P.; Mastropietro, A.; Pasculli, G.; Tieri, P.; Vergni, D. NIAPU: Network-informed adaptive positive-unlabeled learning for disease gene identification. Bioinformatics 2023, 39, btac848. [Google Scholar] [CrossRef] [PubMed]
- Fung, G.P.C.; Yu, J.X.; Lu, H.; Yu, P.S. Text classification without negative examples revisit. IEEE Trans. Knowl. Data Eng. 2005, 18, 6–20. [Google Scholar] [CrossRef]
- Li, F.Y.; Dong, S.Y.; Leier, A.; Han, M.Y.; Guo, X.D.; Xu, J.; Wang, X.Y.; Pan, S.R.; Jia, C.Z.; Zhang, Y.; et al. Text classification without negative examples revisit Positive-unlabeled learning in bioinformatics and computational biology: A brief review. Brief. Bioinform. 2022, 23, 1–13. [Google Scholar]
- de Souza, M.C.; Nogueira, B.M.; Rossi, R.G.; Marcacini, R.M.; Dos Santos, B.N.; Rezende, S.O. A network-based positive and unlabeled learning approach for fake news detection. Mach. Learn. 2022, 111, 3549–3592. [Google Scholar] [CrossRef] [PubMed]
- Jaskie, K.; Martin, J.; Spanias, A. PV Fault Detection Using Positive Unlabeled Learning. Appl. Sci. 2021, 11, 5599. [Google Scholar] [CrossRef]
- Yang, W.T.; Chen, C.T.; Sang, C.Y.; Huang, S.H. Reinforced pu-learning with hybrid negative sampling strategies for recommendation. ACM Trans. Intell. Syst. Technol. 2023, 14, 1–25. [Google Scholar] [CrossRef]
- Manevitz, L.M.; Yousef, M. One-class SVMs for document classification. J. Mach. Learn. Res. 2001, 2, 139–154. [Google Scholar]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.H.; Chen, W.J.; Liu, L.M.; Deng, N.Y. Laplacian unit-hyperplane learning from positive and unlabeled examples. Inf. Sci. 2015, 314, 152–168. [Google Scholar] [CrossRef]
- Zhou, K.; Xue, G.R.; Yang, Q.; Yu, Y. Learning with positive and unlabeled examples using topic-sensitive PLSA. IEEE Trans. Knowl. Data Eng. 2009, 22, 46–58. [Google Scholar] [CrossRef]
- Liu, B.; Dai, Y.; Li, X.; Lee, W.S.; Yu, P.S. Building text classifiers using positive and unlabeled examples. In Proceedings of the Third IEEE International Conference on Data Mining, Melbourne, FL, USA, 19–22 November 2003; pp. 179–186. [Google Scholar]
- Ke, T.; Li, M.; Zhang, L.; Lv, H.; Ge, X. Construct a biased SVM classifier based on Chebyshev distance for PU learning. J. Intell. Fuzzy Syst. 2020, 39, 3749–3767. [Google Scholar] [CrossRef]
- Zhang, Y.; Ju, X.; Tian, Y. Nonparallel hyperplane support vector machine for pu learning. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014; pp. 703–708. [Google Scholar]
- Bai, F.; Yuan, Y. L1-norm Nonparallel Support Vector Machine for PU Learning. In Proceedings of the 2018 IEEE 23rd International Conference on Digital Signal Processing (DSP), Shanghai, China, 19–21 November 2018; pp. 1–5. [Google Scholar]
- Luo, C.; Zhao, P.; Chen, C.; Qiao, B.; Du, C.; Zhang, H.Y.; Wu, W.; Cai, H.W.; He, B.; Rajmohan, S.; et al. Pulns: Positive-unlabeled learning with effective negative sample selector. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; pp. 8784–8792. [Google Scholar]
- Liu, B.; Lee, W.S.; Yu, P.S.; Li, X. Partially supervised classification of text documents. ICML 2002, 2, 387–394. [Google Scholar]
- Yu, H.; Han, J.; Chang, K.C.C. PEBL: Positive example based learning for web page classification using SVM. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 239–248. [Google Scholar]
- Li, X.; Liu, B. Learning to classify texts using positive and unlabeled data. In Proceedings of the 18th International Joint Conference on Artificial Intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 587–592. [Google Scholar]
- Liu, B.; Liu, Q.; Xiao, Y. A new method for positive and unlabeled learning with privileged information. Appl. Intell. 2022, 52, 2465–2479. [Google Scholar] [CrossRef]
- Zhang, B.; Zuo, W. Reliable Negative Extracting Based on kNN for Learning from Positive and Unlabeled Examples. J. Comput. 2009, 4, 94–101. [Google Scholar] [CrossRef]
- Mangasarian, O.L. Unsupervised classification via convex absolute value inequalities. Optimization 2015, 64, 81–86. [Google Scholar] [CrossRef]
- Angelov, P. Anomaly detection based on eccentricity analysis. In Proceedings of the 2014 IEEE Symposium on Evolving and Autonomous Learning Systems (EALS), Orlando, FL, USA, 9–12 December 2014. [Google Scholar]
- Ilievski, I.; Akhtar, T.; Feng, J.; Shoemaker, C. Efficient hyperparameter optimization for deep learning algorithms using deterministic rbf surrogates. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Tian, Y.; Qi, Z.; Ju, X.; Shi, Y.; Liu, X. Nonparallel support vector machines for pattern classification. IEEE Trans. Cybern. 2013, 44, 1067–1079. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Ju, X.; Qi, Z. Efficient sparse nonparallel support vector machines for classification. Neural Comput. Appl. 2014, 24, 1089–1099. [Google Scholar] [CrossRef]
- Jung, C.; Shen, Y.; Jiao, L. Learning to rank with ensemble ranking SVM. Neural Process. Lett. 2015, 42, 703–714. [Google Scholar] [CrossRef]
- Angelov, P. Outside the box: An alternative data analytics framework. J. Autom. Mob. Robot. Intell. Syst. 2014, 8, 29–35. [Google Scholar] [CrossRef]
- Saw, J.G.; Yang, M.C.; Mo, T.C. Chebyshev inequality with estimated mean and variance. Am. Stat. 1984, 38, 130–132. [Google Scholar] [CrossRef]
- Mangasarian, O.L. Absolute value equation solution via concave minimization. Optim. Lett. 2007, 1, 3–8. [Google Scholar] [CrossRef]
- Lee, W.S.; Liu, B. Learning with positive and unlabeled examples using weighted logistic regression. In Proceedings of the Twentieth International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003; pp. 448–455. [Google Scholar]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 6 March 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).