Abstract
The Mann–Whitney effect is a measure for comparing survival distributions between two groups. The Mann–Whitney effect is interpreted as the probability that a randomly selected subject in a group survives longer than a randomly selected subject in the other group. Under the independence assumption of two groups, the Mann–Whitney effect can be expressed as the traditional integral formula of survival functions. However, when the survival times in two groups are not independent of each other, the traditional formula of the Mann–Whitney effect has to be modified. In this article, we propose a copula-based approach to compute the Mann–Whitney effect with parametric survival models under dependence of two groups, which may arise in the potential outcome framework. In addition, we develop a Shiny web app that can implement the proposed method via simple commands. Through a simulation study, we show the correctness of the proposed calculator. We apply the proposed methods to two real datasets.
Keywords:
censoring; copula; Hand’s paradox; Mann–Whitney effect; potential outcome; stress–strength model; survival analysis; survival function; treatment effect; two-sample comparison MSC:
62-04; 62D20; 62F10; 62N01; 62N03; 62N05
1. Introduction
When comparing the survival times of two independent groups, the Mann–Whitney parameter plays an important role in the two-sample problem [1]. The Mann–Whitney parameter, say, p, is defined as the probability that a random subject from one group (with survival time in group 1) survives longer than an independent random subject from the other group (with survival time in group 2), plus one-half the probability that the two subjects survive at the same time (tie):
When researchers verify the superiority of a treatment over another, they examine whether the effect exceeds the null difference, . For instance, when they obtain , this effect is transformed to of Cohen’s d according to well-known benchmark values [2]. Therefore, it can be interpreted as a large effect. The Mann–Whitney effect relates to important statistical ideas, such as, the Mann–Whitney test [3], hazard ratios, and win ratio [4]. The Mann–Whitney test examines the null hypothesis vs. . The hazard ratio is the main effect measure of the Cox proportional hazards model, which is a typical statistical model in survival analysis. The win ratio w is given by the odds of p; that is, . That is, , or equivalently , implies a protective survival effect for group 1.
The problem of estimating the parameter p plays an important part in survival and reliability analysis. The basic idea was first studied by Birnbaum [5]. They illustrated an attractive relationship between the Mann–Whitney statistic and the stress–strength model. Efron [1] first proposed a nonparametric estimator (Efron’s estimator) for p under independent censoring. Since then, this topic has been investigated by several researchers. In the following, we refer to some recent studies in the field of survival and reliability analyses. Dobler & Pauly [6] modified Efron’s estimator for p under small sample sizes. Emura & Hsu [7] proposed a copula-graphic estimator for p and suggested the Mann–Whitney test to compare two survival distributions in the presence of dependent censoring. Biswas et al. [8] introduced the Bayesian estimation of p for the log-Lindley distribution. Rubarth et al. [9] proposed estimating the Mann–Whitney effects in factorial clustered data. Hu et al. [10] developed methodologies for constructing fixed-accuracy confidence intervals of p when and follow geometric and the exponential distributions, respectively. de la Cruz et al. [11] studied a estimation procedure of the stress–strength model for the two independent unit-half-normal distributions with different shape parameters. Patil et al. [12] investigated the effect of dependence of the variables on p in the stress-strength model with the exponential margins. Nowak et al. [13] proposed a group sequential method for estimating the Mann–Whitney parameter. Singh et al. [14] studied the estimator of p in point, interval, and Bayesian estimations when the stress variables follow geometric and Lindley distribution. All the methods assumed that and are independent.
When and are independent of each other and continuous, one can estimate p with the marginal distributions based on the following integral:
That is, one can estimate p by estimating two marginal survival functions, and . However, this is not the case when and are dependent; the phenomenon is sometimes called “Hand’s paradox” [15]. This showed that the paradox arises when and are regarded as potential outcomes in the causal inference framework. Therefore, p in the integral cannot be interpreted as the true treatment effect. Moreover, the dependence of outcomes from observation to observation is well known in factorial, paired, and cross-over designs [16,17].
Since p is not identifiable solely from independently sampled data, Fan & Park [18] suggested a bound for p under all possible dependence structures for and . Alternatively, Fay et al. [19] reformulated p such that it can be identified from randomized treatment assignments. Computing p under various dependence structures gives the researchers additional information for their decision making about the behavior of p when the outcomes are not independent. However, to estimate the true p, we must model the bivariate survival function of and . A copula is often used to model joint distributions of dependent survival times [20,21]. Here, the major challenge is to derive the formula of p under copula models and its extension to allow for a limited follow-up length for survival times.
In this article, we propose a model for the bivariate survival function by using parametric copulas and parametric marginal distributions. Our focus is to study p when there is dependence between and . Therefore, we focus on assessing how p vary under various dependences modeled by copulas. We then derive a new formula for computing p under a parametric copula. We also propose a new formula for p under the restricted follow-up. To make the proposed computation method for p to be easily performed by users, we develop a Shiny-based web app. Furthermore, we validate the accuracy of the proposed computation method and Shiny web app by simulations. We finally analyze real data, where the proposed copula-based estimators are compared with Efron’s estimator (benchmark).
The rest of the paper is organized as follows. In Section 2, we define copula-based models and introduce several well-known copula families. In this section, we show that one can compute p by a theorem given by Emura & Pan [22], and we extend the theorem to compute p when the follow-up time is restricted up to time . In Section 3, we introduce a Shiny web app in the R software version 4.2.3 that can compute p via simple commands. In Section 4, we describe a simulation study to show the correctness of the proposed calculator for p. In Section 5, we illustrate a meaningful application of our proposed method using survival data. The computer code for the simulations and data analyses is available in Supplementary Materials.
2. Proposed Method
In this section, we first introduce copula-based bivariate survival models for and . We then propose our method for computing the Mann–Whitney effect p in Equation (1) under the copula models.
2.1. Survival Copula Models for Dependent Survival Time
According to Sklar [23], any bivariate distribution function for can be formulated by using a copula. A bivariate copula is a bivariate distribution function for two uniformly distributed variables on [24,25]. In many applications of copulas on survival analysis, bivariate survival functions are modeled via survival copulas [20,24,26,27]. Below, we introduce a survival copula model for a bivariate survival function .
Let and be continuous survival times with marginal survival functions and , respectively. We model the bivariate survival function of and using a survival copula C:
This representation is useful since two marginal survival functions and are separated from the dependence structure C. Under the survival copula model (2), the copula C is a bivariate distribution function for and , namely . Note that the survival copula model (2) gives a different model from the copula model unless the copula is radially symmetric, i.e., .
We will consider the following well-known families of bivariate copulas.
- 1.
- The independence copula:
- 2.
- The Clayton copula [28]:
- 3.
- The Gumbel copula [29]:
- 4.
- The Frank copula [30]:
- 5.
- The Farlie–Gumbel–Morgenstern (FGM) copula [31]:
- 6.
- The Gumbel–Barnett (GB) copula [24,32,33]:
In Figure 1, we present scatter plots for generated from various copulas with selected values of . The Clayton copula (Figure 1b,c) shows lower tail dependence, the Gumbel copula (Figure 1d) shows upper tail dependence, Frank copula (Figure 1e,f) shows symmetric dependence around the median, and the FGM copula (Figure 1g,h) is similar to the Frank copula; both copulas are radially symmetric. Unlike other copulas, the GB copula exhibits negative dependence only (Figure 1i).
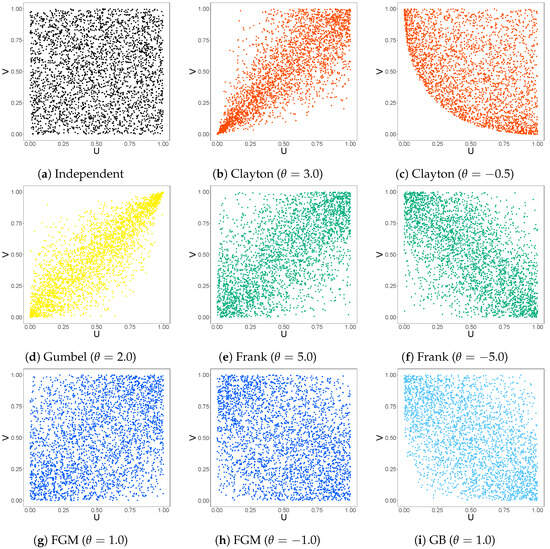
Figure 1.
Scatter plots of 3000 data points generated from the copula distribution with parameter .
These copulas have been applied to survival data and other data analyses. The Clayton copula was applied to survival data with dependent censoring. For instance, Schneider et al. [34] modeled dependence between survival and dependent censoring times in the survival data of tuberculosis cure. The Clayton, Gumbel, and Frank copulas were also applied to dependently censored data in clinical trials or observational studies [35,36,37]. The Gumbel, Frank, and FGM copulas were often used in competing risks models on survival data analysis [26,38,39,40]. Copulas were also applied to multivariate meta-analysis; Shih et al. and Shih et al. [41,42] proposed bivariate Clayton, FGM, and Gumbel models for bivariate meta-analysis. The Gumbel–Barnett copula has the simple form and is suitable for modeling negative dependence [24,32]. Therefore, it is important to consider a variety of copulas for dependent survival times.
To see the strength of dependence in a copula, can be transformed to Kendall’s . Kendall’s is a well-known measure to assess the dependence between two variables [20,24]. Kendall’s does not depend on the marginals, and is solely determined by the copula (by ). Appendix A provides the formulas of Kendall’s for the Clayton, Gumbel, Frank, FGM, and GB copulas. Therefore, Kendall’s is advantageous over the Pearson correlation for and .
2.2. Proposed Method for Computing p
In this section, we propose a new formula for computing p under the survival copula model (2). Let and . For computing p, we will use the conditional distribution function for U given , which is the partial derivative of C with respect to v:
Then, by slightly modifying the theorem given by Emura & Pan [22], p can be expressed as the univariate integral on :
We note that the theorem of Emura & Pan [22] is not directly applicable to the survival copula model (2) since that theorem is designed for the copula model .
In order to compute p by the above formulas, we need to specify , , and . One can specify and by continuous parametric models that will be discussed in Section 2.4. One can try different values for in a sensitivity analysis. Note that the above calculations are not applicable for discrete parametric models for and .
2.3. Computing p with Follow-Up Time
In this section, we assume that every subject has a common follow-up time . For survival data, the follow-up period is often limited. When a subject survives longer than the follow-up period, one may treat the survival time of the subject as equal to the follow-up period [6,43,44]. This means that we define the Mann–Whitney effect for min and min. We now obtain p with the follow-up time from the following theorem, a straightforward expansion of the theorem of Emura & Pan [22].
Theorem 1.
The Mann–Whitney effect p with a follow-up time τ is written as the univariate integral:
Furthermore, tends to p as . That is,
Appendix B provides the formulas of p and for the Clayton, Gumbel, Frank, FGM, and GB copulas.
2.4. Marginal Survival Distributions
To compute p and , we considered the following parametric marginal distributions for the group :
- 1.
- The exponential distribution:where is a rate parameter.
- 2.
- The Weibull distribution:where is a scale parameter and is a shape parameter.
- 3.
- The gamma distribution:where is a scale parameter and is a shape parameter, and is the gamma function, and is the lower incomplete gamma function. The gamma distribution has no simple closed-form expression for the inverse survival function. Therefore, one can use approximations for the inverse survival function. In this article, we use the R software version 4.2.3 function “qgamma” to calculate .
- 4.
- The log-normal distribution:where is a location parameter and is a scale parameter. Note that has no simple closed-form expression for the inverse survival function. Therefore, one can use approximations for the inverse survival function. In this article, we use the R software function “qlnorm” to calculate .
- 5.
- The Burr III distribution:where are shape parameters.
In Figure 2, we present survival curves of the exponential, Weibull, gamma, log-normal, and Burr III distributions with different parameters. These plots show that these distributions can represent almost any continuous survival curve that will be encountered in practice.
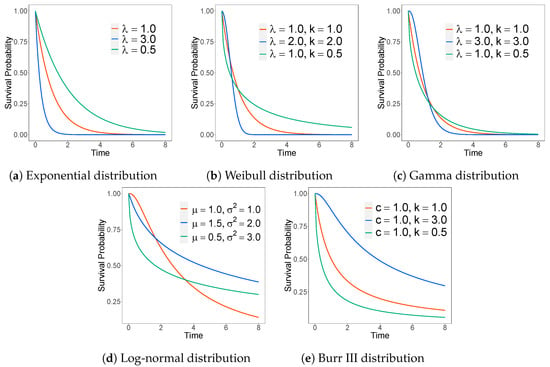
Figure 2.
The plots for parametric survival functions.
Example 1.
Let the marginals be the exponential distributions with parameter . Assume that and are independent. Then, by Theorem 1 with , p is given by
Example 2.
Let the marginals be the exponential distributions with parameter . Assume that is the Clayton copula with parameter . Then, Kendall’s τ is given by
and by Theorem 1 with , p is given by
When , is given by
When , . Here, we computed the last two equations by a numerical integration by the R software version 4.2.3 function “integrate”.
Parameters for the marginal distributions can be estimated by maximum likelihood estimators (MLEs) when the survival data are available in two groups (Section 5).
2.5. Sensitivity Analysis by Copulas
To comprehensively cover the possible dependence structures between and , we select the Clayton, Gumbel, Frank, FGM, and GB copulas, and set their parameters. Table 1 contains positive dependence and negative dependence with weak and strong correlations, as well as the independence. However, the selection of an appropriate copula may be difficult unless both and are observed for the same subject (e.g., by cross-over designs). This is the case for the data examples (Section 5), where and are observed for different subjects. Let Z be the group indicator ( when is observed; when is observed). What we observe is one of and , namely, . As and are never observed simultaneously, the copula for and are not identifiable [18,19]. This means that copula model selection and goodness-of-fit test are not feasible. Therefore, as one cannot specify a single copula, we suggest computing p under all these copulas and dependence parameters to see how p changes under various dependence. Such sensitivity analyses allow researchers to obtain the bounds of p under the possible dependence structures.

Table 1.
Selection of copulas and their parameters.
3. Software and Web App
We developed a Shiny-based web app to implement the proposed method for computing p and . The app is available at (https://nkosuke.shinyapps.io/shiny_survival/ accessed on 7 April 2024) and can be used in any environment, including smartphones. Using this app, users can choose a marginal survival distribution, copula, and the relevant parameters to compute p and . Our app is easy to use without knowledge of the R software version 4.2.3. The app works without data, because it does not estimate the parameters of the marginals and copula. All relevant parameters are entered by users. The app can compute p and across different parametric distributions (Section 2.4) and copula models (Section 2.5).
3.1. Input
The web app requires users to select input values to compute p and . The left panel of Figure 3 shows input icons, where users can select marginal distributions from the exponential, Weibull, gamma, log-normal, and Burr III distributions and a copula from the Clayton, Gumbel, Frank, FGM, and GB copulas. One can choose marginal distributions and copulas, set their parameters, and choose the language displayed on the screen in the input panels on the left-hand of the app (Figure 3). Furthermore, users can set a follow-up time .
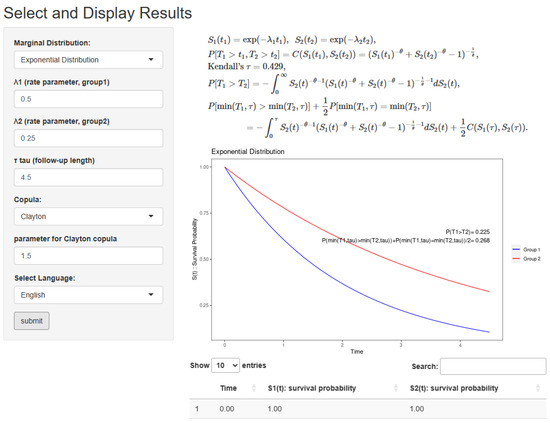
Figure 3.
The web app showing the results for computing p and under the exponential distribution.
3.2. Output
This app displays key formulas, survival curves of two groups, the values of p and , and the value of Kendall’s . These formulas include marginal and bivariate survival functions and formulas of p and based on the input values. The theoretical values of p and are displayed together with survival curves.
3.3. Example of Using the App
Users may set the marginal survival distribution = “Exponential Distribution”, , , , copula = “Clayton”, and the language displayed on the screen “English”, and push “submit” button, and then they can obtain . Figure 3 displays the web app in this setting. Appendix C provides further examples for users.
4. Simulation Studies
To show the correctness of the proposed calculator for p and , we conduced a simulation study. In particular, we tried to confirm the formula of Theorem 1 under a variety of marginal distributions and copulas. For the simulation study, we set the marginal survival functions to be the exponential distributions with , the Weibull distributions with , the gamma distributions with , the log-normal distributions with , and the Burr III distributions with . Furthermore, we set the copula parameters, the Clayton copula with , the Gumbel copula with , the Frank copula with , the FGM copula with , the GB copula with , and follow-up time . We chose the copulas and their parameters to cover both positive and negative dependence. We generated 100,000 pairs where M = 100,000, from the bivariate survival function based on the aforementioned setting, and calculated the Monte Carlo simulation values defined as
Table 2 shows that the simulation values are nearly equal to the theoretical values computed by the formula of Theorem 1 for every setting. Note that the standard errors (SEs) due to the uncertainty of the Monte Carlo values are less than in all settings, which are negligible. As the positive dependence between and gets strong, the value of p and approaches 1. Moreover, even though the values of the Kendall’s are equivalent, it is possible for to vary from a copula model to others due to distinct characteristics of copulas. In conclusion, our simulations show that Theorem 1 is correct, and the Shiny web app based on Theorem 1 is reliable.

Table 2.
Comparison of the theoretical value and the simulation value (SE < 0.002) for calculating defined in Theorem 1. (The exponential, Weibull, gamma, log-normal, and Burr III distributions).
5. Data Analysis
In this section, we apply our proposed methods to a tongue cancer dataset and a prostate cancer dataset. The two datasets are publicly available and anonymized. The purpose of the data analyses is to show how the proposed methods are implemented and how the results offer new insights beyond Efron’s traditional estimator for the Mann–Whitney effect.
Before analyzing the real datasets, we introduce basic notations and ideas for estimating p by using censored data. We consider survival times for two groups, a group indicator ( for group 1 and for group 2), and censoring time for . The sample size for each group is , . With , we observe is , , and for . In this observation, only one of , , and is observed ( and are never observed simultaneously) for each i, making it difficult to identify a copula for . Without specifying a copula for possibly dependent survival times , one can still estimate the marginal distributions. Using the exponential distribution, we obtained the MLE of the exponential hazard rate by
Then, by applying the values of the MLE to the proposed Shiny web app, we obtained the estimators and , where was chosen appropriately (Section 5.1 and Section 5.2). The estimators were computed under various copulas as one cannot specify a single copula (see Section 2.5). On the other hand, under the independence assumption of and , Efron’s estimator [1] of p is
where and is a Kaplan–Meier (KM) estimator for group . However, these benchmark estimates are subject to the independence of two groups. Therefore, the proposed estimator is useful to examine the sensitivity under a variety of dependence structures via copulas. We apply a jackknife estimator of standard error (SE) to measure the estimators’ uncertainty, and employ the normal approximation to obtain p-values for testing .
5.1. Tongue Cancer Data
The tongue dataset is available in the R software version 4.2.3 package KMsurv. It has 80 observations and contains: type (tumor DNA profile: 1 = aneuploid tumor, 2 = diploid tumor), time (time to death or on-study time (weeks)), and death (event indicator: 0 = alive, 1 = dead). It contains observations in the DNA-aneuploid tumor group (), and observations in the DNA-diploid tumor group (). We considered the follow-up time and obtained . The tongue cancer data resulted in and . In Figure 4, the KM estimators of each group and the estimated exponential survival curves are plotted.
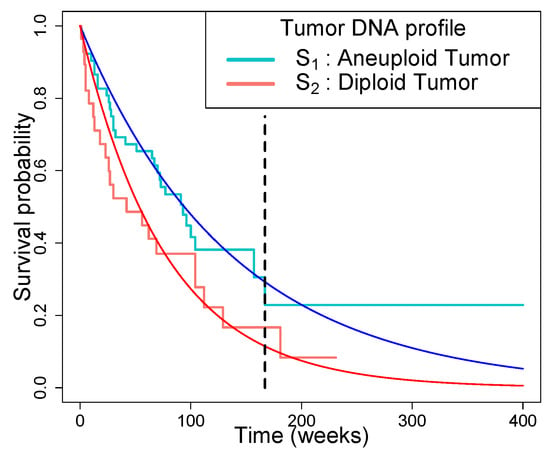
Figure 4.
KM estimators for the DNA-aneuploid tumor and the DNA-diploid tumor group and the exponential survival curves with the MLEs of exponential hazard rate (darker blue and red lines), . The vertical line signifies the follow-up time .
We conducted sensitivity analyses using a copula-based approach (see Section 2.5). We calculated and by Theorem 1 under weak, strong positive, and negative independence. We calculated via the web app (Figure 5). Table 3 shows the output under the independent, Clayton, Gumbel, Frank, FGM, and GB copula with parameter . The results for all scenarios are summarized in Table 3. We obtained the ranging from to , which is equivalent to Cohen’s d being greater than or equal to . Therefore, we concluded that subjects in the DNA-aneuploid tumor group survive longer than in those the DNA-diploid tumor group. This conclusion did not change under any of the conducted dependence structures.
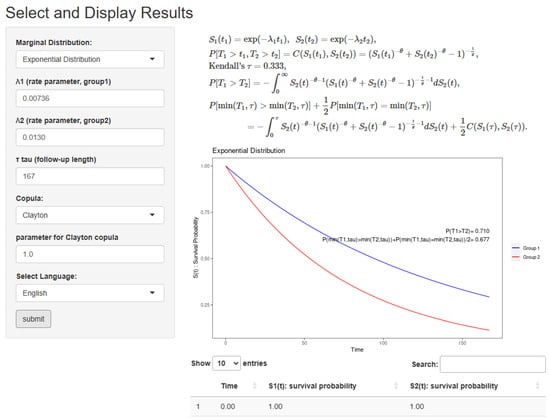
Figure 5.
Example for the tongue cancer dataset on the app. This setting is marginal distribution: “Exponential”, , copula: “Clayton”, copula parameter: , and language: “English”.

Table 3.
Estimates for fitting the KM estimator (independent) and with exponential marginal survival distributions (the independent, Clayton, Gumbel, Frank, FGM, GB copulas) for the tongue cancer dataset.
5.2. Prostate Cancer Data
The prostate cancer data are available in the R software version 4.2.3 package asaur [45]. They have 14,294 observations and contain grade (moderately differentiated and poorly differentiated), survTime (time from diagnosis to death or last date known alive), and status (event indicator: 0 = censored, 1 = death from prostate cancer). They contain = 10,988 observations in the moderately differentiated group (), and = 3306 observations in the poorly differentiated group ().
The prostate cancer data resulted in , , and . In Figure 6, we plot the KM estimators of each group and estimated exponential survival curves. We calculated by Theorem 1 with copulas and several parameters. We calculated under the independent, Clayton, Gumbel, Frank, FGM, and GB copulas with parameter via the web app (Figure 7). The results for all scenarios are summarized in Table 4. We obtained the ranging from to , which is equivalent to Cohen’s d being equal to . Therefore, we concluded that subjects in the moderately differentiated group survive longer than those in the poorly differentiated group. The range of is narrower than one of tongue cancer dataset, because the large difference of survival functions may not be influenced by copulas.
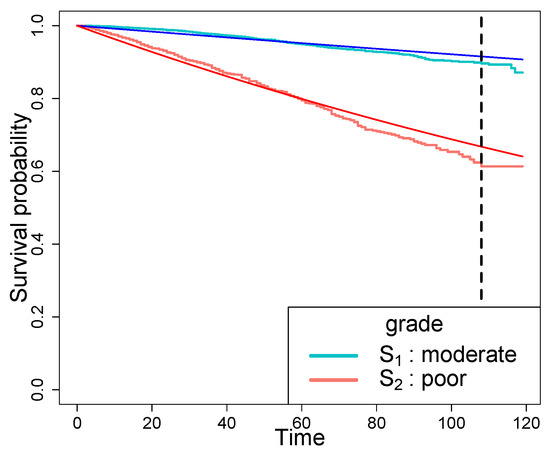
Figure 6.
KM estimators for the moderately differentiated and the poorly differentiated group and exponential survival curves with the MLEs of exponential hazard rate (darker blue and red lines), . The vertical line signifies the follow-up time .
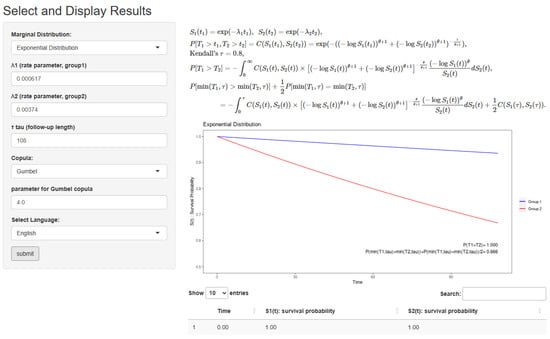
Figure 7.
Example for the tongue cancer dataset on the app. This setting is marginal distribution: “Exponential”, , copula: “Gumbel”, copula parameter: , and language: “English”.

Table 4.
Estimates for fitting the KM estimator (independent) and with the exponential marginal survival distributions (the independent, Clayton, Gumbel, Frank, FGM, GB copulas) for the prostate cancer dataset.
6. Conclusions
The Mann–Whitney effect has been widely used for survival analysis, which can provide a meaningful measure of treatment effects on survival outcomes. However, the Mann–Whitney effect may not be interpreted as the true treatment effect under the dependence of the two survival times. In this article, we proposed a parametric copula-based approach for estimating the Mann–Whitney effect p under dependence structures for two survival times. We derived the formulas of p under a variety of copulas and marginal survival functions and modified it by with as the follow-up time. We also introduced a web-based calculator for p and for users. Our simulation studies demonstrate the correctness of the proposed calculator under a variety of parametric marginal survival distributions and copulas. The results of the data analyses show that the proposed method provides possible changes in p and under various dependence and enables the examination of the sensitivity.
In the examples of real datasets, we obtained under the Clayton, Gumbel, Frank, FGM, and GB copulas with varying parameters. The value of ranged from to in the tongue cancer dataset and from to in the prostate cancer dataset. We obtained narrow ranges whose lower bounds did not include the null value of . The results show that, under a variety of dependence structures, the interpretation of the Mann–Whitney effect does not change. This result is consistent with previous studies showing that Hand’s paradox does not occur under a strictly monotonic effect [15,46]. The considered dependence may not affect decision making in clinical research or practice. Although more complex dependence structures with various copulas might be considered, the conclusion may not change significantly.
On computing the Mann–Whitney effect under dependence, there are several previous works (Table 5). However, these works focused on specific combinations of marginals and copulas. The advantage of our article is that it can be applied to various marginals and copulas, not just to a specific one. Our app allows readers to verify the behavior of the Mann–Whitney effect under various dependences.

Table 5.
Recent works on the Mann–Whitney effect with the copula models and marginal models.
The main limitation of the present article is that we only discussed the “parametric” approach. Because the proposed method uses extrapolated parameters to compute the Mann–Whitney effect, the result strongly depends on the model assumptions of the marginals and copulas and the characteristics of the extrapolated parameter. However, in practice, researchers may use the “semiparametric” or “nonparametric” approaches [17]. In future work, we will examine the method of computing p without parametric assumptions and expand it to nonparametric or semiparametric models such as Cox regression. The anticipated challenge of nonparametric approach is that the empirical copula, which is a nonparametric approach to copula models, is often nonsmooth and not a genuine copula. Another extension is to include covariates or secondary outcomes, including time-varying effects in the model, which helps obtain narrow bounds for treatment effects [54,55,56]. Another limitation is that only one-parameter bivariate copulas and noninformative censoring were implemented. Multiparameter or multivariate copulas deserve attention [24,32,57]. There are also several recent works on copula-based approaches for dependent censoring [58,59,60]. If censoring is not independent of survival, the usual MLE and KM estimators are biased (hence, the estimators in Section 5 are all biased). Furthermore, the proposed method for two-sample comparison may be extended to multigroup comparisons using the factorial designs by adopting the relative treatment effects of Brunner & Puri and Dobler & Pauly [43,61].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math12101453/s1, the R code for simulations and data analyses.
Author Contributions
Conceptualization, K.N. and T.E.; Methodology, K.N. and T.E.; Software, K.N. and Y.-C.L.; Resources, G.-Y.L.; Writing—original draft, K.N., R.U. and T.E.; Visualization, K.N.; Supervision, T.E.; Funding acquisition, R.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [JSPS KAKENHI] grant number [22K11948], grant number [20H04147], and grant number [23K20374].
Data Availability Statement
As all data in Section 5 use publicly available data, written informed consent was not required.
Acknowledgments
We thank the editor and three reviewers for their time to comments on our paper. The comments from the reviewers greatly helped improve the presentation of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Kendall’s τ
Under the copula model (2), Kendall’s for and is expressed as
Kendall’s of each copula is expressed as follows.
- 1.
- The independence copula:
- 2.
- The Clayton copula:
- 3.
- The Gumbel copula:
- 4.
- The Frank copula:
- 5.
- The FGM copula:
- 6.
- The GB copula:
Appendix B. Examples of p and pτ with Different Copulas
Equation (3) with different copulas is computed by the following formulas:
- 1.
- The Clayton copula:
- 2.
- The Gumbel copula:
- 3.
- The Frank copula:
- 4.
- The FGM copula:
- 5.
- The GB copula:
Equation (4) with different copulas is computed by the following formulas:
- 1.
- The Clayton copula:
- 2.
- The Gumbel copula:
- 3.
- The Frank copula:
- 4.
- The FGM copula:
- 5.
- The GB copula:
Appendix C. Examples of Using the Shiny Web App
This appendix gives two examples of using the Shiny web app.
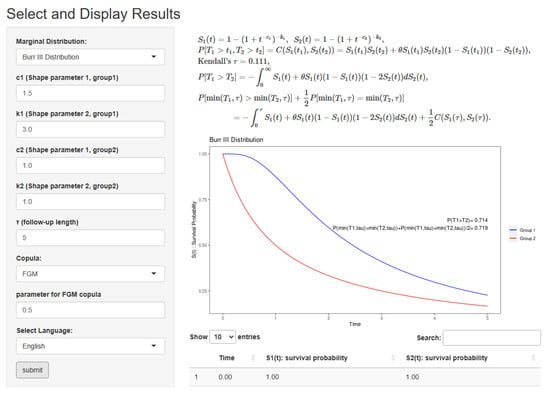
Figure A1.
The web app showing the results for computing p and under the Burr III distributions.
Example A1.
Users set the marginal survival distribution = “Burr III Distribution”, , , , copula = “FGM”, and the language displayed on the screen “English”, and push the “submit” button, and then they can obtain Kendall’s τ , , and . Figure A1 displays the web app in this setting.
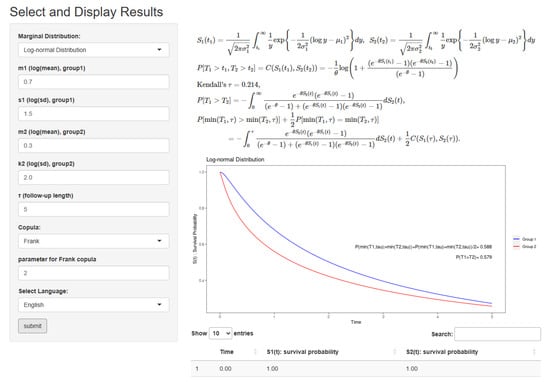
Figure A2.
The web app showing the results for computing p and under the log-normal distribution.
Example A2.
Users set the marginal survival distribution = “Log-normal Distribution”, , , , copula = “Frank”, and the language displayed on the screen “English”, and push the “submit” buttom, and then they can obtain Kendall’s τ, , and . Figure A2 displays the web app in this setting.
References
- Efron, B. The two sample problem with censored data. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; Volume 4, pp. 831–853. [Google Scholar]
- Rahlfs, V.W.; Zimmermann, H.; Lees, K.R. Effect Size Measures and Their Relationships in Stroke Studies. Stroke 2014, 45, 627–633. [Google Scholar] [CrossRef][Green Version]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Pocock, S.J.; Ariti, C.A.; Collier, T.J.; Wang, D. The win ratio: A new approach to the analysis of composite endpoints in clinical trials based on clinical priorities. Eur. Heart J. 2011, 33, 176–182. [Google Scholar] [CrossRef]
- Birnbaum, Z.W. On a use of the Mann-Whitney statistic. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, 1954–1955; University of California Press: Berkeley, BA, USA,, 1956; Volume I, pp. 13–17. [Google Scholar]
- Dobler, D.; Pauly, M. Bootstrap- and permutation-based inference for the Mann-Whitney effect for right-censored and tied data. TEST 2018, 27, 639–658. [Google Scholar] [CrossRef]
- Emura, T.; Hsu, J. Estimation of the Mann-Whitney effect in the two-sample problem under dependent censoring. Comput. Statist. Data Anal. 2020, 150, 106990. [Google Scholar] [CrossRef]
- Biswas, A.; Chakraborty, S.; Mukherjee, M. On estimation of stress-strength reliability with log-Lindley distribution. J. Stat. Comput. Simul. 2021, 91, 128–150. [Google Scholar] [CrossRef]
- Rubarth, K.; Sattler, P.; Zimmermann, H.G.; Konietschke, F. Estimation and Testing of Wilcoxon-Mann-Whitney Effects in Factorial Clustered Data Designs. Symmetry 2022, 14, 244. [Google Scholar] [CrossRef]
- Hu, J.; Zhuang, Y.; Goldiner, C. Fixed-accuracy confidence interval estimation of P(X<Y) under a geometric-exponential model. Jpn. J. Stat. Data Sci. 2021, 4, 1079–1104. [Google Scholar] [CrossRef]
- de la Cruz, R.; Salinas, H.S.; Meza, C. Reliability Estimation for Stress-Strength Model Based on Unit-Half-Normal Distribution. Symmetry 2022, 14, 837. [Google Scholar] [CrossRef]
- Patil, D.; Naik-Nimbalkar, U.V.; Kale, M.M. Effect of Dependency on the Estimation of P[Y>X] in Exponential Stress-strength Models. Austrian J. Stat. 2022, 51, 10–34. [Google Scholar] [CrossRef]
- Nowak, C.P.; Mütze, T.; Konietschke, F. Group sequential methods for the Mann-Whitney parameter. Stat. Methods Med. Res. 2022, 31, 2004–2020. [Google Scholar] [CrossRef]
- Singh, B.; Nayal, A.S.; Tyagi, A. Estimation of P [Y< Z] under Geometric-Lindley model. Ric. Mat. 2023, 1–32. [Google Scholar] [CrossRef]
- Hand, D.J. On Comparing Two Treatments. Am. Stat. 1992, 46, 190–192. [Google Scholar] [CrossRef]
- Cochran, W.G.; Cox, G.M. Experimental Designs, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA; Chapman & Hall, Ltd.: London, UK, 1957; p. xiv+617. [Google Scholar]
- Dobler, D.; Möllenhoff, K. A nonparametric relative treatment effect for direct comparisons of censored paired survival outcomes. Stat. Med. 2024; early view. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Park, S.S. Sharp bounds on the distribution of treatment effects and their statistical inference. Econom. Theory 2010, 26, 931–951. [Google Scholar] [CrossRef]
- Fay, M.P.; Brittain, E.H.; Shih, J.H.; Follmann, D.A.; Gabriel, E.E. Causal estimands and confidence intervals associated with Wilcoxon-Mann-Whitney tests in randomized experiments. Stat. Med. 2018, 37, 2923–2937. [Google Scholar] [CrossRef]
- Emura, T.; Matsui, S.; Rondeau, V. Survival Analysis with Correlated Endpoints; SpringerBriefs in Statistics; Springer: Singapore, 2019; p. xvii+118. [Google Scholar] [CrossRef]
- Li, D.; Hu, X.J.; Wang, R. Evaluating association between two event times with observations subject to informative censoring. J. Amer. Statist. Assoc. 2023, 118, 1282–1294. [Google Scholar] [CrossRef]
- Emura, T.; Pan, C. Parametric likelihood inference and goodness-of-fit for dependently left-truncated data, a copula-based approach. Statist. Pap. 2020, 61, 479–501. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2006; p. xiv+269. [Google Scholar] [CrossRef]
- Geenens, G. (Re-)Reading Sklar (1959);A Personal View on Sklar’s Theorem. Mathematics 2024, 12, 380. [Google Scholar] [CrossRef]
- Escarela, G.; Carrière, J.F. Fitting competing risks with an assumed copula. Stat. Methods Med. Res. 2003, 12, 333–349. [Google Scholar] [CrossRef] [PubMed]
- Petti, D.; Eletti, A.; Marra, G.; Radice, R. Copula link-based additive models for bivariate time-to-event outcomes with general censoring scheme. Comput. Statist. Data Anal. 2022, 175, 107550. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–151. [Google Scholar] [CrossRef]
- Gumbel, E.J. Distributions des valeurs extrêmes en plusieurs dimensions. Publ. Inst. Statist. Univ. Paris 1960, 9, 171–173. [Google Scholar]
- Frank, M.J. On the simultaneous associativity of F(x,y) and x + y − F(x,y). Aequationes Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Morgenstern, D. Einfache Beispiele zweidimensionaler Verteilungen. Mitteilungsbl. Math. Statist. 1956, 8, 234–235. [Google Scholar]
- Chesneau, C. On the Gumbel-Barnett extended Celebioglu-Cuadras copula. Jpn. J. Stat. Data Sci. 2023, 6, 759–781. [Google Scholar] [CrossRef]
- Toparkus, A.; Weißbach, R. Testing Truncation Dependence: The Gumbel-Barnett Copula. arXiv 2024, arXiv:2305.19675. [Google Scholar]
- Schneider, S.; dos Reis, R.C.P.; Gottselig, M.M.F.; Fisch, P.; Knauth, D.R.; Vigo, A. Clayton copula for survival data with dependent censoring: An application to a tuberculosis treatment adherence data. Stat. Med. 2023, 42, 4057–4081. [Google Scholar] [CrossRef]
- Sun, T.; Ding, Y. Copula-based semiparametric regression method for bivariate data under general interval censoring. Biostatistics 2021, 22, 315–330. [Google Scholar] [CrossRef]
- Moradian, H.; Larocque, D.; Bellavance, F. Survival forests for data with dependent censoring. Stat. Methods Med. Res. 2019, 28, 445–461. [Google Scholar] [CrossRef] [PubMed]
- Farzana, W.; Basree, M.M.; Diawara, N.; Shboul, Z.A.; Dubey, S.; Lockhart, M.M.; Hamza, M.; Palmer, J.D.; Iftekharuddin, K.M. Prediction of Rapid Early Progression and Survival Risk with Pre-Radiation MRI in WHO Grade 4 Glioma Patients. Cancers 2023, 15, 4636. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y. Semiparametric marginal regression analysis for dependent competing risks under an assumed copula. J. R. Stat. Soc. Ser. B Stat. Methodol. 2010, 72, 235–251. [Google Scholar] [CrossRef]
- Shih, J.; Emura, T. Likelihood-based inference for bivariate latent failure time models with competing risks under the generalized FGM copula. Comput. Statist. 2018, 33, 1293–1323. [Google Scholar] [CrossRef]
- Kawakami, R.; Michimae, H.; Lin, Y. Assessing the numerical integration of dynamic prediction formulas using the exact expressions under the joint frailty-copula model. Jpn. J. Stat. Data Sci. 2021, 4, 1293–1321. [Google Scholar] [CrossRef]
- Shih, J.; Konno, Y.; Chang, Y.; Emura, T. Estimation of a common mean vector in bivariate meta-analysis under the FGM copula. Statistics 2019, 53, 673–695. [Google Scholar] [CrossRef]
- Shih, J.; Konno, Y.; Chang, Y.; Emura, T. Copula-Based Estimation Methods for a Common Mean Vector for Bivariate Meta-Analyses. Symmetry 2022, 14, 186. [Google Scholar] [CrossRef]
- Dobler, D.; Pauly, M. Factorial analyses of treatment effects under independent right-censoring. Stat. Methods Med. Res. 2020, 29, 325–343. [Google Scholar] [CrossRef] [PubMed]
- Emura, T.; Ditzhaus, M.; Dobler, D.; Murotani, K. Factorial survival analysis for treatment effects under dependent censoring. Stat. Methods Med. Res. 2024, 33, 61–79. [Google Scholar] [CrossRef]
- Moore, D.F. Applied Survival Analysis Using R; Springer: Berlin/Heidelberg, Germany, 2016; Volume 473. [Google Scholar]
- Greenland, S.; Fay, M.P.; Brittain, E.H.; Shih, J.H.; Follmann, D.A.; Gabriel, E.E.; Robins, J.M. On causal inferences for personalized medicine: How hidden causal assumptions led to erroneous causal claims about the D-value. Am. Statist. 2020, 74, 243–248. [Google Scholar] [CrossRef]
- Domma, F.; Giordano, S. A copula-based approach to account for dependence in stress-strength models. Statist. Pap. 2013, 54, 807–826. [Google Scholar] [CrossRef]
- Gao, J.; An, Z.; Liu, B. A dependent stress-strength interference model based on mixed copula function. J. Mech. Sci. Technol. 2016, 30, 4443–4446. [Google Scholar] [CrossRef]
- de Andrade, B.B.; do Nascimento, A.R.; Rathie, P.N. Parametric and nonparametric inference for the reliability of copula-based stress-strength models. Qual. Reliab. Eng. Int. 2020, 36, 2249–2267. [Google Scholar] [CrossRef]
- Rathie, P.N.; de Sena Monteiro Ozelim, L.C.; de Andrade, B.B. Portfolio Management of Copula-Dependent Assets Based on P(Y < X) Reliability Models: Revisiting Frank Copula and Dagum Distributions. Stats 2021, 4, 1027–1050. [Google Scholar] [CrossRef]
- James, A.; Chandra, N.; Sebastian, N. Stress-strength reliability estimation for bivariate copula function with rayleigh marginals. Int. J. Syst. Assur. Eng. Manag. 2023, 14, 196–215. [Google Scholar] [CrossRef]
- Shang, L.; Yan, Z. Reliability estimation stress-strength dependent model based on copula function using ranked set sampling. J. Radiat. Res. Appl. Sci. 2024, 17, 100811. [Google Scholar] [CrossRef]
- Lima, R.K.; Quintino, F.S.; da Fonseca, T.A.; de Sena Monteiro Ozelim, L.C.; Rathie, P.N.; Saulo, H. Assessing the Impact of Copula Selection on Reliability Measures of Type P(X < Y) with Generalized Extreme Value Marginals. Modelling 2024, 5, 180–200. [Google Scholar] [CrossRef]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Internat. Econom. Rev. 2006, 47, 527–556. [Google Scholar] [CrossRef]
- Almeida, C.; Czado, C. Efficient Bayesian inference for stochastic time-varying copula models. Comput. Statist. Data Anal. 2012, 56, 1511–1527. [Google Scholar] [CrossRef]
- Yin, Y.; Cai, Z.; Zhou, X. Using secondary outcome to sharpen bounds for treatment harm rate in characterizing heterogeneity. Biom. J. 2018, 60, 879–892. [Google Scholar] [CrossRef]
- Susam, S.O. A multi-parameter Generalized Farlie-Gumbel-Morgenstern bivariate copula family via Bernstein polynomial. Hacet. J. Math. Stat. 2022, 51, 618–631. [Google Scholar] [CrossRef]
- Deresa, N.W.; Van Keilegom, I. A multivariate normal regression model for survival data subject to different types of dependent censoring. Comput. Statist. Data Anal. 2020, 144, 106879. [Google Scholar] [CrossRef]
- Jo, J.H.; Gao, Z.; Jung, I.; Song, S.Y.; Ridder, G.; Moon, H.R. Copula graphic estimation of the survival function with dependent censoring and its application to analysis of pancreatic cancer clinical trial. Stat. Methods Med. Res. 2023, 32, 944–962. [Google Scholar] [CrossRef] [PubMed]
- Emura, T.; Chen, Y. Analysis of Survival Data with Dependent Censoring: Copula-Based Approaches; Springer: Berlin/Heidelberg, Germany, 2018; Volume 450. [Google Scholar]
- Brunner, E.; Puri, M.L. Nonparametric methods in factorial designs. Statist. Pap. 2001, 42, 1–52. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).