Dual-Graph-Regularization Constrained Nonnegative Matrix Factorization with Label Discrimination for Data Clustering
Abstract
:1. Introduction
2. Related Works
2.1. NMF
2.2. CNMF
2.3. GNMF
2.4. DNMF
2.5. DCNMF
2.6. GNMFLD
3. Proposed DCNMFLD
3.1. DCNMFLD
3.2. Optimization
| Algorithm 1 DCNMFLD. |
| Input: matrix . The regularization parameters , and . The number of neighbors . The clustering number . The maximum iteration number . |
Output: matrices and .
|
3.3. Convergence Analysis
3.4. Computation Complexity Analysis
4. Experiments
4.1. Experiments on the Yale Face Dataset
4.2. Experiments on the ORL Dataset
4.3. Experiments on the Jaffe Dataset
4.4. Experiments on the Isolet5 Dataset
4.5. Experiments on the YaleB Dataset
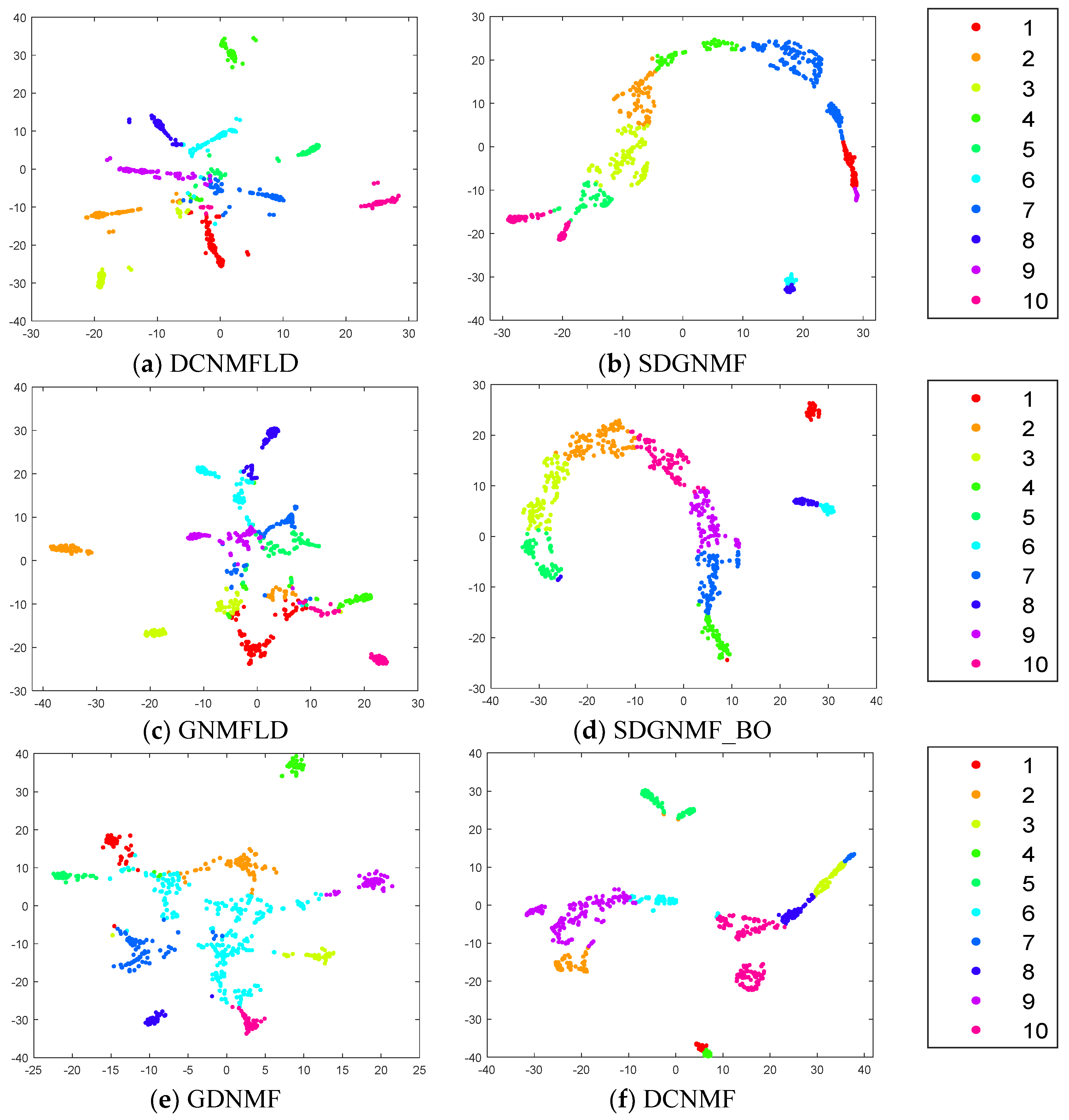
4.6. Visualization Comparison
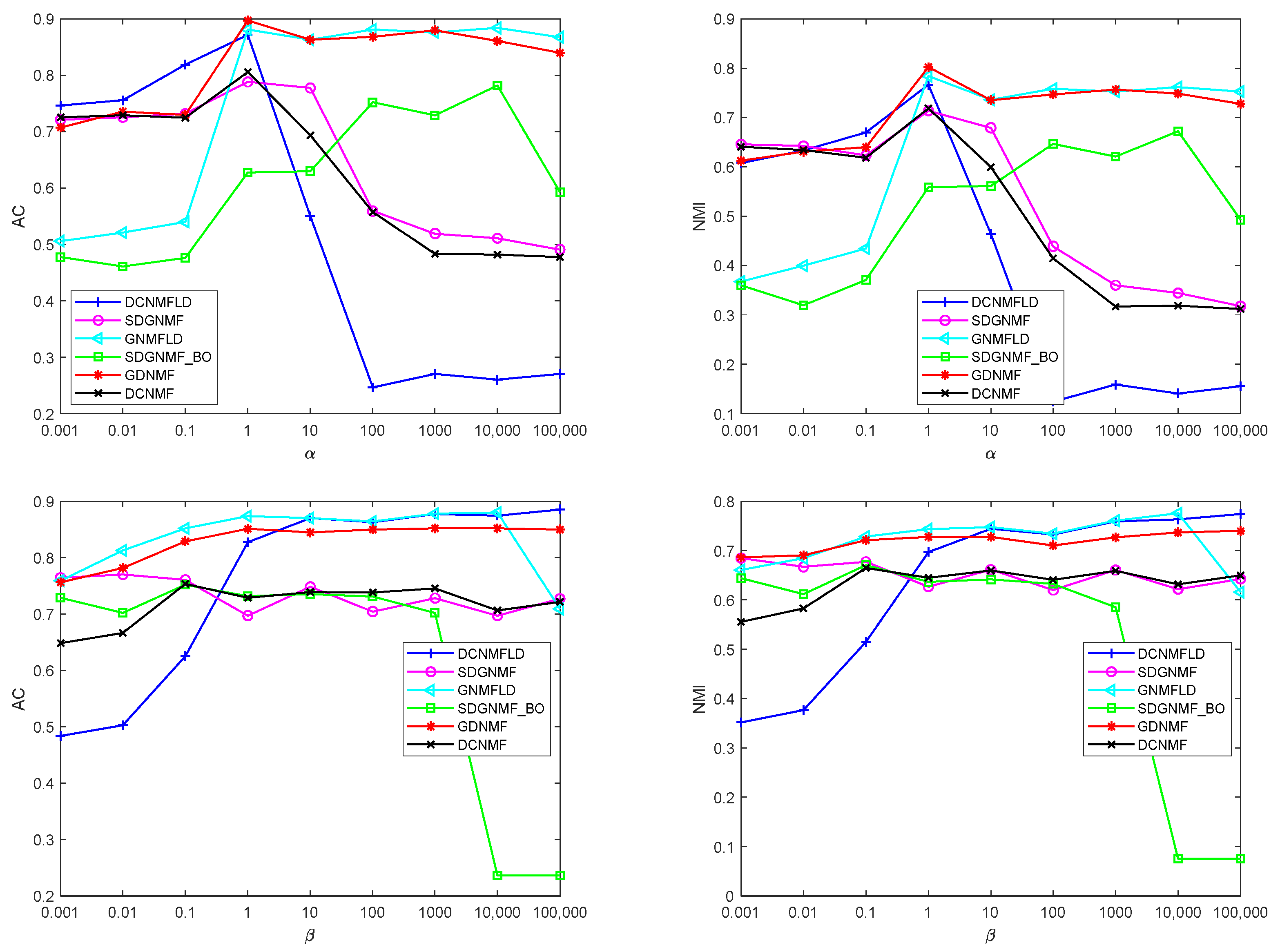
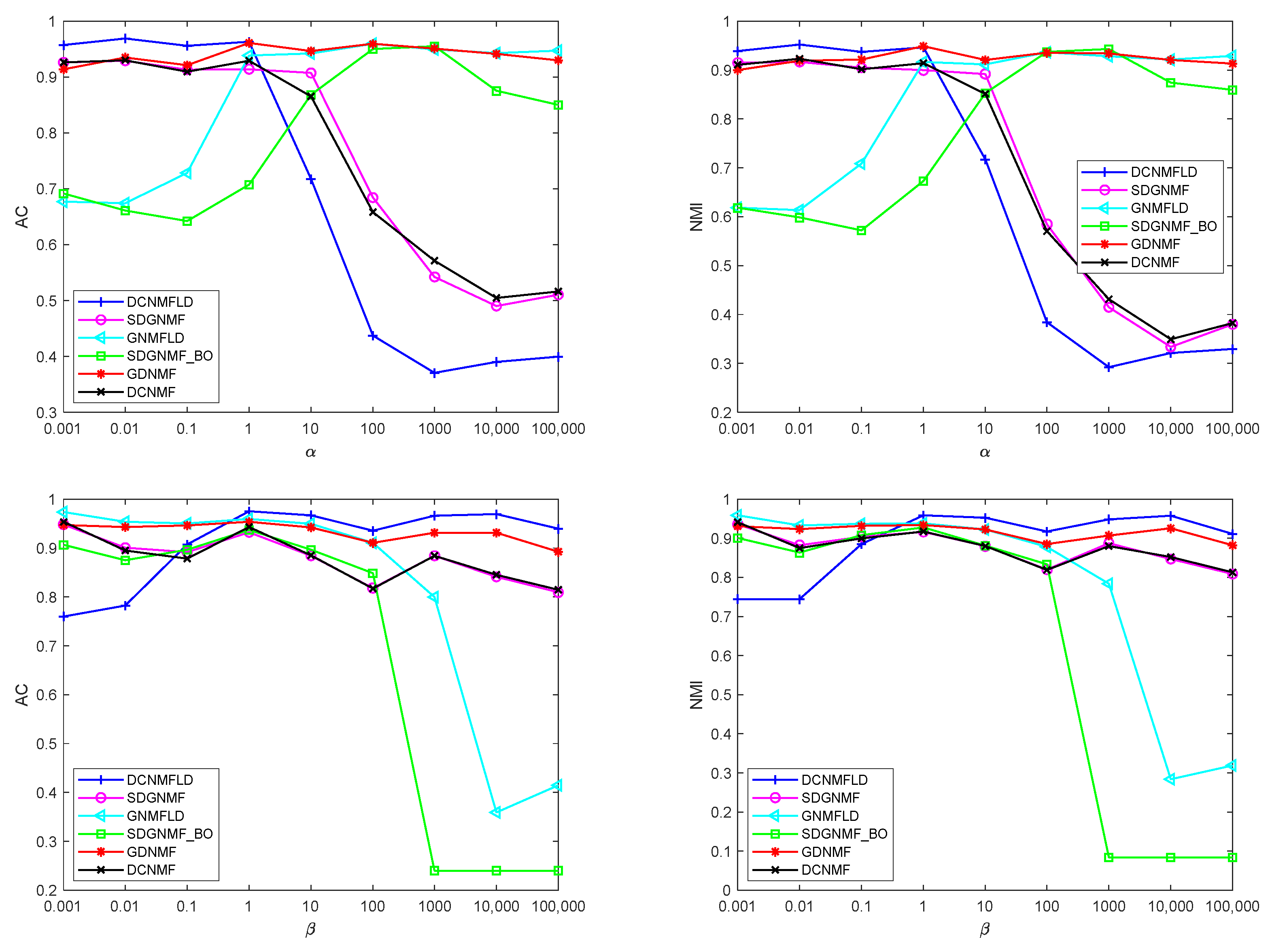
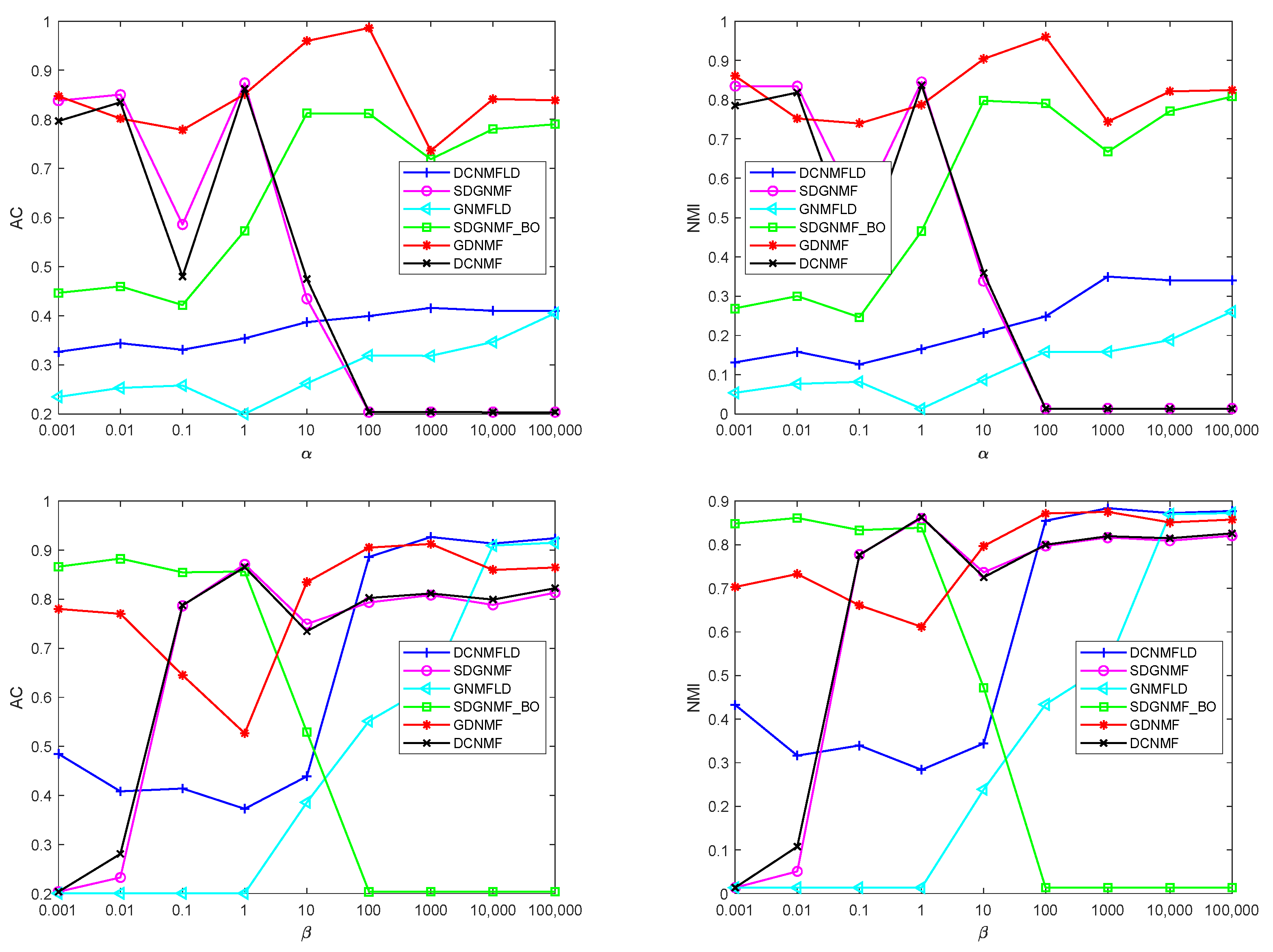
4.7. Parameter Selection
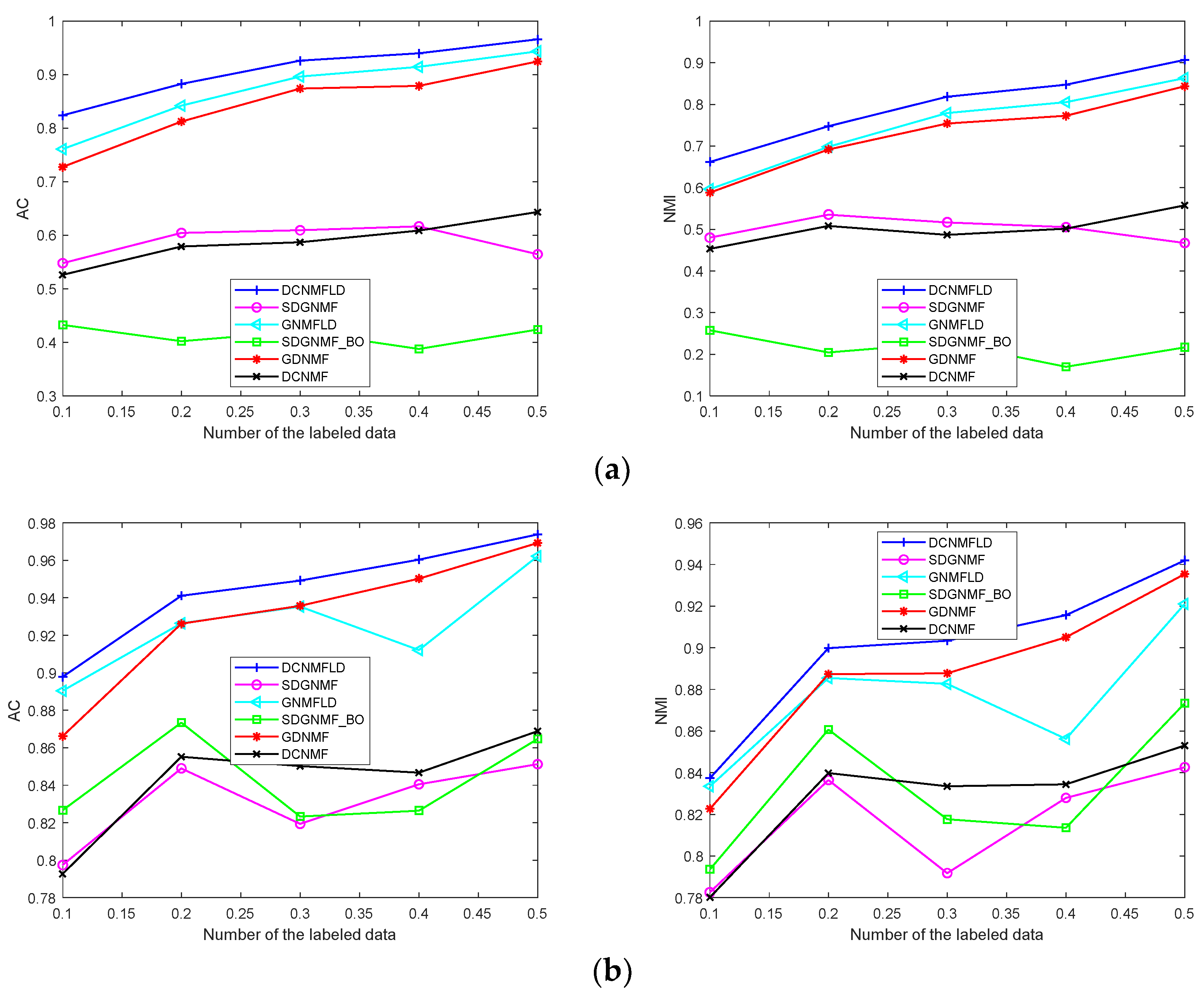
4.8. Relation with the Labeled Data Proportion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, D.; He, X.; Wu, X.; Han, J. Non-negative matrix factorization on manifold. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 63–72. [Google Scholar]
- Lai, Z.; Xu, Y.; Chen, Q.; Yang, J.; Zhang, D. Multilinear sparse principal component analysis. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1942–1950. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Lai, Z.; Xu, Y.; Li, X.; Yuan, C. Nonnegative discriminant matrix factorization. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 1392–1405. [Google Scholar] [CrossRef]
- Kirby, M.; Sirovich, L. Application of the karhunen loeve procedure for the characterization of human faces. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 103–108. [Google Scholar] [CrossRef]
- Dan, K. A singularly valuable decomposition: The svd of a matrix. Coll. Math. J. 1996, 27, 2–23. [Google Scholar]
- Belhumeur, P.N.; Hespanha, J.; Kriegman, D.J. Eigenfaces vs fisher faces: Recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- Xu, W.; Gong, Y. Document clustering by concept factorization. In Proceedings of the 27th Annual International ACM SIGIR Conference on Research and Development in INFORMATION Retrieval, SIGIR’04, Sheffield, UK, 25–29 July 2004; pp. 202–209. [Google Scholar]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2001, 13, 556–562. [Google Scholar]
- Li, S.Z.; Hou, X.W.; Zhang, H.J.; Cheng, Q.S. Learning spatially localized, parts-based representation, In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. CVPR 2001, Kauai, HI, USA, 8–14 December 2001; pp. 207–212. [Google Scholar]
- Xu, W.; Gong, Y. Document clustering based on non-negative matrix factorization. In Proceedings of the 26th Annual International ACM SIGIR Conference on Research and Development in Informaion Retrieval, SIGIR’03, Toronto, ON, Canada, 28 July–1 August 2003. [Google Scholar]
- Shahnaz, F.; Berry, M.W.; Pauca, V.P.; Plemmons, R.J. Document clustering using nonnegative matrix factorization. Inf. Process. Manag. 2006, 42, 373–386. [Google Scholar] [CrossRef]
- Kim, W.; Chen, B.; Kim, J.; Pan, Y.; Park, H. Sparse nonnegative matrix factorization for protein sequence motif discovery. Expert Syst. Appl. 2011, 38, 13198–13207. [Google Scholar] [CrossRef]
- Shashua, A.; Hazan, T. Non-negative tensor factorization with applications to statistics and computer vision. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 792–799. [Google Scholar]
- Lu, N.; Miao, H. Structure constrained nonnegative matrix factorization for pattern clustering and classification. Neurocomputing 2016, 171, 400–411. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J. Document clustering using locality preserving indexing. IEEE Trans. Knowl. Data Eng. 2005, 17, 1624–1637. [Google Scholar] [CrossRef]
- Kim, J.; Park, H. Sparse Nonnegative Matrix Factorization for Clustering. Available online: https://faculty.cc.gatech.edu/~hpark/papers/GT-CSE-08-01.pdf (accessed on 1 August 2023).
- He, C.; Fei, X.; Cheng, Q.; Li, H.; Hu, Z.; Tang, Y. A survey of community detection in complex networks using nonnegative matrix factorization. IEEE Trans. Comput. Soc. Syst. 2021, 9, 440–457. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, H.; Li, G.; Zhao, J.; Huo, J.; Yin, J. Multi-view clustering based on graph-regularized nonnegative matrix factorization for object recognition. Inf. Sci. 2018, 432, 463–478. [Google Scholar] [CrossRef]
- Wu, W.; Kwong, S.; Zhou, Y.; Jia, Y.; Gao, W. Nonnegative matrix factorization with mixed hypergraph regularization for community detection. Inf. Sci. 2018, 435, 263–281. [Google Scholar] [CrossRef]
- Wang, J.Y.; Bensmail, H.; Gao, X. Multiple graph regularized nonnegative matrix factorization. Pattern Recognit. 2013, 46, 2840–2847. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar]
- Shang, F.; Jiao, L.; Wang, F. Graph dual regularization non-negative matrix factorization for co-clustering. Pattern Recognit. 2012, 45, 2237–2250. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Lee, H.; Yoo, J.; Choi, S. Semi-supervised nonnegative matrix factorization. IEEE Signal Process. Lett. 2010, 17, 4–7. [Google Scholar]
- Liu, H.; Wu, Z.; Li, X.; Cai, D.; Huang, T.S. Constrained nonnegative matrix factorization for image representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1299–1311. [Google Scholar] [CrossRef]
- Babaee, M.; Tsoukalas, S.; Babaee, M.; Rigoll, G.; Datcu, M. Discriminative Nonnegative Matrix Factorization for dimensionality reduction. Neurocomputing 2015, 173, 212–223. [Google Scholar] [CrossRef]
- Chen, P.; He, Y.; Lu, H.; Wu, L. Constrained Non-negative Matrix Factorization with Graph Laplacian. In Proceedings of the International Conference on Neural Information Processing: 22nd International Conference, ICONIP 2015, Istanbul, Turkey, 9–12 November 2015. [Google Scholar]
- Li, H.; Zhang, J.; Shi, G.; Liu, J. Graph-based discriminative nonnegative matrix factorization with label information. Neurocomputing 2017, 266, 91–100. [Google Scholar] [CrossRef]
- Sun, J.; Cai, X.; Sun, F.; Hong, R. Dual graph-regularized constrained nonnegative matrix factorization for image clustering. KSII Trans. Internet Inf. Syst. 2017, 11, 2607–2627. [Google Scholar]
- Sun, J.; Wang, Z.; Sun, F.; Li, H. Sparse dual graph-regularized nmf for image co-clustering. Neurocomputing 2018, 316, 156–165. [Google Scholar] [CrossRef]
- Li, S.T.; Li, W.G.; Hu, J.W.; Li, Y. Semi-supervised bi-orthogonal constraints dual-graph regularized nmf for subspace clustering. Appl. Intell. 2021, 52, 3227–3248. [Google Scholar] [CrossRef]
- Xing, Z.; Ma, Y.; Yang, X.; Nie, F. Graph regularized nonnegative matrix factorization with label discrimination for data clustering. Neurocomputing 2021, 440, 297–309. [Google Scholar] [CrossRef]
- Xing, Z.; Wen, M.; Peng, J.; Feng, J. Discriminative semi-supervised non-negative matrix factorization for data clustering. Eng. Appl. Artif. Intell. 2021, 103, 104289. [Google Scholar] [CrossRef]
- Li, H.; Gao, Y.; Liu, J.; Zhang, J.; Li, C. Semi-supervised graph regularized nonnegative matrix factorization with local coordinate for image representation. Signal Process. Image Commun. 2022, 102, 116589. [Google Scholar] [CrossRef]
- Dong, Y.; Che, H.; Leung, M.F.; Liu, C.; Yan, Z. Centric graph regularized log-norm sparse non-negative matrix factorization for multi-view clustering. Signal Process. 2024, 217, 109341. [Google Scholar] [CrossRef]
- Liu, C.; Wu, S.; Li, R.; Jiang, D.; Wong, H.S. Self-Supervised Graph Completion for Incomplete Multi-View Clustering. IEEE Trans. Knowl. Data Eng. 2023, 35, 9394–9406. [Google Scholar] [CrossRef]



| Methods | Label Hard Constraint | One-Hot Scaling | Data Graph | Feature Graph |
|---|---|---|---|---|
| GNMFLD | × | √ | √ | × |
| DCNMF | √ | × | √ | √ |
| DCNMFLD | √ | √ | √ | √ |
| Algorithm | Overall Cost | Number of Regularization Graphs |
|---|---|---|
| DCNMFLD | 2 | |
| DCNMF [31] | 2 | |
| SDGNMF [32] | 2 | |
| SDGNMF_BO [33] | 2 | |
| GNMFLD [34] | 1 | |
| GDNMF [30] | 1 |
| Type | Name | Size | Dimension | Of Classes |
|---|---|---|---|---|
| Face | Yale 1 | 165 | 1024 | 15 |
| Face | ORL 2 | 400 | 1024 | 40 |
| Face | Jaffe 3 | 213 | 1024 | 10 |
| Face | YaleB 4 | 2414 | 1024 | 38 |
| Sound | Isolet5 5 | 1559 | 617 | 26 |
| c | Accuracy (%) | Normalized Mutual Information (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | |
| 2 | 98.41 | 96.14 | 97.96 | 93.18 | 97.27 | 75.91 | 92.65 | 93.39 | 91.24 | 80.73 | 88.16 | 50.06 |
| 3 | 93.33 | 85.76 | 93.94 | 79.24 | 91.67 | 63.49 | 81.35 | 69.94 | 82.96 | 59.75 | 77.29 | 41.92 |
| 4 | 91.36 | 85.46 | 89.77 | 82.61 | 88.18 | 79.77 | 79.80 | 74.32 | 78.42 | 69.22 | 75.93 | 67.16 |
| 5 | 87.18 | 74.91 | 85.64 | 71.27 | 83.73 | 73.82 | 75.01 | 65.75 | 73.82 | 62.36 | 71.37 | 64.33 |
| 6 | 85.08 | 71.29 | 83.71 | 70.61 | 80.83 | 70.15 | 75.09 | 67.37 | 74.59 | 64.76 | 72.68 | 66.68 |
| 7 | 84.61 | 68.83 | 81.95 | 69.16 | 75.91 | 67.34 | 74.53 | 66.37 | 73.14 | 64.60 | 69.29 | 65.09 |
| 8 | 81.82 | 68.24 | 78.98 | 69.03 | 72.10 | 68.30 | 73.46 | 67.19 | 71.42 | 65.31 | 67.88 | 66.00 |
| 9 | 81.47 | 67.02 | 78.79 | 65.96 | 73.08 | 69.14 | 73.74 | 67.79 | 72.35 | 65.13 | 68.08 | 68.12 |
| 10 | 80.82 | 66.14 | 78.82 | 65.00 | 72.91 | 66.68 | 74.52 | 67.91 | 73.21 | 65.50 | 69.35 | 67.51 |
| Avg. | 87.12 | 75.98 | 85.51 | 74.01 | 81.74 | 70.51 | 77.80 | 71.11 | 76.80 | 66.37 | 73.34 | 61.87 |
| c | Accuracy (%) | Normalized Mutual Information (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | |
| 2 | 98.50 | 98.75 | 99.00 | 95.25 | 99.50 | 97.50 | 94.56 | 95.05 | 96.26 | 86.58 | 97.58 | 91.61 |
| 3 | 97.33 | 95.83 | 97.67 | 93.67 | 96.83 | 94.83 | 95.25 | 92.31 | 95.33 | 89.73 | 94.81 | 90.47 |
| 4 | 98.00 | 96.38 | 96.25 | 91.63 | 96.25 | 95.00 | 96.84 | 94.58 | 94.09 | 88.09 | 93.75 | 92.42 |
| 5 | 96.60 | 96.40 | 96.40 | 88.80 | 96.30 | 96.20 | 95.05 | 94.94 | 95.21 | 89.96 | 94.72 | 94.61 |
| 6 | 95.58 | 92.83 | 95.33 | 88.67 | 94.08 | 93.58 | 94.40 | 92.11 | 93.81 | 89.17 | 92.76 | 93.07 |
| 7 | 94.21 | 91.57 | 94.86 | 89.71 | 90.43 | 91.07 | 93.27 | 91.46 | 93.38 | 91.01 | 91.32 | 91.29 |
| 8 | 96.06 | 91.19 | 94.63 | 84.50 | 89.75 | 90.06 | 95.28 | 92.12 | 93.56 | 89.56 | 91.14 | 91.16 |
| 9 | 93.83 | 87.00 | 93.39 | 84.78 | 87.67 | 86.22 | 94.18 | 90.47 | 93.01 | 89.49 | 89.87 | 90.14 |
| 10 | 94.05 | 87.05 | 91.75 | 86.00 | 89.05 | 85.10 | 93.69 | 90.47 | 91.40 | 89.58 | 90.69 | 89.53 |
| Avg. | 96.02 | 93.00 | 95.48 | 89.22 | 93.32 | 92.18 | 94.72 | 92.61 | 94.01 | 89.24 | 92.96 | 91.59 |
| c | Accuracy (%) | Normalized Mutual Information (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | |
| 2 | 99.76 | 95.98 | 99.88 | 99.88 | 99.88 | 75.72 | 98.62 | 86.16 | 99.29 | 99.29 | 99.29 | 34.48 |
| 3 | 97.68 | 97.44 | 97.68 | 94.90 | 97.14 | 89.22 | 92.39 | 92.37 | 92.56 | 89.09 | 91.16 | 79.68 |
| 4 | 98.83 | 96.60 | 98.78 | 98.25 | 98.72 | 96.77 | 96.89 | 94.52 | 96.87 | 96.48 | 96.62 | 93.73 |
| 5 | 97.95 | 96.41 | 98.00 | 94.59 | 97.63 | 97.67 | 95.61 | 94.16 | 95.70 | 91.97 | 94.88 | 95.05 |
| 6 | 96.21 | 96.13 | 96.41 | 93.21 | 96.02 | 95.24 | 92.81 | 92.95 | 93.17 | 89.99 | 92.54 | 91.79 |
| 7 | 96.95 | 95.69 | 96.44 | 94.44 | 96.55 | 96.28 | 94.47 | 93.35 | 93.82 | 92.35 | 93.86 | 93.46 |
| 8 | 96.66 | 92.89 | 96.51 | 92.14 | 93.57 | 94.58 | 94.25 | 92.02 | 93.95 | 91.94 | 92.30 | 92.78 |
| 9 | 96.38 | 86.30 | 96.14 | 92.60 | 91.44 | 91.17 | 94.09 | 88.28 | 93.74 | 91.58 | 91.74 | 91.58 |
| 10 | 96.83 | 89.44 | 96.62 | 90.42 | 92.98 | 89.65 | 94.95 | 90.78 | 94.66 | 91.51 | 92.79 | 91.58 |
| Avg. | 97.47 | 94.10 | 97.38 | 94.49 | 95.99 | 91.81 | 94.90 | 91.62 | 94.86 | 92.69 | 93.91 | 84.90 |
| c | Accuracy (%) | Normalized Mutual Information (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | |
| 2 | 99.96 | 88.00 | 99.83 | 89.46 | 99.79 | 90.04 | 99.69 | 74.52 | 98.97 | 68.30 | 98.55 | 79.33 |
| 3 | 97.53 | 89.00 | 97.25 | 94.33 | 96.39 | 96.22 | 94.43 | 83.40 | 93.92 | 91.69 | 93.77 | 94.24 |
| 4 | 92.71 | 86.66 | 91.71 | 83.79 | 89.75 | 85.87 | 87.09 | 83.37 | 85.60 | 80.02 | 85.20 | 83.14 |
| 5 | 93.15 | 82.62 | 92.48 | 85.78 | 92.26 | 83.02 | 89.21 | 83.77 | 88.95 | 84.91 | 88.98 | 83.52 |
| 6 | 91.84 | 83.08 | 91.44 | 86.43 | 90.99 | 78.91 | 88.36 | 83.13 | 88.04 | 85.48 | 88.64 | 78.91 |
| 7 | 88.68 | 77.73 | 87.79 | 80.34 | 86.09 | 79.71 | 85.60 | 81.50 | 84.84 | 82.76 | 85.21 | 82.02 |
| 8 | 92.46 | 79.76 | 91.92 | 84.52 | 88.73 | 80.41 | 89.58 | 83.86 | 89.08 | 86.19 | 88.81 | 84.85 |
| 9 | 85.85 | 74.52 | 85.03 | 75.05 | 82.95 | 72.98 | 84.36 | 79.99 | 83.86 | 80.46 | 84.05 | 79.25 |
| 10 | 83.58 | 71.91 | 82.19 | 72.45 | 77.73 | 72.60 | 82.30 | 77.73 | 82.02 | 77.13 | 81.48 | 78.09 |
| Avg. | 91.75 | 81.48 | 91.07 | 83.57 | 89.41 | 82.20 | 88.96 | 81.25 | 88.36 | 81.88 | 88.30 | 82.59 |
| c | Accuracy (%) | Normalized Mutual Information (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | |
| 2 | 98.41 | 96.14 | 97.96 | 93.18 | 97.27 | 75.91 | 92.65 | 93.39 | 91.24 | 80.73 | 88.16 | 50.06 |
| 3 | 93.33 | 85.76 | 93.94 | 79.24 | 91.67 | 63.49 | 81.35 | 69.94 | 82.96 | 59.75 | 77.29 | 41.92 |
| 4 | 91.36 | 85.46 | 89.77 | 82.61 | 88.18 | 79.77 | 79.80 | 74.32 | 78.42 | 69.22 | 75.93 | 67.16 |
| 5 | 87.18 | 74.91 | 85.64 | 71.27 | 83.73 | 73.82 | 75.01 | 65.75 | 73.82 | 62.36 | 71.37 | 64.33 |
| 6 | 85.08 | 71.29 | 83.71 | 70.61 | 80.83 | 70.15 | 75.09 | 67.37 | 74.59 | 64.76 | 72.68 | 66.68 |
| 7 | 84.61 | 68.83 | 81.95 | 69.16 | 75.91 | 67.34 | 74.53 | 66.37 | 73.14 | 64.60 | 69.29 | 65.09 |
| 8 | 81.82 | 68.24 | 78.98 | 69.03 | 72.10 | 68.30 | 73.46 | 67.19 | 71.42 | 65.31 | 67.88 | 66.00 |
| 9 | 81.47 | 67.02 | 78.79 | 65.96 | 73.08 | 69.14 | 73.74 | 67.79 | 72.35 | 65.13 | 68.08 | 68.12 |
| 10 | 80.82 | 66.14 | 78.82 | 65.00 | 72.91 | 66.68 | 74.52 | 67.91 | 73.21 | 65.50 | 69.35 | 67.51 |
| Avg. | 87.12 | 75.98 | 85.51 | 74.01 | 81.74 | 70.51 | 77.80 | 71.11 | 76.80 | 66.37 | 73.34 | 61.87 |
| DCNMFLD | SDGNMF | GNMFLD | SDGNMF_BO | GDNMF | DCNMF | |
|---|---|---|---|---|---|---|
| Yale | (1, 100,000) | (1, 0.01) | (10,000, 10,000) | (10,000, 0.1) | (1, 1000) | (1, 0.1) |
| ORL | (0.01, 1) | (0.01, 0.001) | (100, 0.001) | (1000, 1) | (1, 1) | (0.01, 0.001) |
| Jaffe | (0.1, 1000) | (10, 1) | (1000, 1000) | (1000, 0.1) | (1000, 1000) | (1, 0.01) |
| YaleB | (10, 100) | (1, 10,000) | (100, 100) | (100,000, 0.01) | (10,000, 100) | (1, 100) |
| Isolet5 | (1000, 1000) | (1, 1) | (100,000, 100,000) | (10, 0.01) | (100, 1000) | (1, 1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, Y.; Li, C. Dual-Graph-Regularization Constrained Nonnegative Matrix Factorization with Label Discrimination for Data Clustering. Mathematics 2024, 12, 96. https://doi.org/10.3390/math12010096
Li J, Li Y, Li C. Dual-Graph-Regularization Constrained Nonnegative Matrix Factorization with Label Discrimination for Data Clustering. Mathematics. 2024; 12(1):96. https://doi.org/10.3390/math12010096
Chicago/Turabian StyleLi, Jie, Yaotang Li, and Chaoqian Li. 2024. "Dual-Graph-Regularization Constrained Nonnegative Matrix Factorization with Label Discrimination for Data Clustering" Mathematics 12, no. 1: 96. https://doi.org/10.3390/math12010096
APA StyleLi, J., Li, Y., & Li, C. (2024). Dual-Graph-Regularization Constrained Nonnegative Matrix Factorization with Label Discrimination for Data Clustering. Mathematics, 12(1), 96. https://doi.org/10.3390/math12010096






