Solving the Matrix Exponential Function for Special Orthogonal Groups SO(n) up to n = 9 and the Exceptional Lie Group G₂

Abstract

In this work the matrix exponential function is solved analytically for the special orthogonal groups $SO\left(n\right)$ up to $n=9$. The number of occurring k-th matrix powers gets limited to $0\le k\le n-1$ by exploiting the Cayley–Hamilton relation. The corresponding expansion coefficients can be expressed as cosine and sine functions of a vector-norm V and the roots of a polynomial equation that depends on a few specific invariants. Besides the well-known case of $SO\left(3\right)$, a quadratic equation needs to be solved for $n=4,5$, a cubic equation for $n=6,7$, and a quartic equation for $n=8,9$. As an interesting subgroup of $SO\left(7\right)$, the exceptional Lie group $G_2$ of dimension 14 is constructed via the matrix exponential function through a remarkably simple constraint on an invariant, $\xi =1$. The traces of the $SO\left(n\right)$-matrices arising from the exponential function are sums of cosines of several angles. This feature confirms that the employed method is equivalent to exponentiation after diagonalization, but avoids complex eigenvalues and eigenvectors and operates only with real-valued quantities.

1. Introduction

The matrix exponential function is a basic and versatile tool in order to compute the entire manifold of elements from a (compact) matrix Lie group, as they enter, e.g., in lattice gauge theories and effective field theories. Besides the use of efficient algorithms for numerically computing the matrix exponential function, analytical formulas that provide an exact solution can also be helpful and advantageous. For special unitary $SU\left(2\right)$ matrices the result of evaluating the matrix exponential function, $U=exp(i\overrightarrow{\tau }·\overrightarrow{v})=\mathbf{1}cos|\overrightarrow{v}|+i\overrightarrow{\tau }·\widehat{v}sin\left|\overrightarrow{v}\right|$, with $\overrightarrow{\tau }=({\tau }_1,{\tau }_2,{\tau }_3)$ the Pauli matrices, is well known and frequently used in effective field theories [1] where U comprises three low-energy excitations (e.g., pions) and thus serves as the basic field variable. In a recent work [2] the solution of the matrix exponential function has been extended to the $SU\left(3\right)$ group with eight real parameters. By employing the Cayley–Hamilton relation the required matrix powers could be reduced to the zeroth, first and second. The resulting analytical formula involved the sum over three real roots of a cubic equation, corresponding thus to the so-called irreducible case, where one employs for its solution the trisection of an angle. This straightforward solution should be compared with the overly long expositions about an analytic $SU\left(3\right)$ matrix in ref. [3]. When going to the special unitary group $SU\left(4\right)$ with 15 real parameters, the analytical formula involved the sum over four real roots of a quartic equation. The associated cubic resolvent equation with three positive roots belonged again to the irreducible case. By imposing the pertinent condition on $SU\left(4\right)$ matrices one could also treat the symplectic group $Sp\left(2\right)$ with ten real parameters. Since the roots occurred as two pairs of opposite signs, this simplified the analytical formula for $Sp\left(2\right)$ matrices considerably. An outlook on the situation with semi-analytical formulas for $SU\left(5\right)$, $SU\left(6\right)$, and $Sp\left(3\right)$ has also been given in ref. [2].

The purpose of the present work is to continue the approach of ref. [2] by solving the matrix exponential function analytically for the special orthogonal groups $SO\left(n\right)$ up to $n=9$. Again, by exploiting the Cayley–Hamilton relation for the elements of the Lie algebra $so\left(n\right)$ (i.e., antisymmetric $n\times n$ matrices), the number of required matrix powers ranges from 0 up to $n-1$. The corresponding expansion coefficients will be expressed as cosine and sine functions of a vector-norm $V=|\overrightarrow{v}|$ and the roots $y_j$ of a polynomial equation that depends on some specific invariants (the determinant and the traces of even matrix powers). Putting aside the almost trivial cases of $SO\left(2\right)$ and $SO\left(3\right)$, a quadratic equation needs to be solved for $n=4,5$, a cubic equation for $n=6,7$, and a quartic equation for $n=8,9$ (where the latter leads to a cubic resolvent equation). The exceptional Lie group $G_2\subset SO\left(7\right)$ of dimension 14 (and rank 2), defined as the automorphism group of the octonions, is constructed via the matrix exponential function by first deriving seven homogeneous linear relations for the 21 parameters of a general $so\left(7\right)$ Lie algebra element. These restricting relations translate into a remarkably simple constraint on an invariant, $\xi =1$. The calculation of the trace of the $SO\left(n\right)$-matrices arising from the exponential function, gives as a result a simple sum of cosines of several angles, which specify the associated conjugation class as a point on a maximal torus $SO\left(2\right)\times \cdots \times SO\left(2\right)$.

In the following one uses the generators $J_a,a=1,\dots ,n(n-1)/2$ (i.e., basis elements of the Lie algebra $so\left(n\right)$), where the antisymmetric $n\times n$ matrix $J_a$ has exactly one entry 1 above the diagonal that is reflected to a $-1$ below the diagonal. These generators are normalized as tr$\left(J_a{J}_b\right)=-2{\delta }_{ab}$. Following a gradually extended strategy one works from the easy case $n=3$ up to $n=9$, with an insertion after $SO\left(7\right)$ that treats in detail the interesting subgroup $G_2\subset SO\left(7\right)$. In perspective, one remarks that for higher $n=10,11$ analogous semi-analytical formulas could be written down to solve the matrix exponential function, but these involve a sum over the five (positive) roots of quintic equation for which no algebraic solution formulas in terms of radicals of its coefficients exist.

2. SO(3)

Elements of the three-dimensional Lie algebra $so\left(3\right)$ are antisymmetric $3\times 3$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{ccc}0& v_1& v_2\\ -v_1& 0& v_3\\ -v_2& -v_3& 0\end{array}\right),$$

(1)

with the length $V=\sqrt{v_1^2+v_2^2+v_3^2}$ of the three-component real vector $\overrightarrow{v}$. The normalized matrix $\Sigma =\overrightarrow{J}·\widehat{v}=\overrightarrow{J}·\overrightarrow{v}/V$ satisfies the relation ${\Sigma }^3=-\Sigma$, and therefore, all powers of $\Sigma$ can be reduced to the first two. The matrix exponential function for the special orthogonal group $SO\left(3\right)$ takes the following simple form

$$R_3\left(\overrightarrow{v}\right)=exp(\overrightarrow{J}·\overrightarrow{v})=\mathbf{1}+sinV\overrightarrow{J}·\widehat{v}+(1-cosV){(\overrightarrow{J}·\widehat{v})}^2,$$

(2)

where $\mathbf{1}$ denotes the $3\times 3$ unit matrix. The formula in Equation (2) describes a right-handed rotation in three-dimensional space about the axis $\overrightarrow{n}=(-v_3,v_2,-v_1)/V$ with an angle $\phi =V$. Starting from the linear transformation $(\overrightarrow{J}·\widehat{v})\overrightarrow{x}=\overrightarrow{n}\times \overrightarrow{x}$, one reproduces the well-known formula [4] for the rotation of a three-component vector $\overrightarrow{x}$: $R_3\overrightarrow{x}=\overrightarrow{n}(\overrightarrow{n}·\overrightarrow{x})+cos\phi (\overrightarrow{x}-\overrightarrow{n}(\overrightarrow{n}·\overrightarrow{x}))+sin\phi \overrightarrow{n}\times \overrightarrow{x}$, sorted into pieces parallel and perpendicular to the axis $\overrightarrow{n}$. The involved rotation angle follows also directly from the trace, tr$R_3\left(\overrightarrow{v}\right)=1+2cosV$. Note that $\phi =V$ parametrizes at fixed $\widehat{v}$ a so-called maximal torus $SO\left(2\right)={\mathbf{S}}^1$ (circle line) in $SO\left(3\right)={\mathbf{RP}}^3$ (three-dimensional real projective space [5]). For comparison, the almost trivial result for $SO\left(2\right)$-rotations in a plane reads:

$$R_2\left(v\right)=exp\left(Iv\right)=\mathbf{1}cosv+Isinv,I=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),I^2=-\mathbf{1}$$

(3)

with the trace, tr$R_2\left(v\right)=2cosv$, of this $2\times 2$ rotation matrix.

3. SO(4)

Elements of the six-dimensional Lie algebra $so\left(4\right)$ are antisymmetric $4\times 4$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{cccc}0& v_1& v_2& v_3\\ -v_1& 0& v_4& v_5\\ -v_2& -v_4& 0& v_6\\ -v_3& -v_5& -v_6& 0\end{array}\right),$$

(4)

with the corresponding length $V=\sqrt{v_1^2+v_2^2+v_3^2+v_4^2+v_5^2+v_6^2}$ of the six-component real vector $\overrightarrow{v}$. For any antisymmetric matrix, the traces of its odd powers vanish altogether. Based on the relation tr$\left({\Sigma }^2\right)=-2$ the characteristic polynomial [6] of the normalized matrix $\Sigma =\overrightarrow{J}·\widehat{v}=\overrightarrow{J}·\overrightarrow{v}/V$ is given by

$$P_4\left(x\right)=x^4+x^2+\eta ,$$

(5)

with the invariant

$$\eta =\det (\overrightarrow{J}·\widehat{v})={\left(\frac{v_1{v}_6-v_2{v}_5+v_3{v}_4}{v_1^2+v_2^2+v_3^2+v_4^2+v_5^2+v_6^2}\right)}^2\ge 0.$$

(6)

The four roots of the equation $P_4\left(x\right)=0$ are the eigenvalues of $\Sigma$ and these must be purely imaginary since $\Sigma =-{\Sigma }^{†}$ is antihermitean (actually it is real antisymmetric). This fact about the roots implies for the solutions $-x_{\pm }^2$ of the intermediate quadratic equation (in $y=-x^2$) the inequality

$$-2x_{\pm }^2=1\pm \sqrt{1-4\eta }\ge 0,$$

(7)

from which one deduces the allowed range $0\le \eta \le 1/4$ for the determinant $\eta$. As a consequence of the Cayley–Hamilton relation ${\Sigma }^4=-{\Sigma }^2-\eta \mathbf{1}$ the number of independent matrix powers that get produced by the exponential series is limited to the first three (including the $4\times 4$ unit-matrix $\mathbf{1}$). Starting at order n with ${\Sigma }^n={\alpha }_n\mathbf{1}+{\beta }_n\Sigma +{\gamma }_n{\Sigma }^2+{\delta }_n{\Sigma }^3$ and multiplying with $\Sigma$, one obtains via the mentioned relation the expansion coefficients at order $n+1$. The resulting linear recursion reads in matrix-vector notation

$$\left(\begin{array}{c}{\alpha }_{n+1}\\ {\beta }_{n+1}\\ {\gamma }_{n+1}\\ {\delta }_{n+1}\end{array}\right)=M_4\left(\begin{array}{c}{\alpha }_n\\ {\beta }_n\\ {\gamma }_n\\ {\delta }_n\end{array}\right),M_4=\left(\begin{array}{cccc}0& 0& 0& -\eta \\ 1& 0& 0& 0\\ 0& 1& 0& -1\\ 0& 0& 1& 0\end{array}\right),$$

(8)

and the initial values are ${\alpha }_0=1,{\beta }_0=0,{\gamma }_0=0,{\delta }_0=0$. By diagonalization the exponential series $exp\left(V{M}_4\right)={\sum }_{k=0}^{\infty }{\left(V{M}_4\right)}^k/k!$ can be solved, but when using Mathematica, the routine MatrixExp[ , ] gives the result directly in terms of RootSum[ , ]. After multiplication with $(1,0,0,0)$ from the right, one obtains the four-component vector of expansion coefficient with respect to $(\mathbf{1},\Sigma ,{\Sigma }^2,{\Sigma }^3)$. Putting all the pieces together, one ends up with the following analytical formula for $SO\left(4\right)$ rotation matrices:

$$\begin{array}{ccc}\hfill R_4\left(\overrightarrow{v}\right)=exp(\overrightarrow{J}·\overrightarrow{v})& =& \frac{1}{1-2z}\{\left[(1-z)cos\left(V\sqrt{z}\right)-zcos\left(V\sqrt{1-z}\right)\right]\mathbf{1}\hfill \\ & & +\left[\frac{1-z}{\sqrt{z}}sin\left(V\sqrt{z}\right)-\frac{z}{\sqrt{1-z}}sin\left(V\sqrt{1-z}\right)\right]\overrightarrow{J}·\widehat{v}\hfill \\ & & +\left[cos\left(V\sqrt{z}\right)-cos\left(V\sqrt{1-z}\right)\right]{(\overrightarrow{J}·\widehat{v})}^2\hfill \\ & & +\left[\frac{1}{\sqrt{z}}sin\left(V\sqrt{z}\right)-\frac{1}{\sqrt{1-z}}sin\left(V\sqrt{1-z}\right)\right]{(\overrightarrow{J}·\widehat{v})}^3\}.\hfill \end{array}$$

(9)

The auxiliary parameter z is introduced via the relation $\eta =z(1-z)$ to the determinant $\eta$. Since Equation (9) is invariant under the substitution $z\to 1-z$, one can restrict the values of z to the interval $0\le z\le 1/2$, taking the solution $z=(1-\sqrt{1-4\eta })/2$. Note that the four expansion coefficients in Equation (9) depend only on V and z. Calculating the trace of the special orthogonal $4\times 4$ matrix, tr$R_4\left(\overrightarrow{v}\right)=2cos\left(V\sqrt{z}\right)+2cos\left(V\sqrt{1-z}\right)$, reveals that the two involved rotation angles are ${\phi }_1=V\sqrt{1-z}$ and ${\phi }_2=V\sqrt{z}$, which satisfy the conditions ${\phi }_1\ge {\phi }_2$, ${\phi }_1^2+{\phi }_2^2=V^2$ and ${\phi }_1{\phi }_2=\sqrt{\eta }{V}^2$. Both angles specify to which element on a maximal torus $SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1$ in $SO\left(4\right)={\mathbf{S}}^3\times {\mathbf{RP}}^3$ the given rotation matrix $R_4\left(\overrightarrow{v}\right)$ is related by conjugation [5]. Note that a conventional maximal torus in $SO\left(4\right)$ consists of independent rotations that take place in the $x_1{x}_2$-plane and the $x_3{x}_4$-plane of four-dimensional space.

4. SO(5)

Elements of the ten-dimensional Lie algebra $so\left(5\right)$ are antisymmetric $5\times 5$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{ccccc}0& v_1& v_2& v_3& v_4\\ -v_1& 0& v_5& v_6& v_7\\ -v_2& -v_5& 0& v_8& v_9\\ -v_3& -v_6& -v_8& 0& v_{10}\\ -v_4& -v_7& -v_9& -v_{10}& 0\end{array}\right),$$

(10)

with the corresponding norm $V=\sqrt{v_1^2+\cdots +v_{10}^2}$ of the ten-component real vector $\overrightarrow{v}$. Since the determinant of $\overrightarrow{J}·\overrightarrow{v}$ vanishes (in all odd dimensions), det$(\overrightarrow{J}·\overrightarrow{v})=0$, one has as a new invariant for $so\left(5\right)$-matrices the trace of the fourth power, $\xi =\mathrm{tr}\left({\Sigma }^4\right)$, where $\Sigma =\overrightarrow{J}·\widehat{v}=\overrightarrow{J}·\overrightarrow{v}/V$. The invariant $\xi$ enters the characteristic polynomial [6] of degree five

$$P_5\left(x\right)=x^5+x^3+x\left(\frac{1}{2}-\frac{\xi }{4}\right).$$

(11)

Again all its roots (including zero) must be purely imaginary. This fact implies for the solutions $-x_{\pm }^2$ of the intermediate quadratic equation (in $y=-x^2$) the inequality

$$-2x_{\pm }^2=1\pm \sqrt{\xi -1}\ge 0,$$

(12)

from which one deduces the allowed range of $\xi$ as the interval $1\le \xi \le 2$. Based on the Cayley–Hamilton relation ${\Sigma }^5=-{\Sigma }^3+\Sigma (\xi -2)/4$ one constructs the $5\times 5$ iteration matrix as

$$M_5=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 1& 0& 0& 0& \xi /4-1/2\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& -1\\ 0& 0& 0& 1& 0\end{array}\right),$$

(13)

with which one can solve $exp\left(V{M}_5\right)$ and multiply with $(1,0,0,0,0)$. It is furthermore advantageous to parametrize $\xi =1+{cos}^{2}2\theta$ in terms of an angle $\theta$, that is taken from the interval $0\le \theta \le \pi /4$, namely $\theta =\frac{1}{2}arccos\sqrt{\xi -1}$. Putting all the pieces together, the solution of the matrix exponential function for the $SO\left(5\right)$ rotation group reads

$$\begin{array}{ccc}\hfill R_5\left(\overrightarrow{v}\right)& =& exp(\overrightarrow{J}·\overrightarrow{v})=\mathbf{1}+\frac{1}{cos2\theta }\{\left[\frac{{cos}^2\theta }{sin\theta }sin(Vsin\theta )-\frac{{sin}^2\theta }{cos\theta }sin(Vcos\theta )\right]\overrightarrow{J}·\widehat{v}\hfill \\ & & +\left[\frac{1}{{sin}^2\theta }-\frac{1}{{cos}^2\theta }+{tan}^2\theta cos(Vcos\theta )-{cot}^2\theta cos(Vsin\theta )\right]{(\overrightarrow{J}·\widehat{v})}^2\hfill \\ & & +\left[\frac{sin(Vsin\theta )}{sin\theta }-\frac{sin(Vcos\theta )}{cos\theta }\right]{(\overrightarrow{J}·\widehat{v})}^3\hfill \\ & & +\left[\frac{1-cos(Vsin\theta )}{{sin}^2\theta }-\frac{1-cos(Vcos\theta )}{{cos}^2\theta }\right]{(\overrightarrow{J}·\widehat{v})}^4\},\hfill \end{array}$$

(14)

where $\mathbf{1}$ denotes the $5\times 5$ unit matrix. Note, again that the four expansion coefficients depend only on V and $\theta$. The occurring trigonometric functions of $\theta$ are related to the invariant $\xi \in [1,2]$ by the relations

$$\begin{array}{c}cos2\theta =\sqrt{\xi -1},sin\theta =\frac{\sqrt{1-\sqrt{\xi -1}}}{\sqrt{2}},cos\theta =\frac{\sqrt{1+\sqrt{\xi -1}}}{\sqrt{2}},\hfill \\ tan\theta =\frac{1-\sqrt{\xi -1}}{\sqrt{2-\xi }},cot\theta =\frac{1+\sqrt{\xi -1}}{\sqrt{2-\xi }}.\hfill \end{array}$$

(15)

By calculating the trace of the special orthogonal matrix, tr$R_5\left(\overrightarrow{v}\right)=1+2cos(Vcos\theta )+2cos(Vsin\theta )$, one recognizes that the two involved rotation angles are ${\phi }_1=Vcos\theta$ and ${\phi }_2=Vsin\theta$, subject to the conditions ${\phi }_1\ge {\phi }_2$, ${\phi }_1^2+{\phi }_2^2=V^2$ and ${\phi }_1{\phi }_2=\sqrt{2-\xi }{V}^2/2$. Again, these two angles specify the conjugation class [5] of $R_5\left(\overrightarrow{v}\right)$ as a point on the maximal torus $SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1$ in $SO\left(5\right)$. By convention, such a maximal torus consists of independent rotations in the $x_1{x}_2$-plane and the $x_3{x}_4$-plane of five-dimensional space.

5. SO(6)

Elements of the 15-dimensional Lie algebra $so\left(6\right)$ are antisymmetric $6\times 6$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{cccccc}0& v_1& v_2& v_3& v_4& v_5\\ -v_1& 0& v_6& v_7& v_8& v_9\\ -v_2& -v_6& 0& v_{10}& v_{11}& v_{12}\\ -v_3& -v_7& -v_{10}& 0& v_{13}& v_{14}\\ -v_4& -v_8& -v_{11}& -v_{13}& 0& v_{15}\\ -v_5& -v_9& -v_{12}& -v_{14}& -v_{15}& 0\end{array}\right),$$

(16)

with the corresponding norm $V=\sqrt{v_1^2+\cdots +v_{15}^2}$ of the 15-component real vector $\overrightarrow{v}$. The characteristic polynomial [6] of $\Sigma =\overrightarrow{J}·\widehat{v}$ is of degree six and it reads

$$P_6\left(x\right)=x^6+x^4+x^2\left(\frac{1}{2}-\frac{\xi }{4}\right)+\eta ,$$

(17)

with coefficients $\xi =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^4$ and $\eta =\det (\overrightarrow{J}·\widehat{v})$. The substitution $y=-x^2$ leads to a cubic polynomial (of a half degree)

$${\tilde{P}}_3\left(y\right)=y^3-y^2+y\left(\frac{1}{2}-\frac{\xi }{4}\right)-\eta ,$$

(18)

whose three roots $y_1,y_2,y_3\ge 0$ all have to be positive, since those of $P_6\left(x\right)=0$ are the purely imaginary eigenvalues of the antihermitean $6\times 6$ matrix $\Sigma$. Figure 1 shows the generic behavior of such a cubic polynomial. From ${\tilde{P}}_3\left(0\right)=-\eta \le 0$ one learns first $\eta \ge 0$, and the fact that the positions of the local minimum and maximum at $y_{\pm }$ lie on the positive y-axis, leads to the inequality

$$6y_{\pm }=2\pm \sqrt{3\xi -2}\ge 0,$$

(19)

from which one deduces the allowed range $2/3\le \xi \le 2$ for the invariant $\xi$. Moreover, the product $\tilde{P}\left(y_{+}\right)\tilde{P}\left(y_{-}\right)\le 0$ is negative, and this condition gives rise to a further inequality:

$${(3\xi -2)}^3\ge {(9\xi +108\eta -10)}^2.$$

(20)

The resulting allowed range for the invariants $\xi$ and $\eta$ is the bounded region shown in Figure 2, from which one deduces also the maximal value ${\eta }_{\max }=1/27$. With three positive real roots, the cubic polynomial equation ${\tilde{P}}_3\left(y\right)=0$ corresponds to the so-called irreducible case, where the problem is effectively solved by the trisection of an angle. The ansatz $y_1=(1+\sqrt{3\xi -2}cos\psi )/3$ leads to a determining equation for $cos3\psi$, that is immediately solved by

$$\psi =\frac{1}{3}arccos\frac{9\xi +108\eta -10}{{(3\xi -2)}^{3/2}},$$

(21)

with $\psi \in [0,\pi /3]$. Note, that the inequality derived in Equation (20) guarantees that the argument of the arc-cosine function lies between $-1$ and 1. The other two roots are given by

$$y_{2,3}=\frac{1}{6}\left[2+\sqrt{3\xi -2}\left(\pm \sqrt{3}sin\psi -cos\psi \right)\right],$$

(22)

and with this assignment, the three roots are ordered as $y_1\ge y_2\ge y_3\ge 0$.

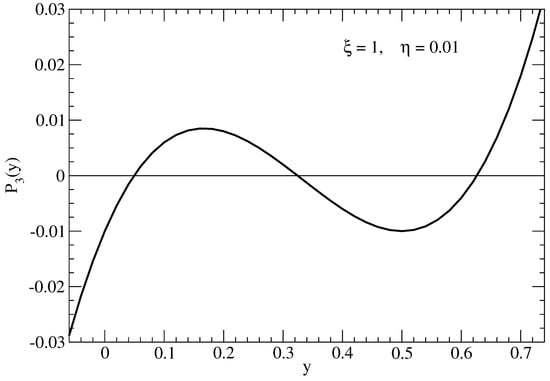
Figure 1. Generic behavior of the cubic polynomial ${\tilde{P}}_3\left(y\right)=y^3-y^2+y(1/2-\xi /4)-\eta$.

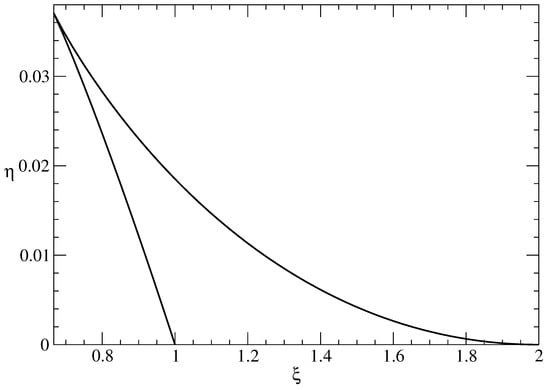
Figure 2. The allowed values of the invariants $\xi$ and $\eta$ for $so\left(6\right)$ lie inside the bounded region. The enclosed area in the $\xi \eta$-plane amounts to $1/120$, and the circumference of the tricorn measures $2.6695$.

Based on the Cayley–Hamilton relation ${\Sigma }^6=-{\Sigma }^4+{\Sigma }^2(\xi -2)/4-\eta \mathbf{1}$ one constructs the $6\times 6$ iteration matrix as

$$M_6=\left(\begin{array}{cccccc}0& 0& 0& 0& 0& -\eta \\ 1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& \xi /4-1/2\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0& -1\\ 0& 0& 0& 0& 1& 0\end{array}\right),$$

(23)

with which one can solve $exp\left(V{M}_6\right)$ and multiply with $(1,0,0,0,0,0)$. One ends up with the following analytical formula for the matrix exponential function $so\left(6\right)\to SO\left(6\right)$:

$$\begin{array}{ccc}\hfill R_6\left(\overrightarrow{v}\right)=exp(\overrightarrow{J}·\overrightarrow{v})& =& \sum _{j=1}^3\frac{1}{3y_j^2-2y_j+1/2-\xi /4}\left\{\frac{\eta }{y_j}\mathbf{1}+(1-y_j){(\overrightarrow{J}·\widehat{v})}^2+{(\overrightarrow{J}·\widehat{v})}^4\right\}\hfill \\ & & \times \left\{cos\left(V\sqrt{y_j}\right)\mathbf{1}+\frac{1}{\sqrt{y_j}}sin\left(V\sqrt{y_j}\right)\overrightarrow{J}·\widehat{v}\right\},\hfill \end{array}$$

(24)

where the sum goes over the three positive roots of the cubic equation ${\tilde{P}}_3\left(y\right)=0$. Note, that the denominator of the prefactor is the derivative ${\tilde{P}}_3^{\prime }\left(y_j\right)$, and one finds a remarkable factorization for the terms with (up to fifth) powers of $\overrightarrow{J}·\widehat{v}$. When taking the trace of the special orthogonal matrix $R_6\left(\overrightarrow{v}\right)$ one obtains

$$\mathrm{tr}{R}_6\left(\overrightarrow{v}\right)=\sum _{j=1}^3\frac{cos\left(V\sqrt{y_j}\right)}{3y_j^2-2y_j+1/2-\xi /4}\left\{\frac{6\eta }{y_j}+2(y_j-1)+\xi \right\}=2\sum _{j=1}^{3}cos\left(V\sqrt{y_j}\right),$$

(25)

where the final expression is obtained by eliminating $\eta$ in favor of the root $y_j$, using its determining equation ${\tilde{P}}_3\left(y_j\right)=0$. The three angles ${\phi }_j=V\sqrt{y_j}$ satisfy the conditions ${\phi }_1\ge {\phi }_2\ge {\phi }_3$, ${\phi }_1^2+{\phi }_2^2+{\phi }_3^2=V^2$ (due to the root-sum $y_1+y_2+y_3=1$), ${\phi }_1{\phi }_2{\phi }_3=\sqrt{\eta }{V}^3$. In $SO\left(6\right)$ the maximal torus $SO\left(2\right)\times SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1\times {\mathbf{S}}^1$ is three-dimensional and by convention, the three independent rotations occur in the $x_1{x}_2$-plane, $x_3{x}_4$-plane, and $x_5{x}_6$-plane of six-dimensional space.

6. SO(7)

Elements of the 21-dimensional Lie algebra $so\left(7\right)$ are antisymmetric $7\times 7$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{ccccccc}0& v_1& v_2& v_3& v_4& v_5& v_6\\ -v_1& 0& v_7& v_8& v_9& v_{10}& v_{11}\\ -v_2& -v_7& 0& v_{12}& v_{13}& v_{14}& v_{15}\\ -v_3& -v_8& -v_{12}& 0& v_{16}& v_{17}& v_{18}\\ -v_4& -v_9& -v_{13}& -v_{16}& 0& v_{19}& v_{20}\\ -v_5& -v_{10}& -v_{14}& -v_{17}& -v_{19}& 0& v_{21}\\ -v_6& -v_{11}& -v_{15}& -v_{18}& -v_{20}& -v_{21}& 0\end{array}\right),$$

(26)

with the corresponding norm $V=\sqrt{v_1^2+\cdots +v_{21}^2}$ of the 21-component real vector $\overrightarrow{v}$. The characteristic polynomial [6] of $\Sigma =\overrightarrow{J}·\widehat{v}$ is of degree seven and it reads

$$P_7\left(x\right)=x^7+x^5+x^3\left(\frac{1}{2}-\frac{\xi }{4}\right)+x\left(\frac{1-\zeta }{6}-\frac{\xi }{4}\right),$$

(27)

with in addition to $\xi =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^4$ a new invariant $\zeta =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^6$. Besides the trivial root $x=0$ of $P_7\left(x\right)$ the other purely imaginary ones are found via the substitution $y=-x^2$ from the cubic polynomial

$${\tilde{P}}_3\left(y\right)=y^3-y^2+y\left(\frac{1}{2}-\frac{\xi }{4}\right)+\frac{\zeta -1}{6}+\frac{\xi }{4}.$$

(28)

It has the same form as the cubic polynomial in Equation (18) relevant for $so\left(6\right)$ after identifying the constant term with $-\eta$. Although det$(\overrightarrow{J}·\widehat{v})=0$ in $so\left(7\right)$, this connection motivates to introduce the auxiliary parameter

$${\eta }_7=\frac{1-\zeta }{6}-\frac{\xi }{4}\ge 0.$$

(29)

The steps to construct the three positive roots $y_1,y_2,y_3$ of ${\tilde{P}}_3\left(y\right)=0$ are the same as in the previous section about $so\left(6\right)$. One just replaces $\eta$ by ${\eta }_7$ and gets for the trisected angle $\psi$ the modified expression

$$\psi =\frac{1}{3}arccos\frac{8-18(\xi +\zeta )}{{(3\xi -2)}^{3/2}},$$

(30)

and the inequality in Equation (20) turns into ${(3\xi -2)}^3\ge 4{[4-9(\xi +\zeta )]}^2$. The resulting allowed range for the invariants $\xi$ and $\zeta$ is the thin bounded region shown in Figure 3, from which one deduces also the extremal values ${\zeta }_{\max }=-2/9$ and ${\zeta }_{\min }=-2$. Note, that this bounded region is obtained from the one shown in Figure 2 by the shear-transformation $\zeta =1-6\eta -3\xi /2$ from the $\xi \eta$-plane to the $\xi \zeta$-plane.

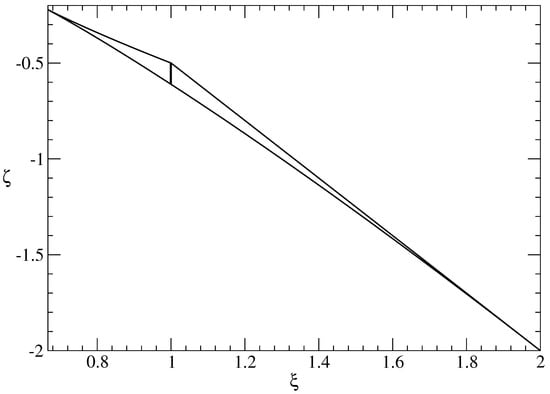
Figure 3. The allowed values of the invariants $\xi$ and $\zeta$ for $so\left(7\right)$ lie inside the thin bounded region. The enclosed area in the $\xi \zeta$-plane amounts to $1/20$, and the circumference of the tricorn measures $4.4612$. The short vertical line at $\xi =1$ of length $1/9$ corresponds to the subgroup $G_2\subset SO\left(7\right)$.

Based on the Cayley–Hamilton relation ${\Sigma }^7=-{\Sigma }^5+{\Sigma }^3(\xi -2)/4-{\eta }_7\Sigma$ one constructs the $7\times 7$ iteration matrix as

$$M_7=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& -{\eta }_7\\ 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& \xi /4-1/2\\ 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& -1\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right),$$

(31)

with which one can solve $exp\left(V{M}_7\right)$ and multiply with $(1,0,0,0,0,0,0)$. One ends up with the following analytical formula for the matrix exponential function $so\left(7\right)\to SO\left(7\right)$:

$$\begin{array}{ccc}\hfill R_7\left(\overrightarrow{v}\right)& =& exp(\overrightarrow{J}·\overrightarrow{v})=\mathbf{1}+\frac{1}{{\eta }_7}\left\{\left(\frac{1}{2}-\frac{\xi }{4}\right){(\overrightarrow{J}·\widehat{v})}^2+{(\overrightarrow{J}·\widehat{v})}^4+{(\overrightarrow{J}·\widehat{v})}^6\right\}\hfill \\ & & +2\sum _{j=1}^3{\left[7y_j^3-5y_j^2+\frac{3}{4}(2-\xi )y_j-{\eta }_7\right]}^{-1}\left\{\frac{{\eta }_7}{y_j}\mathbf{1}+(1-y_j){(\overrightarrow{J}·\widehat{v})}^2+{(\overrightarrow{J}·\widehat{v})}^4\right\}\hfill \\ & & \times \left\{\sqrt{y_j}sin\left(V\sqrt{y_j}\right)\overrightarrow{J}·\widehat{v}-cos\left(V\sqrt{y_j}\right){(\overrightarrow{J}·\widehat{v})}^2\right\},\hfill \end{array}$$

(32)

where the sum goes over the three positive roots of the cubic equation ${\tilde{P}}_3\left(y\right)=0$ in Equation (28) and ${\eta }_7=(1-\zeta )/6-\xi /4$ is an auxiliary parameter. Again one finds a remarkable factorization for the terms with (up to sixth) powers of $\overrightarrow{J}·\widehat{v}$. Note, also the extra terms outside the sum in addition to the $7\times 7$ unit-matrix $\mathbf{1}$. Taking the trace of the special orthogonal matrix $\mathrm{tr}{R}_7\left(\overrightarrow{v}\right)$ one finds the result

$$\mathrm{tr}{R}_7\left(\overrightarrow{v}\right)=1+2\sum _{j=1}^{3}cos\left(V\sqrt{y_j}\right),$$

(33)

where this short expression is obtained by first using $\zeta =1-3\xi /2-6{\eta }_7$, and then eliminating ${\eta }_7$ in favor of the root $y_j$ through the equation ${\tilde{P}}_3\left(y_j\right)=0$. The three angles ${\phi }_j=V\sqrt{y_j}$ appearing in Equation (33) satisfy the conditions ${\phi }_1\ge {\phi }_2\ge {\phi }_3$, ${\phi }_1^2+{\phi }_2^2+{\phi }_3^2=V^2$, ${\phi }_1{\phi }_2{\phi }_3=\sqrt{{\eta }_7}{V}^3$ and they parametrize a three-dimensional maximal torus $SO\left(2\right)\times SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1\times {\mathbf{S}}^1$ in $SO\left(7\right)$. By convention, the three independent rotations take place in the $x_1{x}_2$-plane, $x_3{x}_4$-plane, and $x_5{x}_6$-plane of seven-dimensional space.

7. Exceptional Lie Group ${\mathit{G}}_{\mathbf{2}}$

The special orthogonal group $SO\left(7\right)$ of dimension 21 (and rank 3) has an interesting subgroup, namely the exceptional Lie group $G_2$ of dimension 14 (and rank 2). From the point of view of geometrical symmetries, $G_2$ is interpreted as the automorphism group of the octonions $\mathbf{O}$, which form an eight-dimensional real division algebra spanned by 1 and seven imaginary units ${\mathbf{i}}_j,j=1,\dots ,7$. The multiplication ∗ of two imaginary units is anticommutative

$${\mathbf{i}}_j\ast {\mathbf{i}}_k+{\mathbf{i}}_k\ast {\mathbf{i}}_j=-2{\delta }_{jk}1,$$

(34)

and non-associative for higher products. The multiplication rule for two different imaginary units reads

$${\mathbf{i}}_j\ast {\mathbf{i}}_k=\sum _{l=1}^7{f}_{jkl}{\mathbf{i}}_l,j\ne k\ne l,$$

(35)

with totally antisymmetric structure constants $f_{jkl}$. Among 480 equivalent realizations a possible choice is to set $f_{jkl}=1$ for the cyclic index-combinations $ijk$ = 123, 145, 176, 246, 257, 347, 365.

An automorphism of $\mathbf{O}$ is defined as a linear transformation to seven new imaginary units:

$${\mathbf{i}}_j^{\prime }=\sum _{m=1}^7{S}_{jm}{\mathbf{i}}_m,$$

(36)

which leaves the entire multiplication table invariant. From anticommutativity ${\mathbf{i}}_j^{\prime }\ast {\mathbf{i}}_k^{\prime }+{\mathbf{i}}_k^{\prime }\ast {\mathbf{i}}_j^{\prime }=-2{\delta }_{jk}1$ one deduces ${\sum }_{m=1}^7{S}_{jm}{S}_{km}={\delta }_{jk}$, thus S is a $7\times 7$ orthogonal matrix. Since $S=-\mathbf{1}$ changes the sign in Equation (35) and $O\left(7\right)=SO\left(7\right)\times \{-\mathbf{1},\mathbf{1}\}$ as a group, one arrives at the necessary condition $S\in SO\left(7\right)$. From the multiplication rule involving the structure constant $f_{jkl}$ one derives the set of coupled cubic equations

$$\sum _{m,n,o=1}^7{S}_{jm}{S}_{kn}{S}_{lo}{f}_{mno}=f_{jkl},$$

(37)

which states that $G_2$ is the invariance group of an alternating trilinear form in seven variables. Note, that orthogonality has been used to bring all three S-matrices onto the left-hand side of Equation (37). In order to deduce the implication of Equation (37) on the Lie algebra elements one considers infinitesimal transformations $S_{jm}={\delta }_{jm}+ϵT_{jm}+\dots$ with $T=\overrightarrow{J}·\overrightarrow{v}\in so\left(7\right)$. The resulting linear equations read

$$\sum _{m=1}^7\left(T_{jm}{f}_{mkl}+T_{km}{f}_{mlj}+T_{lm}{f}_{mjk}\right)=0.$$

(38)

By analyzing these 343 equations in packages of 49, one obtains from $l=1$ six linear relations for the components of $\overrightarrow{v}$, from $l=2$ one further linear relation, but no further constraints from $l=3,4,5,6,7$. The resulting seven homogeneous linear relations for the 21 components of $\overrightarrow{v}$ read

$$\begin{array}{c}{v}_{12}=v_5-v_9,v_{13}=v_6+v_8,v_{14}=v_{11}-v_3,v_{15}=-v_4-v_{10},\hfill \\ v_{19}=v_1+v_{18},v_{20}=v_2-v_{17},v_{21}=v_7+v_{16},\hfill \end{array}$$

(39)

and these specify how the 14-dimensional exceptional Lie algebra ${\mathbf{g}}_2$ can be projected out of the 21-dimensional Lie algebra $so\left(7\right)$. After introducing 14 new parameters $w_1,\dots ,w_{14}$ via

$$\begin{array}{ccc}& & w_{1,8}=v_1\pm v_{18},w_{2,9}=v_2\mp v_{17},w_{3,10}=v_3\mp v_{11},w_{4,11}=v_4\pm v_{10},\hfill \\ & & w_{5,12}=v_5\mp v_9,w_{6,13}=v_6\pm v_8,w_{7,14}=v_7\pm v_{16},\hfill \end{array}$$

(40)

the length square of the yet 21-component vector $\overrightarrow{v}$ becomes a sum of 14 squares:

$$\begin{array}{ccc}\hfill V^2& =& \frac{3}{2}(w_1^2+w_2^2+w_3^2+w_4^2+w_5^2+w_6^2+w_7^2)\hfill \\ & & +\frac{1}{2}(w_8^2+w_9^2+w_{10}^2+w_{11}^2+w_{12}^2+w_{13}^2+w_{14}^2).\hfill \end{array}$$

(41)

More interesting is the effect of the seven linear relations in Equation (39) on the invariants $\xi$ and $\zeta$. The explicit calculation gives tr${(\overrightarrow{J}·\overrightarrow{v})}^4={(\overrightarrow{v}·\overrightarrow{v})}^2$, which translates into the remarkable constraint

$$\xi =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^4=1,\mathrm{for}{\mathbf{g}}_2\subset so\left(7\right),$$

(42)

whereas the other invariant $\zeta =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^6$ is confined to the small interval $-11/18\le \zeta \le -1/2$ (see Figure 3). The expressions for the three positive roots $y_j$ and the angle $\psi$ simplify accordingly to

$$y_1=\frac{1}{3}(1+cos\psi ),y_{2,3}=\frac{1}{6}\left(2\pm \sqrt{3}sin\psi -cos\psi \right),\psi =\frac{1}{3}arccos(-10-18\zeta ).$$

(43)

As a result, the matrix exponential function for the exceptional (real) Lie algebra ${\mathbf{g}}_2$ and corresponding compact Lie group $G_2$ is solved analytically by the formula in Equation (32), setting $\xi =1$ and ${\eta }_7=-(1+2\zeta )/12$ (ranging over the interval $0\le {\eta }_7\le 1/54$) and implementing the linear relations written in Equation (39) into V and $\widehat{v}$.

The ${\mathbf{g}}_2$-constraint $\xi =1$ implies for the three roots the additional relation $y_1^2+y_2^2+y_3^2=1/2$. This translates into a constraint on the angles ${\phi }_j=V\sqrt{y_j}$:

$$\begin{array}{ccc}& & 2({\phi }_1^4+{\phi }_2^4+{\phi }_3^4)-{({\phi }_1^2+{\phi }_2^2+{\phi }_3^2)}^2\hfill \\ & & =({\phi }_1+{\phi }_2+{\phi }_3)({\phi }_1+{\phi }_2-{\phi }_3)({\phi }_1-{\phi }_2+{\phi }_3)({\phi }_1-{\phi }_2-{\phi }_3)=0,\hfill \end{array}$$

(44)

which in view of the chosen ordering is solved by ${\phi }_1={\phi }_2+{\phi }_3$. Consequently, the trace of $G_2$-matrices in $SO\left(7\right)$ is given by

$$\mathrm{tr}{R}_{G_2}\left(\overrightarrow{v}\right)=1+2\left[cos({\phi }_2+{\phi }_3)+cos{\phi }_2+cos{\phi }_3\right],$$

(45)

and the two independent angles ${\phi }_2,{\phi }_3$ parametrize a two-dimensional maximal torus $SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1$ in $G_2$. Stated differently, by passing to the subgroup $G_2\subset SO\left(7\right)$ the angle for the rotation in the $x_1{x}_2$-plane is fixed to the sum of the rotation angles in the $x_3{x}_4$- and $x_5{x}_6$-planes, ${\phi }_1={\phi }_2+{\phi }_3$.

8. SO(8)

Elements of the 28-dimensional Lie algebra $so\left(8\right)$ are antisymmetric $8\times 8$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{cccccccc}0& v_1& v_2& v_3& v_4& v_5& v_6& v_7\\ -v_1& 0& v_8& v_9& v_{10}& v_{11}& v_{12}& v_{13}\\ -v_2& -v_7& 0& v_{14}& v_{15}& v_{16}& v_{17}& v_{18}\\ -v_3& -v_9& -v_{14}& 0& v_{19}& v_{20}& v_{21}& v_{22}\\ -v_4& -v_{10}& -v_{15}& -v_{19}& 0& v_{23}& v_{24}& v_{25}\\ -v_5& -v_{11}& -v_{16}& -v_{20}& -v_{23}& 0& v_{26}& v_{27}\\ -v_6& -v_{12}& -v_{17}& -v_{21}& -v_{24}& -v_{26}& 0& v_{28}\\ -v_7& -v_{13}& -v_{18}& -v_{22}& -v_{25}& -v_{27}& -v_{28}& 0\end{array}\right),$$

(46)

with the corresponding norm $V=\sqrt{v_1^2+\cdots +v_{28}^2}$ of the 28-component real vector $\overrightarrow{v}$. The characteristic polynomial [6] of $\overrightarrow{J}·\widehat{v}$ is of degree eight and it reads

$$P_8\left(x\right)=x^8+x^6+x^4\left(\frac{1}{2}-\frac{\xi }{4}\right)+x^2\left(\frac{1-\zeta }{6}-\frac{\xi }{4}\right)+\eta ,$$

(47)

with the invariants $\xi =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^4,\zeta =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^6$ and $\eta =\det (\overrightarrow{J}·\widehat{v})$ forming its coefficients. By setting $y=-x^2$ one is led to a quartic polynomial

$${\tilde{P}}_4\left(y\right)=y^4-y^3+y^2\left(\frac{1}{2}-\frac{\xi }{4}\right)+y\left(\frac{\zeta -1}{6}+\frac{\xi }{4}\right)+\eta ,$$

(48)

whose four roots $y_1,y_2,y_3,y_4\ge 0$ all have to be positive, since those of $P_8\left(x\right)=0$ are the purely imaginary eigenvalues of the antihermitean $8\times 8$ matrix $\overrightarrow{J}·\widehat{v}$. The determination of the four roots $y_j$ proceeds via three auxiliary quantities ${\Theta }_1,{\Theta }_2,{\Theta }_3$ in the following way [7]

$$y_{1,2}=\frac{1}{4}\left[1+\sqrt{{\Theta }_1}\pm \left(\sqrt{{\Theta }_2}+\sqrt{{\Theta }_3}\right)\right],y_{3,4}=\frac{1}{4}\left[1-\sqrt{{\Theta }_1}\pm \left(\sqrt{{\Theta }_2}-\sqrt{{\Theta }_3}\right)\right],$$

(49)

where the product of the three square-roots must fulfill the condition $\sqrt{{\Theta }_1}\sqrt{{\Theta }_2}\sqrt{{\Theta }_3}=1/3-\xi -4\zeta /3$. This means that if the right-hand side is negative, $3\xi +4\zeta >1$, one square-root must be chosen as negative. The three positive $\Theta$-values are the roots of the cubic resolvent polynomial

$$R_3(\Theta )={\Theta }^3+{\Theta }^2(1-2\xi )+\Theta \left(\frac{5}{3}-64\eta -4\xi +{\xi }^2-\frac{8\zeta }{3}\right)-\frac{1}{9}{\left(3\xi +4\zeta -1\right)}^2.$$

(50)

The solution of $R_3(\Theta )=0$ belongs again to the irreducible case and is performed with the trigonometric ansatz

$$\Theta =\frac{1}{3}\left(2\xi -1+2\sqrt{192\eta +8\zeta +8\xi +{\xi }^2-4}cos\psi \right).$$

(51)

The determining equation for $cos3\psi$ yields for the trisected angle $\psi$ the result

$$\psi =\frac{1}{3}arccos\frac{8(1-36\eta -3\zeta +3{\zeta }^2)-{\xi }^3+42{\xi }^2+12\xi (5\zeta +48\eta -3)}{{(192\eta +8\zeta +8\xi +{\xi }^2-4)}^{3/2}},$$

(52)

and the three auxiliary quantities ${\Theta }_1,{\Theta }_2,{\Theta }_3$ follow by evaluating Equation (51) at the angles $\psi$ and $\psi \pm 2\pi /3$. The necessary conditions that the radicand in Equation (52) is positive, and that the numerator is smaller in magnitude than the denominator following from considering the local minimum and maximum located at ${\Theta }_{\pm }=(2\xi -1\pm \sqrt{192\eta +8\zeta +8\xi +{\xi }^2-4})/3\ge 0$ together with $R_3\left({\Theta }_{+}\right)R_3\left({\Theta }_{-}\right)\le 0$. One should remark here that the cubic polynomial $R_3(\Theta )$ has actually the same form as ${\tilde{P}}_3\left(y\right)$ shown in Figure 1. Considering the coefficients of the quadratic terms in Equations (48) and (50) one deduces from the positivity of all roots the inequalities $2-\xi \ge 0$ and $1-2\xi \le 0$, which lead to the range $1/2\le \xi \le 2$ for the invariant $\xi$. In a further detailed study (e.g., at fixed $\xi$) one finds for the other two invariants the intervals $0\le \eta \le 1/64$ and $-2\le \zeta \le -1/8$, pertinent to the case of $so\left(8\right)$. Altogether the bounded region of allowed values in $\xi \eta \zeta$-space fills a volume of $0.001385\simeq 1/722$. The less obvious boundary values ${\eta }_{\min }=0,{\eta }_{\max }=1/64,{\zeta }_{\min }=-2,{\zeta }_{\max }=-1/8$ are confirmed by observing that this volume would decrease, if the integration intervals were narrowed, but stay constant when they are widened.

Based on the Cayley–Hamilton relation ${\Sigma }^8=-{\Sigma }^6+{\Sigma }^4(\xi -2)/4+{\Sigma }^2[\xi /4+(\zeta -1)/6]-\eta \mathbf{1}$ one constructs the $8\times 8$ iteration matrix as

$$M_8=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& -\eta \\ 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& \xi /4+(\zeta -1)/6\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& \xi /4-1/2\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& -1\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right),$$

(53)

with which one can solve $exp\left(V{M}_8\right)$ and multiply with $(1,0,0,0,0,0,0,0)$. This way one derives the following analytical formula for the matrix exponential function $so\left(8\right)\to SO\left(8\right)$:

$$\begin{array}{ccc}\hfill R_8\left(\overrightarrow{v}\right)=exp(\overrightarrow{J}·\overrightarrow{v})& =& \sum _{j=1}^4{\left[4y_j^3-3y_j^2+y_j\left(1-\frac{\xi }{2}\right)+\frac{\xi }{4}+\frac{\zeta -1}{6}\right]}^{-1}\hfill \\ & & \times \left\{cos\left(V\sqrt{y_j}\right)\mathbf{1}+\frac{1}{\sqrt{y_j}}sin\left(V\sqrt{y_j}\right)\overrightarrow{J}·\widehat{v}\right\}\hfill \\ & & \times \left\{-\frac{\eta }{y_j}\mathbf{1}+\left(\frac{\xi }{4}-\frac{1}{2}+y_j-y_j^2\right){(\overrightarrow{J}·\widehat{v})}^2+(y_j-1){(\overrightarrow{J}·\widehat{v})}^4-{(\overrightarrow{J}·\widehat{v})}^6\right\},\hfill \end{array}$$

(54)

where the sum goes over the four positive roots of the quartic equation ${\tilde{P}}_4\left(y\right)=0$. Note that the denominator of the prefactor is the derivative ${\tilde{P}}_4^{\prime }\left(y_j\right)$, and one gets a remarkable factorization for the terms with (up to seventh) powers of $\overrightarrow{J}·\widehat{v}$. The trace of the orthogonal matrix $R_8\left(\overrightarrow{v}\right)$ comes out as

$$\mathrm{tr}{R}_8\left(\overrightarrow{v}\right)=2\sum _{j=1}^{4}cos\left(V\sqrt{y_j}\right),$$

(55)

where the simplification is achieved by eliminating each summand $\eta$ in favor of the root $y_j$ through the equation ${\tilde{P}}_4\left(y_j\right)=0$. The four angles ${\phi }_j=V\sqrt{y_j}$ specify to which element on a four-dimensional maximal torus $SO\left(2\right)\times SO\left(2\right)\times SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1\times {\mathbf{S}}^1\times {\mathbf{S}}^1$ a given $SO\left(8\right)$-matrix $R_8\left(\overrightarrow{v}\right)$ is related by conjugation [5].

9. SO(9)

Elements of the 36-dimensional Lie algebra $so\left(9\right)$ are antisymmetric $9\times 9$ matrices of the form

$$\overrightarrow{J}·\overrightarrow{v}=\left(\begin{array}{ccccccccc}0& v_1& v_2& v_3& v_4& v_5& v_6& v_7& v_8\\ -v_1& 0& v_9& v_{10}& v_{11}& v_{12}& v_{13}& v_{14}& v_{15}\\ -v_2& -v_9& 0& v_{16}& v_{17}& v_{18}& v_{19}& v_{20}& v_{21}\\ -v_3& -v_{10}& -v_{16}& 0& v_{22}& v_{23}& v_{24}& v_{25}& v_{26}\\ -v_4& -v_{11}& -v_{17}& -v_{22}& 0& v_{27}& v_{28}& v_{29}& v_{30}\\ -v_5& -v_{12}& -v_{18}& -v_{23}& -v_{27}& 0& v_{31}& v_{32}& v_{33}\\ -v_6& -v_{13}& -v_{19}& -v_{24}& -v_{28}& -v_{31}& 0& v_{34}& v_{35}\\ -v_7& -v_{14}& -v_{20}& -v_{25}& -v_{29}& -v_{32}& -v_{34}& 0& v_{36}\\ -v_8& -v_{15}& -v_{21}& -v_{26}& -v_{30}& -v_{33}& -v_{35}& -v_{36}& 0\end{array}\right),$$

(56)

with the corresponding norm $V=\sqrt{v_1^2+\cdots +v_{36}^2}$ of the 36-component real vector $\overrightarrow{v}$. The characteristic polynomial [6] of $\overrightarrow{J}·\widehat{v}$ is of degree nine and it reads

$$P_9\left(x\right)=x^9+x^7+x^5\left(\frac{1}{2}-\frac{\xi }{4}\right)+x^3\left(\frac{1-\zeta }{6}-\frac{\xi }{4}\right)+x\left(\frac{1}{24}-\frac{\xi +\chi }{8}+\frac{{\xi }^2}{32}-\frac{\zeta }{6}\right),$$

(57)

with a new invariant, $\chi =\mathrm{tr}{(\overrightarrow{J}·\widehat{v})}^8$, the trace of the eighth matrix power. Besides the trivial root $x=0$ of $P_9\left(x\right)$, the other purely imaginary ones are found via the substitution $y=-x^2$ from the quartic polynomial

$${\tilde{P}}_4\left(y\right)=y^4-y^3+y^2\left(\frac{1}{2}-\frac{\xi }{4}\right)+y\left(\frac{\zeta -1}{6}+\frac{\xi }{4}\right)+\frac{1}{24}-\frac{\xi +\chi }{8}+\frac{{\xi }^2}{32}-\frac{\zeta }{6},$$

(58)

which after identification of the constant term with $\eta$ is identical to ${\tilde{P}}_4\left(y\right)$ in Equation (48) pertinent to the case of $so\left(8\right)$. Therefore, when working with the auxiliary parameter

$${\eta }_9=\frac{1}{24}-\frac{\xi +\chi }{8}+\frac{{\xi }^2}{32}-\frac{\zeta }{6}\ge 0,$$

(59)

the construction of the four positive roots $y_1,y_2,y_3,y_4$ can be copied from the previous section by making merely the substitution $\eta \to {\eta }_9$. The denominator of the arc-cosine function in Equation (52) becomes this way

$$192{\eta }_9+8\zeta +8\xi +{\xi }^2-4=7{\xi }^2-16\xi -24(\zeta +\chi )+4,$$

(60)

while the numerator polynomial turns into

$$\begin{array}{c}8(1-36{\eta }_9-3\zeta +3{\zeta }^2)-{\xi }^3+42{\xi }^2+12\xi (5\zeta +48{\eta }_9-3)\hfill \\ ={\xi }^2(17\xi -39)+12\xi (2-3\zeta -6\chi )+12(2\zeta +2{\zeta }^2+3\chi )-4,\hfill \end{array}$$

(61)

where the corresponding ranges are $1/2\le \xi \le 2$, $-2\le \zeta \le -1/8$, and $0\le {\eta }_9\le 1/64$. The allowed region in $\xi \zeta \chi$-space fills a volume of $0.01108\simeq 8/722$, and within this region, the invariant $\chi$ takes on values from the interval $1/32\le \chi \le 2$.

Based on the Cayley–Hamilton relation ${\Sigma }^9=-{\Sigma }^7+{\Sigma }^5(\xi -2)/4+{\Sigma }^3[\xi /4+(\zeta -1)/6]-\Sigma {\eta }_9$ one constructs the $9\times 9$ iteration matrix as

$$M_9=\left(\begin{array}{ccccccccc}0& 0& 0& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& -{\eta }_9\\ 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& \xi /4+(\zeta -1)/6\\ 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& \xi /4-1/2\\ 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& -1\\ 0& 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right),$$

(62)

with which one can solve $exp\left(V{M}_9\right)$ and multiply with $(1,0,0,0,0,0,0,0,0)$. This way one derives the following analytical formula for the matrix exponential function $so\left(9\right)\to SO\left(9\right)$:

$$\begin{array}{ccc}\hfill R_9\left(\overrightarrow{v}\right)& =& exp(\overrightarrow{J}·\overrightarrow{v})=\mathbf{1}+\frac{1}{{\eta }_9}\left\{\left(\frac{1-\zeta }{6}-\frac{\xi }{4}\right){(\overrightarrow{J}·\widehat{v})}^2+\left(\frac{1}{2}-\frac{\xi }{4}\right){(\overrightarrow{J}·\widehat{v})}^4+{(\overrightarrow{J}·\widehat{v})}^6+{(\overrightarrow{J}·\widehat{v})}^8\right\}\hfill \\ & & +2\sum _{j=1}^4{\left[9y_j^4-7y_j^3+\frac{5}{4}{y}_j^2(2-\xi )+\frac{y_j}{4}(3\xi +2\zeta -2)+{\eta }_9\right]}^{-1}\hfill \\ & & \times \left\{\frac{{\eta }_9}{y_j}\mathbf{1}+\left(\frac{1}{2}-\frac{\xi }{4}-y_j+y_j^2\right){(\overrightarrow{J}·\widehat{v})}^2+(1-y_j){(\overrightarrow{J}·\widehat{v})}^4+{(\overrightarrow{J}·\widehat{v})}^6\right\}\hfill \\ & & \times \left\{cos\left(V\sqrt{y_j}\right){(\overrightarrow{J}·\widehat{v})}^2-\sqrt{y_j}sin\left(V\sqrt{y_j}\right)\overrightarrow{J}·\widehat{v}\right\}.\hfill \end{array}$$

(63)

The calculation of the trace of the orthogonal matrix $R_9\left(\overrightarrow{v}\right)$ gives the result

$$\mathrm{tr}{R}_9\left(\overrightarrow{v}\right)=1+2\sum _{j=1}^{4}cos\left(V\sqrt{y_j}\right),$$

(64)

where one first uses $\chi =1/3-\xi +{\xi }^2/4-4\zeta /3-8{\eta }_9$ and then eliminates ${\eta }_9$ in favor of the root $y_j$ via the equation ${\tilde{P}}_4\left(y_j\right)=0$. The four angles ${\phi }_j=V\sqrt{y_j}$ specify to which element on a four-dimensional maximal torus $SO\left(2\right)\times SO\left(2\right)\times SO\left(2\right)\times SO\left(2\right)={\mathbf{S}}^1\times {\mathbf{S}}^1\times {\mathbf{S}}^1\times {\mathbf{S}}^1$ a given $SO\left(9\right)$-matrix $R_9\left(\overrightarrow{v}\right)$ is related by conjugation [5]. By convention, the independent rotations take place in the $x_1{x}_2$-plane, $x_3{x}_4$-plane, $x_5{x}_6$-plane, and $x_7{x}_8$-plane of nine-dimensional space.

10. Conclusions

In this work the matrix exponential function has been solved analytically for the special orthogonal groups $SO\left(n\right)$ up to $n=9$. By exploiting the Cayley–Hamilton relation for the elements of the underlying Lie algebra $so\left(n\right)$ (i.e., antisymmetric real $n\times n$ matrices) the number of required matrix powers ranges from 0 up to $n-1$. The pertinent expansion coefficients have been expressed as cosine and sine functions of a vector norm $V=|\overrightarrow{v}|$ and the roots $y_j$ of a polynomial equation that depended on some specific invariants (the determinant and the traces of even matrix powers). A quadratic equation needed to be solved for $n=4,5$, a cubic equation for $n=6,7$, and a quartic equation for $n=8,9$ (where the latter leads to a cubic resolvent equation of irreducible type). The exceptional Lie group $G_2\in SO\left(7\right)$ of dimension 14, defined as the automorphism group of the octonions, has been constructed via the matrix exponential function by first deriving seven linear relations for the 21 parameters of a general $so\left(7\right)$ Lie algebra element. These linear relations turned into a remarkably simple constraint on the invariant $\xi =\mathrm{t}r{(\overrightarrow{J}·\widehat{v})}^4=1$.

It is hoped that the given analytical formulas will be useful to generate the full manifold of special orthogonal $SO\left(n\right)$-matrices and (exceptional) $G_2$-matrices in various applications, such as lattice gauge theories [8,9,10,11] and effective field theories [1,12].