Generalized Halanay Inequalities and Asymptotic Behavior of Nonautonomous Neural Networks with Infinite Delays
Abstract
1. Introduction
2. Preliminaries and Model Description
3. Main Results
- (C.4)
- For , there exist constants and such thatwhere
- (C.5)
- For ,andwhere, were introduced in Theorem 1.
- (C.4′)
- For , there exist constants and such that
- (C.5′)
- For , there exist constants , and such that
- (C.6)
- For , there exist positive constants , such thatand there exists such that
- (C.7)
- For , there exist constants and such thatThen,and
- (C.1′)
- For each , , , and are all continuous functions defined on .
- (C.6′)
- For each ,
- (C.7′)
- For , there exists a such that
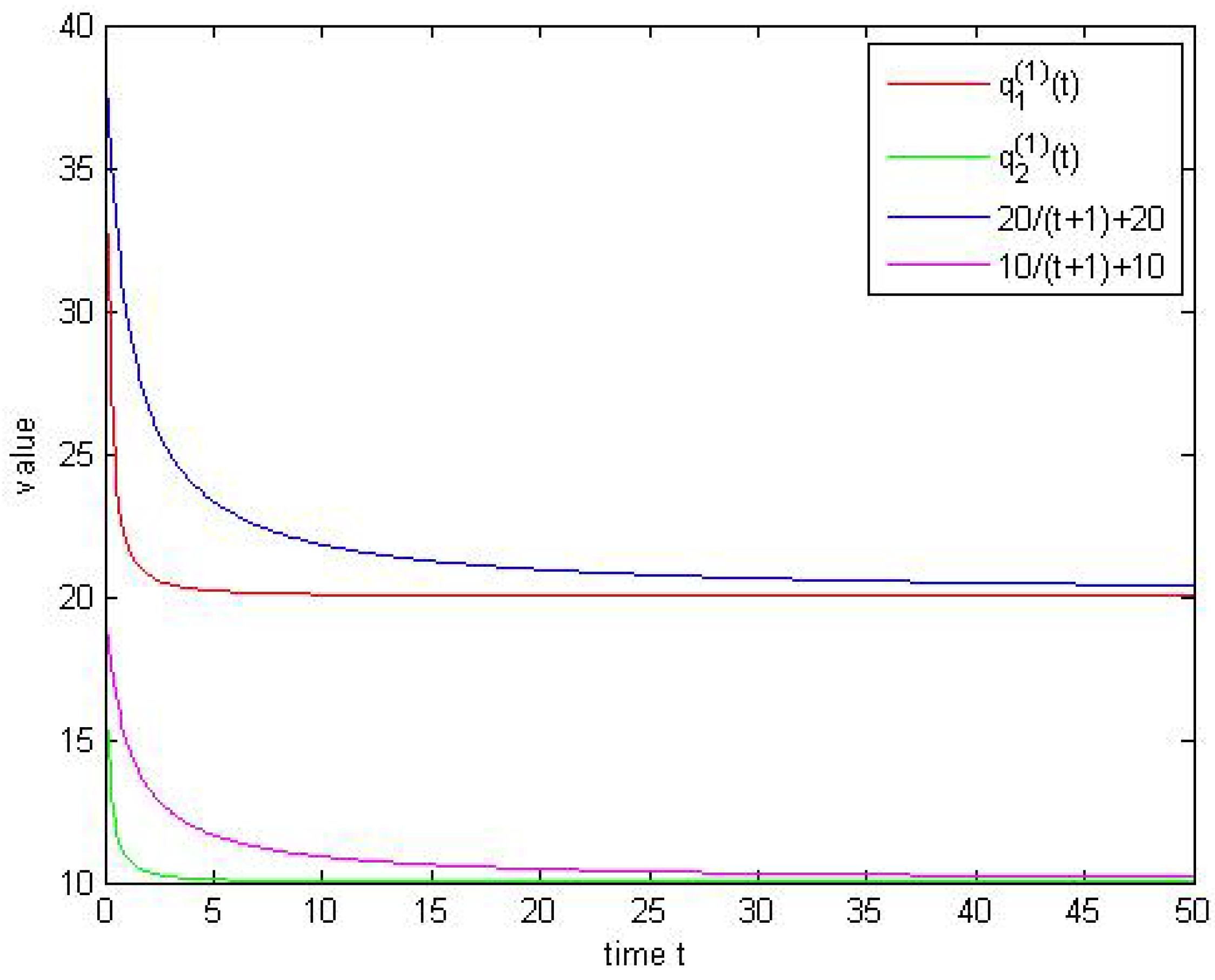
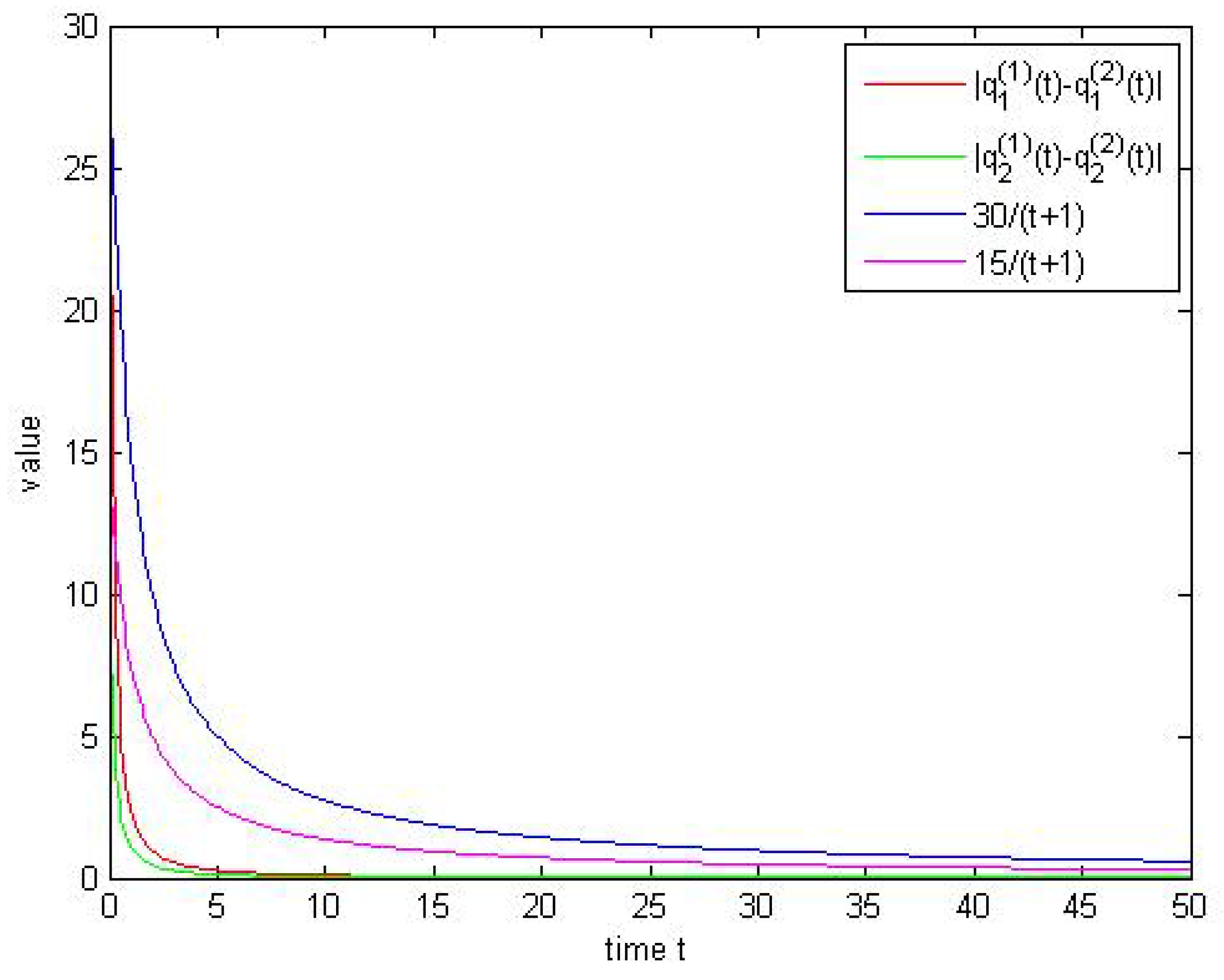
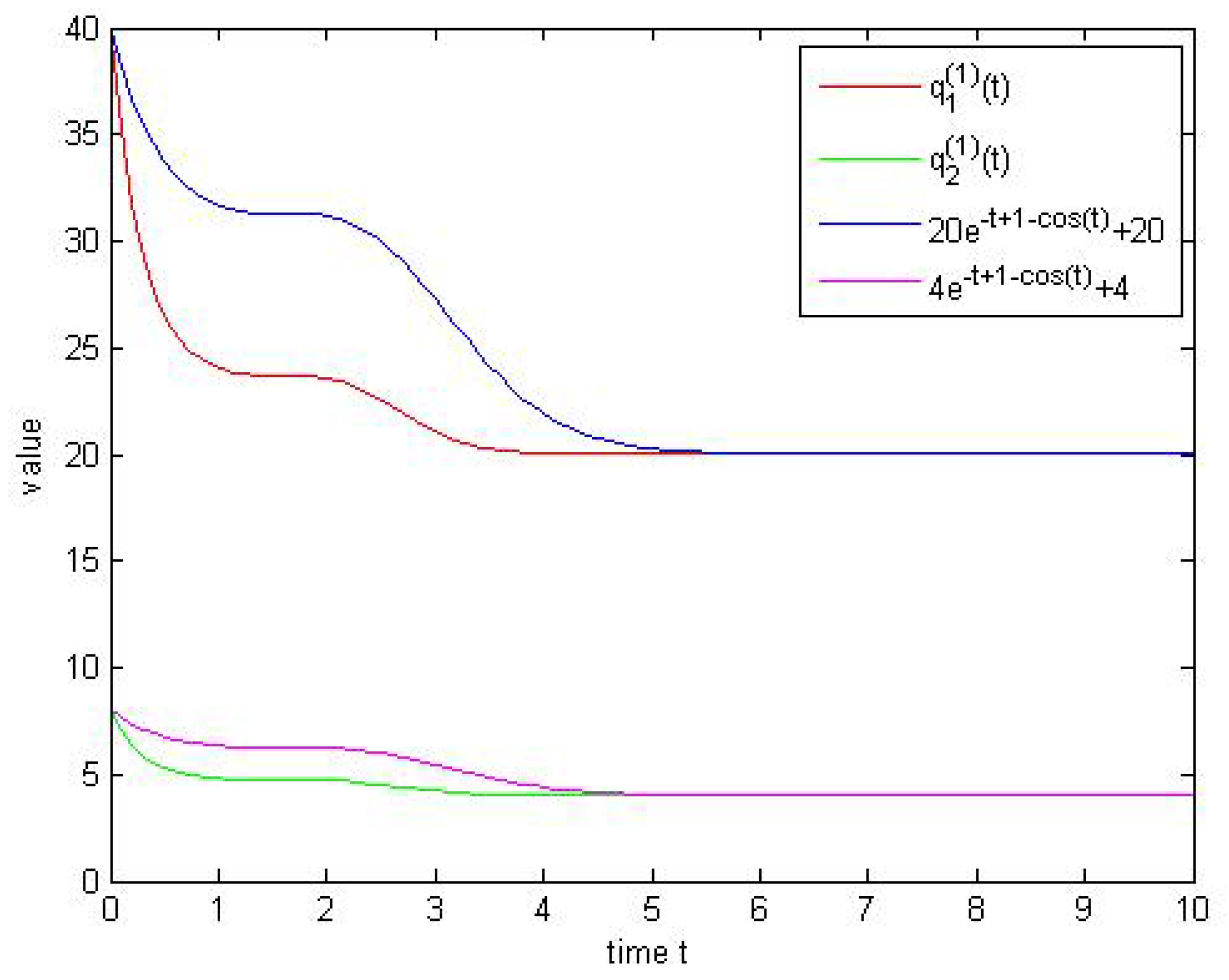
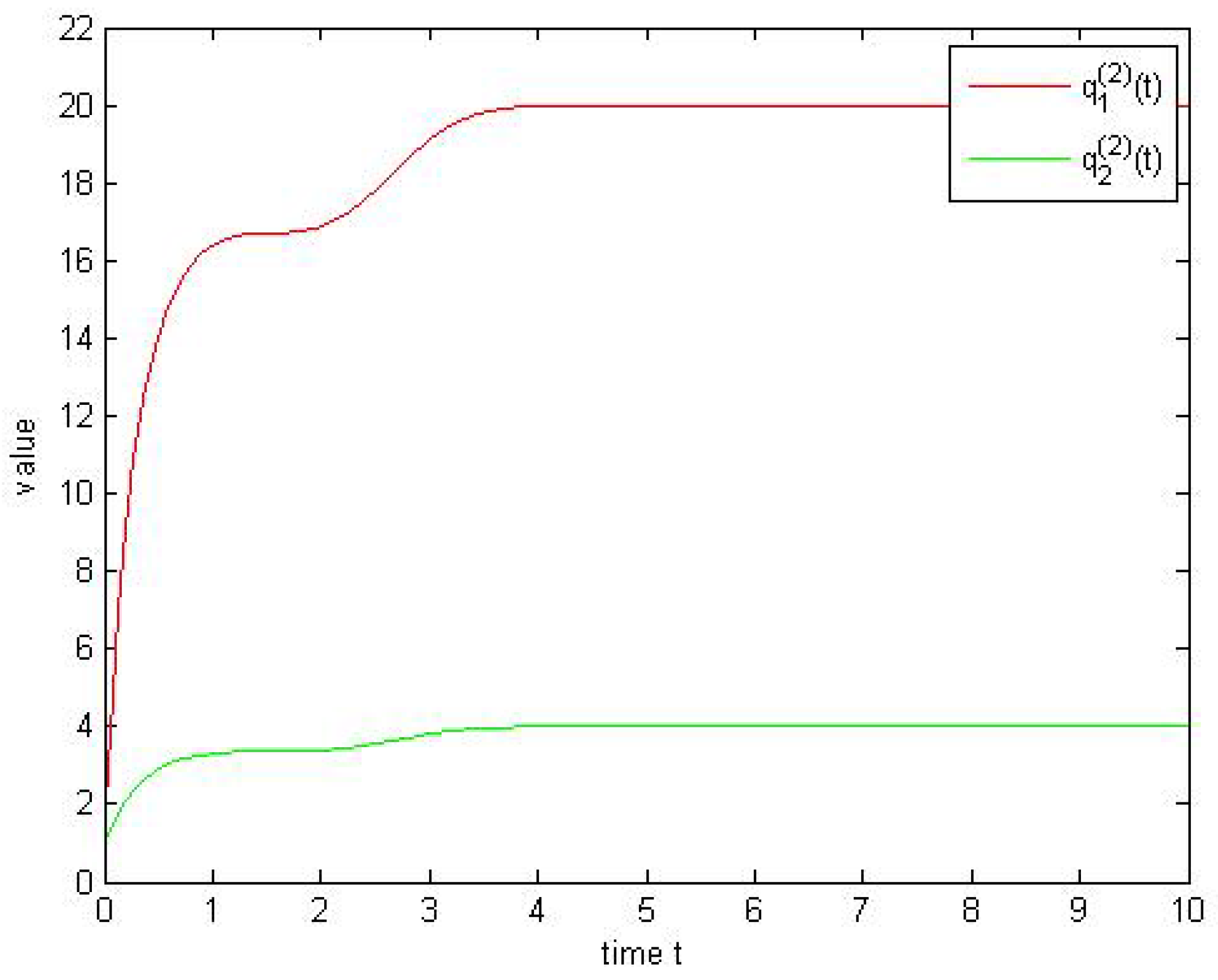
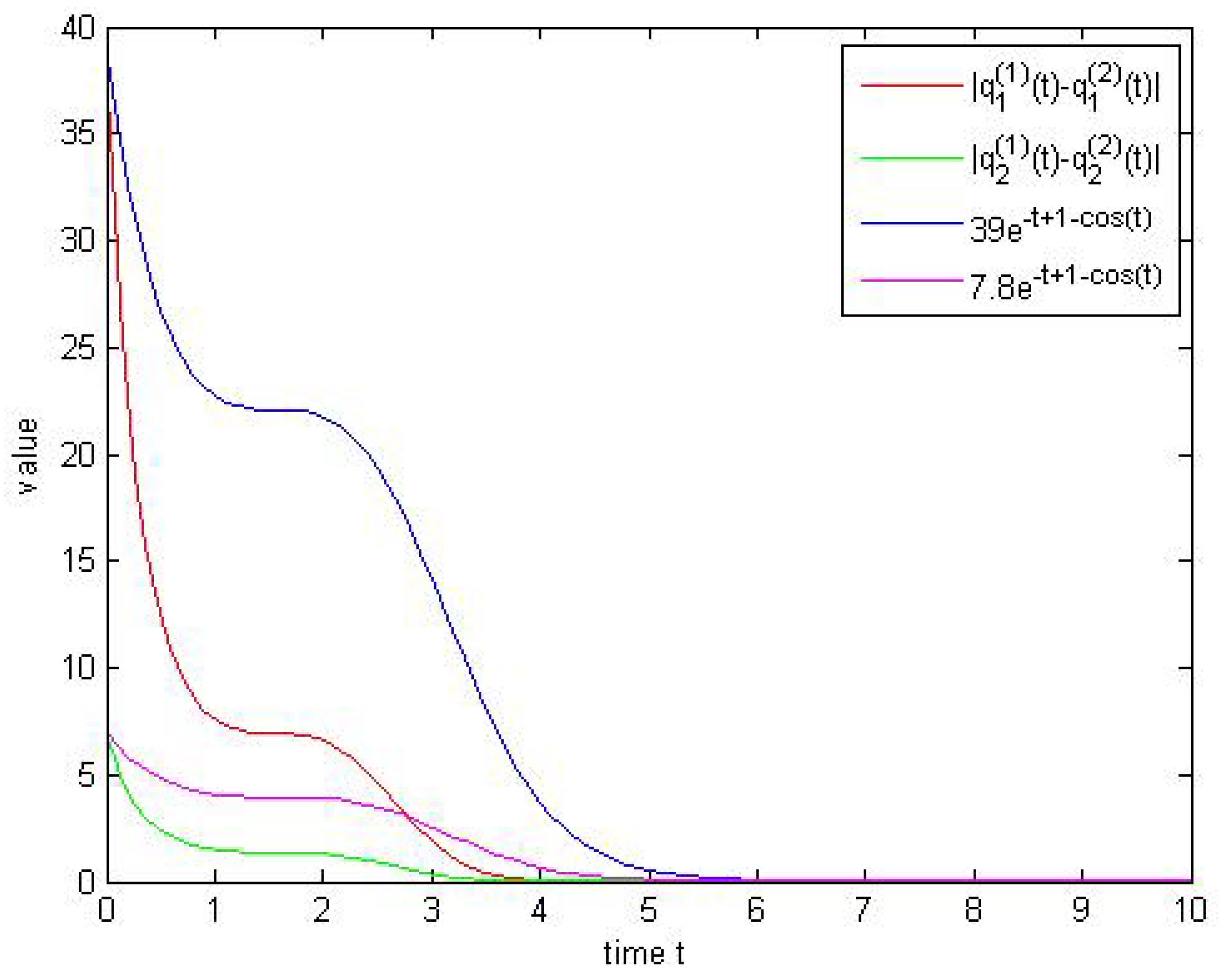
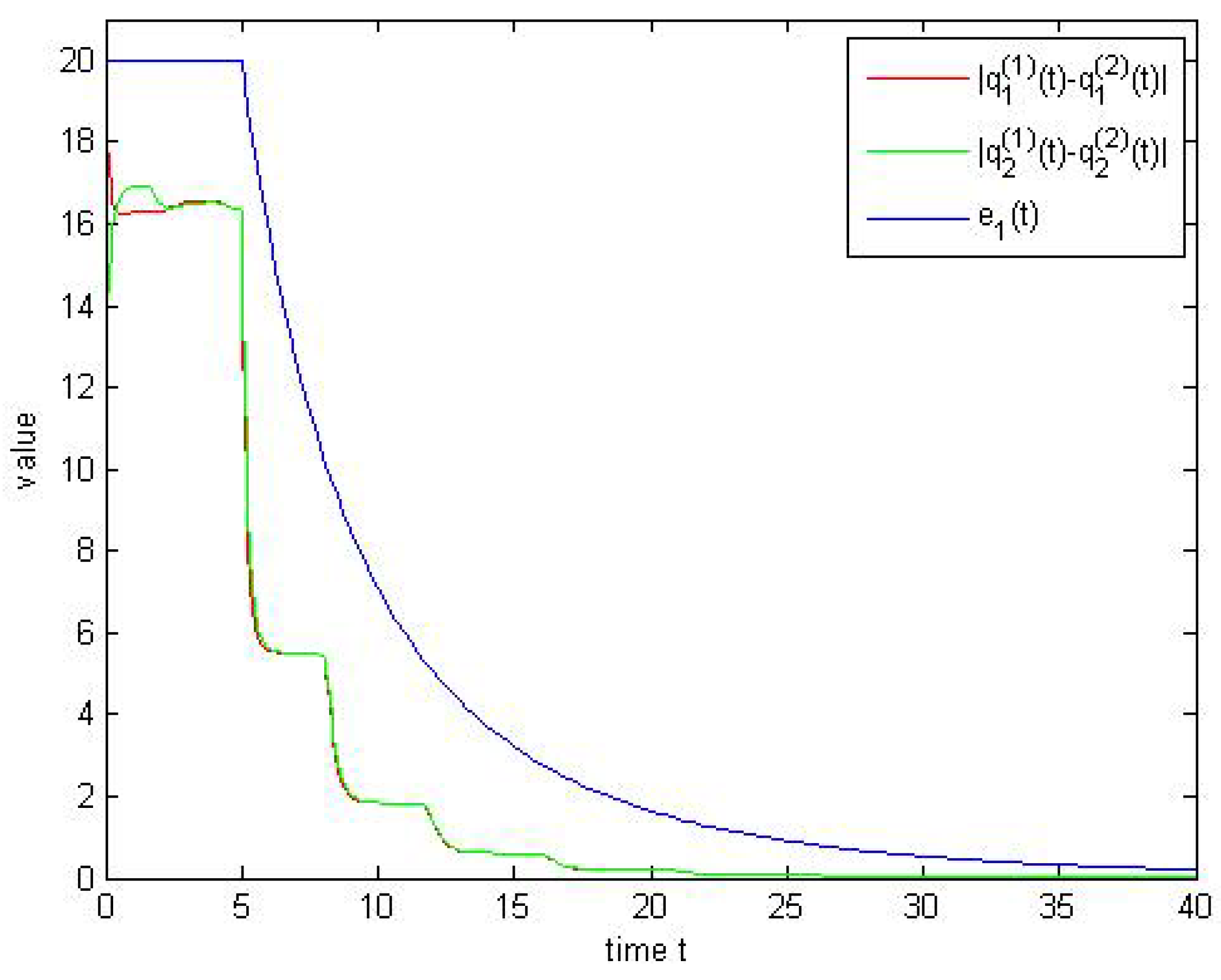
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Feng, G.; Duan, S.; Liu, L. Multilayer rtd-memristor-based cellular neural networks for color image processing. Neurocomputing 2015, 162, 150–162. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Teoh, E.K.; Mital, D.P. Pattern recognition by homomorphic graph matching using Hopfield neural networks. Image Vis. Comput. 2015, 13, 45–60. [Google Scholar] [CrossRef]
- Liu, D.; Michel, A.N. Cellular neural networks for associative memories. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1993, 40, 119–121. [Google Scholar] [CrossRef]
- Feng, Z.; Lam, J. Stability and dissipativity analysis of distributed delay cellular neural networks. IEEE Trans. Neural Netw. 2011, 22, 976–981. [Google Scholar] [CrossRef]
- Hien, L.V.; Phat, V.N.; Trinh, H. On global dissipativity of nonautonomous neural networks with multiple proportional delays. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Zhao, Z. Global dissipativity of neural networks with both variable and unbounded delays. Chaos Solitons Fractals 2005, 25, 393–401. [Google Scholar] [CrossRef]
- Zeng, H.; He, Y.; Shi, P.; Wu, M.; Xiao, S. Dissipativity analysis of neural networks with time-varying delays. Neurocomputing 2015, 16, 741–746. [Google Scholar] [CrossRef]
- Chen, A.; Cao, J. Existence and attractivity of almost periodic solutions for cellular neural networks with distributed delays and variable coefficients. Appl. Math. Comput. 2003, 134, 125–140. [Google Scholar]
- Ding, K.; Zhu, Q. Intermittent static output feedback control for stochastic delayed-switched positive systems with only partially measurable information. IEEE Trans. Autom. Control 2023, 68, 8150–8157. [Google Scholar] [CrossRef]
- Xiao, Q.; Huang, T.; Zeng, Z. Stabilization of nonautonomous recurrent neural networks with bounded and unbounded delays on time scales. IEEE Trans. Cybern. 2019, 50, 4307–4317. [Google Scholar] [CrossRef]
- Zhu, Q. Stabilization of stochastic nonlinear delay systems with exogenous disturbances and the event-triggered feedback control. IEEE Trans. Autom. Control 2019, 64, 3764–3771. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Q. Stability analysis of discrete-time semi-Markov jump linear systems with time delay. IEEE Trans. Autom. Control 2023, 68, 6758–6765. [Google Scholar] [CrossRef]
- Fan, L.; Zhu, Q.; Zheng, W. Stability analysis of switched stochastic nonlinear systems with state-dependent delay. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Q.; Zheng, W. Exponential stability of stochastic nonlinear delay systems subject to multiple periodic impulses. IEEE Trans. Autom. Control 2023. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, Q. Adaptive event-triggered fuzzy control for stochastic highly nonlinear systems with time delay and non-triangular structure interconnections. IEEE Trans. Fuzzy Syst. 2023. [Google Scholar] [CrossRef]
- Cao, J.; Zhou, D. Stability analysis of delayed cellular neural networks. Neural Netw. 1998, 11, 1601–1605. [Google Scholar] [CrossRef]
- Cao, J. New results concerning exponential stability and periodic solutions of delayed cellular neural networks. Phys. Lett. A 2003, 307, 136–147. [Google Scholar] [CrossRef]
- Mohamad, S.; Gopalsamy, K. Exponential stability of continuous-time and discrete-time cellular neural networks with delays. Appl. Math. Comput. 2003, 135, 17–38. [Google Scholar] [CrossRef]
- Sun, L.; Tang, Y.; Wang, W.; Shen, S. Stability analysis of time-varying delay neural networks based on new integral inequalities. J. Frankl. Inst. 2020, 357, 10828–10843. [Google Scholar] [CrossRef]
- Zeng, Z.; Wang, J.; Liao, X. Global asymptotic stability and global exponential stability of neural networks with unbounded time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2005, 52, 168–173. [Google Scholar]
- Zhang, B.; Lam, J.; Xu, S. Stability analysis of distributed delay neural networks based on relaxed Lyapunov-Krasovskii functionals. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1480–1492. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, X.; Xu, J. Delay-dependent exponential stability of cellular neural networks with time-varying delays. Chaos Solitons Fractals 2005, 23, 1363–1369. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, J. New conditions for global exponential stability of cellular neural networks with delays. Neural Netw. 2005, 18, 1332–1340. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.; Zhang, H. New delay-dependent global exponential stability criterion for cellular-type neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2009, 56, 250–254. [Google Scholar]
- Zhou, L.; Zhang, Y. Global exponential periodicity and stability of recurrent neural networks with multi-proportional delays. ISA Trans. 2016, 60, 89–95. [Google Scholar] [CrossRef]
- Jiang, H.; Cao, J. Global exponential stability of periodic neural networks with time-varying delays. Neurocomputing 2006, 70, 343–350. [Google Scholar] [CrossRef]
- Jiang, H.; Teng, Z. Global exponential stability of cellular neural networks with time-varying coefficients and delays. Neural Netw. 2004, 17, 1415–1425. [Google Scholar] [CrossRef]
- Jiang, H.; Teng, Z. Boundedness and global stability for nonautonomous recurrent neural networks with distributed delays. Chaos Solitons Fractals 2006, 30, 83–93. [Google Scholar] [CrossRef]
- Long, S.; Li, H.; Zhang, Y. Dynamic behavior of nonautonomous cellular neural networks with time-varying delays. Neurocomputing 2015, 168, 846–852. [Google Scholar] [CrossRef]
- Rehim, M.; Jiang, H.; Li, Z.; Teng, Z. Boundedness and stability for nonautonomous cellular neural networks with delay. Neural Netw. 2004, 17, 1017–1025. [Google Scholar] [CrossRef]
- Yu, T.; Cao, D.; Liu, S.; Chen, H. Stability analysis of neural networks with periodic coefficients and piecewise constant arguments. J. Frankl. Inst. 2016, 353, 409–425. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, X.; Xu, J. Global exponential stability for nonautonomous cellular neural networks with delays. Phys. Lett. A 2006, 351, 153–160. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, X.; Xu, J. Global exponential stability for nonautonomous cellular neural networks with unbounded delays. Phys. Lett. A 2009, 39, 1144–1151. [Google Scholar] [CrossRef]
- Li, H.; Zhang, W.; Li, C.; Zhang, W. Global asymptotical stability for a class of non-autonomous impulsive inertial neural networks with unbounded time-varying delay. Neural Comput. Appl. 2019, 31, 6757–6766. [Google Scholar] [CrossRef]
- Hien, L.V.; Son, D.T.; Trinh, H. New generalized Halanay inequalities with applications to stability of nonlinear non-autonomous time-delay systems. Nonlinear Dyn. 2015, 82, 563–575. [Google Scholar] [CrossRef]
- Jiang, M.; Mu, J.; Huang, D. Globally exponential stability and dissipativity for nonautonomous neural networks with mixed time-varying delays. Neurocomputing 2016, 205, 421–429. [Google Scholar] [CrossRef]
- Liu, B.; Lu, W.; Chen, T. Generalized Halanay inequalities and their applications to neural networks with unbounded time-varying delays. IEEE Trans. Neural Netw. 2011, 22, 1508–1513. [Google Scholar] [CrossRef]
- Lu, B.; Jiang, H.; Abdurahman, A.; Hu, C. Global generalized exponential stability for a class of nonautonomous cellular neural networks via generalized Halanay inequalities. Neurocomputing 2016, 214, 1046–1052. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, D.; Lu, Y. Generalized Halanay Inequalities and Asymptotic Behavior of Nonautonomous Neural Networks with Infinite Delays. Mathematics 2024, 12, 155. https://doi.org/10.3390/math12010155
Ruan D, Lu Y. Generalized Halanay Inequalities and Asymptotic Behavior of Nonautonomous Neural Networks with Infinite Delays. Mathematics. 2024; 12(1):155. https://doi.org/10.3390/math12010155
Chicago/Turabian StyleRuan, Dehao, and Yao Lu. 2024. "Generalized Halanay Inequalities and Asymptotic Behavior of Nonautonomous Neural Networks with Infinite Delays" Mathematics 12, no. 1: 155. https://doi.org/10.3390/math12010155
APA StyleRuan, D., & Lu, Y. (2024). Generalized Halanay Inequalities and Asymptotic Behavior of Nonautonomous Neural Networks with Infinite Delays. Mathematics, 12(1), 155. https://doi.org/10.3390/math12010155




