Stability of Traveling Fronts in a Neural Field Model
Abstract
1. Introduction
2. Materials and Methods
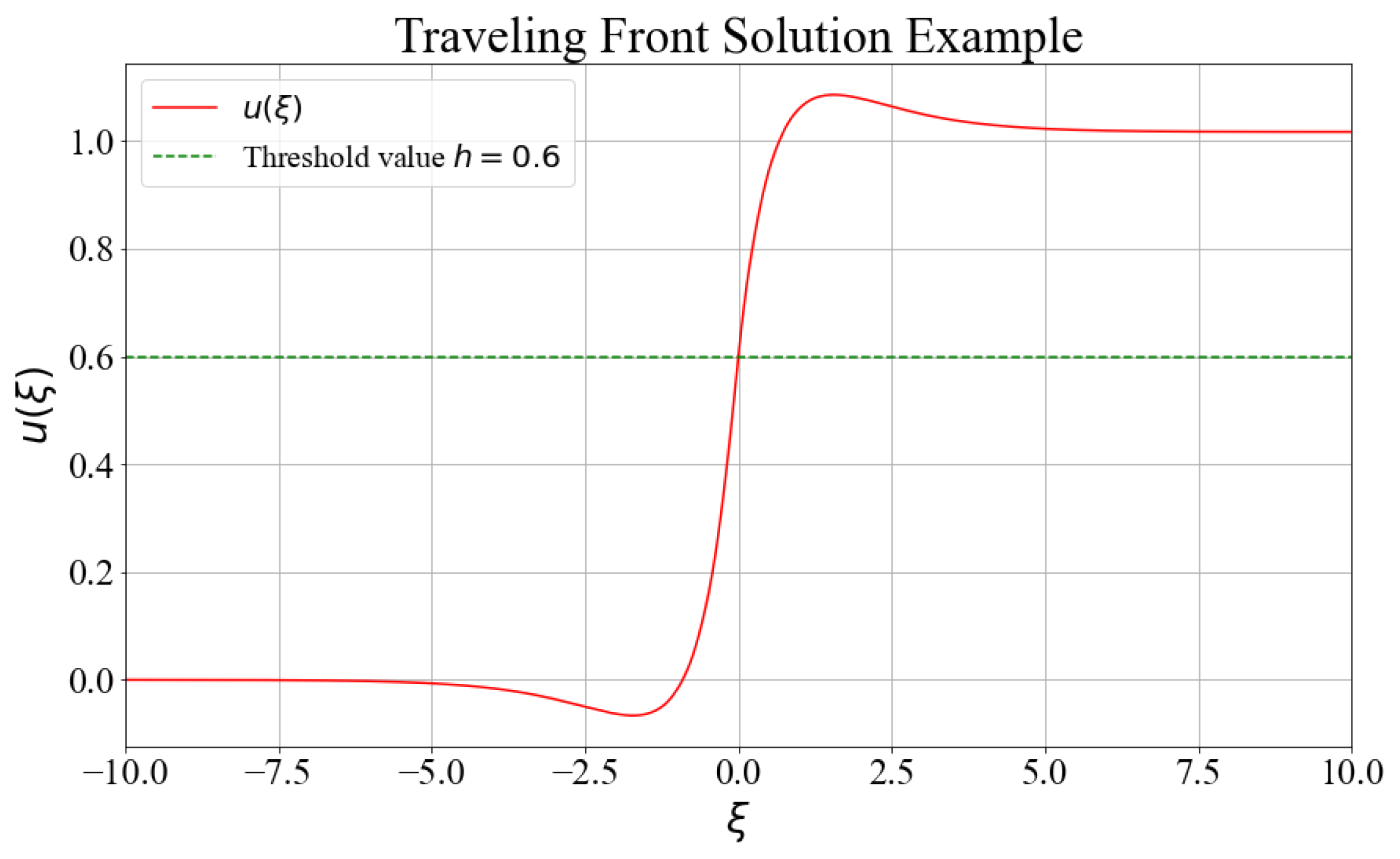
2.1. Coupling Function, Gain Function, and Front Solutions Considered
- on an interval , and ,
- is decreasing on ,
- on ,
- is continuous on , and is integrable on ,
- has a unique minimum on such that , and is strictly increasing on .
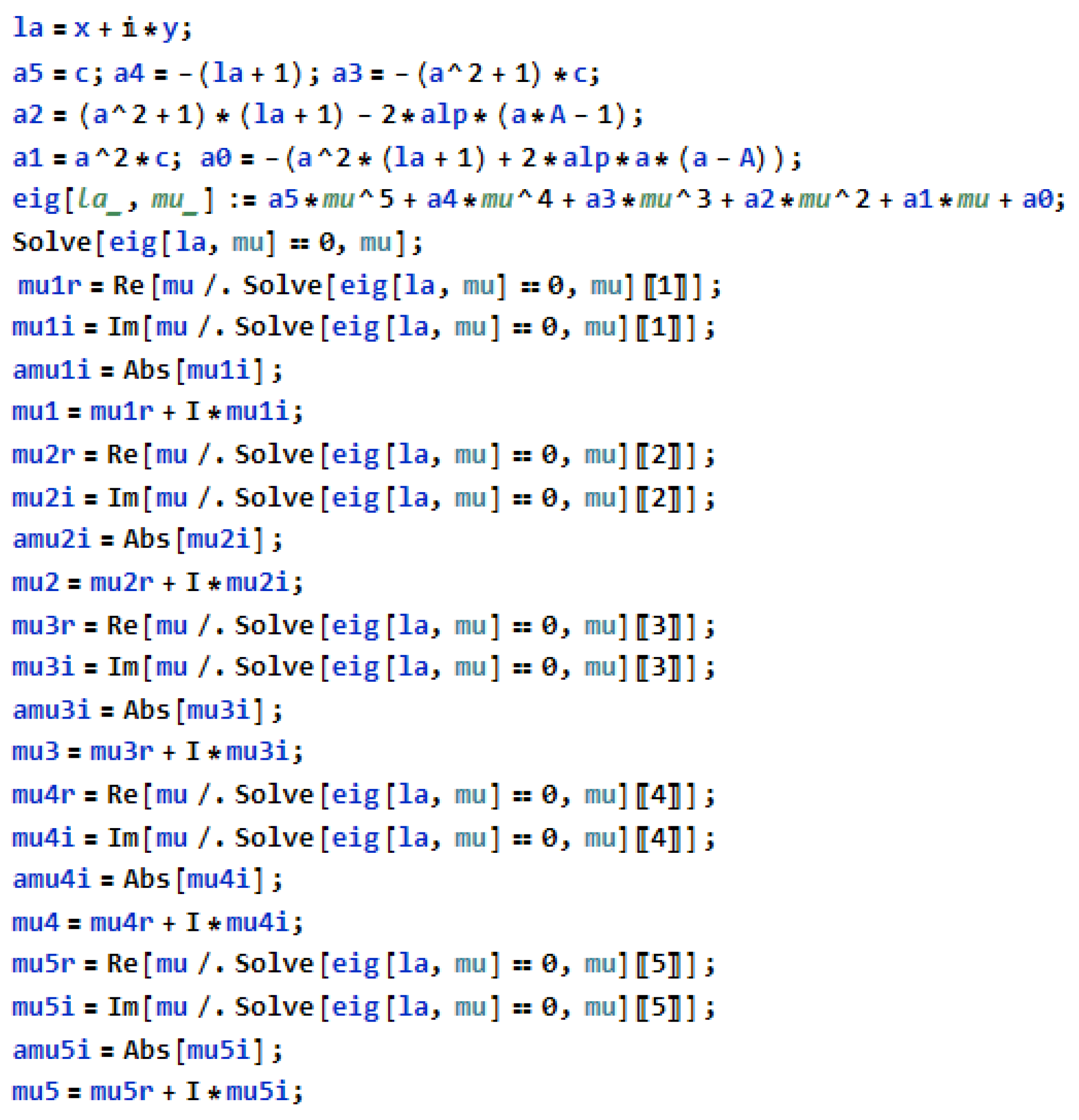
2.2. Formation of the 5th Order ODE
2.3. Matching Conditions for the ODE
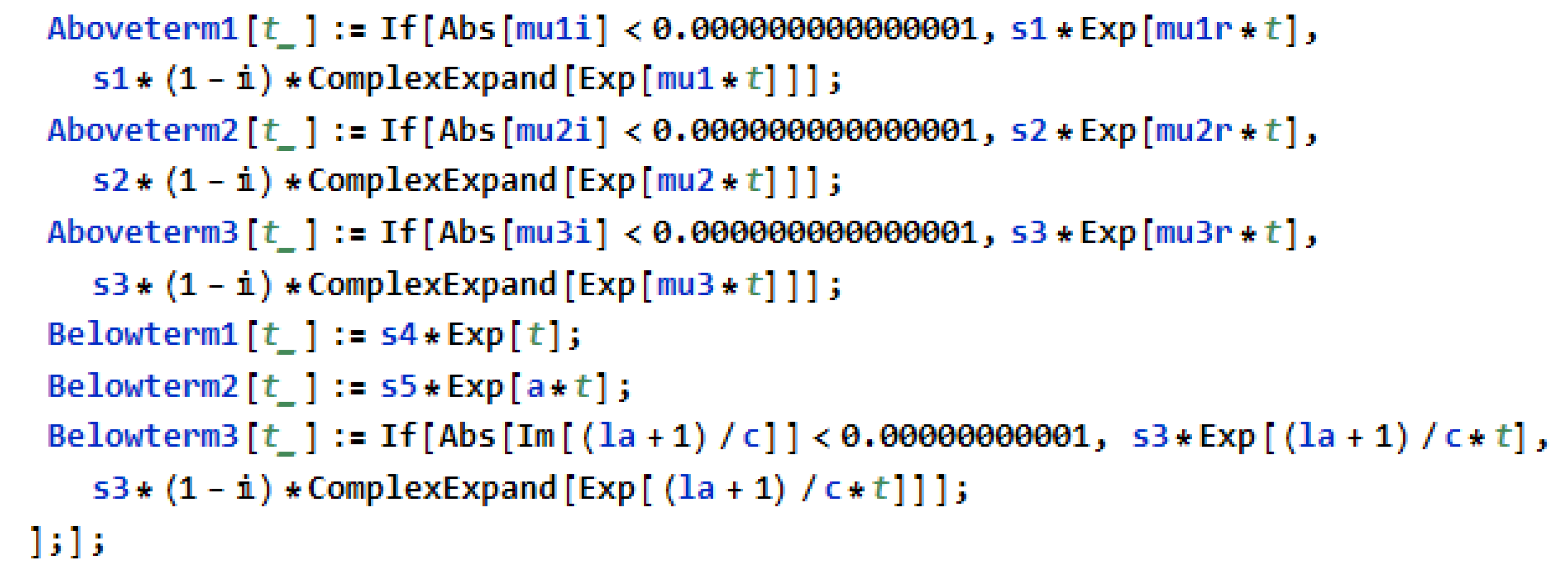
2.4. Forms for Eigenfunction
2.4.1. Eigenfunction Forms When ()
- If , then is the transition between either cases 1 and 2, cases 2 and 4, or cases 3 and 4.
- For the first two transitions mentioned above, the repeated roots are . The solution form is
- If the transition is between case 3 and case 4, the solution form is the same as case 3.
- If , then is the transition between either cases 4 and 5, cases 6 and 8, or cases 7 and 8.
- For the transition from 4 to 5 or 6 to 8, the repeated roots are . The solution form is the same as case 6.
- For the transition from 7 to 8, the solution form is the same as case 7.
2.4.2. Eigenfunction Forms When ()
2.5. Evans Function for Stability Analysis
3. Results
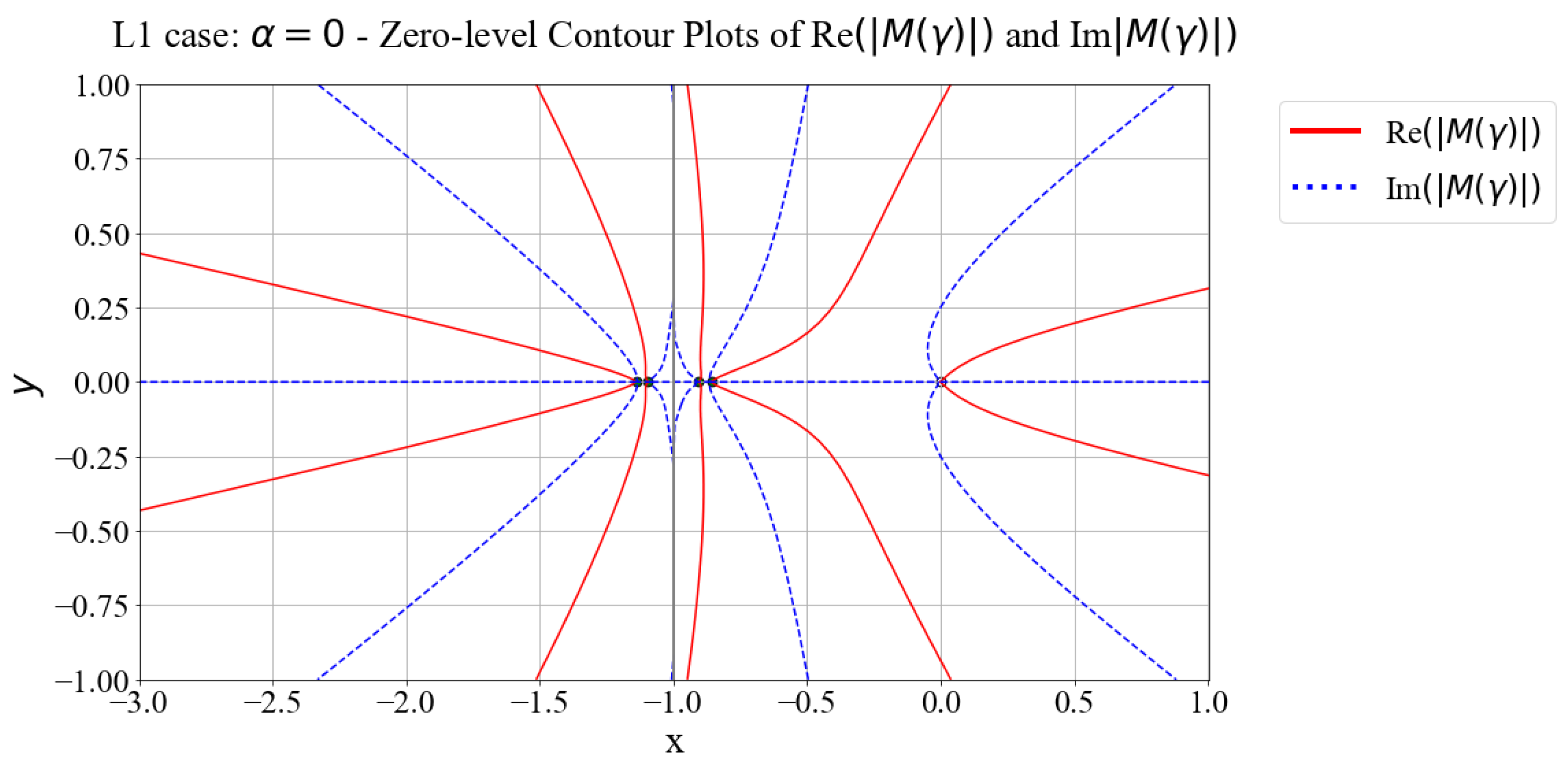
3.1. Case L1 Analysis
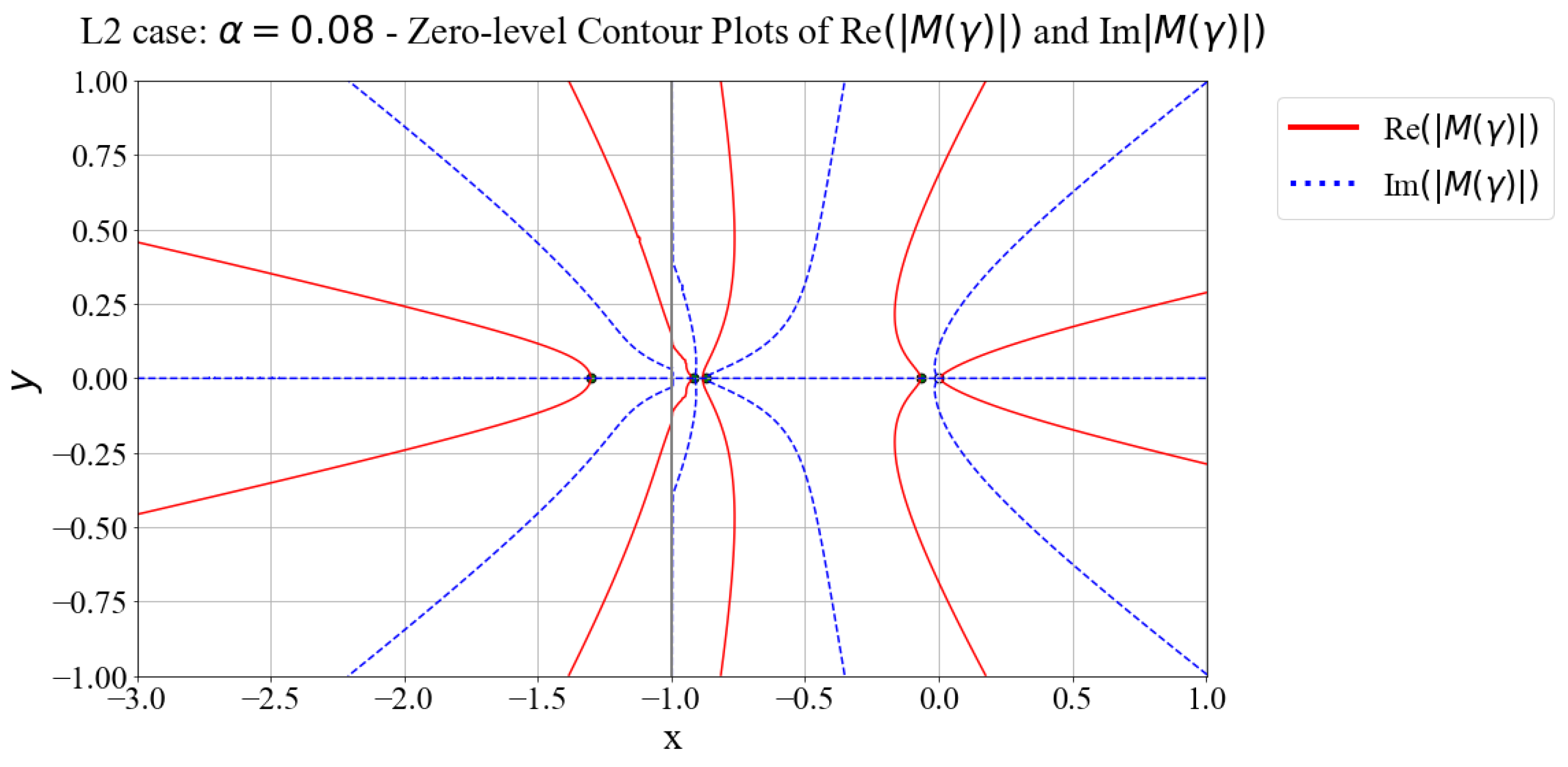
3.2. Case L2 Analysis
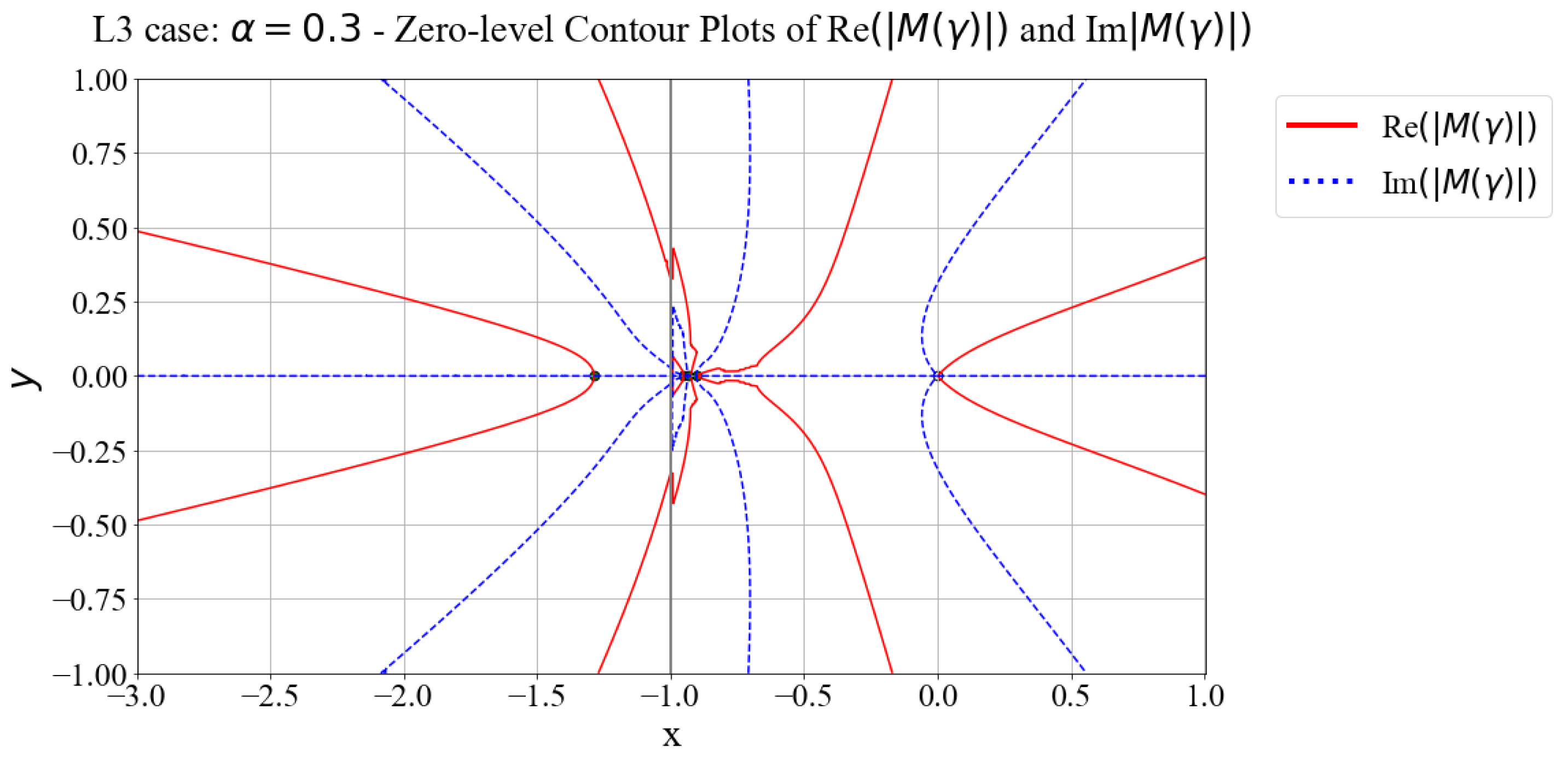
3.3. Case L3 Analysis
3.4. Case L4 Analysis
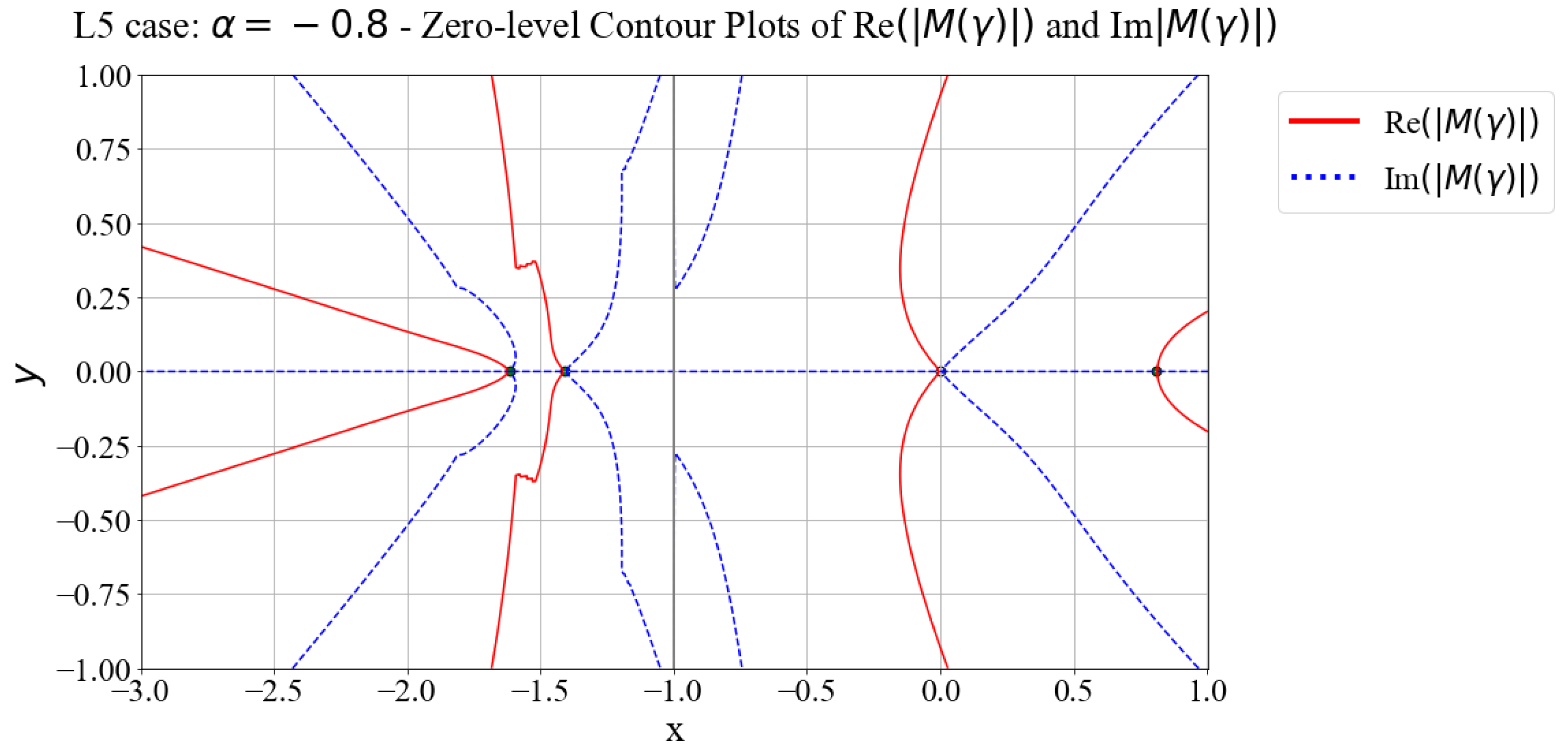
3.5. Case L5 Analysis
3.6. Case L6 Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Details of (16c), (16d) in Lemma (1)
Appendix B. Examples of M(γ) Used in the Evans Function in Equation (38)








Appendix C. Explicit Matrix: L1 Case, α = 0, γ ∈
References
- Bai, L.; Huang, X.; Yang, Q.; Wu, J.Y. Spatiotemporal patterns of an evoked network oscillation in neocortical slices: Coupled local oscillators. J. Neurophysiol. 2006, 96, 2528–2538. [Google Scholar] [CrossRef] [PubMed]
- Connors, B.W.; Amitai, Y. Generation of epileptiform discharge by local circuits of neocortex. In Epilepsy: Models, Mechanisms, and Concepts; Schwartkroin, P.A., Ed.; Cambridge University Press: Cambridge, UK, 1993; pp. 388–423. [Google Scholar]
- Chervin, R.D.; Pierce, P.A.; Connors, B.W. Periodicity and directionality in the propagation of epileptiform discharges across discharges across neocortex. J. Neurophysiol. 1988, 60, 1695–1713. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Chow, C. Existence and stability of standing pulses in neural networks: I. Existence. SIAM J. Appl. Dyn. Syst. 2005, 4, 217–248. [Google Scholar] [CrossRef]
- Pfurscheller, G.; Graimann, B.; Huggins, J.E.; Levine, S.P.; Schuh, L.A. Spatiotemporal patterns of beta desynchronization and gamma synchronization in cotricographic data during self-paced movement. Clin. Neurophysiol. 2003, 114, 1226–1236. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Neuper, C.; Brunner, C.; da Silva, F.L. Beta rebound after different types of motor imagery in man. Neurosci. Lett. 2005, 378, 156–159. [Google Scholar] [CrossRef]
- Sandstede, B. Evans functions and nonlinear stability of travelling waves in neuronal network models. Int. J. Bifurc. Chaos 2007, 17, 2693–2704. [Google Scholar] [CrossRef]
- Amari, S. Dynamics of Pattern Formation in Lateral-Inhibition Type Neural Fields. Biol. Cybern. 1977, 27, 77–87. [Google Scholar] [CrossRef]
- Ermentrout, G.B.; McLeod, B.J. Existence and uniqueness of traveling waves for a neural network. Proc. R. Soc. Edinb. Sect. A Math. 1993, 123A, 461–478. [Google Scholar] [CrossRef]
- Zhang, L. On stability of traveling wave solutions in synaptically coupled neuronal networks. Differ. Integral Equ. 2003, 16, 513–536. [Google Scholar] [CrossRef]
- Guo, Y. Existence and Stability of Traveling Fronts in a Lateral Inhibition Neural Network. SIAM J. Appl. Dyn. Syst. 2012, 11, 1543–1582. [Google Scholar] [CrossRef]
- Coombes, S.; Owen, M.R. Evans functions for integral neural field equations with Heaviside firing rate function. SIAM J. Appl. Dyn. Syst. 2004, 3, 574–600. [Google Scholar] [CrossRef]
- Coombes, S.; Schmidt, H.; Bojak, I. Interface dynamics in planar neural field models. J. Math. Neurosci. 2012, 2, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Coombes, S.; Thul, R.; Laing, C. Neural Field Models with Threshold Noise. J. Math. Neurosci. 2016, 6, 3. [Google Scholar]
- Coombes, S.; Avitabile, D.; Gokce, A. The Dynamics of Neural Fields on Bounded Domains: An Interface Approach for Dirichlet Boundary Conditions. J. Math. Neurosci. 2017, 7, 12. [Google Scholar]
- Cook, B.; Peterson, A.; Woldman, W.; Terry, J. Neural Field Models: A mathematical overview and unifying framework. Math Neuro. Appl. 2022, 2, 1–67. [Google Scholar] [CrossRef]
- Qin, Z.; Fu, Q.; Jin, D.; Peng, J. A Looming Perception Model Based on Dynamic Neural Field. 2022. Available online: https://ssrn.com/abstract=4248213 (accessed on 28 January 2023).
- González-Ramírez, L.R. On the existence of traveling fronts in the fractional-order Amari neural field model. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106790. [Google Scholar] [CrossRef]
- Laing, C.R.; Troy, w.C.; Gutkin, B.; Ermentrout, G.B. Multiple Bumps in a Neuronal Model of Working Memory. SIAM J. Appl. Math. 2002, 63, 62–97. [Google Scholar] [CrossRef]
- Laing, C.R.; Troy, W.C. Two-bump Solutions of Amari-type Models of Neuronal Pattern Formation. Phys. D Nonlinear Phenom. 2003, 178, 190–218. [Google Scholar] [CrossRef]
- Janson, S. Resultant and Discriminant of Polynomials. 2010. Available online: http://www2.math.uu.se/~svante/papers/sjN5 (accessed on 19 March 2020).
- Evans, J.W. Nerve axon equations, I: Linear approximations. Indiana Univ. Math. J. 1972, 21, 877–955. [Google Scholar] [CrossRef]
- Evans, J.W. Nerve axon equations, II: Stability at rest. Indiana Univ. Math. J. 1972, 22, 75–90. [Google Scholar] [CrossRef]
- Evans, J.W. Nerve axon equations, III: Stability of the nerve impulse. Indiana Univ. Math. J. 1972, 22, 577–594. [Google Scholar] [CrossRef]
- Evans, J.W. Nerve axon equations, IV: The stable and unstable impulse. Indiana Univ. Math. J. 1975, 24, 1169–1190. [Google Scholar] [CrossRef]
- Zhang, L. Existence, uniqueness and exponential stability of traveling wave solutions of some integral differential equations arising from neuronal networks. J. Differ. Equ. 2004, 197, 162–196. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macaluso, D.; Guo, Y. Stability of Traveling Fronts in a Neural Field Model. Mathematics 2023, 11, 2202. https://doi.org/10.3390/math11092202
Macaluso D, Guo Y. Stability of Traveling Fronts in a Neural Field Model. Mathematics. 2023; 11(9):2202. https://doi.org/10.3390/math11092202
Chicago/Turabian StyleMacaluso, Dominick, and Yixin Guo. 2023. "Stability of Traveling Fronts in a Neural Field Model" Mathematics 11, no. 9: 2202. https://doi.org/10.3390/math11092202
APA StyleMacaluso, D., & Guo, Y. (2023). Stability of Traveling Fronts in a Neural Field Model. Mathematics, 11(9), 2202. https://doi.org/10.3390/math11092202





