Logarithmic Coefficients Inequality for the Family of Functions Convex in One Direction ^†

Abstract

The logarithmic coefficients play an important role for different estimates in the theory of univalent functions. Due to the significance of the recent studies about the logarithmic coefficients, the problem of obtaining the sharp bounds for the modulus of these coefficients has received attention. In this research, we obtain sharp bounds of the inequality involving the logarithmic coefficients for the functions of the well-known class $\mathcal{G}$ and investigate a majorization problem for the functions belonging to this family. To prove our main results, we use the Briot–Bouquet differential subordination obtained by J.A. Antonino and S.S. Miller and the result of T.J. Suffridge connected to the Alexander integral. Combining these results, we give sharp inequalities for two types of sums involving the modules of the logarithmical coefficients of the functions of the class $\mathcal{G}$ indicating also the extremal function. In addition, we prove an inequality for the modulus of the derivative of two majorized functions of the class $\mathcal{G}$, followed by an application.

1. Introduction

Let $\mathbb{D}:=\left\{\zeta \in \mathbb{C}:\left|\zeta \right|<1\right\}$ denote the open unit disk of the complex plane $\mathbb{C}$ and let $\mathcal{A}$ be the family of functions f analytic in $\mathbb{D}$ of the form

$$f\left(\zeta \right)=\zeta +\sum _{n=2}^{\infty }{a}_n{\zeta }^n,\zeta \in \mathbb{D}.$$

(1)

Further, let $\mathcal{S}$ be the subclass of $\mathcal{A}$ consisting of all univalent functions in $\mathbb{D}$. Then, the logarithmic coefficients ${\gamma }_n:={\gamma }_n\left(f\right)$ of the function $f\in \mathcal{S}$ are defined with the aid of the following series expansion

$$log{\displaystyle \frac{f\left(\zeta \right)}{\zeta }}=2\sum _{n=1}^{\infty }{\gamma }_n\left(f\right){\zeta }^n,\zeta \in \mathbb{D}.$$

(2)

These coefficients play an important role for various estimates in the theory of univalent functions, and note that we use ${\gamma }_n$ instead of ${\gamma }_n\left(f\right)$. Kayumov [1] solved Brennan’s conjecture for conformal mappings with the help of studying the logarithmic coefficients. The significance of the logarithmic coefficients follows from Lebedev–Milin inequalities ([2], Chapter 2) where estimates of the logarithmic coefficients were applied to obtain bounds on the coefficients of f. Milin [2] conjectured the inequality

$$\sum _{m=1}^n\sum _{k=1}^m\left(k|{\gamma }_k{|}^2-\frac{1}{k}\right)\le 0(n=1,2,3,\cdots )$$

that implies Robertson’s conjecture [3] and hence Bieberbach’s conjecture [4], which is the well-known coefficient problem of the univalent function theory. De Branges [5] proved the Bieberbach’s conjecture by establishing Milin’s conjecture. In [6], the authors determined bounds on the difference of the modules of successive coefficients for some classes defined by subordination and using the logarithmic coefficients. In addition, as the application of the developed methods with the logarithmic asymptotics [7], the connection of the created theory with the entire functions theory [8] would be interesting for readers (see also [9]).

The rotation of the Koebe function $k\left(z\right)=z{(1-e^{i\theta })}^{-2}$ for each real $\theta$ has the logarithmic coefficients ${\gamma }_n=e^{i\theta n}/n$, $n\ge 1$. If $f\in \mathcal{S}$, then by using the Bieberbach inequality and the Fekete–Szegö inequality (see [10], Theorem 3.8), we have

$$|{\gamma }_1|\le 1,|{\gamma }_2|={\displaystyle \frac{1}{2}}\left|a_3-{\displaystyle \frac{1}{2}}{a}_2^2\right|\le {\displaystyle \frac{1}{2}}\left(1+2e^{-2}\right)=0.635\cdots ,$$

respectively. It was proved in Theorem 4 in [11] that the logarithmic coefficients ${\gamma }_n$ of every function $f\in \mathcal{S}$ satisfy the inequality ${\displaystyle \sum _{n=1}^{\infty }}{\left|{\gamma }_n\right|}^2\le {\displaystyle \frac{{\pi }^2}{6}},$ and the equality is obtained for the Koebe function. For class starlike functions, the relation $|{\gamma }_n|\le 1/n$ holds but is not true for the full class $\mathcal{S}$, even in the order of magnitude (see [10], Theorem 8.4). However, the problem of the best upper bounds for the logarithmic coefficients of univalent functions for $n\ge 3$ is still a concern.

A function $f\in \mathcal{A}$ is said to be convex, if it satisfies the inequality

$$Re\left(1+\frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}\right)>0,\zeta \in \mathbb{D}.$$

We denote the class which consists of all convex functions by $\mathcal{C}$ (for example, see [12,13]).

For $\gamma \in (0,1]$, the authors [14] defined the family $\mathcal{G}\left(\gamma \right)$ consisting of all $f\in \mathcal{A}$ satisfying the inequality

$$Re\left(1+{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right)<1+\frac{\gamma }{2},\zeta \in \mathbb{D}.$$

They reported that $\mathcal{G}\left(\gamma \right)$ is a subfamily of ${\mathcal{S}}^{*}$ of the starlike functions. Ozaki in [15] studied the class $\mathcal{G}:=\mathcal{G}\left(1\right)$ and proved that functions in $\mathcal{G}$ are univalent in the unit disk $\mathbb{D}$. An extension of $\mathcal{G}\left(\gamma \right)$ and some geometric properties of $\mathcal{G}$-like convex in one direction, close-to-convex, and starlike were reported (see, for example, [16] and the references cited therein). In [17], the researchers obtained the bounds of the logarithmic coefficients for particular subfamilies of univalent functions and found the sharp upper bound for ${\gamma }_n$ when $n=1,2,3$ if f belongs to the family $\mathcal{G}\left(\gamma \right)$ (see also [18]). Logarithmic coefficients problem was also considered for the another well-known classes, for example see [12,19,20,21,22,23,24,25].

We recall that if f and F are two analytic functions in $\mathbb{D}$, the function f is subordinate to F, written $f\left(\zeta \right)\prec F\left(\zeta \right)$, if there exists an analytic function $\omega$ in $\mathbb{D}$ with $\omega \left(0\right)=0$ and $\left|\omega \right(\zeta \left)\right|<1$, such that $f\left(\zeta \right)=F\left(\omega \left(\zeta \right)\right)$ for all $\zeta \in \mathbb{D}$. The function $\omega$ that satisfies this property is called a subordination function (see [26], p. 125). It is well-known that if F is univalent in $\mathbb{D}$, then $f\left(\zeta \right)\prec F\left(\zeta \right)$ if and only if $f\left(0\right)=F\left(0\right)$ and $f\left(\mathbb{D}\right)\subset F\left(\mathbb{D}\right)$ (see [27], p. 15).

It is well-known that if k and h are analytic functions in $\mathbb{D}$, we say that k is majorized by h in $\mathbb{D}$ (see [28]), written $k\left(\zeta \right)\ll h\left(\zeta \right)$, if there exists a function $\mu$ analytic in $\mathbb{D}$, such that $\left|\mu \right(\zeta \left)\right|<1$ and $k\left(\zeta \right)=\mu \left(\zeta \right)h\left(\zeta \right)$, for all $\zeta \in \mathbb{D}$.

In the current study, using the recent results from Antonino and Miller [26] for the Briot–Bouquet differential subordination, we give sharp inequalities for two types of sums involving the modules of the logarithmical coefficients of the functions of the class $\mathcal{G}$ and indicating the extremal function. In addition, we prove an inequality for the modulus of the derivative of two majorized functions of this class, followed by a particular case.

2. Main Results

We will prove our first main result by applying the next lemmas.

Lemma 1

([10], Theorem 6.2, p. 192). Let $f\left(\zeta \right)={\displaystyle \sum _{n=1}^{\infty }}{a}_n{\zeta }^n$ and $g\left(\zeta \right)={\displaystyle \sum _{n=1}^{\infty }}{b}_n{\zeta }^n$ be analytic in $\mathbb{D}$, and suppose that $f\left(\zeta \right)\prec g\left(\zeta \right)$ where g is univalent in $\mathbb{D}$. Then,

$$\sum _{k=1}^n|a_k{|}^2\le \sum _{k=1}^n|b_k{|}^2,n\in \mathbb{N}.$$

The next lemma deals to the well-known Briot–Bouquet differential equation and differential subordination:

Lemma 2

([26], Theorem 9, p. 135). Let $h_{*}$ and $q_{*}$ be given by

$$h_{*}\left(\zeta \right)=\frac{1+(2\eta -1)\zeta }{1-\zeta }\mathit{and}{q}_{*}\left(\zeta \right)=\frac{(2\eta -1)\zeta }{(1-\zeta )-{(1-\zeta )}^{2\eta }}.$$

(3)

If χ is an analytic function in $\mathbb{D}$ with $\chi \left(0\right)=1$, and ω is a subordination function such that

$$\chi \left(\zeta \right)+{\displaystyle \frac{\zeta {\chi }^{\prime }\left(\zeta \right)}{\chi \left(\zeta \right)}}=h_{*}\left(\omega \left(\zeta \right)\right),\zeta \in \mathbb{D},$$

then the differential equation

$${\phi }^{\prime }\left(\zeta \right)=\frac{\phi \left\{1-\omega +2\eta (\omega -\phi )-\left[(2\eta -1)\omega +1\right]{(1-\phi )}^{2\eta }\right\}}{\zeta (1-\omega )\left\{1-\left[(2\eta -1)\phi +1\right]{(1-\phi )}^{2\eta -1}\right\}},$$

(4)

with $\phi \left(0\right)=0$, has a solution φ analytic in $\mathbb{D}$ such that $\chi \left(\zeta \right)=q_{*}\left(\phi \left(\zeta \right)\right)$. Furthermore, if

(i)

φ is also a subordination function,

or

(ii)

φ is a non-extendable solution in ${\mathbb{D}}_r:=\left\{\zeta \in \mathbb{C}:\left|\zeta \right|<r\right\}$, $0<r\le 1$, that satisfies

$$\ell \equiv \frac{{\zeta }_0{\phi }^{\prime }\left({\zeta }_0\right)}{\phi \left({\zeta }_0\right)}\notin (1,+\infty ),$$

where $\left|\phi \right({\zeta }_0\left)\right|$ is a maximum of $\left|\phi \right(\zeta \left)\right|$ on $\partial {\mathbb{D}}_r$,

then, $\chi \left(\zeta \right)\prec q_{*}\left(\zeta \right)$. In these cases, we have the sharp result

$$\chi \left(\zeta \right)+{\displaystyle \frac{\zeta {\chi }^{\prime }\left(\zeta \right)}{\chi \left(\zeta \right)}}\prec h_{*}\left(\zeta \right)\Rightarrow \chi \left(\zeta \right)\prec q_{*}\left(\zeta \right).$$

Using the notations of Theorem 3.1d of [27] (see also [29]), this theorem can be formulated for the special case $a=0$ and $n=1$, with $F\left(\zeta \right):=\zeta p^{\prime }\left(\zeta \right)$, as follows:

Lemma 3.

Let h be starlike in $\mathbb{D}$, with $h\left(0\right)=0$. If F is analytic in $\mathbb{D}$, with $F\left(0\right)=0$, and satisfies

$$F\left(\zeta \right)\prec h\left(\zeta \right),$$

then,

$${\int }_0^{\zeta }\frac{F\left(t\right)}{t}\mathrm{d}t\prec {\int }_0^{\zeta }\frac{h\left(t\right)}{t}\mathrm{d}t=:q\left(\zeta \right).$$

Moreover, the function q is convex and is the best dominant.

In the next result, we prove the inequalities involving the modules of the logarithmic coefficients for functions of the family $\mathcal{G}$.

Theorem 1.

Let the function $f\in \mathcal{G}$, let ω be the subordination function such that

$$1+{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}={\displaystyle \frac{1-2\omega \left(\zeta \right)}{1-\omega \left(\zeta \right)}},\zeta \in \mathbb{D}$$

(5)

and let φ the analytic solution in $\mathbb{D}$ of the differential equation

$${\phi }^{\prime }\left(\zeta \right)=\frac{\phi \left[1-\omega -(\omega -\phi )-\left(-2\omega +1\right){(1-\phi )}^{-1}\right]}{\zeta (1-\omega )\left[1-\left(-2\phi +1\right){(1-\phi )}^{-2}\right]},$$

(6)

with $\phi \left(0\right)=0$. Furthermore, if φ satisfies one of the conditions $\left(i\right)$ or $\left(ii\right)$ of Lemma 2, then, the logarithmic coefficients of the function f fulfill the inequalities

$$\sum _{n=1}^{\infty }{\left|{\gamma }_n\right|}^2\le \sum _{n=1}^{\infty }\frac{1}{n^2{4}^{n+1}}$$

(7)

and

$$\sum _{n=1}^{\infty }{n}^2{\left|{\gamma }_n\right|}^2\le \frac{1}{12}.$$

(8)

The equalities in these relations are attained for the function $f_0\left(\zeta \right)=\zeta -{\zeta }^2/2$.

Proof. 

Suppose $f\left(\zeta \right)=\zeta +{\displaystyle \sum _{n=2}^{\infty }}{a}_n{\zeta }^n\in \mathcal{G}$, and let $\omega$ the subordination function considered by (5). If we define the function $p\left(\zeta \right):=\zeta f^{\prime }\left(\zeta \right)/f\left(\zeta \right)$ with $\zeta \in \mathbb{D}$, then (5) is equivalent to

$$p\left(\zeta \right)+{\displaystyle \frac{\zeta p^{\prime }\left(\zeta \right)}{p\left(\zeta \right)}}=h\left(\omega \left(\zeta \right)\right),\zeta \in \mathbb{D}$$

where the function $h\left(\zeta \right):=(1-2\zeta )/(1-\zeta )$ is obtained from $h_{*}$ defined by (3) for $\eta =-1/2$.

On the other the hand, the function $q\left(\zeta \right)={\displaystyle \frac{2(1-\zeta )}{2-\zeta }}$ obtained from $q_{*}$ given by (3) for $\eta =-1/2$ is an analytic solution in $\mathbb{D}$ of the differential equation

$$q\left(\zeta \right)+{\displaystyle \frac{\zeta q^{\prime }\left(\zeta \right)}{q\left(\zeta \right)}}={\displaystyle \frac{1-2\zeta }{1-\zeta }}.$$

Now, we will prove that

$$\frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}=p\left(\zeta \right)\prec q\left(\zeta \right).$$

For $\eta =-1/2$, the differential Equation (4) will have the form (6) of the assumption of our theorem, and we easily see that for $\eta =-1/2$ all the assumptions of Lemma 2 are satisfied. Since we assumed that $\phi$ satisfies one of the conditions (i) or (ii) of Lemma 2, from this lemma it follows that $p\left(\zeta \right)\prec q\left(\zeta \right)$, and we have the sharp result

$$p\left(\zeta \right)+\frac{\zeta p^{\prime }\left(\zeta \right)}{p\left(\zeta \right)}\prec h\left(\zeta \right)\Rightarrow p\left(\zeta \right)\prec q\left(\zeta \right).$$

Therefore, we obtained the sharp subordination

$${\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\prec \frac{2(1-\zeta )}{2-\zeta }={\displaystyle \frac{\zeta f_0^{\prime }\left(\zeta \right)}{f_0\left(\zeta \right)}}=:q\left(\zeta \right)=1-\sum _{n=1}^{\infty }\frac{1}{2^n}{\zeta }^n.$$

(9)

If we define the function $H\left(\zeta \right):={\displaystyle \frac{f\left(\zeta \right)}{\zeta }}$ which is an analytic function in $\mathbb{D}$ with $H\left(0\right)=1$, using (9), it fulfills the equivalent subordination

$${\displaystyle \frac{\zeta H^{\prime }\left(\zeta \right)}{H\left(\zeta \right)}}={\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}-1\prec q\left(\zeta \right)-1=:\tilde{\omega }\left(\zeta \right).$$

We have $\tilde{\omega }\left(0\right)=0$, ${\tilde{\omega }}^{\prime }\left(0\right)\ne 0$, and

$$Re\frac{\zeta {\tilde{\omega }}^{\prime }\left(\zeta \right)}{\tilde{\omega }\left(\zeta \right)}=Re{\displaystyle \frac{\zeta q^{\prime }\left(\zeta \right)}{q\left(\zeta \right)-1}}=Re{\displaystyle \frac{2}{2-\zeta }}>\frac{2}{3}>0,\zeta \in \mathbb{D},$$

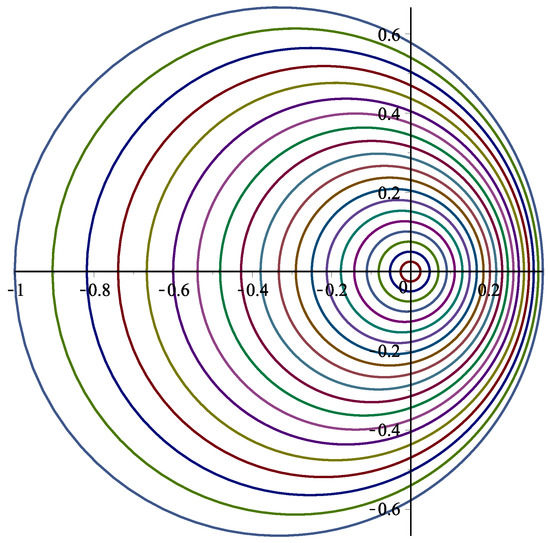
hence $\tilde{\omega }$ is a starlike univalent function in $\mathbb{D}$ (Figure 1).

Figure 1. The image of $\tilde{\omega }\left(\mathbb{D}\right)$.

Now, let us set in Lemma 3 the functions

$$F\left(\zeta \right):={\displaystyle \frac{\zeta H^{\prime }\left(\zeta \right)}{H\left(\zeta \right)}},h\left(\zeta \right):=\tilde{\omega }\left(\zeta \right).$$

Since $\tilde{\omega }$ is starlike in $\mathbb{D}$ with $\tilde{\omega }\left(0\right)=0$ and $F\left(0\right)=0$ (because $H\left(0\right)=1$), we only need to prove that F is analytic in $\mathbb{D}$. Since the function $f\in \mathcal{G}\subset \mathcal{S}$ which implies that $f\left(\zeta \right)\ne 0$ for $\zeta \in \mathbb{D}\setminus \left\{0\right\}$ and ${\zeta }_0=0$ is a simple zero for f. Hence, $H\left(\zeta \right)={\displaystyle \frac{f\left(\zeta \right)}{\zeta }}\ne 0$ for all $\zeta \in \mathbb{D}$, consequently F is analytic in $\mathbb{D}$. Thus, all the assumptions of Lemma 3 hold and using this lemma we obtain that

$${\int }_0^{\zeta }{\displaystyle \frac{H^{\prime }\left(t\right)}{H\left(t\right)}}\mathrm{d}t\prec {\int }_0^{\zeta }{\displaystyle \frac{\tilde{\omega }\left(t\right)}{t}}\mathrm{d}t$$

and so

$$logH\left(\zeta \right)-logH\left(0\right)\prec {\int }_0^{\zeta }{\displaystyle \frac{\tilde{\omega }\left(t\right)}{t}}\mathrm{d}t,$$

that is

$$log{\displaystyle \frac{f\left(\zeta \right)}{\zeta }}\prec {\int }_0^{\zeta }{\displaystyle \frac{\tilde{\omega }\left(t\right)}{t}}\mathrm{d}t.$$

Moreover, it is well-known that if $\tilde{\omega }$ is starlike (univalent) in $\mathbb{D}$, then ${\displaystyle {\int }_0^{\zeta }{\displaystyle \frac{\tilde{\omega }\left(t\right)}{t}}\mathrm{d}t}$ is convex (univalent) in $\mathbb{D}$, and conversely. Denoting with ${\gamma }_n$ the logarithmic coefficients of f given by (2), the previous subordination could be written as

$$\sum _{n=1}^{\infty }2{\gamma }_n{\zeta }^n\prec \sum _{n=1}^{\infty }\frac{1}{n{2}^n}{\zeta }^n.$$

(10)

Since the function ${\displaystyle {\int }_0^{\zeta }{\displaystyle \frac{\tilde{\omega }\left(t\right)}{t}}\mathrm{d}t}$ is univalent in $\mathbb{D}$, by using Lemma 1 the relation (10) implies

$$\sum _{n=1}^{k}4{\left|{\gamma }_n\right|}^2\le \sum _{n=1}^k\frac{1}{n^2{2}^{2n}}\le \sum _{n=1}^{\infty }\frac{1}{n^2{2}^{2n}},k\in \mathbb{N},$$

and taking $k\to \infty$ we conclude that

$$\sum _{n=1}^{\infty }{\left|{\gamma }_n\right|}^2\le {\displaystyle \frac{1}{4}}\sum _{n=1}^{\infty }\frac{1}{n^2{2}^{2n}}.$$

Thus, the required inequality (7) is proved.

To prove our theorem’s second relation, from (2) and (9) we conclude

$$\sum _{n=1}^{\infty }2n{\gamma }_n{\zeta }^n=\zeta {\displaystyle \frac{\mathrm{d}}{\mathrm{d}\zeta }}\left(log{\displaystyle \frac{f\left(\zeta \right)}{\zeta }}\right)={\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}-1\prec q\left(\zeta \right)-1=\tilde{\omega }\left(\zeta \right).$$

According to Lemma 1 this subordination leads to

$$\sum _{n=1}^{k}4n^2{\left|{\gamma }_n\right|}^2\le \sum _{n=1}^k\frac{1}{2^{2n}}\le \sum _{n=1}^{\infty }\frac{1}{2^{2n}},k\in \mathbb{N},$$

and letting $k\to +\infty$ the assertion (8) is proved.

Finally, it is sufficient to consider the equality

$${\displaystyle \frac{\zeta f_0^{\prime }\left(\zeta \right)}{f_0\left(\zeta \right)}}=\frac{2(1-\zeta )}{2-\zeta }$$

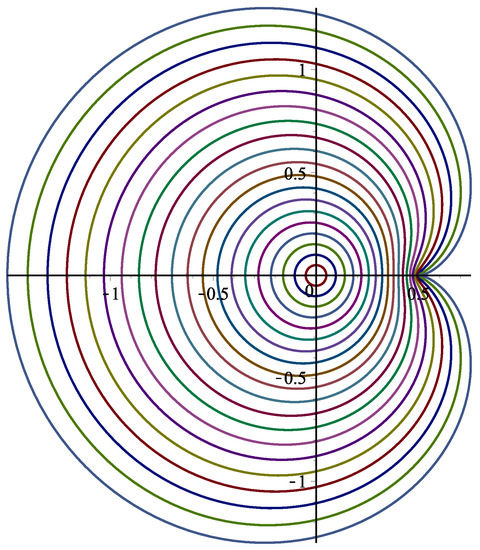
to prove the sharpness of these bounds. In fact, the above relation concludes that $f_0\left(\zeta \right)=\zeta -{\zeta }^2/2$. Using the definition of the class $\mathcal{G}$, a simple computation shows that $f_0\in \mathcal{G}$ (see $f_0\left(\mathbb{D}\right)$ in Figure 2) and

$$\frac{1}{2}log\frac{f_0\left(\zeta \right)}{\zeta }=\sum _{k=1}^{\infty }-\frac{1}{k{2}^{k+1}}{\zeta }^k,\zeta \in \mathbb{D}.$$

Hence, ${\gamma }_n=-{\displaystyle \frac{1}{n{2}^{n+1}}}$, $n\in \mathbb{N}$ and thus

$$|{\gamma }_n{|}^2={\displaystyle \frac{1}{n^2{4}^{n+1}}},n\in \mathbb{N},$$

therefore, we have

$$\sum _{n=1}^{\infty }{\left|{\gamma }_n\right|}^2=\sum _{n=1}^{\infty }\frac{1}{n^2{4}^{n+1}}.$$

Figure 2. The image of $f_0\left(\mathbb{D}\right)$.

Similarly, we obtain

$$n^2{\left|{\gamma }_n\right|}^2={\displaystyle \frac{1}{4^{n+1}}},n\in \mathbb{N},$$

hence

$$\sum _{n=1}^{\infty }{n}^2{\left|{\gamma }_n\right|}^2=\sum _{n=1}^{\infty }{\displaystyle \frac{1}{4^{n+1}}}=\frac{1}{12}.$$

□

The next corollary present the solution of a majorization problem for the family $\mathcal{G}$.

Corollary 1.

Let $h\in \mathcal{A}$ and $f\in \mathcal{G}$, such that h is majorized by f in $\mathbb{D}$. If we suppose that φ, the analytic solution in $\mathbb{D}$ of the differential Equation (6) with $\phi \left(0\right)=0$, satisfies either condition $\left(i\right)$ or $\left(ii\right)$ of Lemma 2, then $|h^{\prime }\left(\zeta \right)|\le |f^{\prime }\left(\zeta \right)|$ for $\left|\zeta \right|\le r_{*}=0.3472963553\cdots$, where $r_{*}$ is the smallest positive root of the equation

$$r^3-3r+1=0.$$

(11)

Proof. 

If $f\left(\zeta \right)=\zeta +{\displaystyle \sum _{n=2}^{\infty }}{a}_n{\zeta }^n\in \mathcal{G}$ according to the proof of Theorem 1, namely to (9), we have

$${\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\prec \frac{2(1-\zeta )}{2-\zeta }=q\left(\zeta \right).$$

We have $q^{\prime }\left(0\right)\ne 0$, and

$$1+Re\frac{\zeta q^{″}\left(\zeta \right)}{q^{\prime }\left(\zeta \right)}=Re{\displaystyle \frac{2+\zeta }{2-\zeta }}>0,\zeta \in \mathbb{D},$$

hence q is a convex univalent function in $\mathbb{D}$. Further, since $q\left(\overline{\zeta }\right)=\overline{q\left(\zeta \right)}$ for all $\zeta \in \mathbb{D}$ it follows that $q\left(\mathbb{D}\right)$ is symmetric with respect to the real axis. Thus, combining with the fact that q is convex in $\mathbb{D}$ it follows that

$$min\left\{Req\left(\zeta \right):\left|\zeta \right|\le r\right\}=q(-r)$$

or

$$min\left\{Req\left(\zeta \right):\left|\zeta \right|\le r\right\}=q\left(r\right),r\in (0,1).$$

We have

$$q\left(r\right)<q(-r),r\in (0,1)$$

and therefore,

$$min\left\{Req\left(\zeta \right):\left|\zeta \right|\le r\right\}=q\left(r\right)=\underset{\left|\zeta \right|=r}{min}\left|q\left(\zeta \right)\right|,r\in (0,1).$$

Since $q\left(\zeta \right)\ne 0$ for $\zeta \in \mathbb{D}$, from the principle of the maximum of the module of an analytic function it follows

$$\underset{\left|\zeta \right|=r}{min}\left|q\left(\zeta \right)\right|=\frac{2(1-r)}{2-r},0<r<1$$

and we have $f\in {\mathcal{S}}^{*}\left(q\right)$ with the notations of [30].

From the assumption $h\left(\zeta \right)\ll f\left(\zeta \right)$, by using Lemma 4 of [30] we obtain that $|h^{\prime }\left(\zeta \right)|\le |f^{\prime }\left(\zeta \right)|$ for all $\zeta$ in the disk $\left|\zeta \right|\le r_{*}$, where $r_{*}$ is the smallest positive root of the equation

$$-2r+\frac{2(1-r)}{2-r}\left(1-r^2\right)=0,r\in (0,1)$$

that is equivalent to (11), and this completes our proof. □

Example 1.

If we consider the functions $f_0\left(\zeta \right)=\zeta -{\zeta }^2/2$ and

$$h\left(\zeta \right)=\frac{\zeta -{\zeta }^2/2}{3+\zeta },$$

then h is majorized by $f_0$ by $\mu \left(\zeta \right)={\displaystyle \frac{1}{3+\zeta }}$. Further, if we suppose that φ the analytic solution in $\mathbb{D}$ of the differential Equation (6) with $\phi \left(0\right)=0$ satisfies either condition $\left(i\right)$ or $\left(ii\right)$ of Lemma 2; then from Corollary 1, we have

$$\left|\frac{{\zeta }^2+6\zeta -6}{2{(3+\zeta )}^2}\right|\le |1-\zeta |$$

for $\left|\zeta \right|\le r_{*}$.

3. Conclusions

In this paper, due to the importance of logarithmic coefficients that was stated in Section 1, we find the sharp bounds of the inequality involving the logarithmic coefficients for the functions of the class $\mathcal{G}$. For this purpose, we used the well-known Rogosinski’s Theorem ([10], Theorem 6.2, p. 192), the Suffridge theorem regarding the subordination-preserving property of Alexander integral, combined with the recent results of Antonino and Miller [26] for the Briot–Bouquet differential subordination.

Further, as a consequence of the intermediate results of the proof of out theorem, we proved an inequality for the derivative of two majorized functions of the class $\mathcal{G}$ that holds in an enough small open disk with center in the origin.

As an open problem, we recommended to the readers to give a method for obtaining the conclusion of Theorem 1 without using the additional assumptions of [26] given by (5) and (6). Another interesting open problem is to find the corresponding upper bounds to (7) and (8) for the general class $\mathcal{G}\left(\gamma \right)$ with $\gamma \in (0,1]$.