State Feedback with Integral Control Circuit Design of DC-DC Buck-Boost Converter
Abstract
1. Introduction
- The state-feedback with integral control law is designed based on an ideal small-signal model and tested with a nonlinear power converter model that includes all parasitic components;
- The realization of the proposed control circuit has been introduced using op-amps, resistors, and a capacitor;
- The closed-loop SIMULINK model and the corresponding closed-loop Simscape power converter circuit have been simulated in MATLAB to validate the design approach;
- The transient characteristics, tracking performance, and disturbance rejection capability of the proposed control circuit have been investigated.
2. Mathematical Model of Inverting DC-DC Buck-Boost Converter
2.1. Nonlinear Model
2.2. Linearized State-Space Averaged Model
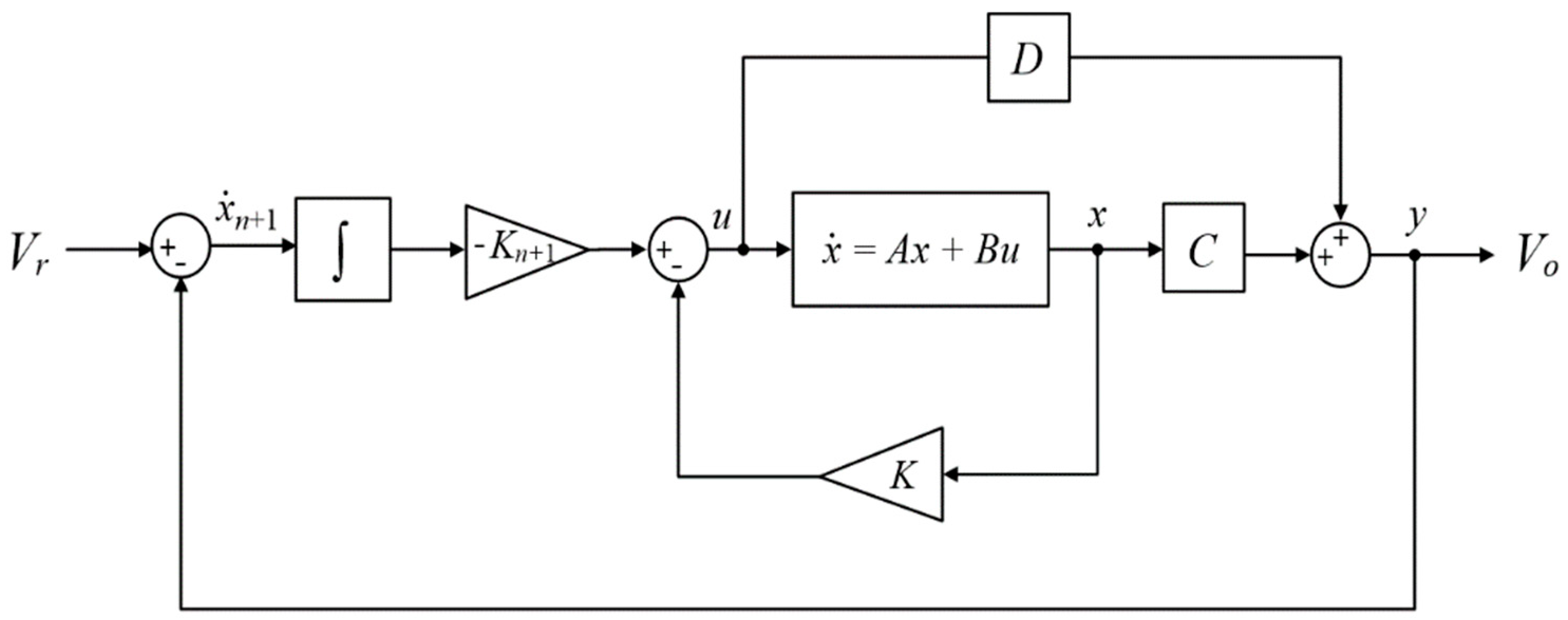
3. State-Feedback with Integral Control Design
3.1. Control Law Design
3.2. Controller Gains Selection
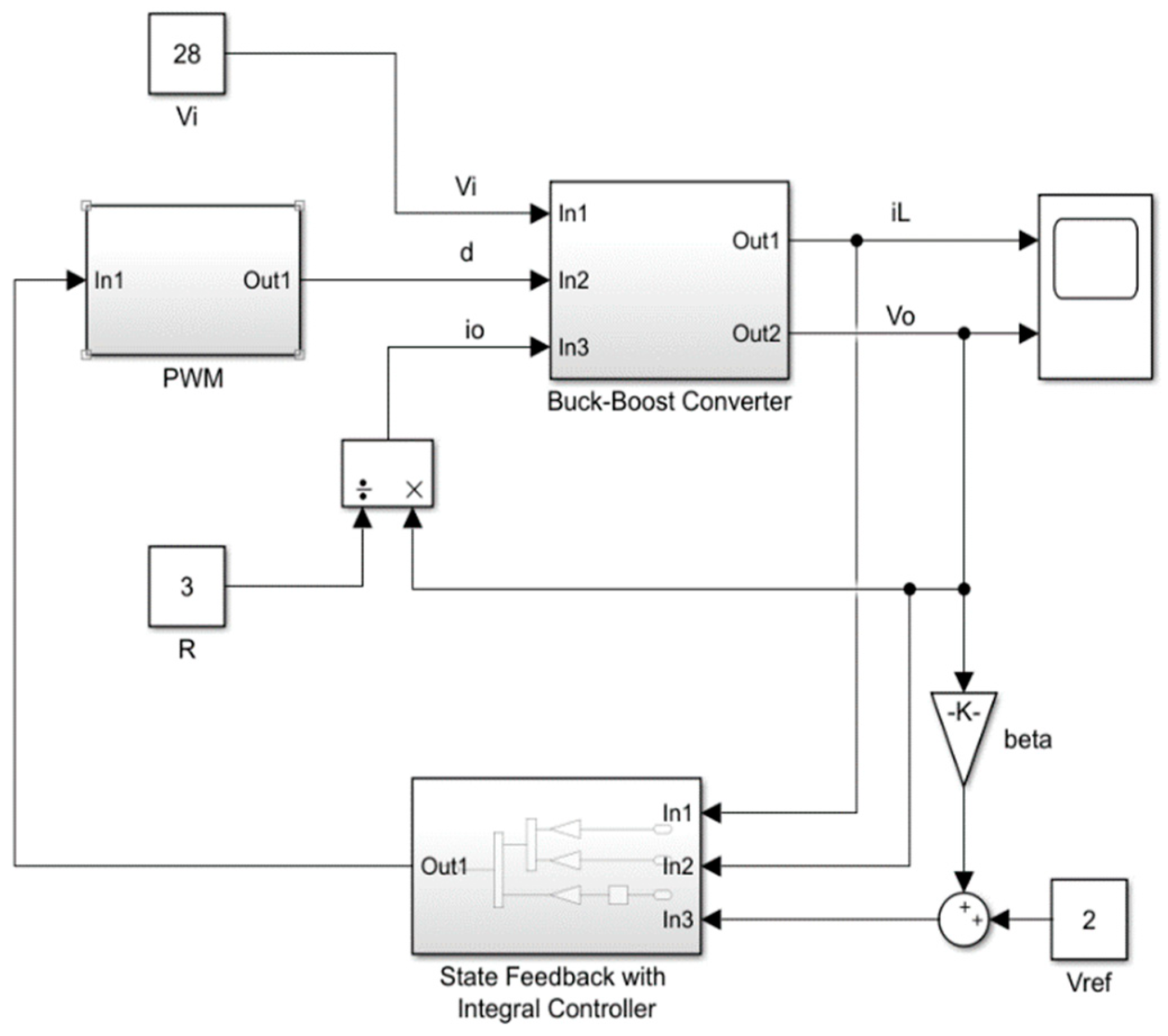
3.3. Structure of Proposed Control System
- Pulse-Width Modulator: The PWM subsystem contains a comparator that compares the state feedback with integral control law with the ramp voltage VT to generate the duty cycle dT that drives the nonlinear power converter model;
- Power Converter: The large-signal non-ideal dc-dc buck-boost converter model is built in MATLAB/SIMULINK using s-function based on the state-space equations given in (1) and (2). The nonlinear model emulates the dc-dc buck-boost converter dynamics;
- State Feedback with Integral Controller: The controller subsystem comprises the state feedback with integral control law given in (10) along with the state feedback controller gains defined in (24).
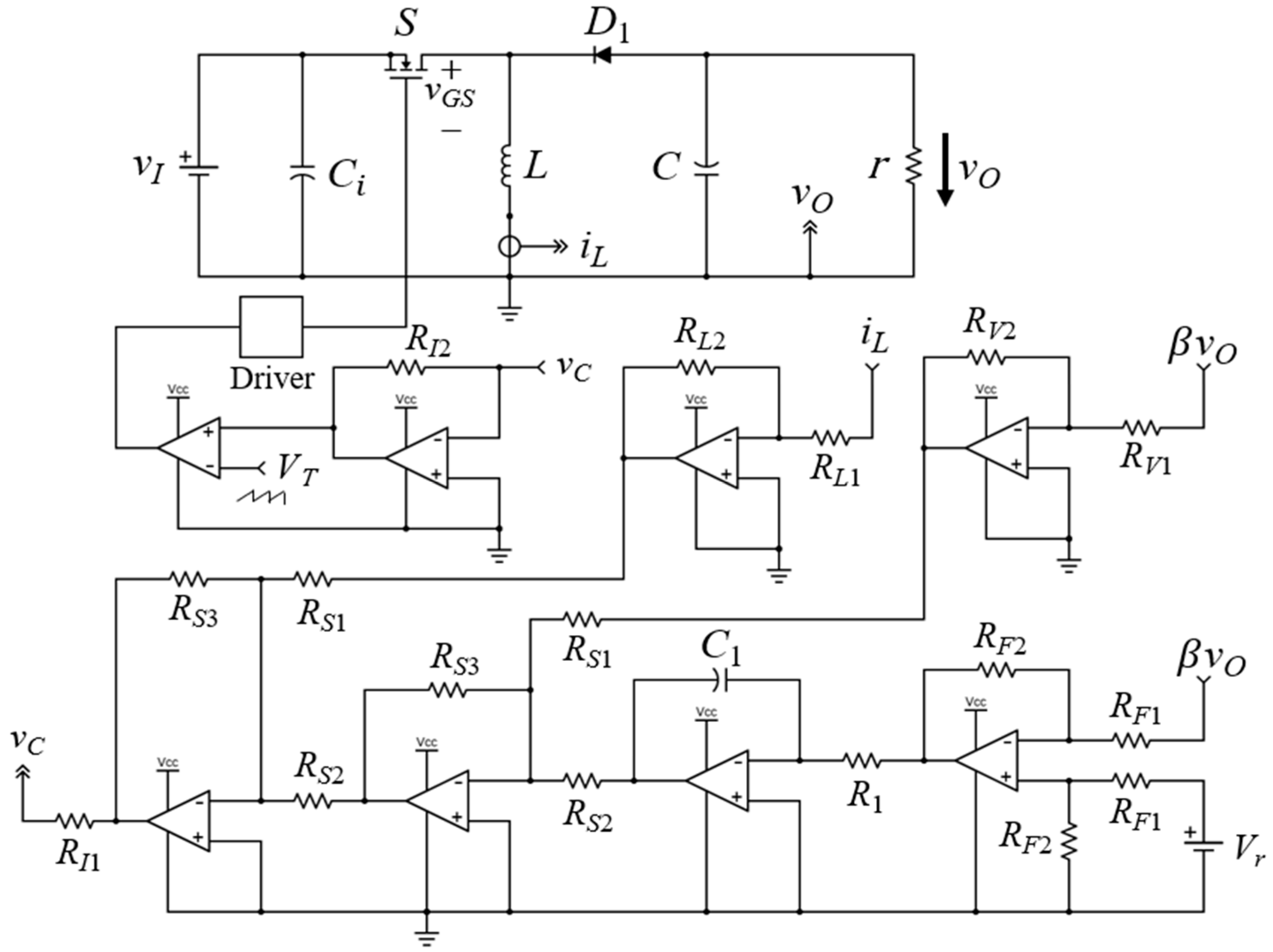
4. Realization of Analog Control Circuit
- Voltage sensor gain : The buck-boost converter is designed to convert 28 V to 12 V. If the reference voltage 2 V, then the feedback network gain is ;
- Summing, inverting, and differential op-amps: The gain of the summing, inverting, and differential op-maps in the control circuit is unity. Thus, the resistors of the summing op-amps , , and , inverting op-amp and , and differential op-amp and are set to 5.1 kΩ;
- Pulse-Width Modulator: The peak ramp voltage is set to 2 V, whereas the switching frequency is 100 kHz.
- Inductor current gain : In the control design section, the gain of the inductor current has been computed as 0.011. Since the gain , the resistor and can be set to 100 kΩ and 1.1 kΩ, respectively;
- Output voltage gain : In the control design section, the gain of the output voltage has been computed as 0.17. Since the gain , the resistor and can be set to 100 kΩ and 17 kΩ, respectively;
- Integral gain : As reported in [26], the integral gain is defined as . In the control design section, the gain has been computed as 600. If the resistor is assumed to be 33 kΩ, then the capacitor is 56 nF;
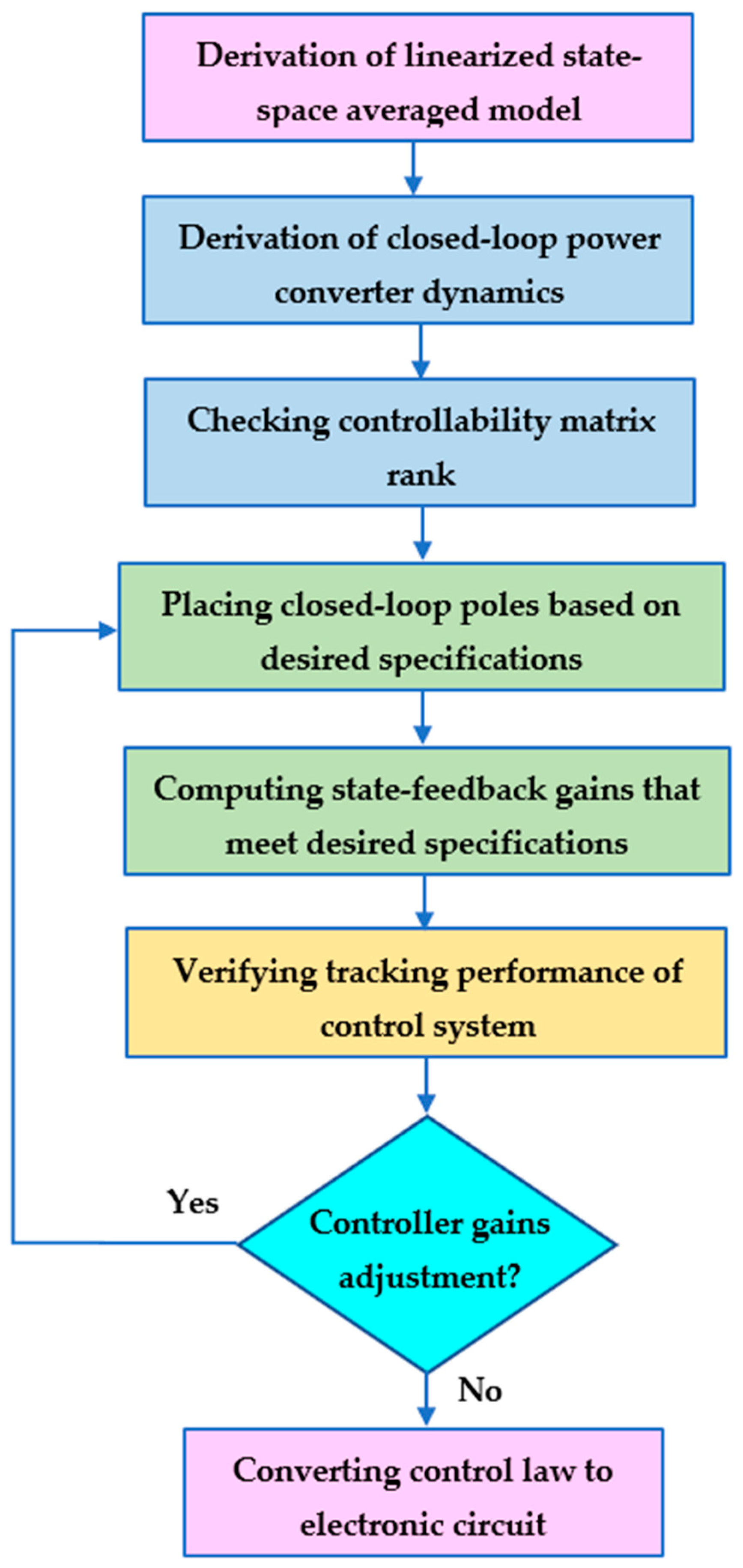
5. Flowchart of State-Feedback with Integral Control Design
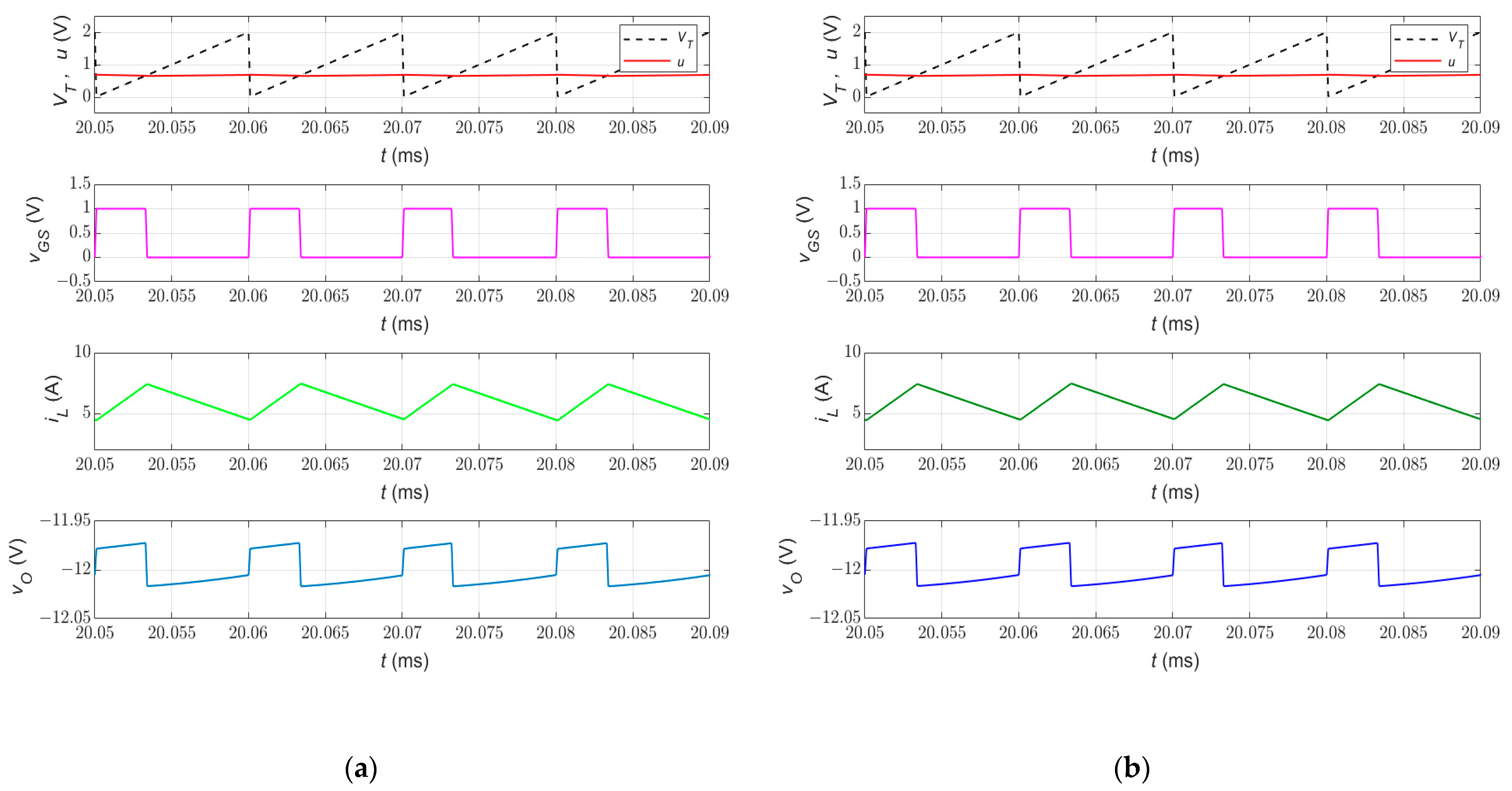
6. Results and Discussion
6.1. Validation of Control Design Approach
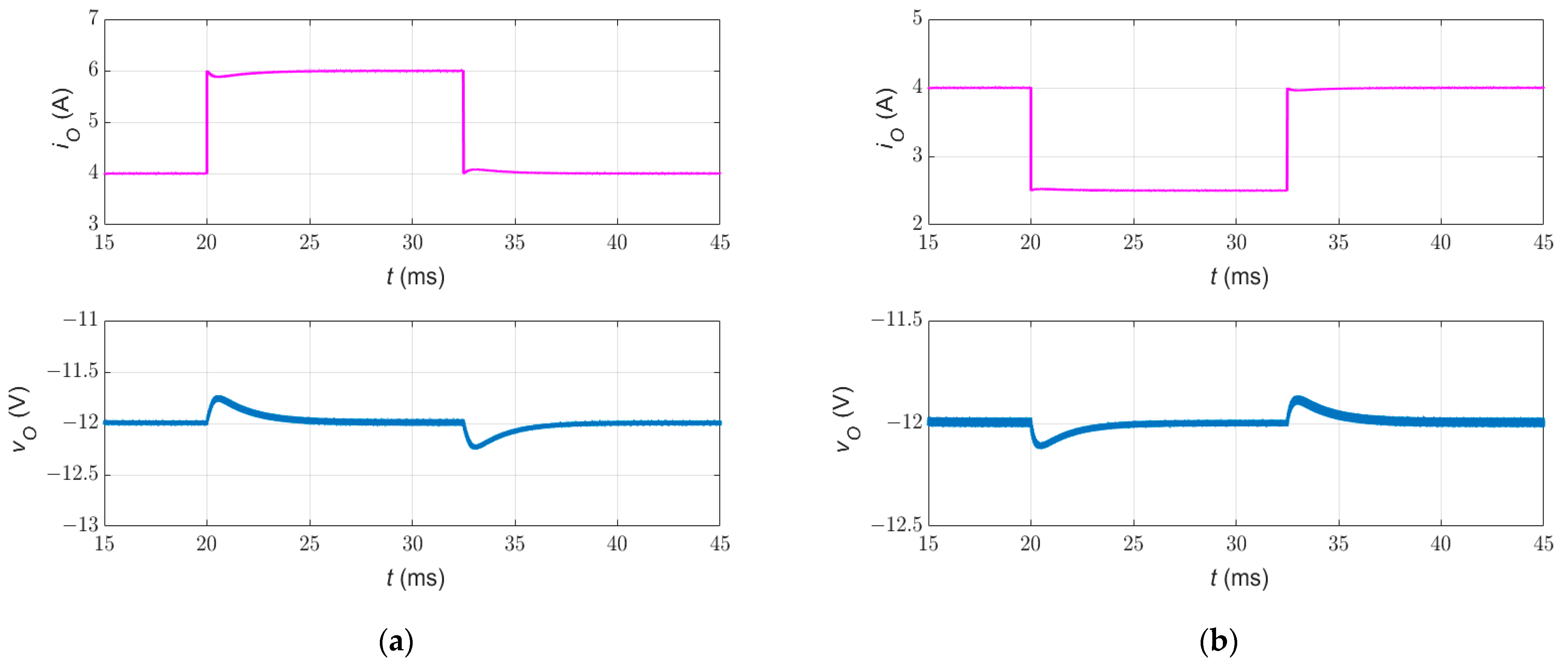
6.2. Rejection of Line and Load Variations
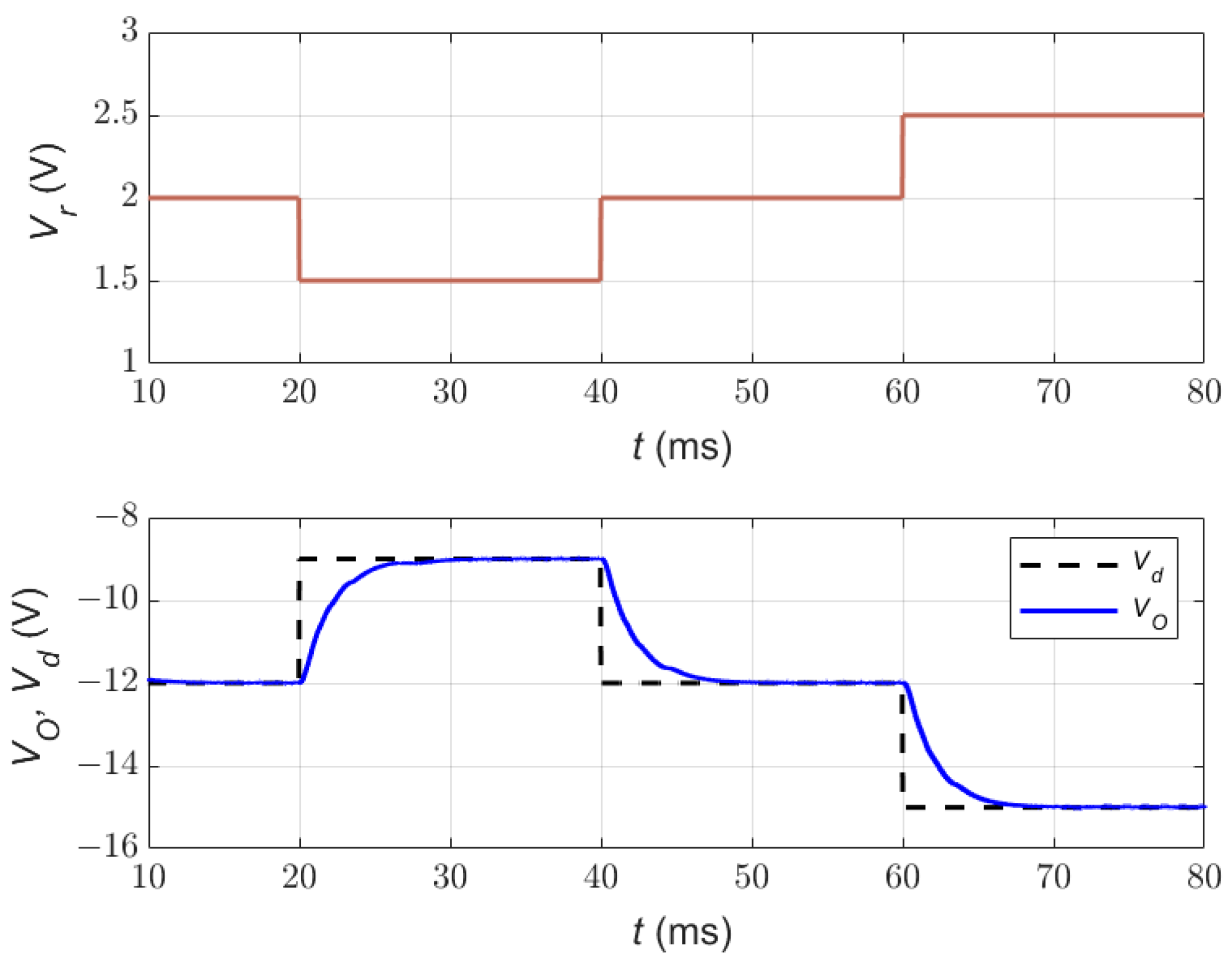
6.3. Tracking of Time-Varying Reference Voltage
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of Acronyms | |
| PWM | pulse-width modulated |
| EV | electric vehicle |
| NIOC | neural inverse optimal control |
| EKF | extended Kalman filter |
| MPC | model predictive control |
| LHP | left-half-plane |
| CPL | constant power load |
| HIL | hardware-in-the-loop |
| CCM | continuous conduction mode |
| MOSFET | metal-oxide-semiconductor field-effect transistor |
| ESR | equivalent series resistance |
| PO | percentage overshoot |
| characteristic polynomial | |
| EMC | electromagnetic compatibility |
| EMI | electromagnetic interference |
| List of Symbols | |
| S | MOSFET |
| D1 | Diode |
| L | Inductor |
| C | Output capacitor |
| Inductor ESR | |
| Capacitor ESR | |
| Diode forward resistance | |
| Diode threshold voltage | |
| MOSFET on-resistance | |
| Large-signal input voltage | |
| Large-signal output voltage | |
| r | Large-signal load resistance |
| Large-signal load current | |
| Large-signal time interval when S is ON | |
| Large-signal time interval when S is OFF | |
| Large-signal inductor current | |
| Large-signal capacitor voltage | |
| Steady-state input voltage | |
| Steady-state output voltage | |
| Steady-state load resistance | |
| Steady-state inductor current | |
| Steady-state time interval when S is ON | |
| Steady-state time interval when S is OFF | |
| Small-signal ac inductor current | |
| Small-signal ac capacitor voltage | |
| Small-signal ac duty cycle | |
| State variables vector | |
| State matrix | |
| Input matrix | |
| Output matrix | |
| Direct transmission matrix | |
| Controllability matrix | |
| u | System input |
| y | System output |
| Desired reference voltage | |
| Constant gains vector | |
| Zeros vector | |
| ts | Settling time |
| Damping ratio | |
| Natural frequency | |
| Desired closed-loop poles vector | |
| Voltage sensor gain | |
| Peak ramp voltage | |
| Switching frequency | |
| Inductor current gain | |
| Output voltage gain | |
| Integral gain | |
References
- Ruz-Hernandez, J.A.; Djilali, L.; Canul, M.A.R.; Boukhnifer, M.; Sanchez, E.N. Neural Inverse Optimal Control of a Regenerative Braking System for Electric Vehicles. Energies 2022, 15, 8975. [Google Scholar] [CrossRef]
- Sankar, R.S.R.; Deepika, K.K.; Alsharef, M.; Alamri, B. A Smart ANN-Based Converter for Efficient Bidirectional Power Flow in Hybrid Electric Vehicles. Electronics 2022, 11, 3564. [Google Scholar] [CrossRef]
- Danyali, S.; Aghaei, O.; Shirkhani, M.; Aazami, R.; Tavoosi, J.; Mohammadzadeh, A.; Mosavi, A. A New Model Predictive Control Method for Buck-Boost Inverter-Based Photovoltaic Systems. Sustainability 2022, 14, 11731. [Google Scholar] [CrossRef]
- Murillo-Yarce, D.; Riffo, S.; Restrepo, C.; González-Castaño, C.; Garcés, A. Model Predictive Control for Stabilization of DC Microgrids in Island Mode Operation. Mathematics 2022, 10, 3384. [Google Scholar] [CrossRef]
- Kahani, R.; Jamil, M.; Iqbal, M.T. Direct Model Reference Adaptive Control of a Boost Converter for Voltage Regulation in Microgrids. Energies 2022, 15, 5080. [Google Scholar] [CrossRef]
- Jiang, Y.; Jin, X.; Wang, H.; Fu, Y.; Ge, W.; Yang, B.; Yu, T. Optimal Nonlinear Adaptive Control for Voltage Source Converters via Memetic Salp Swarm Algorithm: Design and Hardware Implementation. Processes 2019, 7, 490. [Google Scholar] [CrossRef]
- Hamed, S.B.; Hamed, M.B.; Sbita, L.; Bajaj, M.; Blazek, V.; Prokop, L.; Misak, S.; Ghoneim, S.S.M. Robust Optimization and Power Management of a Triple Junction Photovoltaic Electric Vehicle with Battery Storage. Sensors 2022, 22, 6123. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, H.; Huang, X.; Lorenz, R.D. Inverse-System Decoupling Control of DC/DC Converters. Energies 2019, 12, 179. [Google Scholar] [CrossRef]
- Solsona, J.A.; Jorge, S.G.; Busada, C.A. Modeling and Nonlinear Control of dc–dc Converters for Microgrid Applications. Sustainability 2022, 14, 16889. [Google Scholar] [CrossRef]
- Broday, G.R.; Lopes, L.A.C.; Damm, G. Exact Feedback Linearization of a Multi-Variable Controller for a Bi-Directional DC-DC Converter as Interface of an Energy Storage System. Energies 2022, 15, 7923. [Google Scholar] [CrossRef]
- Broday, G.R.; Damm, G.; Pasillas-Lépine, W.; Lopes, L.A.C. A Unified Controller for Multi-State Operation of the Bi-Directional Buck–Boost DC-DC Converter. Energies 2021, 14, 7921. [Google Scholar] [CrossRef]
- Csizmadia, M.; Kuczmann, M.; Orosz, T. A Novel Control Scheme Based on Exact Feedback Linearization Achieving Robust Constant Voltage for Boost Converter. Electronics 2023, 12, 57. [Google Scholar] [CrossRef]
- Chen, P.; Liu, J.; Xiao, F.; Zhu, Z.; Huang, Z. Lyapunov-Function-Based Feedback Linearization Control Strategy of Modular Multilevel Converter–Bidirectional DC–DC Converter for Vessel Integrated Power Systems. Energies 2021, 14, 4691. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Silva-Ortigoza, R. Control Design Techniques in Power Electronics Devices; Springer: London, UK, 2006. [Google Scholar]
- Bajoria, N.; Sahu, P.; Nema, R.K.; Nema, S. Overview of different control schemes used for controlling of DC-DC converters. In Proceedings of the 2016 International Conference on Electrical Power and Energy Systems (ICEPES), Bhopal, India, 14–16 December 2016; pp. 75–82. [Google Scholar]
- Gkizas, G.; Yfoulis, C.; Amanatidis, C.; Stergiopoulos, F.; Giaouris, D.; Ziogou, C.; Voutetakis, S.; Papadopoulou, S. Digital state-feedback control of an interleaved DC-DC boost converter with bifurcation analysis. Cont. Eng. Pract. 2018, 73, 100–111. [Google Scholar] [CrossRef]
- Pegueroles-Queralt, J.; Bianchi, F.D.; Gomis-Bellmunt, O. A Power Smoothing System Based on Supercapacitors for Renewable Distributed Generation. IEEE Trans. Ind. Electron. 2015, 62, 343–350. [Google Scholar] [CrossRef]
- Hajizadeh, A.; Shahirinia, A.H.; Namjoo, N.; Yu, D.C. Self-tuning indirect adaptive control of non-inverting buck-boost converter. IET Power Electron. 2015, 8, 2299–2306. [Google Scholar] [CrossRef]
- Czarkowski, D.; Kazimierczuk, M.K. Application of state feedback with integral control to pulse-width modulated push-pull DC-DC convertor. IEE Proc.-Control Theory Appl. 1994, 141, 99–103. [Google Scholar] [CrossRef]
- Abdurraqeeb, A.M.; Al-Shamma’a, A.A.; Alkuhayli, A.; Noman, A.M.; Addoweesh, K.E. RST Digital Robust Control for DC/DC Buck Converter Feeding Constant Power Load. Mathematics 2022, 10, 1782. [Google Scholar] [CrossRef]
- Koundi, M.; El Idrissi, Z.; El Fadil, H.; Belhaj, F.Z.; Lassioui, A.; Gaouzi, K.; Rachid, A.; Giri, F. State-Feedback Control of Interleaved Buck–Boost DC–DC Power Converter with Continuous Input Current for Fuel Cell Energy Sources: Theoretical Design and Experimental Validation. World Electr. Veh. J. 2022, 13, 124. [Google Scholar] [CrossRef]
- Al-Baidhani, H.; Salvatierra, T.; Ordonez, R.; Kazimierczuk, M.K. Simplified nonlinear voltage-mode control of PWM DC-DC buck converter. IEEE Trans. Energy Conv. 2021, 36, 431–440. [Google Scholar] [CrossRef]
- Al-Baidhani, H.; Kazimierczuk, M.K. Simplified Double-Integral Sliding-Mode Control of PWM DC-AC Converter with Constant Switching Frequency. Appl. Sci. 2022, 12, 10312. [Google Scholar] [CrossRef]
- Al-Baidhani, H.; Kazimierczuk, M.K.; Ordóñez, R. Nonlinear Modelling and Control of PWM DC-DC Buck-Boost Converter for CCM. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1374–1379. [Google Scholar]
- Golnaraghi, F.; Kuo, B. Automatic Control Systems, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Kazimierczuk, M.K. Pulse-Width Modulated DC-DC Power Converters, 2nd ed.; John Wiley & Sons: Chichester, UK, 2016. [Google Scholar]
- Al-Baidhani, H.; Kazimierczuk, M.K. Simplified Nonlinear Current-Mode Control of DC-DC Cuk Converter for Low-Cost Industrial Applications. Sensors 2023, 23, 1462. [Google Scholar] [CrossRef]



| Control Technique | Advantages | Disadvantages | References |
|---|---|---|---|
| Neural inverse optimal control (NIOC) |
|
| [1] |
| Artificial neural network-based control | [2] | ||
| Model predictive control (MPC) |
| Practical implementation has not been discussed. | [3] |
| Centralized MPC |
| High-cost control system implementation. | [4] |
| Direct model reference adaptive control | Robustness against voltage and frequency variations. | Complexity of control system implementation. | [5] |
| Optimal adaptive control | Estimation of uncertainties and disturbances | High-cost control system implementation (dSPACE). | [6] |
| Lyapunov-based nonlinear control | Robustness against load variations. | Practical implementation has not been covered. | [7] |
| Inverse-system decoupling control | Disturbance rejection capability. | Design procedure of control circuit has not been provided. | [8] |
| Feedback linearization control | Mitigation of CPL and zero dynamics. | Design procedure of control circuit has not been provided. | [9,10,11,12,13] |
| State-feedback control via pole placement | Placement of closed-loop poles at desired locations. | Steady-state error issue. Design procedure of control circuit has not been provided. | [14,15,16,17,18] |
| State-feedback with integral control | State variables regulation and steady-state error elimination. | Design procedure of control circuit has not been introduced. High-cost control system implementation (dSPACE). | [19] |
| pole placement control with sensitivity function | Mitigation of CPL and non-minimum phase issue. | [20] |
| Description | Parameter | Value |
|---|---|---|
| Inductor | L | 30 μH |
| Output capacitor | C | 2.2 mF |
| Load resistance | R | (1.2–12) Ω |
| Inductor ESR | rL | 0.050 Ω |
| Output capacitor ESR | rC | 0.006 Ω |
| MOSFET on-resistance | rDS | 0.110 Ω |
| Diode forward resistance | rF | 0.020 Ω |
| Diode threshold voltage | VF | 0.700 V |
| Input voltage | VI | 28 ± 4 V |
| Output voltage | VO | 12 V |
| Switching frequency | fs | 100 kHz |
| Disturbance Type (∆iO, ∆vI, ∆Vr) | Overshoot/Undershoot (%) | Settling Time (ms) | Output Voltage (V) |
|---|---|---|---|
| 4 A to 6.0 A | 2 | 4 | −12 |
| 4 A to 2.5 A | 1 | 3.5 | −12 |
| 28 V to 33 V | 2.6 | 5.5 | −12 |
| 28 V to 23 V | 3.5 | 5.5 | −12 |
| 2 V to 2.5 V | 0 | 5.5 | −15 |
| 2 V to 1.5 V | 0 | 5.5 | −9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Baidhani, H.; Sahib, A.; Kazimierczuk, M.K. State Feedback with Integral Control Circuit Design of DC-DC Buck-Boost Converter. Mathematics 2023, 11, 2139. https://doi.org/10.3390/math11092139
Al-Baidhani H, Sahib A, Kazimierczuk MK. State Feedback with Integral Control Circuit Design of DC-DC Buck-Boost Converter. Mathematics. 2023; 11(9):2139. https://doi.org/10.3390/math11092139
Chicago/Turabian StyleAl-Baidhani, Humam, Abdullah Sahib, and Marian K. Kazimierczuk. 2023. "State Feedback with Integral Control Circuit Design of DC-DC Buck-Boost Converter" Mathematics 11, no. 9: 2139. https://doi.org/10.3390/math11092139
APA StyleAl-Baidhani, H., Sahib, A., & Kazimierczuk, M. K. (2023). State Feedback with Integral Control Circuit Design of DC-DC Buck-Boost Converter. Mathematics, 11(9), 2139. https://doi.org/10.3390/math11092139










