Abstract
Applications of non-Newtonian fluids have been widespread across industries, accompanied by theoretical developments in engineering and mathematics. This paper studies a two-dimensional multi-term time fractional viscoelastic non-Newtonian fluid model by using two autonomous consecutive spectral collocation strategies. A modification of the spectral approach is implemented, leading to an algebraic system of equations able to obtain an approximate symmetric solution for the model. Numerical examples illustrate the effectiveness of the technique in terms of accuracy and convergence.
Keywords:
time fractional non-Newtonian fluid model; collocation method; spectral method; Gauss-type quadrature; modern technologies MSC:
35P05; 65M70; 76A05
1. Introduction
Fractional calculus has been proven more effective than the classical integer calculus for describing a variety of natural scenarios [1], and emerged as a crucial tool within the scope of mathematical modeling [2,3], with a plethora of applications [4,5]. Indeed, several anomalous phenomena and complex systems in multiple areas have been studied using fractional differential equations [6], since they have advantages over the integer-order ones for describing real processes with memory [7].
A Newtonian fluid is a type of fluid that obeys Newton’s law of viscosity, which states that the shear stress of a fluid is directly proportional to its rate of shear strain. In other words, the viscosity of a Newtonian fluid remains constant regardless of the applied shear stress or strain rate. This makes Newtonian fluids relatively simple to model and analyze mathematically. Examples of Newtonian fluids include water, air, and most oils. However, many real-world fluids exhibit non-Newtonian behavior, where the viscosity changes with the applied stress or strain rate. These fluids require more complex models to describe their behavior.
Non-Newtonian fluid models are used to describe fluids that do not follow the traditional Newtonian model of viscosity. These fluids often exhibit complex behavior, such as shear-thinning or shear-thickening, where the viscosity of the fluid changes depending on the applied force. There are many different models used to describe these types of fluids, including the Power-law model, the Herschel-Bulkley model, and the Casson model. These models are often used in engineering and scientific applications, such as in the design of non-Newtonian fluids for use in food products, cosmetics, and even in hydraulic fracturing fluids for oil and gas exploration. By understanding the behavior of non-Newtonian fluids, we can better design and optimize processes that rely on these materials.
Over the last few decades, non-Newtonian fluids have been widely used in engineering applications. Non-Newtonian fluids’ constitutive equations are significantly more complex than those describing Newtonian ones. Fractional differential equations have been adopted to describe non-Newtonian fluids, since they are well-suited for dealing with viscoelastic properties [8], yielding results in accordance to experimental data [9,10].
The flow of an incompressible Oldroyd-B fluid [11] bounded by two rigid plates is described by the following model, which is one of the most significant:
where is the velocity field (meter/second), represents the relaxation time (second), is the retardation time (second), and stand for the dynamic viscosity (Pascal·second), and is the density of the fluid.
Sutton [12] summarized its fundamental electromagnetic properties. When exposed to a magnetic field, under the assumption of low magnetic Reynolds number, the flow of a Oldroyd-B fluid between two infinite parallel rigid plates is challenging to model. Khan et al. [13] investigated the generalized Oldroyd-B fluid in a porous medium with the influence of Hall current. Zheng et al. [14] explored the interaction of two plates with slip boundaries and achieved the exact solution for the flow magnetohydrodynamics by some transform techniques.
The exact solution of the generalized Oldroyd-B fluid was obtained using generalized G- or H-functions [14,15]. Fetecau et al. [16] derived an exact solution for a two-dimensional fluid model. However, because multi-term fractional fluid models are difficult to solve analytically, many researchers studied alternative approaches [17,18] based on numerical methods. Finite difference [19,20], finite element [21,22], finite volume [23,24], and spectral methods [25,26] have been the most commonly used for solving fractional equations.
In the last four decades, spectral methods [27,28,29] have been widely used in several areas. Firstly, techniques based on Fourier expansion were applied, namely for dealing with simple geometric area and periodic boundary conditions. Afterwards, sophisticated techniques were developed, and spectral methods emerged as powerful tools to solve different kinds of problems. Indeed, due to their thoroughness and exponential rates of convergence, spectral methods reveal superiority when compared with their counterparts. They include the collocation [30,31], tau [32], Galerkin [33], and Petrov-Galerkin [34] variants. Regardless of the technique adopted, spectral methods express the problem as a finite series of several functions. Then, the coefficients are chosen such that the absolute error is minimized as well as possible. In the spectral collocation technique [35,36], the numerical solution is implemented in order to almost satisfying the problem. On the other hand, the residuals are permitted to be zero at the collocation points.
Spectral schemes can be applied to a wide range of problems, including integral and integro-differential equations [37], fractional differential equations [38], optimal control, and variational problems. However, global spectral schemes [39] have received little attention, when compared to other classical methods, as finite difference and finite element, for solving fractional order differential equations. Although the approach has disadvantages like the inability to represent physical processes in spectral space and parallelizing difficulties on distributed memory computers, it is highly accurate, converges quickly, and is straightforward.
In this paper we propose a spectral method for approximating a fractional non-Newtonian fluid model (FNNFM). The solution of the model is expressed as a limited expansion of shifted Legendre polynomials for the independent variables, and the residuals are estimated at the shifted Legendre quadrature points. The proposed collocation scheme is investigated for both temporal and spatial discretizations. The shifted Legendre collocation method is proposed, with a suitable modification for treating the intial-boundary, for spatial and temporal discretization. This treatment improves greatly the accuracy of the scheme. The solutions of the problem are approximated as a finite expansion of shifted Legendre polynomials for the discretization of the spatial and temporal variables. Consequently, the spatial and temporal derivatives of this finite expansion are evaluated explicitly at some quadrature nodes. The resulting equations, when combined with the initial conditions, generate a system of algebraic equations that can be solved by any suitable method. In addition, we investigate the effectiveness of the proposed technique in terms of accuracy and convergence.
The paper is structured into 5 sections. Section 2 presents some preliminary tools as well as information about shifted Legendre polynomials. Section 3 introduces the spectral collocation method to solve the time FNNFM. Section 4 presents some numerical examples to illustrate the effectiveness and accuracy of the technique. Section 5 summarizes some conclusions.
2. Adopted Notation and Preliminary Concepts
2.1. Caputo Fractional Derivative
Definition 1.
Given a function , its Caputo fractional derivative [40] is:
whereand
is the Gamma function.
2.2. Brief Introduction to Shifted Legendre Polynomials
A class of mathematical functions known as Legendre polynomials is crucial in many branches of physics and engineering. They are defined as solutions to the Legendre’s equation, a particular differential equation that frequently appears in spherical symmetry-related issues. The polynomials are orthogonal in the range [−1, 1], so unless they are identical, their inner product over this range is zero. Numerous fields, including quantum mechanics, electromagnetism, and signal processing, as well as approximation theories and numerical methods for solving differential equations, use Legendre polynomials. The Legendre polynomials fulfil the Rodrigues formula, meaning that [41,42]
with pth derivative given by
where
The property of orthogonality [43] is written as
Using the Legendre-Gauss-Lobatto quadrature, ref. [43] we obtain
for .
Let us express the discrete inner product by means of the expression
Definition 2.
The shifted Legendre polynomial is given by [44]
Theorem 1.
For , a complete -orthogonal system is obtained [45]
where.
Corollary 1.
Let be the finite space of fractional-polynomials. Using (9), the function can be obtained as
3. Solving the Time FNNFM
The time FNNFM [46,47] is dealt with the Gauss–Lobatto and the Gauss–Radau shifted Legendre collocation techniques [43], yielding:
where and are constants and , , and
Expression (10) represents various types of fractional diffusion equations. The generalized Oldroyd-B fluid model (1), the time fractional diffusion-wave equation [48] (), and the generalized Maxwell fluid model [49] () are some particular cases. A detailed derivation of the flow problem is discussed in reference [47].
The truncated solution is
where and are shift Legendre polynomials (see [50,51] for more details).
The time derivatives are then computed as
where [52]. Moreover, the space derivatives are
The derivative is calculated as:
where [45,51]
with
Also, we get
At selected quadrature nodes, we get
where and are Gauss-Lobatto and Gauss-Radau shifted Legendre collocation nodes, respectively.
Besides, the provided conditions can be written as
The Equation (10) is closest to zero at the nodes.
where
and
Additionally
This results in a system of algebraic equations that is simple to solve.
4. Some Numerical Examples
We illustrate the proposed spectral approach by solving two examples.
Example 1.
We consider the multi-term time fractional viscoelastic non-Newtonian fluid model [53]
The included conditions are specified in a way that where
Relying on -errors, the results obtained with the proposed technique are compared with those in [53], and are summarized in Table 1. We verify that the new procedure yields better numerical results. The tables show that the numerical results and exact solution are well-aligned, proving the efficacy of our numerical approach and supporting the theoretical analysis. We plot a few graphs to show the dynamic properties of the generalized non-Newtonian fluid and to observe the effects of various physical parameters on the velocity field.

Table 1.
The -errors of Example 1 for various values of .
Figure 1 and Figure 2 depict the numerical solution and absolute error of Example 1, respectively. The similarity between the numerical and the exact solutions is illustrated in Figure 3. Also, Figure 3 depicts the relationship between time and velocity, and the increase in flow velocity. Figure 4 and Figure 5 reveal the - and -curves associated with the absolute errors, respectively. In addition, the convergence error decay is shown in Figure 6.
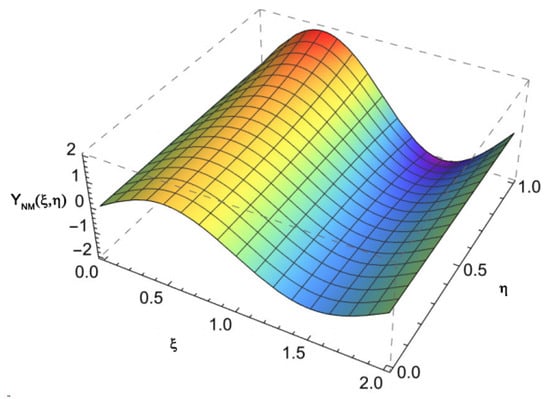
Figure 1.
The solution of Example 1, with , .
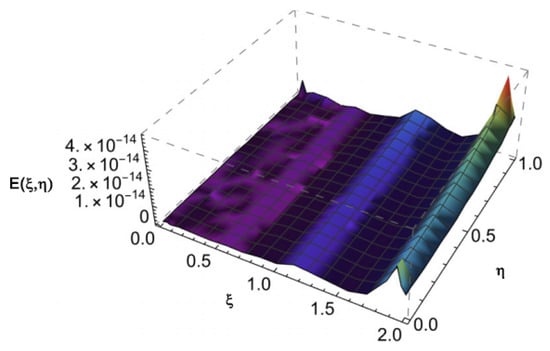
Figure 2.
The absolute error of Example 1, with , .
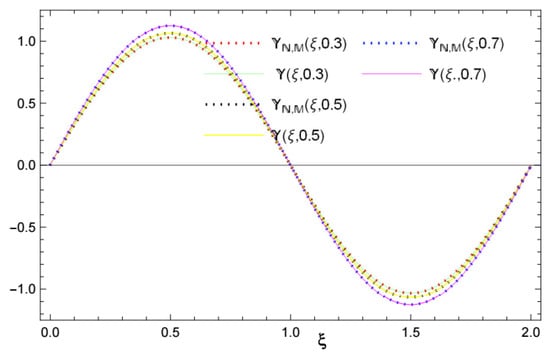
Figure 3.
The numerical and the exact solutions, and , along the -direction of Example 1, with .
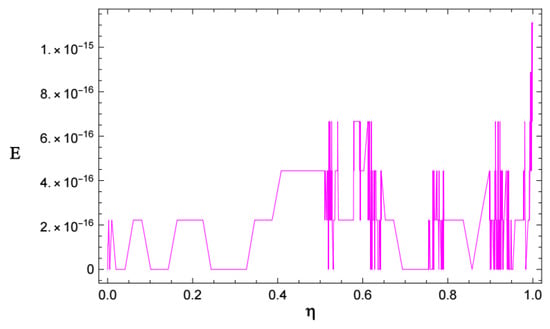
Figure 4.
The absolute error of Example 1, with .
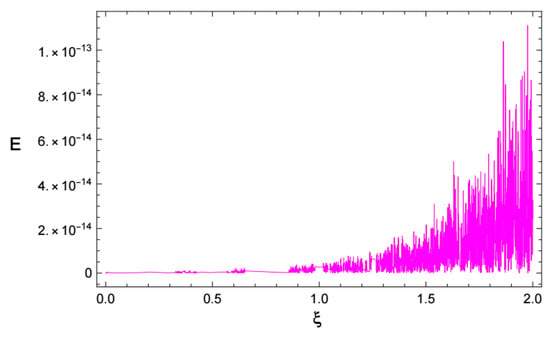
Figure 5.
The absolute error of Example 1, with .
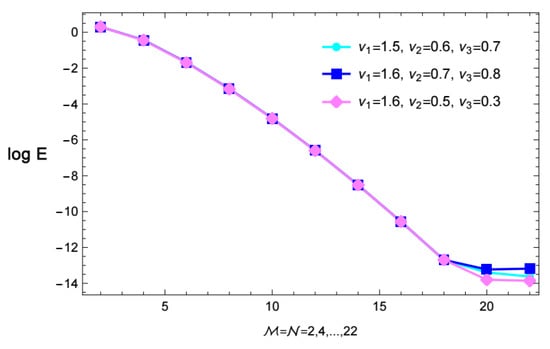
Figure 6.
Convergence error of Example 1, expressed in log scale.
Example 2.
We consider the multi-term time fractional diffusion equation [47]
The included conditions are specified in a way that where
The results with the proposed technique are compared with those in [47] and listed in Table 2 in terms of -error. We verify that the accuracy of the solutions with the new technique is superior to that with the alternative method.

Table 2.
The -error of Example 2 for various values of .
Figure 7 and Figure 8 depict the numerical solution and the absolute errors of Example 2, respectively. The similarity between the numerical and exact solutions is illustrated in Figure 9. Also, Figure 9 depicts the relationship between time and velocity, and the increase in flow velocity. Figure 10 and Figure 11 reveal the - and -curves associated with absolute errors, respectively. In addition, the decay of the convergence error is shown in Figure 12.
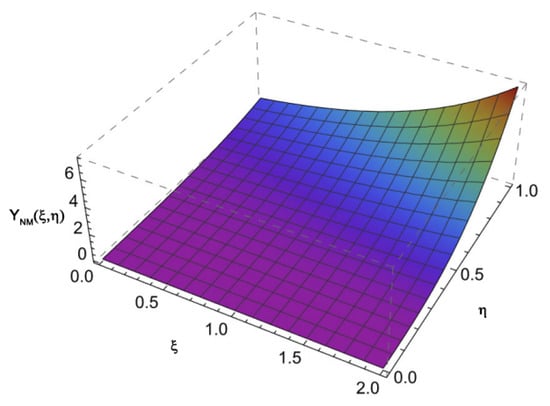
Figure 7.
The solution of Example 2, with .
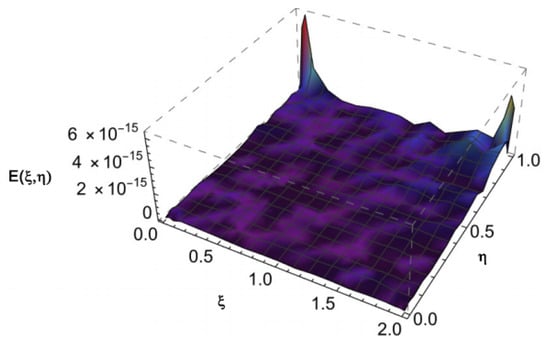
Figure 8.
The absolute error of Example 2, with .
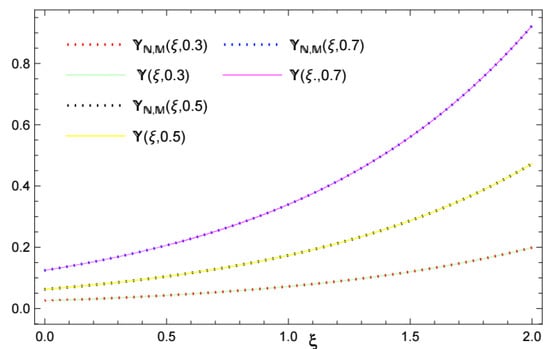
Figure 9.
The approximate and exact solutions, and , of Example 2, with .
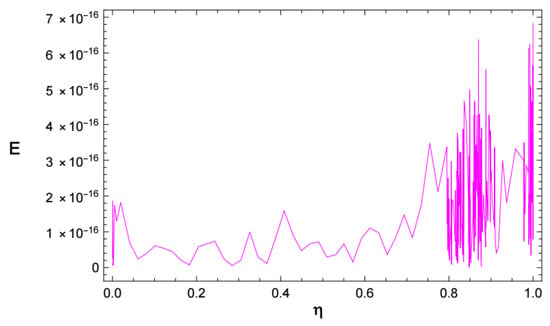
Figure 10.
The absolute error of Example 2, with .
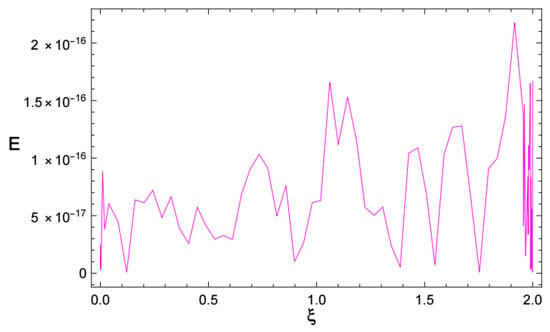
Figure 11.
The absolute error of Example 2, with .
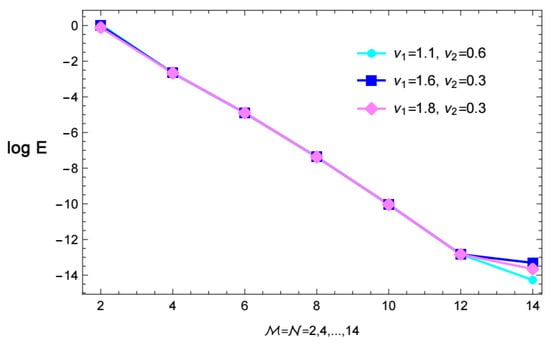
Figure 12.
Convergence error of Example 2, expressed in log scale.
5. Conclusions
We proposed an accurate technique for solving two-dimensional multi-term time fractional viscoelastic non-Newtonian fluid model. To exemplify the technique’s implementation and effectiveness, a theoretical analysis was provided, along with a set of numerical tests. Based on the results obtained though the examples, we can deduce that our method is extremely precise and dependable. More fractional order concerns can be incorporated into the existing discussion. The results are completely compatible with the expected values of the technique, evidencing exponential convergence.
Author Contributions
Investigation, Methodology and Writing-original draft, M.M.A.-S. and M.A.A.; Software and Conceptualization, M.M.A.-S. and M.A.A.; Writing-review and editing, A.M.L.; visualization and supervision, M.A.A. and A.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
The Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia has funded this project under grant no. (G:194-130-1443).
Data Availability Statement
Data sharing is not applicable to this article, as no datasets were generated or analyzed during the current study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations and Symbols
| Velocity field (meter/second) | |
| Relaxation time (second) | |
| Retardation time (second) | |
| Dynamic viscosity (Pascal-second) | |
| Constant density of the fluid | |
| Legendre polynomials | |
| Weight function of Legendre polynomials | |
| Orthogonality constant of Legendre polynomials | |
| Christoffel numbers of the Legendre-quadrature formula | |
| Orthogonality constant of shifted Legendre polynomials | |
| Space (meter) and time (second) | |
| Shifted Legendre polynomials | |
| FNNFM | Fractional non-Newtonian fluid model |
References
- Singh, S.; Devi, V.; Tohidi, E.; Singh, V.K. An efficient matrix approach for two-dimensional diffusion and telegraph equations with Dirichlet boundary conditions. Phys. A Stat. Mech. Appl. 2020, 545, 123784. [Google Scholar] [CrossRef]
- West, B.J. Nature’s Patterns and the Fractional Calculus; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2017; Volume 2. [Google Scholar]
- Liu, Y. A new method for converting boundary value problems for impulsive fractional differential equations to integral equations and its applications. Adv. Nonlinear Anal. 2019, 8, 386–454. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Babatin, M.M.; Alnahdi, A.S.; Taha, T. Legendre spectral collocation technique for fractional inverse heat conduction problem. Int. J. Mod. Phys. C 2022, 33, 2250065. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Lopes, A.M. Spectral Solutions for Fractional Black–Scholes Equations. Math. Probl. Eng. 2022, 2022. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: London, UK, 2010. [Google Scholar]
- Leonenko, N.N.; Meerschaert, M.M.; Sikorskii, A. Fractional pearson diffusions. J. Math. Anal. Appl. 2013, 403, 532–546. [Google Scholar] [CrossRef] [PubMed]
- Bagley, R.L.; Torvik, P. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Makris, N.; Constantinou, M. Fractional-derivative Maxwell model for viscous dampers. J. Struct. Eng. 1991, 117, 2708–2724. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Shah, N.A.; Wakif, A.; Mahanthesh, B.; Sivaraj, R.; Koríko, O.K. Ratio of Momentum Diffusivity to Thermal Diffusivity: Introduction, Meta-Analysis, and Scrutinization; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Jiang, Y.; Qi, H.; Xu, H.; Jiang, X. Transient electroosmotic slip flow of fractional Oldroyd-B fluids. Microfluid. Nanofluid. 2017, 21, 7. [Google Scholar] [CrossRef]
- Sutton, G.W.; Sherman, A. Engineering Magnetohydrodynamics; Courier Dover Publications: Oxford, UK, 2006. [Google Scholar]
- Khan, M.; Maqbool, K.; Hayat, T. Influence of Hall current on the flows of a generalized Oldroyd-B fluid in a porous space. Acta Mech. 2006, 184, 1–13. [Google Scholar] [CrossRef]
- Zheng, L.; Liu, Y.; Zhang, X. Slip effects on MHD flow of a generalized Oldroyd-B fluid with fractional derivative. Nonlinear Anal. Real World Appl. 2012, 13, 513–523. [Google Scholar] [CrossRef]
- Jiang, X.; Qi, H. Thermal wave model of bioheat transfer with modified Riemann–Liouville fractional derivative. J. Phys. A Math. Theor. 2012, 45, 485101. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C.; Kamran, M.; Vieru, D. Exact solutions for the flow of a generalized Oldroyd-B fluid induced by a constantly accelerating plate between two side walls perpendicular to the plate. J. Non-Newton. Fluid Mech. 2009, 156, 189–201. [Google Scholar] [CrossRef]
- Zaky, M.A.; Doha, E.H.; Taha, T.M.; Baleanu, D. New recursive approximations for variable-order fractional operators with applications. arXiv 2018, arXiv:1804.01198. [Google Scholar] [CrossRef]
- Bhrawy, A.; Doha, E.; Baleanu, D.; Hafez, R. A highly accurate Jacobi collocation algorithm for systems of high-order linear differential–difference equations with mixed initial conditions. Math. Methods Appl. Sci. 2015, 38, 3022–3032. [Google Scholar] [CrossRef]
- Ding, H.; Li, C. Fractional-compact numerical algorithms for Riesz spatial fractional reaction-dispersion equations. Fract. Calc. Appl. Anal. 2017, 20, 722–764. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Li, H.; Li, J.; He, S. A two-grid mixed finite element method for a nonlinear fourth-order reaction–diffusion problem with time-fractional derivative. Comput. Math. Appl. 2015, 70, 2474–2492. [Google Scholar] [CrossRef]
- Zhao, Y.; Bu, W.; Huang, J.; Liu, D.Y.; Tang, Y. Finite element method for two-dimensional space-fractional advection–dispersion equations. Appl. Math. Comput. 2015, 257, 553–565. [Google Scholar] [CrossRef]
- Simmons, A.; Yang, Q.; Moroney, T. A finite volume method for two-sided fractional diffusion equations on non-uniform meshes. J. Comput. Phys. 2017, 335, 747–759. [Google Scholar] [CrossRef]
- Jia, J.; Wang, H. A fast finite volume method for conservative space-fractional diffusion equations in convex domains. J. Comput. Phys. 2016, 310, 63–84. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A.; Baleanu, D.; Amin, A.Z. A spectral technique for solving two-dimensional fractional integral equations with weakly singular kernel. Hacet. J. Math. Stat. 2018, 47, 553–566. [Google Scholar]
- Zayernouri, M.; Karniadakis, G.E. Fractional spectral collocation method. SIAM J. Sci. Comput. 2014, 36, A40–A62. [Google Scholar] [CrossRef]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M. On spectral methods for solving variable-order fractional integro-differential equations. Comput. Appl. Math. 2018, 37, 3937–3950. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Amin, A.; Lopes, A.M. Fractional-order shifted Legendre collocation method for solving non-linear variable-order fractional Fredholm integro-differential equations. Comput. Appl. Math. 2022, 41, 2. [Google Scholar] [CrossRef]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.Z.M.; Baleanu, D. Spectral technique for solving variable-order fractional Volterra integro-differential equations. Numer. Methods Partial Differ. Equ. 2018, 34, 1659–1677. [Google Scholar]
- Abdelkawy, M.A.; Amin, A.Z.M.; Babatin, M.M.; Alnahdi, A.S.; Zaky, M.A.; Hafez, R.M. Jacobi spectral collocation technique for time-fractional inverse heat equations. Fractal Fract. 2021, 5, 115. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Amin, A.Z.; Bhrawy, A.H.; Machado, J.A.T.; Lopes, A.M. Jacobi collocation approximation for solving multi-dimensional Volterra integral equations. Int. J. Nonlinear Sci. Numer. Simul. 2017, 18, 411–425. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. A fractional-order Jacobi tau method for a class of time-fractional PDEs with variable coefficients. Math. Methods Appl. Sci. 2016, 39, 1765–1779. [Google Scholar] [CrossRef]
- Hafez, R.M.; Zaky, M.A. High-order continuous Galerkin methods for multi-dimensional advection–reaction–diffusion problems. Eng. Comput. 2020, 36, 1813–1829. [Google Scholar] [CrossRef]
- Hafez, R.M.; Zaky, M.A.; Hendy, A.S. A novel spectral Galerkin/Petrov–Galerkin algorithm for the multi-dimensional space–time fractional advection–diffusion–reaction equations with nonsmooth solutions. Math. Comput. Simul. 2021, 190, 678–690. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations. Comput. Math. Appl. 2017, 73, 1100–1117. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. An improved collocation method for multi-dimensional space–time variable-order fractional Schrödinger equations. Appl. Numer. Math. 2017, 111, 197–218. [Google Scholar] [CrossRef]
- Eslahchi, M.R.; Dehghan, M.; Parvizi, M. Application of the collocation method for solving nonlinear fractional integro-differential equations. J. Comput. Appl. Math. 2014, 257, 105–128. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Doha, E.H.; Bhrawy, A.H.; Amin, A.Z. Efficient pseudospectral scheme for 3D integral equations. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2017, 18, 199–206. [Google Scholar]
- Ezz-Eldien, S.; Wang, Y.; Abdelkawy, M.; Zaky, M.; Aldraiweesh, A.; Machado, J.T. Chebyshev spectral methods for multi-order fractional neutral pantograph equations. Nonlinear Dyn. 2020, 100, 3785–3797. [Google Scholar] [CrossRef]
- Abdelkawy, M. Numerical solutions for fractional initial value problems of distributed-order. Int. J. Mod. Phys. C (IJMPC) 2021, 32, 2150096. [Google Scholar] [CrossRef]
- Abdelkawy, M.A. Shifted Legendre spectral collocation technique for solving stochastic Volterra–Fredholm integral equations. Int. J. Nonlinear Sci. Numer. Simul. 2021, 24, 123–136. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Ezz-Eldien, S.S.; Doha, E.H.; Abdelkawy, M.A.; Baleanu, D. Solving fractional optimal control problems within a Chebyshev–Legendre operational technique. Int. J. Control 2017, 90, 1230–1244. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods: Fundamentals in Single Domains; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Bhrawy, A.; Zaky, M.; Tenreiro Machado, J. Efficient Legendre spectral tau algorithm for solving the two-sided space–time Caputo fractional advection–dispersion equation. J. Vib. Control 2016, 22, 2053–2068. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A.; Baleanu, D. New numerical approximations for space-time fractional Burgers’ equations via a Legendre spectral-collocation method. Rom. Rep. Phys. 2015, 67, 340–349. [Google Scholar]
- Liu, Y.; Yin, X.; Feng, L.; Sun, H. Finite difference scheme for simulating a generalized two-dimensional multi-term time fractional non-Newtonian fluid model. Adv. Differ. Equ. 2018, 2018, 442. [Google Scholar] [CrossRef]
- Feng, L.; Liu, F.; Turner, I.; Zhuang, P. Numerical methods and analysis for simulating the flow of a generalized Oldroyd-B fluid between two infinite parallel rigid plates. Int. J. Heat Mass Transf. 2017, 115, 1309–1320. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
- Zheng, L.; Zhao, F.; Zhang, X. Exact solutions for generalized Maxwell fluid flow due to oscillatory and constantly accelerating plate. Nonlinear Anal. Real World Appl. 2010, 11, 3744–3751. [Google Scholar] [CrossRef]
- Zaky, M.A.; Abdelkawy, M.A.; Ezz-Eldiene, S.S.; Dohaf, E.H. Pseudospectral methods for the Riesz space-fractional Schrödinger equation. Fract.-Order Model. Dyn. Syst. Appl. Optim. Signal Process. Control 2021, 2, 323–353. [Google Scholar]
- Abdelkawy, M.; Alyami, S. Legendre-Chebyshev spectral collocation method for two-dimensional nonlinear reaction-diffusion equation with Riesz space-fractional. Chaos Solitons Fractals 2021, 151, 111279. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Abdelkawy, M.A. A fully spectral collocation approximation for multi-dimensional fractional Schrödinger equations. J. Comput. Phys. 2015, 294, 462–483. [Google Scholar] [CrossRef]
- Feng, L.; Liu, F.; Turner, I.; Zheng, L. Novel numerical analysis of multi-term time fractional viscoelastic non-Newtonian fluid models for simulating unsteady MHD Couette flow of a generalized Oldroyd-B fluid. Fract. Calc. Appl. Anal. 2018, 21, 1073–1103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).