On Fractional-Order Discrete-Time Reaction Diffusion Systems
Abstract
:1. Introduction
2. Preliminaries
- where c is a constant.
- .
- .
- Discrete Leibniz integral law
- Caputo fractional difference of a constant x
3. The Fractional Discrete Lengyl–Epstein Reaction–Diffusion System
- (1) describes the iodization of malonic acid (MA).
- (2) describes the oxidation of iodide ions by free chlorine dioxide radicals.
- (3) describes an interaction between chlorite and iodide ions created in the (1) and (2) processes to produce iodine.
4. Local Stability
4.1. Local Stability of the Free Diffusions System
- If and
- If and
- If , we can see that . As a result, the eigenvalues’ negativity is dependent on the sign of , and the eigenvalues and are real and may be represented as
- –
- If then, we haveAs a result, . Since both eigenvalues are real, it is obvious that As a consequence, based on Theorem 2, the equilibrium is asymptotically stable.
- –
- If then, we haveTherefore, . Based on Theorem 2, system (18) is unstable.
- If , then,We may discuss the solutions based on the sign of .
- If , as , cannot be equal to zero. The sign of the eigenvalues is the same as the sign of . As a result, is asymptotically stable for all if and unstable if .
4.2. Local Stability of the Diffusion System
- If and
- If and , in addition the eigenvaluessatisfy
- If , then, . The two solutions of the equation are both negative. Thus, and the roots of (35) areNote that the solutions are real and In addition, if , then This leads towhich ensures is asymptotically stable.
- If , we have This returns us to the previous scenario, again, for Hence, and are negative and must meet the conditions of Theorem 2.
5. Global Stability
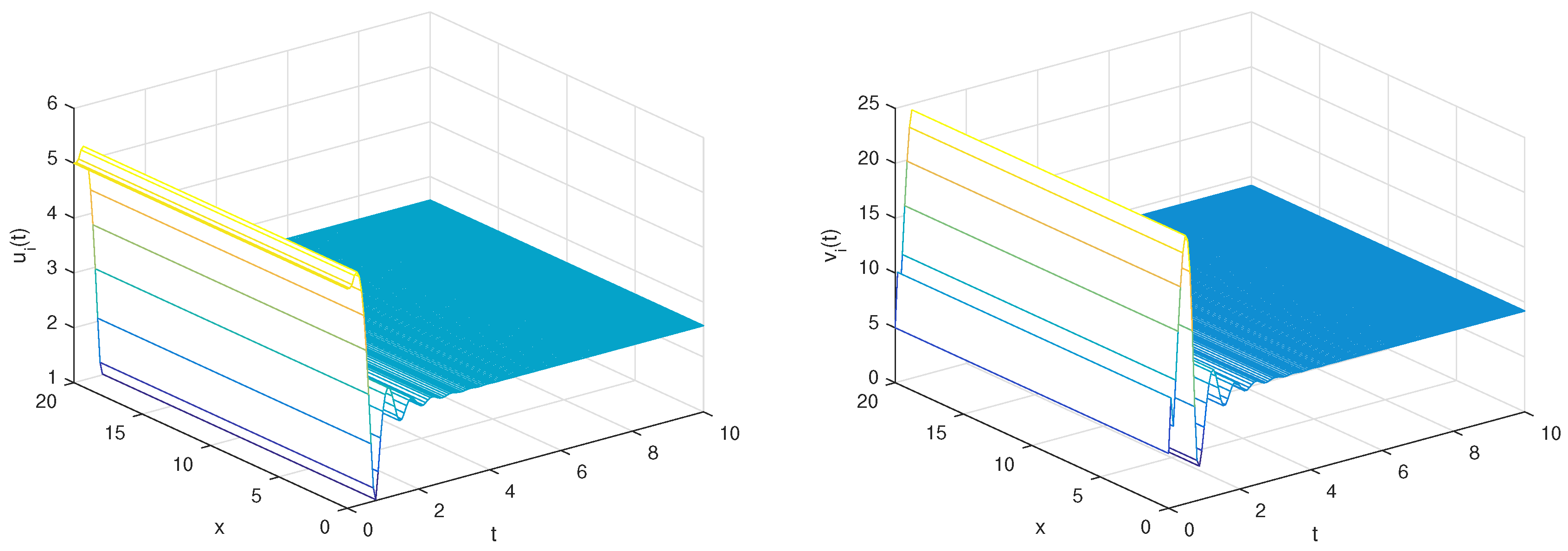
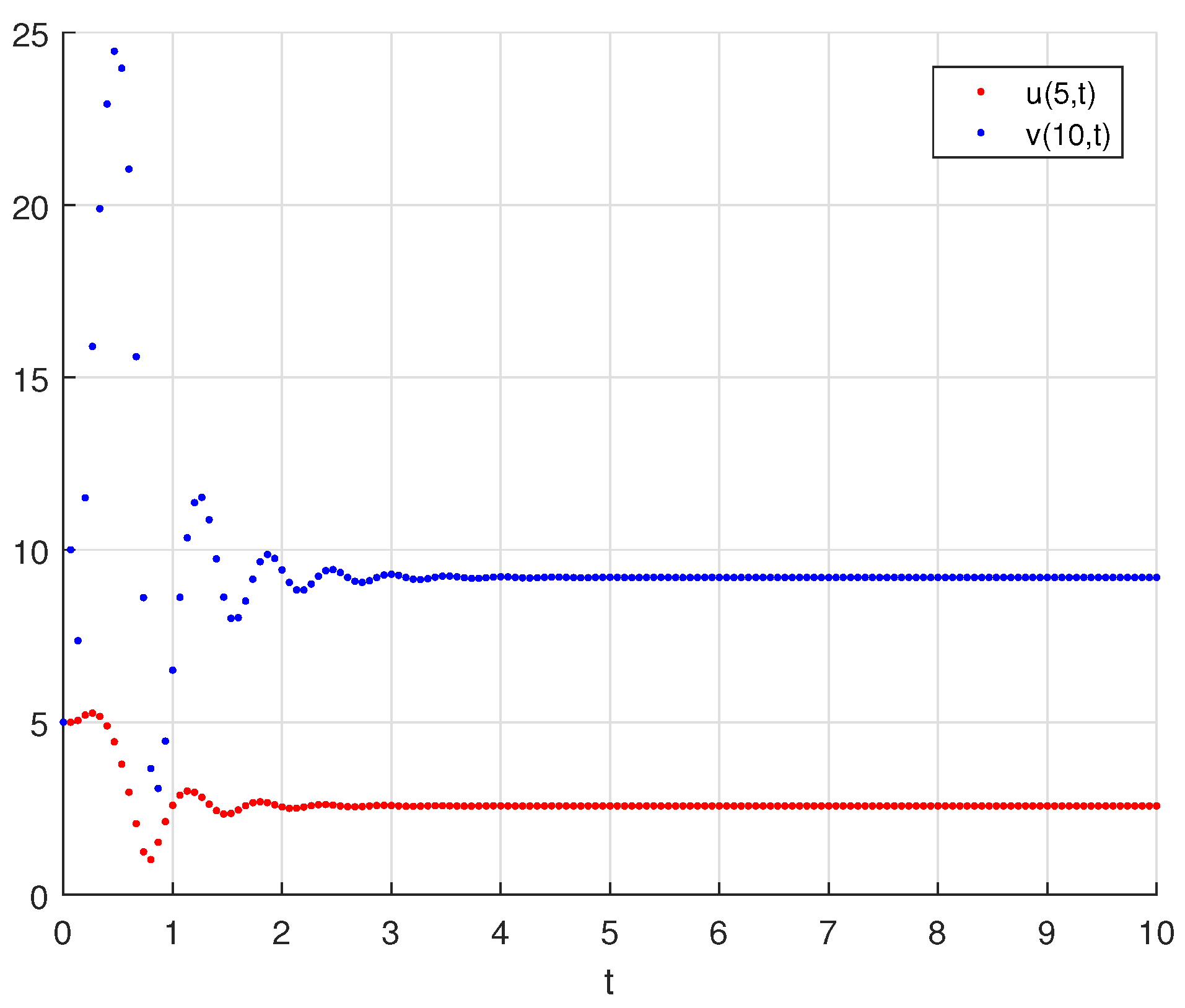
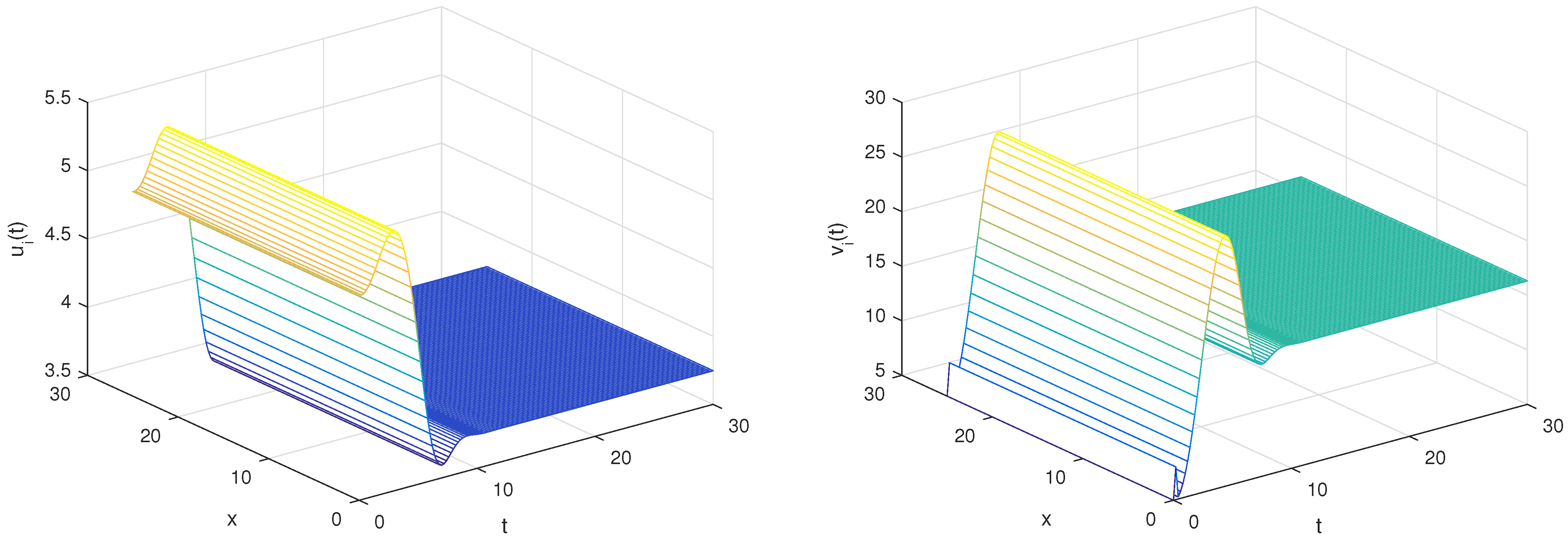
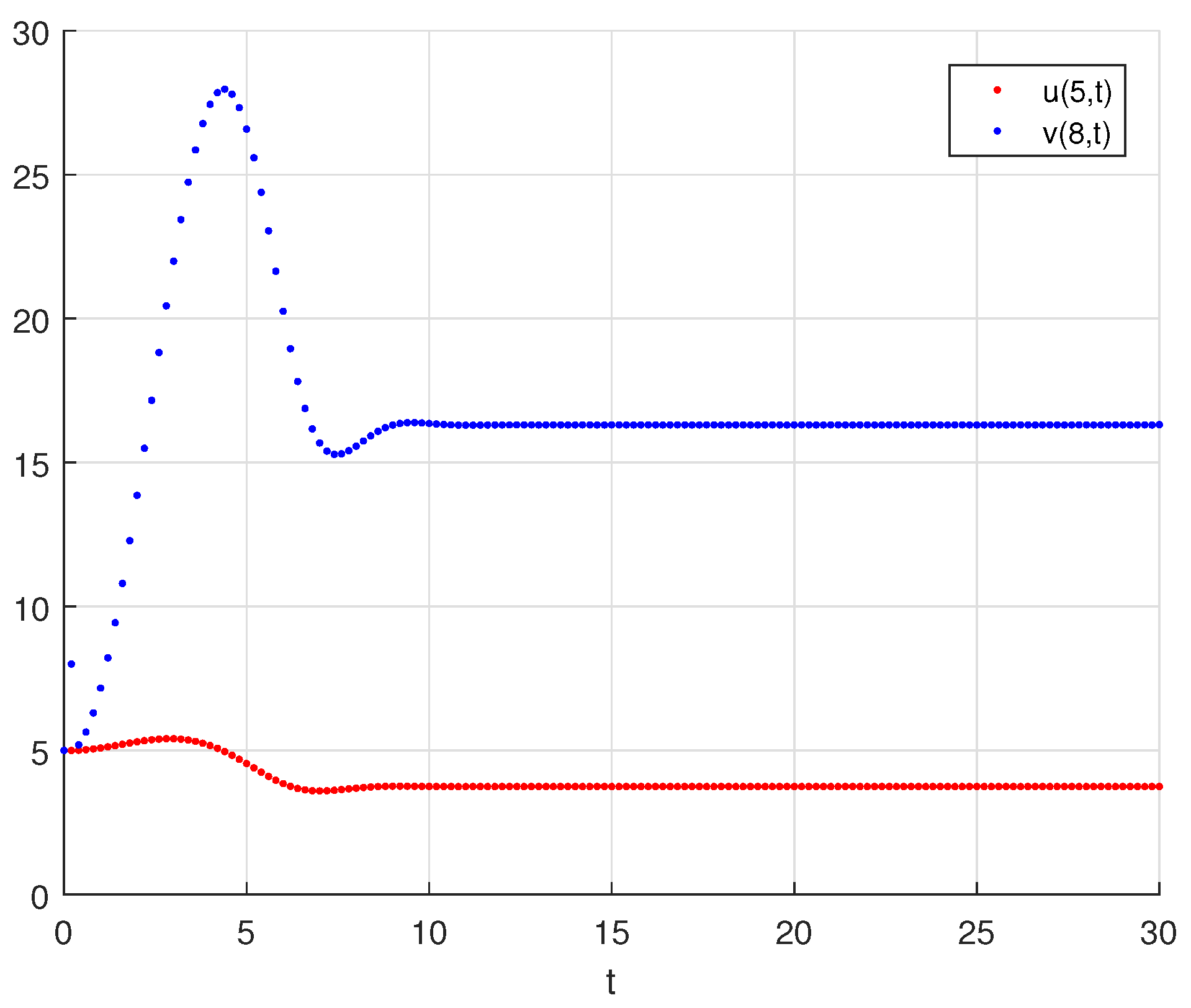
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bailey, J.E. Mathematical modeling and analysis in biochemical engineering: Past accomplishments and future opportunities. Biotechnol. Prog. 1998, 14, 8–20. [Google Scholar] [CrossRef]
- Zaheri, S.; Hassanipour, F. A comprehensive approach to the mathematical modeling of mass transport in biological systems: Fundamental concepts and models. Int. J. Heat Mass Transf. 2020, 158, 119777. [Google Scholar] [CrossRef]
- Azizi, T. Mathematical Modeling with Applications in Biological Systems, Physiology, and Neuroscience; Kansas State University: Manhattan, KS, USA, 2021. [Google Scholar]
- Siettos, C.I.; Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 2013, 4, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Brauer, F.; Castillo-Chavez, C.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: New York, NY, USA, 2012; Volume 2, No. 40. [Google Scholar]
- Yang, C.; Wang, J. A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math. Biosci. Eng. MBE 2020, 17, 2708. [Google Scholar] [CrossRef] [PubMed]
- Frunzo, L.; Garra, R.; Giusti, A.; Luongo, V. Modeling biological systems with an improved fractional Gompertz law. Commun. Nonlinear Sci. Numer. Simul. 2019, 74, 260–267. [Google Scholar] [CrossRef]
- Das, P.; Upadhyay, R.K.; Das, P.; Ghosh, D. Exploring dynamical complexity in a time-delayed tumor-immune model. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 123118. [Google Scholar] [CrossRef]
- Escudero, C. The fractional keller–segel model. Nonlinearity 2006, 19, 2909. [Google Scholar] [CrossRef]
- Das, P.; Mukherjee, S.; Das, P.; Banerjee, S. Characterizing chaos and multifractality in noise-assisted tumor-immune interplay. Nonlinear Dyn. 2020, 101, 675–685. [Google Scholar] [CrossRef]
- Das, P.; Das, P.; Mukherjee, S. Stochastic dynamics of Michaelis–Menten kinetics based tumor-immune interactions. Phys. Stat. Mech. Its Appl. 2020, 541, 123603. [Google Scholar] [CrossRef]
- Das, S.; Das, P.; Das, P. Dynamics and control of multidrug-resistant bacterial infection in hospital with multiple delays. Commun. Nonlinear Sci. Numer. Simul. 2020, 89, 105279. [Google Scholar] [CrossRef]
- Henry, I.; Wearne, S.L. Fractional reaction–diffusion. Physics A 2000, 276, 448–455. [Google Scholar] [CrossRef]
- Henry, B.I.; Wearne, S.L. Existence of Turing instabilities in a two-species fractional reaction–diffusion system. SIAM J. Appl. Math. 2002, 62, 870–887. [Google Scholar] [CrossRef]
- Gafiychuk, V.V.; Datsko, B.Y.; Izmajlova, Y.Y. Analysis of the dissipative structures in reaction–diffusion systems with fractional derivatives. Math. Methods Phys. Mech. Fields 2006, 49, 109–116. [Google Scholar]
- Seki, K.; Wojcik, M.; Tachiya, M. Fractional reaction–diffusion equation. J. Chem. Phys. 2003, 119, 2165. [Google Scholar] [CrossRef]
- West, B.J. Fractional Calculus View of Complexity: Tomorrow’s Science; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Baleanu, D.; Mustafa, O.G. Asymptotic Integration and Stability: For Ordinary, Functional and Discrete Differential Equations of Fractional Order; World Scientific: Singapore, 2015; Volume 4. [Google Scholar]
- Wu, G.C.; Baleanu, D.; Zeng, S.D.; Deng, Z.G. Discrete fractional diffusion equation. Nonlinear Dyn. 2015, 80, 281–286. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D.; Xie, H.P.; Zeng, S.D. Discrete fractional diffusion equation of chaotic order. Int. J. Bifurc. Chaos 2016, 26, 1650013. [Google Scholar] [CrossRef]
- Lengyel, I.; Epstein, I.R. A chemical approach to designing Turing patterns in reaction-diffusion systems. Proc. Natl. Acad. Sci. USA 1992, 89, 3977–3979. [Google Scholar] [CrossRef]
- Lengyel, I.; Epstein, I.R. Modeling of Turing structures in the chlorite–iodide–malonic acid–starch reaction system. Science 1991, 251, 650–652. [Google Scholar] [CrossRef]
- Kepper, P.D.; Epstein, I.R.; Kustin, K.; Orban, M. Systematic design of chemical oscillators. Part 8. Batch oscillations and spatial wave patterns in chlorite oscillating systems. J. Phys. Chem. 1982, 86, 170–171. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Bull. Math. Biol. 1990, 52, 153–197. [Google Scholar] [CrossRef]
- Lisena, B. On the global dynamics of the Lengyel–Epstein system. Appl. Math. Comput. 2014, 249, 67–75. [Google Scholar] [CrossRef]
- Zheng, J. Time optimal controls of the Lengyel–Epstein model with internal control. Appl. Math. Optim. 2014, 70, 345–371. [Google Scholar] [CrossRef]
- Zheng, J. Optimal control problem for Lengyel–Epstein model with obstacles and state constraints. Nonlinear Anal. Model. Control 2016, 21, 18–39. [Google Scholar] [CrossRef]
- Yi, F.; Wei, J.; Shi, J. Global asymptotical behavior of the Lengyel–Epstein reaction–diffusion system. Appl. Math. Lett. 2009, 22, 52–55. [Google Scholar] [CrossRef]
- Zafar, Z.U.A. RETRACTED ARTICLE: Fractional order Lengyel–Epstein chemical reaction model. Comput. Appl. Math. 2019, 38, 1–16. [Google Scholar] [CrossRef]
- Ouannas, A.; Wang, X.; Pham, V.T.; Grassi, G.; Huynh, V. Synchronization results for a class of fractional-order spatiotemporal partial differential systems based on fractional Lyapunov approach. Bound. Value Probl. 2019, 2019, 74. [Google Scholar] [CrossRef]
- Mesdoui, F.; Shawagfeh, N.; Ouannas, A. Global synchronization of fractional-order and integer-order N component reaction diffusion systems: Application to biochemical models. Math. Methods Appl. Sci. 2021, 44, 1003–1012. [Google Scholar] [CrossRef]
- Daşbaşı, B.; Daşbaşı, T. Mathematical analysis of Lengyel-Epstein chemical reaction model by fractional-order differential equation’s system with multi-orders. Int. J. Sci. Eng. Investig. 2017, 6, 78–83. [Google Scholar]
- Xu, L.; Zhao, L.J.; Chang, Z.X.; Feng, J.T.; Zhang, G. Turing instability and pattern formation in a semi-discrete Brusselator model. Mod. Phys. Lett. 2013, 27, 1350006. [Google Scholar] [CrossRef]
- Kelley, W.G.; Peterson, A.C. Difference Equations: An Introduction with Applications; Academic Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Baleanu, D.; Wu, G.C.; Bai, Y.R.; Chen, F.L. Stability analysis of Caputo–like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Abdeljawad, T. Different type kernel h-fractional differences and their fractional h-sums. Chaos Solitons Fractals 2018, 116, 146–156. [Google Scholar] [CrossRef]
- Čermák, J.; Nechvátal, L. On a problem of linearized stability for fractional difference equations. Nonlinear Dyn. 2021, 104, 1253–1267. [Google Scholar] [CrossRef]
| a | b | Case | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 15 | 4 | 7 | 1 | 10 | 0.025 | stable | |||
| 20 | 9 | 7 | 7 | 8 | 0.26 | stable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almatroud, O.A.; Hioual, A.; Ouannas, A.; Grassi, G. On Fractional-Order Discrete-Time Reaction Diffusion Systems. Mathematics 2023, 11, 2447. https://doi.org/10.3390/math11112447
Almatroud OA, Hioual A, Ouannas A, Grassi G. On Fractional-Order Discrete-Time Reaction Diffusion Systems. Mathematics. 2023; 11(11):2447. https://doi.org/10.3390/math11112447
Chicago/Turabian StyleAlmatroud, Othman Abdullah, Amel Hioual, Adel Ouannas, and Giuseppe Grassi. 2023. "On Fractional-Order Discrete-Time Reaction Diffusion Systems" Mathematics 11, no. 11: 2447. https://doi.org/10.3390/math11112447
APA StyleAlmatroud, O. A., Hioual, A., Ouannas, A., & Grassi, G. (2023). On Fractional-Order Discrete-Time Reaction Diffusion Systems. Mathematics, 11(11), 2447. https://doi.org/10.3390/math11112447






