Abstract
Auxetic honeycomb has unique mechanical properties such as good energy absorption capacity, tensile strength and fracture toughness, etc. Therefore, honeycomb with a negative Poisson’s ratio is used widely in medical, biological, aerospace and other fields. This honeycomb has large deformations in energy absorption and vibration reduction. It is very important to study the nonlinear constitutive of the honeycomb structure. Therefore, this paper establishes the nonlinear constitutive relationship of the auxetic honeycomb structure under large deformations. This constitutive relation includes the in-plane stress, in-plane strain, Young’s modulus and Poisson’s ratio of the negative Poisson’s ratio honeycomb. The finite element model of the negative Poisson’s ratio honeycomb cells is established, and the calculated results of finite element model are compared with that of the theoretical calculation results. On this basis, the influence of the geometric parameters on the mechanical properties of the structure is studied. The results of this paper will provide a theoretical basis for the further study of the auxetic honeycomb sandwich structure and provide a basis for the engineering application of honeycomb structures.
Keywords:
negative Poisson’s ratio; honeycomb; nonlinear constitutive; equivalent mechanical parameters MSC:
74M20
1. Introduction
As a lightweight material structure, the honeycomb structure not only has high specific stiffness and specific strength, but also has good thermal insulation, vibration isolation, energy absorption and impact resistance [1,2]. It has been widely used in aerospace, vehicles [3], construction [4], bridges and national defense. The honeycomb sandwich structure is composed of periodically arranged honeycomb cells as the core layer and a thin skin. Most of the honeycomb cores of the sandwich are considered as homogeneous materials when calculating their equivalent elastic parameters. Gibson et al. [5] gave the basic theory of foam and honeycomb structures and put forward the classical theory of calculating the equivalent elastic modulus of the honeycomb core layer. The main calculated methods of equivalent parameters include the energy method, the stiffness matrix method, the integral method and theoretical calculation through the traditional mechanics of the materials. Zhang et al. [6] constructed a butterfly honeycomb structure and derived its equivalent parameters using the energy method. Wu et al. [7] carried out deflection and strain analysis on the deformation of semi-reentrant honeycomb and established four equivalent theories based on the consideration of bending, tensile, hinged, shear deformation and wall thickness.
The honeycomb with a negative Poisson’s ratio has better mechanical properties than traditional honeycombs. Therefore, it is of great practical significance to study the relationship between the microstructure geometry and the macroscopic structural mechanical properties of negative Poisson’s ratio honeycomb. In 1987, Lakes [8] designed polyurethane foam materials with negative Poisson’s ratio characteristics. Since then, the research of negative Poisson’s ratio materials has developed rapidly. Zhou et al. [9] evaluated the effective elastic properties of multiphase composites by numerical method. Wang et al. [10] extracted the structural parameters of the unit and studied the mechanical properties of the three-dimensional star structure by theoretical derivation, numerical and experimental methods. Pagliocca et al. [11] introduced orthogonal perforation mechanical metamaterials with different characteristics and studied the mechanical properties. Xue et al. [12] improved the mechanical properties of the honeycomb lattice structure by adding struts. Hou et al. [13] derived the analytical formula of dynamic compressive strength according to the periodic collapse principle of unit structure. Chen et al. [14] designed a three-dimensional structure with an adjustable Poisson’s ratio and an adjustable thermal expansion coefficient which shows high stiffness. Chen et al. [15] studied the elastic behavior of honeycomb and its dependence on geometric parameters. Serban [16] studied the Poisson’s ratio of an elastomeric structure with different structural parameters under axial strain. Valle et al. [17] used the classical Timoshenko beam theory to design the auxiliary element through topological analysis. Harkati et al. [18] conducted a parametric study on the multiple-entry honeycomb structure with variable stiffness and Poisson’s ratio effect.
The honeycomb will show nonlinear characteristics under large deformation. Therefore, linear elasticity cannot accurately describe the mechanical behavior of the structure in the elastic stage. Geometric nonlinearity needs to be considered. Han et al. [19] optimized the energy absorption of the overall structure by adjusting the material distribution in the large deformation region and the small deformation region. Ciepielewski et al. [20] studied the stress of aluminum honeycomb sandwich materials under static and dynamic compressive loads. Qi et al. [21] studied the three-dimensional chiral structure under large deformation conditions through theoretical and experimental innovation. Farrugia et al. [22] studied the possible negative Poisson’s ratio effect of square and rectangular honeycombs under large deformation conditions. Hong [23] used the third-order shear deformation theory to study the nonlinear static bending and nonlinear free vibration behavior of functionally graded plates under strong loads. Taherkhani et al. [24] studied the cell geometry effect on Poisson’s ratio under the large tension of the auxetic structure. Zhu et al. [25] studied the potential deformation mechanism of reinforced structures under different geometric parameters through finite element analysis under large deformation conditions. Teng et al. [26] studied the influence on geometric parameters of three-dimensional honeycomb under large deformation through a structural deformation mode and energy absorption performance. Du et al. [27] found that the nonlinear mechanical behavior is closely related to the rib bending in the metamaterial foam and the maximum tensile strain is caused by the stiffener. Yin et al. [28] studied the nonlinear mechanics of periodic network materials and gave the change of Poisson’s ratio and the tensile stiffness with change of microstructure geometries. Lan et al. [29,30] gave the in-plane mechanical performance of a thin-walled honeycomb structure and analyzed the elastic-plastic deformation of the honeycomb.
Honeycomb will produce large deformation as absorbing energy. However, there are few studies on the nonlinear constitutive relationship of auxetic honeycomb under large deformation. Based on existing research, this paper establishes the nonlinear constitutive relationship of a negative Poisson’s ratio honeycomb structure under large deformation. By introducing the Almansi strain and using an elliptic integral to represent the bending deformation of the honeycomb wall, the equivalent mechanical parameter formula of concave hexagonal auxetic honeycomb cells under elastic buckling is derived, including the in-plane stress, strain, Young’s modulus and Poisson’s ratio. The results of the finite element model are compared with the results of the theoretical calculation. On this basis, the influence of the geometric parameters of the negative Poisson’s ratio honeycomb on the mechanical properties of the structure is studied.
2. Equivalent Parameters
A cell of concave hexagonal honeycomb with a negative Poisson’s ratio is shown in Figure 1; the lengths of the straight wall and inclined wall are, respectively, expressed as h and l, the thickness of the wall is t, the angle between the inclined wall and the horizontal plane is the cell angle , and the angle between the inclined wall and the vertical plane is .
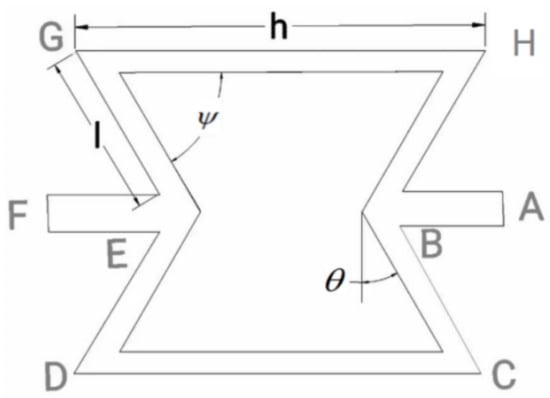
Figure 1.
Concave hexagonal auxetic honeycomb cell.
The relative density of the honeycomb with a negative Poisson’s ratio can be calculated by the ratio of the actual volume of honeycomb (V*) to the volume occupied by the honeycomb structure (V0) [29]:
The deformation of the auxetic honeycomb is mainly realized by the bending deformation of the inclined wall. Therefore, the inclined wall of the honeycomb is selected as the main research object as the equivalent parameters are calculated. When the honeycomb cell is subjected to uniaxial compression in the y direction, the deformation mode of the inclined wall is shown in Figure 2. According to the force analysis, the inclined wall is loaded with the concentrated force P and the corresponding bending moment is M. It can be observed that the inclined wall is symmetrically deformed. Therefore, half of the inclined wall is taken to study the deformation of the honeycomb. Point O in Figure 2 is the midpoint of the inclined wall.
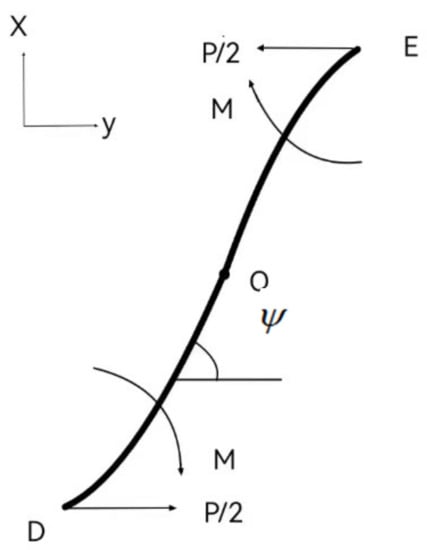
Figure 2.
Bending deformation of inclined wall of honeycomb cell under y-axis pressure.
Write the differential equation of the deflection curve of the beam under compression in Figure 2 as follows:
where Es is the Young’s modulus of the material, I is the moment of inertia of the inclined wall, α is the bending angle of the honeycomb, s is the curvilinear coordinates of the inclined wall, and Ψ is the curvilinear coordinates of the inclined wall. The dimensionless Equation (2) can be obtained:
where , , can be obtained by integrating Equation (3)
by giving the following boundary conditions:
where β is the angle of the inclined wall in the deformation process.
It can be solved as
Substituting Equation (6) into Equation (4) for simplification, we can obtain
Substitute the polynomial in the root sign of Equation (7): The dimensionless force ζ in Equation (7) can be simplified by the first kind of elliptic integral F after substitution:
where the first elliptic integral F and the second elliptic integral E are denoted by
among them, the integral upper limit . At the same time, through the elliptic integral element, the separation variable S in Equation (7) can be obtained:
The honeycomb inclined wall deformation S can be obtained by solving Equation (11). By projecting the deformation of the inclined wall S to the x-axis and the y-axis respectively, the deformation of the inclined wall in two directions X and Y expressed by the elliptic integral can be obtained:
When the honeycomb is under tension, the sign of in Equations (4)–(12) needs to be changed into a plus sign.
The deformation force of the honeycomb elastic stage is expressed by Euler stress when loaded in x direction,
When the loaded is in y direction, is it expressed as
The Almansi strain is used to represent the strain value of the honeycomb cell in each direction as follows:
where X, Y are obtained by Equations (12) and (13).
The Young’s modulus and Poisson’s ratio can be calculated according to the stress and strain values
In the above formulas, the value of stress is given by formula Equations (14) and (15), and the value of strain is given by formula Equations (16)–(19). In this section, the bending deformation of a negative Poisson’s ratio honeycomb cell is represented by the elliptic integral and the nonlinear deformation is represented by Almansi strain. The equivalent Young’s modulus and Poisson’s ratio of a negative Poisson’s ratio honeycomb cell are derived. The following section will compare the calculation results with the finite element model.
3. Finite Element Verification
In order to verify the correctness of the above nonlinear equivalent mechanical parameter formulas, the finite element model of negative Poisson’s ratio concave hexagonal honeycomb cell is established. The honeycomb cell size is as follows: h = 20 mm, l = 10 mm, t = 1 mm, and the in-plane depth of honeycomb is b = 10 mm. Ansys finite element software is used for simulation, and explicit dynamics Ls-dyna analysis is used. The matrix material is aluminum. The material parameters are density ρ = 2700 kg/m3, Poisson’s ratio μ = 0.33, and elastic modulus E = 69 GPa. The honeycomb cell is assumed to be an ideal elastoplastic model. The displacement is given for stretching and the analysis time is 0.01 s. When the honeycomb specimen is impacted, the bottom of the specimen is fixed and the top of the specimen is applied with displacement. The mesh convergence is considered in the meshing process of finite element software. The simulation results of the multi-grid size model show that when the grid size is less than 0.4 mm, the total deformation-equivalent stress curve of the honeycomb remains basically unchanged, as shown in Figure 3. Therefore, the mesh size for the finite element model in this paper is selected as 0.4 mm.
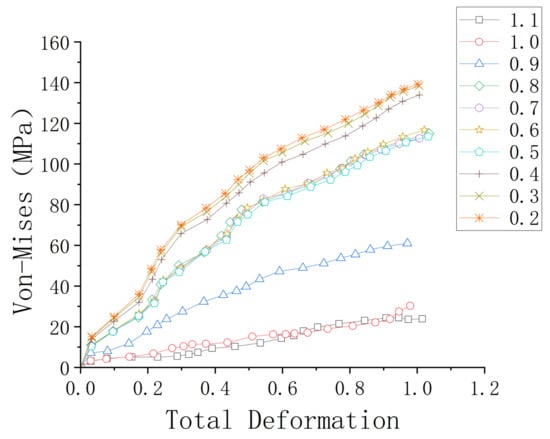
Figure 3.
The mesh convergence of finite element model.
When the 2 mm displacement is compressed along the y direction, the comparison results of the Young’s modulus and the Poisson’s ratio of the negative Poisson’s ratio honeycomb are shown in Figure 4. It can be seen from Figure 4a that the theoretical calculation of the equivalent Young’s modulus and Poisson’s ratio are consistent with the calculation results of the concave hexagonal honeycomb cell modeled by the finite element solid element. The Poisson’s ratio of the theoretical calculation in Figure 4b is about −0.95, and the result of the finite element model calculation is about −1. The error is within the acceptable range. The cause of the error may be due to the difference between the meshing and the finite element software. It has been proven that the correctness of the nonlinear constitutive for the negative Poisson’s ratio honeycomb, derived in this paper. It can be seen from Figure 4 that the Young’s modulus decreases with the increase of strain, and Poisson’s ratio decreases first and then increases slightly with the increase of strain. Therefore, the mechanical parameters of honeycomb change with the increase of strain.
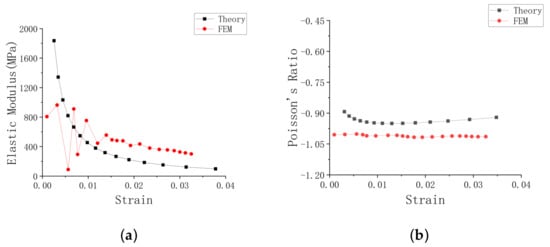
Figure 4.
Comparison of theoretical and finite element results. (a) Young’s modulus, (b) Poisson’s ratio.
4. Parametric Analysis
In order to further study the mechanical properties of negative Poisson’s ratio honeycomb cells in the nonlinear elastic stage, this paper compares the results with that in the literature and carries out parameter analysis. The effects of honeycomb cell angle, thickness-to-length ratio and ratio of straight arm length to inclined wall length on the Young’s modulus and Poisson’s ratio of the honeycomb are studied.
4.1. Comparison of Linear and Nonlinear Equivalent Parameters
In Section 2, the nonlinear elastic equivalent mechanical parameters of negative Poisson’s ratio honeycomb are calculated by introducing the Almansi strain and an elliptic integral. The theoretical and finite element results in Figure 4 show that the deformation of honeycomb is nonlinear. The nonlinear terms of the strain Equations (16)–(19) in Section 2 are removed and compared with the linear elastic equivalent parameters calculated by Zhang et al. [31] as shown in Figure 5. It can be seen from Figure 5 that the linear elastic equivalent Young’s modulus and Poisson’s ratio calculated in the literature are constant. When the strain is about 0.02, the equivalent Young’s modulus and Poisson’s ratio are very close to the theoretical calculation results in this paper. This also proves the correctness of the theoretical formula derived in this paper. At the same time, it shows that the honeycomb deformation is nonlinear, and considering the nonlinearity can better describe the deformation of the honeycomb. Comparing Figure 4 and Figure 5, it can be seen that the influence of the elliptic integral is greater than that of the nonlinear part of the Almansi strain.
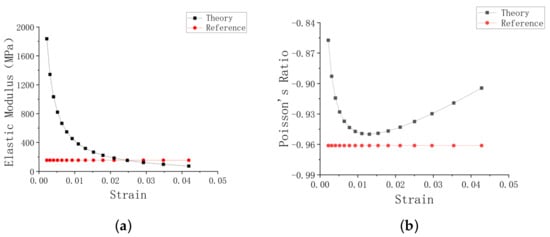
Figure 5.
Comparison of this paper and literature. (a) Young’s modulus, (b) Poisson’s ratio.
4.2. Effect of Honeycomb Cell Angle on Mechanical Parameters
Considering four honeycomb angles as 30°, 45°, 60° and 75°, the remaining geometric parameters are l = 10 mm, h = 20 mm, b = 10 mm and t = 1 mm. The material parameter is Es = 69 MPa. A displacement of 2 mm is given to analyze the influence of cell angle change on the equivalent parameters of the honeycomb. The stress cloud of the honeycomb cell is shown in Figure 6. It can be seen that the deformation of the honeycomb cell with different cell angles shows a negative Poisson’s ratio effect. The strain at the node position connected by the straight wall and the inclined wall is the largest and the inclined wall bears the main deformation.
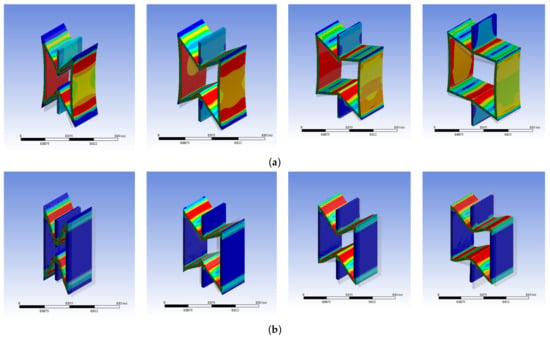
Figure 6.
Honeycomb cell stress under different cell angles (30°, 45°, 60°, 75°). (a) Compression in y direction, (b) Stretch in x direction.
Figure 7 shows the change of the Young’s modulus of the honeycomb cell under different cell angles when the honeycomb cell is loaded in y and x directions, respectively. It can be seen from Figure 7a that when the honeycomb is loaded in the y direction, the Young’s modulus begins to stabilize after the strain is greater than 0.01, and the Young’s modulus of 30° is the largest while the Young’s modulus of 45° is the smallest. The variation of Young’s modulus with strain is roughly the same at different honeycomb cell angles. It can be seen from Figure 7b that the negative Poisson’s ratio honeycomb with 75° cell angle shows different trends when loaded in the x direction. This is mainly because the cell angle is too large, the overall structure of the honeycomb is close to the square during the stretching process. The stress cloud changes as shown in Figure 6b.
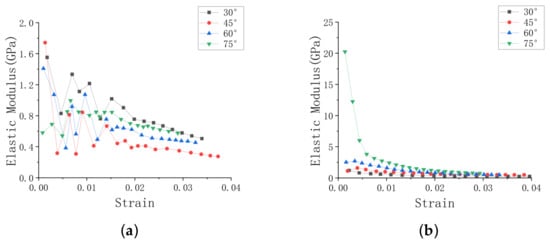
Figure 7.
Young’s modulus under different honeycomb angles. (a) Loading in y direction, (b) Loading in x direction.
Figure 8 shows the variation in Poisson’s ratio with honeycomb cell angle. It can be seen from Figure 8a that when loaded in the y direction, the Poisson’s ratio gradually decreases as the strain increases, and the Poisson’s ratio of the honeycomb cell gradually decreases as the cell angle decreases. When the cell angle is less than 45°, the decreasing trend of Poisson’s ratio is more obvious. When the angle is greater than 45°, the decreasing trend of Poisson’s ratio is not obvious. It can be seen from Figure 8b that when loading in the x direction, the Poisson’s ratio of honeycomb with cell angles of 60° gradually increases with the increase of strain, while the Poisson’s ratio of honeycomb with other cell angles gradually decreases.
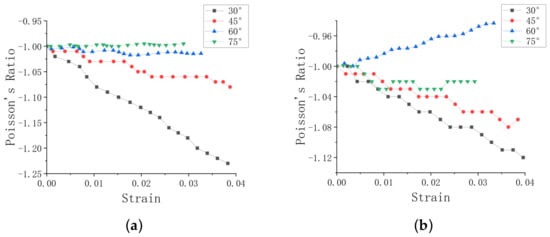
Figure 8.
Poisson’s ratio under different honeycomb angles. (a) Loading in y direction, (b) loading in x direction.
4.3. Effect of Thickness-to-Length Ratio t/l on Mechanical Parameters
The honeycomb thickness-to-length ratios t/l are 0.1, 0.2, 0.4 and 0.6, respectively. Other geometric parameters are = 60°, l = 10 mm, h = 20 mm and b = 10 mm, and the material parameter is Es = 69 MPa. The deformation of the honeycomb cell loaded in two directions is shown in Figure 9. It can be seen from Figure 9a that the stress value inside the honeycomb is the largest, and the diffusion to the periphery gradually decreases. The symmetrical deformation of the inclined wall is more obvious when loading in the x direction.
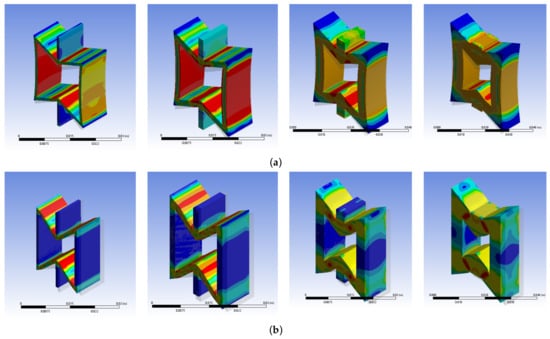
Figure 9.
Honeycomb cell stress under different thickness-to-length ratio t/l (0.1, 0.2, 0.4, 0.6). (a) Compression in y direction, (b) stretch in x direction.
Figure 10 shows the change of the Young’s modulus when the honeycomb is loaded in y and x directions, respectively. The thickness-to-length ratio t/l has a significant effect on the Young’s modulus of the negative Poisson’s ratio honeycomb. The Young’s modulus gradually decreases with the increase of strain. At the same strain value, the Young’s modulus will gradually increase with the increase of the thickness-length ratio. Compared with that of the y-direction loading, the honeycomb has a larger strain value and a larger Young’s modulus loaded in the x-direction, which is due to the anisotropy of the honeycomb.
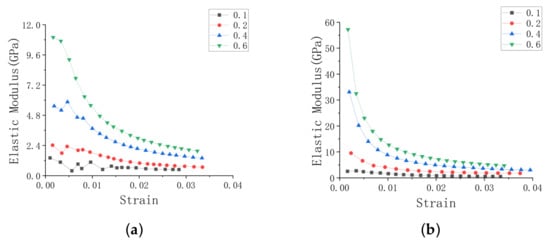
Figure 10.
Young’s modulus under different thickness-to-length ratio t/l. (a) Loading in y direction, (b) loading in x direction.
The change of Poisson’s ratio under different thickness-to-length ratios is shown in Figure 11. Figure 11a shows that the Poisson’s ratio of the honeycomb decreases gradually with the increase of strain. As the thickness-to-length ratio increases, the Poisson’s ratio of the honeycomb gradually decreases. Figure 11b shows the effect of the thickness-to-length ratio on the Poisson’s ratio of the honeycomb loaded in the x direction. As the strain increases, the Poisson’s ratio gradually increases. When the thickness-to-length ratio is greater than 0.2, the Poisson’s ratio of the honeycomb increases gradually.
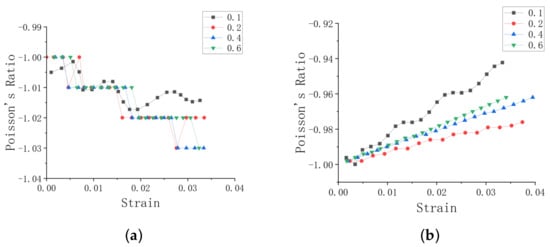
Figure 11.
Poisson’s ratio under different thickness-to-length ratio t/l. (a) Loading in y direction, (b) loading in x direction.
4.4. Effect of the Ratio of Straight Wall to Inclined Wall h/l on Mechanical Parameters
The stress under different ratios of straight wall to inclined wall is shown in Figure 12. The geometric parameters are = 60°, l = 10 mm, t = 20 mm and b = 10 mm, and the material parameters are Es = 69 MPa. The ratio of honeycomb straight wall to inclined wall is adjusted to 1.2, 1.5, 1.8 and 2.4. Different straight wall lengths have little effect on the deformation of the honeycomb. The main deformation of the honeycomb is achieved by the deformation of the inclined wall, so the inclined wall bears most of stress.
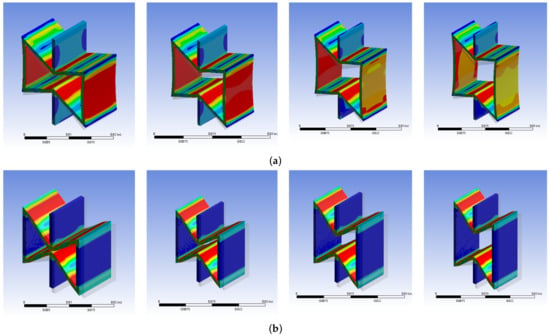
Figure 12.
Honeycomb cell stress under different ratios of straight wall to inclined wall h/l (1.2, 1.5, 1.8, 2.4). (a) Compression in y direction, (b) stretch in x direction.
Figure 13 is the result of the Young’s modulus when the honeycomb is loaded in both y and x directions. With the increase of strain value, the Young’s modulus of honeycomb decreases gradually. In the case of y-direction loading, the Young’s modulus of the honeycomb is the largest when h/l is 2.4. When the load is in x direction, the Young’s modulus of the honeycomb decreases with the increase of h/l. However, the above trend is not obvious. This is because the length of the straight wall increases, the length of the inclined wall does not change and the main deformation of the honeycomb depends on the bending deformation of the inclined wall—so the change of Young’s modulus is not obvious.
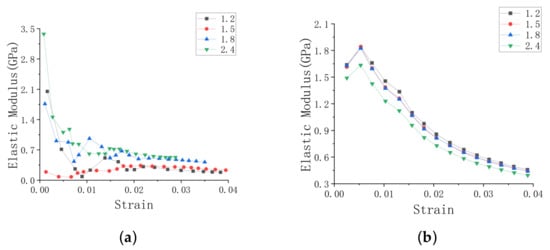
Figure 13.
Young’s modulus under different the ratios of straight wall to inclined wall h/l. (a) Loading in y direction, (b) loading in x direction.
Figure 14 shows the Poisson’s ratios of honeycombs with different ratios of straight and inclined walls. The Poisson’s ratio of honeycomb decreases with the increase of the ratio of straight wall to inclined wall. The difference between the maximum Poisson’s ratio and the minimum Poisson’s ratio is 0.02 in the y direction, as shown in Figure 14a. The change of the Poisson’s ratio in the x direction is larger, and the difference between the maximum Poisson’s ratio and the minimum Poisson’s ratio is 0.06, as shown in Figure 14b.
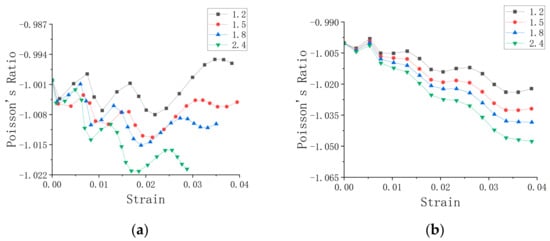
Figure 14.
Poisson’s ratio under different the ratios of straight wall to inclined wall h/l. (a) Loading in y direction, (b) loading in x direction.
In summary, with the increase of honeycomb wall thickness, the Young’s modulus of honeycomb decreases gradually. The Young’s modulus of honeycomb with a negative Poisson’s ratio is most affected by the thickness of honeycomb wall. When the wall thickness is 0.6, the Young’s modulus of the honeycomb is 10 times higher than that of the wall thickness of 0.1. E2 is higher than E1. As the cell angle decreases, the thickness and the straight wall increase, ν1 gradually increases and ν2 gradually decreases. The Poisson’s ratio of honeycomb is most affected by cell angle, followed by t/l. Compared with ν1, ν2 is more likely to receive the influence of honeycomb structure parameters.
5. Conclusions
In this paper, the nonlinear constitutive relation of the concave hexagonal honeycomb with a negative Poisson’s ratio is given and compared with the finite element model and the literature. The influence of the cell parameters on the mechanical parameters of the honeycomb is studied. The conclusions are as follows:
- The elliptic integral was used to represent the nonlinear bending deformation of the honeycomb wall and the Almansi strain was used to represent the nonlinear strain. The nonlinear constitutive relationship of the negative Poisson’s ratio honeycomb was obtained. Based on this, the equivalent mechanical parameters were calculated to compare with the mechanical parameters of the honeycomb cell calculated by the finite element model established by the solid element. The two were consistent, which verifies the correctness of the theoretical formula.
- By comparing the theoretical results calculated in this paper with the linear elastic equivalent mechanical parameters in the literature, it was found that when the strain is about 0.02, the equivalent Young’s modulus and Poisson’s ratio calculated by the two methods were very close. At the same time, it can be concluded that when considering the nonlinear deformation of honeycomb, the mechanical properties of honeycomb under load can be described more accurately.
- The variations in Young’s modulus and Poisson’s ratio was studied when the parameters of the honeycomb cell changed, including the cell angle of honeycomb cell, the thickness-length ratio of honeycomb wall and the ratio of straight wall to inclined wall.
The results obtained in this paper will provide a theoretical basis for the further study of the negative Poisson’s ratio honeycomb sandwich structure, and also provide a basis for the engineering application of the honeycomb structure.
Author Contributions
Conceptualization, J.Z.; methodology, J.Z. and Q.M.; software, Q.M.; validation, J.Z. and Q.M.; formal analysis, J.Z. and Q.M.; investigation, J.Z. and Q.M.; resources, J.Z. and Q.M.; data curation, Q.M.; writing—original draft preparation, Q.M. and J.Z.; writing—review and editing, J.Z. and Q.M.; supervision, J.Z.; funding acquisition, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the support of National Natural Science Foundation of China No. 12272057.
Data Availability Statement
Data available with request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, N.; Deng, Q.; Li, X. Deformation behaviors and energy absorption of composite re-entrant honeycomb cylindrical shells under axial load. Materials 2021, 14, 7129. [Google Scholar] [CrossRef] [PubMed]
- Gong, X.B.; Ren, C.W.; Liu, Y.H.; Sun, J.; Xie, F. Impact response of the honeycomb sandwich structure with different Poisson’s ratios. Materials 2022, 15, 6982. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.J.; Liu, P.; Kang, Z. A novel mechanical metamaterial with simultaneous stretching- and compression-expanding property. Mater. Des. 2021, 208, 109930. [Google Scholar] [CrossRef]
- Shah, I.A.; Khan, R.; Koloor, S.S.R.; Petru, M.; Badshah, S.; Ahmad, S.; Amjad, M. Finite element analysis of the ballistic impact on auxetic sandwich composite human body armor. Materials 2022, 15, 2064. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Zhang, Z.W.; Tian, R.L.; Zhang, X.L.; Wei, F.Y.; Yang, X.W. A novel butterfly-shaped auxetic structure with negative Poisson’s ratio and enhanced stiffness. J. Mater. Sci. 2021, 56, 14139–14156. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.G.; Cai, W.; Guo, K.L.; Zhu, L. Dynamic responses and energy absorption of sandwich panel with aluminium honeycomb core under ice wedge impact. Int. J. Impact Eng. 2022, 162, 104137. [Google Scholar] [CrossRef]
- Lakes, R. Deformation mechanisms in negative Poisson’s ratio materials: Structural aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Li, X.P.; Gao, L. Design of multiphase auxetic metamaterials by a parametric color level set method. Compos. Struct. 2022, 287, 115385. [Google Scholar] [CrossRef]
- Wang, W.W.; Dai, S.J.; Zhao, W.Z.; Wang, C.Y.; Zhang, Z.Y. Topology design and equivalent mechanical properties of a three-dimensional star-shaped auxetic structure. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2022, 236, 1108–1121. [Google Scholar] [CrossRef]
- Pagliocca, N.; Uddin, K.Z.; Anni, I.A.; Shen, C.; Youssef, G.; Koohbor, B. Flexible planar metamaterials with tunable Poisson’s ratios. Mater. Des. 2022, 215, 110446. [Google Scholar] [CrossRef]
- Xue, Y.Y.; Gao, P.X.; Zhou, L.; Han, F.S. An enhanced three-dimensional auxetic lattice structure with improved property. Materials 2020, 13, 1008. [Google Scholar] [CrossRef]
- Hou, X.H.; Deng, Z.C.; Zhang, K. Dynamic crushing strength analysis of auxetic honeycombs. Acta Mech. Solida Sin. 2016, 29, 490–501. [Google Scholar] [CrossRef]
- Chen, M.M.; Fu, M.H.; Lan, L.H.; Sheshenin, S.V. A novel 3D structure with tunable Poisson’s ratio and tailorable coefficient of thermal expansion based on a tri-material triangle unit. Compos. Struct. 2020, 253, 112803. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, B.B.; Fu, M.H.; Lan, L.H.; Zhang, W.Z. Doubly unusual 3D lattice honeycomb displaying simultaneous negative and zero Poisson’s ratio properties. Smart Mater. Struct. 2018, 27, 045003. [Google Scholar] [CrossRef]
- Şerban, D.A.; Qian, G. Variation of Poisson’s ratio with axial strain for three-dimensional reentrant auxetic structures. J. Mater. Process. Technol. 2022, 2022, 2623601. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe, L.E. Design and characterization of asymmetric cell structure of auxetic material for predictable directional mechanical response. Materials 2022, 15, 1841. [Google Scholar] [CrossRef]
- Harkati, E.; Daoudi, N.; Bezazi, A.; Haddad, A.; Scarpa, F. In-plane elasticity of a multi re-entrant auxetic honeycomb. Compos. Struct. 2017, 180, 130–139. [Google Scholar] [CrossRef]
- Han, D.; Ren, X.; Zhang, Y.; Yu, Z.X.; Gang, Z.X.; Luo, C.; Min, X.Y. Lightweight auxetic metamaterials: Design and characteristic study. Compos. Struct. 2022, 293, 115706. [Google Scholar] [CrossRef]
- Ciepielewski, R.; Gieleta, R.; Miedzinska, D. Experimental study on static and dynamic response of aluminum honeycomb sandwich structures. Materials 2022, 15, 1793. [Google Scholar] [CrossRef]
- Qi, D.X.; Zhang, P.; Wu, W.W.; Xin, K.H.; Liao, H.T.; Li, Y.; Xiao, D.B.; Xia, R. Innovative 3D chiral metamaterials under large deformation: Theoretical and experimental analysis. Int. J. Solids Struct. 2020, 202, 787–797. [Google Scholar] [CrossRef]
- Farrugia, P.S.; Gatt, R.; Mizzi, L.; Grima, J.N. Auxetic behavior obtained through the large deformations of variants of the rectangular grid. Mech. Adv. Mater. Struct. 2021, 30, 262–271. [Google Scholar] [CrossRef]
- Hong, N.T.; Pizzarelli, M. Nonlinear static bending and free vibration analysis of bidirectional functionally graded material plates. J. Aerosp Eng. 2020, 2020, 8831366. [Google Scholar] [CrossRef]
- Taherkhani, B.; Anaraki, A.P.; Kadkhodapour, J.; Rezaei, S.; Tu, H. Large deformation of TPU re-entrant auxetic structures designed by TO approach. J. Elastomers Plast. 2020, 53, 347–369. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Jiang, S.H.; Lu, F.C.; Ren, X. A novel enhanced anti-tetra-missing rib auxetic structure with tailorable in-plane mechanical properties. Eng. Struct. 2022, 262, 114399. [Google Scholar] [CrossRef]
- Teng, X.C.; Ren, X.; Zhang, Y.; Jiang, W.; Pan, Y.; Zhang, X.G.; Zhang, X.Y.; Xie, Y.M. A simple 3D re-entrant auxetic metamaterial with enhanced energy absorption. Int. J. Mech. Sci. 2022, 229, 107524. [Google Scholar] [CrossRef]
- Du, L.M.; Luo, S.D.; Xu, Y. Understanding nonlinear behaviors of auxetic foams using X-ray tomography and pore structure analysis. Mech. Mater. 2022, 165, 104196. [Google Scholar] [CrossRef]
- Yin, Y.F.; Zhao, Z.; Li, Y.H. Theoretical and experimental research on anisotropic and nonlinear mechanics of periodic network materials. J. Mech. Phys. Solids 2021, 152, 104458. [Google Scholar] [CrossRef]
- Lan, L.H.; Sun, J.; Hong, F.L.; Wang, D.Y.; Zhang, Y.S.; Fu, M.H. Nonlinear constitutive relations of thin-walled honeycomb structure. Mech. Mater. 2020, 149, 103556. [Google Scholar] [CrossRef]
- Lan, L.H.; Luo, W.L.; Sun, J.; Liu, D.Y.; Fu, M.H. Analytical investigation on elastic–plastic deformation of reentrant honeycomb structures. AIAA J. 2021, 59, 3735–3747. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhu, X.F.; Yang, X.D.; Zhang, W. Transient nonlinear responses of an auxetic honeycomb sandwich plate under impact loads. Int. J. Impact Eng. 2019, 134, 103383. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).