Abstract
Survival after out-of-hospital cardiac arrest (OHCA) is contingent on time-sensitive interventions taken by onlookers, emergency call operators, first responders, emergency medical services (EMS) personnel, and hospital healthcare staff. By building integrated cardiac resuscitation systems of care, measurement systems, and techniques for assuring the correct execution of evidence-based treatments by bystanders, EMS professionals, and hospital employees, survival results can be improved. To aid in OHCA prognosis and treatment, we develop a hybrid agnostic explanation TabNet (HAE-TabNet) model to predict OHCA patient survival. According to the results, the HAE-TabNet model has an “Area under the receiver operating characteristic curve value” (ROC AUC) score of 0.9934 (95% confidence interval 0.9933–0.9935), which outperformed other machine learning models in the previous study, such as XGBoost, k-nearest neighbors, random forest, decision trees, and logistic regression. In order to achieve model prediction explainability for a non-expert in the artificial intelligence field, we combined the HAE-TabNet model with a LIME-based explainable model. This HAE-TabNet model may assist medical professionals in the prognosis and treatment of OHCA patients effectively.
Keywords:
hybrid model; TabNet; machine learning; LIME; explainable AI; out-of-hospital cardiac arrest (OHCA) MSC:
68T01; 68T09; 68T07
1. Introduction
Sudden cardiac arrest, also known as out-of-hospital cardiac arrest (OHCA), happens when a person’s heart suddenly stops beating for no apparent reason outside of a medical facility. OHCA is considered a serious public health burden across the world, with around 30,000 cases handled by emergency medical services (EMS) in the Republic of Korea each year [1]. Only 10% of approximately 400,000 Americans who have this illness survive [2]. OHCA causes more premature deaths for men (2.04 million years) and women (1.29 million years) than all other malignancies and most other main causes of mortality [3]. OHCA is the patient’s initial and sole sign of cardiovascular illness in many circumstances [4]. Due to its abrupt onset, high prevalence, and low resuscitation success rates, OHCA is an urgent public health problem that has to be addressed.
Survival after cardiac arrest is contingent on time-sensitive interventions taken by onlookers, emergency call operators, first responders, emergency medical services (EMS) personnel, and hospital healthcare staff. By building integrated cardiac resuscitation systems of care, measurement systems, and techniques for assuring the correct execution of evidence-based treatments by bystanders, EMS professionals, and hospital employees, survival results can be improved [5]. The “chain of survival” for OHCA outcomes includes important “bridges” of intervention, such as witnessed arrest, bystander-initiated cardiopulmonary resuscitation (CPR), community-accessible defibrillation, dispatcher-assisted CPR, shorter EMS response intervals, initial defibrillate cardiac rhythm, the quality of CPR, return of spontaneous circulation (ROSC) in the field, and post-resuscitation care [6,7]. To enhance survival outcomes, research goals might be directed by identifying sensitive points throughout the continuum of care.
In recent years, deep learning methods have demonstrated superior performance in areas of critical care, such as hospital cardiac arrest prediction, severity evaluation, and OHCA outcome prediction [8,9,10,11,12]. Cho et al. [8] proposed a deep learning-based early warning system with 0.865 of the area under the receiver operating characteristic curve (ROC AUC) and 0.066 of the area under the precision-recall curve (PRC AUC), which outperformed the modified early warning score (ROC AUC: 0.682, PRC AUC: 0.010) and decreased the number of examines needed and the mean alarm count per day by 69.2% and 59.6%, respectively. Additionally, an algorithm based on deep learning [9] outperformed traditional triage tools and effectively predicted patients’ requirements to obtain critical care during emergency medical services. The ROC AUC of the algorithm to predict critical care was 0.867, which outperformed the emergency severity index (0.839), the Korean triage and acuity system (0.824), the national early warning score (0.741), and the modified early warning score (0.696). Kwon et al. [10] developed a deep learning-based out-of-hospital cardiac arrest prognostic system (DCAPS) for predicting neurologic recovery and survival to discharge. The ROC AUC of DCAPS for predicting neurologic recovery was 0.953, whereas it was 0.901 for predicting survival discharge. In another study, Kwon et al. [11] validated that a deep learning-based triage and acuity score identifies high-risk patients more accurately than existing triage and acuity scores using a large national dataset. A multicenter study [12] utilized a deep learning-based early warning system to identify patients at risk of in-hospital cardiac arrest, achieving great sensitivity and a low false-alarm rate. This deep learning-based early warning system (ROC AUC: 0.850, PRC AUC: 0.044) outperformed the modified early warning score (ROC AUC: 0.603, AUPRC: 0.003), the random forest model (ROC AUC: 0.780, PRC AUC: 0.014), and logistic regression model (ROC AUC: 0.613, PRC AUC: 0.007). Moreover, this model reduced the number of alarms by 82.2%, 13.5%, and 42.1% compared with the modified early warning system, random forest, and logistic regression, respectively, at the same sensitivity. The capacity of deep learning models to automatically learn features from input data is a key attribute [11]. Consequently, a predictive system for OHCA may be constructed by combining deep learning and patient and paramedic data to predict OHCA patient outcomes and assist medical professionals in making therapeutic decisions.
Although deep learning models are capable of learning complicated data structures, deep networks generalize less well on tabular datasets than other traditional machine learning models [13]. To solve the restrictions of deep learning models on tabular data, Arik et al. [14] introduced TabNet, a revolutionary canonical deep tabular learning architecture. TabNet uses single deep learning, multi-step processing, sequential attention, and gradient descent to build a novel architecture that achieves both high accuracy and model interpretability in contrast to more conventional deep learning methods. Recent medical research has utilized TabNet to predict outcomes such as pulmonary embolism [15], concomitant epilepsy [16], breast cancer [17], tacrolimus daily dosage in kidney transplant recipients [18], lapatinib dosing regimen in breast cancer patients [19], and memory development. In several of these studies, TabNet was found to perform better than the competing models. This is because of the advantages of the TabNet model’s design [14], which develops a sequential multi-step architecture in which each phase, contributes to decision-making on the selection of critical attributes. TabNet is quite similar to ensemble models since it can build larger dimensions and more stages. Nevertheless, increasing the number of phases would increase model complexity. In addition, like other deep learning models, TabNet is hyperparameter-sensitive. Therefore, hyperparameter fine-tuning is essential for achieving more outstanding outcomes.
In addition to making accurate predictions from tabular data, TabNet is also interpretable [14]. This addresses a major problem with the complicated, non-linear, and uninterpretable “black-box” design typically used in deep learning [20]. Even if a “black-box” model produces positive outcomes, there may be concerns about its reliability and transparency, particularly in the healthcare industry. According to model dependency, eXplainable Artificial Intelligence (XAI) interpretability approaches are classified as model-agnostic or model-specific [21]. TabNet belongs to the model-specific group of intrinsic interpretability methods. Knowing the inner workings of a model-specific interpretable model, such as TabNet, allows us to have a deeper understanding of the outcomes [14]. However, the model would need to be retrained in order to regain the explanations [22]. If not properly optimized, this might affect the model performance in a real-world setting. Contrarily, model-agnostic approaches ignore model structure. It may be applied to any machine learning or deep learning classifiers considered “black-box” models without affecting their performance [23].
The recently developed framework known as the local interpretable model-agnostic explanation (LIME) may be used with any black-box classification model to generate an explanation for a singular manifestation [24]. This technique finds the fewest features that most strongly influence the likelihood of a single-class outcome for a single observation while also presenting a local explanation for the classification. Although the LIME has been utilized in the previous classification models in healthcare, it is still being determined how well healthcare practitioners would comprehend and accept LIME explanations.
In this research, we developed a hybrid agnostic explanation TabNet (HAE-TabNet) model to predict the survival outcome of OHCA patients. HAE-TabNet combined a LIME-based explainability model with the TabNet model. Our combined model could be interpreted more easily and intuitively than the native interpretation feature of the TabNet model in the local explanation. We also compared HAE-TabNet with other traditional machine learning models.
2. Materials and Methods
2.1. Data Source
The current study utilized data from the Out-of-Hospital Cardiac Arrest Surveillance database, which is maintained by the Korean Centers for Disease Control and Prevention (Korean CDC) in South Korea. The Out-of-Hospital Cardiac Arrest Surveillance database is introduced on the website (https://www.kdca.go.kr/ accessed on 23 April 2023). OHCA data are national statistics; therefore, the data cannot be utilized publicly and can only be used after submitting an IRB and research plan to the Ministry of Health and Welfare of the Republic of Korea and gaining approval for data usage. The study was designed as a retrospective, nationwide, population-based observational analysis, covering the period from January to December 2018. The Korean CDC Institutional Review Board approved the study in 2018 after it adhered to the Declaration of Helsinki’s requirements (IRB protocol code 0439001, date of approval 31 January 2018). Due to the retrospective nature of the study and the examination of anonymous clinical data, informed consent was waived. Improving the Reporting of Observational Studies in Epidemiology produced a checklist for observational studies, which was included in the study’s approach. The Out-of-Hospital Cardiac Arrest Surveillance database is a population-based registry of out-of-hospital cardiac arrest patients that are assessed by emergency medical services. The Korean CDC provided clinical data on out-of-hospital cardiac arrest patients for hospital management and discharge outcomes. Information on out-of-hospital cardiac arrest patients was acquired from emergency medical services records. Korean CDC medical record reviewers analyzed the medical records of all out-of-hospital cardiac arrest patients admitted to emergency rooms and hospitals. Patient demographic information such as age, sex, and underlying diseases such as hypertension, diabetes mellitus, and chronic kidney disease (CKD), as well as locations of cardiopulmonary resuscitation, bystander cardiopulmonary resuscitation, post-cardiac arrest care, survival, and neurological outcomes, were all gathered through the use of a well-designed survey form. The Utstein Style guidelines and the Resuscitation Outcome Consortium Project were used to create the registry form. Detailed descriptions are presented by Yang et al. [25].
2.2. Data Preprocessing
Prior to fitting the model, the dataset needed to be preprocessed. The raw data collection includes 216 columns of identifying data for a total of 30,179 patients. We first removed 26 unnecessary columns related to the serial number and date/time variables. The categorical variables in the dataset were then encoded via label encoding. In this study, we created a new column depending on the following circumstance. Patients whose emergency room treatment results and post-hospitalization results were alive were classified as “survival”, and those who died or were discharged with no hope were classified as “death”. We chose this new column as the target feature and gave it the label “Survival”.
Columns with 50% null values were eliminated from the dataset in order to account for missing values. After that, only the “CPR in the emergency room” column still included missing values. The “most frequent” strategy handled these null values in this column. After removing unnecessary columns and handling missing values, the dataset was reduced to 30,179 patients with 30 variables and the target feature.
Out of a total of 30,179 samples, only 3870 patients were labeled as “survival”, whereas 26,309 were labeled as “dead” (87.2%) in the target feature. Consequently, we used the SMOTE-ENN [26] approach to rebalance the dataset. The synthetic minority over-sampling technique (SMOTE) method, introduced by Chawla et al. [27], is an improved solution for imbalanced data. In essence, the SMOTE algorithm creates new samples by randomly interpolating between a small number of samples and those samples’ neighbors. In order to improve the classification impact of an unbalanced data collection, the ratio of imbalanced data is boosted by producing a given number of artificial minority samples [28]. The fundamental concept of edited nearest neighbor (ENN) [29] is to exclude samples whose class is dissimilar to the majority class of its k-nearest neighbors. The algorithm’s primary goal is to eliminate the majority of the noise samples. In principle, the SMOTE-ENN technique combines the SMOTE capacity to produce synthetic instances for the minority class with the ENN ability to eliminate observations from both classes that are detected as belonging to a different class between its k-nearest neighbor majority class and the observation’s class.
Before applying the SMOTE-ENN method, the dataset was stratify-split randomly into a training set and a test set, with a ratio of 80:20, in order to complete the basic setup for the model to learn. Only the training dataset was artificially balanced by the SMOTE-ENN method. The test set was unaltered to assess model performance on representative data. The variables of the dataset are shown in Table 1.

Table 1.
Variables and their description.
2.3. Development of a TabNet-Based OHCA Survival Outcome Prediction Model
TabNet [14] is a deep neural network designed to learn from tabular data. A comprehensive overview of the TabNet architecture is given in Figure 1. The architecture of this model aids in feature selection and increases the model’s ability to learn high-dimensional characteristics.
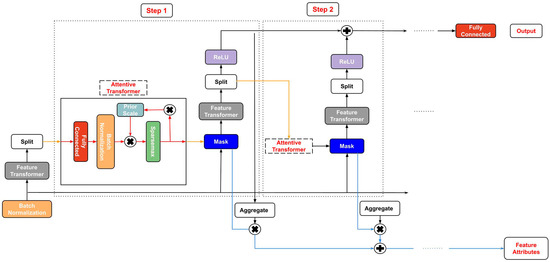
Figure 1.
The architecture of the TabNet model.
TabNet design consists of sequential multi-steps (). The step uses the processed information from the step to identify which features to employ and produce the processed feature representation that is aggregated and utilized for the overall decision-making. The dataset with given batch size () and D-dimensional characteristics () is provided as model input without performing any global feature normalization. The data is then delivered to a feature transformer after passing via a batch normalization (BN) layer.
A D-dimensional feature vector is processed in every ith step, with each step’s output going to a feature transformer block. This feature transformer block has several levels that are either common to all decision steps or specific to a particular decision step. A BN layer, a gated liner unit (GLU) activation, and fully connected (FC) layers are all present in every block. The GLU is also linked to a normalization residual connection, which reduces the variation over the whole network. This multi-layered block improves the parameter efficiency of the network and contributes to feature selection.
An attentive transformer includes four layers: FC, BN, prior scales, and sparsemax. The input is forwarded to a fully connected layer after batch normalization. It is then multiplied by the prior scale. The prior scales layer gathers the corresponding feature magnitudes that were utilized before the present decision phase, as follows:
where is the relaxation parameter.
The job of an attentive transformer is to figure out the mask layer for the current step by using the outcome of the previous step. The most important features are sparsely chosen using the learnable mask (). As a result, the learning capacity of a decision step is not squandered on pointless features to make the model parameter efficient. Due to the multiplicative nature of the masking procedure, an attentive transformer is employed to create the masks from the previously processed features, as follows:
where the layer is utilized for coefficient normalization resulting in sparse feature selection (when (See Reference [23]), is the previous scale’s item, and is the trainable function used to represent the FC and BN layers. To aid in learning the model, the characteristics with are not used. The following is a proposal for sparsity regularization () in the form of entropy to regulate the sparsity of the chosen features further:
where is a small number for numerical stability.
The mask vector is passed to the feature transformer, which analyzes the filtered features and separates the data into two outputs, as seen below:
where is the information for the following step for the following attentive transformer and is the output of the decision step.
TabNet also provides model-specific local and global reasons for interpretability. To create a scalar, the model first adds the step’s output vector. This scalar conveys the significance of this step to the outcome. For instance, the final outcome’s contribution from the Z decision step for the X sample is calculated using:
When the results of each step are combined for a single X sample, the local feature significance is determined. Nevertheless, the global aggregate feature importance mask Y of the normalized feature is calculated as follows:
In this research, the HAE-TabNet model was built by pytorch_tabnet version 4.0. Figure 2 depicts a schematic representation of the model process. Specifically, we used the stratified 10-fold cross-validation (CV) technique to assess the quality of machine learning models. When employing a k-fold CV, the dataset is divided into k sections of equal size, and cases are selected at random for each section. Each subgroup is divided into a part for training and a reminder for the test set. During the k evaluations of the model, each group is used once as the test set. Each subset is split into groups with roughly the same class labels as the initial dataset during stratified k-fold cross-validation.
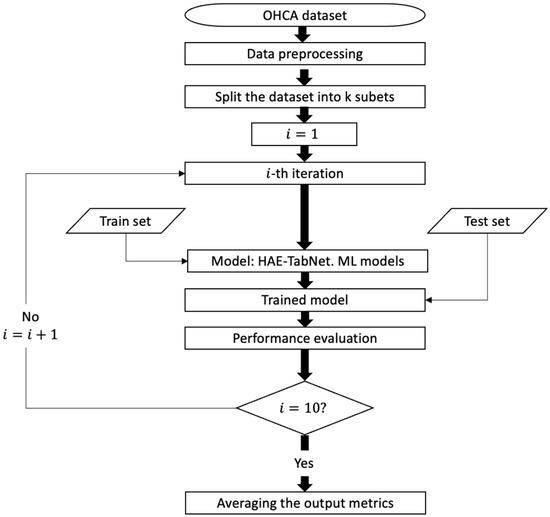
Figure 2.
Process flow diagram for the HAE-TabNet model.
2.4. Hyperparameter Fine-Tuning Method: Bayesian Optimization
Hyperparameter fine-tuning via trial and error is time-consuming and frequently produces unsatisfactory outcomes [30]. Therefore, reliable tuning techniques are crucial, particularly when the objective of the optimization is to find the most excellent value at the sample point for an unknown function, as in [31]:
where stands for the sampling point, stands for the search region around , stands for the unidentified objective function, and stands for the location where the unidentified objective function should be maximized.
Bayesian optimization (BO) is a more effective hyperparameter optimization approach than the typical grid search (GS) and random search (RS) methods. Every assessment in GS and RS iterations is independent of previous evaluations, which increases the time wasted in evaluating poorly performing areas of the hyperparameter search field. BO solves this problem by combining prior knowledge about the with sample locations to estimate the following distribution of the objective function using the Bayes theorem. This posterior information is subsequently employed in the search for the global optimal value.
BO involves two primary phases, which are as follows [32]:
- Phase 1: By selecting a few data points at random, the BO algorithm tries to fit a surrogate function across the . A Gaussian process (GP) is used to update the surrogate function and generate the posterior distribution over the because of its versatility, robustness, accuracy, and analytic tractability.
- Phase 2: Using the posterior distribution created in Phase 1, an acquisition function is developed. This function explores new parts of the search space and exploits existing regions with optimal results. Until a stopping threshold is reached, the exploration and exploitation processes will continue, and the surrogate model will be updated with new results. The goal is to maximize the acquisition function in order to find the next sampling point.
In this study, the hyperparameters inside the HAE-TabNet model were fine-tuned by BO as follows:
- “n_d” (Number of features in the output of each decision step): This hyperparameter controls the size of the output space for each decision step, which can affect the model’s ability to capture complex patterns in the data. A larger value for “n_d” can increase the capacity of the model, but may also increase the risk of overfitting. A typical range for “n_d” is between 4 and 128.
- “n_a” (Number of features in the attention function for each decision step): This hyperparameter controls the size of the attention network in each decision step, which can affect the model’s ability to focus on relevant features for prediction. A larger value for “n_a” can improve the quality of the attention mechanism, but may also increase the computational cost. A typical range for n_a is between 4 and 128.
- “n_steps” (Number of decision steps in the network): This hyperparameter controls the depth of the TabNet model, which can affect its ability to capture hierarchical relationships in the data. A larger value for “n_steps” can increase the capacity of the model, but may also increase the risk of overfitting. A typical range for “n_steps” is between 1 and 10.
- “gamma” (Sparsity regularization coefficient): This hyperparameter controls the degree of sparsity in the feature selection process. A larger value for “gamma” can increase the sparsity of the model, but may also decrease its ability to capture important features. A typical range for gamma is between 0.8 and 2.0.
- “n_independent” (Number of independent GLU (gated linear unit) activations per feature): This hyperparameter controls the number of independent nonlinear transformations for each feature. A larger value for “n_independent” can increase the complexity of the model, but may also increase the risk of overfitting. A typical range for n_independent is between 1 and 10.
- “n_shared” (Number of shared GLU activations for all features): This hyperparameter controls the number of shared nonlinear transformations for all features. A larger value for “n_shared” can increase the capacity of the model, but may also increase the computational cost. A typical range for “n_shared” is between 1 and 10.
- “momentum” (Batch normalization momentum): This hyperparameter controls the momentum for the batch normalization layer, which can affect the stability and convergence of the optimization process. A larger value for “momentum” can improve the stability of the model, but may also increase the risk of overfitting. A typical range for “momentum” is between 0.02 and 0.3.
- “batch_size” (The size of each batch used for training the model): A larger value for “batch_size” can improve the efficiency of the optimization process, but may also increase the risk of overfitting. A typical range for “batch_size” is between 16 and 256.
- “virtual_batch_size” (The size of the virtual batch used for training the model): This hyperparameter can be used to simulate larger batch sizes without increasing memory usage. A larger value for “virtual_batch_size” can improve the stability of the optimization process, but may also increase the computational cost. A typical range for “virtual_batch_size” is between 16 and 256.
- “patience”: The number of epochs to wait before early stopping if the validation loss does not improve. This hyperparameter can be used to prevent overfitting and improve the efficiency of the optimization process. A larger value for ‘patience’ can improve stability. A range for “patience” is between 5 to 25.
2.5. Performance Metrics
The most often used terminologies for a binary classification test are accuracy, precision, recall, and F1-score, which all offer statistical evaluation of the performance of a classifier model. These metrics were calculated as follows:
where Truenegative and Truepositive denote the correct predictions for dead (class 0) and survival (class 1), respectively, and Falsenegative and Falsepositive denote the incorrect predictions for dead and survival accordingly.
Accuracy = (Truepositive + Truenegative)/(Truepositive + Truenegative + Falsepositive + Falsenegative)
Precision = Truepositive/(Truepositive + Falsepositive)
Recall = Truepositive/(Truepositive + Falsenegative)
F1 score = 2 * (Precision * Recall) * (Precision + Recall)
Additionally, we also utilized the “Area under the receiver operating characteristic curve value” (ROC AUC) to assess the model’s performance. The ROC AUC is defined as:
where and denote the true positive rate and false positive rate for a threshold .
In our investigation, it was assumed that a model with the greatest ROC AUC had the best predictive capacity. If the ROC AUC remained stable, the model with the highest recall was considered the best.
2.6. Prediction Performance Comparison
Five machine learning models, including XGBoost [33], k-nearest neighbors [34], random rorest [35], decision trees [36], and logistic regression [37], are used as benchmarks for comparison in order to validate the prediction performance of the proposed method. These techniques were utilized and evaluated in the field of cardiac arrest prediction in previous studies [10,12,38,39]. The same training set and test set are used for all models’ evaluations. Notably, the BO method also yields the optimal settings for these benchmarks. The hyperparameters of the HAE-TabNet model and these benchmark models are described in Table 2. The brief features of the benchmark machine learning models are as follows:

Table 2.
Hyperparameters of the HAE-TabNet model and benchmark models.
- XGBoost (XGB): XGB is a popular gradient-boosting algorithm widely used in regression and classification tasks. It uses a combination of multiple decision trees to make predictions, and it is known for its high performance and accuracy. XGB is particularly good at handling large datasets and handling missing data. Some notable features of XGB include its ability to handle different types of data, including both categorical and numerical data, and its ability to perform feature selection to identify the most important features for prediction.
- K-nearest neighbors (KNN): KNN is a simple and effective algorithm for both regression and classification problems. It works by finding the k-nearest data points to a new observation and using their values to predict the outcome of that observation. KNN is often used for problems with non-linear decision boundaries and can be effective in low-dimensional datasets. One of the key features of KNN is that it is easy to understand and implement, but it can be computationally expensive for large datasets.
- Random forest (RF): RF is an ensemble learning algorithm that uses multiple decision trees to make predictions. It is particularly good at handling high-dimensional datasets and can handle both categorical and continuous data. RF is known for its ability to reduce overfitting and handle missing data, and it can be used for both regression and classification tasks.
- Decision tree (DT): DT is a simple yet powerful algorithm for both regression and classification problems. It works by recursively splitting the data based on the most informative feature at each node until a stopping criterion is reached. DT is easy to interpret and can handle both categorical and continuous data.
- Logistic regression (LR): LR is a popular algorithm for binary classification problems. It works by estimating the probability of the outcome variable given the input variables, and it uses a logistic function to transform this probability into a binary outcome. LR is easy to interpret and can handle both categorical and continuous data.
2.7. Local Interpretable Model-Agnostic Explanations (LIMEs)
The LIME [24] method allows for the approximation of any black-box machine learning model with a local, interpretable model to account for each individual prediction. The idea was inspired by a 2016 study [24] in which the authors disturbed the initial data points, put them into a black-box model, and then examined the associated outcomes. The extra data points were then given a weight by the algorithm in proportion to the initial point. Finally, a prediction model incorporating the sample weights was fitted to the dataset. The trained explanation model might subsequently be used to explain each raw data point.
The primary goal is to present a trustworthy and interpretable explanation. To achieve this, the LIME tries to minimize the following objective function:
where is an original model, g is the interpretable model, represents the original observation, denotes the proximity measure from all permutations to the original observation, the component is a measure of the unfaithfulness of in approximating in the locality defined by π, and is a measure of model complexity. In this study, we chose a specific instance to analyze in order to show how the LIME model works with the HAE-TabNet model to predict an OHCA patient’s survival outcome.
3. Results
3.1. Performances of the HAE-TabNet Model
After rebalancing the training set by the SMOTE-ENN technique, the number of “dead” labels became 19,625, and the number of “survival” labels was 20,879. The test set with 12,918 values was not transformed.
The HAE-TabNet with optimized hyperparameters received 0.9858 ± 0.002 of ROC AUC on the initial imbalanced training set, whereas the ROC AUC of the proposed model on the rebalanced training set was 0.9934 ± 0.001. Other evaluation metrics also increased significantly. Specifically, accuracy, precision, recall, and F1-score were 0.9611 ± 0.002, 0.9681 ± 0.002, 0.9623 ± 0.002, and 0.9652 ± 0.002, respectively, on the rebalanced dataset. On the imbalanced dataset, they were only 0.9572 ± 0.003, 0. 9031 ± 0.004, 0.8339 ± 0.005, and 0.8669 ± 0.005, respectively. In addition to the improvement in ROC AUC, other scores also increased significantly between the imbalanced dataset and the balanced dataset. As detailed in Table 3, the performance of other benchmark machine learning models was also greatly enhanced on the balanced dataset in comparison to the imbalanced dataset.

Table 3.
Performance of the HAE-TabNet model and other benchmark models (95% confidence interval).
Table 3 demonstrated that the ROC AUC of XGB, KNN, RF, DT, and LR were 0.9909 ± 0.001, 0.9854 ± 0.001, 0.9894 ± 0.001, 0.9205 ± 0.003, and 0.9469 ± 0.003, respectively. On the test set, the HAE-TabNet model’s ROC AUC was also higher than other machine learning models, with a value of 0.9930 ± 0.001 displayed in Figure 3. The ROC AUC of the HAE-TabNet outperformed all other benchmark models on both the training set and the test set. Moreover, the HAE-TabNet model also had the highest accuracy on the training set.
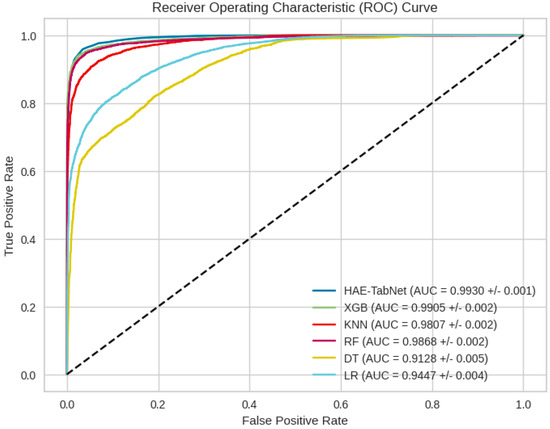
Figure 3.
All models’ ROC curves on the test dataset.
3.2. Evaluation of HAE-TabNet’s Feature Masks
Figure 4 illustrates which features are chosen between the first and fourth decision steps. The brighter color indicates that the feature is given more weight in this decision step. Figure 4 also demonstrates that each decision step will assign a unique weight to each feature, reflecting the instance-wise idea. For instance, in the first decision step, denoted as mask 0, the top three features (features 1, 16, and 8) received high scores, but the noise from other irrelevant features was also captured. The second decision step, denoted by mask 1, was more beneficial because it emphasized the important features while assigning zero weight to irrelevant features. In the subsequent step, as depicted by masks 2 and 3, the noise features were nearly eliminated, and only the essential features were displayed. The internal mask is a fundamental component of TabNet, and it is easy to use and obtain. Compared to other benchmark models that perform similarly in this study, TabNet outperformed them in offering comprehensive model insights without the need for extra software.
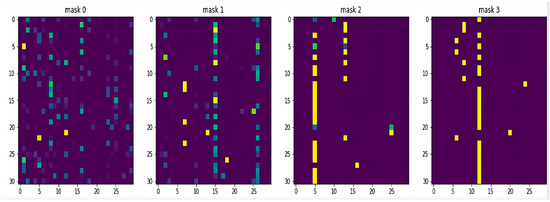
Figure 4.
HAE-TabNet’s local feature importance mask.
3.3. Evaluation of LIME-HAE-TabNet
Figure 5 depicts a description of an OHCA patient with a predicted outcome of survival. Figure 5c summarizes the patient’s state and contributing circumstances. We noticed that only the first eight features would contribute to prediction, so we summarize the states of patients only including ten out of thirty features. The patient’s states in Figure 5c can be explained below:
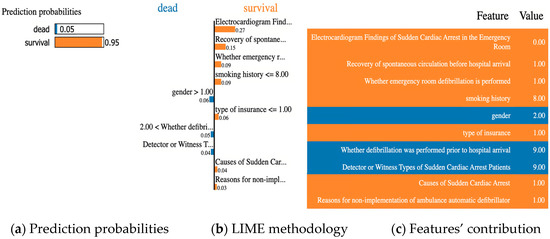
Figure 5.
Example of an OHCA patient with prediction result as “survival”.
- Electrocardiogram findings of sudden cardiac arrest in the emergency room = 0 (rhythm after recovery of spontaneous circulation (state of recovery of spontaneous circulation at the time of visit));
- Recovery of spontaneous circulation before hospital arrival = 1 (recovery of spontaneous circulation);
- Whether emergency room defibrillation is performed = 1 (not conducted);
- smoking history = 8 (does not exist);
- Gender = 2 (female);
- Type of insurance = 1 (national health insurance);
- Whether defibrillation was performed prior to hospital arrival = 9 (unknown);
- Detector or witness types of sudden cardiac arrest patients = 9 (unknown);
- Causes of sudden cardiac arrest = 1 (disease);
- Reasons for non-implementation of ambulance automatic defibrillator = 1 (indication).
Based on this patient’s state, the HAE-TabNet predicted that the survival rate would be 95%, as shown in Figure 5a. Figure 5b depicts the LIME methodology. The blue bars represent the variables that significantly contribute to the prediction’s rejection, whereas the orange bars represent the states and factors that considerably contribute to the prediction’s support. According to the explanation, at the time of the prediction, “Electrocardiogram Findings of Sudden Cardiac Arrest in the Emergency Room” was the target’s main factor and state that most contributed to the prediction, with a weight of 0.27.
4. Discussion
Through validation, this study demonstrated that the accurate performance of the deep learning model, HAE-TabNet, was excellent for predicting the survival outcome of OHCA patients. The most important finding from this study was that the proposed model outperformed other traditional machine learning models such as XGB, KNN, RF, DT, and LR on the medical tabular data. Moreover, this hybrid model combined with the LIME can help medical professionals without expert knowledge in the field of data analysis understand the AI model’s decision easily.
For professionals in the field of data science, understanding and evaluating TabNet’s mask in Figure 4 is not a matter. However, for medical professionals who are not specialized in the field of artificial intelligence, understanding TabNet’s mask is quite complicated. Compared to TabNet’s original explanatory model, our model is more intuitive and easier to understand. Medical professionals only need to compare code values to understand the model’s interpretation quickly and easily. Thereby, combined with specialized knowledge, doctors can verify the reliability of the model, as well as apply the model to the prognosis and treatment of patients effectively.
A few comparable investigations merit additional discussion. Seki et al. [40] used 53 variables to create a machine learning method for one-year survival after OHCA. The simulation performed well. (ROC AUC 0.94). Although only OHCA with an assumed cardiac etiology was included, the prediction tool’s utility was still constrained, and it is unlikely that any practitioner will be able to input data on 53 factors while performing ongoing CPR. In order to forecast mortality after OHCA among patients who attained ROSC, Kwon et al. [10] combined a variety of machine learning techniques with logistic regression models. Even though the model had a high ROC AUC (0.95) because it only included patients with ROSC, its applicability in the ED is constrained because the majority of patients with prolonged ROSC are moved to the ICU for additional care, and prognostications are frequently made at a later stage. The same restriction applies to a number of other prediction tools (Miracle2 [41], OHCA [42], TTM [43], and CAHP [44]), which can only be used to forecast brain function in patients who have OHCA and ROSC. They are useless to clinicians who are dealing with OHCA patients who do not have ROSC. Our proposed prediction model is compatible with all common data of OHCA patients and has a higher ROC AUC (0.9934 ± 0.001 on the training set, 0.9930 ± 0.001 on the test set) than previous research.
There is conflicting evidence regarding whether skilled medical professionals are more accurate than current scoring methods at distinguishing survivors from non-survivors. (APACHE, SAPS, MPM) [45]. When evaluating survival 24 h after ICU admission, ICU physicians performed better than the current scoring systems. However, the ability to predict outcomes was only moderately correct for both doctors and scoring systems [46]. According to the data, prognosis projections frequently rely on clinical judgment rather than objective information [47], which can occasionally be deceptive. Medical professionals only correctly predicted the time to death 20% of the time (within 33% of real survival), frequently made overly optimistic predictions (63%), and underestimated survival times by a factor of 5 on average [47], according to data from prognosis assessments in terminally ill patients. As a result, it suggested that prediction tools are needed in medicine to ensure objective accuracy.
5. Limitations
The following are some of the limitations of this study. First, the dataset contains multiple absent values, necessitating the elimination of numerous variables. We utilized the TabNet model, which has the capacity for self-supervised learning so that in future research we can use this technique to manage missing values in this dataset. Second, our analysis was conducted using all available data features without performing any feature engineering. Further research should focus on employing feature engineering techniques to improve the performance of the predictive models. We recommend that future studies consider using Bayesian linear regression based on a Poisson (or a negative binomial) distribution [48] to model the count of survival outcomes as a function of various features in the dataset. By quantifying the impact of each feature on survival outcomes, this approach can help identify the most important features for improving outcomes in OHCA patients. Additionally, the Bayesian framework allows for the incorporation of uncertainty, providing a more robust understanding of the relationships between features and outcomes. Thirdly, TabNet is a model of deep learning, so fine-tuning requires considerable effort. Therefore, we cannot fine-tune the TabNet model with a wider range and more hyperparameters. Finally, due to the use of various samples and the determination of which local data points are incorporated into the local model, LIME’s explanations are not always stable or consistent. In the future, this model must be evaluated by medical professionals.
6. Conclusions
This research presents a reliable HAE-TabNet model that can help medical professionals predict OHCA patients’ survival outcomes and understand the model’s interpretation quickly and easily. Our proposed model achieved good performance with a 0.9934 ± 0.001 ROC AUC score in the training dataset and a 0.9930 ± 0.001 ROC AUC score in the test dataset. Combined with specialized knowledge, medical doctors can verify the reliability of the model, as well as apply the model to the prognosis and treatment of patients effectively. In the future, more research on enhancing the LIME and the characteristics that increase its trust among physicians is required for "black-box" machine learning predictive technologies to be broadly implemented in healthcare.
Author Contributions
Conceptualization, H.V.N. and H.B.; software, H.V.N.; methodology, H.V.N. and H.B.; validation, H.V.N. and H.B.; investigation, H.V.N. and H.B.; writing—original draft preparation, H.V.N.; formal analysis, H.B.; writing—review and editing, H.B.; visualization, H.V.N.; supervision, H.B.; project administration, H.B.; funding acquisition, H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2018R1D1A1B07041091 and NRF-2021S1A5A8062526).
Institutional Review Board Statement
The study was carried out in accordance with the Helsinki Declaration and was approved by the Korean Workers’ Compensation and Welfare Service’s Institutional Review Board (or Ethics Committee) (protocol code 0439001, date of approval 31 January 2018).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are provided at the request of the corresponding author. These data are not publicly available because researchers need to obtain permission from the Korean Centers for Disease Control and Prevention.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roh, S.-Y.; Choi, J.-I.; Park, S.H.; Kim, Y.G.; Shim, J.; Kim, J.-S.; Han, K.D.; Kim, Y.-H. The 10-Year Trend of Out-of-Hospital Cardiac Arrests: A Korean Nationwide Population-Based Study. Korean Circ. J. 2021, 51, 866. [Google Scholar] [CrossRef] [PubMed]
- Daya, M.R.; Schmicker, R.H.; Zive, D.M.; Rea, T.D.; Nichol, G.; Buick, J.E.; Brooks, S.; Christenson, J.; MacPhee, R.; Craig, A.; et al. Out-of-hospital cardiac arrest survival improving over time: Results from the Resuscitation Outcomes Consortium (ROC). Resuscitation 2015, 91, 108–115. [Google Scholar] [CrossRef]
- Stecker, E.C.; Reinier, K.; Marijon, E.; Narayanan, K.; Teodorescu, C.; Uy-Evanado, A.; Gunson, K.; Jui, J.; Chugh, S.S. Public Health Burden of Sudden Cardiac Death in the United States. Circ. Arrhythmia Electrophysiol. 2014, 7, 212–217. [Google Scholar] [CrossRef]
- Adabag, A.S.; Peterson, G.; Apple, F.S.; Titus, J.; King, R.; Luepker, R.V. Etiology of Sudden Death in the Community: Results of Anatomical, Metabolic, and Genetic Evaluation. Am. Heart J. 2010, 159, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Nichol, G.; Soar, J. Regional cardiac resuscitation systems of care. Curr. Opin. Crit. Care 2010, 16, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Adnet, F.; Triba, M.N.; Borron, S.W.; Lapostolle, F.; Hubert, H.; Gueugniaud, P.-Y.; Escutnaire, J.; Guenin, A.; Hoogvorst, A.; Marbeuf-Gueye, C.; et al. Cardiopulmonary Resuscitation Duration and Survival in Out-of-Hospital Cardiac Arrest Patients. Resuscitation 2017, 111, 74–81. [Google Scholar] [CrossRef]
- Kashiura, M.; Hamabe, Y.; Akashi, A.; Sakurai, A.; Tahara, Y.; Yonemoto, N.; Nagao, K.; Yaguchi, A.; Morimura, N. Applying the Termination of Resuscitation Rules to Out-of-Hospital Cardiac Arrests of Both Cardiac and Non-Cardiac Etiologies: A Prospective Cohort Study. Crit. Care 2016, 20, 49. [Google Scholar] [CrossRef]
- Cho, K.-J.; Kwon, O.; Kwon, J.; Lee, Y.; Park, H.; Jeon, K.-H.; Kim, K.-H.; Park, J.; Oh, B.-H. Detecting Patient Deterioration Using Artificial Intelligence in a Rapid Response System. Crit. Care Med. 2020, 48, e285–e289. [Google Scholar] [CrossRef]
- Kang, D.-Y.; Cho, K.-J.; Kwon, O.; Kwon, J.; Jeon, K.-H.; Park, H.; Lee, Y.; Park, J.; Oh, B.-H. Artificial Intelligence Algorithm to Predict the Need for Critical Care in Prehospital Emergency Medical Services. Scand. J. Trauma Resusc. Emerg. Med. 2020, 28, 17. [Google Scholar] [CrossRef]
- Kwon, J.; Jeon, K.-H.; Kim, H.M.; Kim, M.J.; Lim, S.; Kim, K.-H.; Song, P.S.; Park, J.; Choi, R.K.; Oh, B.-H. Deep-Learning-Based out-of-Hospital Cardiac Arrest Prognostic System to Predict Clinical Outcomes. Resuscitation 2019, 139, 84–91. [Google Scholar] [CrossRef]
- Kwon, J.; Lee, Y.; Lee, Y.; Lee, S.; Park, H.; Park, J. Validation of Deep-Learning-Based Triage and Acuity Score Using a Large National Dataset. PLoS ONE 2018, 13, e0205836. [Google Scholar] [CrossRef]
- Kwon, J.; Lee, Y.; Lee, Y.; Lee, S.; Park, J. An Algorithm Based on Deep Learning for Predicting In-Hospital Cardiac Arrest. J. Am. Heart Assoc. 2018, 7, e008678. [Google Scholar] [CrossRef]
- Shwartz-Ziv, R.; Armon, A. Tabular Data: Deep Learning Is Not All You Need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Arik, S.Ö.; Pfister, T. TabNet: Attentive Interpretable Tabular Learning. Proc. AAAI Conf. Artif. Intell. 2021, 35, 6679–6687. [Google Scholar] [CrossRef]
- Cahan, N.; Marom, E.M.; Soffer, S.; Barash, Y.; Konen, E.; Klang, E.; Greenspan, H. Weakly Supervised Multimodal 30-Day All-Cause Mortality Prediction for Pulmonary Embolism Patients. In Proceedings of the 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI), Kolkata, India, 28–31 March 2022. [Google Scholar] [CrossRef]
- Asadi-Pooya, A.A.; Kashkooli, M.; Asadi-Pooya, A.; Malekpour, M.; Jafari, A. Machine Learning Applications to Differentiate Comorbid Functional Seizures and Epilepsy from Pure Functional Seizures. J. Psychosom. Res. 2022, 153, 110703. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, H.; He, J.; Pan, Q.; Zhao, W. An Causal XAI Diagnostic Model for Breast Cancer Based on Mammography Reports. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Houston, TX, USA, 9–12 December 2021. [Google Scholar] [CrossRef]
- Zhang, Q.; Tian, X.; Chen, G.; Yu, Z.; Zhang, X.; Lu, J.; Zhang, J.; Wang, P.; Hao, X.; Huang, Y.; et al. A Prediction Model for Tacrolimus Daily Dose in Kidney Transplant Recipients With Machine Learning and Deep Learning Techniques. Front. Med. 2022, 9. [Google Scholar] [CrossRef]
- Yu, Z.; Ye, X.; Liu, H.; Li, H.; Hao, X.; Zhang, J.; Kou, F.; Wang, Z.; Wei, H.; Gao, F.; et al. Predicting Lapatinib Dose Regimen Using Machine Learning and Deep Learning Techniques Based on a Real-World Study. Front. Oncol. 2022, 12. [Google Scholar] [CrossRef]
- Vilone, G.; Longo, L. Notions of Explainability and Evaluation Approaches for Explainable Artificial Intelligence. Inf. Fusion 2021, 76, 89–106. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A Review of Machine Learning Interpretability Methods. Entropy 2020, 23, 18. [Google Scholar] [CrossRef]
- Yang, G.; Ye, Q.; Xia, J. Unbox the Black-Box for the Medical Explainable AI via Multi-Modal and Multi-Centre Data Fusion: A Mini-Review, Two Showcases and Beyond. Inf. Fusion 2022, 77, 29–52. [Google Scholar] [CrossRef]
- Alves, M.A.; Castro, G.Z.; Oliveira, B.A.S.; Ferreira, L.A.; Ramírez, J.A.; Silva, R.; Guimarães, F.G. Explaining Machine Learning Based Diagnosis of COVID-19 from Routine Blood Tests with Decision Trees and Criteria Graphs. Comput. Biol. Med. 2021, 132, 104335. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why Should I Trust You. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Yang, W.; Kim, J.-G.; Kang, G.-H.; Jang, Y.-S.; Kim, W.; Choi, H.-Y.; Lee, Y. Prognostic Effect of Underlying Chronic Kidney Disease and Renal Replacement Therapy on the Outcome of Patients after Out-of-Hospital Cardiac Arrest: A Nationwide Observational Study. Medicina 2022, 58, 444. [Google Scholar] [CrossRef] [PubMed]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-Sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Mi, Y. Imbalanced Classification Based on Active Learning SMOTE. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 944–949. [Google Scholar] [CrossRef]
- Beckmann, M.; Ebecken, N.F.F.; Pires de Lima, B.S.L. A KNN Undersampling Approach for Data Balancing. J. Intell. Learn. Syst. Appl. 2015, 7, 104–116. [Google Scholar] [CrossRef]
- Massaoudi, M.; Refaat, S.S.; Chihi, I.; Trabelsi, M.; Oueslati, F.S.; Abu-Rub, H. A Novel Stacked Generalization Ensemble-Based Hybrid LGBM-XGB-MLP Model for Short-Term Load Forecasting. Energy 2021, 214, 118874. [Google Scholar] [CrossRef]
- Shi, R.; Xu, X.; Li, J.; Li, Y. Prediction and Analysis of Train Arrival Delay Based on XGBoost and Bayesian Optimization. Appl. Soft Comput. 2021, 109, 107538. [Google Scholar] [CrossRef]
- Kulshrestha, A.; Krishnaswamy, V.; Sharma, M. Bayesian BILSTM Approach for Tourism Demand Forecasting. Ann. Tour. Res. 2020, 83, 102925. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Peterson, L. K-Nearest Neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning; Springer: Berlin/Heidelberg, Germany, 2012; pp. 157–175. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A Survey of Decision Tree Classifier Methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Krizmaric, M.; Verlic, M.; Stiglic, G.; Grmec, S.; Kokol, P. Intelligent analysis in predicting outcome of out-of-hospital cardiac arrest. Comput. Methods Programs Biomed. 2009, 95, S22–S32. [Google Scholar] [CrossRef]
- Lee, Y.; Kwon, J.; Lee, Y.; Park, H.; Cho, H.; Park, J. Deep Learning in the Medical Domain: Predicting Cardiac Arrest Using Deep Learning. Acute Crit. Care 2018, 33, 117–120. [Google Scholar] [CrossRef]
- Seki, T.; Tamura, T.; Suzuki, M. Outcome Prediction of Out-of-Hospital Cardiac Arrest with Presumed Cardiac Aetiology Using an Advanced Machine Learning Technique. Resuscitation 2019, 141, 128–135. [Google Scholar] [CrossRef]
- Pareek, N.; Kordis, P.; Beckley-Hoelscher, N.; Pimenta, D.; Kocjancic, S.T.; Jazbec, A.; Nevett, J.; Fothergill, R.; Kalra, S.; Lockie, T.; et al. A Practical Risk Score for Early Prediction of Neurological Outcome after Out-of-Hospital Cardiac Arrest: MIRACLE2. Eur. Heart J. 2020, 41, 4508–4517. [Google Scholar] [CrossRef] [PubMed]
- Adrie, C.; Cariou, A.; Mourvillier, B.; Laurent, I.; Dabbane, H.; Hantala, F.; Rhaoui, A.; Thuong, M.; Monchi, M. Predicting Survival with Good Neurological Recovery at Hospital Admission after Successful Resuscitation of Out-of-Hospital Cardiac Arrest: The OHCA Score. Eur. Heart J. 2006, 27, 2840–2845. [Google Scholar] [CrossRef]
- Martinell, L.; Nielsen, N.; Herlitz, J.; Karlsson, T.; Horn, J.; Wise, M.P.; Undén, J.; Rylander, C. Early Predictors of Poor Outcome after Out-of-Hospital Cardiac Arrest. Crit. Care 2017, 21, 96. [Google Scholar] [CrossRef]
- Maupain, C.; Bougouin, W.; Lamhaut, L.; Deye, N.; Diehl, J.-L.; Geri, G.; Perier, M.-C.; Beganton, F.; Marijon, E.; Jouven, X.; et al. The CAHP (Cardiac Arrest Hospital Prognosis) Score: A Tool for Risk Stratification after out-of-Hospital Cardiac Arrest. Eur. Heart J. 2015, 37, 3222–3228. [Google Scholar] [CrossRef]
- Keegan, M.T.; Gajic, O.; Afessa, B. Severity of Illness Scoring Systems in the Intensive Care Unit. Crit. Care Med. 2011, 39, 163–169. [Google Scholar] [CrossRef]
- Sinuff, T.; Adhikari, N.K.J.; Cook, D.J.; Schünemann, H.J.; Griffith, L.E.; Rocker, G.; Walter, S.D. Mortality Predictions in the Intensive Care Unit: Comparing Physicians with Scoring Systems. Crit. Care Med. 2006, 34, 878–885. [Google Scholar] [CrossRef]
- Farinholt, P.; Park, M.; Guo, Y.; Bruera, E.; Hui, D. A Comparison of the Accuracy of Clinician Prediction of Survival Versus the Palliative Prognostic Index. J. Pain Symptom Manag. 2018, 55, 792–797. [Google Scholar] [CrossRef] [PubMed]
- Casini, L.; Roccetti, M. Reopening Italy’s Schools in September 2020: A Bayesian Estimation of the Change in the Growth Rate of New SARS-CoV-2 Cases. BMJ Open 2021, 11, e051458. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).