ConvGRU-RMWP: A Regional Multi-Step Model for Wave Height Prediction
Abstract
1. Introduction
- (1)
- The model needs to output the predicted values of multiple locations simultaneously, which is a pixel-level prediction. Achieving accurate pixel-level spatial output not only requires the model to have strong spatio-temporal feature extraction capabilities but also needs to be able to correctly resolve the extracted deep spatial features to the output map of the same size. For the regional wave height prediction task, direct prediction from the image representation is not suitable, but the deep features should be decoded using the same network layers with gradually increasing output resolution [28]. Thus, regional wave height prediction places high demands on the model structure.
- (2)
- Performing multi-step prediction while guaranteeing pixel-level regional wave height output is a challenging task. Current regional wave height prediction models, especially CNN-like models, generally perform single-step prediction. Some studies also exist that use independent modeling of individual moments to achieve multi-step prediction, and this approach has difficulty in maintaining high-accuracy prediction at the more backward moments [29].
2. Data and Methods
2.1. Experimental Data Sources
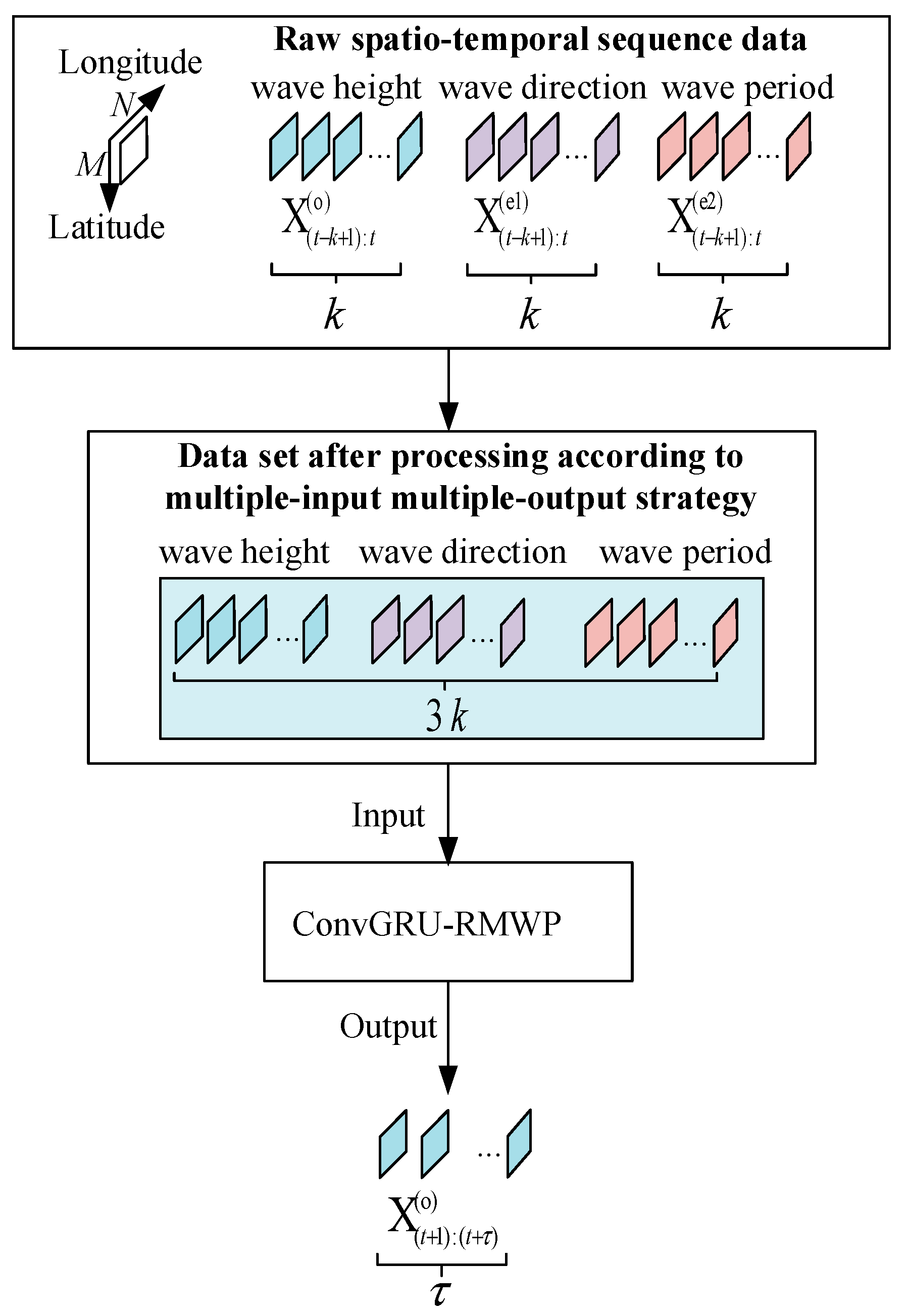
2.2. Multi-Input Multi-Output Strategy (MIMO)
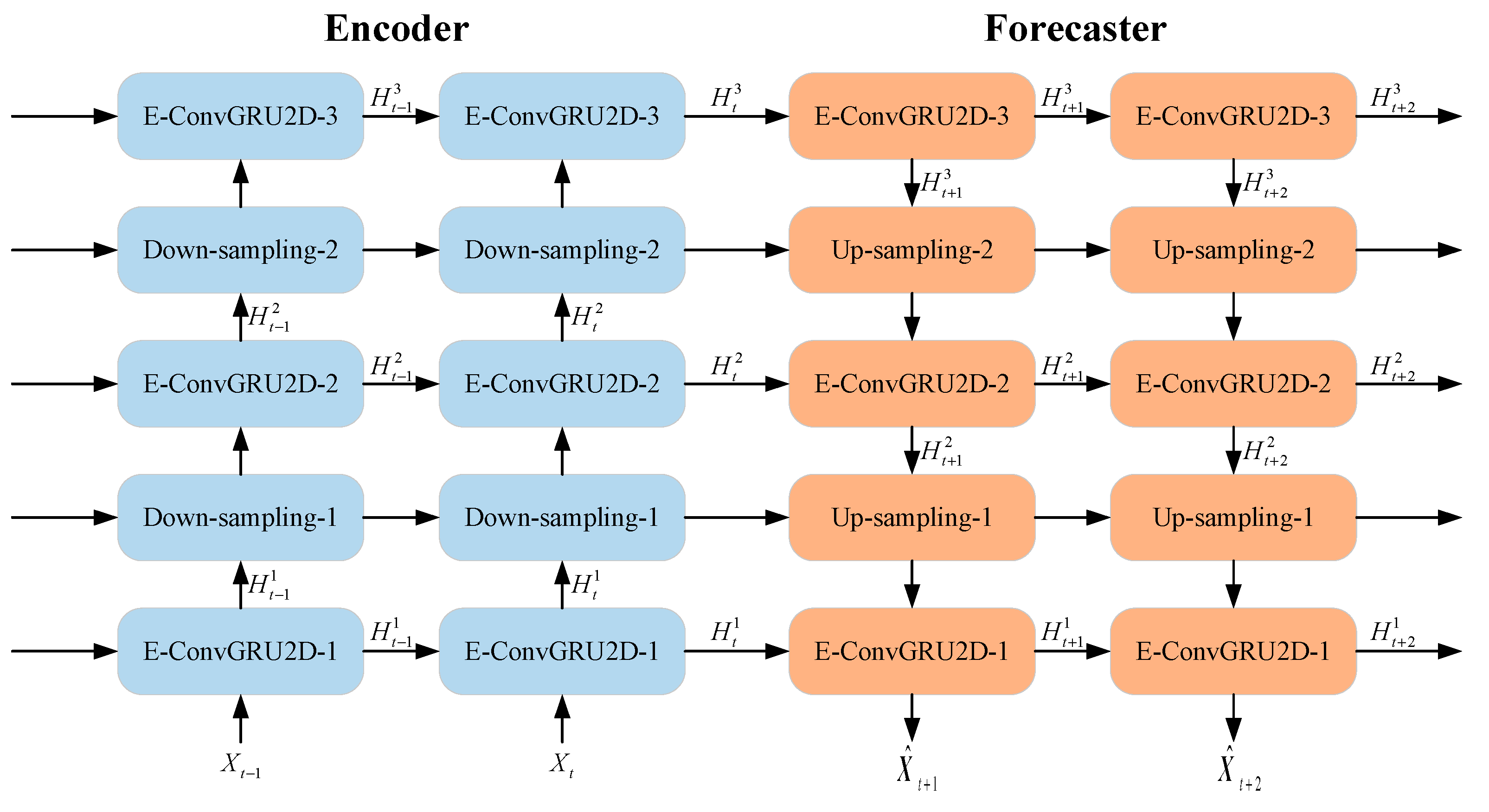
2.3. Multi-Step Spatio-Temporal Prediction Method
3. Model Building and Experimental Setup
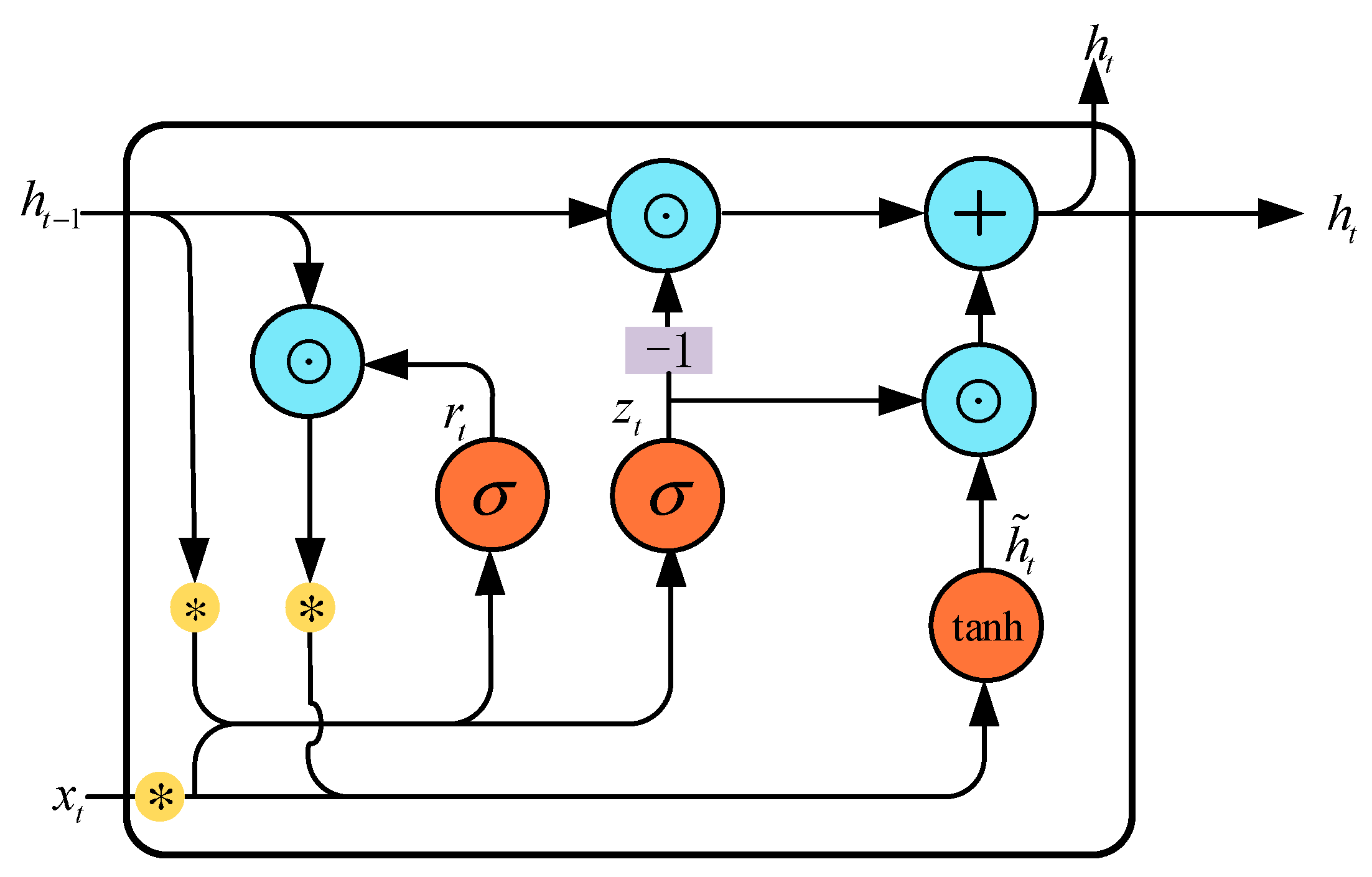
3.1. ConvGRU Network
3.2. Model Building
3.3. Loss Function and Model Setup
3.4. Experimental Setup and Evaluation Indicators
4. Results and Discussion
4.1. Optimal Setting of Hyperparameters
4.2. Comparison of Prediction Errors for Different Input Steps
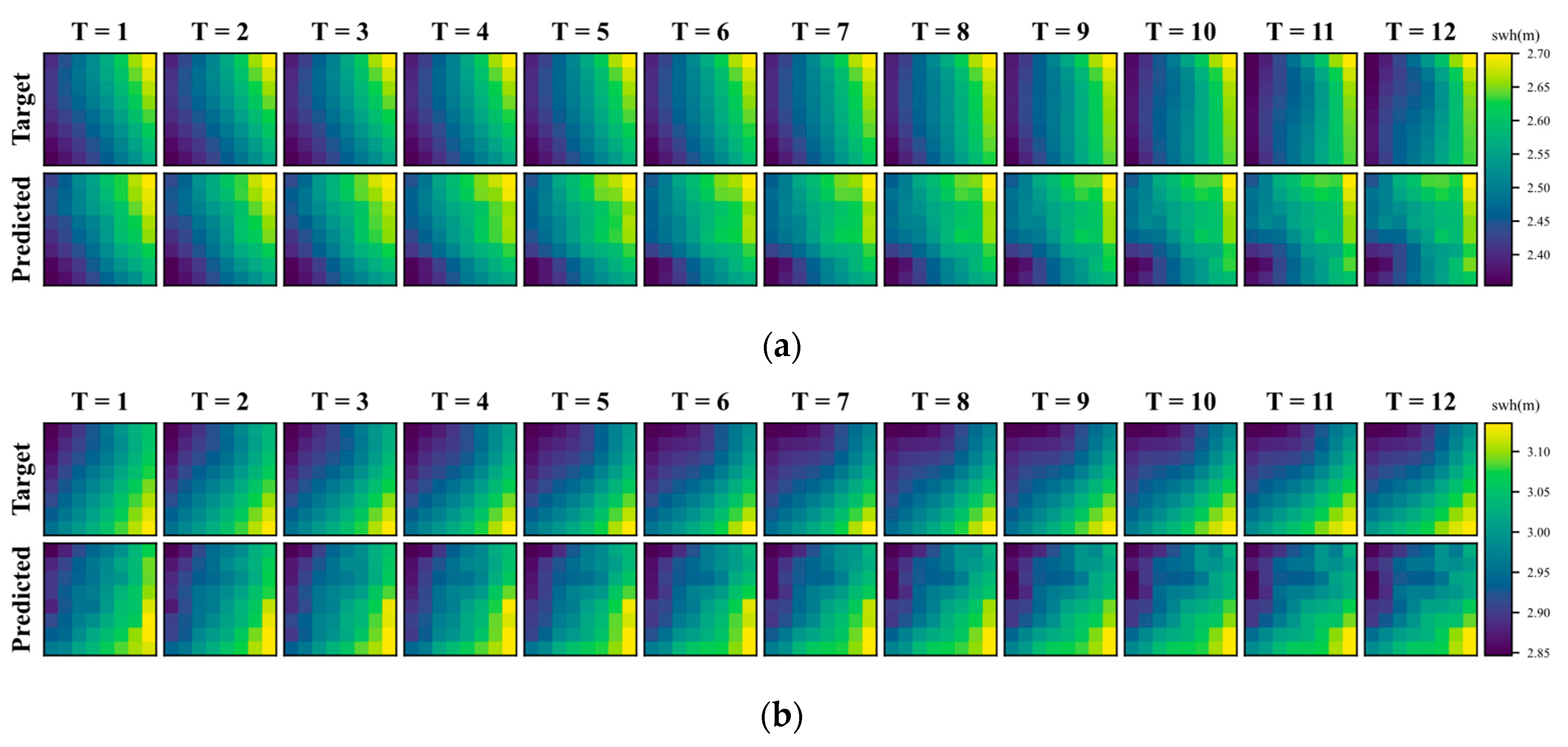
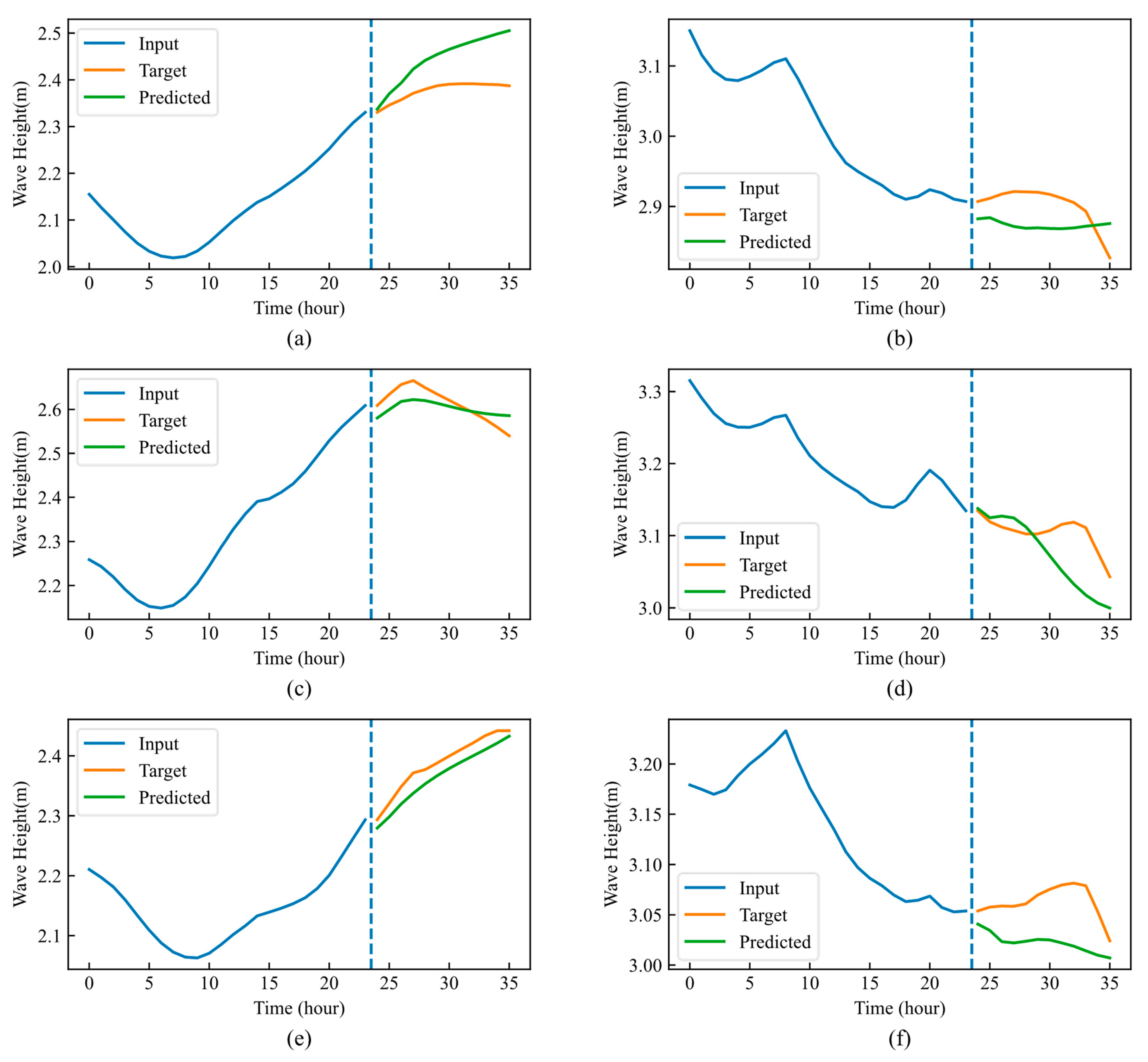
4.3. Predicted Results
4.4. Ablation Experiments
4.4.1. Impact of Exogenous Variables
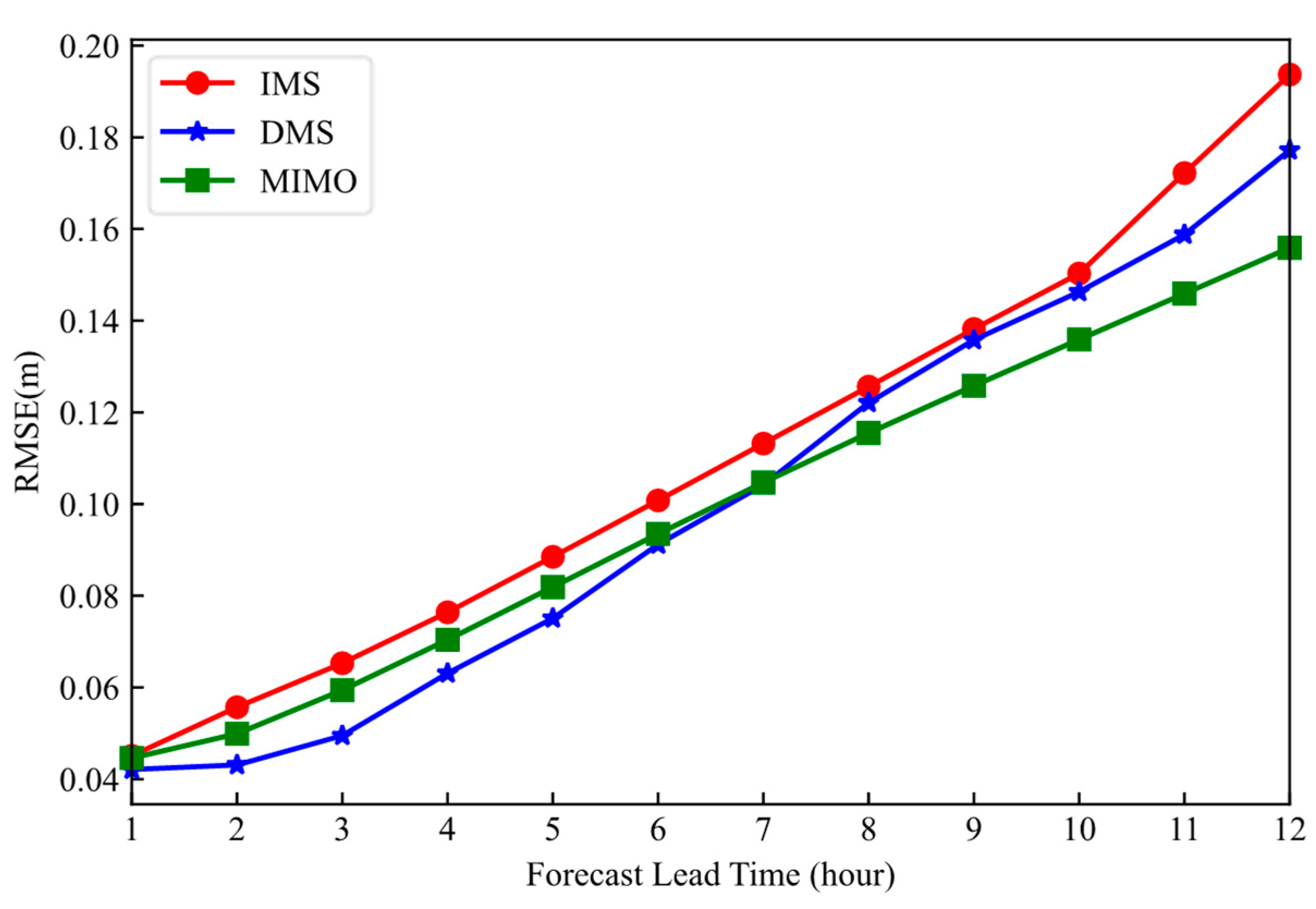
4.4.2. Impact of Multiple Input—Multiple Output Strategy (MIMO)
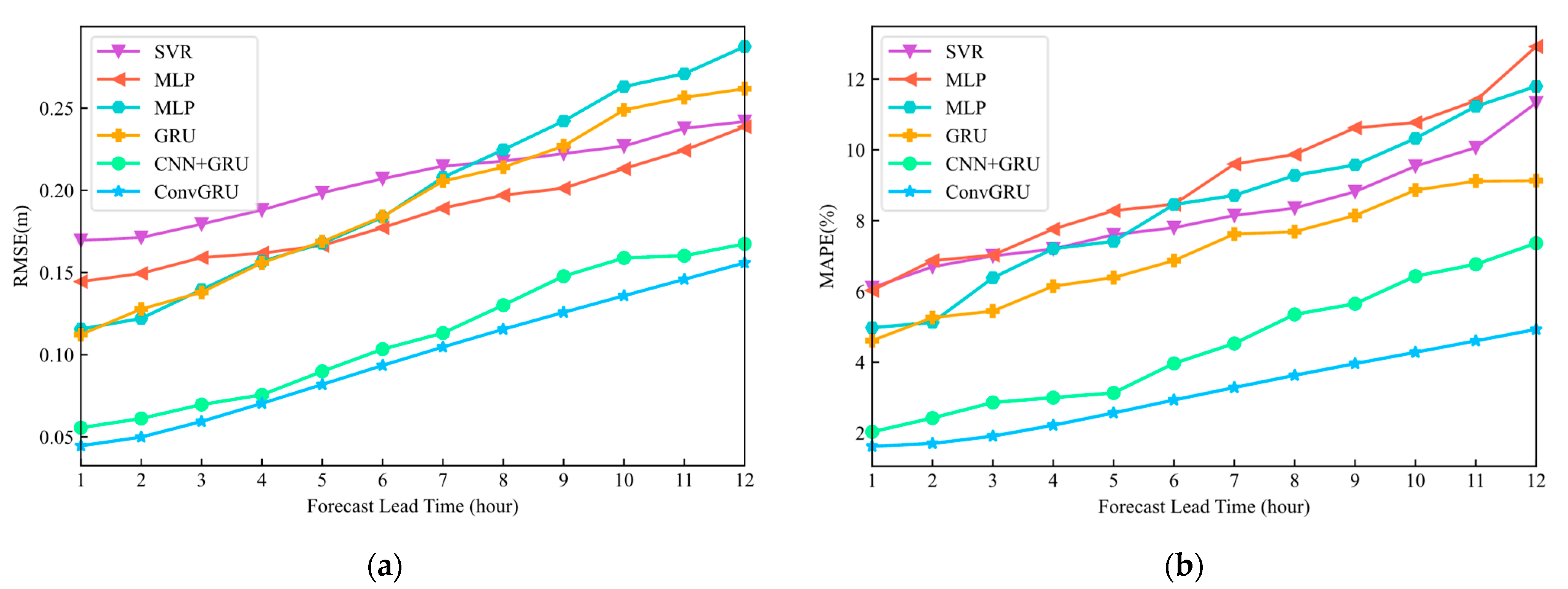
4.5. Comparison of Different Models and Prediction Results
- (1)
- SVR is a form of SVM applied to regression problems. SVR treats the regression problem as an optimization problem by constructing a hyperplane that minimizes the distance to sample points in the sample space. However, unlike the general regression model, SVR incorporates fault tolerance for outlier samples to improve generalization [38,39]. In the experiments, SVR uses an rbf kernel with kernel coefficients taken as the reciprocal of the number of sample features and a penalty parameter of 1. Multi-step prediction is achieved using the DMS strategy.
- (2)
- MLP has good nonlinear regression because it can theoretically approximate any nonlinear function through the nonlinear activation of multilayer neurons and the fully connected structure [24,25]. Moreover, the fully connected structure enables the MLP to perform multi-step prediction using the MIMO strategy. The MLP uses three network layers with 200, 400, and 12 neurons in the experiment.
- (3)
- LSTM is a classical RNN model that uses a gating mechanism to control the forgetting and selection of memory states [18]. Unlike GRU, LSTM has two states. The cell state is responsible for preserving the long-term information of the time series, and the hidden state is the output on the current time step. To handle both states, the LSTM has one more control gate than the GRU and thus has a larger number of parameters for the same setup. The network structure used is a single LSTM layer—Dropout layer—fully connected output layer. The LSTM layer size is 400, and the tanh activation function is used. The Dropout layer discard rate is 0.2, and the fully connected layer size is 12, using linear activation. The model is trained at batch size = 32, learning rate = 0.0001.
- (4)
- GRU enables the transfer of information memory between time steps through a circular connection structure along the time axis. GRU not only captures the temporal correlation between multidimensional time series efficiently but also has a faster training speed than LSTM [40]. Since the structure of LSTM and GRU is more similar, the same grid structure and training hyperparameters as LSTM are used for GRU in the experiments.
- (5)
- CNN+GRU adds a convolutional layer shared on the time axis to GRU to achieve successive extraction of spatial and temporal structures. At each time step, the spatial features are extracted using the convolutional layer to transform the input information of a single moment into a one-dimensional sequence containing spatial information. Thereafter, the temporal structure of the one-dimensional sequence at each moment is extracted using GRU, and the single-step regional prediction results are output.
4.6. Applicability of the Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, C.; Shiotani, S. Numerical ship navigation based on weather and ocean simulation. Ocean Eng. 2013, 69, 44–53. [Google Scholar] [CrossRef]
- Chen, B.; Kou, Y.; Wang, Y.; Zhao, D.; Liu, S.; Liu, G.; Han, X. Analysis of storm surge characteristics based on stochastic process. AIMS Math. 2021, 6, 1177–1190. [Google Scholar] [CrossRef]
- Chen, C.; Sasa, K. Statistical analysis of waves’ effects on ship navigation using high-resolution numerical wave simulation and shipboard measurements. Ocean Eng. 2021, 229, 108757. [Google Scholar] [CrossRef]
- Camus, P.; Losada, I.; Izaguirre, C.; Espejo, A.; Menéndez, M.; Pérez, J. Statistical wave climate projections for coastal impact assessments. Earth’s Future 2017, 5, 918–933. [Google Scholar] [CrossRef]
- Camus, P.; Menendez, M.; Mendez, F.J.; Izaguirre, C.; Espejo, A.; Canovas, V.; Perez, J.; Rueda, A.; Losada, I.J.; Medina, R. A weather-type statistical downscaling framework for ocean wave climate. J. Geophys. Res. Ocean. 2014, 119, 7389–7405. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium, Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Bridges, T.J. Waves in Oceanic and Coastal Waters. Q. J. R. Meteorol. Soc. 2008, 134, 1947–1948. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions: 1. Model description and validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch III in the Mediterranean Sea. Ocean Model. 2015, 90, 82–94. [Google Scholar] [CrossRef]
- Rogers, W.E.; Hwang, P.A.; Wang, D.W. Investigation of wave growth and decay in the SWAN model: Three Regional-Scale applications. J. Phys. Oceanogr. 2003, 33, 366–389. [Google Scholar] [CrossRef]
- Samiksha, S.V.; Jancy, L.; Sudheesh, K.; Kumar, V.S.; Shanas, P.R. Evaluation of wave growth and bottom friction parameterization schemes in the SWAN based on wave modelling for the central west coast of India. Ocean Eng. 2021, 235, 109356. [Google Scholar] [CrossRef]
- Bingölbali, B.; Jafali, H.; Akpınar, A.; Bekiroğlu, S. Wave energy potential and variability for the south west coasts of the Black Sea: The WEB-based wave energy atlas. Renew. Energy 2020, 154, 136–150. [Google Scholar] [CrossRef]
- Li, A.; Guan, S.; Mo, D.; Hou, Y.; Hong, X.; Liu, Z. Modeling wave effects on storm surge from different typhoon intensities and sizes in the South China Sea. Estuar. Coast. Shelf Sci. 2020, 235, 106551. [Google Scholar] [CrossRef]
- Zhou, W.; Shan, D.; Yang, J. The Modeling of Interval-Valued Time Series: A Method Based on Fuzzy Set Theory and Artificial Neural Networks. Int. J. Comput. Intell. Appl. 2019, 18, 1950002. [Google Scholar] [CrossRef]
- Jäger, W.S.; Nagler, T.; Czado, C.; McCall, R.T. A Statistical Simulation Method for Joint Time Series of Non-Stationary Hourly Wave Parameters. Coast. Eng. 2019, 146, 14–31. [Google Scholar] [CrossRef]
- Asma, S.; Sezer, A.; Ozdemir, O. MLR and ANN models of significant wave height on the west coast of India. Comput. Geosci. 2012, 49, 231–237. [Google Scholar] [CrossRef]
- Makarynskyy, O.; Pires-Silva, A.A.; Makarynska, D.; Ventura-Soares, C. Artificial neural networks in wave predictions at the west coast of Portugal. Comput. Geosci. 2005, 31, 415–424. [Google Scholar] [CrossRef]
- Gao, S.; Huang, J.; Li, Y.; Liu, G.; Bi, F.; Bai, Z. A forecasting model for wave heights based on a long short-term memory neural network. Acta Oceanol. Sin. 2021, 40, 62–69. [Google Scholar] [CrossRef]
- Choi, H.; Park, M.; Son, G.; Jeong, J.; Park, J.; Mo, K.; Kang, P. Real-time significant wave height estimation from raw ocean images based on 2D and 3D deep neural networks. Ocean Eng. 2020, 201, 107129. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, W.; Lu, Y.; Wang, Y.; Zhou, Y.; Hui, N.; Dong, C. ConvLSTM-Based wave forecasts in the South and East China Seas. Front. Mar. Sci. 2021, 8, 740. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Kong, X.; Lee, K.Y. Wind speed forecasting using deep neural network with feature selection. Neurocomputing 2020, 397, 393–403. [Google Scholar] [CrossRef]
- Gu, C.; Li, H. Review on Deep Learning Research and Applications in Wind and Wave Energy. Energies 2022, 15, 1510. [Google Scholar] [CrossRef]
- Song, T.; Han, R.; Meng, F. A significant wave height prediction method based on deep learning combining the correlation between wind and wind waves. Front. Mar. Sci. 2022, 9, 983007. [Google Scholar] [CrossRef]
- James, S.C.; Zhang, Y.; O’Donncha, F. A machine learning framework to forecast wave conditions. Coast. Eng. 2018, 137, 1–10. [Google Scholar] [CrossRef]
- Feng, X.; Ma, G.; Su, S.F.; Huang, C.; Boswell, M.K.; Xue, P. A multi-layer perceptron approach for accelerated wave forecasting in Lake Michigan. Ocean Eng. 2020, 211, 107526. [Google Scholar] [CrossRef]
- Pirhooshyaran, M.; Snyder, L.V. Forecasting, hindcasting and feature selection of ocean waves via recurrent and sequence-tosequence networks. Ocean Eng. 2020, 207, 107424. [Google Scholar] [CrossRef]
- Yu, J.; Lu, Z.; Wei, H. Numerical study of a CNN-based model for regional wave prediction. Ocean Eng. 2022, 255, 111400. [Google Scholar] [CrossRef]
- Vandenhende, S.; Georgoulis, S.; Van Gansbeke, W.; Proesmans, M.; Dai, D.; Van Gool, L. Multi-task learning for dense prediction tasks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3614–3633. [Google Scholar] [CrossRef]
- Liu, J.; Xu, L.; Chen, N. A spatiotemporal deep learning model ST-LSTM-SA for hourly rainfall forecasting using radar echo images. J. Hydrol. 2022, 609, 127748. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Ben Taieb, S.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef]
- Carr, C.M.; Yavary, M.; Yavary, M. Wave agitation studies for port expansion-Salalah, Oman. In Proceedings of the Ports 2004: Port Development in the Changing World, Houston, TX, USA, 23–26 May 2004; pp. 1–10. [Google Scholar]
- Anoop, T.R.; Kumar, V.S.; Shanas, P.R.; Johnson, G. Surface Wave Climatology and Its Variability in the North Indian Ocean Based on ERA-Interim Reanalysis. J. Atmos. Oceans Technol. 2015, 32, 1372–1385. [Google Scholar] [CrossRef]
- Rashmi, R.; Aboobacker, V.; Vethamony, P.; John, M. Co-existence of wind seas and swells along the west coast of India during non-monsoon season. Ocean Sci. 2013, 9, 281. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Yang, J. Forecasting of significant wave height based on gated recurrent unit network in the Taiwan strait and its adjacent waters. Water 2021, 13, 86. [Google Scholar] [CrossRef]
- Zhang, D.; Kabuka, M.R. Combining Weather Condition Data to Predict Traffic Flow: A GRU Based Deep Learning Approach. IET Intell. Transp. Syst. 2018, 12, 578–585. [Google Scholar] [CrossRef]
- Dai, G.; Ma, C.; Xu, X. Short-term Traffic Flow Prediction Method for Urban Road Sections Based on Space-time Analysis and GRU. IEEE Access 2019, 7, 143025–143035. [Google Scholar] [CrossRef]
- Fan, S.; Xiao, N.; Dong, S. A novel model to predict significant wave height based on long short-term memory network. Ocean Eng. 2020, 205, 107298. [Google Scholar] [CrossRef]
- Mahjoobi, J.; Adeli, E. Prediction of significant wave height using regressive support vector machines. Ocean Eng. 2009, 36, 339–347. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Z.; Feng, Z. Short-term offshore wind speed forecast by seasonal ARIMA—A comparison against GRU and LSTM. Energy 2021, 227, 120492. [Google Scholar] [CrossRef]

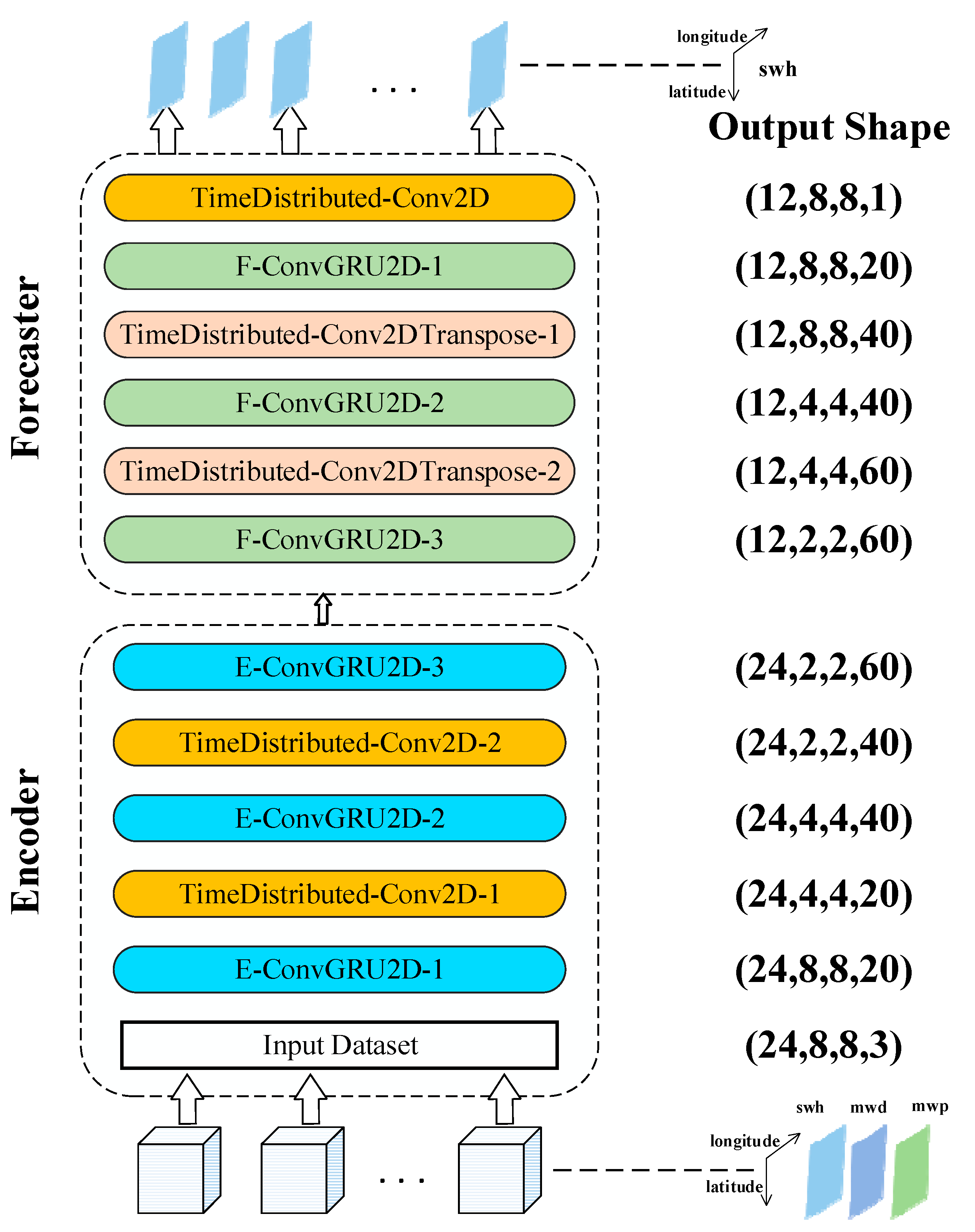


| Parts | Network Layer | Filters | Kernel_Size | Strides |
|---|---|---|---|---|
| Input | Input-1 | |||
| Encoder | E-ConvGRU2D-1 | 20 | 2 | 1 |
| TimeDistributed-Conv2D-1 | 20 | 2 | 2 | |
| E-ConvGRU2D-2 | 40 | 2 | 1 | |
| TimeDistributed-Conv2D-2 | 40 | 2 | 2 | |
| E-ConvGRU2D-3 | 60 | 2 | 1 | |
| Forecaster | F-ConvGRU2D-3 | 60 | 2 | 1 |
| TimeDistributed-Conv2DTranspose-2 | 60 | 3 | 1 | |
| F-ConvGRU2D-2 | 40 | 2 | 1 | |
| TimeDistributed-Conv2DTranspose-1 | 40 | 2 | 2 | |
| F-ConvGRU2D-1 | 20 | 2 | 1 | |
| output | TimeDistributed-Conv2D | 1 | 1 | 1 |
| Learning Rate | Batch Size | MRMSE | MMAE | MMAPE |
|---|---|---|---|---|
| 0.001 | 12 | 0.0986 | 0.0710 | 3.1375 |
| 24 | 0.1003 | 0.0742 | 3.3980 | |
| 36 | 0.1005 | 0.0772 | 3.7344 | |
| 48 | 0.1086 | 0.0781 | 3.4124 | |
| 0.0001 | 12 | 0.1037 | 0.0751 | 3.3259 |
| 24 | 0.1096 | 0.0796 | 3.5492 | |
| 36 | 0.1192 | 0.0912 | 4.1226 | |
| 48 | 0.1259 | 0.0924 | 4.0918 |
| Input Step | Error | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 12 | RMSE | 0.0625 | 0.0621 | 0.0710 | 0.0802 | 0.0905 | 0.1009 | 0.1112 | 0.1211 | 0.1310 | 0.1410 | 0.1513 | 0.1618 | 0.1070 |
| MAE | 0.0521 | 0.0508 | 0.0580 | 0.0653 | 0.0731 | 0.0810 | 0.0886 | 0.0959 | 0.1032 | 0.1108 | 0.1186 | 0.1268 | 0.0853 | |
| MAPE | 2.6415 | 2.5395 | 2.8811 | 3.1963 | 3.5357 | 3.8824 | 4.2226 | 4.5467 | 4.8738 | 5.2075 | 5.5558 | 5.9160 | 4.0832 | |
| 18 | RMSE | 0.0586 | 0.0613 | 0.0666 | 0.0753 | 0.0846 | 0.0943 | 0.1038 | 0.1131 | 0.1222 | 0.1314 | 0.1409 | 0.1506 | 0.1002 |
| MAE | 0.0470 | 0.0480 | 0.0508 | 0.0567 | 0.0630 | 0.0699 | 0.0767 | 0.0833 | 0.0898 | 0.0965 | 0.1034 | 0.1105 | 0.0746 | |
| MAPE | 2.2392 | 2.2435 | 2.3417 | 2.5848 | 2.8528 | 3.1510 | 3.4457 | 3.7356 | 4.0225 | 4.3119 | 4.6123 | 4.9241 | 3.3721 | |
| 24 | RMSE | 0.0446 | 0.0499 | 0.0594 | 0.0704 | 0.0819 | 0.0935 | 0.1047 | 0.1155 | 0.1258 | 0.1359 | 0.1459 | 0.1559 | 0.0986 |
| MAE | 0.0345 | 0.0372 | 0.0428 | 0.0501 | 0.0583 | 0.0667 | 0.0748 | 0.0826 | 0.0902 | 0.0975 | 0.1049 | 0.1122 | 0.0710 | |
| MAPE | 1.6250 | 1.7045 | 1.9111 | 2.2194 | 2.5661 | 2.9332 | 3.2848 | 3.6306 | 3.9610 | 4.2808 | 4.6043 | 4.9291 | 3.1375 | |
| 30 | RMSE | 0.0667 | 0.0702 | 0.0778 | 0.0872 | 0.0976 | 0.1081 | 0.1187 | 0.1292 | 0.1397 | 0.1501 | 0.1607 | 0.1712 | 0.1149 |
| MAE | 0.0559 | 0.0590 | 0.0646 | 0.0716 | 0.0796 | 0.0874 | 0.0951 | 0.1027 | 0.1103 | 0.1179 | 0.1257 | 0.1337 | 0.0920 | |
| MAPE | 2.8505 | 2.9459 | 3.1930 | 3.5026 | 3.8721 | 4.2303 | 4.5832 | 4.9276 | 5.2784 | 5.6257 | 5.9892 | 6.3630 | 4.4468 | |
| 36 | RMSE | 0.0531 | 0.0573 | 0.0645 | 0.0752 | 0.0859 | 0.0975 | 0.1088 | 0.1200 | 0.1310 | 0.1416 | 0.1522 | 0.1625 | 0.1041 |
| MAE | 0.0390 | 0.0414 | 0.0463 | 0.0540 | 0.0614 | 0.0698 | 0.0779 | 0.0861 | 0.0942 | 0.1023 | 0.1103 | 0.1183 | 0.0751 | |
| MAPE | 1.8427 | 1.9254 | 2.1101 | 2.4518 | 2.7490 | 3.1248 | 3.4698 | 3.8315 | 4.1820 | 4.5358 | 4.8873 | 5.2410 | 3.3626 |
| Input Variables | MRMSE | MMAE | MMAPE |
|---|---|---|---|
| swh | 0.1091 | 0.0802 | 3.5561 |
| swh,mwd | 0.1075 | 0.0785 | 3.4959 |
| swh,mwd,mwp | 0.0986 | 0.0710 | 3.1375 |
| Model | Error | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVR | RMSE | 0.1696 | 0.1713 | 0.1795 | 0.1881 | 0.1986 | 0.2071 | 0.2148 | 0.2178 | 0.2224 | 0.2269 | 0.2378 | 0.2419 | 0.2063 |
| MAE | 0.1576 | 0.1612 | 0.1676 | 0.1838 | 0.1912 | 0.2043 | 0.2069 | 0.2096 | 0.2143 | 0.2208 | 0.2249 | 0.2284 | 0.1976 | |
| MAPE | 6.1076 | 6.6984 | 7.0042 | 7.1985 | 7.6037 | 7.8020 | 8.1490 | 8.3553 | 8.8201 | 9.5414 | 10.0658 | 11.3289 | 8.2229 | |
| MLP | RMSE | 0.1445 | 0.1495 | 0.1591 | 0.1618 | 0.1665 | 0.1773 | 0.1892 | 0.1971 | 0.2013 | 0.2132 | 0.2244 | 0.2387 | 0.1852 |
| MAE | 0.1292 | 0.1398 | 0.1449 | 0.1456 | 0.1575 | 0.1692 | 0.1755 | 0.1813 | 0.1950 | 0.2018 | 0.2144 | 0.2257 | 0.1733 | |
| MAPE | 6.0294 | 6.8732 | 7.0264 | 7.7628 | 8.2841 | 8.4627 | 9.6008 | 9.8731 | 10.6233 | 10.7755 | 11.3936 | 12.9243 | 9.1358 | |
| LSTM | RMSE | 0.1156 | 0.1221 | 0.1396 | 0.1568 | 0.1678 | 0.1837 | 0.2079 | 0.2247 | 0.2422 | 0.2632 | 0.2710 | 0.2875 | 0.1985 |
| MAE | 0.1126 | 0.1298 | 0.1396 | 0.1407 | 0.1586 | 0.1662 | 0.1689 | 0.1725 | 0.1885 | 0.2156 | 0.2259 | 0.2338 | 0.1717 | |
| MAPE | 4.9765 | 5.1250 | 6.3860 | 7.2080 | 7.4165 | 8.4579 | 8.7160 | 9.2815 | 9.5755 | 10.3267 | 11.2312 | 11.7987 | 8.3750 | |
| GRU | RMSE | 0.1123 | 0.1278 | 0.1380 | 0.1559 | 0.1688 | 0.1841 | 0.2056 | 0.2141 | 0.2270 | 0.2489 | 0.2565 | 0.2619 | 0.1917 |
| MAE | 0.0999 | 0.1146 | 0.1219 | 0.1361 | 0.1442 | 0.1550 | 0.1727 | 0.1765 | 0.1866 | 0.2053 | 0.2107 | 0.2137 | 0.1614 | |
| MAPE | 4.6107 | 5.2614 | 5.4458 | 6.1504 | 6.3911 | 6.8728 | 7.6227 | 7.6893 | 8.1477 | 8.8649 | 9.1178 | 9.1318 | 7.1089 | |
| CNN+GRU | RMSE | 0.0556 | 0.0612 | 0.0697 | 0.0756 | 0.0899 | 0.1034 | 0.1132 | 0.1302 | 0.1478 | 0.1589 | 0.1602 | 0.1675 | 0.1111 |
| MAE | 0.0421 | 0.0496 | 0.0509 | 0.0631 | 0.06716 | 0.0705 | 0.0891 | 0.0951 | 0.1205 | 0.1321 | 0.1406 | 0.1489 | 0.0891 | |
| MAPE | 2.0321 | 2.4231 | 2.8621 | 3.0012 | 3.1326 | 3.9682 | 4.5312 | 5.3521 | 5.6531 | 6.4325 | 6.7675 | 7.3654 | 4.4600 | |
| Conv GRU | RMSE | 0.0446 | 0.0499 | 0.0594 | 0.0704 | 0.0819 | 0.0935 | 0.1047 | 0.1155 | 0.1258 | 0.1359 | 0.1459 | 0.1559 | 0.0986 |
| MAE | 0.0345 | 0.0372 | 0.0428 | 0.0501 | 0.0583 | 0.0667 | 0.0748 | 0.0826 | 0.0902 | 0.0975 | 0.1049 | 0.1122 | 0.0710 | |
| MAPE | 1.6250 | 1.7045 | 1.9111 | 2.2194 | 2.5661 | 2.9332 | 3.2848 | 3.6306 | 3.9610 | 4.2808 | 4.6043 | 4.9291 | 3.1375 |
| Sea Areas | MAX (m) | MEAN (m) | VAR (m2) | STD (m) | MRMSE | MMAE | MMAPE |
|---|---|---|---|---|---|---|---|
| C | 3.5578 | 1.5766 | 0.2450 | 0.4950 | 0.0814 | 0.0631 | 4.2154 |
| D | 5.0784 | 2.2308 | 0.3066 | 0.5538 | 0.1248 | 0.0862 | 3.9586 |
| Original | 5.9778 | 2.2551 | 0.4121 | 0.6420 | 0.0986 | 0.0710 | 3.1375 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Zhang, H.; Hu, S.; Shi, J.; Geng, J.; Su, Y. ConvGRU-RMWP: A Regional Multi-Step Model for Wave Height Prediction. Mathematics 2023, 11, 2013. https://doi.org/10.3390/math11092013
Sun Y, Zhang H, Hu S, Shi J, Geng J, Su Y. ConvGRU-RMWP: A Regional Multi-Step Model for Wave Height Prediction. Mathematics. 2023; 11(9):2013. https://doi.org/10.3390/math11092013
Chicago/Turabian StyleSun, Youjun, Huajun Zhang, Shulin Hu, Jun Shi, Jianning Geng, and Yixin Su. 2023. "ConvGRU-RMWP: A Regional Multi-Step Model for Wave Height Prediction" Mathematics 11, no. 9: 2013. https://doi.org/10.3390/math11092013
APA StyleSun, Y., Zhang, H., Hu, S., Shi, J., Geng, J., & Su, Y. (2023). ConvGRU-RMWP: A Regional Multi-Step Model for Wave Height Prediction. Mathematics, 11(9), 2013. https://doi.org/10.3390/math11092013







