Abstract
Non-negative matrix factorization (NMF) is widely used as a powerful matrix factorization tool in data representation. However, the traditional NMF, measured by Euclidean distance or Kullback–Leibler distance, does not take into account the internal implied geometric information of the dataset and cannot measure the distance between samples as well as possible. To remedy the defects, in this paper, we propose the NMF method with Earth mover’s distance as a metric, for short GSNMF-EMD. It combines graph regularization and smooth constraints. The GSNMF-EMD method takes into account the intrinsic implied geometric information of the dataset and can produce more sparse and stable local solutions. Experiments on two specific image datasets showed that the proposed method outperforms related state-of-the-art methods.
Keywords:
non-negative matrix factorization (NMF); Earth mover’s distance (EMD); graph regularized; L1/2 sparsity-constrained MSC:
68U10; 62H30; 15A69
1. Introduction
The non-negative matrix factorization (NMF) method has been widely used in various fields of feature learning and has become one of the most popular methods, among which are text clustering [1,2,3], digital image processing [4,5,6,7,8,9], face recognition [10], and signal analytics [11,12]. Due to the wide range of practical properties of NMF, numerous scholars have proposed some improvements to the original NMF: Imposing different constraints on the two factor matrices. For example, P. O. Hoyer [13] proposed NMF with sparseness constraints, which improve the accuracy of the parts-based representation compared to the basic NMF. Cai et al. [14] proposed a manifold-based NMF (GNMF) method that respects the geometric structure information hidden inside the dataset. He et al. [15] proposed a robust NMF method with sparse constraints in order to deal with both sparse and Gaussian noise. Kong et al. [16] added the -norm constraint and proposed a robust non-negative matrix decomposition algorithm. Huang et al. [17] proposed a new unsupervised learning model that takes into account the overall and local structure of the data space, called NMF with robustness. Pan et al. [18] introduced an orthogonal non-negative matrix factorization. Luo et al. [19] applied NMF to the collaborative filtering problem and proposed a regularized single-element-based model (RSNMF) that achieves computational complexity reduction and accuracy improvement for large industrial datasets. Sun et al. [20] analyzed the generalization performance of the NMF algorithm from the perspective of algorithm stability and gave bounds on the generalization error.
The vast majority of the various NMF-based variants mentioned above use the Euclidean norm or the K-L divergence [21] to measure the minimization distance between the product of two factor matrices and the original matrix. A shortcoming of the above NMF-based approaches is that either the intrinsic structure of the dataset or the distance between samples is ignored. To remedy the shortcoming, many researchers have tried to adopt new metrics. Recently, correntropy has proven to be a very effective approximation measure by virtue of its stability against outliers or noise [22,23,24,25,26]. For example, Yu et al. [26] proposed the correntropy-based, hypergraph-regularized NMF (CHNMF) method using correlation entropy. The method is used for clustering and feature extraction of multi-cancer integrated data with better robustness. Another measure, called the Earth mover’s distance (EMD), has also attracted great interest. EMD not only provides a better measure of the distance between samples but also has good robustness [27,28]. In [28], the authors showed that EMD has good performance in tasks involving large distortions, such as geometric deformations, illumination changes, or heavy intensity noise.
Rubner et al. [29] constructed an image comparison framework that better accounts for perceptual similarity than other previously proposed methods by combining EMD with a vector quantization-based distribution representation scheme. Sandler et al. [30,31] proposed an EMDNMF algorithm that minimizes the EMD error between the data and the product of factor matrices. The main advantage of this method is enhanced robustness. In order to improve the efficiency and accuracy of approximate EMD calculations, Atasu et al. provided new theoretical and practical results in [32]. Qu et al. [33] proposed a novel EMD method to detect false data injection attacks in smart grids to improve power-system security.
In this paper, the NMF algorithm is improved based on the EMD distance and the use of graph-regularization terms and sparse constraints, which can discover the geometric structure information inherent in the dataset and produce a smooth and more accurate solution. We call it graph-regularized, sparsity-constrained NMF with EMD metric (GSNMF-EMD). In view of numerous literature showing that -NMF provides sparser and more accurate results than those delivered using the norm [34,35,36,37,38], we also chose the norm as the sparse constraint. The graph-regularization constraint uncovers the implied semantics while focusing on preserving information about the intrinsic geometric structure of the dataset. Furthermore, update rules and convergence proofs of the GSNMF-EMD algorithm are presented. Experimental results on real datasets demonstrate the validity and accuracy of our proposed multiplicative update algorithm.
The rest of the paper is organized as follows: In Section 2, we present some of the related work. In Section 3, we propose a multiplicative update rule for the GSNMF-EMD model and prove its convergence. We report some experimental results on two image datasets in Section 4. The parameter selection is provided in Section 5. Finally, we briefly summarize in Section 6.
2. Related Work
In this section, we review the EMD metric and the NMF with the Earth Mover’s distance metric (EMDNMF in short). We use bold capital letters to denote matrices and lowercase letters to denote vectors. For example, is an matrix, is the j- column vector, and is the -th entry of matrix . Let x, y, be the generalized K-L divergence between and , where represents element-wise division and denotes the transpose operation.
2.1. EMD
EMD was first proposed for certain vision problems by Peleg et al. [39]. EMD is an efficient metric based on an optimal transportation problem solution. To be precise, this is the minimum cost that must be paid to convert one distribution into another. Since it can manipulate the variable-length representation of the distribution, it effectively avoids the quantization and other typical histogram binning problems, causing it to be more robust than histogram matching techniques.
Definition 1
([29]). Let be two normalized histograms with . Let be an distance metric matrix. is a transport matrix. We call
an Earth mover’s distance (EMD) between and .
Despite EMD having many good properties, its calculations based on the well-known solution to the transportation problem are very expensive. Recent years, some scholars have done fruitful work to improve the operation efficiency. Based on Equation (1), Marco Cuturi [40] proposed a maximum entropy perspective. He smoothed the solution to the EMD problem by adding an entropy-regularization term. Based on the excellent results of Cuturi, Frogner [41] replaced the equality constraint with a soft penalty in terms of K-L divergence. He obtained an unconstrained approximate transmission problem. The specific form is:
where = is the entropy of , and and are the regularization parameters. When are normalized vectors, Equation (2) can approximate Cuturi’s algorithm closely for large enough . Moreover, Frogner obtains the optimal solution of Equation (2) by borrowing Cuturi’s results; that is, the optimal solution is a diagonal scaling of a matrix . The specific form is:
where ⨀ denotes element-wise multiplication. The gradient of Equation (2) is given by
2.2. EMDNMF
Considering n non-negative histograms with m bins, the histogram is expressed in matrix form as , where the j- histogram is the j- column of the matrix. The matrix may be decomposed into a product of and , where and are defined as the basis and coefficient matrices, respectively. In many cases, the low-dimensional approximation is more valuable than the exact decomposition. Let , . Optimizing the exact EMD throughout the iterative solution process is expensive and makes it difficult to guarantee that . Equation (2) describes a regularized approximation which can be calculated quickly and efficiently, even with unnormalized data. Fortunately, implies that is the sum of distances between the feature histograms. Based on Equation (2), the objective function of EMDNMF can be expressed as:
3. GSNMF-EMD
3.1. The Objective Function
To explicitly explain how to discover information about the geometric structure implied by the dataset, the low-dimensional representation of the original data relative to the basis matrix is . A reasonable assumption is that if two data points and are close to each other in the intrinsic geometric structure of the dataset, then these two points and are also close to each other in the new basis matrix [42]. For each data point , we can use a 0–1 weighting scheme to generate a k-nearest neighbor graph, which in turn generates a weight matrix according to the graph theory [43,44]. Given a graph with n vertices, where each vertex corresponds to a data point, the edge weight matrix is defined as follows:
where denotes the set of k nearest neighbors of the data point . Thus, the formula used to measure the smoothed representation of the lower dimension is
Combining Equations (6) and (7), we get another objective function:
where is the regularization parameter.
To obtain a sparser and more accurate solution, the first issue to be addressed is: Should a sparse constraint be imposed on the basis matrix or the coefficient matrix ? In this paper, we choose the sparsity constraint on the coefficients . Numerous results have shown that the proposed regularity is both easier to solve than the regularity and more sparse and stable than the regularity [35,36,37], and it is also computationally efficient. Based on the above graph-regularization term and sparsity constraint, the final objective function of graph-regularized, sparsity-constrained NMF with the Earth mover’s distance metric (GSNMF-EMD) is given as:
where is the regularization and is the regularization parameter.
3.2. Multiplicative Update Rules
The objective function Equation (9) is not convex in both and . Therefore, to find the global minimum is a difficult task, and fortunately we can find an iterative update algorithm to obtain a locally optimal solution. Similar to [14,45], we obtained the two-step multiplicative update rule that can maintain non-negativity and find a local minimum.
Theorem 1.
The objective function ϝ in Equation (9) has the following update rules:
where is the -entry of the optimal transportation matrix between and defined in Equation (3). Furthermore, the objective function ϝ is nonincreasing and permanent under these update rules if and only if and are at a stationary point.
Now the specific procedure for finding the local optimal and of GSNMF-EMD is summarized in Algorithm 1.
| Algorithm 1 GSNMF-EMD algorithm. |
|
3.3. Convergence Analysis
In this section, we will draw on the ideas of [14,45] and cite the relevant theory as Definition 2 and Lemma 1.
Definition 2
([45]). is an auxiliary function for , if the conditions and are satisfied.
Lemma 1
([45]). If Ψ is an auxiliary function of , then is nonincreasing under the update
By fixing the matrix , we transform the objective function as
With fixed , can similarly be rewritten under the update rules for . We only prove that is nonincreasing under the update rule of Equation (10), and Equation (11) can be proved in similar way.
Lemma 2.
Let , and . Then, function
is an auxiliary function for .
Proof.
It can be seen from reference [41], is convex. We use the convexity for one by one and obtain
which implies . Therefore, Lemma 2 is proved. □
Proof.
(Proof of Theorem 1.) The gradient satisfies Equation (6). Let the gradient of with respect to be zero. We can obtain . The equations are such that . We have
Similarly, we can construct . Use the same update method as V. We get
Combine Lemma 1 and Lemma 2. Theorem 1 is obtained. □
4. Experiments
In this section, we compare the data-clustering results of two popular datasets with the related most well-known methods, such as K-means, NMF [45], GNMF [14], and EMDNMF [30], to evaluate the performance of the proposed GSNMF-EMD algorithm.
4.1. Datasets
We evaluated the clustering performance on two widely used datasets, COIL20 and MNIST. The basic information of these two datasets is presented in Table 1.

Table 1.
Statistics of the datasets used in our experiment.
- COIL20 (https://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php, accessed on: 26 June 2022 ): The COIL20 dataset contains 1440 gray images of 20 objects—that is, 72 images of each object acquired from different angles. The images we use here are limited to a size of .
- MNIST (http://yann.lecun.com/exdb/mnist/, accessed on: 26 June 2022): The MNIST handwritten digit dataset comes from Yann LeCun’s web page and contains a training set of examples and a test set of examples. The size of the images we used here was .
4.2. Evaluation Metric
We used two of the most popular evaluation metrics to evaluate the clustering performance of the GSNMF-NMF algorithm. One metric was ACC (clustering accuracy), and the other was (mutual information). ACC measures the proportion of correctly classified data points in a clustering task, and NMI measures the mutual information between the true labels of the data points and the cluster assignments. These two metrics are commonly used in clustering tasks because they provide an easy-to-understand measure of the quality of the clustering results. In the context of NMF, ACC and NMI are used to evaluate the quality of the clusters that are produced by the algorithm. ACC is based on the principle of evaluating the clustering performance by comparing the clustering labels of each sample with the labels provided by the dataset, which is defined as [5,9,11,42], etc., as follows:
where is the delta function that equals one if and equals zero otherwise, n is the total number of samples, and map is the permutation mapping function that maps each cluster label to the equivalent label from the data corpus.
The between the two clusters C and , which is defined as in [5,10,42], etc., it is defined as follows:
where C is a set of true labels; is a set of clustering labels obtained from a specific clustering algorithm; denotes the joint probability that this arbitrarily selected document belongs to the clusters and at the same time, as opposed to and , which denote the probabilities of a document belonging to the clusters and , respectively. The other metric is the NMI (normalized mutual information) [5,9,11,42]. It is expressed as follows
and are the entropies of C and , respectively.
4.3. Performance Evaluations and Comparisons
To demonstrate the performance of our proposed method in improving image clustering, we compared the GSNMF-EMD algorithm with the following four classical clustering algorithms.
- K-means: Canonical K-means clustering method (K-means in short).
- NMF: [45]: The original NMF is considered to be the baseline algorithm and only imposes non-negative constraints on the two factor matrices.
- GNMF: [42]: Graph-regularized NMF (GNMF in short) with Euclidean distance. It adds graph-regularization constraints to NMF, taking into account information about the geometric structure of the data space. The regularization parameter is set to 10.
- EMDNMF: [30]: NMF with EMD (EMDNMF in short). We set the and to 100 and 0.1, respectively; meanwhile, we used the 2D distance of pixels’ location of the image as the ground metric.
- GSNMF-EMD: Graph-regularized sparsity-constrained NMF with the Earth mover’s distance metric (GSNMF-EMD in short). We set the , , , and to 100, 0.1, 20, and 1.8, respectively. Meanwhile, we use the 2D distances among pixels’ locations in the image as the ground metric.
In order to demonstrate the clustering performance, we compare our method with K-means, NMF, GNMF, and EMDNMF methods under the same iterations and with the same well-known datasets. In all experiments, we used the 0-1 weighting scheme for constructing the k-nearest neighbor graph with . Table 2 and Table 3 show the ACC and NMI results on the COIL20 and MNIST datasets, respectively, including those of GSNMF-EMD and the four comparison algorithms. For each given cluster number k, 20 test and 100 iterations runs were conducted on different randomly chosen clusters. The average performance is reported in the Table 2 and Table 3. Figure 1 and Figure 2 show the clustering results for the COIL20 and MNIST datasets in graphical form, and we can see from these experiments that our algorithm has high performance.

Table 2.
Clustering performance on the COIL20 dataset.

Table 3.
Clustering performance on the MNIST dataset.
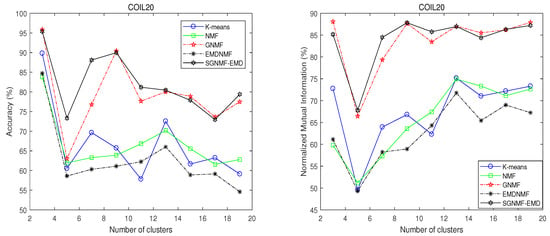
Figure 1.
Clustering performance comparisons on the COIL20 dataset.
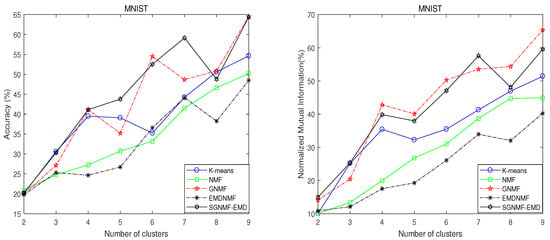
Figure 2.
Clustering performance comparisons on the MNIST dataset.
The GSNMF-EMD method and GNMF method are better than the NMF and EMDNMF methods. This is because graph regularization can respect the geometric information implied by the dataset. Meanwhile, the -smoothing-constraint method in GSNMF-EMD can produce more accurate and smoother solutions. In addition, the GSNMF-EMD method has good perceptual similarity and robustness, thereby having better performance than GNMF and the other three methods.
5. Parameter Selection
GSNMF-EMD has four essential regularization parameters: and , when both values of and are equal to zero. The new model degrades to the EMDNMF method [30]. In this experiment, based on the algorithm of graph theory, we set the number of nearest neighbors on all datasets to five. There are four regularization parameters, as in [14,17,42]. It is very interesting and meaningful to explore the influences of their changes on the clustering results. Of course, there are many combined results of these four parameters, which requires a large number of numerical experiments. In this section, we mainly investigate the sensitivity of , and , with the iterations set to 100 and the number of clusters set to eight. Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 demonstrate the ACC and NMI of GSNMF-EMD with different and or and on COIL20.
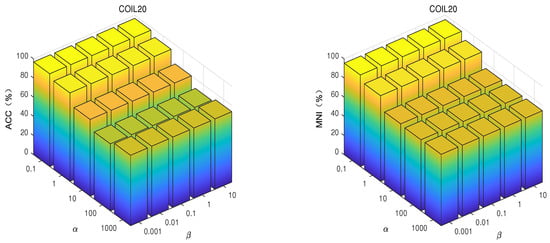
Figure 3.
With fixed and , ACC and NMI of GSNMF-EMD with different and and the same number of clusters on the COIL20 dataset.
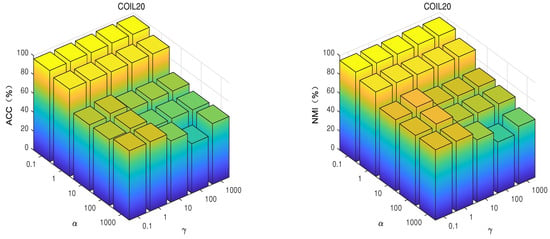
Figure 4.
With fixed and , ACC and NMI of GSNMF-EMD with different and and the same number of clusters on the COIL20 dataset.
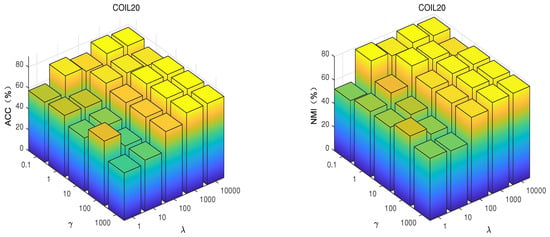
Figure 5.
With fixed and , ACC and NMI of GSNMF-EMD with different and , and the same number of clusters on the COIL20 dataset.
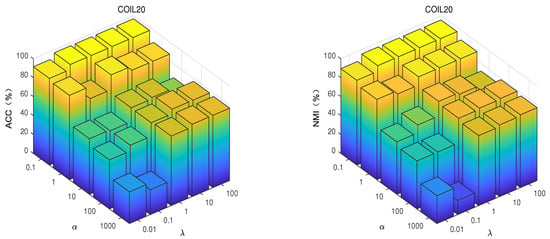
Figure 6.
With fixed and , ACC and NMI of GSNMF-EMD with different and and the same number of clusters on the COIL20 dataset.
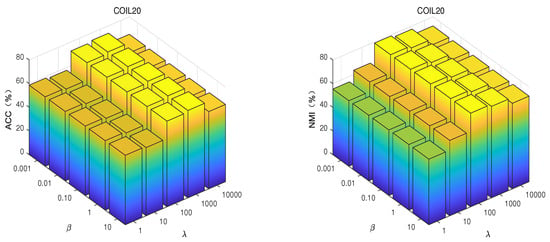
Figure 7.
With fixed and , ACC and NMI of GSNMF-EMD with different and and the same number of clusters on the COIL20 dataset.
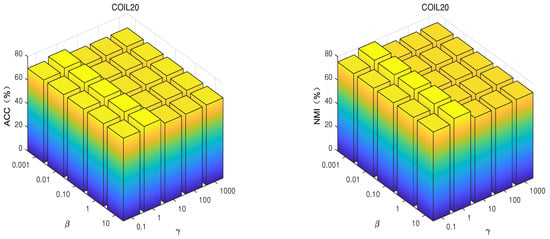
Figure 8.
With fixed and , ACC and NMI of GSNMF-EMD with different and and the same number of clusters on the COIL20 dataset.
As shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, the performance of the algorithm is influenced by the parameters. It can be seen that the performance of GSNMF-EMD is relatively stable with respect to the parameter . In general, can be selected from the range [0.001, 10]. The effect of on GSNMF-EMD is small. When the value of is within [0.1, 1], GSNMF-EMD achieves consistently good performances. However, when is greater than 10, the performance of our algorithm degrades. When the value of is within [1, 10,000], the performance of the GSNMF-EMD improves as increases. In particular, when is greater than 10, the performance of GSNMF-EMD stabilizes due to a slower increase, so the range of can be set to [10, 10,000]. Overall, the performance of the GSNMF-EMD algorithm can remain relatively stable as the parameters are transformed, and in most cases, it is more accurate than any other algorithm we tested. Based on the experimental results, we conclude that all the regularization parameters in the algorithm can control the clustering performance. Therefore, if certain parameters are not set to reasonable values, the clustering performance may be relatively low.
Figure 9a,b show reconstructions of face images from the COIL20 database and handwritten digits from the MNIST database, respectively. From Figure 9, we can see that our algorithm has good reconstruction performance.
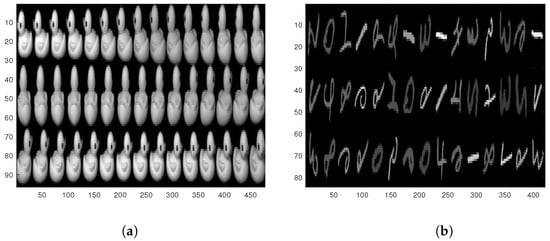
Figure 9.
Some of the reconstructed images. (a): Reconstructions of face images from the COIL20 database. (b): Reconstructions of handwritten digits from the MNIST database.
6. Conclusions
We proposed a new algorithm called graph-regularized, sparsity-constrained NMF with the Earth mover’s distance metric (GSNMF-EMD). GSNMF-EMD builds the geometric structures of the data distribution and sparsity constraints and incorporates them into EMDNMF as the additional regularization terms. The experimental results showed that it can have more clustering power than lots of NMF-based algorithms. Meanwhile, the results also showed that GSNMF-EMD is more stable and works more accurately and rapidly than the original EMD.
In the end, there are two issues that may lead to more interesting work in the future. Firstly, the normalization assumption of the histograms is not essential for GSNMF-EMD. This is because the algorithm proposed by EMD is not limited to the normalized case. Therefore, GSNMF-EMD has the potential ability to deal with occlusions, which is an important problem in local descriptors. Secondly, using our algorithm for hyperspectral analysis is also a good research direction, and finally, as indicated in [29], GSNMF-EMD can also be modeled as a network flow problem, and that would be worthy work, full of research significance.
Author Contributions
Conceptualization, S.L. and Q.L.; methodology, S.L. and L.L.; software, Q.L. and Z.C.; writing—original draft preparation, S.L.; writing—review and editing, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Natural Science Foundation of China under Grants 12161020 and 12061025; and partially funded by the Natural Science Foundation of the Educational Commission of Guizhou Province under Grant Qian-Jiao-He KY Zi [2021]298, and Guizhou Provincial Science and Technology Projects (QKHJC-ZK[2023]YB245), GYU-KYZ(2019-2020)PT06-04, under the Guiyang Municipal Bureau of Science and Technology (No. K1930000701225).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shahnaz, F.; Berry, M.W.; Pauca, V.P.; Plemmons, R.J. Document clustering using nonnegative matrix factorization. Inf. Process Manag. 2006, 42, 373–386. [Google Scholar] [CrossRef]
- Pei, X.; Wu, T.; Chen, C. Automated graph regularized projective nonnegative matrix factorization for document clustering. IEEE Trans. Cybern. 2014, 44, 1821–1831. [Google Scholar]
- Chen, Z.; Li, L.; Peng, H.; Liu, Y.; Yang, Y. Attributed community mining using joint general non-negative matrix factorization with graph Laplacian. Phys. A 2018, 495, 324–335. [Google Scholar] [CrossRef]
- Yang, J.; Yang, S.; Fu, Y.; Li, X.; Huang, T. Non-negative graph embedding. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Anchorage, Alaska, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Dai, X.; Su, X.; Zhang, W.; Xue, F.; Li, H. Robust Manhattan non-negative matrix factorization for image recovery and representation. Inf. Sci. 2020, 527, 70–87. [Google Scholar] [CrossRef]
- Li, Z.; Tang, J.; He, X. Robust structured nonnegative matrix factorization for image representation. IEEE Trans. Neural. Netw. Learn. Syst. 2017, 29, 1947–1960. [Google Scholar] [CrossRef]
- Gong, M.; Jiang, X.; Li, H.; Tan, K.C. Multiobjective sparse non-negative matrix factorization. IEEE Trans. Cybern. 2018, 49, 2941–2954. [Google Scholar] [CrossRef]
- Guan, N.; Tao, D.; Luo, Z.; Yuan, B. Online nonnegative matrix factorization with robust stochastic approximation. IEEE Trans. Neural. Netw. Learn. Syst. 2012, 23, 1087–1099. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Peng, H.; Liu, Y.; Yang, Y. A novel digital watermarking based on general non-negative matrix factorization. IEEE Trans. Multimedia 2018, 20, 1973–1986. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Peng, H.; Liu, Y.; Zhu, H.; Yang, Y. Sparse general non-negative matrix factorization based on left semi-tensor product. IEEE Access. 2019, 7, 81599–81611. [Google Scholar] [CrossRef]
- Fu, X.; Huang, K.; Sidiropoulos, N.D.; Ma, W.K. Nonnegative matrix factorization for signal and data analytics: Identifiability, algorithms, and applications. IEEE Signal. Proc. Mag. 2019, 36, 59–80. [Google Scholar] [CrossRef]
- Vaswani, N.; Bouwmans, T.; Javed, S.; Narayanamurthy, P. Robust subspace learning: Robust PCA, robust subspace tracking, and robust subspace recovery. IEEE Signal. Proc. Mag. 2018, 35, 32–55. [Google Scholar] [CrossRef]
- Hoyer, P.O. Nonnegative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar]
- Qian, W.; Hong, B.; Cai, D.; He, X.; Li, X. Non-Negative Matrix Factorization with Sinkhorn Distance. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-16), New York, NY, USA, 9–15 July 2016; pp. 1960–1966. [Google Scholar]
- He, W.; Zhang, H.; Zhang, L. Sparsity-regularized robust non-negative matrix factorization for hyperspectral unmixing. IEEE J. Sel. Top. Appl. Earth. Obs. Remote. Sens. 2016, 9, 4267–4279. [Google Scholar] [CrossRef]
- Kong, D.; Ding, C.; Huang, H. Robust nonnegative matrix factorization using l21-norm. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 673–682. [Google Scholar]
- Huang, Q.; Yin, X.; Chen, S.; Wang, Y.; Chen, B. Robust nonnegative matrix factorization with structure regularization. Neurocomputing 2020, 412, 72–90. [Google Scholar] [CrossRef]
- Pan, J.; Ng, M.K. Orthogonal nonnegative matrix factorization by sparsity and nuclear norm optimization. SIAM J. Matrix Anal. Appl. 2018, 39, 856–875. [Google Scholar] [CrossRef]
- Luo, X.; Zhou, M.; Xia, Y.; Zhu, Q. An efficient non-negative matrix-factorization-based approach to collaborative filtering for recommender systems. IEEE Trans. Industr. Inform. 2014, 10, 1273–1284. [Google Scholar]
- Sun, H.C.; Yang, J. The Generalization of Non-Negative Matrix Factorization Based on Algorithmic Stability. Electronics 2023, 12, 1147. [Google Scholar] [CrossRef]
- Venkatesan, R.C.; Plastino, A. Deformed statistics Kullback—Leibler divergence minimization within a scaled Bregman framework. Phys. Lett. A 2011, 375, 4237–4243. [Google Scholar] [CrossRef]
- He, R.; Zheng, W.S.; Hu, B.G. Maximum correntropy criterion for robust face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1561–1576. [Google Scholar]
- Wang, J.J.Y.; Wang, X.; Gao, X. Non-negative matrix factorization by maximizing correntropy for cancer clustering. BMC Bioinform. 2013, 14, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, C.; Xiang, S.; Zhu, F. Robust hyperspectral unmixing with correntropy-based metric. IEEE Trans. Image Process. 2015, 24, 4027–4040. [Google Scholar] [CrossRef]
- Peng, S.; Ser, W.; Lin, Z.; Chen, B. Robust sparse nonnegative matrix factorization based on maximum correntropy criterion. In Proceedings of the IEEE International Symposium on Circuits and Systems, Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Yu, N.; Wu, M.J.; Liu, J.X.; Zheng, C.H.; Xu, Y. Correntropy-based hypergraph regularized NMF for clustering and feature selection on multi-cancer integrated data. IEEE Trans. Cybern. 2020, 51, 3952–3963. [Google Scholar] [CrossRef] [PubMed]
- Pele, O.; Werman, M. Fast and robust earth mover’s distances. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 460–467. [Google Scholar]
- Ling, H.; Okada, K. An efficient earth mover’s distance algorithm for robust histogram comparison. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 840–853. [Google Scholar] [CrossRef]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The earth mover’s distance as a metric for image retrieval. Int. J. Comput. Vision. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Sandler, R.; Lindenbaum, M. Nonnegative matrix factorization with earth mover’s distance metric. In Proceedings of the Computer Vision and Pattern Recognition Conference, Miami, FL, USA, 20–25 June 2009; pp. 1873–1880. [Google Scholar]
- Sandler, R.; Lindenbaum, M. Nonnegative matrix factorization with earth mover’s distance metric for image analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1590–1602. [Google Scholar] [CrossRef]
- Atasu, K.; Mittelholzer, T. Linear-complexity data-parallel earth mover’s distance approximations. ICML 2019, 97, 364–373. [Google Scholar]
- Qu, Z.W.; Yang, J.C.; Lang, Y.S.; Wang, Y.J.; Han, X.M.; Guo, X.Y. Earth Mover Distance based detection of false data injection attacks in smart grids. Energies 2022, 15, 1733. [Google Scholar] [CrossRef]
- Lu, X.; Wu, H.; Yuan, Y.; Yan, P.; Li, X. Manifold regularized sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote 2012, 51, 2815–2826. [Google Scholar] [CrossRef]
- Qian, Y.; Jia, S.; Zhou, J.; Robles-Kelly, A. Hyperspectral unmixing via L1/2 sparsity-constrained nonnegative matrix factorization. IEEE Trans. Geosci. Remote 2011, 49, 4282–4297. [Google Scholar] [CrossRef]
- Xu, Z.B.; Zhang, H.; Wang, Y.; Xu, Y.; Yong, L. L1/2 regularizer. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Wang, W.; Qian, Y.; Tang, Y.Y. Hypergraph-regularized sparse NMF for hyperspectral unmixing. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2016, 9, 681–694. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Topics Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef]
- Werman, M.; Peleg, S.; Rosenfeld, A. A distance metric for multidimensional histograms. Comput. Vis. Image. Underst. 1985, 32, 328–336. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. Proc. Adv. Neural Inf. Process. Syst. 2013, 26, 2292–2300. [Google Scholar]
- Frogner, C.; Zhang, C.; Mobahi, H.; Araya, M.; Poggio, T.A. Learning with a Wasserstein loss. Proc. Adv. Neural Inf. Process. Syst. 2015, 28, 2044–2052. [Google Scholar]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar]
- Chung, F.R. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Proceedings of the Advances in Neural Information Processing Systems, Denver, CO, USA, 3–6 November 2001; Volume 14, pp. 585–591. [Google Scholar]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Proceedings of the International Conference on Neural Information Processing Systems, Denver, CO, USA, 28–30 November 2000; Volume 13, pp. 556–562. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).