BooLSPLG: A Library with Parallel Algorithms for Boolean Functions and S-Boxes for GPU

Abstract

In this paper, we present a library with sequential and parallel functions for computing some of the most important cryptographic characteristics of Boolean and vectorial Boolean functions. The library implements algorithms to calculate the nonlinearity, algebraic degree, autocorrelation, differential uniformity and related tables of vectorial Boolean functions. For the sake of completeness, we provide the mathematical basis of these algorithms. Furthermore, we compare the performance of the parallel functions from the developed software with the corresponding sequential functions and with analogous functions from the well-known SageMath and SET packages. Functions from BooLSPLG can be used to develop efficient algorithms for constructing Boolean and vectorial Boolean functions with good cryptographic properties. The parallel part of the library is implemented using a CUDA parallel programming model for recent NVIDIA GPU architectures. BooLSPLG is an open-source software library written in CUDA C/C++ with explicit documentation, test examples, and detailed input and output descriptions of all functions, both sequential and parallel, and it is available online.

1. Introduction

The main subjects which we consider in this paper are Boolean and vectorial Boolean functions (S-boxes) with good cryptographic properties. There is a substantial body of research on S-boxes with eight or fewer variables that are embedded in the most popular ciphers [1], but not much is known about larger S-boxes, despite the interest in them [2,3,4]. One of the reasons for this is the computationally difficult evaluation of their cryptographic properties. The construction of such types of objects is very important, but in most cases it is also a computationally expensive issue.

Some of the construction methods are based on checking for proper parameters between huge amounts of candidates [5]. The cryptographic parameters which we investigate in this paper are nonlinearity, algebraic degree, autocorrelation, and differential uniformity. The computation of these parameters is related to Fourier-type transforms such as Walsh–Hadamard and Möbius (Reed-Muller) transforms [6,7]. The algorithms, known as butterfly algorithms, that implement these fast, discrete transforms are very efficient [8]. Moreover, these algorithms are suitable for parallelization in SIMD (single instruction, multiple data) computer architectures.

For this type of parallelization, using modern graphics processing units (GPUs) together with CUDA (compute unified device architecture) [9] is natural and very effective. GPUs are usually specialized for manipulating high-resolution computer graphics, but their structure makes them suitable for processing large amounts of data. This feature of GPUs is a great advantage for deep learning [10], neural systems [11], molecular modeling [12], etc.

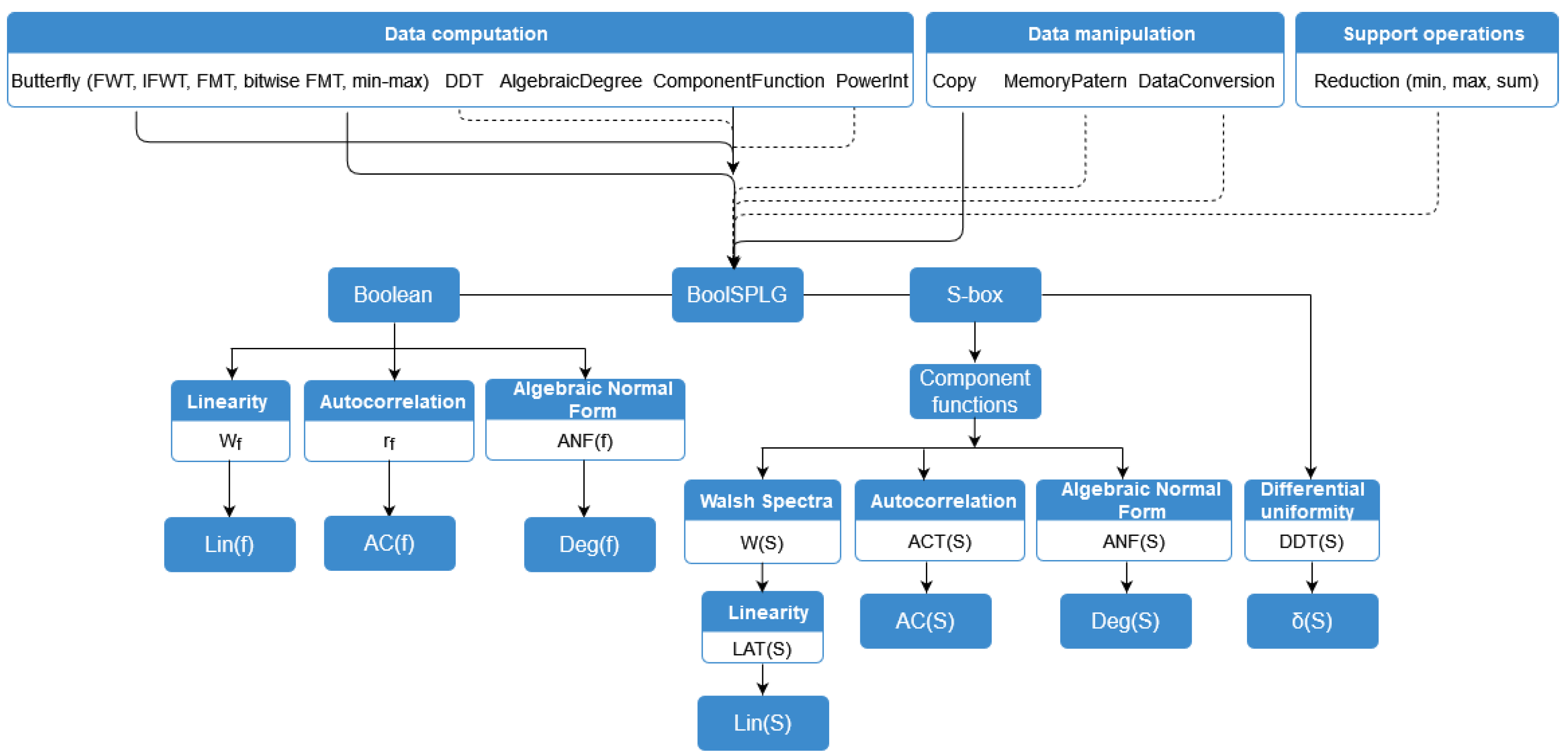
For this paper, we developed a library BoolSPLG with C/C++ functions. It can be used to study important cryptographic properties of Boolean functions with n variables and bijective $n\times n$ S-boxes for $n\le 20$. BoolSPLG computes the following cryptographic parameters of the Boolean and vectorial Boolean functions: the Walsh spectrum of a Boolean function, the linearity of a Boolean function, the Walsh Spectrum of an S-box, the linear approximation table of an S-box, the linearity of an S-box, the autocorrelation spectrum of a Boolean function, the autocorrelation of a Boolean function, the autocorrelation spectrum of an S-box, the autocorrelation of an S-box, the algebraic normal form of a Boolean function, the algebraic normal form of an S-box, the algebraic degree of a Boolean function, the algebraic degree of an S-box, the difference distribution table of an S-box, and the differential uniformity of an S-box and a component function of an S-box. All of the basic functions have two versions—sequential and parallel. All these features can be used for project development by anyone who knows the C/C++ programming language but is not so familiar with CUDA C.

The effectiveness of the developed library is based on the optimal use of the capabilities of the GPU architecture and on the properties of the CUDA platform as well. Building an optimized and portable parallel library requires various strategies so that it can be used not only for computing the properties of Boolean and vector Boolean functions, but also for implementation in another software. We will focus on some of the basic features for building the library.

First, developing a parallel library requires an efficient consecutive algorithm which is suitable for parallel implementation. Our research is focused on the cryptographic properties of vector Boolean functions. These are mainly calculated by butterfly algorithms, and such methods are appropriate for parallelization.

Second, GPUs and the CUDA platform have a great advantage—they possess huge computing power for large amounts of data. However, implementing optimized software is a complex task. One of the main problems is related to the transfer of data from the main memory to the GPU memory and vice versa. This is a time-consuming process, sometimes commensurate with the calculation time. Therefore, each of the functions is tailored to this fact. If the algorithm consists of several parallel steps, data transfer is conducted only at the beginning and the end of the function. The other technique that shortens the transfer time is compressing the data to bitwise representation.

Another peculiarity in the implementation of the library functions is using the fast memories of the GPU. The CUDA platform provides access to the global memory of the graphic card and also to the much faster shared and local memories. In order to perform calculations on variables located on the shared or local memory, additional steps are necessary to move the data from variables located on global memory. However, due to the throughput-oriented organization of the CUDA API, this turns out to be much more efficient than directly using global memory variables for calculations.

The functions of the library are adapted to the size of the processed data. In the case of S-boxes of fewer variables, simultaneous parallel computations are made on all component functions defined by the considered S-box. For larger parameters, component functions are processed separately.

Many of the library’s features also use the cutting-edge techniques of the ever-updating CUDA interface. A good example of this are the shuffle operations, which allow for the direct passing of the values of local variables from one thread to another. The use of bitwise calculations, where possible, provides another degree of parallelism and further optimization of the library functions.

In addition, BoolSPLG can be used for training research, to view the characteristics of the video card, and to compare parallel and sequential performance. For example, we used it to study bijective S-boxes with $n\le 18$ variables and good cryptographic properties which were derived from linear codes with quasi-cyclic structures in ref. [13].

There are many libraries and mathematical software for computing the cryptographic properties of Boolean and vectorial Boolean functions developed for sequential CPU computation. As examples, we point out SageMath [14], MATLAB [15], VBF Library [16], PEIGEN [17], or SET (S-box Evaluation Tool) [18]. A detailed review of the software related to the cryptographic characteristics of the S-boxes is made in [16]. This software is good for training purposes and basic calculations but is not as fast as parallel implementation, especially for large ($n\ge 8$) S-boxes.

In terms of linear algebra GPU tools, we can mention cuBLAS [19] and cuSPARSE [20]. There are GPU libraries for butterfly algorithms, such as BPLG [21], NVIDIA’s cuFFT [22], but most of them are for signal processing (fast Fourier transform, Hartley transform, etc.) and not for vector Boolean functions. Examples of parallel software related to cryptography include Eval16BitSbox and the algorithms in Refs. [23,24]. Ref. [24] discusses only the linear approximation tables (LAT) of S-boxes and offers a different approach to their calculation. In addition, the authors evaluate and compare their work with other known software in this area. The implementation of Ref. [24] is in CUDA, which allows us to compare it with our software library BoolSPLG. We would like to point out that the computation time for LAT of $16\times 16$ S-boxes in Ref. [24] is close (comparable) to the computation time with a function of our library and is much less than the other presented software.

The paper is organized as follows. The main definitions connected to Boolean and vectorial Boolean functions are given in Section 2. In Section 3, we present some advantages of the CUDA programming platform. Basic facts and information about the data organization and the algorithms used is provided in Section 4. Section 5 presents some experimental results as well as a comparison of the calculation times of the considered library to SageMath and SET packages. A short conclusion and directions for future improvements to the presented library are given in Section 6.

2. Main Definitions and Preliminaries

In this section, we present the terminology and definitions we follow (see Refs. [8,25,26]).

Let ${\alpha }_0,{\alpha }_1\cdots {\alpha }_{2^n-1}$ be the vectors of the n-dimensional vector space ${\mathbb{F}}_2^n$ over the field ${\mathbb{F}}_2=\{0,1\}$ in lexicographic order. There is a one-to-one correspondence between the vectors of ${\mathbb{F}}_2^n$ and integers in $[0;2^n-1]$, which allows us to switch from a vector to an integer and vice versa. The Hamming weight $w_H\left(v\right)$ of a vector v is the number of its nonzero coordinates.

A Boolean function f of n variables is a mapping from ${\mathbb{F}}_2^n$ into ${\mathbb{F}}_2$. The Hamming distance $d_H(f,g)$ between two Boolean functions f and g is the number of function values in which they differ. Two natural representations of a Boolean function are its truth table $TT\left(f\right)$ and its algebraic normal form $ANF\left(f\right)$. Any Boolean function f of n variables is uniquely determined by its truth table $TT\left(f\right)=(f\left({\alpha }_0\right),f\left({\alpha }_1\right)\cdots f\left({\alpha }_{2^n-1}\right))$. Another way of uniquely representing a Boolean function f is by means of a polynomial with n variables, called its algebraic normal form (ANF), whose monomials have the form $x_{i_1}{x}_{i_2}\cdots x_{i_k}$, $1\le i_1<i_2<\cdots <i_k\le n$, $0\le k\le n$ [8].

Denote by $x^u$ the monomial $x_1^{u_1}{x}_2^{u_2}\cdots x_n^{u_n}$, where $u\in \mathbb{Z}$, $0\le u\le 2^n-1,u=(u_1,u_2,\cdots ,u_n)\in {\mathbb{F}}_2^n$. Then the algebraic normal form of f is a polynomial

$${\displaystyle f\left(x\right)=f(x_1,x_2,\cdots ,x_n)=\underset{u=0}{\overset{2^n-1}{⨁}}{a}_n{x}^u.}$$

(1)

The degree of $ANF\left(f\right)$ is called the algebraic degree $\mathit{deg}\left(f\right)$ of the Boolean function f, and it is equal to the maximum number of variables of the terms $x^u$, or

$${\displaystyle deg\left(f\right)=max\left\{w_H\left(u\right)\right|a_u=1\},\mathrm{where}f\left(x\right)=\underset{u=0}{\overset{2^n-1}{⨁}}{a}_n{x}^u.}$$

The Boolean functions $a_0\oplus a_1{x}_1\oplus a_2{x}_2\oplus \cdots \oplus a_n{x}_n=a_0\oplus l_a\left(x\right)$ of algebraic degree at most 1 play a special role in our investigations, and they are called affine, while $l_a\left(x\right)$ are called linear.

Obviously, $ANF\left(f\right)$ can be associated with the binary ($2^n$-dimensional) vector $f^{ANF}\in {\mathbb{F}}_2^{2^n}$ whose coordinates are the coefficients in (1) following the lexicographical order [27].

Associated with the Boolean function f is the function $\widehat{f}={(-1)}^f=1-2f$ whose function values belong to the set $\{-1;1\}$. The corresponding vector that contains the function’s values of $\widehat{f}$ is called the polarity truth table ($PTT$) of the function f.

Definition 1.

Walsh (Hadamard, Walsh–Hadamard, Walsh–Fourier) transform $f^W$ of the Boolean function f is the integer-valued function $f^W:{\mathbb{F}}_2^n\to \mathbb{Z}$, defined by

$$f^W\left(a\right)=\sum _{x\in {\mathbb{F}}_2^n}{(-1)}^{f\left(x\right)\oplus l_a\left(x\right)}=\sum _{x\in {\mathbb{F}}_2^n}\widehat{f}\left(x\right){\widehat{l}}_a\left(x\right)=2^n-2d_H(f,l_a),$$

where $a=(a_1,\cdots ,a_n)\in {\mathbb{F}}_2^n$.

The function $\widehat{f}\left(x\right)$ can be recovered by the inverse Walsh transform:

$$\widehat{f}\left(x\right)=2^{-n}\sum _{a\in {\mathbb{F}}_2^n}\left(f^W\right)\left(a\right){(-1)}^{a·x}.$$

The values of $f^W$ are called Walsh coefficients of the Boolean function f. For any Boolean function f and any vector $a\in {\mathbb{F}}_2^n$, we have $-2^n\le f^W\left(a\right)\le 2^n$. The functions $l_a\left(x\right)$ and ${\overline{l}}_a\left(x\right)=l_a\left(x\right)\oplus 1$ have the maximal and minimal Walsh coefficients, namely $l_a^W\left(a\right)=2^n$ and ${\overline{l}}_a^W\left(a\right)=-2^n$.

The vector $W_f=(f^W\left({\alpha }_0\right),f^W\left({\alpha }_1\right)\cdots f^W\left({\alpha }_{2^n-1}\right))$ is called the Walsh spectrum of the Boolean function and is denoted by $W_f$. The Walsh spectrum measures the distance to the linear and affine functions.

The linearity of a Boolean function f is the maximum absolute value of a Walsh coefficient of f: $Lin\left(f\right)=max\left\{\right|f^W\left(a\right)\left|\right|a\in {\mathbb{F}}_2^n\}$. The Parseval’s Equality ${\sum }_{a\in {\mathbb{F}}_2^n}{\left(f^W\left(a\right)\right)}^2=2^{2n}$ gives that $Lin\left(f\right)\ge 2^{n/2}$ [8]. Functions attaining this lower bound are called bent functions.

Another important parameter which is closely connected with linearity is nonlinearity.

Nonlinearity$nl\left(f\right)$ of the Boolean function f is the minimum Hamming distance from f to the nearest affine function:

$$nl\left(f\right)=min\left\{d_H(f,g)\right|g-\mathrm{affine}\mathrm{function}\}.$$

The relation between the linearity and nonlinearity of the Boolean function f is given by the equality $Lin\left(f\right)=2^n-2nl\left(f\right)$ [8]. Obviously, minimum linearity corresponds to maximum nonlinearity.

Definition 2.

Autocorrelation function of the Boolean function f (auto-correlation of f with a shift w) is the function $r_f:{\mathbb{F}}_2^n\to \mathbb{Z}$ defined by:

$$r_f\left(w\right)=\sum _{x\in {\mathbb{F}}_2^n}{(-1)}^{f\left(x\right)\oplus f(x\oplus w)},$$

where $w\in {\mathbb{F}}_2^n$.

The expression of the autocorrelation values $r_f\left(w\right)$ for all $w\in F_2^n$ in terms of the Walsh coefficients [6] is equal to

$$r_f\left(w\right)=2^{-n}\sum _{u\in {\mathbb{F}}_2^n}{\left(f^W\left(u\right)\right)}^2{(-1)}^{u·w}.$$

For any Boolean function f and any vector $w\in {\mathbb{F}}_2^n$ we have $-2^n\le r_f\left(w\right)\le 2^n$ and $r_f\left(0\right)=2^n$. The vector of the autocorrelation values $r_f\left(w\right)$ is referred to as its autocorrelation spectrum of the function f.

The absolute indicator of a Boolean function f of n variable, denoted by $AC\left(f\right)$, is the maximum absolute value of an autocorrelation value and is defined by $AC\left(f\right)=max\left\{\right|r_f\left(w\right)\left|\right|w\in {\mathbb{F}}_2^n\}$.

The Sylvester–Hadamard matrix (or Walsh–Hadamard matrix) of order $2^n$, denoted by $H_n$, is generated by the recursive relation:

$$H_0=1,H_1=\left(\begin{array}{cc}1& \hfill 1\\ 1& \hfill -1\end{array}\right),H_n=\left(\begin{array}{cc}{H}_{n-1}& \hfill H_{n-1}\\ H_{n-1}& \hfill -H_{n-1}\end{array}\right)=H_1\otimes H_{n-1}forn>1,$$

where ⊗ denotes the Kronecker product. The i-th row (column) of $H_n$ is a PTT of the linear function $l_i$. So $W_f^t=H_n.PTT{\left(f\right)}^t$ and $PTT{\left(f\right)}^t=2^{-n}{H}_n{W}_f^t.$

Fast Walsh transform (FWT) is usually used to calculate the Walsh spectrum. It is based on matrix vector multiplication and can be given by a butterfly diagram. The theoretical base of the FWT is given by Good [28] and it follows from a suitable factorization of $H_n$.

A similar approach can be used to calculate the fast Möbius transform (FMT). This transform gives the coefficients of ANF(f) from the truth table of the Boolean function f and vice versa. It is based on the following matrices:

$$A_0=1,A_1=\left(\begin{array}{cc}1& \hfill 0\\ 1& \hfill 1\end{array}\right)A_n=\left(\begin{array}{cc}{A}_{n-1}& \hfill 0\\ A_{n-1}& \hfill A_{n-1}\end{array}\right)=A_1\otimes A_{n-1}forn>1.$$

Actually, the i-th column of $A_n$ is the truth table of the monomial $m_i=x^{{\alpha }_i}$. Using these matrices, we have ${\left(f^{ANF}\right)}^t=A_n.{\left(TT\left(f\right)\right)}^t$ and $TT{\left(f\right)}^t=A_n.{\left(f^{ANF}\right)}^t.$ The complexity of the algorithms for both fast Walsh and Möbius transforms is $O\left(n{2}^n\right)$, and they require $O\left(2^n\right)$ memory units.

A vectorial Boolean function $S:{\mathbb{F}}_2^n\to {\mathbb{F}}_2^m$ (also called $(n,m)$ S-box or shortly S-box) can be represented by the vector $(f_1,f_2,\cdots ,f_m)$, where $f_i$ are Boolean functions of n variables, $i=1,2,\cdots ,m$. The functions $f_i$ are called the coordinate functions of the S-box. Then the $m\times 2^n$ matrix

$$G_S=\left(\begin{array}{c}TT\left(f_1\right)\\ ⋮\\ TT\left(f_m\right)\end{array}\right)$$

represents the considered S-box, where $TT\left(f_i\right)$ is the truth table of the Boolean function $f_i$, $i=1,\cdots ,m$. An S-box is bijective if $n=m$ and S is an invertible function.

In order to study the cryptographic properties of a vectorial Boolean function f related to linearity, algebraic degree, and autocorrelation, we need to consider all non-zero linear combinations of the coordinate functions of the S-box, denoted by

$$S_b=b·G_S=b_1{f}_1\oplus \cdots \oplus b_m{f}_m,$$

where $b=(b_1,\cdots ,b_m)\in {\mathbb{F}}_2^m$. These are the component functions of the S-box S.

The Walsh spectrum of S is defined as the collection of all of the Walsh spectra of the component functions of S. The linearity and nonlinearity of the vectorial Boolean function are defined as

$$Lin\left(S\right)=\underset{b\in {\mathbb{F}}_2^m\setminus \left\{0\right\}}{max}Lin\left(S_b\right),nl\left(S\right)=\underset{b\in {\mathbb{F}}_2^m\setminus \left\{0\right\}}{min}nl\left(S_b\right).$$

In order to obtain the important parameters of an S-box, we use four tables, namely a linear approximation table (LAT), a difference distribution table (DDT), an autocorrelation table (ACT), and a table with the algebraic degrees (ADT) of the monomials in the component Boolean functions of the considered S-box. We define these tables below.

The $2^n\times 2^m$ table whose entries are defined by

$$L_{a,b}=\left|\{x\in {\mathbb{F}}_2^n:S_b\left(x\right)=a·x-2^{n-1}\}\right|,a\in {\mathbb{F}}_2^n,b\in {\mathbb{F}}_2^m,$$

is called its linear approximation table and is also denoted by $LAT\left(S\right)$. The elements of $LAT\left(S\right)$ show the relationship between the inputs and outputs of the S-box. Since $S_b^W\left(a\right)=2L_{a,b}$, the Walsh spectrum and the linear approximation table of an S-box are closely related, and by computing one of these parameters, we obtain the other. Therefore, we actually compute the Walsh spectrum instead of the $LAT\left(S\right)$ in order to find the linearity and nonlinearity of S.

Another important parameter related to an S-box S is its algebraic degree. We define this as the maximum among all degrees of the component functions, or $\mathit{deg}\left(S\right)={max}_{b\in {\mathbb{F}}_2^m\setminus \left\{0\right\}}\mathit{deg}\left(S_b\right)$. The minimum degree is also important regarding algebraic attacks. Therefore, we define the maximal and the minimal algebraic degree of the vectorial Boolean function S as

$$max\mathit{deg}\left(S\right)=\underset{b\in {\mathbb{F}}_2^m\setminus \left\{0\right\}}{max}\mathit{deg}\left(S_b\right),min\mathit{deg}\left(S\right)=\underset{b\in {\mathbb{F}}_2^m\setminus \left\{0\right\}}{min}\mathit{deg}\left(S_b\right).$$

Autocorrelation spectrum $ACT$ of the vectorial Boolean function S is defined as the collection of all autocorrelation spectra of its component functions. In fact, we consider $ACT\left(S\right)$ as a $2^n\times 2^m$ autocorrelation matrix, whose columns represent the autocorrelation functions of all component Boolean functions of S. The autocorrelation (or the maximal absolute autocorrelation value) $AC\left(S\right)$ is defined as:

$$AC\left(S\right)=\underset{b\in {\mathbb{F}}_2^m\setminus \left\{0\right\}}{max}\left|r\left(S_b\right)\right|.$$

The difference distribution table (DDT) is a $2^n\times 2^m$ table whose entries are defined as

$$DDT{\left(S\right)}_{\alpha ,\beta }=\left|\right\{x\in {\mathbb{F}}_2^n,\alpha \in {\mathbb{F}}_2^n\setminus \left\{0\right\},\beta \in {\mathbb{F}}_2^m|S\left(x\right)\oplus S(x\oplus \alpha )=\beta \}|.$$

(2)

The differential uniformity denoted by $\delta \left(S\right)$ is defined as the largest value in its difference distribution table not counting the first entry in the first row, or

$$\delta \left(S\right)=\underset{\alpha \ne 0,\beta }{max}DDT{\left(S\right)}_{\alpha ,\beta }.$$

We are looking for S-boxes that have a differential uniformity as low as possible. It is well known that $\delta \left(S\right)$ takes only even values in the interval $[2^{n-m},2^n]$. The smallest possible value of $\delta$ in the case of bijective S-boxes $(n=m)$ is 2.

3. GPU and CUDA

One way to understand the difference between CPU and GPU is to compare the ways they process tasks. Usually, CPU consists of a few cores optimized for sequential serial processing. They have powerful ALU, large caches, and sophisticated control. Modern NVIDIA GPUs have their own memory, a massively parallel architecture consisting of thousands of smaller cores and designed for handling multiple tasks simultaneously. These cores have a throughput-oriented design with small caches, simple control, and energy-efficient ALUs, and they require a massive number of threads to tolerate latency. A GPU is very convenient when manipulating large data or using a high number of threads in single-instruction multiple-data (SIMD) programming model [29].

The CUDA programming platform allows programmers to interact directly with GPUs and run parallel parts of programs using the advantages of GPU architecture [9]. CUDA C is a programming language close to C by syntax, but conceptually and semantically it is quite different from C. The source code for CUDA applications consists of a mixture of conventional C/C++ host code and GPU device functions.

The processing of the data flow has several steps. At the highest level, we have a master process which runs on the CPU and performs the following steps: prepares data for manipulation, allocates memory on GPU, copies data from the host (CPU) to the GPU global memory, launches multiple instances of the execution “kernel” on GPU, copies data from the GPU memory to the host, deallocates all memory, and terminates. In a program, a parallel GPU part can be activated many times with different data and manipulations.

Functions for parallel execution on GPU are written in units called kernels. Syntactically, a kernel is a function of a programming language that is very similar to the C/C++ language functions. However, semantically, it is used by several directions. Its header initiates a grid of threads that practically performs the parallel execution of the calculations. The definition of a kernel header, which contains the type of grid, is given as follows:

$$kernel\_name<<<gridblocks,threadsperblock>>>(\dots ),$$

where “$kernel\_name$” is a usual name (identifier) and ‘grid blocks’ and ‘threads per block’ are positive integers. After the header, each kernel consists of a program code that refers to the single thread of the grid. Any thread has its own number in the grid of threads. According to this number, it is determined which part of the data will be calculated by the particular thread. Kernels are executed over the stream of data by many threads on a device in parallel. Thread is a process that performs series of programming instructions and it is a single instance of the kernel. Threads are organized into blocks, which are sets of threads that can communicate and synchronize their execution. Maximum 1024 threads per block can be launched. Multiple blocks can be executed simultaneously. First, a configuration of the kernel (number of blocks and number of threads per block inside) has to be made in order to launch it. Blocks and threads per block form a grid. All threads run the same code.

The threads are executed in groups of 32 threads called “wraps”. Usually, all of the threads in the wrap execute the same instruction at the same time. The difference is only input data, which depends on the unique number of any thread in block and any block in a grid.

The memory model has the following features. Each thread has access to the slowest global memory, but threads from different blocks can communicate with it. Each block has its own memory called shared which serves the communication between all of the threads in one block and is much faster than the global one. Each thread uses a small amount of fast local memory. The variables in the global memory, unlike the others, are preserved even after the terminating execution of each kernel.

We would like to mention some features of the CUDA model that are especially important for the efficiency of GPU calculations. Creating and destroying threads takes a negligible amount of time but only states which resources will be needed, so they do not affect performance. The time required to transfer data from the main memory to the global GPU memory and vice versa in many cases turns out to significantly lengthen the duration of calculations. Therefore, the master process has to manage the overall performance by running different kernels sequentially (if possible) without intermediate data transfer and only returning the final result.

4. Strategies in Algorithms and Data Organization

In order to discuss the implemented strategies and how the data is organized in the memory, it is necessary to show the model of the library BoolSPLG. Its structure is presented in Figure 1.

4.1. Data Organization

One way to represent the $n\times n$ vectorial Boolean function S that we use is through the truth tables of its coordinate functions. Therefore, an $n\times 2^n$ matrix is needed. For convenience, we use the integers corresponding to the binary representation of the columns of this matrix, so S is defined by the integer vector $(s_0,s_1,\cdots ,s_{2^n-1})$. This representation has several advantages: data from the main memory is transferred to the GPU memory much faster, and the value of the function S for the input vector $v\in {\mathbb{F}}_2^n$ corresponds to the v-th coordinate of the array.

Any vector $a\in {\mathbb{F}}_2^n$ defines the component function $S_a$ as a linear combination of rows of the matrix corresponding to S. The truth table of the component function $S_a$ can be calculated in the following way:

$$TT\left(S_a\right)=(a·s_0,a·s_1,\cdots ,a·s_{2^n-1}).$$

4.2. Strategies in Algorithms

Effective sequential algorithms serve as a basis for parallel implementation. An in-depth examination of such algorithms, in some cases with different approaches, has been conducted in Ref. [30]. For the relationship between the different linear and differential characteristics, see Ref. [31]. The time complexity of the fast Walsh and Möbius transforms of a Boolean function is $O\left(n{2}^n\right)$, and the required memory is $O\left(2^n\right)$.

The fast Walsh Transform (FWT) is the main tool (part) of the functions in the library related to the linear characteristics of the the vectorial Boolean functions. In order to apply the fast Walsh transform to a Boolean function with n variables, we consider its truth tables as an integer array of length $2^n$. The algorithm requires n steps. In the i-th step, the sum and the difference of the integers from the jth and rth cells (depending on i) of the current tuple must be written in the jth and rth cells of the new tuple. Therefore, the same array and variables can be used for the result of the calculations of all of its steps. Each thread can calculate the values of two elements without communicating with other threads. When using shared memory, it is convenient to calculate several steps of FWT on one thread on a given part of the array. A detailed description is presented in Ref. [32].

When calculating the linearity, nonlinearity, or LAT of a vectorial Boolean function S, we need all of its components’ functions (not only the coordinate functions). For small n, we list all of the component functions in an array of size $2^{2n}$. After the first n steps of the fast Walsh transform are applied to this array, we obtain the Walsh spectrum of S. This is enough to find the linearity (nonlinearity) of the vectorial Boolean function. The result is obtained by finding the minimum element in the set of absolute values of the coordinates of the obtained vector (by reduction). For larger values of n (when the hardware resource of the GPU is insufficient), in order to determine the linearity of the vector Boolean function S, the Walsh transform of each component Boolean function has to be calculated separately (see Algorithm 1).

Algorithm 1: Linearity of an S-box.
Input:	An S-box $S\_box$
Output:	The linearity $Lin(S\_box)$
sequential	copy $S\_box$ (as it is represented) to GPU memory
sequential	$Lin(S\_box)=0$
sequential	for all component Boolean functions of $S\_box$ do
	{
parallel	get TT of current component function f
parallel	calculate $W^f$ (the Walsh spectrum of f)
parallel	compute the linearity of f
parallel	update the value of $Lin(S\_box)$ // using one thread
	}
sequential	copy linearity of S-box in RAM memory

For the autocorrelation properties of S-boxes with $n>10$, we use the following Algorithm 2.

Algorithm 2: The autocorrelation of an S-box.
Input:	An S-box $S\_box$
Output:	$AC(S\_box)$
sequential	copy $S\_box$ to GPU memory
sequential	current autocorrelation value $AC(S\_box)=0$
sequential	for all component Boolean functions of $S\_box$ do
	{
parallel	get TT of current component function f
parallel	calculate $W^f$ and $g={\left(W^f\right)}^2$
parallel	compute $2^{-n}{W}^g$
parallel	update the value of $AC(S\_box)$
	}
sequential	copy $AC(S\_box)$ in RAM memory

We would like to note the following points in the calculation of the algebraic degree of a Boolean function. Since $ANF\left(f\right)$ can also be computed via a fast Möbius transform from the truth table of a Boolean function, this can be achieved using only bitwise operations. Compared to Walsh transform, this is a very significant advantage and allows us to use bitwise representation of the truth tables. Note that the i-th coordinate of the vector of $ANF\left(f\right)$ corresponds to the monomial $x^i$, and the degree of this monomial is equal to the Hamming weight of i. This can easily be calculated from a single thread. A detailed description of the corresponding parallel butterfly algorithms is given in Ref. [33].

From the definition of DDT for a vectorial Boolean function, we can directly derive a basic algorithm. We enumerate all of the values of the input difference $\Delta$. For each possible difference, we initialize to zero an array $DD{T}_{\Delta }\left(S\right)$ of $2^n$ cells, one for each possible output difference. Then, for each pair $(x,x\oplus \Delta )$ with the prescribed input difference, its output difference $S\left(x\right)\oplus S(x\oplus \Delta )$ is computed and the corresponding counter in $DD{T}_{\Delta }\left(S\right)$ is incremented. The runtime for sequential implementation is $O\left(2^{2n}\right)$.

In our parallel implementation, each thread calculates only one output difference $S\left(x\right)\oplus S(x\oplus \Delta )$. The second part, increasing the value of the corresponding DDT cell, is more difficult. More than one thread can yield the same value for the output difference. Therefore, they have to write the results in the same time, and to avoid "race conditions", we use so-called atomic operators.

For S-boxes of less than 15 variables, all of the tables that we used are generated and accessible through the functions of the library.

In this case, the DDT for all of the input differences is generated in parallel. For S-boxes of more than 14 variables, the rows for each of the tables are generated sequentially (see Algorithm 3), but the elements of one row are generated in parallel.

Algorithm 3: The differential uniformity of an S-box
Input:	An S-box $S\_box$
Output:	$\delta (S\_box)$
sequential	copy $S\_box$ to GPU memory
sequential	$\delta (S\_box)=2^n$
sequential	for all $\Delta \in {\mathbb{F}}_2^n$ do
	{
parallel	compute $DD{T}_{\Delta }(S\_box)$
parallel	find current $\delta (S\_box)$
	}
sequential	copy $\delta (S\_box)$ in RAM memory

5. Experimental Results

A server with two different GPU devices was used to evaluate the efficiency of the implemented library. Their parameters are listed in

Table 1. Description of the used CPU and GPU devices.

Environment:	Platform
CPU	Intel Xeon E5-2640, 2.50 GHz
Memory	48 GB DDR3 1333 MHz
OS	Windows 7, 64-bit
IDE/Compiler	MSVC 2019
CUDA SDK	10.2
GPU Driver	V 471.96
GPU	Nvidia TITAN X (Pascal)	GeForce GTX TITAN
	Device 0	Device 1
Architecture	Pascal	Kepler
CUDA Cores	3584	2688
Boost Clock	1531 MHz	876 MHz
Memory Speed	10 Gbps	6 Gbps
Global Memory	12 GB GDDR5X	6 GB GDDR5
Memory Bandwidth	480 (GB/s)	288.38 (GB/s)

. One of the GPUs, presented as Device 0, is much more powerful than the other (Device 1).

The average times for calculating the considered cryptographic parameters per 100 randomly generated invertible S-boxes with n variables for any $n=8,9,\dots ,20$ were obtained. The results for the different parameters were systematized in

Table 2. Computing linearity.

Size	CPU (ms)	Device 0 (ms)	CPU vs. Dev 0	Device 1 (ms)	CPU vs. Dev 1
$2^8$ (256)	0.863	0.223	×3.86	0.14336	×6
$2^9$ (512)	7.654	0.340	×22.51	0.3576	×21.4
$2^{10}$ (1024)	15.855	0.318	×49.85	1.1442	×13.8
$2^{11}$ (2048)	68.343	62.774	×1	72	×1
$2^{12}$ (4096)	314.927	149.562	×2.1	186.106	×1.68
$2^{13}$ (8192)	1257.97	287.688	×4.83	347.72	×3.6
$2^{14}$ (16,384)	5686.84	622.29	×9.13	759.53	×7.5
$2^{15}$ (32,768)	24,083.8	1239.54	×19.42	2141.55	×11.2
$2^{16}$ (65,536)	99,800.3	2446.03	×40.8	6289.8	×15.86
$2^{17}$ (131,072)	442,678	6165.59	×71.8	22,772	×19.43
$2^{18}$ (262,144)	1,677,921	22,029.27	×76.1	90,089	×18.62
$2^{19}$ (524,288)	7,562,247	90,786.66	×83.29	375,519	×20.13
$2^{20}$ (1,048,576)	29,638,868	418,942	×70.7	1,618,402	×18.3

,

Table 3. Computing autocorrelation.

Size	CPU (ms)	Device 0 (ms)	CPU vs. Dev 0	Device 1 (ms)	CPU vs. Dev 1
$2^8$ (256)	2.020	0.206	×9.8	0.319	×6.3
$2^9$ (512)	14.212	0.435	×32.67	0.393	×36.13
$2^{10}$ (1024)	37.940	0.463	×81.94	1.462	×25.95
$2^{11}$ (2048)	185.673	132.284	×1.4	144.06	×1.28
$2^{12}$ (4096)	771.527	209.130	×3.68	253.18	×3
$2^{13}$ (8192)	3142.98	503.77	×6.23	418.54	×7.5
$2^{14}$ (16,384)	13,555.2	866.02	×15.65	1094.63	×12.3
$2^{15}$ (32,768)	57,324.5	1931.21	×29.68	3189.85	×18
$2^{16}$ (65,536)	238,216.4	3813.45	×62.46	9621.8	×24.76
$2^{17}$ (131,072)	1,060,294	9396.38	×112.84	34,810.46	×30.45
$2^{18}$ (262,144)	3,832,308	33,814.94	×113.33	133,629.15	×28.67
$2^{19}$ (524,288)	16,860,299	138,108.15	×122.1	566,914	×29.7
$2^{20}$ (1,048,576)	68,227,870	629,515	×108.38	2,411,828	×28.2

,

Table 4. Computing differential uniformity.

Size	CPU (ms)	Device 0 (ms)	CPU vs. Dev 0	Device 1 (ms)	CPU vs. Dev 1
$2^8$ (256)	0.282	0.208	×1	0.136	×2
$2^9$ (512)	1.908	0.432	×4.416	0.351	×5.4
$2^{10}$ (1024)	3.591	0.366	×9.811	1.053	×3.4
$2^{11}$ (2048)	14.269	0.705	×20.23	1.313	×10.8
$2^{12}$ (4096)	69.932	1.710	×40.89	2.914	×24
$2^{13}$ (8192)	245.719	5.773	×42.56	11.27	×22
$2^{14}$ (16,384)	998.174	21.022	×47.48	37.64	×27
$2^{15}$ (32,768)	4059.71	990.88	×4.1	1497.6	×2.7
$2^{16}$ (65,536)	18,307.9	1924.91	×9.5	4345	×4.2
$2^{17}$ (131,072)	86,983.9	4206.78	×20.68	14,988.47	×5.8
$2^{18}$ (262,144)	453,136	14,319.73	×31.64	55,269.61	×8.2
$2^{19}$ (524,288)	1,925,444	61,572	×31.27	283,692	×6.7
$2^{20}$ (1,048,576)	9,312,785	730,660	×12.7	1,531,534	×6

and

Table 5. Computing degree—$deg\left(S\right)$–deg_ bitwise (S).

Size	CPU (ms)	Device 0	Device 0	CPU vs. Dev0	CPU vs. Dev0	Device 1	Device 1	CPU vs. Dev1	CPU vs. Dev1
		Base (ms)	Bitwise	Base	Bitwise	Base (ms)	Bitwise	Base	Bitwise
$2^8$	1.127	0.122	0.115	×9.23	×9.8	0.3193	0.2692	×3.5	×14.1
$2^9$	10.099	0.201	0.202	×49.9	×49	0.7321	0.3087	×13.6	×32.46
$2^{10}$	20.396	0.318	0.142	×64.1	×143.6	1.1814	0.7277	×17.2	×28
$2^{11}$	102.390	76.042	12.447	×1.3	×8.2	78.66	23.71	×1.3	×4.3
$2^{12}$	369.589	162.987	28.963	×2.2	×12.7	220.58	42.9	×1.6	×8.6
$2^{13}$	1754.26	307.870	54.385	×5.69	×32.2	366	65.68	×4.8	×26.9
$2^{14}$	6822.06	720.525	279.5	×9.4	×24.45	822.66	767.35	×8.3	×8.9
$2^{15}$	28,395.3	1410.75	489.42	×20.1	×58	2221	2658.13	×12.78	×10.6
$2^{16}$	117,070.8	2961.87	1593.99	×39.5	×73.5	6400	9964	×18.29	×11.74
$2^{17}$	492,150.2	6421.09	6470	×76.6	×76	22,974	26,110	×21.42	×18.84
$2^{18}$	1,699,950	22,824.7	12,011.3	×74.48	×141.53	84,706	56,085	×20	×30.1
$2^{19}$	7,327,083	90,603.8	32,384.5	×80.87	×226.2	356,180	122,500	×20.5	×59.8
$2^{20}$	29,481,099	416,376	83,943	×70.8	×351.2	1,530,321	478,612	×19.2	×61.59

. The first column in each table shows the size of the considered S-box. The second column contains the average time required to find the parameter with a sequential program using a single CPU core. The next column shows the time required to find the corresponding parameter using Device 0. Then, the speedup found between the sequential and parallel implementation methods is given by the formula

$$S_p=\frac{T_0\left(n\right)}{T_p\left(n\right)},$$

where n is the number of variables in the S-box, $T_0\left(n\right)$ is the execution time of the fastest known sequential algorithm, and $T_p\left(n\right)$ is the execution time of the parallel algorithm. The speedup of the parallel algorithm is given in the columns CPU vs. Dev0 and CPU vs. Dev1, respectively. For example, the linearity of an S-box of size $2^8$ is calculated for 0.863 ms by the CPU, while Device 0 performs the calculation for about 0.223 ms. This means it gives a 3.86-times better executing time, written in the table as $\times 3.86$.

It should be noted that the time required for parallel implementation includes the time used for data transfer from RAM to device memory and vice versa. The next two columns provide the execution time of Device 2 and the corresponding acceleration. The test results show the following: Using parallel implementation is much more efficient for S-boxes with larger parameters. In parallel implementation, the algebraic degree is calculated the fastest and the $DDT$ is calculated the slowest. Device 0 gives much better acceleration in most cases.

As can be seen, for S-boxes with particular sizes, the speedup drops. This occurs due to the CUDA memory hierarchy model. The functions in the library generate the following tables related to S-boxes: a linear approximation table LAT(S), an autocorrelation table ACT(S), a table with the algebraic degrees of the monomials in the component Boolean functions ADT(S), and a difference distribution table (DDT). In the case of S-boxes with less than 11 variables, all component functions are calculated simultaneously (LAT, ACT, and ADT). The necessary transformations of the functions to one vector saved in the global memory are also performed simultaneously. For S-boxes with 11 or more variables, the component functions are generated one after the other. Further, in the case of S-boxes with more than 14 variables, the rows of the DDT table are generated sequentially, and this takes more time as well.

One million randomly generated invertible 16-bit S-boxes have been studied.

Table 6. Test evaluation between bijective 16-bit QCS-boxes and randomly generated 16-bit S-boxes.

S-Boxes	Lin	nl	$\mathit{\delta }$	$\mathit{deg}\left(\mathit{S}\right)$ (max)	$\mathit{AC}\left(\mathit{S}\right)$	Number
QCS-boxes, $n=16$
C2, $M_1$, m = 13,107, r = 5	512	32,512	4	15	512	5
S-boxes, random	1532	32,002	22	15	2344, 2248	2
$n=16$	1532	32,002	20	15	2568–2208	34
	1532	32,002	18	15	2432–2224	39
S-boxes, random	1528	32,004	20	15	2504–2232	23
$n=16$	1528	32,004	18	15	2416–2264	17
S-boxes, random	1524	32,006	20	15	2512–2240	8
$n=16$	1524	32,006	18	15	2392–2216	7
S-boxes, random	1520	32,008	20	15	2288, 2280, 2184	3
$n=16$	1520	32,008	18	15	2352–2264	5
S-boxes, random	1516	32,010	20	15	2280	1
$n=16$	1516	32,010	18	15	2312	1

provides information on the best S-boxes in terms of the considered cryptographic parameters. For comparison, the table also presents the parameters of one S-box generated in a different way from a quasi-cyclic code.

In addition, we compared the parallel version of the presented library with the packages SageMath v9.8 and SET. In

Table 7. Calculation times of BoolSPLG, Sage, and SET.

	Lin			$\mathit{\delta }$			deg			AC
Size	Sage	SET	BoolSPLG	Sage	SET	BoolSPLG	Sage	SET	BoolSPLG	SET	BoolSPLG
$2^8$	0.66 s	2 ms	0.22 ms	0.096 s	0.4 ms	0.2 ms	0.12 s	3 ms	0.1 ms	2 ms	0.2 ms
$2^9$	1.94 s	5 ms	0.34 ms	0.35 s	2 ms	0.4 ms	0.14 s	18 ms	0.2 ms	7 ms	0.4 ms
$2^{10}$	7.2 s	39 ms	0.32 ms	1.44 s	8 ms	0.3 ms	0.18 s	52 ms	0.1 ms	48 ms	0.4 ms
$2^{11}$	26.3 s	246 ms	62 ms	6.2 s	83 ms	0.7 ms	0.22 s	374 ms	12 ms	0.4 s	132 ms
$2^{12}$	99 s	1.5 s	149 ms	29 s	0.5 s	1.7 ms	0.39 s	2.3 s	28 ms	2.7 s	209 ms
$2^{13}$	N/A	7.9 s	284 ms	N/A	2.1 s	5.7 ms	1 s	12.4 s	54 ms	14 s	503 ms
$2^{14}$	N/A	66 s	662 ms	N/A	9.9 s	21 ms	1.6 s	91 s	279 ms	102 s	866 ms

are given the calculation times of the following cryptographic parameters of the S-boxes: linearity, differential uniformity, algebraic aegree, and autocorrelation. The computing environment for BoolSPLG and SET is presented in Table 1, while for SageMath we used SageMathCell. Computing the linearity and the differential uniformity of S-boxes of sizes bigger than $2^{12}$ is not possible in SageMath. The calculation of autocorrelation is also not included in this package.

6. Conclusions and Future Work

In this article, a C++ library with sequential and parallel functions, implemented in CUDA C and designed to analyze large vectorial Boolean functions from cryptographic perspective, was presented. The parallel functions for many of the parameters are up to 60 times faster, which makes them convenient to use in ambitious research projects. The library has several opportunities for development. One is in the direction of universality. We plan to expand it so that it can be used for any type of vectorial Boolean function, not just bijective.

Another direction is to present more detailed information about the studied cryptographic parameters. For example, S-boxes that have the same differential uniformity but different differential spectra can perform differently in terms of resistance against differential attacks. Thus, some design criteria impose restrictions on the differential spectra of the S-box. The other example is related to algebraic degree. Note that, different from the notion of algebraic degree, the minimum among all degrees of the coordinate functions does not equal the minimum among all degrees of the component functions. Moreover, the number of component and coordinate functions with minimum (or maximal) degree is also important for some of the cases. In the current version, the library only calculates the value of the smallest (or largest) degrees of the component functions.

In the parallel functions of the current implementation, the calculations are conducted in two ways. One way (for smaller parameters) is to perform calculations for all of the component functions simultaneously. The other is to perform calculations for each of the component functions separately. In cases where the component functions are not of sufficient size, the second method of calculation does not provide good acceleration (as can be seen from the experimental results). In this case, it is more efficient to make calculations on appropriate groups of component functions.