A Second-Order Accurate Numerical Approximation for a Two-Sided Space-Fractional Diffusion Equation
Abstract
1. Introduction
2. The Classical CN Difference Scheme for the One-Dimensional Two-Sided Space-Fractional Diffusion Equation and Its Consistency
- (i)
- .
- (ii)
- , for .
- (iii)
- for any .
- (iv)
- , for .
- (v)
- for any .
3. Stability and Convergence of the Classical Fractional CN Method
- Step 1: On the spatially coarse grid h, solve using this CN difference format method to obtain the numerical solution on the coarse grid.
- Step 2: On the spatially fine grid with the same , solve again using this CN difference format method to obtain the numerical solution on the fine grid.
- Step 3: The Richard extrapolation solution, which can be written in the following form .
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sokolov, L.M.; Klafer, J.; Blumen, A. Fractional kinetics. Phys. Today 2002, 55, 48–54. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering, Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Kirchner, J.W.; Feng, X.; Neal, C. Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 2000, 403, 524–527. [Google Scholar] [CrossRef]
- Raberto, M.; Scalas, E.; Mainardi, F. Waiting-times and returns in high-frequency financial data: An empirical study. Phys. Stat. Mech. Its Appl. 2002, 314, 749–755. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Turner, I.; Anh, V.; Burrage, K. A semi-alternating direction method for a 2-D fractional FitzHugh-Nagumo monodomain model on an approximate irregular domain. J. Comput. Phys. 2015, 293, 252–263. [Google Scholar] [CrossRef]
- Li, S.; Cao, W.; Wang, Y. On spectral Petrov-Galerkin method for solving optimal control problem governed by a two-sided fractional diffusion equation. Comput. Math. Appl. 2022, 107, 104–116. [Google Scholar] [CrossRef]
- She, Z.H.; Qu, H.D.; Liu, X. Stability and convergence of finite difference method for two-sided space-fractional diffusion equations. Comput. Math. Appl. 2021, 89, 78–86. [Google Scholar] [CrossRef]
- Hao, Z.P.; Lin, G.; Zhang, Z.Q. Error estimates of a spectral Petrov-Galerkin method for two-sided fractional reaction-diffusion equations. Appl. Math. Comput. 2020, 374, 125045. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Z. Fractional spectral collocation method for optimal control problem governed by space fractional diffusion equation. Appl. Math. Comput. 2019, 350, 331–347. [Google Scholar] [CrossRef]
- Gunzburger, M.; Wang, J. Error analysis of fully discrete finite element approximations to an optimal control problem governed by a time-fractional PDE. SIAM J. Control. Optim. 2019, 57, 241–263. [Google Scholar] [CrossRef]
- Ozbilge, E.; Kanca, F.; Zbilge, E. Inverse Problem for a Time Fractional Parabolic Equation with Nonlocal Boundary Conditions. Mathematics 2022, 10, 1479. [Google Scholar] [CrossRef]
- Feng, L.B.; Zhuang, P.; Liu, F.; Turner, I. Stability and convergence of a new finite volume method for a two-sided space-fractional diffusion equation. Appl. Math. Comput. 2015, 257, 52–65. [Google Scholar] [CrossRef]
- Liu, X.Y.; Liu, Z.H.; Fu, X. Relaxation in nonconvex optimal control problems described by fractional differential equations. J. Math. Anal. Appl. 2014, 409, 446–458. [Google Scholar] [CrossRef]
- Jia, J.; Wang, H. Fast finite difference methods for space-fractional diffusion equations with fractional derivative boundary conditions. J. Comput. Phys. 2015, 293, 359–369. [Google Scholar] [CrossRef]
- Lai, J.J.; Liu, H.Y. On a Novel Numerical Scheme for Riesz Fractional Partial Differential Equations. Mathematics 2021, 9, 1–14. [Google Scholar] [CrossRef]
- Chen, H.B.; Gan, S.Q.; Xu, D.; Liu, Q.W. A second-order BDF compact difference scheme for fractional-order Volterra equation. Int. J. Comput. Math. 2016, 93, 1140–1154. [Google Scholar] [CrossRef]
- Ma, C.Y.; Shiri, B.; Wu, G.C.; Baleanu, D. New fractional signal smoothing equations with short memory and variable order. Optik 2020, 218, 164507. [Google Scholar] [CrossRef]
- Shiri, B.; Kong, H.; Wu, G.C. Adaptive Learning Neural Network Method for Solving Time-Fractional Diffusion Equations. Neural Comput. 2022, 34, 971–990. [Google Scholar] [CrossRef]
- Qu, W.; Lei, S.L.; Vong, S.W. A note on the stability of a second order finite difference scheme for space fractional diffusion equations, Numerical Algebra. Control. Optim. 2014, 4, 317–325. [Google Scholar]
- Sitho, S.; Ntouyas, S.K.; Sudprasert, C.; Tariboon, J. Integro-Differential Boundary Conditions to the Sequential -Hilfer and -Caputo Fractional Differential Equations. Mathematics 2023, 11, 867. [Google Scholar] [CrossRef]
- Hakkar, N.; Dhayal, R.; Debbouche, A.; Torres, D.F.M. Approximate Controllability of Delayed Fractional Stochastic Differential Systems with Mixed Noise and Impulsive Effects. Fractal Fract. 2023, 7, 104. [Google Scholar] [CrossRef]
- Chen, S.; Liu, F.; Jiang, X.; Turner, I.; Anh, V. A fast semi-implicit difference method for a nonlinear two-sided space-fractional diffusion equation with variable diffusivity coefficient. Appl. Math. Comput. 2015, 257, 591–601. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Meerschaert, M.M.; Sikorskii, A. Stochastic Models for Fractional Calculus; De Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Tadjeran, C.; Meerschaert, M.M. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications; Gordon Breach: London, UK, 1993. [Google Scholar]
- Isaacson, E.; Keller, H.B.; Weiss, G.H. Analysis of Numerical Methods; Wiley: New York, NY, USA, 1966. [Google Scholar]
- Tadjeran, C.; Meerschaert, M.M.; Scheffler, P. A second-order accurate numerical approximation for the fractional diffusion equation. J. Comput. Phys. 2006, 213, 205–213. [Google Scholar] [CrossRef]
- Richtmyer, R.D.; Morton, K.W. Difference Methods for Initial-Value Problems; Krieger Publishing: Malabar, FL, USA, 1994. [Google Scholar]


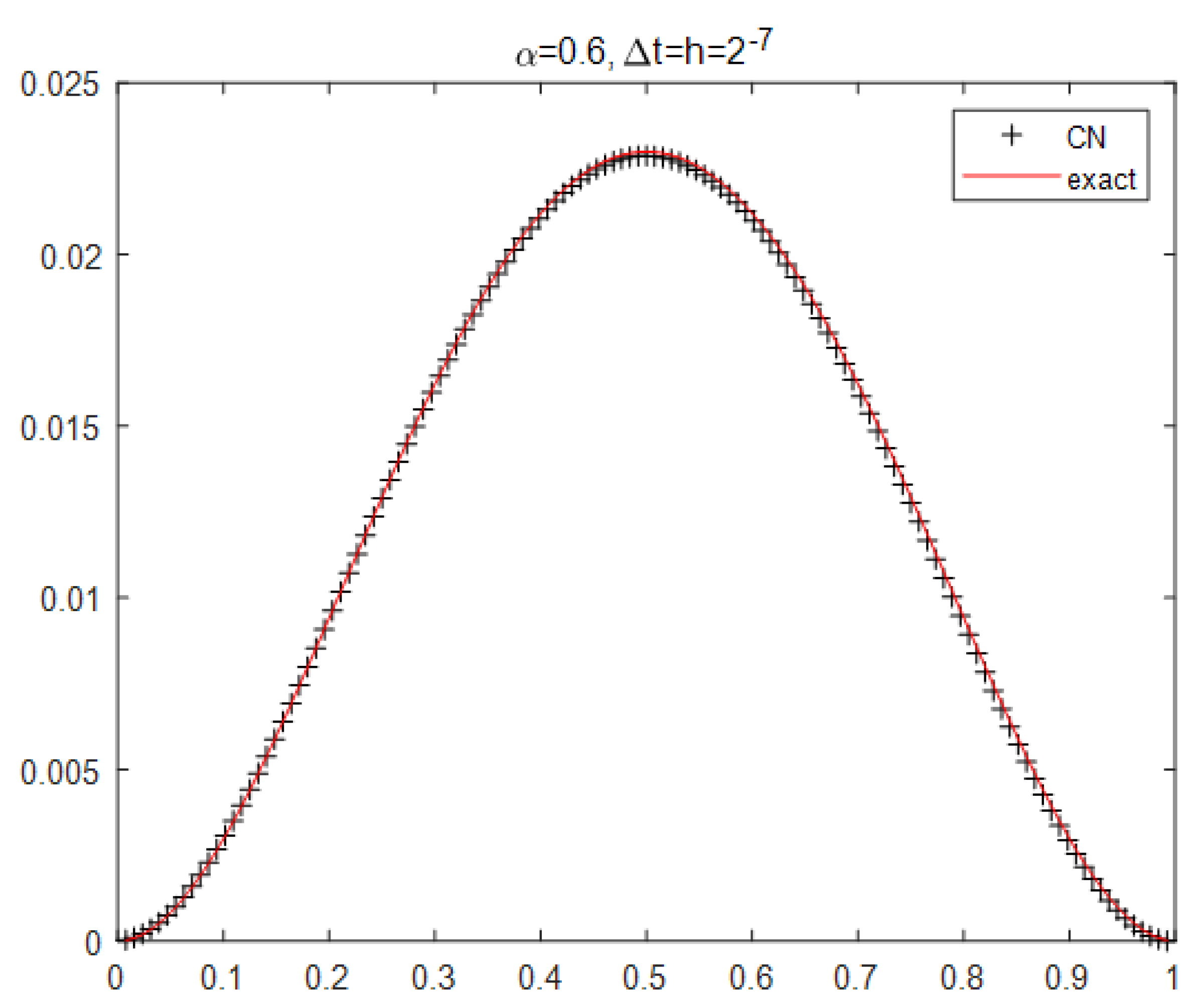

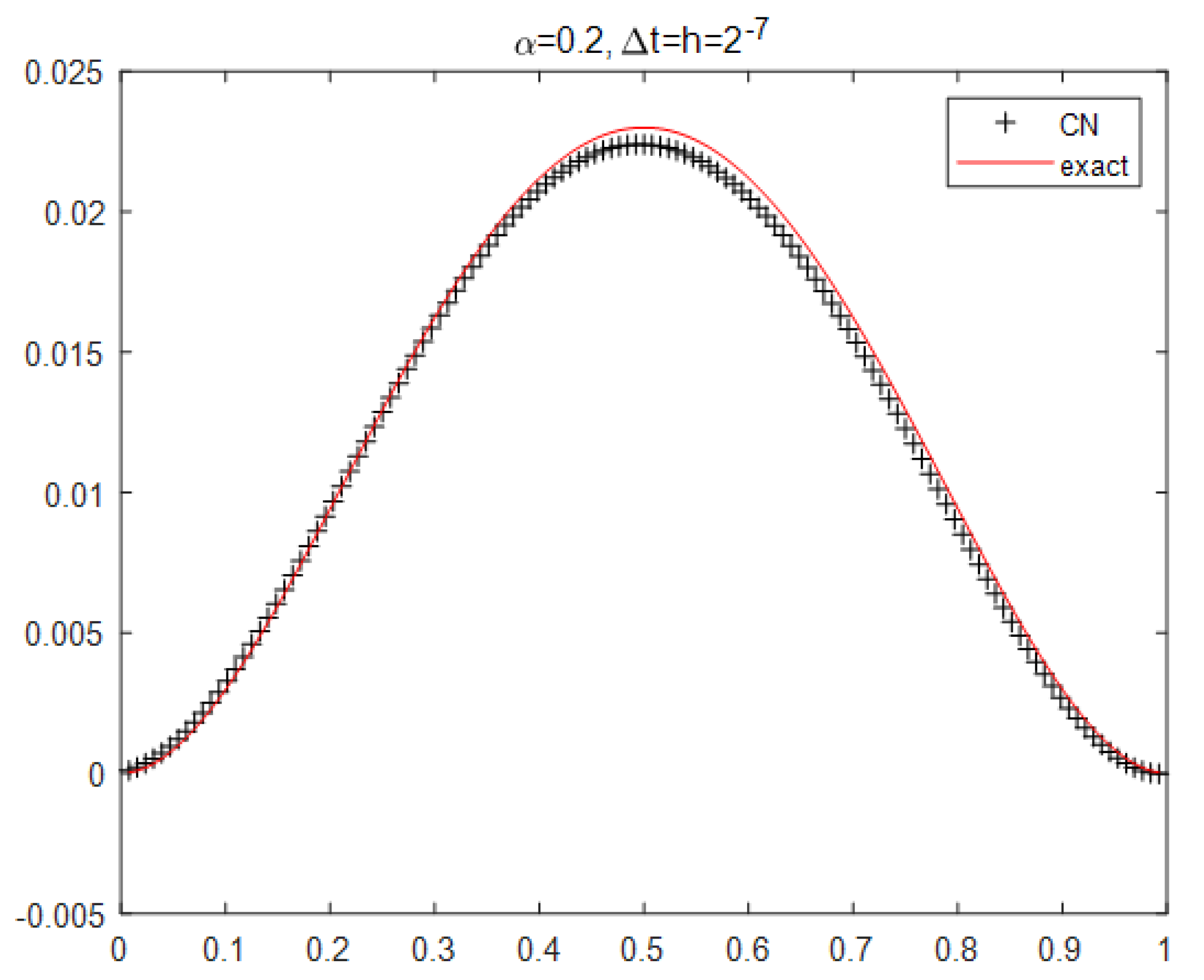
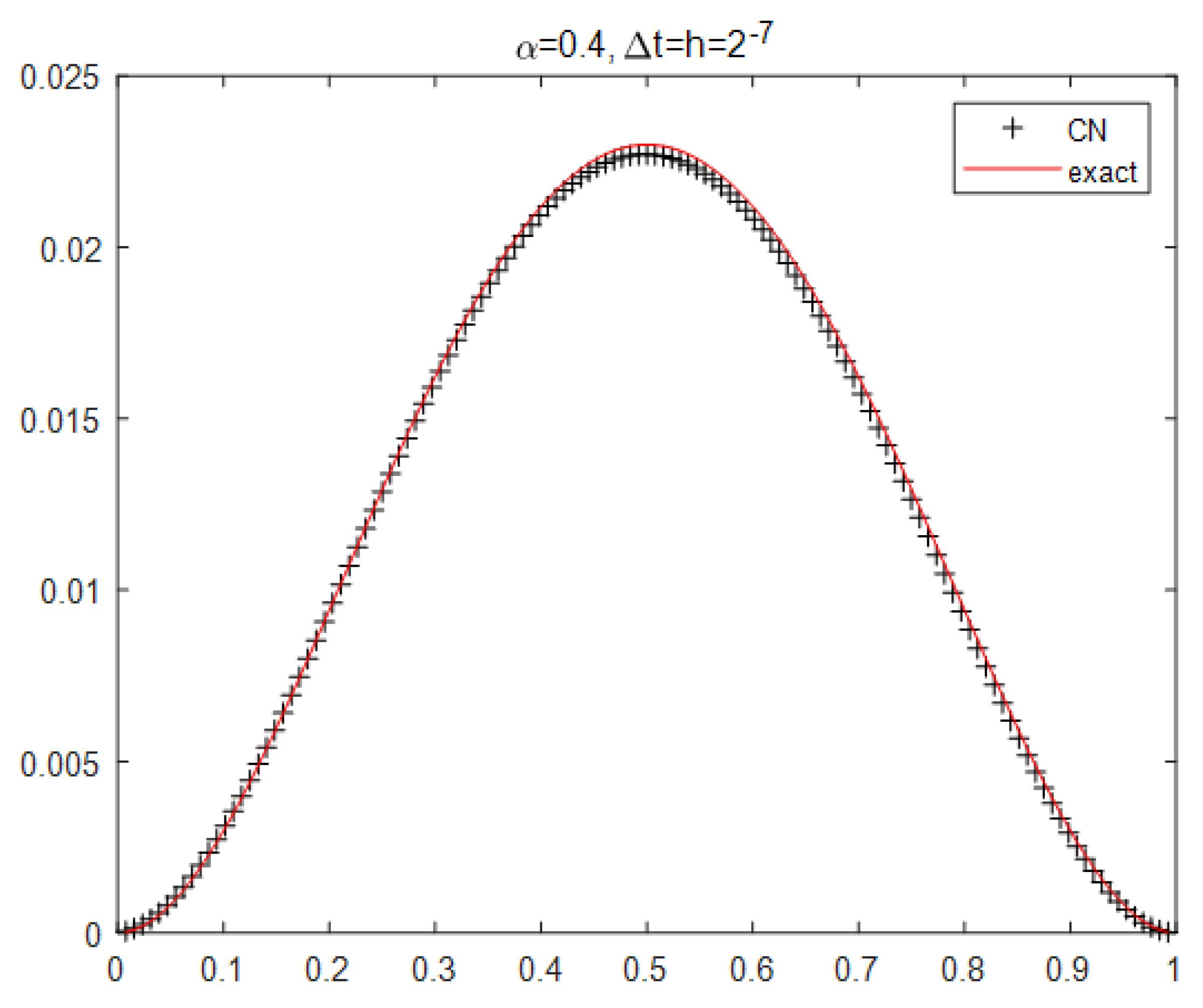


| 7.5340 | - | 4.2000 | - | 1.9000 | - | |
| 4.2214 | 1.78 | 2.4000 | 1.75 | 1.2000 | 1.83 | |
| 2.2199 | 1.90 | 1.3000 | 1.85 | 6.565 | 1.58 | |
| 1.1356 | 1.95 | 6.4325 | 2.02 | 3.4039 | 1.93 | |
| 5.7351 | 1.98 | 3.2425 | 1.98 | 1.7301 | 1.97 |
| 7.7198 | - | 7.4596 | - | |
| 4.0338 | 1.91 | 1.7406 | 4.29 | |
| 2.4992 | 1.61 | 4.1151 | 4.23 | |
| 1.3734 | 1.82 | 9.7767 | 4.21 |
| 8.3000 | - | 3.8000 | - | 1.3000 | - | |
| 5.0000 | 1.66 | 2.3000 | 1.75 | 9.1101 | 1.43 | |
| 2.7000 | 1.85 | 1.2000 | 1.85 | 5.1674 | 1.76 | |
| 1.4000 | 1.93 | 6.4069 | 2.02 | 2.7250 | 1.90 | |
| 7.1602 | 1.96 | 3.2564 | 1.98 | 1.3953 | 1.95 |
| 7.1922 | - | 6.5386 | - | |
| 1.8018 | 3.99 | 1.5769 | 4.15 | |
| 1.3921 | 1.29 | 3.7662 | 4.19 | |
| 8.2345 | 1.69 | 8.2345 | 4.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Yin, X.; Chen, Y.; Hou, M. A Second-Order Accurate Numerical Approximation for a Two-Sided Space-Fractional Diffusion Equation. Mathematics 2023, 11, 1838. https://doi.org/10.3390/math11081838
Liu T, Yin X, Chen Y, Hou M. A Second-Order Accurate Numerical Approximation for a Two-Sided Space-Fractional Diffusion Equation. Mathematics. 2023; 11(8):1838. https://doi.org/10.3390/math11081838
Chicago/Turabian StyleLiu, Taohua, Xiucao Yin, Yinghao Chen, and Muzhou Hou. 2023. "A Second-Order Accurate Numerical Approximation for a Two-Sided Space-Fractional Diffusion Equation" Mathematics 11, no. 8: 1838. https://doi.org/10.3390/math11081838
APA StyleLiu, T., Yin, X., Chen, Y., & Hou, M. (2023). A Second-Order Accurate Numerical Approximation for a Two-Sided Space-Fractional Diffusion Equation. Mathematics, 11(8), 1838. https://doi.org/10.3390/math11081838









