On the Construction of Exact Numerical Schemes for Linear Delay Models

Abstract

Exact numerical schemes have previously been obtained for some linear retarded delay differential equations and systems. Those schemes were derived from explicit expressions of the exact solutions, and were expressed in the form of perturbed difference systems, involving the values at previous delay intervals. In this work, we propose to directly obtain expressions of the same type for the fundamental solutions of linear delay differential equations, by considering vector equations with vector components corresponding to delay-lagged values at previous intervals. From these expressions for the fundamental solutions, exact numerical schemes for arbitrary initial functions can be proposed, and they may also facilitate obtaining explicit exact solutions. We apply this approach to obtain an exact numerical scheme for the first order linear neutral equation $x^{\prime }\left(t\right)-\gamma x^{\prime }(t-\tau )=\alpha x\left(t\right)+\beta x(t-\tau )$, with the general initial condition $x\left(t\right)=\phi \left(t\right)$ for $-\tau \le t\le 0$. The resulting expression reduces to those previously published for the corresponding retarded equations when $\gamma =0$.

1. Introduction

Differential equations are essential modelling tools in science and engineering, with a vast majority of applications requiring the use of numerical methods, due to the lack of exact solutions or practical computable expressions for them. Finite difference schemes are some of the most widely used methods to compute numerical approximate solutions of ordinary or partial differential equations (e.g., [1,2,3]), transforming the original continuous differential problems into difference equations or systems.

In [4], Potts considered a seemingly simple question, whether, given a linear ordinary differential equation (ODE), a linear ordinary difference equation (OΔE) could be determined with the same general solution, that is, satisfying that, for any step-size h defining the discretization $t_n=nh$, the numerical values computed with the OΔE, $x_n$, coincide with the continuous solution $x\left(t\right)$ at those points, i.e., $x_n=x\left(t_n\right)$. With positive answers for linear ODE and systems given by Potts [4], and for general ODE by Mickens [5,6], an exact difference scheme is defined as one for which the solution to the OΔE has the same general solution as the associated ODE.

Exact difference schemes for particular problems, or groups of problems [7], are ideal, as there are no truncation errors and there are no issues regarding the order of convergence or stability. More importantly, since they reproduce the values of exact solutions in the discrete mesh, the dynamic properties of the continuous solutions are faithfully preserved by the numerical method. By constructing exact schemes for different examples of simple ODE, it was shown that commonly used standard numerical schemes for these equations [4,6], which were not exact, could have stability problems and/or could produce numerical solutions with dynamic properties different from the continuous solutions they were supposed to reproduce.

There is no general procedure on how to construct exact schemes for particular problems, and, since having an exact scheme essentially equates to having an exact solution, it cannot be expected to obtain exact schemes for most problems. However, as pointed out in [6], examples of exact schemes for a variety of equations may give “useful information on modeling rules for realistic situations where exact solutions are not known a priori”. This basic idea was developed by Mickens to propose “nonstandard modeling rules” for difference schemes, resulting in the so-called nonstandard finite difference (NSFD) methods [8]. NSFD methods have been increasingly used in all kind of problems, including ordinary, partial, fractional, and delay differential equations (see [8,9,10,11,12] and references therein), with a special focus on applications in population models and epidemiology, since they can be designed to preserve critical dynamic properties of these models (e.g., [13,14,15,16,17,18,19]).

In real world systems, completely instantaneous responses, if any, are hardly found, and although in most situations they can be safely assumed in models, there are many problems where the presence of delays and lagged responses heavily affect the systems’ dynamics, requiring the use of delay differential equations (see, e.g., [20,21,22,23,24] and references therein). Although exact schemes have been constructed for many different non-delay differential equations and systems (see ([12], Chapter 10)), for delay differential equations (DDE) they are limited to the linear first order retarded scalar initial value problem [25,26],

$$\begin{array}{ccc}\hfill x^{\prime }\left(t\right)& =& \alpha x\left(t\right)+\beta x(t-\tau ),t>0,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill x\left(t\right)& =& \phi \left(t\right),-\tau \le t\le 0,\hfill \end{array}$$

(2)

and also to the corresponding vector problem [27,28].

In [26,27], explicit constructive exact solutions were used to express the value of $x(t+h)$ as a function of $x\left(t\right)$ and previous values. The resulting expression included all previous $\tau -$lagged values, i.e., $x(t-k\tau )$, and also an integral term with the initial function $\phi \left(t\right)$, reflecting the infinite dimensional nature of delay equations, and from that expression an exact numerical solution was presented in the form of a perturbed difference system. The aim of the present work is to show that, assuming these properties for exact numerical solutions of linear DDE, they could be directly constructed without the requirement of having a previous expression for the exact solutions. As a proof of concept, we will consider the neutral equation

$$x^{\prime }\left(t\right)-\gamma x^{\prime }(t-\tau )=\alpha x\left(t\right)+\beta x(t-\tau ),t>0,$$

(3)

with the initial condition (2), obtaining an expression for its exact numerical solution and generalizing the expression given in [26] for the particular case $\gamma =0$.

Thus, this work may be considered an extension of the results on exact numerical schemes presented in [26] for the scalar retarded Equation (1), extended in [27] to systems of retarded equations, with two main novelties. Firstly, the proposed new approach is to derive exact numerical schemes without prior knowledge of the exact solution, which we expect could be applied to more complex DDE; and, secondly, we use the construction of an exact scheme for the neutral Equation (3), not previously obtained and including the exact scheme given in [26], as a particular case.

We would like to stress the significance of both the new results developed in this work and the new methodology used in the process. To our knowledge, we present the first example of an exact numerical scheme for a neutral delay equation. Additionally, we are not aware of an exact constructive solution for the neutral DDE (3) that would allow to derive an exact scheme following the process used in previous works.

2. Methods and Results

To facilitate reading, and clarify the type of expressions that are sought for the exact numerical solutions of (3), in the next lemma we recall the results obtained in [26] for the retarded problems (1) and (2), in the equivalent form of the simplified expression given in [27] for the corresponding vector problem with commuting matrix coefficients, which include the scalar equation considered in [26] as a particular case.

Lemma 1.

Let $h>0$ such that $Nh=\tau$, for some integer $N\ge 1$. Writing $t_n\equiv nh$ and $x_n\equiv x\left(t_n\right)$, for $n\ge -N$, the numerical solution for $-N\le n\le 0$ is given by $x_n=\phi \left(t_n\right)$, and for $(m-1)\tau \le nh<m\tau$ and $m\ge 1$ it is given by

$$\begin{array}{cc}\hfill x_{n+1}=x(t_n+h)& ={\mathrm{e}}^{\alpha h}\sum _{k=0}^{m-1}\frac{{\beta }^k{h}^k}{k!}{x}_{n-kN}\hfill \\ & +\frac{{\beta }^m}{(m-1)!}{\int }_{t_n-m\tau }^{t_n-m\tau +h}{(t_n-m\tau +h-s)}^{m-1}{\mathrm{e}}^{\alpha (t_n-m\tau +h-s)}\phi \left(s\right)ds,\hfill \end{array}$$

(4)

which defines an exact numerical scheme for problem (1) and (2).

Consider Equation (3) with the initial condition (2), with $\phi \left(t\right)\in C^1\left([-\tau ,0]\right)$. Then, the solution $x\left(t\right)$ is continuous in $(0,\infty )$ and of class $C^1$ in each interval $\left[\right(k-1)\tau ,(k-1\left)\tau \right]$, $k\in \mathbb{N}$ ([29], Theorem 5.1). For $(m-1)\tau <t<m\tau$, write $u=t-(m-1)\tau$, and let $X\left(u\right)={(x_m\left(u\right),\dots ,x_1\left(u\right))}^T$ be the vector of functions $x_k$ defined by $x_k\left(u\right)=x((k-1)\tau +u)=x(t-k\tau )$.

We also consider the fundamental solution $f\left(t\right)$, satisfying (3) with initial values $f\left(t\right)=0$ for $t\in [-\tau ,0)$ and $f\left(0\right)=1$, which exists and is unique ([29], p. 146), and let $F\left(u\right)={(f_m\left(u\right),\dots ,f_1\left(u\right))}^T$ be the corresponding vector of functions $f_k\left(u\right)=f((k-1)\tau +u)$. Then, for $k=1$, one has $f_1^{\prime }\left(u\right)=f^{\prime }\left(u\right)=\alpha f\left(u\right)=\alpha f_1\left(u\right)$, since $f(u-\tau )=f^{\prime }(u-\tau )=0$; while for $k>1$ it holds that

$$\begin{array}{cc}\hfill f_k^{\prime }\left(u\right)-\gamma f_{k+1}^{\prime }\left(u\right)=& f^{\prime }(t-k\tau )-\gamma f^{\prime }(t-(k+1)\tau )\hfill \\ & =\alpha f(t-k\tau )+\beta f(t-(k+1)\tau )=\alpha f_k\left(u\right)+\beta f_{k+1}\left(u\right).\hfill \end{array}$$

(5)

Hence, letting C and B be the m dimensional upper triangular matrices

$$C=\left(\begin{array}{cccccc}1& -\gamma & 0& \cdots & 0& 0\\ 0& 1& -\gamma & \cdots & 0& 0\\ 0& 0& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & 1& -\gamma \\ 0& 0& 0& \cdots & 0& 1\end{array}\right),B=\left(\begin{array}{cccccc}\alpha & \beta & 0& \cdots & 0& 0\\ 0& \alpha & \beta & \cdots & 0& 0\\ 0& 0& \alpha & \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & \cdots & ⋮\\ 0& 0& 0& \cdots & \alpha & \beta \\ 0& 0& 0& \cdots & 0& \alpha \end{array}\right),$$

(6)

the vector of fundamental solutions satisfies the equation $C{F}^{\prime }\left(u\right)=BF\left(u\right)$ or, equivalently, since C is invertible, $F^{\prime }\left(u\right)=AF\left(u\right)$, with $A=C^{-1}B$. Therefore, for $0<h\le \tau$ and $(m-1)\tau \le t\le m\tau -h$, one gets

$$F(u+h)={\mathrm{e}}^{Ah}F\left(u\right),$$

(7)

and the first element in this equation provides the expression of $f(t+h)$ in terms of $f(t-k\tau )$, $k=0\dots m-1$.

It can easily be checked that the matrices $C^{-1}=\left(c_{ij}^{-1}\right)$ and $A=\left(a_{ij}\right)$ are upper triangular matrices with non-zero elements given by

$$c_{ii+k}^{-1}={\gamma }^k,i=1\dots m,k=0\dots m-i$$

(8)

and

$$a_{ii}=\alpha ,i=1\dots m;a_{ii+k}=(\beta +\alpha \gamma ){\gamma }^{k-1},i=1\dots m-1,k=1\dots m-i.$$

(9)

Thus, it is obvious that ${\mathrm{e}}^{Ah}$ is also an upper triangular matrix, and it is not difficult to see that the main diagonal elements are equal to ${\mathrm{e}}^{\alpha h}$. By computing ${\mathrm{e}}^{Ah}$ for increasing dimension values, and by analysing the results, one can guess a general expression for all the elements in this matrix, as shown in our next theorem.

Theorem 1.

Let $Q\left(u\right)=\left(q_{ij}\left(u\right)\right)$ be the m-dimensional upper triangular matrix with nonzero elements $q_{ii}\left(u\right)={\mathrm{e}}^{\alpha u}$, for $i=1\dots m$, and

$$q_{pp+k}\left(u\right)={\mathrm{e}}^{\alpha u}\sum _{r=1}^k\frac{{\gamma }^{k-r}{(\beta +\alpha \gamma )}^r{u}^r}{r!}\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right),p=1\dots m,k=1\dots m-p.$$

(10)

Then, $Q\left(u\right)$ satisfies $Q^{\prime }\left(u\right)=AQ\left(u\right)$ and $Q\left(0\right)=I$, where I is the m-dimensional identity matrix, and, hence, $Q\left(u\right)={\mathrm{e}}^{Au}$.

Proof. 

It is obvious that $Q\left(0\right)=I$, and that both $Q^{\prime }\left(u\right)$ and $AQ\left(u\right)$ are upper triangular matrices. Additionally, the diagonal elements are easily found to be $\alpha {\mathrm{e}}^{\alpha h}$ in both cases.

We will show next that the elements in row p and column $p+k$, with $1\le p\le m-1$ and $1\le k\le m-p$, in both matrices $Q^{\prime }\left(u\right)$ and $AQ\left(u\right)$ are equal. For $Q^{\prime }\left(u\right)$ one has

$$\begin{array}{cc}\hfill q_{pp+k}^{\prime }\left(u\right)& =\alpha q_{pp+k}\left(u\right)+{\mathrm{e}}^{\alpha u}\sum _{r=1}^k\frac{{\gamma }^{k-r}{(\beta +\alpha \gamma )}^r{u}^{r-1}}{(r-1)!}\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right)\hfill \\ & =\alpha q_{pp+k}\left(u\right)+{\mathrm{e}}^{\alpha u}{\gamma }^{k-1}(\beta +\alpha \gamma )+{\mathrm{e}}^{\alpha u}\sum _{r=1}^{k-1}\frac{{\gamma }^{k-1-r}{(\beta +\alpha \gamma )}^{r+1}{u}^r}{\left(r\right)!}\left(\genfrac{}{}{0pt}{}{k-1}{r}\right).\hfill \end{array}$$

(11)

Writing $A=\left(a_{ij}\right)$ and taking into account that both A and $Q\left(u\right)$ are upper triangular matrices, the corresponding element in the product $AQ\left(u\right)$ is computed as

$$\begin{array}{c}\sum _{j=0}^k{a}_{pp+j}{q}_{p+jp+k}\left(u\right)\hfill \\ =\alpha q_{pp+k}\left(u\right)+\sum _{j=1}^{k-1}(\beta +\alpha \gamma ){\gamma }^{j-1}{\mathrm{e}}^{\alpha u}\sum _{r=1}^{k-j}\frac{{\gamma }^{k-j-r}{(\beta +\alpha \gamma )}^r{u}^r}{\left(r\right)!}\left(\genfrac{}{}{0pt}{}{k-j-1}{r-1}\right)+(\beta +\alpha \gamma ){\gamma }^{k-1}{\mathrm{e}}^{\alpha u}\hfill \\ =\alpha q_{pp+k}\left(u\right)+{\mathrm{e}}^{\alpha u}{\gamma }^{k-1}(\beta +\alpha \gamma )+{\mathrm{e}}^{\alpha u}\sum _{j=1}^{k-1}\sum _{r=1}^{k-j}\frac{{\gamma }^{k-1-r}{(\beta +\alpha \gamma )}^{r+1}{u}^r}{\left(r\right)!}\left(\genfrac{}{}{0pt}{}{k-j-1}{r-1}\right)\hfill \end{array}$$

(12)

and we only need to prove that the last terms in (11) and (12) are equivalent. Using the binomial identity ([30], p. 619, 26.3.7).

$$\sum _{i=n}^m\left(\genfrac{}{}{0pt}{}{i}{n}\right)=\left(\genfrac{}{}{0pt}{}{m+1}{n+1}\right),$$

(13)

one gets

$$\begin{array}{c}\sum _{j=1}^{k-1}\sum _{r=1}^{k-j}\frac{{\gamma }^{k-1-r}{(\beta +\alpha \gamma )}^{r+1}{u}^r}{\left(r\right)!}\left(\genfrac{}{}{0pt}{}{k-j-1}{r-1}\right)=\sum _{s=1}^{k-1}\sum _{r=1}^s\frac{{\gamma }^{k-1-r}{(\beta +\alpha \gamma )}^{r+1}{u}^r}{\left(r\right)!}\left(\genfrac{}{}{0pt}{}{s-1}{r-1}\right)\hfill \\ \hfill =\sum _{r=1}^{k-1}\frac{{\gamma }^{k-1-r}{(\beta +\alpha \gamma )}^{r+1}{u}^r}{\left(r\right)!}\sum _{s=r}^{k-1}\left(\genfrac{}{}{0pt}{}{s-1}{r-1}\right)=\sum _{r=1}^{k-1}\frac{{\gamma }^{k-1-r}{(\beta +\alpha \gamma )}^{r+1}{u}^r}{\left(r\right)!}\left(\genfrac{}{}{0pt}{}{k-1}{r}\right)\end{array}$$

(14)

and the proof is complete.  □

Hence, the expression for $f(t+h)$ follows as given in our next Theorem.

Theorem 2.

Let $0<h\le \tau$ and $(m-1)\tau \le t\le m\tau -h$ for $m\ge 1$. Then, the fundamental solution $f\left(t\right)$ of (3) satisfies

$$f(t+h)=e^{\alpha h}\left(f\left(t\right)+\sum _{k=1}^{m-1}\left(\sum _{r=1}^k\frac{{\gamma }^{k-r}{(\beta +\alpha \gamma )}^r{h}^r}{r!}\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right)\right)f(t-k\tau )\right).$$

(15)

Proof. 

From (7), $f(t+h)$ is the first element in the vector $F(t+h)$, and the right-hand term in (15) is simply the first element in the product ${\mathrm{e}}^{Ah}F\left(u\right)$, using the expressions for the elements of ${\mathrm{e}}^{Ah}$ given in Theorem 1.  □

We now seek an expression similar to (15) for the solution of (3) with the general initial condition (2). In this case, for $k=1$ one has

$$x_1^{\prime }\left(u\right)=x^{\prime }\left(u\right)=\alpha x\left(u\right)+\beta \phi (u-\tau )+\gamma {\phi }^{\prime }(u-\tau )=\alpha x_1\left(u\right)+\beta \phi (u-\tau )+\gamma {\phi }^{\prime }(u-\tau ),$$

(16)

and for $k>1$, similarly to (5), one has $x_k^{\prime }\left(u\right)-\gamma x_{k-1}^{\prime }(u-\tau )=\alpha x_k\left(u\right)+\beta x_{k-1}(u-\tau )$. Therefore, considering the m-dimensional vector $\Phi \left(u\right)={(0,\dots 0,\gamma {\phi }^{\prime }(u-\tau )+\beta \phi (u-\tau ))}^T$, one has the non-homogeneous equation

$$X^{\prime }\left(u\right)=AX\left(u\right)+B^{-1}\Phi \left(u\right),$$

(17)

which can be used to obtain the expression for $x(t+h)$ given in our next theorem.

Theorem 3.

Let $0<h\le \tau$ and $(m-1)\tau \le t\le m\tau -h$ for $m\ge 1$. Then, writing $F\left(s\right)=\gamma {\phi }^{\prime }\left(s\right)+\beta \phi \left(s\right)$, the solution $x\left(t\right)$ of (3), with the initial condition (2), satisfies

$$\begin{array}{cc}\hfill x(t+h)& =e^{\alpha h}\left(x\left(t\right)+\sum _{k=1}^{m-1}\left(\sum _{r=1}^k\frac{{\gamma }^{k-r}{(\beta +\alpha \gamma )}^r{h}^r}{r!}\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right)\right)x(t-k\tau )\right)\hfill \\ & +{\int }_{t-m\tau }^{t-m\tau +h}\left({\gamma }^{m-1}+\sum _{k=1}^{m-1}\sum _{r=1}^k\frac{{\gamma }^{m-1-r}{(\beta +\alpha \gamma )}^r{(t-m\tau +h-s)}^r\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right)}{r!}\right)e^{\alpha (t-m\tau +h-s)}F\left(s\right)ds.\hfill \end{array}$$

(18)

Proof. 

Let G be the constant vector ${({\gamma }^{m-1},{\gamma }^{m-2},\dots ,\gamma ,1)}^T$ and $\Psi \left(u\right)$ the vector $\Psi \left(u\right)=({\phi }^{\prime }(u-\tau )+\beta \phi (u-\tau ))G$. It can easily be checked that $B^{-1}\Phi \left(u\right)=\Psi \left(u\right)$. Then, since ${\mathrm{e}}^{Au}$ is a fundamental matrix solution of (17), one has

$$\begin{array}{cc}\hfill X(u+h)& ={\mathrm{e}}^{A(u+h)}X\left(0\right)+{\int }_0^{u+h}{\mathrm{e}}^{A(u+h-v)}\Psi \left(v\right)dv\hfill \\ & ={\mathrm{e}}^{Ah}\left({\mathrm{e}}^{Au}X\left(0\right)+{\int }_0^u{\mathrm{e}}^{A(u-v)}\Psi \left(v\right)dv\right)+{\int }_u^{u+h}{\mathrm{e}}^{A(u+h-v)}\Psi \left(v\right)dv\hfill \\ & ={\mathrm{e}}^{Ah}X\left(u\right)+{\int }_u^{u+h}{\mathrm{e}}^{A(u+h-v)}\Psi \left(v\right)dv.\hfill \end{array}$$

(19)

Hence, for t in $\left[\right(m-1)\tau ,m\tau ]$, writing $u=t-(m-1)\tau$ and $s=v-\tau$, one gets

$$X(t-(m-1)\tau +h)={\mathrm{e}}^{Ah}X(t-(m-1)\tau )+{\int }_{t-m\tau }^{t-m\tau +h}{\mathrm{e}}^{A(t-m\tau +h-s)}G({\phi }^{\prime }\left(s\right)+\beta \phi \left(s\right))ds.$$

(20)

Then, since $x_{m-1}(t-(m-1)\tau +h)=x((m-1)\tau +t-(m-1)\tau +h)=x(t+h)$, the expression given in (18) is obtained as the first element on the right-hand side of (20), using the expressions for ${\mathrm{e}}^{Ah}$ and ${\mathrm{e}}^{A(t-m\tau +h-s)}$ given in Theorem 1.  □

From Theorem 3, an exact numerical scheme can immediately be obtained, as given in the following corollary.

Corollary 1.

Let $h>0$, such that $Nh=\tau$ for some integer $N\ge 1$. Writing $t_n\equiv nh$ and $x_n\equiv x\left(t_n\right)$ for $n\ge -N$, the numerical solution for $-N\le n\le 0$ is given by $x_n=\phi \left(t_n\right)$, and for $(m-1)\tau \le nh<m\tau$ and $m\ge 1$ by

$$\begin{array}{cc}\hfill x_{n+1}& =e^{\alpha h}{x}_n+\sum _{k=1}^{m-1}\left(\sum _{r=1}^k\frac{{\gamma }^{k-r}{(\beta +\alpha \gamma )}^r{h}^r}{r!}\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right)\right)x_{n-kN}\hfill \\ & +{\int }_{t_n-m\tau }^{t_n-m\tau +h}\left({\gamma }^{m-1}+\sum _{k=1}^{m-1}\sum _{r=1}^k\frac{{\gamma }^{m-1-r}{(\beta +\alpha \gamma )}^r{(t_n-m\tau +h-s)}^r\left(\genfrac{}{}{0pt}{}{k-1}{r-1}\right)}{r!}\right)e^{\alpha (t_n-m\tau +h-s)}F\left(s\right)ds,\hfill \end{array}$$

(21)

with $F\left(s\right)$ as in Theorem 3, and where the summations are understood to be empty when $m=1$, defines an exact numerical scheme for (3) with the initial condition (2).

Remark 1.

When $\gamma =0$, i.e., for the retarded initial value problems (1) and (2), all the terms with γ in (21), except those corresponding to ${\gamma }^{k-r}$ with $k=r$, are zero, and the expression given in Corollary 1 reduces to that previously obtained for this case, recalled in Lemma 1.

Example 1.

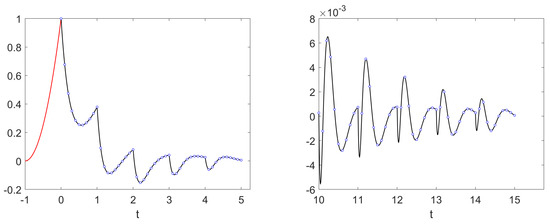
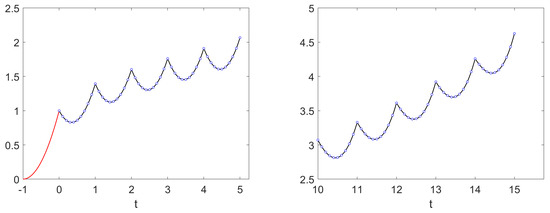
Figure 1 and Figure 2 present two examples of numerical solutions computed with the exact scheme given in Corollary 1 superimposed to the exact continuous solutions obtained by step-by-step integration of Equation (3) with $x(t-\tau )$ and $x^{\prime }(t-\tau )$ as computed in the previous interval. As shown in these figures, the numerical solutions perfectly match the exact continuous solutions, either when the exact solution is asymptotically stable (Figure 1) or when it is unstable (Figure 2).

3. Discussion

In previous works [26,27], exact numerical solutions for retarded first order DDE were derived from explicit expressions of the exact solutions. These type of expressions are usually constructed by using the method of steps to obtain solutions in successive delay intervals [29], and then guessing a possible general form of the solution, which can hopefully be formally proven to be correct. Once an expression for the explicit solution is available, it still needs to be transformed into an expression relating the value of the solution at $t+h$ with previously computed values. The whole process can be cumbersome, especially when more complex equations than those considered in [26,27] are to be tackled.

The main idea of this work was to use the information obtained about the form of the exact schemes derived in [26,27], i.e., that they can be given in the form of a perturbed difference system including all previous $\tau$-lagged values, to try and directly construct an exact numerical solution without requiring previous knowledge of the continuous solution.

As shown by the expression given in Corollary 1, the envisaged strategy was proven to be successful by obtaining an exact numerical scheme for the first order neutral DDE (3), with the general initial condition (2). The expression given in Corollary 1 generalises previous results for retarded scalar equations [26], reducing to them when $\gamma =0$. Additionally, to our knowledge, it constitutes the first example of an exact scheme for a neutral DDE.

Although not in the objectives of this work, we note that the expressions given in Theorems 2 and 3 may also help the construction of explicit expressions for the exact continuous solutions, reversing the process previously used to derive exact numerical solutions. Instead of using the method of steps, which may imply solving increasingly complex non-homogeneous ODE, one could use a recursive process to express the solution in one interval in terms of the previous ones.

The form of the exact solutions obtained in this and previous works as perturbed difference systems, including an integral term depending on the initial function, seem unavoidable except for particular simple initial functions that could be integrated exactly, and this reflects the infinite dimensional nature of delay equations. In [26,27], to avoid the computation of the integral terms, a family of NSFD schemes of as high an order as needed, derived from the given exact schemes, was proposed and shown to be dynamically consistent with the continuous solutions. The strategy followed there was not directly applied to the neutral equation considered in this work, as all terms in (3) corresponding to previously computed vales, $x_{n-kN}$, include coefficients of order h, in contrast to the retarded case, where they were of order $h^k$.

As part of future work we consider the use of the recursive expressions given in Theorems 2 and 3 to construct exact solutions and analysing the best approach to derive efficient NSFD methods from the exact schemes, as mentioned above, but also testing the applicability of the proposed approach to directly derive exact schemes to higher order equations or to problems with random terms.