Horizontal Axis Wind Turbine Weather Vane Aerodynamic Characteristics: Delayed Detached Eddy Simulation and Experimental Approach

Abstract

The known differential yaw error of horizontal axis wind turbines is clearly linked to weather vane fluctuations, arising out of the deflection of the onrushing wind flow from the rotating blades. Since the problem has not been resolved as the control systems still present this problem, it should be considered as an actual difficulty requiring deeper studies of the weather vane’s aerodynamic features, including the modeling of its deviations. This paper focuses on the computational fluid dynamics and experimental study of the aerodynamic characteristics of the weather vane located on the nacelle top of horizontal axis wind turbines. Computational fluid dynamics simulation is based on the k-ω Shear Stress Transport turbulence model and the Delayed Detached Eddy Simulation. The numerical simulation and laboratory experiment arrangements are demonstrated in detail. The new scientific results obtained during the research include the validation of the numerical experiment, demonstration of the differences in forming the wake structures for the used models on the studied angles of attack and comparison of the mean values of the moment and power spectral densities for all cases, which demonstrated a good correlation between the Delayed Detached Eddy Simulation data and the experiment. The time spent on the preparation of numerical experiments using different models was accurately estimated, to give an understanding of man-hour resources. The obtained moment values for the weather vane are applied for further mathematical modeling of the systems intended for the reduction in the differential yaw error. The applicability of the Delayed Detached Eddy Simulation approach was proved by the simulation of the aerodynamic characteristics of complexly streamlined bodies, but at the same time, it showed an extended calculation period. The results obtained during the study expand upon the experience of using numerical simulation when studying horizontal axis wind turbines and may be used to build mathematical models of yaw control systems.

1. Introduction

Wind power currently covers a considerable share of electricity generation in a number of countries. Global annual investments in the renewable energy segment reached USD 259 billion in 2022 as announced in [1].

The increase in electricity generation is one of the main goals of wind power developers around the world. In general, there are two ways that could be used in this area. There is a simple but the expensive method, which is to increase the installed capacity of wind farms, and this approach is working. The global wind power growth from 2020 to 2021 was estimated to be 93 gigawatts according to the Global Wind Energy Council [2]. Another method is to improve a single installation. Works in this area are concentrated primarily on the increment in the wind turbine’s lifetime, and improvements in the aerodynamic and electrodynamic characteristics of the components, especially the rotor and generator.

One of the main problems in the operation of horizontal axis wind turbines is the permanent determination of the direction of the wind flow since the electric generation of any wind turbine depends on the swept area and reaches its maximum when the onrushing air flow vector is perpendicular to the wind rotor plane it rotates in. When the wind direction changes, the yaw control system reads as an appeared error, and if and when it is sensitive enough, then the system gives a command to turn the nacelle with the rotor to the right position. The accurate yawing reduces the power losses and, at the same time, structural loads, which may shorten the wind turbine’s lifetime significantly.

Scientists from countries with developed wind power have continue their research to improve the accuracy of rotor orientation. Kim and Dalhoff (2014) in [3] presented a patent analysis of the state of the field, showing that the main directions of development are focused on the design of new types of mechanisms and control systems to reduce stress. Newer researches have not really changed the areas of development but are more concerned with the intelligent control issues such as advanced model predictive control (Song, 2019) [4] and neural-network-based fault detection systems for pitch and yaw control (El-Mallawany, 2019) [5]. The intelligent systems presented in these studies have huge potential in terms of the installations of the next generation, but they still have a number of disadvantages associated with the limited set of cases for training.

A new type of orientation sensor, LiDAR (light detection and ranging), presented by Scholbrock et al. (2015) in [6] showed great potential for its usage in wind farm yaw control systems and is currently being used for megawatt-class installations. However, the huge disadvantage of this type of yaw control is its high cost. The authors also noted that the differences in positioning accuracy with classical-weather-vane-based systems can be neglected by the implementation of a bias correction function.

Another research team was involved in a project that intended to study of the nature of the yawing differential (periodically changing) error caused by the deflection of the air flow by the rotating blades [7,8,9,10]. A mathematic compensator, built-in as a separate block in the control software, was developed for this case on the basis of studying the behavior of a weather vane. This approach led to a decrease in the error of yawing by up to 2 degrees. The study focused on mathematical simulation based on aerodynamic data obtained by experimental and numerical methods.

Due to the lack of aerodynamic data for a weather vane in open sources, this article presents both an experimental and a numerical study along with a comparison of the approaches to reach a conclusion about the feasibility of their usage for studying a wind turbine’s operation. Being able to obtain the aerodynamic characteristics of a complex streamlined body that are close to real, is still a common problem in many research areas. However, it can be resolved partly or in full by numerical simulation. The main modeling approaches for obtaining the required data on different levels are as follows:

• Solution of Reynolds-averaged Navier–Stokes equations (RANS). The k-ɛ and k-ω Shear Stress Transport (SST) turbulence models are the most commonly used in engineering projects;
• Large eddy simulation (LES);
• Detached eddy simulations (DES) and different modifications;
• Direct numerical simulation (DNS) approach, which is used primarily in the academic area, while not being practical enough for engineering calculations.

DES is the most promising method, rapidly developing and acquiring various modifications such as Detached DES (DDES), Zonal DES (ZDES), etc. [11,12]. At the moment, the application of the method affects the study of the geometry of simple and medium complexity. In the research [13], two modifications of DES (DDES and Zonal DES) were studied using the examples with channel flow and profile flow on a small angle of attack (AoA), and showed a significant advantage of the DDES approach over ZDES. In paper [14], a mesh study of iced wings was performed with good correspondence between the data obtained from DDES and the experiment, and, in addition, some valuable recommendations regarding the construction of a computational grid were given. According to the literature analysis, the most used modification is Delayed Detached Eddy Simulation (DDES). It is worth noting that most of the studies were performed on the Spalart–Allmaras (SA) modification of DES. The SA model, in some cases, loses in terms of the accuracy of the description of the boundary flows of the k-ω SST model; therefore, a modification of the k-ω SST is preferable. As a consequence, the k-ω SST modification of DDES was used in the present study based on the ANSYS Fluent software package.

The project is divided into several stages. First, we give a short theory of the DDES approach using governing equations. Here, we describe the geometry and finite volume mesh preparation process, including mesh zones, highlighting the boundary layer modeling and spatial resolution assessment, as well as the boundary conditions and time step selections. This contains some new elements in the preparation of a numerical experiment, such as a hybrid approach to the creation of a computational grid and the study of its resolution. Such details are often overlooked when describing the method. Second, we give a description of the experiment. Finally, we present the results of the research with analysis. We also make a conclusion on the applicability of computational fluid dynamics (CFD) for this specific case with some other general conclusions. Further research steps are also proposed on the basis of the material presented in this article.

2. Delayed Detached Eddy Simulation

DES was first introduced in 1997 by Spalart [15]. This approach was designed to mitigate the next shortcomings of the Reynolds-averaged Navier–Stokes (RANS) and Large Eddy Simulation (LES) methods:

• The inability of RANS to provide an acceptable accuracy when calculating flows with large separation zones;
• The high computational cost of LES. To resolve the boundary layer, which contains a lot of small energy-carrying vortices, appropriate spatial and temporal resolution is required.

Notwithstanding these, both of the methods are widely used in engineering and scientific projects due to their main advantages:

• RANS is capable of a quite accurate resolving of the boundary layer with a low computational cost as reported in [16,17];
• LES demonstrates a physically close representation of turbulence in accordance with [18].

According to these statements, DES was developed as a hybrid approach that uses RANS in the near-wall region and LES for the stall one. This approach demonstrates a good agreement with the experimental data presented in [19]. It has a good ratio of performance to computational costs and is therefore widely used on modern personal computers.

The well-known problem of DES is grid-induced separation, the physics of which is described in [20]. The Delayed Detached Eddy Simulation (DDES) was introduced to mitigate this problem according to [21].

2.1. Theory

In this research, the Shear Stress Transport k-ω formulation of DDES was employed as recommended in [22]. This approach is described by Equations (1) and (2), showing a good ratio of compliance between the experimental data and calculation cost, compared with another modern LES approach [23].

Turbulence kinetic energy:

$$\frac{\partial k}{\partial t}+\frac{\partial k}{\partial x_j}\left({\overline{\upsilon }}_{j}k\right)=P^k-{\beta }^{*}k\omega +\frac{\partial }{\partial x_j}\left[\left(v+\frac{v_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right],$$

(1)

Specific dissipation rate:

$$\frac{\partial \omega }{\partial t}+\frac{\partial \omega }{\partial x_j}\left({\overline{\upsilon }}_j\omega \right)=\frac{\partial }{\partial x_j}\left[\left(v+\frac{v_t}{{\sigma }_{\omega }}\right)\frac{\partial \omega }{\partial x_j}\right]+\alpha \frac{P^k}{{\nu }_t}-\beta {\omega }^2+2(1-F_1)\frac{{\sigma }_{\omega 2}}{\omega }\frac{\partial k}{\partial x_i}\frac{\partial \omega }{\partial x_i},$$

(2)

The selected model is suitable for simulating both parts of the boundary layer: outer with the k-ɛ model in a free-flow zone, thus avoiding the known problem of the standard k-ω model being too sensitive to the free-stream condition as per [24], and inner by k-ω, with better behavior on adverse pressure gradients.

The action mechanism of k-ω SST DDES is based on using the «switch» in a modified dissipation term (3):

$$\begin{gathered} \epsilon =-{\beta }^{*}k\omega \to {\beta }^{*}k\omega \cdot F_{DES}, \\ {F}_{DES}=\left[\max \left(\frac{L_t}{C_{DES}\Delta }\left(1-f_{DDES}\right),1\right)-1\right] \end{gathered}$$

(3)

where Δ—largest cell size (4):

$$\Delta =\max \left({\Delta }_x,{\Delta }_y,{\Delta }_z\right),$$

(4)

ƒ_DDES—shielding function and L_t is the turbulent length scale (5):

$$L_t=\frac{\sqrt{k}}{{\beta }^{*}\cdot \omega },$$

(5)

Thus, when ƒ_DDES = 0 and/or C_DESΔ > L_t, the solution is obtained by means of RANS. Otherwise, Large Eddy Simulation is used.

2.2. Studied Geometry

The geometry under study is a HAWT weather vane (Figure 1) of the following size: 0.25 m × 0.02 m × 0.06 m. Since the bottom part of the vane rack does not influence torque occurrence but generates an additional turbulence that complicates calculation, it was decided not to consider it in the numerical simulation.

2.3. Mesh Preparation

The finite volume method starts from dividing the study area into simple geometric shapes. The structure of the cells to be analyzed by computer has a setting with a simple function inside each. Thus the more cells, the more accurate the calculation is. At the same time, the growth in the number of cells is accompanied by an increase in time and cost of computer resources. When working with CFD, the problem often appears in the determination of optimal ratio between the accuracy of solution and the resources spent to obtain it. The following description presents the process of generating optimal mesh for simulation.

2.3.1. Mesh Regions’ Description

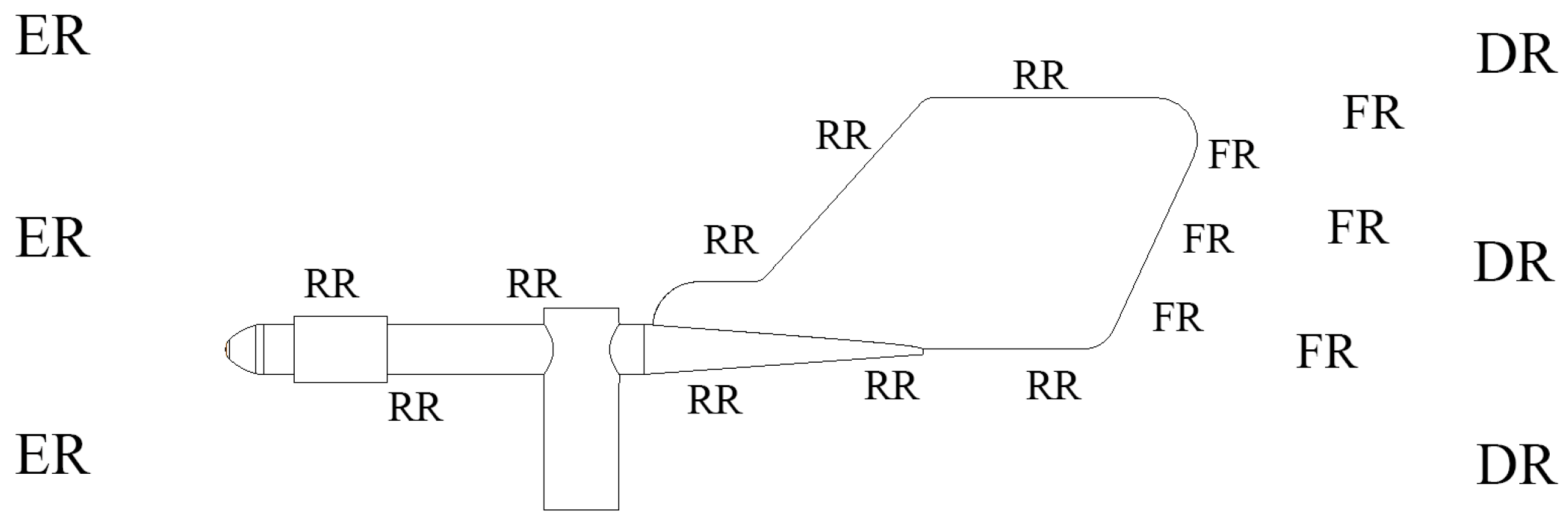
According to [25], it is advisable to highlight zones where the proper mesh should be generated in all of them. The geometry can then be analyzed, identifying the corresponding zones, as shown in Figure 2.

The Euler region (ER) is a place with almost no disturbance of the flow, so there is no need for a dense mesh. The RANS region (RR) incudes viscous and outer regions (not indicated due to their small sizes). This part has the same mesh requirements as basic RANS modeling faces. As soon as the disturbance of flow caused by obstacles appears, the LES region (LR) is involved. LES region consists of Focus region (FR) and Departure (DR) region. FR is a zone of high turbulence because of strong separation effects. To achieve a good resolution in all mesh directions, the cells in FR should be of a cubic form. DR is an extension of FR and does not require 100% of turbulence structures to be resolved; thus, the mesh is incremented, allowing RANS to be switched on.

2.3.2. Hybrid Approach

The mesh model for the flow streaming around the weather vane is difficult to study using hexahedral cells, i.e., structured mesh. That is why a hybrid mesh was used for the current study.

The hybrid mesh (Figure 3) represents a tetrahedral mesh with prismatic layer in the geometrical area to be studied, and hexahedral mesh in the rest of the region. To create this mesh, the computational domain was divided into blocks, in which the mesh sizes were set according to the region types (Figure 2).

2.3.3. Boundary Layer

Meshes required for implementation of DDES in the near-wall region, coincide with meshes required for solving the RANS equations. They are considerably larger than the meshes needed for calculating a small near-wall vortices in the framework of LES. Thus, the preparation of mesh in the near-wall region was made according to RANS concept.

The thickness of the boundary layer (BL) was calculated using the Schlichting Formula (6) for a developed turbulent BL and was further used to create the inflation layer.

$$\begin{gathered} h=0.37\cdot l\cdot \left(\frac{1}{{\mathrm{Re}}_L{}^{\frac{1}{5}}}\right), \\ \mathrm{Re}=U_{\infty }\cdot l\cdot \frac{\rho }{\mu } \end{gathered}$$

(6)

where $U_{\infty }$—stream velocity, l—characteristic size, ρ—air density equal to 1.225 kg/m³, $\mu$—dynamic viscosity is 1.85 × 10⁻⁵ kg/m s.

To ensure the required value of y⁺ = 1 (location of the first cell in viscous sublayer), thickness of first near-wall cell was calculated using formula (7):

$$\Delta y=\frac{y^{+}\mu }{\rho U_{\tau }},$$

(7)

where $U_{\tau }$—friction velocity (8):

$$U_{\tau }=\sqrt{\frac{{\tau }_{\omega }}{\rho }},$$

(8)

where τ_ω—wall shear stress (9):

$${\tau }_w=0.5\cdot C_f\cdot \rho \cdot U_{\infty }{}^2,$$

(9)

2.4. Spatial Resolution

Mesh resolution has crucial influence on the accuracy of the calculation results as reported in [26,27,28]. To create a mesh with good resolution, it is necessary to conduct a preliminary RANS simulation. This also provides valuable data, such as pressure and velocity fields for subsequent transient simulation, accelerating final calculations. Thus, all steady simulations are performed until convergence reaches value 1 × 10⁻⁴ of residuals and stabilization of monitored values, such as mass flow rate on outlet.

In accordance with the recommendation of Pope in [29], about 80% of resolved turbulence kinetic energy (TKE) should be achieved for better quality of solution. According to Young-Person’s Guide [25], it is necessary to have at least 5 cells on turbulent length scale (5) to resolve such level of turbulent kinetic energy.

As a result, a finite volume mesh was iteratively refined in weather vane bounded area to have at least 5 cells per L_t in FR volume. Changing resolution fields with mesh refinement for AoA = 15° case can be seen in Figure 4.

As can be seen from Figure 4, it was not possible to achieve 100% coverage of FR mesh with the required resolution. The tail stall region near wall has low resolution, which should not affect further simulation due to calculation of a near-wall layer by RANS k-ω SST forces. Rest of FR has resolution of about required value of 5. The same preparation of mesh was fulfilled for all other cases.

2.5. Temporal Resolution

It should be noted that temporal resolution has to match the spatial one. The Courant–Friedrichs–Lewy condition (10) is used to evaluate the correctness of chosen time step in transient calculations:

$$C=\frac{U_{\infty }\cdot \Delta t}{\Delta x},$$

(10)

where $U_{\infty }$—magnitude of velocity, Δt—is time step, Δx—characteristic length, equal to the pitch of mesh at the trailing edge of weather vane.

The value of Courant number is equal to 1, which means that one time step particle motion corresponds to one mesh step. An acceptable estimation of Courant number for calculations of complex aerodynamics is considered to be a value that does not exceed ‘1′ in FR. According to this assessment, the integration step was set up during the simulation to achieve the required Courant–Friedrichs–Lewy CFL level.

The total time of each simulation was 5 complete passes of the air mass through the computational domain. The observed values were averaged for the last two passes.

2.6. Boundary Conditions

The domain of 2 m × 0.5 m × 0.5 m size includes both inlet and outlet. The study was made at flow rate of 10 m/s from inlet since this speed is optimal for the operation of most megawatt-class HAWTs. A zero-pressure outlet was used with a reverse flow from neighborhood-cell condition turned on to enhance a solver robustness. No-slip wall condition, applied for all walls, implies a zero roughness.

2.7. Monitors Setup

The axial torque was monitored during simulation. To monitor the convergence, in addition to the residuals and CFL in FR, stabilization of the mass flow rate was monitored through outlet.

3. Experimental Research

The experimental study was performed using a small-size aerodynamic pipe (Figure 5a). The air flow is moved in a closed looped tunnel, driven by centrifugal fan (1). The wind tunnel has an open working area (2) with the following dimensions: 300 mm × 300 mm × 250 mm. The open working area ensures the constancy of the total pressure and eliminates the influence of the walls on the measured characteristics, which contributes to the similarity of the experimental conditions and real object. This pipe was calibrated by measuring the wind speed at 9 cross-sectional positions (Figure 5b) using a telescopic anemometer probe (Figure 5c). The required air flow velocity was achieved by changing the rotation speed of the suction turbine by frequency controller. The torque (force) on the vane shaft was measured by strain gauge providing accuracy up to 0.01 g. The reading frequency was set to 1 kHz.

Next, the results and discussion are presented to finalize the research.

4. Results and Discussion

Validation of the spatial resolution starts with an evaluation of the Yplus value on the weather vane’s surface.

Table 1. Yplus, Courant–Friedrichs–Lewy number and turbulence kinetic energy ratio in Focus Region distribution.

AoA	Yplus			CFL in FR			TKE Ratio
	Min	Max	Face Avg.	Min	Max	Face Avg.	FR Avg.
0°	0.021	0.846	0.328	0.300	7.795	0.699	89.1%
5°	0.032	0.941	0.366	0.273	8.342	0.718	65.4%
10°	0.037	1.056	0.395	0.229	9.029	0.726	64.5%
15°	0.042	0.961	0.400	0.258	9.390	0.961	49%
20°	0.057	1.07	0.435	0.246	6.825	0.855	51%
45°	0.065	1.082	0.440	0.137	7.475	1.052	71%

consists of Yplus data for all cases studied in this work. The readings satisfy the following condition: the first near-wall cell enters the viscous sublayer, excluding the usage of near-wall functions by the solver.

The second part of the table shows the values of the Courant number in the FR. During the simulation, the size of the time step was adjusted depending on the volume-averaged CFL. As the angle of attack increases, the CFL increases as well, so a reduction in the time step corresponding to the design case is required. Compliance with the requirements for the CFL value was achieved on optimized meshes with a gradual decrease in the time step from 1 × 10⁻³ to 1 × 10⁻⁴.

In the obtained data, there is a sharp increase in the volume-averaged Courant number at a 15 degrees angle of attack, and a slight decrease at 20 degrees. This phenomenon can be explained by the transition from a near-separated flow around to a developed turbulent one at an AoA = 45°, with periodic stall (lower and upper edges with swirling vortex shedding, absent in the k-ω SST case), which disappears with an increase in the angle of attack, turning to a stable one over the entire surface of the weather vane (Figure 6).

The next point in the validation of the spatial resolution is to determine the level of resolved TKE. As was previously noted, it is advisable for this to be higher than 80%, which is indicated to achieve good quality of the simulation. The level of resolved turbulence was estimated by calculating the ratio of the resolved turbulence k_res to the sum of the resolved and modeled components in the FR.

The reduced percentage of TKE resolution was probably obtained due to the inaccurate preliminary estimation of the spatial resolution when creating the mesh due to the non-100% correspondence of the shape of the cells to the cube. However, the used meshes give a relatively high level of resolution, and the resulting moment values are in good compliance with the experimental values (Figure 7).

In addition to the above-described validation steps, an integral error was determined in accordance with the methodology presented in [30,31]. The calculation took into account the usage of the second-order scheme and a maximum error level of 1%. The results are summarized in

Table 2. Accumulated error and reliability estimation for calculated cases.

AoA	Accumulated Error, %	$\mathbf{Reliability} \left(\frac{{\mathit{n}}_{\mathbf{max}}}{\mathit{n}}\right)$
0	8.73333 × 10−5	17,481.5
5	6.5029 × 10−5	31,530.06
10	6.5029 × 10−5	31,530.06
15	5.13081 × 10−5	50,648.49
20	5.13081 × 10−5	50,648.49
45	4.02481 × 10−5	82,309.1

.

According to the results obtained, it can be argued that the accumulated error is small, and due to the high value of reliability (ratio of maximum allowable number of time steps to actual number), the numerical simulation can be significantly extended without the significant impact of errors, if necessary.

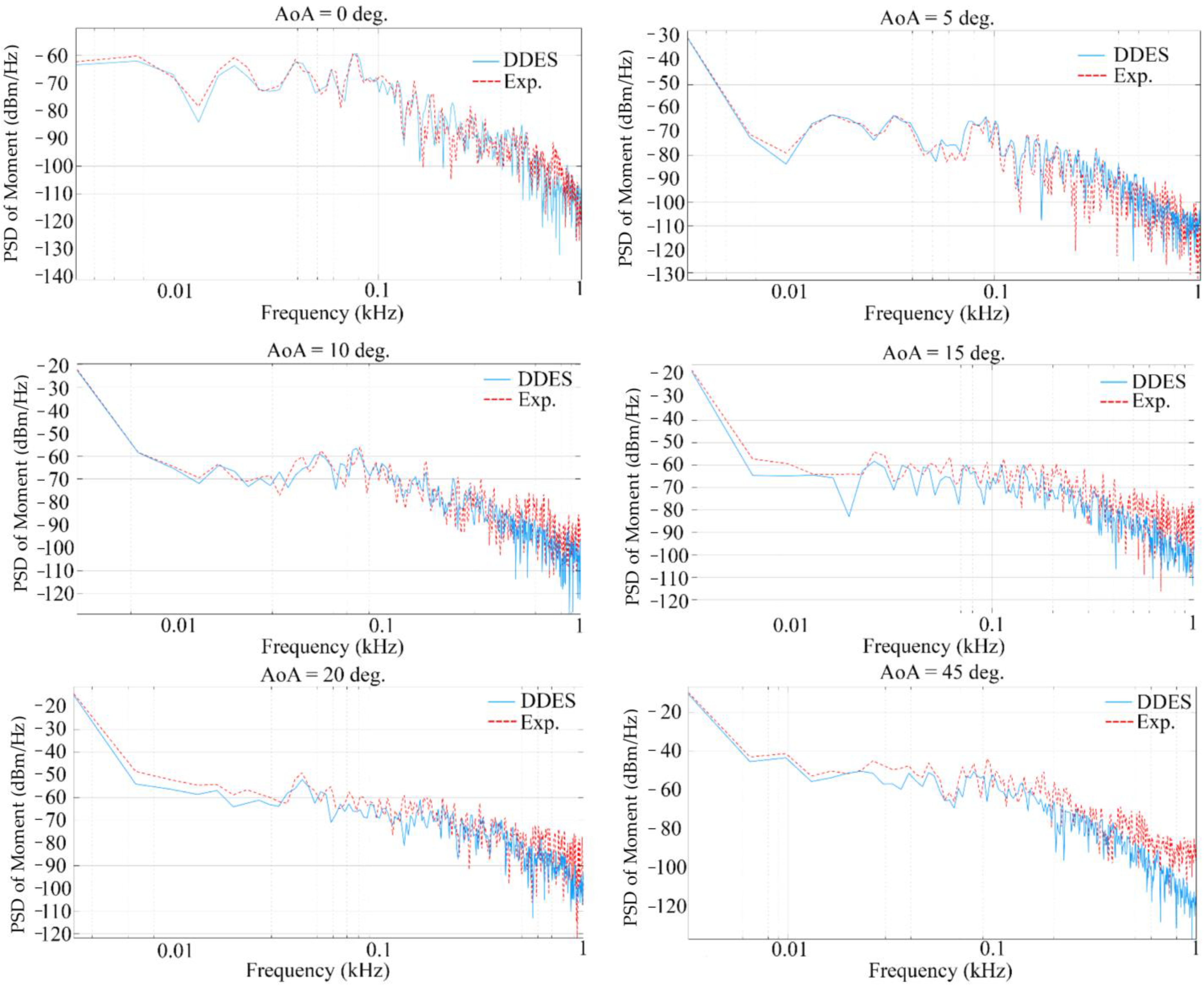
For the analysis of the experimental and numerical data, power spectral density (PSD) graphs were obtained using Welch’s method (Figure 8). The comparison showed the similarity in the frequencies of weather vane oscillations caused by the shedding of vortices with different kinetic energies, which indicates the similarity in the aerodynamics of the vortices simulated in CFD and obtained from the experiment. For the cases requiring most computation, the biggest difference is observed in the high-frequency spectrum (100–1000 Hz) with low amplitude, which in numerical simulation corresponds to frequencies of the smallest eddies modeled by the subgrid model. According to the Kolmogorov turbulent cascade, these vortices have low energy and do not strongly affect the characteristics. For angles of attack of 10, 15, 20 and 45 degrees, there is a noticeable increasing the difference in the mid-frequency part of the spectrum (10–100 Hz). In the low-frequency spectrum, the greatest deviation is observed for angles of 15 and 20 degrees, and the angle of attack of 45 degrees shows a smaller level of deviation. Thus, the obtained differences in the averaged values are explained by the differences in low- and mid-frequency spectra. It is also necessary to take into account the influence of the flow pulsations in the wind tunnel due to the open type of working area. The pulsations introduce additional fluctuations to the kinetic energy of the flow, which in turn affects the shape of the boundary layer and the subsequent difference in aerodynamic characteristics. From the CFD point of view, the error can be explained by the insufficient resolution of the grid, and as a consequence, by the lowered turbulent kinetic energy ratio. To obtain similar PSDs in these areas, a significant mesh refinement and decrease in time step are required, which transfers the simulation into the DNS class.

In addition, an assessment of the time spent on the preparation and calculation of the numerical experiment and the full-scale one was performed during the study. The DDES preparation time consists of three main steps.

The first stage is the preparation of the geometry. In the case of RANS and DDES, it takes the same time and directly depends on its complexity.

At the second stage, the finite volume mesh is prepared. RANS requires a mesh independence test, which requires several meshes with different densities. To prepare the final DDES mesh, it is not advisable to perform mesh independence tests due to excessive time costs. In this study, we applied a method, according to which the optimal mesh resolution was obtained based on the results of preliminary RANS modeling with successive mesh refinement in FR. As noted above, the preliminary RANS simulations also allow speeding up of the DDES. Thus, the preparation of the final mesh requires approximately the same refinement steps, but for DDES, this procedure is associated with a large number of operations.

The third stage is the simulation. DDES, compared to RANS k-ω SST, requires several thousand time steps to obtain statistically averaged values, each of which converge to the required level of residuals for several iterations per time step. Steady-state aerodynamic performance in RANS rarely requires more than 500 iterations. It is important to note the need to monitor the Courant number in the FR for DDES, setting the time step according to the observed values.

The value of the time costs that cannot be estimated includes the time of loading the results for processing in a postprocessor, which is significantly higher for DDES due to the larger amount of data.

The final distribution of time costs in the preparation of one design case is summarized in

Table 3. Reynolds-averaged Navier–Stokes and Delayed Detached Eddy Simulation time costs single case.

Stage №	RANS k-ω SST (h)	DDES (h)
1	3	3
2	7	10
3	5	26
Total:	15	39 (+260%)

.

5. Conclusions

In this paper, the numerical simulation of the weather vane of a horizontal axis wind turbine was performed to obtain the most accurate aerodynamic characteristics at the lowest possible computational costs. To assess the numerical approach, the previous works in this area, related to Detached Eddy Simulation and its modifications, were analyzed. Studies on the geometry of simple and medium complexity have shown the advantage of using Detached Eddy Simulation modification. Unfortunately, in these works, the stage of the preparation of computational grids, as well as the numerical experiment itself, was overlooked or poorly detailed. To fill up the research gap, the Delayed Detached Eddy Simulation was used. It was prepared in accordance with the recommendations given in the literature, using new techniques for the preparation of numerical modeling: a hybrid grid, validation with the study of the degree of resolution of the grids with further iterative correction of low-quality regions. The analysis of the simulation of weather vane aerodynamics showed a positive result in general. The following are the key findings:

• When creating a finite volume mesh for the design case where the angle of attack = 5°, the required resolution was achieved on sufficiently large grids (5 and 5 cells compared to 1 and 6 at angle of attack = 10°). The presence of large stall zones leads to significant increases in mesh density (2 and 6 cells for angle of attack = 45°).
• The largest deviations from the experimental values were obtained for calculated cases at 15 and 20 degrees with the worst turbulence kinetic energy resolution values. However, the error did not exceed 10%, so the recommendation about the need for 80% turbulence kinetic energy resolution can be revised towards lower values to save resources.
• A significant difference in aerodynamic coefficients between Delayed Detached Eddy Simulation and k-w Shear Stress Transport is noticeable starting from low angles of attack because for bluff bodies, the rate of formation of turbulent structures does not allow a second model to adequately reflect the aerodynamics of the studied geometry. The use of the Reynolds-averaged Navier–Stokes to obtain aerodynamic coefficients is reasonable in the absence of strong vortex formation only.
• Delayed Detached Eddy Simulation requires more time to prepare a mesh, and set up and run the simulation. The preparation and calculation of just one case takes approximately 2.5 to 4 times longer than Reynolds-averaged Navier–Stokes. The usage of Delayed Detached Eddy Simulation for urgent applications remains questionable.

The current increase in computer performance leads to the fact that computing power at the moment can allow partial transition to hybrid approaches in aerodynamic calculations of medium complexity. Thus, the modeling approach considered in this article, as well as the results obtained and the conclusions drawn, can already be applied in the engineering practice of numerical modeling for the renewable energy, aircraft and architecture industries.

At the end of this conclusion, it has to be noted that although Delayed Detached Eddy Simulation is more expensive both in terms of preparation and computing resources, the shortcomings can be neglected when using the recommendations of the developers and the described preparation methodology.

Further research of authors can be directed towards a mathematical modeling of yaw control dynamic systems with the usage of the gained results to improve the yaw error compensators algorithms.