Novel Algorithms with Inertial Techniques for Solving Constrained Convex Minimization Problems and Applications to Image Inpainting

Abstract

In this paper, we propose two novel inertial forward–backward splitting methods for solving the constrained convex minimization of the sum of two convex functions, ${\phi }_1+{\phi }_2,$ in Hilbert spaces and analyze their convergence behavior under some conditions. For the first method (iFBS), we use the forward–backward operator. The step size of this method depends on a constant of the Lipschitz continuity of $\nabla {\phi }_1,$ hence a weak convergence result of the proposed method is established under some conditions based on a fixed point method. With the second method (iFBS-L), we modify the step size of the first method, which is independent of the Lipschitz constant of $\nabla {\phi }_1$ by using a line search technique introduced by Cruz and Nghia. As an application of these methods, we compare the efficiency of the proposed methods with the inertial three-operator splitting (iTOS) method by using them to solve the constrained image inpainting problem with nuclear norm regularization. Moreover, we apply our methods to solve image restoration problems by using the least absolute shrinkage and selection operator (LASSO) model, and the results are compared with those of the forward–backward splitting method with line search (FBS-L) and the fast iterative shrinkage-thresholding method (FISTA).

1. Introduction and Preliminaries

In this study, $\mathbb{N}$ and $\mathbb{R}$ denote the set of all positive integers and the set of all real numbers, respectively. Let $\mathcal{H}$ be a real Hilbert space and $Id:\mathcal{H}\to \mathcal{H}$ be the identity operator. The symbols → and ⇀ denote strong convergence and weak convergence, respectively.

The forward–backward splitting method is a popular method for solving the following convex minimization problems:

$$\underset{u\in \mathcal{H}}{min}{\psi }_1\left(u\right)+{\psi }_2\left(u\right),$$

(1)

where ${\psi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ is a convex proper lower semi-continuous function, ${\psi }_1:\mathcal{H}\to \mathbb{R}$ is a convex proper lower semi-continuous and differentiable function, and $\nabla {\psi }_1$ is Lipschitz continuous with constant L.

In 2005, Combettes and Wajs [1] proposed a relaxed forward–backward splitting method as follows:

$$u^{k+1}=u^k+{\beta }_k({prox}_{{\lambda }_k{\psi }_2}(u^k-{\lambda }_k\nabla {\psi }_1\left(u^k\right))-u^k),\forall k\in \mathbb{N},$$

where $u^1\in {\mathbb{R}}^N,$$a\in (0,min(1,\frac{1}{L})),$${\lambda }_k\in [a,\frac{2}{L}-a]$, and ${\beta }_k\in [a,1]$.

In 2016, Cruz and Nghia [2] presented a technique for selecting the stepsize ${\lambda }_k$ that is independent of the Lipschitz constant of $\nabla {\psi }_1$ by using line search process as follows:

We denote ${\mathrm{Linesearch}}_{({\psi }_1,{\psi }_2)}(u,\sigma ,\theta ,\delta )$ as Algorithm 1 with respect to the functions ${\psi }_1$ and ${\psi }_2$ at $u.$ The forward–backward splitting method, FBS-L, where the stepsize ${\lambda }_k$ is generated using Algorithm 1, is as follows:

$$u^{k+1}={prox}_{{\lambda }_k{\psi }_2}(u^k-{\lambda }_k\nabla {\psi }_1\left(u^k\right)),\forall k\in \mathbb{N},$$

where $u^1\in \mathcal{H}$, $\theta \in (0,1),\sigma >0$, $\delta \in (0,\frac{1}{2})$ and ${\lambda }_k:={\mathrm{Linesearch}}_{({\psi }_1,{\psi }_2)}(u^k,\sigma ,\theta ,\delta ).$

Algorithm 1 Let  $u\in \mathcal{H},\theta \in (0,1),\sigma >0$ and $\delta >0.$

Input $\lambda =\sigma .$       While $$\lambda \parallel \nabla {\psi }_1\left({prox}_{\lambda {\psi }_2}(Id-\lambda \nabla {\psi }_1)\left(u\right)\right)-\nabla {\psi }_1\left(u\right)\parallel >\delta \parallel {prox}_{\lambda {\psi }_2}(Id-\lambda \nabla {\psi }_1)\left(u\right)-u\parallel ,$$       do                $\lambda =\theta \lambda .$       End Output $\lambda .$

Inertial techniques are applied in order to speed up the forward–backward splitting method. Various inertial techniques and fixed point methods have been studied, see [3,4,5,6,7,8] for example. Recently, Moudafi, and Oliny [9] introduced an inertial forward–backward splitting method as follows:

$$\begin{array}{cc}\hfill u^{k+1}& ={prox}_{{\lambda }_k{\psi }_2}((u^k+{\alpha }_k(u^k-u^{k-1}))-{\lambda }_k\nabla {\psi }_1(u^k+{\alpha }_k(u^k-u^{k-1}))),\forall k\in \mathbb{N},\hfill \end{array}$$

where $u^0,u^1\in \mathcal{H},$${\lambda }_k\in (0,\frac{2}{L}),$${\alpha }_k\in [0,1).$ The ${\alpha }_k,$ an inertial parameter, controls the momentum $u^k-u^{k-1}.$ In 2009, Beck and Teboulle [3] proposed a fast iterative shrinkage-thresholding algorithm (FISTA) for solving the convex minimization problems, Problem (1) and they also generated the sequence $\left\{u^k\right\}$ as follows:

$$\begin{array}{cc}\hfill y^k& ={prox}_{\frac{1}{L}{\psi }_2}(Id-\frac{1}{L}\nabla {\psi }_1)\left(u^k\right),\hfill \\ \hfill t_{k+1}=\frac{1+\sqrt{1+4t_k^2}}{2},& u^{k+1}=y^k+\left(\frac{t_k-1}{t_{k+1}}\right)(y^k-y^{k-1}),k\in \mathbb{N},\hfill \end{array}$$

when $t_1=1,u^1=y^0\in \mathcal{H}.$

Recently, Cui et al. proposed an inertial three-operator splitting (iTOS) method [10] for solving the following general convex minimization problems:

$$\underset{u\in \mathcal{H}}{min}{\psi }_1\left(u\right)+{\psi }_2\left(u\right)+{\psi }_3\left(u\right),$$

(2)

where ${\psi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ and ${\psi }_3:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ are the convex proper lower semi-continuous functions, ${\psi }_1:\mathcal{H}\to \mathbb{R}$ is the convex proper lower semi-continuous and differentiable function, and $\nabla {\psi }_1$ is Lipschitz continuous with constant L. The iTOS method is defined by the following:

$$\begin{array}{cc}{v}^k\hfill & =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \\ u_{{\psi }_3}^k\hfill & ={prox}_{\lambda {\psi }_3}{v}^k;\hfill \\ u_{{\psi }_2}^k\hfill & ={prox}_{\lambda {\psi }_2}(2u_{{\psi }_3}^k-v^k-\lambda \nabla {\psi }_1\left(u_{{\psi }_3}^k\right));\hfill \\ u^{k+1}\hfill & =v^k+{\beta }_k(u_{{\psi }_2}^k-u_{{\psi }_3}^k),\forall k\in \mathbb{N},\hfill \end{array}$$

(3)

where $u^0,u^1\in \mathcal{H},$$\lambda \in (0,\frac{2}{L}\epsilon ),$$\epsilon \in (0,1),$$\left\{{\alpha }_k\right\}$ is non-decreasing, $0\le {\alpha }_k\le d<1$ and $\forall k\ge 1,$ and $a,b,c>0$ such that

$$c>\frac{d^2(1+d)+db}{1-d^2}\mathrm{and}0<a\le {\beta }_k\le \frac{c-d\left[d\right(1+d)+dc+b]}{\overline{d}c[1+d(1+d)+dc+b]},\mathrm{where}\overline{d}=\frac{1}{2-\epsilon }.$$

They proved the convergence of the iTOS method and applied the method to solve the constrained image inpainting problem as follows:

$$\underset{u\in \mathcal{C}}{min}{\displaystyle \frac{1}{2}}\parallel \mathcal{A}(u-u^0){\parallel }_F^2+\tau {\parallel u\parallel }_{*},$$

(4)

where u is the matrix of known entries $\mathcal{A}\left(u^0\right),$$u^0\in {\mathbb{R}}^{m\times n},$ $\mathcal{A}$ is the linear map that selects a subset of the entries of an $m\times n$ matrix by setting each unknown entry in the matrix to $0,$ and $\mathcal{C}$ is the nonempty closed convex subset of ${\mathbb{R}}^{m\times n}.$ The regularization parameter is $\tau >0,$ ${\parallel ·\parallel }_{*}$ is the nuclear matrix norm, and ${\parallel ·\parallel }_F$ is the Frobenius matrix norm. The constrained image inpainting problem, Problem (4), is equivalent to the following unconstrained image inpainting problem:

$$\underset{u}{min}{\displaystyle \frac{1}{2}}\parallel \mathcal{A}(u-u^0){\parallel }_F^2+\tau {\parallel u\parallel }_{*}+{\delta }_{\mathcal{C}}\left(u\right),$$

(5)

when ${\delta }_{\mathcal{C}}$ is the indicator function.

In this paper, we introduce two novel inertial forward–backward splitting methods for solving the following constraint convex minimization problems:

$$\underset{u\in \mathrm{Argmin}({\psi }_1+{\psi }_2)}{min}{\phi }_1\left(u\right)+{\phi }_2\left(u\right),$$

(6)

where ${\phi }_1:\mathcal{H}\to \mathbb{R},{\psi }_1:\mathcal{H}\to \mathbb{R},{\psi }_1:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ and ${\psi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ are convex proper lower semi-continuous functions. Note that $u^{*}$ is a solution to problem (6) if it satisfies the common minimizers of the following convex minimization problems:

$$\underset{u\in \mathcal{H}}{min}{\phi }_1\left(u\right)+{\phi }_2\left(u\right),\mathrm{and}\underset{u\in \mathcal{H}}{min}{\psi }_1\left(u\right)+{\psi }_2\left(u\right).$$

(7)

Then, we prove the weak convergence of the proposed methods by using the fixed point method and line search technique, respectively. Moreover, we apply our methods for solving constrained image inpainting problem, Problem (4), and compare the performance of our methods with the iTOS method (3).

The basic definitions and Lemmas needed for our paper are let $\psi :\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ be a convex proper lower semi-continuous function. The proximal operator [11,12] of $\psi$, denoted by ${prox}_{\psi }$ is defined for each $u\in \mathcal{H}$, ${prox}_{\psi }u$ is the unique solution of the minimization problem:

$$\underset{z\in \mathcal{H}}{\mathrm{minimize}}\psi \left(z\right)+\frac{1}{2}{\parallel u-z\parallel }^2.$$

(8)

The equivalent form of the proximity operator of $\psi$ from $\mathcal{H}$ to $\mathcal{H}$ can be written as:

$${prox}_{\psi }={(Id+\partial \psi )}^{-1},$$

(9)

when the subdifferential of $\psi$ defined by

$$\partial \psi \left(v\right):=\{u\in \mathcal{H}:\psi (v)+⟨u,z-v⟩\le \psi (z),\forall z\in \mathcal{H}\},\forall v\in \mathcal{H}.$$

We notice that ${prox}_{{\delta }_{\mathcal{C}}}={\mathbb{P}}_{\mathcal{C}},$ when $\mathcal{C}$ is the nonempty closed convex subset of $\mathcal{H}$ and ${\mathbb{P}}_{\mathcal{C}}:\mathcal{H}\to \mathcal{C}$ is the orthogonal projection operator. The following useful fact is also needed:

$$\frac{u-{prox}_{\lambda \psi }\left(u\right)}{\lambda }\in \partial \psi \left({prox}_{\lambda \psi }\left(u\right)\right),\forall u\in \mathcal{H},\lambda >0.$$

(10)

If ${\psi }_1$ is differentiable in $\mathcal{H},$ the solution of the convex minimization problem, Problem (1), is a fixed point of the forward–backward operator, i.e.,

$$\begin{array}{c}\hfill u\in \mathrm{Argmin}({\psi }_1+{\psi }_2)\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}u=\underset{\mathrm{backward}\mathrm{step}}{\underbrace{{prox}_{\lambda {\psi }_2}}}\underset{\mathrm{forward}\mathrm{step}}{\underbrace{(Id-\lambda \nabla {\psi }_1)}}\left(u\right),\end{array}$$

where $\lambda >0.$ Note that the subdifferential operator $\partial \psi$ is a maximal monotone [13] and the operator ${prox}_{\lambda {\psi }_2}(Id-\lambda \nabla {\psi }_1)$ is a nonexpansive mapping where $\lambda \in (0,\frac{2}{L}).$

We consider the following class of Lipschitz continuous and nonexpansive mappings. A mapping $S:\mathcal{H}\to \mathcal{H}$ is said to be Lipschitz continuous if there exists $L>0$ such that

$$\parallel Su-Sv\parallel \le L\parallel u-v\parallel ,\forall u,v\in \mathcal{H}.$$

The mapping S is said to be nonexpansive if S is 1-Lipschitz continuous. If $u=Su,$ then a point $u\in \mathcal{H}$ is said to be fixed point of S The set of all fixed points of S is denoted by $\mathrm{Fix}\left(S\right).$

The mapping $Id-S$ is called demiclosed at zero if sequence $\left\{u^k\right\}$ in $\mathcal{H}$ such that $u^k\rightharpoonup u$, and $u^k-S{u}^k\to 0$ as $k\to \infty$, then $u\in \mathrm{Fix}\left(S\right)$. It is known that if S is a nonexpansive mapping, then $Id-S$ is demiclosed at zero [14]. Let $\{S_k:\mathcal{H}\to \mathcal{H}$ and $S:\mathcal{H}\to \mathcal{H}\}$ be such that $\varnothing \ne \mathrm{Fix}\left(S\right)\subseteq {\bigcap }_{k=1}^{\infty }\mathrm{Fix}\left(S_k\right)$. Then, $\left\{S_k\right\}$ is said to satisfy NST-condition (I) with S [15] if, for all bounded sequence $\left\{u^k\right\}$ in $\mathcal{H}$,

$$\underset{k\to \infty }{lim}\parallel u^k-S_k{u}^k\parallel =0\Rightarrow \underset{k\to \infty }{lim}\parallel u^k-S{u}^k\parallel =0.$$

A sequence $\left\{S_k\right\}$ is said to satisfy the condition (Z) [16,17] if $\left\{u^k\right\}$ is a bounded sequence in $\mathcal{H}$ such that

$$\underset{k\to \infty }{lim}\parallel u^k-S_k{u}^k\parallel =0,$$

it follows that every weak cluster point of $\left\{u^k\right\}$ belongs to ${\bigcap }_{k=1}^{\infty }\mathrm{Fix}\left(S_k\right)$. The following identity in $\mathcal{H}$ will be used in the paper (see [11]): for any $y,z\in \mathcal{H}$ and $\tau \in [0,1],$

$$\begin{array}{cc}\hfill {\parallel \tau y+(1-\tau )z\parallel }^2& ={\tau \parallel y\parallel }^2+{(1-\tau )\parallel z\parallel }^2-\tau (1-\tau ){\parallel y-z\parallel }^2,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\parallel y\pm z\parallel }^2& ={\parallel y\parallel }^2\pm 2⟨y,z⟩+{\parallel z\parallel }^2.\hfill \end{array}$$

(12)

Lemma 1

([4]). Let ${\psi }_1:\mathcal{H}\to \mathbb{R}$ be a convex and differentiable function such that $\nabla {\psi }_1$ is Lipschitz continuous with constant L and ${\psi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ be a convex proper lower semi-continuous function. Let $S_k:={prox}_{{\lambda }_k{\psi }_2}(Id-{\lambda }_k\nabla {\psi }_1)$ and $S:={prox}_{\lambda {\psi }_2}(Id-\lambda \nabla {\psi }_1)$, when $0<{\lambda }_k,\lambda <\frac{2}{L}$ with ${lim}_{k\to \infty }{\lambda }_k=\lambda .$ Then $\left\{S_k\right\}$ satisfies NST-condition (I) with S.

Lemma 2

([5]). Let $\left\{u^k\right\}$ and $\left\{{\alpha }_k\right\}$ be sequences of nonnegative real numbers such that

$$u^{k+1}\le (1+{\alpha }_k)u^k+{\alpha }_k{u}^{k-1},\forall k\in \mathbb{N}.$$

Then $u^{k+1}\le \mathcal{N}·{\prod }_{i=1}^k(1+2{\alpha }_i),\mathrm{when}\mathcal{N}=max\{u^1,u^2\}.$ Moreover, if ${\sum }_{k=1}^{\infty }{\alpha }_k<\infty ,$ then $\left\{u^k\right\}$ is bounded.

Lemma 3

([18]). If $\psi :\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ is a convex proper lower semi-continuous function, then the graph of $\partial \psi$ defined by $\mathrm{Gph}(\partial \psi ):=\left\{\right(u,v)\in \mathcal{H}\times \mathcal{H}:v\in \partial \psi (u\left)\right\}$ is demiclosed, i.e., if the sequence $\left\{(u^k,v^k)\right\}\subset \mathrm{Gph}(\partial \psi )$ satisfies that $u^k\rightharpoonup u$ and $v^k\to v,$ then $(u,v)\in \mathrm{Gph}(\partial \psi ).$

Lemma 4

([19]). Let ${\psi }_1$ and ${\psi }_2$ be convex proper lower semi-continuous functions from $\mathcal{H}$ to $\mathbb{R}\cup \{\infty \}.$ Then for all $u\in dom{\psi }_2$ and $c_2\ge c_1>0,$ we have

$$\begin{array}{cc}\hfill \frac{c_2}{c_1}\parallel u-{prox}_{c_1{\psi }_2}(Id-c_1\nabla {\psi }_1)\left(u\right)\parallel & \ge \parallel u-{prox}_{c_2{\psi }_2}(Id-c_2\nabla {\psi }_1)\left(u\right)\parallel \hfill \\ & \ge \parallel u-{prox}_{c_1{\psi }_2}(Id-c_1\nabla {\psi }_1)\left(u\right)\parallel .\hfill \end{array}$$

Lemma 5

([20]). Let $\left\{u^k\right\}$ and $\left\{v^k\right\}$ be sequences of nonnegative real numbers such that $u^{k+1}\le u^k+v^k,$$\forall k\in \mathbb{N}$. If ${\sum }_{k=1}^{\infty }{v}^k<\infty ,$ then ${lim}_{k\to \infty }{u}^k$ exists.

Lemma 6

([14,21]). Let $\left\{u^k\right\}$ be a sequence in $\mathcal{H}$ such that there exists a nonempty set $\mathsf{\Gamma }\subset \mathcal{H}$ satisfying:

(i)

For every $u^{*}\in \mathsf{\Gamma },$${lim}_{k\to \infty }\parallel u^k-u^{*}\parallel$ exists;

(ii)

${\omega }_w\left(u^k\right)\subset \mathsf{\Gamma },$ where ${\omega }_w\left(u^k\right)$ is the set of all weak-cluster points of $\left\{u^k\right\}.$

Then, $\left\{u^k\right\}$ converges weakly to a point in $\mathsf{\Gamma }.$

2. An Inertial Forward–Backward Splitting Method Based on Fixed Point Inertial Techniques

In this part, we propose an inertial forward–backward splitting method for finding common elements of the convex minimization problem, Problem (7), by using a fixed-point inertial technique and proving a weak convergence of the proposed method.

In the first part, we propose a fixed-point inertial method that approximates the common fixed point of two countable families of nonexpansive mappings. The details and assumptions of the iterative method are represented as:

(A1) 

$\{S_k:\mathcal{H}\to \mathcal{H}\}$ and $\{T_k:\mathcal{H}\to \mathcal{H}\}$ are two countable family of nonexpansive mappings which satisfy condition (Z);

(A2) 

$\mathsf{\Gamma }:={\cap }_{n=1}^{\infty }Fix\left(S_k\right)\cap {\cap }_{n=1}^{\infty }Fix\left(T_k\right)\ne \varnothing .$

Now, we prove the first convergence theorem for Algorithm 2.

Algorithm 2 A fixed-point inertial method.

Le $u^0,u^1\in \mathcal{H}.$ Choose $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\}$ and $\left\{{\gamma }_k\right\}.$        For $k=1,2,...$ do $$\begin{array}{cc}\hfill v^k& =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \end{array}$$ (13) $$\begin{array}{cc}\hfill w^k& =v^k+{\beta }_k(S_k{v}^k-v^k);\hfill \end{array}$$ (14) $$\begin{array}{cc}\hfill u^{k+1}& =(1-{\gamma }_k)S_k{w}^k+{\gamma }_k{T}_k{w}^k,\hfill \end{array}$$ (15)       end for.

Theorem 1.

Let $\left\{x_k\right\}$ be the sequence created by Algorithm 2. Suppose that the sequences $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\}$ and $\left\{{\gamma }_k\right\}$ satisfy the following conditions:

(C1) 

$0<a\le {\beta }_k\le b<1,0<c\le {\gamma }_k\le d<1$$\forall k\in \mathbb{N},$ for some $a,b,c,d\in \mathbb{R}$;

(C2) 

${\alpha }_k\ge 0,$$\forall k\in \mathbb{N}$ and ${\sum }_{k=1}^{\infty }{\alpha }_k<\infty .$

Then the following hold:

(i)

$\parallel u^{k+1}-u^{*}\parallel \le \mathcal{N}{\prod }_{j=1}^k(1+2{\alpha }_j),$ where $\mathcal{N}=max\{\parallel u^1-u^{*}\parallel ,\parallel u^2-u^{*}\parallel \}$ and $u^{*}\in \mathsf{\Gamma }.$

(ii)

$\left\{u^k\right\}$ converges weakly to some element in $\mathsf{\Gamma }.$

Proof. 

(i) Let $u^{*}\in \mathsf{\Gamma }.$ Using (13), we have

$$\parallel v^k-u^{*}\parallel \le \parallel u^k-u^{*}\parallel +{\alpha }_k\parallel u^k-u^{k-1}\parallel .$$

(16)

Using (14) and the nonexpansiveness of $S_k,$ we have

$$\parallel w^k-u^{*}\parallel \le (1-{\beta }_k)\parallel v^k-u^{*}\parallel +{\beta }_k\parallel S_k{v}^k-u^{*}\parallel \le \parallel v^k-u^{*}\parallel .$$

(17)

Using (15) and the nonexpansiveness of $S_k$ and $T_k,$ we obtain

$$\parallel u^{k+1}-u^{*}\parallel \le (1-{\gamma }_k)\parallel S_k{w}^k-u^{*}\parallel +{\gamma }_k\parallel T_k{w}^k-u^{*}\parallel \le \parallel w^k-u^{*}\parallel .$$

(18)

From (16)–(18), we get

$$\begin{array}{cc}\hfill \parallel u^{k+1}-u^{*}\parallel & \le \parallel w^k-u^{*}\parallel \hfill \\ \hfill & \le \parallel v^k-u^{*}\parallel \hfill \\ \hfill & \le \parallel u^k-u^{*}\parallel +{\alpha }_k\parallel u^k-u^{k-1}\parallel .\hfill \end{array}$$

(19)

This implies

$$\begin{array}{c}\hfill \parallel u^{k+1}-u^{*}\parallel \le (1+{\alpha }_k)\parallel u^k-u^{*}\parallel +{\alpha }_k\parallel u^{k-1}-u^{*}\parallel .\end{array}$$

(20)

Applying Lemma 2, we get $\parallel u^{k+1}-u^{*}\parallel \le \mathcal{N}·{\prod }_{j=1}^k(1+2{\alpha }_j),$ where $\mathcal{N}=max\{\parallel u^1-u^{*}\parallel ,\parallel u^2-u^{*}\parallel \}.$

(ii) We conclude that $\left\{u^k\right\}$ is bounded by condition (C2) and that $\left\{v^k\right\}$ and $\left\{w^k\right\}$ are also bounded. This implies ${\sum }_{k=1}^{\infty }{\alpha }_k\parallel u^k-u^{k-1}\parallel <\infty .$ Using (19) and Lemma 5, we obtain that ${lim}_{k\to \infty }\parallel u^k-u^{*}\parallel$ exists. Using (12) and (13), we obtain

$$\begin{array}{cc}\hfill \parallel v^k-u^{*}{\parallel }^2& \le \parallel u^k-u^{*}{\parallel }^2+{\alpha }_k^2\parallel u^k-u^{k-1}{\parallel }^2+2{\alpha }_k\parallel u^k-u^{*}\parallel \parallel u^k-u^{k-1}\parallel .\hfill \end{array}$$

(21)

Using (11), (14), (15), and the nonexpansiveness of $S_k$ and $T_k,$ we obtain

$$\begin{array}{cc}\hfill \parallel w^k-u^{*}{\parallel }^2& =(1-{\beta }_k)\parallel v^k-u^{*}{\parallel }^2+{\beta }_k\parallel S_k{v}^k-u^{*}{\parallel }^2-{\beta }_k(1-{\beta }_k){\parallel v^k-S_k{v}^k\parallel }^2\hfill \\ \hfill & \le \parallel v^k-u^{*}{\parallel }^2-{\beta }_k(1-{\beta }_k){\parallel v^k-S_k{v}^k\parallel }^2,\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill \parallel u^{k+1}-u^{*}{\parallel }^2& \le (1-{\gamma }_k)\parallel S_k{w}^k-u^{*}{\parallel }^2+{\gamma }_k\parallel T_k{w}^k-u^{*}{\parallel }^2-{\gamma }_k(1-{\gamma }_k){\parallel T_k{w}^k-S_k{w}^k\parallel }^2\hfill \\ \hfill & \le \parallel w^k-u^{*}{\parallel }^2-{\gamma }_k(1-{\gamma }_k){\parallel T_k{w}^k-S_k{w}^k\parallel }^2.\hfill \end{array}$$

(23)

From (21)–(23), we obtain

$$\begin{array}{cc}\hfill \parallel u^{k+1}-u^{*}{\parallel }^2& \le \parallel u^k-u^{*}{\parallel }^2+{\alpha }_k^2\parallel u^k-u^{k-1}{\parallel }^2+2{\alpha }_k\parallel u^k-u^{*}\parallel \parallel u^k-u^{k-1}\parallel \hfill \\ \hfill & -{\gamma }_k(1-{\gamma }_k)\parallel T_k{w}^k-S_k{w}^k{\parallel }^2-{\beta }_k(1-{\beta }_k){\parallel v^k-S_k{v}^k\parallel }^2.\hfill \end{array}$$

(24)

From (24) and by condition (C1), ${\sum }_{k=1}^{\infty }{\alpha }_k\parallel u^k-u^{k-1}\parallel <\infty$ and ${lim}_{k\to \infty }\parallel u^k-u^{*}\parallel$ exists, we have

$$\underset{k\to \infty }{lim}\parallel T_k{w}^k-S_k{w}^k\parallel =\underset{k\to \infty }{lim}\parallel v^k-S_k{v}^k\parallel =0\mathrm{and}\mathrm{also}\underset{k\to \infty }{lim}\parallel w^k-v^k\parallel =0.$$

(25)

From (25), we obtain

$$\begin{array}{cc}\hfill \parallel T_k{w}^k-w^k\parallel & \le \parallel T_k{w}^k-S_k{w}^k\parallel +\parallel S_k{w}^k-S_k{v}^k\parallel +\parallel S_k{v}^k-v^k\parallel +\parallel v^k-w^k\parallel \hfill \\ \hfill & \le \parallel T_k{w}^k-S_k{w}^k\parallel +2\parallel w^k-v^k\parallel +\parallel S_k{v}^k-v^k\parallel \to 0\mathrm{as}k\to \infty .\hfill \end{array}$$

(26)

From (13) and ${\sum }_{k=1}^{\infty }{\alpha }_k\parallel u^k-u^{k-1}\parallel <\infty$, we have

$$\parallel v^k-u^k\parallel ={\alpha }_k\parallel u^k-u^{k-1}\parallel \to 0\mathrm{as}k\to \infty .$$

(27)

Since $\left\{u^k\right\}$ is bounded, we obtain ${\omega }_w\left(u^k\right)$ as nonempty. Using (25) and (27), we get ${\omega }_w\left(u^k\right)\subseteq {\omega }_w\left(v^k\right)\subseteq {\omega }_w\left(w^k\right).$ Since $\left\{S_k\right\}$ and $\left\{T_k\right\}$ satisfy the condition (Z), ${lim}_{k\to \infty }\parallel v^k-S_k{v}^k\parallel =0$ and ${lim}_{k\to \infty }\parallel w^k-T_k{w}^k\parallel =0,$ we have ${\omega }_w\left(v^k\right)\subseteq {\cap }_{n=1}^{\infty }Fix\left(S_k\right)$ and ${\omega }_w\left(w^k\right)\subseteq {\cap }_{n=1}^{\infty }Fix\left(T_k\right),$ respectively. So, we get ${\omega }_w\left(u^k\right)\subseteq {\cap }_{n=1}^{\infty }Fix\left(S_k\right)\cap {\cap }_{n=1}^{\infty }Fix\left(T_k\right).$ Using Lemma 6, we conclude that $\left\{u^k\right\}$ converges weakly to a point in $\mathsf{\Gamma }.$ This completes the proof.    □

Remark 1.

Assuming that $S_k=T_k$ for all $k\ge 1,$ the iterative Algorithm 2 becomes the following Algorithm 3:

Algorithm 3 The inertial Picard–Mann hybrid iterative process.

Let $u^0,u^1\in \mathcal{H}.$ Choose $\left\{{\alpha }_k\right\}$ and $\left\{{\beta }_k\right\}.$        For $k=1,2,...$ do $$\begin{array}{cc}\hfill v^k& =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \\ \hfill u^{k+1}& =S_k(v^k+{\beta }_k(S_k{v}^k-v^k)).\hfill \end{array}$$        end for.

Remark 2.

If ${\alpha }_k$ and $S_k=S$ for all $k\ge 1,$ the inertial Picard–Mann hybrid iterative process (Algorithm 3) is reduced to Picard–Mann hybrid iterative process [22].

We are presently in a position to state the inertial forward–backward splitting method and show its convergence properties. We set the standing assumptions used in this method as follows:

(D1) 

${\phi }_1:\mathcal{H}\to \mathbb{R}$ and ${\psi }_1:\mathcal{H}\to \mathbb{R}$ are differentiable and convex functions;

(D2) 

$\nabla {\phi }_1$ and $\nabla {\psi }_1$ are Lipschitz continuous with constants $L_1$ and $L_2,$ respectively;

(D3) 

${\phi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ and ${\psi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ are convex proper lower semi-continuous functions;

(D4) 

$\mathsf{\Theta }:=\mathrm{Argmin}({\phi }_1+{\phi }_2)\cap \mathrm{Argmin}({\psi }_1+{\psi }_2)\ne \varnothing .$

Remark 3.

Let $S_k:={prox}_{{\lambda }_k{\phi }_2}(Id-{\lambda }_k\nabla {\phi }_1)\mathrm{and}S:={prox}_{\lambda {\phi }_2}(Id-\lambda \nabla {\phi }_1).$ If $0<{\lambda }_k,\lambda <\frac{2}{L_1},$ then $S_k$ and S are nonexpansive mappings with $\mathrm{Fix}\left(S\right)=\mathrm{Argmin}({\psi }_1+{\psi }_2)={\bigcap }_{k=1}^{\infty }\mathrm{Fix}\left(S_k\right).$ Moreover, if ${\lambda }_k\to \lambda ,$ by Lemma 1, we obtain that $\left\{S_k\right\}$ satisfies NST-condition (I) with S.

Now, we prove the convergence theorem of Algorithm 4.

Algorithm 4 An inertial forward–backward splitting (iFBS) method.

Let $u^0,u^1\in \mathcal{H}.$ Choose $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\},\left\{{\gamma }_k\right\},\left\{{\lambda }_k\right\}$ and $\left\{{\lambda }_k^{*}\right\}.$        For $k=1,2,...$ do $$\begin{array}{cc}\hfill v^k& =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \\ \hfill w^k& =v^k+{\beta }_k({prox}_{{\lambda }_k{\phi }_2}(Id-{\lambda }_k\nabla {\phi }_1)v^k-v^k);\hfill \\ \hfill u^{k+1}& =(1-{\gamma }_k){prox}_{{\lambda }_k{\phi }_2}(Id-{\lambda }_k\nabla {\phi }_1)w^k+{\gamma }_k{prox}_{{\lambda }_k^{*}{\psi }_2}(Id-{\lambda }_k^{*}\nabla {\psi }_1)w^k,\hfill \end{array}$$        end for.

Theorem 2.

Let $\left\{x_k\right\}$ be the sequence created by Algorithm 4. Suppose that the sequences $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\}$ and $\left\{{\gamma }_k\right\}$ satisfy the following conditions:

(C1)

$0<a\le {\beta }_k\le b<1,0<c\le {\gamma }_k\le d<1$$\forall k\in \mathbb{N},$ for some $a,b,c,d\in \mathbb{R}$;

(C2)

${\alpha }_k\ge 0,$$\forall k\in \mathbb{N}$ and ${\sum }_{k=1}^{\infty }{\alpha }_k<\infty$;

(C3)

$0<{\lambda }_k,\lambda <\frac{2}{L_1},$$0<{\lambda }_k^{*},{\lambda }^{*}<\frac{2}{L_1},$$\forall k\in \mathbb{N}$ such that ${\lambda }_k\to \lambda$ and ${\lambda }_k^{*}\to {\lambda }^{*}$ as $k\to \infty$.

Then the following hold:

(i)

$\parallel u^{k+1}-u^{*}\parallel \le \mathcal{N}{\prod }_{j=1}^k(1+2{\alpha }_j),$ where $\mathcal{N}=max\{\parallel u^1-u^{*}\parallel ,\parallel u^2-u^{*}\parallel \}$ and $u^{*}\in \mathsf{\Theta };$

(ii)

$\left\{u^k\right\}$ converges weakly to some element in $\mathsf{\Theta }.$

Proof. 

Operators $S_k,T_k,S,T:\mathcal{H}\to \mathcal{H}$ are defined as follows:

$$\begin{array}{cc}\hfill S_k:={prox}_{{\lambda }_k{\phi }_2}(Id-{\lambda }_k\nabla {\phi }_1),& S:={prox}_{\lambda {\phi }_2}(Id-\lambda \nabla {\phi }_1),\hfill \\ \hfill T_k:={prox}_{{\lambda }_k^{*}{\psi }_2}(Id-{\lambda }_k^{*}\nabla {\psi }_1)\mathrm{and}& T:={prox}_{{\lambda }^{*}{\psi }_2}(Id-{\lambda }^{*}\nabla {\psi }_1).\hfill \end{array}$$

By applying Remark 3 and condition (C3), we have $\{S_k:\mathcal{H}\to \mathcal{H}\}$ and $\{T_k:\mathcal{H}\to \mathcal{H}\}$, two families of nonexpansive mappings, which satisfy NST-condition (I) with S and $T,$ respectively. This implies that $\left\{S_k\right\}$ and $\left\{T_k\right\}$ satisfy the condition (Z). Therefore, the result is obtained directly from Theorem 1.    □

Remark 4.

If ${\phi }_1={\psi }_1$, ${\phi }_2={\psi }_2$, and ${\lambda }_k={\lambda }_k^{*}$ then the Algorithm 4 is reduced to the method for solving the minimization problem of the sum of two convex function, Problem (1), as follows Algorithm 5:

Algorithm 5 An inertial Picard–Mann forward–backward splitting (iPM-FBS) method.

Let $u^0,u^1\in \mathcal{H}.$ Choose $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\}$ and $\left\{{\lambda }_k\right\}.$        For $k=1,2,...$ do $$\begin{array}{cc}\hfill v^k& =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \\ \hfill w^k& =v^k+{\beta }_k({prox}_{{\lambda }_k{\psi }_2}(Id-{\lambda }_k\nabla {\psi }_1)v^k-v^k);\hfill \\ \hfill u^{k+1}& ={prox}_{{\lambda }_k{\psi }_2}(Id-{\lambda }_k\nabla {\psi }_1)w^k,\hfill \end{array}$$        end for.

3. An Inertial Forward–Backward Splitting Method with Line Search

In this part, we modify the inertial forward–backward splitting method proposed in Section 2 for finding common elements of the convex minimization problem, Problem (7), by using the linesearch technique (Algorithm 1 [2]) and we prove the weak convergence of the proposed method. We set standing assumptions used throughout this part as follows:

(B1) 

${\phi }_1:\mathcal{H}\to \mathbb{R},{\psi }_1:\mathcal{H}\to \mathbb{R},$${\phi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ and ${\psi }_2:\mathcal{H}\to \mathbb{R}\cup \{\infty \}$ are convex proper lower semi-continuous functions and $\mathsf{\Theta }:=\mathrm{Argmin}({\rm Y}:={\phi }_1+{\phi }_2)\cap \mathrm{Argmin}(\Psi :={\psi }_1+{\psi }_2)\ne \varnothing ;$

(B2) 

${\phi }_1$ and ${\psi }_1$ are differentiable on $\mathcal{H}$. The gradient of ${\phi }_1$ and ${\psi }_1$ are uniformly continuous on $\mathcal{H}$.

Lemma 7

([2]). Let $\left\{u^k\right\}$ is a sequence created using the following:

$$u^{k+1}={prox}_{{\lambda }_k{\psi }_2}(Id-{\lambda }_k\nabla {\psi }_1)\left(u^k\right),$$

where ${\lambda }_k:={\mathrm{Linesearch}}_{({\phi }_1,{\phi }_2)}(u^k,\sigma ,\theta ,\delta ).$ Then for each $k\ge 1$ and $u\in \mathcal{H},$

$$\begin{array}{cc}\hfill \parallel u^k{-u\parallel }^2-{\parallel u^{k+1}-u\parallel }^2& \ge 2{\lambda }_k\left[\Psi \left(u^{k+1}\right)-\Psi \left(u\right)\right]+(1-2\delta ){\parallel u^{k+1}-u^k\parallel }^2.\hfill \end{array}$$

Theorem 3.

Let $\left\{u^k\right\}$ be the sequence created using Algorithm 6. Suppose that the sequences $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\}$ and $\left\{{\gamma }_k\right\}$ satisfy the following conditions:

(C1)

$0<a\le {\beta }_k\le b<1,0<c\le {\gamma }_k\le d<1$$\forall k\in \mathbb{N},$ for some $a,b,c,d\in \mathbb{R}$;

(C2)

${\alpha }_k\ge 0,$$\forall k\in \mathbb{N}$ and ${\sum }_{k=1}^{\infty }{\alpha }_k<\infty$.

Then the sequence $\left\{u^k\right\}$ converges weakly to some element in $\mathsf{\Theta }.$

Algorithm 6 An inertial forward–backward splitting method with line search (iFBS-L).

Let $u^0,u^1\in \mathcal{H}.$ Choose $\left\{{\alpha }_k\right\},\left\{{\beta }_k\right\}$ and $\left\{{\gamma }_k\right\}.$        For $k=1,2,...$ do $$\begin{array}{cc}\hfill v^k& =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \\ \hfill w^k& =v^k+{\beta }_k({prox}_{{\lambda }_k{\phi }_2}(Id-{\lambda }_k\nabla {\phi }_1)v^k-v^k);\hfill \\ \hfill u^{k+1}& =(1-{\gamma }_k){prox}_{{\lambda }_k^1{\phi }_2}(Id-{\lambda }_k^1\nabla {\phi }_1)w^k+{\gamma }_k{prox}_{{\lambda }_k^{*}{\psi }_2}(Id-{\lambda }_k^{*}\nabla {\psi }_1)w^k,\hfill \end{array}$$        where ${\lambda }_k:={\mathrm{Linesearch}}_{({\phi }_1,{\phi }_2)}(v^k,\sigma ,\theta ,\delta ),{\lambda }_k^1:={\mathrm{Linesearch}}_{({\phi }_1,{\phi }_2)}(w^k,\sigma ,\theta ,\delta )$ and        ${\lambda }_k^{*}:=$${\mathrm{Linesearch}}_{({\psi }_1,{\psi }_2)}(w^k,\sigma ,\theta ,\delta ),$       end for.

Proof. 

We denote

$$\overline{v^k}:={prox}_{{\lambda }_k{\phi }_2}(Id-{\lambda }_k\nabla {\phi }_1)v^k,\overbrace{w^k}:={prox}_{{\lambda }_k^1{\phi }_2}(Id-{\lambda }_k^1\nabla {\phi }_1)w^k$$

$$\mathrm{and}\overline{w^k}:={prox}_{{\lambda }_k^{*}{\psi }_2}(Id-{\lambda }_k^{*}\nabla {\psi }_1)w^k.$$

Applying Lemma 7, we have for any $k\in \mathbb{N}$ and $u\in \mathcal{H},$

$$\begin{array}{cc}\hfill \parallel v^k{-u\parallel }^2-{\parallel \overline{v^k}-u\parallel }^2& \ge 2{\lambda }_k\left[{\rm Y}\left(\overline{v^k}\right)-{\rm Y}\left(u\right)\right]+(1-2\delta ){\parallel \overline{v^k}-v^k\parallel }^2,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill \parallel w^k{-u\parallel }^2-{\parallel \overbrace{w^k}-u\parallel }^2& \ge 2{\lambda }_k^1\left[{\rm Y}\left(\overbrace{w^k}\right)-{\rm Y}\left(u\right)\right]+(1-2\delta ){\parallel \overbrace{w^k}-w^k\parallel }^2,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill \parallel w^k{-u\parallel }^2-{\parallel \overline{w^k}-u\parallel }^2& \ge 2{\lambda }_k^{*}\left[\Psi \left(\overline{w^k}\right)-\Psi \left(u\right)\right]+(1-2\delta ){\parallel \overline{w^k}-w^k\parallel }^2.\hfill \end{array}$$

(30)

Let $u^{*}\in \mathsf{\Theta }$ and set $u=u^{*}$ in (28)–(30), we have

$$\parallel \overline{v^k}-u^{*}\parallel \le \parallel v^k-u^{*}\parallel ,\parallel \overbrace{w^k}-u^{*}\parallel \le \parallel w^k-u^{*}\parallel \mathrm{and}\parallel \overline{w^k}-u^{*}\parallel \le \parallel w^k-u^{*}\parallel .$$

(31)

From Algorithm 6 and (31), we have

$$\parallel w^k-u^{*}\parallel \le (1-{\beta }_k)\parallel v^k-u^{*}\parallel +{\beta }_k\parallel \overline{v^k}-u^{*}\parallel \le \parallel v^k-u^{*}\parallel .$$

(32)

So, using (31) and (32), we obtain

$$\begin{array}{cc}\hfill \parallel u^{k+1}-u^{*}\parallel & \le (1-{\gamma }_k)\parallel \overbrace{w^k}-u^{*}\parallel +{\gamma }_k\parallel \overline{w^k}-u^{*}\parallel \hfill \\ \hfill & \le \parallel w^k-u^{*}\parallel \hfill \\ \hfill & \le \parallel v^k-u^{*}\parallel \hfill \\ \hfill & \le \parallel u^k-u^{*}\parallel +{\alpha }_k\parallel u^k-u^{k-1}\parallel .\hfill \end{array}$$

(33)

Using Lemma 2 and condition (C2), we have $\left\{u^k\right\}$ is bounded. This implies ${\sum }_{k=1}^{\infty }{\alpha }_k\parallel u^k-u^{k-1}\parallel <\infty .$ Using (19) and Lemma 5, we obtain that ${lim}_{k\to \infty }\parallel u^k-u^{*}\parallel$ exists. Using (11), (28), (30)–(32), we obtain

$$\begin{array}{cc}\hfill \parallel w^k-u^{*}{\parallel }^2& \le (1-{\beta }_k)\parallel v^k-u^{*}{\parallel }^2+{\beta }_k{\parallel \overline{v^k}-u^{*}\parallel }^2\hfill \\ \hfill & \le \parallel v^k-u^{*}{\parallel }^2-{\beta }_k(1-2\delta ){\parallel v^k-\overline{v^k}\parallel }^2,\hfill \end{array}$$

(34)

and

$$\begin{array}{cc}\hfill \parallel u^{k+1}-u^{*}{\parallel }^2& \le (1-{\gamma }_k)\parallel \overbrace{w^k}-u^{*}{\parallel }^2+{\gamma }_k{\parallel \overline{w^k}-u^{*}\parallel }^2\hfill \\ \hfill & \le \parallel w^k-u^{*}{\parallel }^2-{\gamma }_k(1-2\delta ){\parallel \overline{w^k}-w^k\parallel }^2\hfill \\ \hfill & \le \parallel v^k-u^{*}{\parallel }^2-{\beta }_k(1-2\delta )\parallel v^k-\overline{v^k}{\parallel }^2-{\gamma }_k(1-2\delta ){\parallel \overline{w^k}-w^k\parallel }^2\hfill \\ \hfill & \le \parallel u^k-u^{*}{\parallel }^2+{\alpha }_k^2\parallel u^k-u^{k-1}{\parallel }^2+2{\alpha }_k\parallel u^k-u^{*}\parallel \parallel u^k-u^{k-1}\parallel \hfill \\ \hfill & -{\beta }_k(1-2\delta )\parallel v^k-\overline{v^k}{\parallel }^2-{\gamma }_k(1-2\delta ){\parallel \overline{w^k}-w^k\parallel }^2.\hfill \end{array}$$

(35)

Since ${lim}_{k\to \infty }\parallel u^k-u^{*}\parallel$ exiats, ${\sum }_{k=1}^{\infty }{\alpha }_k\parallel u^k-u^{k-1}\parallel <\infty$ and (C2), we have

$$\underset{k\to \infty }{lim}\parallel v^k-\overline{v^k}\parallel =\underset{k\to \infty }{lim}\parallel \overline{w^k}-w^k\parallel =0\mathrm{and}\mathrm{also}\underset{k\to \infty }{lim}\parallel w^k-v^k\parallel =0.$$

(36)

Next, we show that ${\omega }_w\left(u^k\right)\subset \mathsf{\Theta }:=\mathrm{Argmin}({\phi }_1+{\phi }_2)\cap \mathrm{Argmin}({\psi }_1+{\psi }_2).$ Since $\left\{u^k\right\}$ is bounded, we find that ${\omega }_w\left(u^k\right)$ is nonempty. Let $x\in {\omega }_w\left(u^k\right),$ i.e., there exists a subsequence $\left\{u^{k_i}\right\}$ of $\left\{u^k\right\}$ such that $u^{k_i}\rightharpoonup x.$ Since ${lim}_{k\to \infty }\parallel v^k-u^k\parallel =0,$ and (36), we have $\overline{v^{k_i}}\rightharpoonup x$ and $\overline{w^{k_i}}\rightharpoonup x.$

Now, we show that $x\in \mathrm{Argmin}({\phi }_1+{\phi }_2)$ by considering the following two cases.

• Case 1. Suppose that the sequence $\left\{{\lambda }_{k_i}\right\}$ does not converge to zero. Thus there exists $\lambda >0$ such that ${\lambda }_{k_i}\ge \lambda >0.$ Using (B2), we have

  $$\underset{k\to \infty }{lim}\parallel \nabla {\phi }_1\left(v^k\right)-\nabla {\phi }_1\left(\overline{v^k}\right)\parallel =0.$$

  (37)

From (10), we get

$$\frac{v^{k_i}-\overline{v^{k_i}}}{{\lambda }_{k_i}}+\nabla {\phi }_1\left(\overline{v^{k_i}}\right)-\nabla {\phi }_1\left(v^{k_i}\right)\in \partial {\phi }_2\left(\overline{v^{k_i}}\right)+\nabla {\phi }_1\left(\overline{v^{k_i}}\right)=\partial {\rm Y}\left(\overline{v^{k_i}}\right).$$

(38)

Using (36)–(38) and Lemma 3, we get $0\in \partial {\rm Y}\left(x\right),$ that is, $x\in \mathrm{Argmin}({\phi }_1+{\phi }_2).$

• Case 2. Suppose that the sequence $\left\{{\lambda }_{k_i}\right\}$ converges to zero. Define $\widehat{{\lambda }_{k_i}}={\displaystyle \frac{{\lambda }_{k_i}}{\theta }}>{\lambda }_{k_i}>0$ and

  $$\widehat{v^{k_i}}:={prox}_{\widehat{{\lambda }_{k_i}}{\phi }_2}(v^{k_i}-\widehat{{\lambda }_{k_i}}\nabla {\phi }_1\left(v^{k_i}\right)).$$

Using Lemma 4, we have

$$\parallel v^{k_i}-\widehat{v^{k_i}}\parallel \le {\displaystyle \frac{\widehat{{\lambda }_{k_i}}}{{\lambda }_{k_i}}}\parallel v^{k_i}-\overline{v^{k_i}}\parallel ={\displaystyle \frac{1}{\theta }}\parallel v^{k_i}-\overline{v^{k_i}}\parallel .$$

(39)

Since $\parallel v^{k_i}-\overline{v^{k_i}}\parallel \to 0,$ we have $\parallel v^{k_i}-\widehat{v^{k_i}}\parallel \to 0.$ Using (B2), we have

$$\underset{i\to \infty }{lim}\parallel \nabla {\phi }_1\left(v^{k_i}\right)-\nabla {\phi }_1\left(\widehat{v^{k_i}}\right)\parallel =0.$$

(40)

From the definition of Algorithm 1, we have

$$\widehat{{\lambda }_{k_i}}\parallel \nabla {\phi }_1\left(v^{k_i}\right)-\nabla {\phi }_1\left(\widehat{v^{k_i}}\right)\parallel >\delta \parallel v^{k_i}-\widehat{v^{k_i}}\parallel .$$

(41)

Using (40) and (41), we get

$$\underset{i\to \infty }{lim}{\displaystyle \frac{\parallel v^{k_i}-\widehat{v^{k_i}}\parallel }{\widehat{{\lambda }_{k_i}}}}=0.$$

(42)

From (10), we get

$$\frac{v^{k_i}-\widehat{v^{k_i}}}{\widehat{{\lambda }_{k_i}}}+\nabla {\phi }_1(\widehat{v^{k_i}})-\nabla {\phi }_1(v^{k_i})\in \partial {\phi }_2(\widehat{v^{k_i}})+\nabla {\phi }_1(\widehat{v^{k_i}})=\partial {\rm Y}(\widehat{v^{k_i}}).$$

(43)

Since $v^{k_i}\rightharpoonup x$ and $\parallel v^{k_i}-\widehat{v^{k_i}}\parallel \to 0,$ we obtain $\widehat{v^{k_i}}\rightharpoonup x.$ Using (42), (43) and Lemma 3, we have $0\in \partial {\rm Y}\left(x\right),$ that is, $x\in \mathrm{Argmin}({\phi }_1+{\phi }_2).$ From ${lim}_{k\to \infty }\parallel \overline{w^k}-w^k\parallel =0$, using the same proofs as Case 1 and Case 2, we obtain $x\in \mathrm{Argmin}({\psi }_1+{\psi }_2).$ Therefore, $x\in \mathrm{Argmin}({\phi }_1+{\phi }_2)\cap \mathrm{Argmin}({\psi }_1+{\psi }_2),$ i.e., ${\omega }_w\left(u^k\right)\subset \mathsf{\Theta }.$ Using Lemma 6, we have $u^k\rightharpoonup x^{*}$ for some $x^{*}\in \mathsf{\Theta }$. This completes the proof.    □

Remark 5.

If ${\phi }_1={\psi }_1$ and ${\phi }_2={\psi }_2,$ then Algorithm 6 is reduced to the method for solving the minimization problem of the sum of two convex functions, Problem (1), as follows Algorithm 7:

Algorithm 7 An inertial Picard–Mann forward–backward splitting method with line search (iPM-FBS-L).

Let $u^0,u^1\in \mathcal{H}.$ Choose $\left\{{\alpha }_k\right\}$ and $\left\{{\beta }_k\right\}.$       For $k=1,2,...$ do $$\begin{array}{cc}\hfill v^k& =u^k+{\alpha }_k(u^k-u^{k-1});\hfill \\ \hfill w^k& =v^k+{\beta }_k({prox}_{{\lambda }_k{\psi }_2}(Id-{\lambda }_k\nabla {\psi }_1)v^k-v^k);\hfill \\ \hfill u^{k+1}& ={prox}_{{\lambda }_k^1{\psi }_2}(Id-{\lambda }_k^1\nabla {\psi }_1)w^k,\hfill \end{array}$$       where ${\lambda }_k:={\mathrm{Linesearch}}_{({\psi }_1,{\psi }_2)}(v^k,\sigma ,\theta ,\delta ),$ and ${\lambda }_k^1:={\mathrm{Linesearch}}_{({\psi }_1,{\psi }_2)}(w^k,\sigma ,\theta ,\delta )$,       end for.

4. Numerical Examples

The following experiments are executed in MATLAB and run on a PC with Intel Core-i7/16.00 GB RAM/Windows 11/64-bit. For image quality measurements, we utilize the peak signal-to-noise ratio (PSNR) in decibels (dB), which is defined as follows:

$$PSNR:=10{log}_{10}\left(\frac{{255}^2}{\frac{1}{\mathcal{M}}{\parallel u^k-u\parallel }_2^2}\right),$$

where $\mathcal{M}$ and u are the number of image samples and the original image, respectively.

4.1. The Constrained Image Inpainting Problems

In this subsection, we apply the constrained convex minimization problem, Problem (6), to the constrained image inpainting problem, Problem (4). We analyze and illustrate the convergence behavior of the iFBS method (Algorithm 4) and iFBS-L method (Algorithm 6) for the image restoration problem and also compare those methods’ efficiency with that of the iTOS method [10].

In this experiment, we discuss the following constrained image inpainting problem [10]:

$$\underset{u\in \mathcal{C}}{min}{\displaystyle \frac{1}{2}}\parallel {\mathcal{P}}_{\mathsf{\Lambda }}\left(u^0\right)-{\mathcal{P}}_{\mathsf{\Lambda }}\left(u\right){\parallel }_F^2+\tau {\parallel u\parallel }_{*},$$

(44)

where $u^0\in {\mathbb{R}}^{m\times n}$ is a given image. We define ${\mathcal{P}}_{\mathsf{\Lambda }}$ by

$${\mathcal{P}}_{\mathsf{\Lambda }}\left(u^0\right)=\left\{\begin{array}{c}{u}_{ij}^0,(i,j)\in \mathsf{\Lambda },\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.$$

where ${\left\{u_{ij}^0\right\}}_{(i,j)\in \mathsf{\Lambda }}$ are observed, $\mathsf{\Lambda }$ is a subset of the index set $\{1,2,3...,m\}\times \{1,2,3...,n\}$ which indicates where data are available in the image domain, and the rest are missed and $\mathcal{C}=\{u\in {\mathbb{R}}^{m\times n}|u_{ij}\ge 0\}.$

It is obvious that the constrained image inpainting problem, Problem (44), is a special case of the constrained convex minimization problem, Problems (6), i.e., we can set

$${\psi }_1\left(u\right)=0,{\psi }_2\left(u\right)={\delta }_{\mathcal{C}}\left(u\right),{\phi }_1\left(u\right)={\displaystyle \frac{1}{2}}\parallel {\mathcal{P}}_{\mathsf{\Lambda }}\left(u^0\right)-{\mathcal{P}}_{\mathsf{\Lambda }}\left(u\right){\parallel }_F^2,\mathrm{and}{\phi }_2\left(u\right)=\tau {\parallel u\parallel }_{*}.$$

So, we have ${\phi }_1\left(u\right)$ is differentiable and convex, and $\nabla {\phi }_1\left(u\right)={\mathcal{P}}_{\mathsf{\Lambda }}\left(u^0\right)-{\mathcal{P}}_{\mathsf{\Lambda }}\left(u\right)$ is Lipschitz continuous with constant $L=1$. The proximity operator of ${\psi }_2\left(u\right)$ is the orthogonal projection onto the closed convex set $\mathcal{C}$ and the proximity operator of ${\phi }_2\left(u\right)$ can be computed using singular value decomposition (SVD), see [23]. Thus, the iFBS method (Algorithm 4) and iFBS-L method (Algorithm 6) can be employed to solve the constrained image inpainting problem, Problem (44).

In this demonstration, we identify and correct the damaged area of the Wat Chedi Luang image in the default gallery, and we recommend stopping the calculation when

$${\displaystyle \frac{\parallel u^{k+1}-u^k{\parallel }_F}{\parallel u^k{\parallel }_F}}\le ϵ={10}^{-5}\mathrm{or}4000\mathrm{th}\mathrm{iteration}.$$

The suggested parameters setting in Table 1 are used as parameters for the iFBS, iFBS-L, and iTOS methods. It is noted that the sequence ${\alpha }_k$ can be defined with

$$\begin{array}{c}\hfill {\alpha }_k=\left\{\begin{array}{cc}{\rho }_k\hfill & \mathrm{if}1\le k\le 4000;\hfill \\ \frac{1}{2^k}\hfill & \mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

which satisfies the condition (C2).

Table 1. Details of parameters for each method.

Parameters	iFBS Method	iFBS-L Method	iTOS Method
${\alpha }_k$	${\rho }_k=\frac{0.99k}{k+1}$	${\rho }_k=\frac{0.99k}{k+1}$	0.5
${\beta }_k$	$\frac{0.9k}{k+1}$	$\frac{0.9k}{k+1}$	0.3
${\gamma }_k$	$\frac{0.01k}{k+1}$	$\frac{0.01k}{k+1}$	None
${\lambda }_k$ or ${\lambda }_k^1$ or $\lambda$	1	Algorithm 1: $\sigma =1.2,\theta =0.5,\delta =0.4$	1

The PSNR value for the restored images, CPU time (second), and the number of iterations (Iter.) are listed in Table 2.

Table 2. Performance evaluation of the restored images.

$\mathit{\tau }$	Methods	PSNR (dB)	CPU Time (s)	Iter.	$\mathit{\epsilon }$
	iFBS	23.9005	14.4789	569	9.9575$\times {10}^{-6}$
0.1	iFBS-L	23.8190	78.9583	785	9.9691$\times {10}^{-6}$
	iTOS	19.6026	57.3366	4000	4.5363$\times {10}^{-5}$
	iFBS	23.7995	51.5491	902	9.9645$\times {10}^{-6}$
0.01	iFBS-L	23.7980	214.6868	966	9.9645$\times {10}^{-6}$
	iTOS	19.3362	122.0958	4000	4.1767$\times {10}^{-5}$
	iFBS	23.7976	42.8857	1171	9.9442$\times {10}^{-6}$
0.001	iFBS-L	23.8283	350.8687	2410	9.9942$\times {10}^{-6}$
	iTOS	13.0501	86.4161	4000	1.4987$\times {10}^{-5}$

As shown in Table 2, the numerical examples indicate that our proposed methods perform better than the inertial three-operator splitting (iTOS) method [10] in both terms of PSNR performance and the number of iterations. The running time of the iFBS method is less than those of the iFBS-L and iTOS methods. We exhibit the original image, painted image, and restored images in the case of a regularization parameter of $\tau =0.001$ in Figure 1 as a visual demonstration.

Figure 1. The original image, painted image, and restored images in the case of a regularization parameter of $\tau =0.001$.

4.2. The Least Absolute Shrinkage and Selection Operator (LASSO)

In this subsection, we provide numerical results by comparing Algorithm 5 (iPM-FBS), Algorithm 7 (iPM-FBS-L), the FISTA method [3], and the FBS-L method [2] for the image restoration problems by using the LASSO model specified by the formula:

$$\underset{u\in {\mathbb{R}}^N}{min}\left\{{\psi }_1\left(u\right)+{\psi }_2\left(u\right):=\frac{1}{2}{∥\mathcal{B}u-b∥}_2^2+\tau {\parallel u\parallel }_1\right\},$$

(45)

where $\mathcal{B}=\mathcal{RW}$, $\mathcal{R}$ is the kernel matrix, $\mathcal{W}$ is 2-D fast Fourier transform, b is the observed image, $\tau >0$, ${\parallel ·\parallel }_1$ is the $l_1$-norm, and ${\parallel ·\parallel }_2$ is the Euclidean norm.

In this experiment, we use the RGB image test with a size of 256 × 256 pixels as the original image and evaluate the performance of the iPM-FBS, iPM-FBS-L, FISTA, and FBS-L methods in two typical image blurring scenarios which are summarized in Table 3 (see the test images in Figure 2). The parameters for the methods are set in Table 4.

Table 3. Description of image blurring scenarios.

Scenario	Blur Kernel
I	$9\times 9$ Gaussian kernel with standard deviation $\widehat{\sigma }=3$
II	Motion blur specifying with motion length of 15 pixels and motion orientation 7°

Figure 2. The test images. (a) original image, (b) Blurred image in scenario I, and (c) Blurred image in scenario II.

Table 4. Details of parameters for each method.

Parameters	iPM-FBS Method	iPM-FBS-L Method	FBS-L Method
${\alpha }_k$	${\rho }_k=\frac{k}{k+1}$	${\rho }_k=\frac{k}{k+1}$	None
${\beta }_k$	$\frac{0.99k}{k+1}$	$\frac{0.99k}{k+1}$	None
${\lambda }_k$ or ${\lambda }_k^1$	1	Algorithm 1:	Algorithm 1:
		$\sigma =3,\theta =0.9,\delta =0.9$	$\sigma =3,\theta =0.9,\delta =0.9$

In the results from Table 5, it is evident that the iPM-FBS method produces the best PSNR results. We exhibit the restored images in the case of a regularization parameter of $\tau ={10}^{-8}$ in Figure 3 and Figure 4 as a visual demonstration. The PSNR graphs in Figure 5 further show that the iPM-FBS method has considerable advantages in terms of recovery performance when compared to the iPM-FBS-L, FISTA, and FBS-L methods.

Table 5. The comparison of the PSNR performance of four methods at $200\mathrm{th}$ iteration.

Scenario	$\mathit{\tau }$	Methods	PSNR (dB)	CPU Time (s)
I	${10}^{-4}$	iPM-FBS	27.3458	2.8221
		iPM-FBS-L	25.0238	45.1662
		FISTA	26.4149	1.7705
		FBS-L	23.7164	16.3711
	${10}^{-6}$	iPM-FBS	27.7474	2.7711
		iPM-FBS-L	25.2714	46.0352
		FISTA	26.5376	1.8540
		FBS-L	23.7217	16.2916
	${10}^{-8}$	iPM-FBS	27.7549	2.8393
		iPM-FBS-L	25.2768	57.4240
		FISTA	26.5393	1.8649
		FBS-L	23.7218	16.2471
II	${10}^{-4}$	iPM-FBS	35.4960	4.5469
		iPM-FBS-L	28.9786	1171.4283
		FISTA	34.0224	7.6546
		FBS-L	28.3481	43.5701
	${10}^{-6}$	iPM-FBS	35.7536	4.5796
		iPM-FBS-L	29.0315	66.9911
		FISTA	34.1577	2.9429
		FBS-L	28.3597	23.8312
	${10}^{-8}$	iPM-FBS	35.7568	4.7062
		iPM-FBS-L	29.0322	68.0620
		FISTA	34.1591	2.8966
		FBS-L	28.3598	23.1104

Figure 3. The images recovered in scenario I in the case of $\tau ={10}^{-8}$. (a–d) Images recovered using iPM-FBS, iPM-FBS-L, FISTA, and FBS-L, respectively.

Figure 4. The images recovered in scenario II in case of $\tau ={10}^{-8}$. (a–d) Images recovered using iPM-FBS, iPM-FBS-L, FISTA, and FBS-L, respectively.

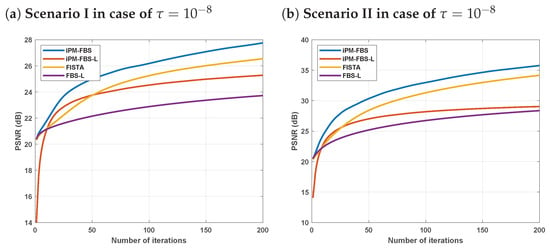
Figure 5. The PSNR comparisons of iPM-FBS, iPM-FBS-L, FISTA, and FBS-L methods.

5. Conclusions

This paper proposed two novel inertial forward–backward splitting methods, the iFBS method and the iFBS-L method, for finding common elements of the convex minimization of the sum of two convex functions in real Hilbert spaces. The key idea was to examine the weak convergence results of the proposed methods by utilizing the fixed point conditions of the forward–backward operators and line search strategies, respectively. The proposed methods were applied to solve image inpainting problems. Numerical simulations showed that our methods (iFBS and iFBS-L) performed better than the inertial three-operator splitting (iTOS) method [10] both in terms of PSNR performance and the number of iterations. Finally, we reduced our methods to solve the convex minimization of the sum of two convex functions, called the iPM-FBS method and iPM-FBS-L method, and applied them to solve image recovery problems. Numerical simulations showed that the iPM-FBS method performed better than the iFBS-L method, FISTA method [3], and FBS-L method [2] in terms of PSNR performance.