An Adaptive-to-Model Test for Parametric Functional Single-Index Model

Abstract

Model checking methods based on non-parametric estimation are widely used because of their tractable limiting null distributions and being sensitive to high-frequency oscillation alternative models. However, this kind of test suffers from the curse of dimensionality, resulting in slow convergence, especially for functional data with infinite dimensional features. In this paper, we propose an adaptive-to-model test for a parametric functional single-index model by using the orthogonality of residual and its conditional expectation. The test achieves model adaptation by sufficient dimension reduction which utilizes functional sliced inverse regression. This test procedure can be easily extended to other non-parametric test methods. Under certain conditions, we prove the asymptotic properties of the test statistic under the null hypothesis, fixed alternative hypothesis and local alternative hypothesis. Simulations show that our test has better performance than the method that does not use functional sufficient dimension reduction. An analysis of COVID-19 data verifies our conclusion.

1. Introduction

Consider the functional single-index regression model

$$\begin{array}{c}\hfill Y=g\left(\langle {\beta }_0,X\rangle \right)+\epsilon ,\end{array}$$

(1)

where Y is a scalar response, X is a predictor function in a functional space $\mathcal{H}$ with an inner product denoted by $\langle ·,·\rangle$, ${\beta }_0\in \mathcal{H}$ is an unknown functional index, $\parallel {\beta }_0\parallel =1$, $\epsilon$ is a scalar random noise and $E\left(\epsilon \right|X)=0$, $g(·)$ is a unknown square integrable continuous function. If the model (1) is correctly specified, Refs. [1,2,3,4] proposed consistent estimates of ${\beta }_0$ and $g(·)$ in different ways. However, compared to non-parametric regression models without specifying the model form of $E\left(Y\right|X)$, parametric functional single-index models are estimated more accurately, especially for functional data with infinite dimension. On the other hand, a wrongly specified model structure would lead to misleading statistical analysis. Therefore, we develop a goodness-of-fit test for model (1) with a given link function $g(·)$. In some cases, the presence of outliers may affect the quality of model fitting, and it is necessary to conduct an outlier test to determine whether outliers exist in the data and then perform the goodness-of-fit test based on the data with outliers removed. The method for the outlier test can be referred to [5], while the primary focus of this paper is on the goodness-of-fit test of model (1).

The special case of the model (1) in which g is linear has been extensively studied. Among them, the research on hypothesis testing has made great progress. For example, testing the nullity of the slope parameter was studied in [6,7,8], and testing whether the conditional expectation of the response given the covariate is almost surely zero or not was considered in [9,10,11]. The model checking method relies on linear model assumptions and is not flexible enough in practical applications. Thus, the proposed model-adaptive approach in this paper overcomes these limitations and offers a more flexible and reliable solution for model checking in parametric functional single-index models. In terms of model testing, the two widely used tests are global smoothing methods based on empirical processes (see [12,13]) and local smoothing methods based on non-parametric estimation (see [9,10,11]). Similar to the conclusion summarized by [14] on vector space, each of these two kinds of tests has advantages and disadvantages. For example, as summarized in [15], the global smoothing methods converge to the limiting distribution at the rate of order $O\left(n^{-1/2}\right)$, which is the faster rate that the existing methods can reach. However, they are insensitive to high-frequency oscillation alternative models and often require the use of resampling techniques to obtain critical values. In contrast, as summarized in [14,16], the local smoothing methods have high power in detecting high-frequency oscillation alternative models, but these methods converge to the limiting distribution at the rate of order $O\left(n^{-1/2}{h}^{-p/4}\right)$, where $p=dim\left(X\right)$. Thus, the local smoothing methods suffer from the curse of dimensionality due to the use of multivariate non-parametric estimation, especially for functional data with infinite dimensional features. To overcome this shortcoming, most of the local smoothing methods mentioned above are based on the semi-metric of the function space to compute univariate non-parametric kernel functions (see [11]), which requires functional principal component analysis for dimensionality reduction. The other method is based on projection technology (see [9,10,17]), which is more complicated for choosing the projection directions. In this paper, we employ sufficient dimension reduction to construct a model adaptive test that achieves a convergence rate of $O\left(n^{-1/2}{h}^{-1/4}\right)$, which is faster compared to that of the locally smooth method when the dimensionality is reduced to 1 under the null hypothesis.

Our aim is to test the parametric model (1) against a parsimonious alternative model class through functional sufficient dimension reduction (FSDR) [18]. We consider the alternative model:

$$\begin{array}{c}\hfill Y=G(\langle \mathit{B},X\rangle )+\epsilon ,\end{array}$$

(2)

where $\mathit{B}=({\beta }_1,\dots ,{\beta }_K)$ is composed of K linearly independent functions in $\mathcal{H}$ and column vectors $\langle \mathit{B},X\rangle ={(\langle {\beta }_1,X\rangle ,\dots ,\langle {\beta }_K,X\rangle )}^{\top }$ is a column vector, $G(·)$ is a function from ${\mathbb{R}}^K\to \mathbb{R}$ and $\epsilon$ is a scalar error independent of X. The FSDR method is based on the above functional multiple index model. Since the FSDR method can effectively use the information between the functional predictor and the response variable, it is widely used in regression models. In the FSDR literature, the subspace spanned by ${\beta }_1,\dots ,{\beta }_K$ is called the functional sufficient dimension reduction subspace, which is first estimated by functional sliced inverse regression (FSIR) in [19]. Then, functional inverse regression [20], functional K-means inverse regression [21] and functional sliced average variance estimation [18,22] were created. For the test problem studied in this paper, when $K>1$, the model (2) is a functional multiple-index model; when $K=1$ and $\mathit{B}={\beta }_0/\parallel {\beta }_0\parallel$, model (2) reduces to the functional single-index model in (1). Therefore, we need construct a test statistic which can adapt to the related model structure through estimating $\mathit{B}$ and its dimension K. In this way, we can achieve that under a null hypothesis, the estimate of $\mathit{B}$ is consistent to ${\beta }_1$, and under an alternative hypothesis, it is consistent to a multiple-index functional $({\beta }_1,\dots ,{\beta }_K)$. To achieve this goal, the most critical step is to determine K. We use the modified BIC criterion introduced in [14] to determine K.

This paper is organized as follows. In Section 2, we construct a test statistic based on the orthogonality of residual and its conditional expectation, which is the extension of the model testing method for vector data in [23] to a functional model. In Section 3, we describe in detail the procedure of identifying and estimating $\mathit{B}$ and its dimension K using the FSIR method. The asymptotic properties under null, alternative and local alternative hypotheses are given in Section 4. Simulation results and a real data analysis are reported in Section 5. The corresponding conclusions and discussions are given in Section 6. All proofs are given in Appendix A.

2. The Test Statistic

To verify the validity of model (1), we should develop an appropriate model checking method. Therefore, for a given $g(·)$, we consider the following null hypothesis

$$\begin{array}{c}\hfill H_0:\exists {\beta }_0\in \mathcal{H},suchthatE\left[Y\right|X]=g\left(\langle {\beta }_0,X\rangle \right),\end{array}$$

(3)

and for any K linearly independent function set $\mathit{B}=({\beta }_1,\dots ,{\beta }_K)$, under model (2), the alternative hypothesis is

$$\begin{array}{c}\hfill H_1:\underset{\beta \in \mathcal{H}}{sup}P\left(E\left[Y\right|X]=E\left[Y\right|\langle \mathit{B},X\rangle ]=g\left(\langle \beta ,X\rangle \right)\right)<1.\end{array}$$

(4)

Without loss of generality, we take $\mathcal{H}=L^2\left([0,1]\right)$. It is worth noting that under $H_0$, $K=1$ and $\mathit{B}=c_1{\beta }_0$ for some constant $c_1$; under $H_1$, $K\ge 1$. Similar to the interpretation of vector spaces introduced in Stute and Zhu [24], the test statistic based on $E[Y-g\left(\langle {\beta }_0,X\rangle \right)|\langle {\beta }_0,X\rangle ]$ is directional, while the test statistic based on $E[Y-g\left(\langle {\beta }_0,X\rangle \right)|\langle \mathit{B},X\rangle ]$ is omnibus. For example, we consider the alternative model: $Y=\langle {\beta }_0,X\rangle +sin\left(\langle {\beta }_1,X\rangle \right)+\epsilon$, where ${\beta }_0$ and ${\beta }_1$ are orthogonal functions. When $E[sin\left(\langle {\beta }_1,X\rangle \right)]=0$, then $E[Y-g\left(\langle {\beta }_0,X\rangle \right)|\langle {\beta }_0,X\rangle ]=0$ providing that $\langle {\beta }_0,X\rangle$ is independent of $\langle {\beta }_1,X\rangle$ and X is a Gaussian process with $E\left(X\right)=0$; similar examples can be found in [14]. Thus, the test based on $E[Y-g\left(\langle {\beta }_0,X\rangle \right)|\langle {\beta }_0,X\rangle ]$ cannot detect the above alternative. Therefore, we can construct a test statistic based on $E[Y-g\left(\langle {\beta }_0,X\rangle \right)|\langle \mathit{B},X\rangle ]$.

Define $\epsilon =Y-g(\langle X,\beta \rangle )$, $E\left(\epsilon \right|\langle \mathit{B},X\rangle )=0$ almost surely under $H_0$ and $P(E\left(\epsilon \right|\langle \mathit{B},X\rangle )=G\left(\langle \mathit{B},X\rangle \right)-g\left(\langle {\beta }_0,X\rangle \right)\ne 0)>0$ under $H_1$. Thus, it is natural to construct a test statistic based on the orthogonality between model’s residuals $\epsilon$ and a non-parametric estimation of $E\left(\epsilon \right|\langle \mathit{B},X\rangle )$. Thus, we construct a test statistic based on $E\left\{\epsilon E\left(\epsilon \right|\langle \mathit{B},X\rangle )\right\}=E\left\{E^2\left(\epsilon \right|\langle \mathit{B},X\rangle )\right\}$.

Given the sample ${\{X_i,Y_i\}}_{i=1}^n$ and $\widehat{\mathit{B}}$ with its structural dimension $\widehat{K}$ (the estimation procedure for $\widehat{\mathit{B}}$ and $\widehat{\mathbf{K}}$ will be introduced in Section 3), the kernel regression estimator of $E\left({\epsilon }_i\right|\langle \mathit{B},X_i\rangle )$ is

$$\begin{array}{c}\hfill \widehat{E}\left({\epsilon }_i\right|\langle \widehat{\mathit{B}},X_i\rangle )=\frac{{\displaystyle \sum _{j\ne i}^n}{\epsilon }_j{K}_h\left(\langle \widehat{\mathit{B}},X_i-X_j\rangle \right)}{{\displaystyle \sum _{j\ne i}^n}{K}_h\left(\langle \widehat{\mathit{B}},X_i-X_j\rangle \right)},\end{array}$$

where $K_h(·)=K(·/h)/h^{\widehat{K}}$ is a $\widehat{K}$-dimensional kernel function, and h is a bandwidth.

When $g(·)$ is known, similar to the estimation methods in [25] (Refs. [26,27,28]’s methods are also available), it is easy to obtain a consistent estimator of $\beta$, which is denoted as $\widehat{\beta }$. Define ${\widehat{\epsilon }}_i\equiv Y_i-g\left(\langle \widehat{\beta },X_i\rangle \right)$. Next, to simplify the formula, let $\widehat{\mathbf{\epsilon }}={({\widehat{\epsilon }}_1,\dots ,{\widehat{\epsilon }}_n)}^{\top }$, $\widehat{U}$ be the $n\times n$ diagonal matrix with $\left(ii\right)$th element ${\widehat{\epsilon }}_i$, ${\widehat{w}}_{ij}\equiv K_h\left(\langle \widehat{\mathit{B}},X_i-X_j\rangle \right)/{\sum }_{l\ne i}^n{K}_h\left(\langle \widehat{\mathit{B}},X_i-X_l\rangle \right)$ and ${\widehat{w}}_{ii}=0$, ${\widehat{W}}_n=\left\{{\widehat{w}}_{ij}\right\}$ be the $n\times n$ matrix with $(i,j)$th element ${\widehat{w}}_{ij}$, where $\widehat{\mathit{B}}$ is an FSDR estimate by [18] in following Section 3. Then, by Proposition 1 and Corollary 1 in [23], the finite sample corrected and standardized quadratic statistic is

$$\begin{array}{c}\hfill T_n^{FSIR}=\frac{{\widehat{\mathbf{\epsilon }}}^{\top }{\widehat{W}}_n^s\widehat{\mathbf{\epsilon }}}{\sqrt{2}s\left(\widehat{U}{\widehat{W}}_n^s\widehat{U}\right)}+\frac{\widehat{K}}{\sqrt{2}s\left({\widehat{W}}_n^s\right)},\end{array}$$

(5)

where ${\widehat{W}}_n^s=({\widehat{W}}_n+{\widehat{W}}_n^{\top })/2$ which satisfies the symmetry condition required in Corollary 1 of [23], $s\left(A\right)={\left({\sum }_{i,j}{a}_{ij}^2\right)}^{1/2}$ is the Frobenius norm of matrix $A=\left(a_{ij}\right)$. We call $\frac{\widehat{K}}{\sqrt{2}s\left({\widehat{W}}_n^s\right)}$ the finite sample correction term (FSC). When $T_n^{FSIR}$ is large enough, the null hypothesis is rejected.

Remark 1. 

This paper mainly extends the problem considered in [14] to the functional data model. In addition to this, there is a clear difference in the construction of the test statistic. For example, [14] constructed the test statistic based on $E\left\{\epsilon E\left(\epsilon \right|{\mathit{B}}^{\top }X)\omega \left({\mathit{B}}^{\top }X\right)\right\}$ for a positive weight $\omega \left({\mathit{B}}^{\top }X\right)$. When $\omega \left({\mathit{B}}^{\top }X\right)$ was the denominator of the non-parametric estimate of $E\left(\epsilon \right|{\mathit{B}}^{\top }X)$, they obtained a simple statistic. Thus, $T_n^{FSIR}$ is different from the test of [14] even without the standardization and the bias correction.

3. Identification and Estimation of $\mathit{B}$ and $\mathit{K}$

Functional sufficient dimension reduction (FSDR) is concerned with the situations where the distribution of Y given X depends on X through a set of linear combinations of X; that is, there is a minimal set of members $\mathit{B}=({\beta }_1,\dots ,{\beta }_K)$ in $\mathcal{H}$, such that $Y\perp X|\langle \mathit{B},X\rangle$. In the applications where the conditional mean is of main interest, we can formulate FSDR through conditional mean as follows

$$\begin{array}{c}\hfill Y\perp E\left(Y\right|X\left)\right|\langle \mathit{B},X\rangle ,\end{array}$$

where ⊥ stands for the conditional independence of Y and $E\left(Y\right|X)$ given $\langle \mathit{B},X\rangle$. This is a fundamental assumption for functional sufficient dimension reduction [19,22,29]. It is worth noting that $Y\perp E\left(Y\right|X\left)\right|\langle \mathit{B},X\rangle$ is equivalent to $E\left(Y\right|X)=E(Y|\langle \mathit{B},X\rangle )$ by Proposition 8.1 in [29]. For any $K\times K$ orthogonal matrix $\mathit{D}$, the above relation is unchanged if we replace $\mathit{B}$ by $\mathit{D}\mathit{B}$, since $E\left(Y\right|\langle \mathit{B},X\rangle )=E\left(Y\right|{\mathit{D}}^{\top }\langle \mathit{B},X\rangle )$. In fact, the identifiable parameter is the space spanned by the columns of $\mathit{B}$.

We denote the column space of $\mathit{B}$ by $span\left(\mathit{B}\right)$. $S_{E\left[Y\right|X]}$ is defined as the central mean subspace and is the intersection of all subspace $span\left(\mathit{B}\right)$ such that $Y\perp E\left(Y\right|X\left)\right|\langle \mathit{B},X\rangle$. $S_{Y|X}$ is defined as the central subspace and is the intersection of all subspace $span\left(\mathit{B}\right)$ of minimal dimension such that $Y\perp X|\langle \mathit{B},X\rangle$. Most of the FSDR methods are looking for central subspace $S_{Y|X}$, such as the FSIR method in [19], FSAVE method in [22], and FSDR via distance covariance in [30]. As proposed in [29] Theorem 8.1, $S_{E\left(Y\right|X)}$ is a subspace of $S_{Y|X}$. To ensure that $S_{Y|X}=S_{E\left(Y\right|X)}$ for $\epsilon$ in model (2), we assume that $\epsilon =G_1\left(\langle \mathit{B},X\rangle \right)\tilde{\epsilon }$, where $G_1(·)$ is an unknown smooth function and $\tilde{\epsilon }\perp X$. $\epsilon \perp X$ is a special case. Next, we uniformly use $S_{Y|X}$ to represent the FSDR space spanned by $\mathit{B}$. Here, we only introduce a popular FSDR method, functional sliced inverse regression (FSIR) which refers to [18], as an example. Of course, other FSDR methods are also applicable.

3.1. A Brief Review on FSIR

Most of the FSDR methods are based on the functional multiple index model (2). As introduced in following Proposition 1, with the FSDR technique, we can achieve with probability tending to 1 $\widehat{K}=1$ under $H_0$; $\widehat{K}\ge 1$ under $H_1$. In the following, we will introduce the specific dimensionality reduction technique of FSIR.

Given $(X,Y)$, by Karhunen–Loéve expansion of X, we have

$$\begin{array}{c}\hfill X=\sum _{j=1}^{\infty }{\xi }_j{\varphi }_j,\end{array}$$

where $E{\xi }_j^2={\gamma }_j$, ${\gamma }_i$ and ${\varphi }_j$ are the eigenvalues and eigenfunctions, respectively, of the covariance operator of X, that is $\Gamma =Var\left(X\right)=E(X\otimes X)$, where for $x,y\in L^2\left([0,1]\right)$, $x\otimes y:L^2\left([0,1]\right)\to L^2\left([0,1]\right)$ is defined by $(x\otimes y)\left(z\right)=\langle x,z\rangle y$. Define $\Gamma S_{Y|X}$ as the space spanned by $\Gamma {\beta }_1,\dots ,\Gamma {\beta }_K$. In addition, we write $\Gamma -Var\left(X\right|Y)\in \Gamma S_{Y|X}$ when $(\Gamma -Var\left(X\right|Y))\beta \in \Gamma S_{Y|X}$ for all $\beta \in L^2\left([0,1]\right)$. To ensure that the estimation of FSIR belongs to the space of $\Gamma S_{Y|X}$, we need the following Lemma (refer to Theorem 1 in [18]).

Lemma 1. 

(a) Suppose for all $b\in L^2\left([0,1]\right)$, the conditional expectation is a linear condition $E\{\langle b,X\rangle |$$\langle \mathit{B},X\rangle \}=c_0+{\sum }_{i=1}^K{c}_i\langle {\beta }_i,X\rangle$ for constants $c_0,\dots ,c_K$, then $E\left(X\right|Y)\in \Gamma S_{Y|X}$; (b) If in addition $Var\left(X\right|\langle \mathit{B},X\rangle )$ is nonrandom, $\Gamma -Var\left(X\right|Y)\in \Gamma S_{Y|X}$.

The conditions in (a) and (b) hold when X is a Gaussian process, although Gaussianity is not necessary. Furthermore, there is no requirement for specific distribution forms in the following theoretical study. In the simulation of Section 4, we will use Gaussian and other continuous distributions.

Since for functional data, the operator ${\Gamma }^{-1}$ is not bounded, we replace ${\Gamma }^{-1}$ by ${(\Gamma +\rho I)}^{-1}$, where $\rho \to 0$ as $n\to \infty$. Then, the FSDR space, which is obtained by FSIR, is the space spanned by the top eigenvectors of

$$\begin{array}{c}\hfill {(\Gamma +\rho I)}^{-1}Var\left(E\left[X\right|Y]\right).\end{array}$$

Given independent and identically distributed samples ${\left\{(X_i,Y_i)\right\}}_{i=1}^n$, referring to [29]’s steps in Section 3 on vector data, we summarize the estimation procedure of functional data as the following algorithm (Algorithm 1).

Algorithm 1: Estimation of $\mathit{B}$

step 1. Compute the sample mean and sample variance functions $\overline{X}\left(t\right)=\frac{1}{n}{\sum }_{i=1}^n{X}_i\left(t\right)$ and ${\widehat{\Gamma }}_n=\frac{1}{n}{\sum }_{i=1}^n[X_i\left(t\right)-\overline{X}\left(t\right)][X_i\left(t^{\prime }\right)-\overline{X}\left(t^{\prime }\right)]$, where $t,t^{\prime }\in [0,1]$, then, define $Z_i\left(t\right)=X_i\left(t\right)-\overline{X}\left(t\right)$, $i=1,\dots ,n$. step 2. Discretize Y: let ${\left(I_{\dot{s}}\right)}_{\dot{s}=1}^{\dot{S}}$ be slice intervals in $[min(Y),max(Y\left)\right]$, define $p_{\dot{s}}=P(Y\in I_{\dot{s}})$ and $e_{\dot{s}}=E\left(Z\right|Y\in I_{\dot{s}})$, $v_{\dot{s}}=Var\left(Z\right|Y\in I_{\dot{s}})$, then, ${\widehat{p}}_{\dot{s}}=E_n\left[I(Y\in I_{\dot{s}})\right]$, ${\widehat{e}}_{\dot{s}}={\sum }_{i=1}^n{Z}_i\left(t\right)I(Y_i\in I_{\dot{s}})/n_{\dot{s}}$, where $E_n(·)$ is the empirical distribution function, $n_s$ is the number of elements that satisfy $Y_i\in I_{\dot{s}}$. step 3. Approximate $Var\left[E\right(Z\left|Y\right)]$ by ${\widehat{\Gamma }}_{\dot{S}}^{FSIR}={\sum }_{\dot{s}=1}^{\dot{S}}{\widehat{p}}_{\dot{s}}{\widehat{e}}_{\dot{s}}\otimes {\widehat{e}}_{\dot{s}}/\dot{S}$. step 4. Let ${\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_r$ and ${\widehat{\lambda }}_1,\dots ,{\widehat{\lambda }}_r$ be the top r eigenvectors and eigenvalues of ${({\widehat{\Gamma }}_n+\rho I)}^{-1}{\widehat{\Gamma }}_{\dot{S}}^{FSIR}$, where $r\ge K$ and ${\widehat{\lambda }}_1\ge {\widehat{\lambda }}_2\ge \dots \ge {\widehat{\lambda }}_r\ge 0$. The sufficient predictors are $$\langle {\widehat{\beta }}_1,Z\rangle ,\dots ,\langle {\widehat{\beta }}_r,Z\rangle .$$

Remark 2. 

The way of discretization in step 2 may affect the outcome of Algorithm 1. A lot of discussions on the discretization were carried out, and some methods were recommended; see [18,31,32], among others.

3.2. Estimating the Structural Dimension $\widehat{K}$

There are several methods to estimate the structural dimension K of $S_{Y|X}$ for vector data. Ref. [33] introduced a Bayesian information criterion (BIC), Refs. [34,35] showed a modified BIC method, and Refs. [36,37] used a bootstrap method. Through simulation, we find that [34]’s method verifies the conclusion of Proposition 1 better. That is,

$$\begin{array}{c}\hfill D\left(k\right)=\frac{n}{2}\frac{{\sum }_{l=1}^k\{log({\widehat{\lambda }}_l+1)-{\widehat{\lambda }}_l\}}{{\sum }_{l=1}^r\{log({\widehat{\lambda }}_l+1)-{\widehat{\lambda }}_l\}}-2C_n\frac{k(k+1)}{2r}.\end{array}$$

(6)

where ${\widehat{\lambda }}_1\ge {\widehat{\lambda }}_2\ge \dots \dots \ge {\widehat{\lambda }}_r\ge 0$ are eigenvalues of ${({\widehat{\Gamma }}_n+\rho I)}^{-1}{\widehat{\Gamma }}_{\dot{S}}^{FSIR}$ and $r\ge K$.

We maximize $D\left(k\right)$ over $k=1,\dots ,r$, and denote the maximizer as $\widehat{K}$. Then, if $C_n/n\to 0$ and $C_n\to \infty$, the estimate $\widehat{K}$ by (6) satisfies: $P(\widehat{K}=1)\to 1$ under $H_0$; $P(\widehat{K}=K\ge 1)\to 1$ under $H_1$; refer to Theorem 4 in [34]. The choice of $C_n=\sqrt{n}$ can ensure the consistency of the estimators under hypotheses $H_0$ and $H_1$.

4. Asymptotic Properties

Define semi-metric $d_{\beta }(x_1,x_2)=\left|\langle \beta ,x_1-x_2\rangle \right|$. The following assumptions are used to prove the asymptotic properties of the test statistic.

Assumption 1. 

${E\parallel X\parallel }^4<\infty$, Γ has eigenvalues ${\lambda }_1>{\lambda }_2>\dots >0$, and $E{\xi }_j^4\le C{\lambda }_j^2$.

Assumption 2. 

For some constants $a,b$ that satisfy $a>1$ and $a-1/2<b$, $j^{-a}\le C{\lambda }_j$, $|{\xi }_{kj}^{*}|\le C{j}^{-b}$, for some $C>0$, where ${\xi }_{kj}^{*}=\langle {\beta }_k,{\varphi }_j\rangle ,j=1,2,\dots$ are the generalized Fourier coefficients of ${\beta }_k,1\le k\le K$.

Assumption 3. 

The regularization parameter is chosen as $\rho \sim n^{-a/(a+2b)}$.

Assumption 4. 

$h=h_n$ is a sequence of positive numbers satisfying $C_2{n}^{-{\tau }_2}<h<C_1{n}^{-{\tau }_1}$ with $0<{\tau }_1<{\tau }_2<1$.

Assumption 5. 

K is an asymmetrical strictly dereasing kernel in $[0,1]$ such that $\exists c_1,c_2>0,c_1{I}_{[0,1]}\left(t\right)<K\left(t\right)<c_2{I}_{[0,1]}\left(t\right)$ for $\forall t\in \mathbb{R}$.

Assumption 6. 

(1) $\mathcal{C}$ is a compact subset of $\mathcal{H}$ such that $X\in \mathcal{C}$, a.s.; (2) $\forall \beta \in {\Theta }_n$ such that $card{\Theta }_n=n^{\alpha }$ with $\alpha >0$, we have $P(d_{\beta }(X_1,X_2)<h|X_1)=C_{X_1,\beta }h+o\left(h\right)$, a.s., where $X_1$ and $X_2$ are independent copies of X; (3) $0<\underset{\beta \in {\Theta }_n}{inf}{C}_{X_1,\beta }\le \underset{\beta \in {\Theta }_n}{sup}{C}_{X_1,\beta }<\infty$, a.s.

Assumption 7. 

Let $g_{\beta }(·)=E\left[Y\right|\langle \beta ,·\rangle ]$. $g_{\beta }$ satisfies, for $\forall \beta$, the Holder-type condition: $\exists C>0,$$\exists b_1>0,\forall (x_1,x_2)\in {\mathcal{C}}^2,|g_{\beta }\left(x_1\right)-g_{\beta }\left(x_2\right)|\le C{d}_{\beta }{(x_1,x_2)}^{b_1}$.

Assumption 8. 

For any positive integer $c_3$, ${E\left(\right|Y|}^{c_3}\left|X\right)\le C_{c_3,X}<\infty$, a.s. and $\exists \varrho >0$, $E\left(Y^2\right|X=x)=\sigma \left(x\right)\ge \varrho$, with $\sigma (·)$ continuous on $\mathcal{C}$.

Assumption 9. 

The density $f(\langle \mathit{B},X\rangle )$ of $\langle \mathit{B},X\rangle$ on its support ${\mathcal{C}}_1$ exists and has two bounded derivatives and satisfies $0<{inf}_{\langle \mathit{B},X\rangle \in {\mathcal{C}}_1}f\left(\langle \mathit{B},X\rangle \right)\le {sup}_{\langle \mathit{B},X\rangle \in {\mathcal{C}}_1}f\left(\langle \mathit{B},X\rangle \right)<\infty$.

Remark 3. 

Assumptions 1–3 are used to obtain $\parallel {\widehat{\beta }}_j-{\beta }_j{\parallel }^2=O_p\left(n^{-(2b-1)/(a+2b)}\right)\equiv O_p\left(r_n^2\right),$$j=1,\dots ,K$ and $r_n=n^{-\frac{2b-1}{2(a+2b)}}$, which was shown in [18]. By choosing the regularization parameter as $\rho \sim n^{-a/(a+2b)}$ in Assumption 3, we aim to balance the bias and variance of the estimator and avoid overfitting. The choice of ρ in this form is motivated by the theoretical analysis of the convergence rates of the FSIR methods. Assumptions 4–8 mainly come from [1], which are necessary assumptions to obtain the following Theorem 1. Assumption 9 is needed for the asymptotic normality of our statistic.

For a given $g(·)$, ${\widehat{\epsilon }}_i=Y_i-g\left(\langle \widehat{\beta },X_i\rangle \right)$. Similar to the proof of [25], under Assumptions 1–3 and $H_0$, we have $\parallel \widehat{\beta }{-\beta \parallel }^2=O_p\left(r_n^2\right)$ for least squares estimate (or penalized likelihood estimation in [38,39], but other assumptions may be needed). Therefore, the limiting behavior of the test statistic can be obtained.

Theorem 1. 

Given Assumptions 1–9, if $n{h}^{1/2}{r}_n^2\to 0$ and $r_n/h\to 0$ as $n\to \infty$, then, under $H_0$, we have

$$T_n^{FSIR}\stackrel{d}{⟶}N(0,1)$$

Proof. 

See Appendix A (Part I).    □

Remark 4. 

It should be noted that although theoretically, we find that $FSC\stackrel{p}{⟶}0$ as $n\to \infty$, through simulation, we found that FSC can improve the power to some degree for finite samples.

We now investigate the power performance of the test statistic $T_n$ under the fixed alternatives model (2). Suppose that under $H_1$, there exists a unique function $\theta \in L^2\left([0,1]\right)$ satisfying $\theta =argmi{n}_{\beta }E{(Y-g\left(\langle \beta ,X\rangle \right))}^2$; then, ${\widehat{\epsilon }}_i=Y-g\left(\langle \theta ,X_i\rangle \right)-\{g\left(\langle \widehat{\beta },X_i\rangle \right)-g\left(\langle \theta ,X_i\rangle \right)\}$.

Theorem 2. 

Under the alternative model (2) and Assumptions 1–9, it holds that $\parallel \widehat{\beta }-\theta \parallel =O_p\left(r_n\right)$ and

$$T_n^{FSIR}\to \infty .$$

Proof. 

See Appendix A (Part II).    □

Next, we consider the following sequence of the local alternative model as

$$\begin{array}{c}\hfill H_{1n}:Y=g\left(\langle {\beta }_0,X\rangle \right)+C_{1n}G\left(\langle \mathit{B},X\rangle \right)+\epsilon ,\end{array}$$

(7)

where $C_{1n}$ goes to zero, $G(·)$ satisfies $E\left[G^2\left(\langle \mathit{B},X\rangle \right)\right]<\infty$ and ${inf}_{\beta \in L^2\left([0,1]\right)}E{[G\left(\langle \mathit{B},X\rangle \right)-g\left(\langle \beta ,X\rangle \right)]}^2>0$.

In order to obtain the main results about the power behaviors under $H_{1n}$ of (7), we need to show the asymptotic property of $\widehat{K}$ when $C_{1n}\to 0$.

Proposition 1. 

Under the local alternative hypothesis $H_{1n}$ in (7) and Assumptions 1–3, when $C_n{h}^{1/2}\to \infty$ ($C_n$ was introduced in (6)), if $C_{1n}=O\left(n^{-1/2}{h}^{-1/4}\right)$, we have $P(\widehat{K}=1)\to 1$.

Proof. 

See Appendix A (Part III).    □

We now present the power performance of our tests under the local alternative hypothesis. Before this, the following condition needs to be met.

Similar to the parameter estimation method under $H_0$, we can obtain the parameter estimate $\widehat{\beta }$ with observations ${\{X_i,Y_i\}}_{i=1}^n$ under $H_{1n}$. Then, we have ${\widehat{\epsilon }}_i={\epsilon }_i+C_{1n}G\left(\langle \mathit{B},X\rangle \right)-\{g\left(\langle \widehat{\beta },X_i\rangle \right)-g\left(\langle {\beta }_0,X_i\rangle \right)\}$.

Theorem 3. 

If Assumptions 1–9 hold, $n{h}^{1/2}{r}_n^2\to 0$ and $r_n/h\to 0$ as $n\to \infty$. Then, under $H_{1n}$, if $C_{1n}=n^{-1/2}{h}^{-1/4}$ and $\parallel \widehat{\beta }-{\beta }_0\parallel =O_p\left(r_n\right)$, we have

$$T_n^{FSIR}\stackrel{d}{⟶}N(\omega ,1),$$

where $\frac{E\left[G^2\left(\langle \mathit{B},X\rangle \right)\right]}{\sqrt{2{\sigma }^{2}E\left[f^{-1}\left(\langle \mathit{B},X\rangle \right)\right]}}$, ${\sigma }^2=Var\left(\epsilon \right)$.

Proof. 

See Appendix A (Part III).    □

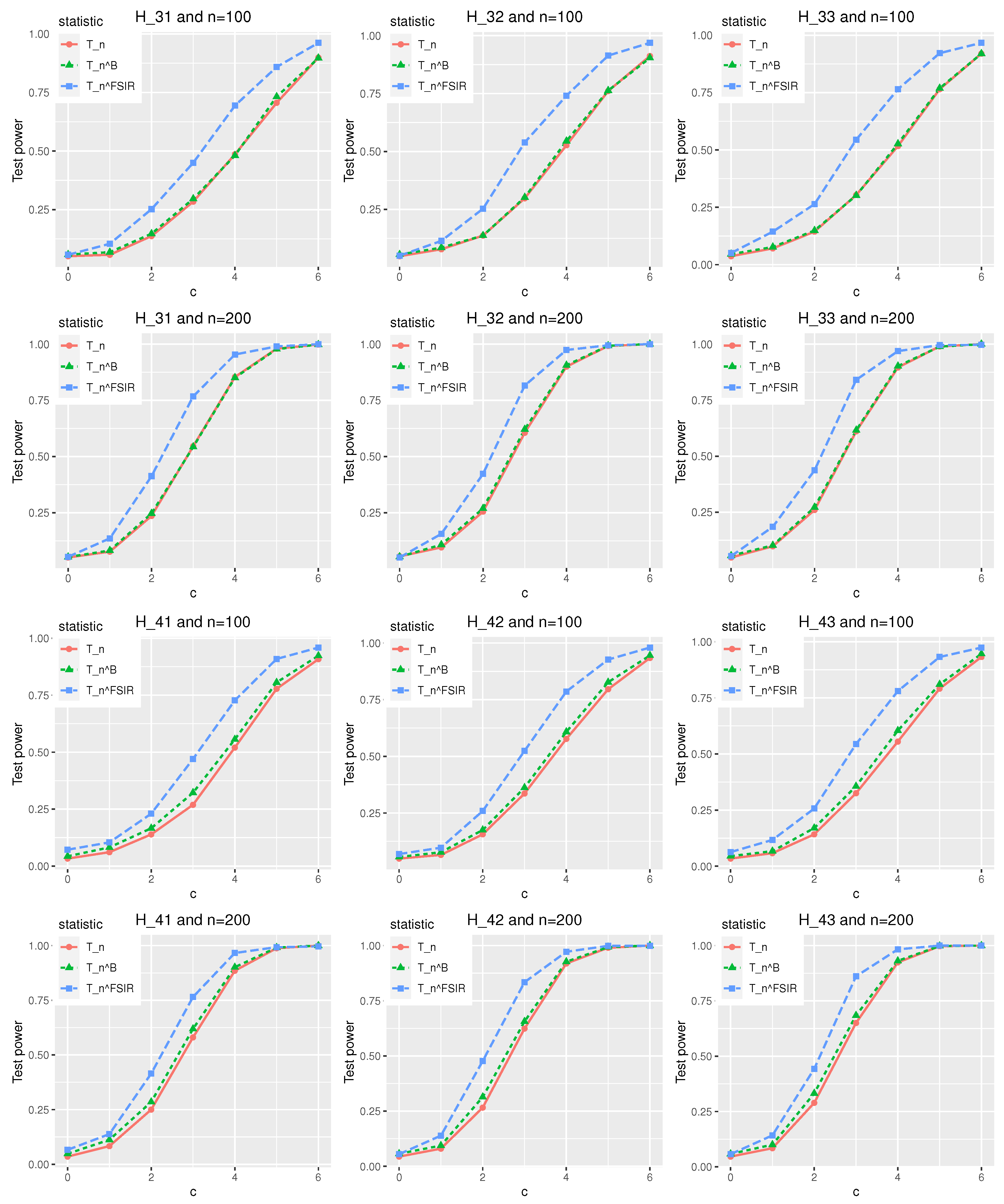
5. Simulations Results and Real Data Analysis

We now perform simulations to check the performance of the proposed test. In the non-parametric estimation, we use the Quartic kernel function $K\left(u\right)=15/16{(1-u^2)}^{2}I(u\in [0,1])$, and the bandwidth h is selected by generalized cross-validation (GCV), which is similar to the method in [40]. Similar to the kernel estimators in Euclid spaces, the choice of the kernel affects less, and other kernel functions are also applicable, such as Gaussian kernel function and Triangular kernel function. The reason for choosing the Quartic kernel function is usually because it has a better fitting effect than the Triangular kernel, and compared to Gaussian kernel function, the Quartic kernel function is relatively more flexible in bandwidth selection. In the functional regression analysis, the optimal bandwidth h can be chosen by the R function $fregre.np$ in the $fda.usc$ package. Since the conclusion in [18] shows that the results are less sensitive to the slice number $\dot{S}$, we choose $\dot{S}=3$ in the simulations if not specifically stated. The regularization parameter is chosen as $\rho =0.02$, which is suggested by the results in [18]. All studies are based on 1000 repetitions, and the significance level is always taken as $\alpha =0.05$. In the following subsections, we check the adequacy of the parametric functional single-index model by considering that $g(·)$ is both linear and nonlinear.

5.1. Study 1: Linear Link Function

When $g(·)$ is a linear function, we need to check the adequacy of the functional linear models (FLM). Among the existing model testing methods for FLM, [13] constructed two test statistics $\mathrm{CvM}$ and $\mathrm{KS}$ based on a random projection empirical process. We also compare the proposed test with the weighted kernel smoothing test suggested in [11], and we denote the test by ${\mathrm{S}}_{\mathrm{n}}$ when its critical value is directly given by the asymptotic normal distribution and ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{B}}$ when its critical value is obtained by bootstrap. In addition, we also extend the method of [11] to sufficient dimension reduction with the kernel function $K(\langle \mathit{B},X_i-X_j\rangle /h)$ and denote the test as ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{FSIR}}$ (see the following Algorithm 2). Similar to ${\mathrm{S}}_{\mathrm{n}}$ and ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{B}}$, we can drop out the FSDR and just use a univariate kernel $K(\parallel X_i-X_j\parallel /h)$ to substitute the multivariate kernel in ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$; then, we obtain the corresponding statistics as ${\mathrm{T}}_{\mathrm{n}}$ and ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{B}}$, respectively. In the simulation, the $\mathrm{KS}$ and $\mathrm{CvM}$ approach can be directly implemented by the $rp.flm.test$ function in R package $fda.usc$ when $g(·)$ is a linear link function, and the number of projections is taken as 3. The bootstrap resampling number is 500 in each case. The specific steps to calculate the test statistic ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ and ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{FSIR}}$ are as follows:   

Algorithm 2: Calculate ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ and ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{FSIR}}$

step 1. To obtain $\widehat{\epsilon }$ in ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ and ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{FSIR}}$, we use the $pfr$ function in the $refund$ package of R for the FLM parameter estimation. step 2. $\widehat{\mathit{B}}$ in the kernel function $K_h\left(\langle \widehat{\mathit{B}},X_i-X_j\rangle \right)$ of the test statistic ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ is estimated by Algorithm 1. step 3. $\widehat{K}$ is determined by (6). When $\widehat{K}=1$, $K_h(·)$ is a one-dimensional kernel function; when $\widehat{K}>1$, $K_h(·)$ is the product of $\widehat{K}$ one-dimensional kernel functions. step 4. Then, we compute $S_n^{FSIR}=\frac{1}{n(n-1)}{\sum }_{j\ne i}^n\frac{1}{h}{K}_h\left(\langle \widehat{\mathit{B}},X_i-X_j\rangle \right){\widehat{\epsilon }}_i{\widehat{\epsilon }}_j$ and $T_n^{FSIR}$ in (5).

We consider the following functional linear link model

$$Y=\langle X,{\beta }_1\rangle +c·m\left(\langle X,\mathit{B}\rangle \right)+\epsilon ,$$

where X is a standard Brownian motion on $[0,1]$ and is observed on a grid of equally spaced 101 points, ${\beta }_j=sin\left(j\pi t\right)$ is the Fourier orthogonal basis with $j=1,2,\dots$, $\epsilon \sim N(0,0.1^2)$, c is a constant, and the null hypothesis $H_0$ holds when $c=0$. We carry out simulations from different perspectives with two examples.

Example 1. 

In this example, our aim is to examine the performance of different test statistics under following alternative models:

• $H_{11}:Y=\langle X,{\beta }_1\rangle +0.2c·cos\left(2\pi \langle X,{\beta }_1\rangle \right)+\epsilon$;
• $H_{12}:Y=\langle X,{\beta }_1\rangle +0.2c·exp(-\langle X,{\beta }_1\rangle )+\epsilon$;
• $H_{13}:Y=\langle X,{\beta }_1\rangle +0.2c·\langle X,{\beta }_1\rangle \langle X,{\beta }_2\rangle +\epsilon$;
• $H_{14}:Y=\langle X,{\beta }_1\rangle +c\left\{exp(-\langle X,{\beta }_2\rangle )+cos\left(\langle X,{\beta }_3\rangle \right)\right\}+\epsilon$;
• $H_{15}:Y=\langle X,{\beta }_1\rangle +c\left\{exp(-\langle X,{\beta }_2\rangle )+cos\left(\langle X,{\beta }_3\rangle \right)+{\langle X,{\beta }_4\rangle }^2\right\}+\epsilon$;
• $H_{16}:Y=\langle X,{\beta }_1\rangle +c\left\{exp(-\langle X,{\beta }_2\rangle )+cos\left(\langle X,{\beta }_3\rangle \right)+{\langle X,{\beta }_4\rangle }^2+{\langle X,{\beta }_5\rangle }^3\right\}+\epsilon$,

where $H_{11}$ and $H_{12}$ are used to examine whether and how much power our test loses by sufficient dimension reduction. $H_{13}$ is the case of the multiplicative effect, $H_{14}$–$H_{16}$ are used to analyze the effect of dimensionality on the different test statistics.

Table A1. Empirical sizes and powers of test statistics under five alternative models in Example 1.

Models	Sample	c	${\mathit{S}}_{\mathit{n}}$	${\mathit{S}}_{\mathit{n}}^{\mathit{B}}$	${\mathit{S}}_{\mathit{n}}^{\mathit{FSIR}}$	${\mathit{T}}_{\mathit{n}}$	${\mathit{T}}_{\mathit{n}}^{\mathit{B}}$	${\mathit{T}}_{\mathit{n}}^{\mathit{FSIR}}$	$\mathit{CvM}$	$\mathit{KS}$
$H_{11}$	$n=100$	0	0.032	0.047	0.035	0.036	0.052	0.042	0.054	0.059
		2	0.175	0.246	0.390	0.186	0.258	0.424	0.136	0.125
		4	0.699	0.771	0.941	0.749	0.814	0.957	0.327	0.270
		6	0.981	0.990	0.997	0.989	0.995	0.999	0.559	0.471
	$n=200$	0	0.038	0.045	0.040	0.039	0.051	0.048	0.052	0.047
		2	0.397	0.492	0.740	0.403	0.531	0.740	0.229	0.196
		4	0.981	0.988	0.999	0.989	0.991	0.999	0.582	0.493
		6	1.000	1.000	1.000	1.000	1.000	1.000	0.812	0.723
$H_{12}$	$n=100$	0	0.032	0.047	0.035	0.036	0.052	0.042	0.054	0.059
		2	0.170	0.217	0.390	0.204	0.250	0.557	0.404	0.299
		4	0.762	0.742	0.590	0.820	0.790	0.650	0.761	0.673
		6	0.978	0.957	0.877	0.983	0.968	0.893	0.893	0.839
	$n=200$	0	0.038	0.045	0.040	0.039	0.051	0.048	0.052	0.047
		2	0.426	0.490	0.798	0.491	0.569	0.935	0.691	0.556
		4	0.989	0.990	0.931	0.997	0.996	0.951	0.972	0.938
		6	1.000	1.000	0.997	1.000	1.000	0.997	0.993	0.989
$H_{13}$	$n=100$	0	0.032	0.047	0.035	0.036	0.052	0.042	0.054	0.059
		2	0.090	0.141	0.123	0.115	0.153	0.198	0.257	0.181
		4	0.453	0.494	0.579	0.528	0.550	0.646	0.634	0.522
		6	0.819	0.798	0.844	0.877	0.848	0.879	0.788	0.710
	$n=200$	0	0.038	0.045	0.040	0.039	0.051	0.048	0.052	0.047
		2	0.187	0.265	0.263	0.270	0.345	0.434	0.503	0.368
		4	0.848	0.877	0.917	0.928	0.932	0.944	0.883	0.818
		6	0.992	0.993	0.995	0.999	0.999	1.000	0.954	0.926
$H_{14}$	$n=100$	0	0.032	0.047	0.035	0.036	0.052	0.042	0.054	0.059
		2	0.117	0.166	0.151	0.146	0.201	0.233	0.195	0.158
		4	0.523	0.547	0.758	0.613	0.624	0.799	0.324	0.279
		6	0.853	0.843	0.950	0.872	0.883	0.954	0.371	0.326
	$n=200$	0	0.038	0.045	0.040	0.039	0.051	0.048	0.052	0.047
		2	0.291	0.375	0.352	0.399	0.486	0.521	0.285	0.235
		4	0.835	0.848	0.977	0.876	0.876	0.985	0.460	0.414
		6	1.000	1.000	1.000	1.000	1.000	0.999	0.509	0.467
$H_{15}$	$n=100$	0	0.032	0.047	0.035	0.036	0.052	0.042	0.054	0.059
		2	0.244	0.314	0.348	0.283	0.350	0.444	0.349	0.278
		4	0.826	0.836	0.937	0.857	0.858	0.956	0.541	0.496
		6	0.881	0.876	0.996	0.883	0.867	0.995	0.570	0.520
	$n=200$	0	0.038	0.045	0.040	0.039	0.051	0.048	0.052	0.047
		2	0.581	0.661	0.704	0.679	0.745	0.832	0.517	0.454
		4	0.896	0.898	1.000	0.898	0.899	0.999	0.717	0.671
		6	1.000	1.000	1.000	1.000	1.000	1.000	0.726	0.687
$H_{16}$	$n=100$	0	0.032	0.047	0.035	0.036	0.052	0.042	0.054	0.059
		2	0.242	0.315	0.343	0.281	0.350	0.479	0.344	0.296
		4	0.730	0.724	0.946	0.755	0.743	0.958	0.530	0.469
		6	0.890	0.880	0.995	0.890	0.882	0.996	0.579	0.528
	$n=200$	0	0.038	0.045	0.040	0.039	0.051	0.048	0.052	0.047
		2	0.582	0.661	0.737	0.676	0.734	0.857	0.529	0.466
		4	0.898	0.897	1.000	0.901	0.902	1.000	0.717	0.670
		6	1.000	1.000	1.000	1.000	1.000	1.000	0.740	0.703

shows the empirical sizes and powers of different test statistics with the nominal size $\alpha =0.05$. Through the comparative analysis in different scenarios, we conclude that: (1) when the critical value is directly given by the asymptotic normal distribution, the empirical sizes of ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ are relatively closer to the pre-specified significance level $\alpha =0.05$, while ${\mathrm{S}}_{\mathrm{n}}$ and ${\mathrm{T}}_{\mathrm{n}}$ are more conservative. (2) ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ has the highest power, except for small and moderate cs in the cases of $H_{12}$ and $H_{13}$. (3) ${\mathrm{S}}_{\mathrm{n}}$, $\mathrm{CvM}$ and $\mathrm{KS}$ test statistics are mainly applicable to the cases of $H_{11}$ and $H_{12}$, see [11,13]. In $H_{11}$ and $H_{12}$, $\mathit{B}={\beta }_1$ under both the null and alternative hypothesis. Therefore, FSDR is not needed in these two alternative models, but we can examine whether and how much the power would be lost if FSDR were used. Comparing the results of using FSDR and not using FSDR in Table A1 for $H_{11}$ and $H_{12}$, it is evident that the use of FSDR would result in some loss of power in $H_{12}$, while ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ still has the highest power under $H_{1n}$. (4) Under the multiplicative effects model $H_{13}$, the considered test statistics remain effective, and the test statistic using FSIR is slightly more powerful for large c and n. (5) From $H_{14}$ to $H_{16}$, the power of the considered test statistic increases to varying degrees with the increasing dimensionality. (6) From $H_{14}$ to $H_{16}$, there is a significant improvement in the powers of almost all test statistics. This indicates that the test statistics are more sensitive to the quadratic model than the high-frequency oscillation model. The power is slightly improved after adding a cubic model from $H_{15}$ to $H_{16}$. (7) The powers of all statistics increase significantly as the sample size increases, and the power of the FSIR method increases more rapidly with increasing c, especially for ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$.

Example 2. 

To analyze the effect of different data from what we considered in Example 1, we take model $Y=\langle X,{\beta }_1\rangle +cexp(-\langle X,{\beta }_2\rangle )+\epsilon$ as an example to analyze the performance of different statistics under the following data generation mechanism (DGM):

• $DG{M}_1:X\sim OrnsteinUhlenbeckprocess,{\beta }_1=sin\left(\pi t\right),{\beta }_2=sin\left(2\pi t\right)$;
• $DG{M}_2:X\sim standardBrownianmotion,{\beta }_1=sin\left(\pi t\right),{\beta }_2=sin\left(2\pi t\right)$;
• $DG{M}_3:X\sim standardBrownianmotion,{\beta }_1=2{(2t-1)}^2-1,{\beta }_2=4{(2t-1)}^3-3(2t-1)$;
• $DG{M}_4:X\sim standardBrownianmotion,{\beta }_1=2{(2t-1)}^2-1,{\beta }_2=sin\left(2\pi t\right)$,

where $\epsilon \sim N(0,0.1^2)$, ${\beta }_1$ and ${\beta }_2$ in ${\mathrm{DGM}}_1-{\mathrm{DGM}}_2$ and ${\mathrm{DGM}}_3$ are the Fourier orthogonal basis and Chebyshev orthogonal basis, respectively, and ${\mathrm{DGM}}_4$ has a non-orthogonal basis.

We present the test results for Example 2 in

Table A2. Empirical sizes and powers of test statistics under four DGM in Example 2.

DGM	Sample	c	${\mathit{S}}_{\mathit{n}}$	${\mathit{S}}_{\mathit{n}}^{\mathit{B}}$	${\mathit{S}}_{\mathit{n}}^{\mathit{FSIR}}$	${\mathit{T}}_{\mathit{n}}$	${\mathit{T}}_{\mathit{n}}^{\mathit{B}}$	${\mathit{T}}_{\mathit{n}}^{\mathit{FSIR}}$	$\mathit{CvM}$	$\mathit{KS}$
$DG{M}_1$	$n=100$	0	0.037	0.045	0.043	0.039	0.044	0.046	0.053	0.049
		2	0.168	0.242	0.258	0.185	0.254	0.370	0.262	0.192
		4	0.667	0.703	0.907	0.716	0.743	0.947	0.417	0.369
		6	0.848	0.843	0.990	0.865	0.851	0.994	0.544	0.486
	$n=200$	0	0.041	0.054	0.038	0.047	0.041	0.053	0.057	0.059
		2	0.401	0.490	0.560	0.442	0.562	0.750	0.396	0.319
		4	0.885	0.884	1.000	0.896	0.895	1.000	0.649	0.601
		6	1.000	1.000	1.000	1.000	1.000	1.000	0.698	0.646
$DG{M}_2$	$n=100$	0	0.039	0.049	0.052	0.038	0.048	0.056	0.050	0.054
		2	0.238	0.298	0.359	0.262	0.310	0.491	0.342	0.266
		4	0.806	0.814	0.966	0.838	0.831	0.985	0.563	0.485
		6	0.875	0.870	0.999	0.884	0.874	0.999	0.666	0.586
	$n=200$	0	0.033	0.061	0.057	0.039	0.046	0.052	0.062	0.049
		2	0.534	0.614	0.730	0.609	0.692	0.867	0.538	0.443
		4	0.897	0.899	1.000	0.897	0.898	1.000	0.725	0.661
		6	1.000	1.000	1.000	1.000	1.000	1.000	0.805	0.773
$DG{M}_3$	$n=100$	0	0.030	0.058	0.044	0.040	0.063	0.052	0.061	0.066
		2	0.059	0.097	0.060	0.059	0.100	0.058	0.113	0.100
		4	0.175	0.251	0.284	0.185	0.252	0.392	0.211	0.177
		6	0.430	0.506	0.794	0.479	0.542	0.882	0.337	0.274
	$n=200$	0	0.036	0.047	0.045	0.038	0.046	0.048	0.054	0.053
		2	0.100	0.165	0.149	0.118	0.192	0.166	0.186	0.165
		4	0.468	0.558	0.683	0.530	0.620	0.818	0.352	0.292
		6	0.778	0.786	0.992	0.812	0.833	0.997	0.501	0.424
$DG{M}_4$	$n=100$	0	0.038	0.054	0.042	0.039	0.053	0.055	0.053	0.061
		2	0.225	0.302	0.266	0.242	0.319	0.245	0.315	0.284
		4	0.781	0.785	0.953	0.819	0.810	0.975	0.564	0.506
		6	0.883	0.872	0.997	0.885	0.875	0.998	0.646	0.591
	$n=200$	0	0.039	0.042	0.041	0.043	0.045	0.051	0.061	0.071
		2	0.527	0.623	0.586	0.619	0.684	0.620	0.513	0.456
		4	0.996	0.997	1.000	0.997	0.997	1.000	0.747	0.686
		6	1.000	1.000	1.000	1.000	1.000	1.000	0.816	0.776

. In ${\mathrm{DGM}}_1$ and ${\mathrm{DGM}}_2$, although X is different, the test results are similar. Comparing the results of ${\mathrm{DGM}}_2-{\mathrm{DGM}}_4$, which has different $\beta$s, we find that the powers in the Chebyshev basis are lower than those in the Fourier basis, while the powers in the case of the non-orthogonal basis are somewhere in between.

5.2. Study 2: Non-Linear Link Function

When $g(·)$ is a given nonlinear function, we only give results of ${\mathrm{T}}_{\mathrm{n}},{\mathrm{T}}_{\mathrm{n}}^{\mathrm{B}}$ and ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$, since ${\mathrm{S}}_{\mathrm{n}}$, ${\mathrm{S}}_{\mathrm{n}}^{\mathrm{B}}$, ${\mathrm{T}}_{\mathrm{n}}$, ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{B}}$, $\mathrm{CvM}$ and $\mathrm{KS}$ are studied for FLM in [11,13]. Except for step 1 in Algorithm 2, the other steps are similar. Step 1 can be implemented in a similar way to functional principal component analysis in [25] when $g(·)$ is known, and $\widehat{\epsilon }$ can be obtained through nonlinear least squares estimation.

We consider the nonlinear link function model:

$$Y=g\left(\langle X,{\beta }_1\rangle \right)+c·m\left(\langle X,\mathit{B}\rangle \right)+\epsilon ,$$

where $g(·)$ is a smooth function. Similar to Study 1, we mainly analyze the performance of the test under different alternative models. The data generation mechanisms are the same as those in ${\mathrm{DGM}}_2$. In order to make our test more widely applicable, we also analyze the case of monotonic and non-monotonic link functions, as demonstrated by the following two examples, respectively.

Example 3. 

In this example, we consider the case where $g(·)$ is monotonic. The following models with the exponential link function are implemented.

• $H_{31}:Y=exp\left(\langle X,{\beta }_1\rangle \right)+c·cos\left(\langle X,{\beta }_2\rangle \right)+\epsilon$;
• $H_{32}:Y=exp\left(\langle X,{\beta }_1\rangle \right)+c·\left(cos\left(\langle X,{\beta }_2\rangle \right)+\left|\langle X,{\beta }_3\rangle \right|\right)+\epsilon$;
• $H_{33}:Y=exp\left(\langle X,{\beta }_1\rangle \right)+c·\left(cos\left(\langle X,{\beta }_2\rangle \right)+\left|\langle X,{\beta }_3\rangle \right|+{\langle X,{\beta }_4\rangle }^2\right)+\epsilon$.

Example 4. 

To examine the power of the test when $g(·)$ is non-monotonic, we analyze the following models with the sin link function,

• $H_{41}:Y=sin\left(\langle X,{\beta }_1\rangle \right)+c·exp\left(\langle X,{\beta }_2\rangle \right)+\epsilon$;
• $H_{42}:Y=sin\left(\langle X,{\beta }_1\rangle \right)+c·\left(exp\left(\langle X,{\beta }_2\rangle \right)+\left|\langle X,{\beta }_3\rangle \right|\right)+\epsilon$;
• $H_{43}:Y=sin\left(\langle X,{\beta }_1\rangle \right)+c·\left(exp\left(\langle X,{\beta }_2\rangle \right)+\left|\langle X,{\beta }_3\rangle \right|+{\langle X,{\beta }_4\rangle }^2\right)+\epsilon$.

We present the results for Examples 3 and 4 in Figure A1. We make three observations. First, for the testing of nonlinear models, the statistic constructed based on the FSIR method always has higher power than others. Second, the difference between monotonic and non-monotonic power is not significant, and the effect of dimensionality on power is not very large, but the differences between ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ and ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{B}},{\mathrm{T}}_{\mathrm{n}}$ in the monotonic cases are more obvious than the non-monotonic cases. For example, the power increment of ${\mathrm{T}}_{\mathrm{n}}^{\mathrm{FSIR}}$ relative to ${\mathrm{T}}_{\mathrm{n}}$ in $H_{33}$ is slightly larger than that in $H_{43}$ when $n=200$. Third, there is a significant increase in power with increasing sample size.

To summarize, through the above examples, including different data generation mechanisms, multiplicative effect models, and monotone/non-monotone cases under functional data, we find that the use of the FSDR method in functional data not only increases the power with the increase of sample size n and deviation parameter c but also improves the power of the test to some extent compared with the method without using FSDR [11,13] even under the multiplicative effect model. The above conclusion is largely consistent with the findings in vector data analysis [14,41,42]. In functional data analysis, similar research has been conducted, such as [43], but Ref. [43]’s method is only applicable to linear models. Our study is not only effective in linear situations but also performs well in nonlinear cases.

5.3. Analysis of the COVID-19 Data

As one of the most important aggregate indicators reflecting the overall macroeconomic operation of each country, Gross Domestic Product (GDP) is an important reference value for decision makers to make rational decisions based on the economic situation. The large shock to the world’s macroeconomy caused by the COVID-19 crisis has imposed tremendous challenges on now accurately forecasting a country’s GDP. Performing relevant data modeling is an important way to make predictions. Goodness-of-fit tests are a prerequisite for accurate modeling. Therefore, when the relationship between the number of new COVID-19 cases per day and the GDP of a country is known, the model can be tested first using the method in this paper, and then the related statistical analysis can be performed. Below, we describe the specific operations.

If X and Y have the following relationship model

$$E\left[Y_i^{GDP}\right|X_i]=g\left(\langle X_i,\beta \rangle \right),$$

where $Y_i$ is the DP growth (annual %) (https://advisor.visualcapitalist.com/gdp-growth-by-country-in-2021/, accessed on 18 January 2023) of country i in 2021, $X_i\left(t\right)$ is the rolling mean of newly confirmed COVID-19 cases (in R package $tidycovid19$) per day as reported by JHU CSSE (https://www.worldbank.org/en/home, accessed on 18 January 2023) in 2021, $i=1,2,\dots ,183$. Rolling mean can be implemented by the $rollmean$ function in the R language and the width of the rolling window is 7; missing values are replaced by the nearby rolling mean. The specific trends of X and Y and the selected countries are shown in Figure A2, where the legend shows the ISO numbers for each country. In the legend of X, we have only indicated the three countries with a high number of confirmed cases. It is worth mentioning that there are more than 183 countries in the world, and we selected 183 countries for our analysis mainly because we excluded those countries that did not publish their GDP in 2021 and had zero cumulative confirmed cases in 2021.

Using the test statistic and parameter values, such as bandwidth and slice number, as mentioned in the simulation, if g is a linear function, the test results are displayed in

Table A3. The p-value of different test statistics in real data analysis.

Statistic	${\mathit{S}}_{\mathit{n}}$	${\mathit{S}}_{\mathit{n}}^{\mathit{B}}$	${\mathit{S}}_{\mathit{n}}^{\mathit{FSIR}}$	${\mathit{T}}_{\mathit{n}}$	${\mathit{T}}_{\mathit{n}}^{\mathit{B}}$	${\mathit{T}}_{\mathit{n}}^{\mathit{FSIR}}$	$\mathit{CvM}$	$\mathit{KS}$
p-value	0.000	0.009	0.000	0.000	0.013	0.000	0.528	0.374

. Table A3 shows that except for $\mathrm{CvM}$ and $KS$, all other statistics reject functional linear models, where $\widehat{K}=3$ with $\mathrm{FSIR}$. These conclusions suggests that a nonlinear model should be used: for example, a functional multi-index model may be appropriate. However, $\mathrm{CvM}$ and $\mathrm{KS}$ fail to detect this nonlinear model structure.

6. Conclusions and Discussion

In this paper, we extend [14]’s method to functional data and construct a different test statistic for checking a single-index model. We theoretically prove the large-sample properties of the constructed test statistic under the null hypothesis, alternative hypothesis, and local alternative hypothesis. In addition, the simulations of Section 4 also show that the FSIR-based statistic has higher power compared to other statistic in most cases and can be used to check the adequacy of functional linear or nonlinear models.

We can extend our methodology to missing, censored or dependent data. For example, the case of missing data can be referred to the method of [41]. Of course, in addition to mean regression, we can also consider the quantile regression or composite quantile regression.