Abstract
Zero-and-one inflated count time series have only recently become the subject of more extensive interest and research. One of the possible approaches is represented by first-order, non-negative, integer-valued autoregressive processes with zero-and-one inflated innovations, abbr. ZOINAR(1) processes, introduced recently, around the year 2020 to the present. This manuscript presents a generalization of ZOINAR processes, given by introducing the zero-and-one inflated power series (ZOIPS) distributions. Thus, the obtained process, named the ZOIPS-INAR(1) process, has been investigated in terms of its basic stochastic properties (e.g., moments, correlation structure and distributional properties). To estimate the parameters of the ZOIPS-INAR(1) model, in addition to the conditional least-squares (CLS) method, a recent estimation technique based on probability-generating functions (PGFs) is discussed. The asymptotic properties of the obtained estimators are also examined, as well as their Monte Carlo simulation study. Finally, as an application of the ZOIPS-INAR(1) model, a dynamic analysis of the number of deaths from the disease COVID-19 in Serbia is considered.
Keywords:
time series; zero-and-one inflation; probability generating functions; parameter estimation; simulation; COVID-19; application MSC:
62M10; 60G10; 60G25
1. Introduction
Integer-valued time series modeling is a very popular research topic, with various applications (cf. [1,2,3,4,5]). One of the most popular approaches in modeling the dynamics of count data is provided by non-negative integer-valued autoregressive (INAR) time series models. This approach started from the famous work by Al-Osh and Alzaid [6], which first introduced the so-called INAR(1) process, and since then many results related to these models have been obtained (cf. [7,8,9,10,11,12,13,14,15,16,17]). One of the recently frequent problems in count data modeling is the presence of inflated zero-and-one values in the data, which can appear in various areas of human activity (e.g., the number of requests for issuing policies, breakdowns in the production process, injury in traffic accidents, etc.). To investigate this and similar problems, Saito et al. [18] and Zhang et al. [19] considered a modification (and generalization) of the traditional Poisson distribution, i.e., the so-called zero-and-one inflated Poisson (ZOIP) distribution. As an example of the application of the ZOIP distribution, the frequency of visits to the dentist in Swedish cities was considered in both mentioned manuscripts. Subsequently, Zhang et al. [20] introduced the multivariate ZOIP distribution, with applications in respect of healthcare demand data in Australia and car portfolio data in France.
Using the ZOIP distributed innovations, Qi et al. [21] introduced the first zero-and-one inflated INAR-based model, named the first-order zero-and-one INAR (ZOINAR(1)) process. Another class of ZOINAR time series, named the ZOIPLINAR process, has recently been introduced by Mohammadi et al. [22], where a Poisson–Lindley distribution of innovations inflated by zero and one is considered. Our main motivation is to introduce a more general form of the ZOINAR process, where the power series (PS) distribution with zero-and-one inflation is observed as its innovations. It should be noted that PS distributions represent a wide family of stochastic distributions, based on which many known integer-valued distributions can be obtained. In this way, the first-order zero-and-one inflated power series INAR process (abbr. ZOIPS-INAR(1) process) is proposed here, and it can be seen as a generalization of the previous ZOINAR models. The definition and the basic stochastic characteristics of this process are described in Section 2 and Section 3.
In order to estimate the parameters of INAR-based processes, various techniques have been developed. Conditional least-squares (CLS) estimation is a commonly utilized method, proposed in [23], as well as the method of conditional maximum likelihood (CML) [24]. However, in [25,26], among other methods, moment-based estimation procedures, i.e., Yule–Walker (YW) equations, are discussed. Nevertheless, to apply any of the aforementioned methods, there is usually an assumption that the estimation functions are given in a closed form and also bounded on some parameter space. As will be seen below, such conditions are not fully met in the case of our ZOIPS-INAR(1) process. Therefore, an alternative and a more contemporary approach, named the probability generating function (PGF) method, is proposed here. PGF estimation was theoretically described by Esquivel [27], first practically applied in Stojanović et al. [28], and recently examined in its general form by Stojanović et al. [29]. In order to apply the PGF method in the parameter estimation of the ZOIPS-INAR(1) process, some basic facts about this estimation method are given in Section 4. In addition, the asymptotic properties and efficiency of the PGF estimators of the ZOIPS-INAR(1) process, under some regulatory conditions, are considered here.
In Section 5, the PGF estimators for some specific ZOIPS innovations are analyzed. As typical members of the PS distributions family, but also for some practical reasons, the Poisson and geometric zero-and-one inflated distributions are considered here. For both of them, Monte Carlo simulations of PGF estimates were calculated and compared with the corresponding CLS estimates, which were taken as initial values for the PGF procedure. The asymptotic properties of both types of estimators are also examined here. The application of the ZOIPS-INAR(1) process in modeling the distribution of the number of deaths from the disease COVID-19 in the Republic of Serbia is presented in Section 6. In addition, by comparing the ZOIPS-INAR(1) model with the standard INAR(1) model, it is shown that the observed actual series has pronounced zero-and-one inflation, and that the proposed model has better efficiency and predictive accuracy. Finally, some concluding remarks are given in Section 7.
2. Structure of the ZOIPS-INAR(1) Process
In this section, similarly as in [28,29,30], we firstly introduce the independent identically distributed (IID) time series with the so-called power series (PS) distribution.
Definition 1.
The IID time series , is PS-distributed if its probability mass distribution (PMF) is as follows:
Here, is the discrete set of values that the series can take, and:
- (i)
- is a function defined on the set ;
- (ii)
- is the (unknown) one-dimensional parameter;
- (iii)
- is the function that depends (only) on θ, and such that it is , when .
Equation (1) can, for particular choices of , and , give some of the most well-known types of discrete distributions (see Table 1 below). Nevertheless, we assume that the condition is fulfilled, as is usual in zero-and-one inflated distributions. Additionally, note that according to , the power series converges in fact on . Nevertheless, the assumption is common for the PMF of PS-distributed series , and we observe the convergence of only on the positive interval . Moreover, in this interval, the function has positive, increasing values, as well as positive derivatives, as follows:

Table 1.
Some specific PS distributions, along with their over-dispersion indices and PGFs.
Equality (2) can be useful for determining the moments of series . For this purpose, we have applied a similar procedure as in Stojanović et al. [28], based on the calculation of the moment-generating function (MGF):
Using (2) and the properties of the MGFs, after some calculations, one obtains:
In doing so, the coefficients , for each , are calculated recursively:
Using the first two moments, obtained by Equation (3), the mathematical expectation and the variance of the random variables (RVs) are obtained as follows:
where . If is the so-called over-dispersion index, then the series is over-dispersed; that is, , if and only if the inequality holds, for any . Hence, the convexity of indicates an overdispersion of the series , as can be seen in Table 1. Moreover, for an arbitrary , we can introduce the first-order PGF of RVs in the following way:
The sum obtained above obviously converges on the interval . In addition, the expression in (5) gives the possibility of the simple calculation of first-order PGFs for PS distributions, which are also given in Table 1.
In the following, we define a zero-and-one inflated distribution for an arbitrary PS-distributed time series .
Definition 2.
Let , be the IID time series with the PS distribution, given by Equation (1). The series , has a zero-and-one inflated power series (ZOIPS) distribution if for some , such that , its PMF is given as follows:
where is the vector of (unknown) parameters.
Note that the ZOIPS distribution is a mixture of three distributions: concentrated in zero, concentrated in one, and the PS distribution of the series . Thus, the PMF of RVs can be written as
where we set or equivalently, . It is obvious that when , the ZOIPS distribution is reduced to the previous PS distribution. For these reasons, we assume that and , so that these coefficients represent, respectively, the additional proportions of zeros and ones compared to those allowed by the PS distribution of the series . Using the previous facts, and similar to Qi et al. [21], for the n-th moments of series one obtains:
Using Equations (4) and (9), similarly as with the PS series , one can obtain the necessary and sufficient conditions for the over-dispersion of the ZOIPS series . According to
the series will be over-dispersed if and only if This condition is more flexible than the “ordinary“ over-dispersion of the series . For instance, if is equally-dispersed, i.e., holds, the inequality is fulfilled when Then, the ZOIPS series will be overdispersed, which is the same result as for the Poisson ZOINAR process introduced in Qi et al. [21].
Finally, using Equations (1), (5) and (6), the first-order PGF of the RVs can be easily obtained. After some simple computations, for an arbitrary , it follows that:
Assuming that the aforementioned notations are valid, we now introduce the INAR-based time series with the ZOIPS-distributed innovations .
Definition 3.
The time series , , represents an INAR(1) process with ZOIPS innovations or, simply, a ZOIPS-INAR(1) process, if it fulfills the recurrence relation:
Here, is the ZOIPS-distributed time series with the PMF given by (6), is an unknown parameter, and
is the binomial thinning operator. More precisely, for an arbitrary non-negative integer-valued RV X, the RVs have Bernoulli’s distribution . In addition, RVs are mutually independent (and also independent of X).
As an illustration, Figure 1 shows the realizations of the ZOIPS series and ZOIPS-INAR(1) process, where a Poisson distribution with the parameter is taken as the PS distribution. As can be easily seen, although the value of the parameter is significantly greater than zero (and one), both time series have emphasized zero-and-one inflation.
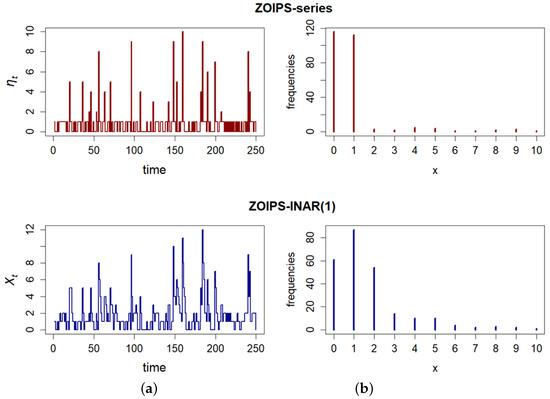
Figure 1.
(a) Dynamics of the ZOIPS series and ZOIPS-INAR(1) process. (b) Empirical frequency distributions of both time series. (Parameters values are: ).
3. Stochastic Properties of the ZOIPS-INAR Process
Based on the mentioned properties of the ZOIPS series , some special properties of the ZOIPS-INAR(1) process can be shown. First, we compute the k-step conditional measures of on . Using some well-known properties of binomial thinning (cf. [31,32]) and Equation (11), for the first-step conditional mean one obtains:
and for the conditional variance:
In the general case, by the method of induction and after some computation, conditional measures of the k-degree can be computed for each . Hence, it follows that:
Theorem 1.
Let be a ZOIPS-INAR(1) process defined by Equation (11). Then, for each the k-step conditional mean and variance for the series are, respectively,
and the autocorrelation function (ACF) at lag k is .
According to Equalities (13), when , the unconditional mean and the variance of RVs can be obtained as follows:
Remark 1.
It can easily be seen that differences and justify equality Thus, similarly to other INAR processes, the series and have the equivalent over-dispersed properties, i.e., they are both at the same time over-, equal- or under-dispersed.
In the following, we examine some characteristics of the distribution of the ZOIPS-INAR(1) process. First of all, we conduct an integer-valued moving average (INMA) representation of infinite order for the series .
Theorem 2.
Proof.
Using the assumptions of the theorem, one can find a constant such that
According to this, it follows that:
and using the definition of the ZOIPS series , given by Equation (6), one obtains:
Hence, the above sum converges uniformly on . Further, the sequence , is monotone and bounded, so Abel’s convergence criterion for infinite sums gives
where the convergence above is uniformly on . According to Theorem 2.1 in Alzaid and Al-Osh [33], condition (15) is sufficient for the equality
Here, and are, respectively, the PGFs of ZOIPS series and ZOIPS-INAR(1) process , and is the vector of (unknown) parameters. Moreover, at least on , the product above converges absolutely. Hence, according to the one-to-one correspondence between the PMFs and PGFs of discrete RVs, it follows that the INMA representation in (14) is equivalent to (16).
To prove the second part of the theorem, note that, using Equation (11), for any it holds that:
According to this, as well as the well-known properties of the binomial thinning operator [31,32], it follows that:
Therefore, the mean-square convergence of the sum in (14) is valid.
To prove the almost certain convergence in (14), we define the event
According to (17) and the definition of the limit value of real functions, we can write the event A as
where Again using (17), for each (fixed) , and , one obtains:
where the expression on the right is the sum of the uncorrelated RVs. Thus, applying the continuity of probability and the definition of the thinning operator (12), for events we have:
By re-applying the continuity property of the probability, as well as the convergence of the product in (16), it follows that i.e., the sum in (14) converges almost surely. □
Remark 2.
Using a similar procedure as in the previous theorem and some general results about the PGFs of non-negative discrete-valued stationary time series (cf. Stojanović et al. [29]), an explicit expression for PGFs of the ZOIPS-INAR(1) process can be obtained. According to Equations (10) and (16), for arbitrary , the series has a PGF of the first order:
Furthermore, suppose that , and , are the so-called overlapping blocks of series . Putting into Equation (17), after some calculations, the explicit expression of the r-dimensional PGF random vector can be obtained:
It can be noted that the PGF of the order will be used in the estimation of parameters of the ZOIPS-INAR(1) process (see Section 4 below).
Let us now consider the Markov properties and marginal distribution of our model.
Theorem 3.
Proof.
According to Equation (11) and the definition of binomial thinning, the conditional distribution of at a given can be expressed as follows:
where
is the PMF of the binomial distribution. Using the definition of the ZOIPS distribution, that is, the PMF of RVs given by Equation (7), one obtains:
where and are, respectively, the PMFs of and . Based on these, we obtain:
It is easy to see that the obtained equality is equivalent to (20), which proves the theorem. □
Remark 3.
Let us recall once again that it is usual to assume that for the zero-and-one distribution, the condition is usually taken. It follows that the first singular part in Equation (20) exists if and only if passes from the state to the non-increasing state . Similarly, the second singular part exists if and only if . Finally, the transition probabilities (20), as well as the use of the conditional probability, give the marginal PMF of the ZOIPS-INAR(1) process:
Thus, the ZOIPS-INAR(1) process is a strictly stationary and ergodic time series.
At the end of this section, similar to Qi et al. [21] and Mohammadi et al. [22], we examine the distribution of the zero-and-one lengths of the ZOIPS-INAR(1) process. Starting with the basic results of the zero-inflated INAR processes (cf. Jazi et al. [34], Wang et al. [35]), we observe the distribution of the “runs”of zeros (resp. ones) in the ZOIPS-INAR(1) process. Thereby, the “runs“ are defined as the number of zeros (resp. ones) between two different non-zeros, i.e., non-one values, respectively. In the following statements, we give the expected lengths and proportions of zeros and ones in our model.
Theorem 4.
The expected lengths of the runs of zeros (resp. ones) for a ZOIPS-INAR(1) process are, respectively, given by:
where and are the functions introduced in Definition 1 for the PS distributions.
Proof.
According to Equation (20), the transition probabilities from zero to zero, and from zero to non-zero values are, respectively,
Since the zero run length is defined as the number of zeros between two non-zero values, it can easily be seen to follow a geometric distribution with parameter . Therefore, the expected length of zero is
where , and the first equality in (21) immediately follows. Similarly, the transition probabilities from one to one and from one to non-one values are, respectively,
Applying the same procedure as before, the second equality in (21) is easily obtained. □
Let us point out that, in the same way as in similar INAR-based models, the expected length of the zero runs in the ZOIPS-INAR(1) process is independent of the parameter .
Theorem 5.
The proportions of zeros and ones in the ZOIPS-INAR(1) process are, respectively,
Proof.
4. Parameter Estimation Procedure
Due to the specific structure, the parameter estimation procedure of the ZOIPS-INAR(1) model is more complex than for the ordinary INAR model. The main reason is that the basic INAR models with ‘ordinary’ PS innovations have (only) two unknown parameters . However, in the non-trivial case, the ZOIPS-INAR(1) process has two additional parameters . Therefore, the structure of this process affects the fact that even some simpler types of estimators, such as YW estimators, cannot be obtained by simple calculation. In previous works on ZOINAR processes, Qi et al. [21] proposed the CML estimation method, while Mohammadi et al. [22] additionally described the CLS estimates. In the following, CLS estimators will also be used as initial values for the PGF estimation procedure, which will now be given more attention.
We emphasize once again that the general aspect of the PGF method was recently described by Stojanović et al. [29]. Accordingly, a specific PGF estimation procedure is examined here, in the case of the ZOIPS-INAR(1) process. The basic idea of the PGF method is close to the empirical characteristic function (ECF) estimation method introduced in [36,37]. It is based on minimizing the ‘distance’ between the theoretical PGF of order , defined by Equations (18) and (19), as well as the corresponding empirical PGF:
where is some finite realization of the ZOIPS-INAR series . Since the ZOIPS-INAR(1) series is stationary and ergodic, hence it follows that:
where is the (unknown) true value of parameter . Thus, is an unbiased estimator of . Further, as the PGF is well-defined at least for all , the objective (minimization) function can be defined as follows:
where and is a weight function, integrable on .
The PGF estimators are then obtained by minimizing the objective function (24) with respect to . In other words, they represent the solutions of the following minimization equation:
where is a regular parameter space of the ZOIPS-INAR(1) process. To solve Equation (25), numerical integration procedures have been used, which are discussed in Section 5. In the following, under some regularity conditions, we examine the consistency and asymptotic normality (AN) of the PGF estimators.
Theorem 6.
Let be the exact value of the parameter λ, and , for arbitrary , the solutions of Equation (25). In addition, assume that the following regularity conditions are fulfilled:
- and for large enough T.
- At the point functionhas a unique minimum .
- is a regular matrix.
- is a non-zero matrix uniformly bounded by a positive ω-integrable function .
Then, the estimator is strictly consistent and AN for the parameter λ.
Proof.
To prove the consistency of the estimator , we firstly check the sufficient conditions for the consistency of the extremum estimators (cf. Newey and McFadden [38]). As it was previously shown that the ZOIPS-INAR(1) series is ergodic, applying Equation (23) and the strong law of large numbers (SLLN) follows:
where “as” denotes the almost sure convergence. Further, under assumption , the closed set is compact, and belongs to its interior. Hence, the functions and are continuous on the compacts and , respectively, and therefore, there exist constants such that
According to these, similarly as in Stojanović et al. [29], one obtains
so the last inequality and Equation (26) imply
Thus, the function converges uniformly and almost surely to . According to these, as well as assumption and Theorem 2.1 in Newey and McFadden [38], it follows that:
that is, the estimator is strictly consistent for .
To prove the AN property of the estimator , note that the first two orders of partial derivatives of the function are continuous functions. Therefore, using the Taylor expansion for at the point , one obtains:
By replacing with , for sufficiently large T, under assumption and the fact that , we have:
Furthermore, according to the properties mentioned above, the function can be differentiated under the sign of the integral, such as:
By taking the mathematical expectations in Equations (28) and (29), one obtains:
where, according to Equation (23), it follows that:
According to assumption , there exists a -integrable function such that
where is the matrix norm on consistent with the Euclidean vector norm. Hence, inequalities
hold, so Equation (30) and SLLN give
Further, note that Equation (28) for the gradient of function can be written as
where
Thereby, according to Equation (23), the equality holds. It can also be shown (cf. Stojanović et al. [39,40]) that
is the finite non-zero limit value if the covariance function , when , is absolutely summable. In the case of the ZOIPS-INAR process, using Theorem 1 we obtain:
Thus, hold for any . By applying the central limit theorem for stationary processes (cf. Billingsley [41]), the convergence that is proved and Equations (31)–(33) give:
where “d” denotes the convergence in the distribution. Finally, according to Equations (27), (31) and (34) it follows that:
which completes the proof of the theorem. □
Remark 4.
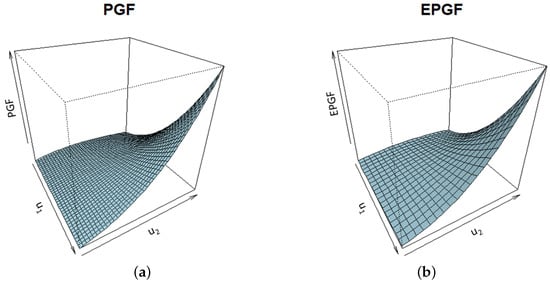
Using similar considerations as in ECF estimates (cf. Knight & Yu [36]), the PGF procedure for estimating the true values of the parameter is based on the realization of the two-dimensional random vector . Then, the objective function represents a double integral with respect to the weight function , and can be numerically approximated by some cubature formulas. For that purpose, it is necessary to determine the two-dimensional PGF (as well as EPGF) of the ZOIPS-INAR(1) series . By replacing in Equation (19), and using Equation (18), the two-dimensional theoretical PGF can be obtained as follows:
where As an illustration, Figure 2 presents the theoretical and empirical PGF of the ZOIPS-INAR(1) process with geometric PS innovations, which were obtained using the ‘R’ function “persp()”.

Figure 2.
3D plots of the two-dimensional PGF (a) and the corresponding EPGF (b) innovations are the ZOIPS series with a geometric PS distribution. (Parameters values are , ).
5. Numerical Simulations
In this section, numerical simulations of the proposed PGF procedure for estimating the unknown parameters of the ZOIPS-INAR(1) process are performed. For this purpose, as previously noted, different PS-distributed series can be observed. As an illustration, but also for practical reasons that are stated in the next section, two different distributions of the series are observed. First it is assumed that RVs have a Poisson distribution, and then they are assumed to have a geometric distribution. For both of these distributions, we generated samples of length , whose size is close to the length of the COVID-19 count series data that will be analyzed in Section 6. These samples were generated through 500 independent Monte Carlo simulations of the PS series as well as the ZOIPS series . After that, according to Equations (11) and (12), the corresponding realizations of the ZOIPS-INAR series were obtained.
Using a similar procedure as in Mohammadi et al. [22], we firstly computed the CLS estimates by minimizing the objective function:
By applying the usual procedure, that is, by solving coupled equations
parameter estimators and can be easily obtained as follows:
In the next step, estimates of the parameters can be obtained by minimizing the objective function:
where and were replaced by their CLS estimators and , respectively. Minimization of the function was conducted using a numerical procedure based on the R-function "nlminb", where the initial values of the parameters were taken randomly from the uniform distribution . The asymptotic properties of the obtained CLS estimates can be proven by applying some basic results of the CLS theory [42,43], in the same way as this was achieved in Mohammadi et al. [22]. The results of these simulations are given in the left part of Table 2, where the minimums (Min.), mean values (Mean), maximums (Max.) and mean squared estimated errors (MSEE ) of the CLS estimates are shown.

Table 2.
Estimated values of parameters of the ZOIPS-INAR process. (True parameters are , ).
Next, the PGF method was applied, with initial values obtained from the previous CLS procedure. The parameter estimates were calculated based on the minimization of the double integral
where is the weight function, and is the two-dimensional PGF of the ZOIPS-INAR(1) process . Using Equation (35), in the case of the series with ZOIPS for the Poisson distribution case, this PGF can be obtained as follows:
Similarly, for the appropriate PGF of the series with ZOIPS for the geometric innovations, one obtains:
It can be observed that these PGFs are not in closed form, but they can be approximated by finite k-term products with an arbitrary precession.
Thereafter, the integral in (37) can be numerically approximated using some of the N-point cubature formulas of the form:
Here, are the cubature nodes, and denotes the appropriate weight coefficients. In this simulation study, we used cubature formulas with nodes, based on Gauss–Legendre orthogonal polynomials and weight function . The numerical construction of these formulas was carried out using the package “Orthogonal polynomials” within the software Mathematica, authored by Cvetković and Milovanović [44]. Next, the objective function (24) was minimized using the “R” procedure for linearly constrained minimization, based on the Nelder–Mead optimization method [45]. Summary statistics of the PGF estimates, which were obtained using the aforementioned estimation procedure and with additional values of the objective function , are shown in the right part of Table 2.
Comparison of the CLS and PGF estimated values indicates that the mean values of CLS estimates are somewhat closer to the true parameter values (only) for the parameter . This is expected, because represents the first correlation of the ZOIPS-INAR(1) series . Since the CLS-estimate , given by the first of Equation (36), is a sampled correlation, it is the most efficient estimate for . However, it is obvious that the other parameter estimates are more efficient in the case when the PGF estimation procedure is applied, as well as that they have smaller mean squared estimation errors (MSEEs).
In addition, the AN test results are shown in Table 2, where the Anderson–Darling normality test was conducted. The test statistic, denoted AD, along with the corresponding p-values, were calculated using the procedure from the R-package “nortest”, authored by Gross [46]. According to the obtained values, it can be seen that the AN property is confirmed for most of the PGF estimates of parameters . However, the CLS estimates of the parameter do not have the AN property, at the significance level of . Therefore, this would be another advantage of the PGF estimates. Certain confirmation of these facts can be observed visually in Figure 3 and Figure 4.
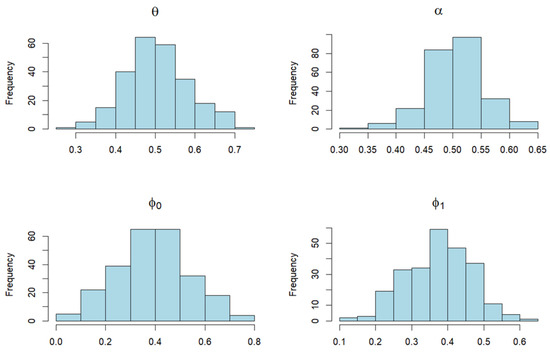
Figure 3.
Histograms of empirical distributions of the PGF estimated parameters of the ZOIPS-INAR(1) process with zero-and-one inflated Poisson PS innovations. (Parameters are the same as in Table 2).
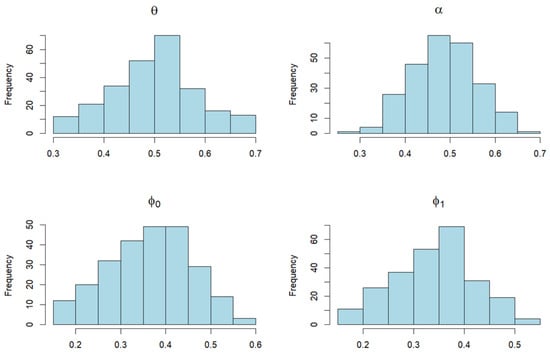
Figure 4.
Histograms of empirical distributions of the estimated parameters of the ZOIPS-INAR(1) process with zero-and-one inflated geometric PS innovations. (Parameters are the same as in Table 2).
6. Application of the Model
Here we point out some possibilities of practical application of the ZOIPS-INAR process in real-world data modeling. In this regard, it is worth noting that the COVID-19 pandemic has received a great deal of attention since its appearance. From a mathematical point of view, various theoretical models have been proposed to investigate this still current problem (for more recent examples, see [47,48,49,50,51,52,53]). To that end, here we explore some additional possibilities in modeling the dynamics of COVID data.
More precisely, we observed an actual count data set, which represents the dynamics of the number of deaths due to COVID-19 in the Republic of Serbia, based on the data of the World Health Organization (WHO) [54], over a period from 1 January 2020 to 31 December 2022. In this way, time series of counting data of length were observed, the dynamics part of which is shown in the diagram in Figure 5. In addition, the autocorrelation function (ACF) and partial autocorrelation function (PACF) of this time series can be seen. Depending on the lag , it is clear that there is an exponentially decreasing autocorrelation, as well as that partial autocorrelation indicates suitable modeling with the INAR process of the order one (or two). Therefore, it could be expected that INAR-based processes can be adequate stochastic models to describe these dynamics.
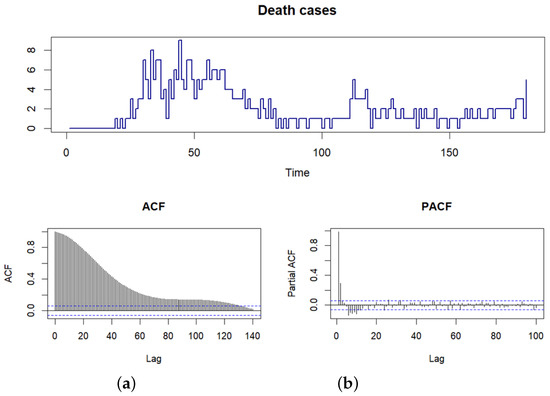
Figure 5.
Graph above: dynamics of the number of deaths caused by the disease COVID-19. Graphs below: autocorrelation (a) and partial autocorrelation (b) of the observed time series.
Furthermore, based on the summary statistics of the data of this time series, shown in Table 3, it can be observed that COVID-19 data have a significant number of zero and one values. Therefore, it could be assumed that the ZOIPS-INAR(1) process can be taken as a suitable stochastic model. In doing so, as members of the PS family, we consider innovations with the Poisson distribution (and the ‘small’ parameter ), and with the geometric distribution. In the following, we first assume Poisson PS-innovations, since a zero-one inflation testing procedure can be applied. In this regard, we point out that the testing procedure here is different than one used in Qi et al. [21]. We form a null hypothesis that a certain INAR time series is not of the ZOI-type; that is, . In that case, according to Theorem 5, that is, Equation (22), the proportions of the occurrences of the zero and one values can be, respectively, expressed as follows:

Table 3.
Summary statistics of the number of deaths per day in the Republic of Serbia, with zero-and-one inflation testing.
Therefore, in the INAR(1) process with ‘ordinary’ Poisson innovations, the zero-and-one proportions are exponentially related to the mean . If we define the so-called sample zero-and-one proportions:
then, according Equations (38) and (39), the so-called zero-and-one test statistics can be taken as follows:
Here, is the sample mean, and , are sample deviations of the statistics , , respectively. By applying some general asymptotic results related to Poisson INAR processes (cf. Weiß et al. [55]), it is shown that the central limit theorem (CLS) holds for these statistics; that is,
Thus, by applying a simple testing procedure based on the standard Gaussian distribution, hypothesis can be verified. The test results are shown in the lower part of Table 3, from which it is evident that in both cases hypothesis was rejected. Thus, the observed count data series can be modeled using the ZOIPS-INAR(1) process.
In a similar way, for the appropriate INAR(1) process with geometric PS-innovations, one obtains:
It can also be seen that the earlier expressions are not in closed form. However, they can be computed approximately with an arbitrary precision.
The estimated values of parameters for both of those PS innovations (Poisson and geometric) are shown in the upper parts of Table 4 and Table 5. In order to compare the ZOIPS-INAR(1) model with the ordinary INAR(1) model, the same estimation procedures were used to fit the observed data, assuming . Note that the INAR(1) model has only two parameters whose estimated values are also shown in Table 4 and Table 5. Thereby, the estimated values of the parameter obtained using the CLS method, as the first sample correlation, are the same for both models. As in the previous simulation study, the PGF estimates were calculated using the previously described two-step estimation procedure. It is worth noting that the estimated parameter values obtained by applying both estimation methods are quite close. At the same time, the relatively small estimated values of the parameter are a consequence of the other small emphasized frequencies of the observed time series, which are not zero and one (and can also be seen in the following Figure 6). However, the estimated values of the parameter are close to 1. This can also be explained by the previously described properties of the observed series, i.e., its significantly high first correlation. Finally, note that by using Equation (7), and similarly as in Mohammadi et al. [22], innovations of the ZOIPS-INAR(1) process can be represented as follows:

Table 4.
Estimated fitting parameters of the considered data with the INAR(1) and ZOIPS-INAR(1) models, along with their goodness-of-fit and predictive statistics. (Poisson distribution is assumed for PS-distributed innovations).

Table 5.
Estimated fitting parameters of the considered data with the INAR(1) and ZOIPS-INAR(1) models, along with their goodness-of-fit and predictive statistics. (Geometric distribution is assumed for PS-distributed innovations).
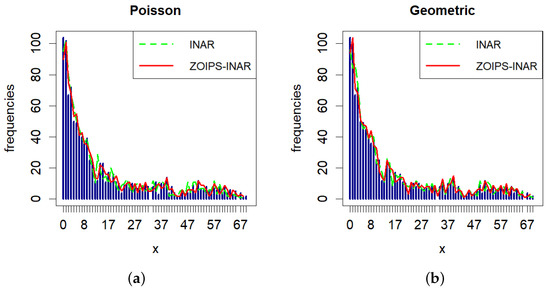
Figure 6.
Frequency distributions of the observed time series and data fitted by INAR(1) and ZOIPS-INAR(1) models: (a) Poisson-distributed innovations; (b) geometric-distributed innovations.
Here, , are the IID Bernoulli time series, also mutually independent of the RVs , and , . Thus, in the observed series, the estimates of are related to the zero-proportion , and the estimates of to the one-proportion .
In addition, we analyzed the efficiency of the fit for both INAR-based models and both estimation procedures. To this end, using the estimated parameters, we generated 500 independent simulations of the INAR(1) and ZOIPS-INAR(1) time series. To check the effectiveness of the fit to real-life data, two typical goodness-of-fit statistics were calculated: the mean squared error of estimation (MSEE) and the Akaike information criterion (AIC). Average values of these statistics, obtained on the basis of the previously described simulations, are shown in the middle parts of Table 4 and Table 5. In both cases, it is noticeable that the MSEE and AIC statistics have relatively close and small estimated values, i.e., the CLS and PGF estimates apparently have similar efficiency. Nevertheless, it is certainly noticeable that the PGF estimates have slightly smaller fitting errors. The goodness-of-fit statistics are also significantly lower in the case when the ZOIPS-INAR(1) model is applied. This means that it is a more suitable stochastic model for fitting the observed real-life time series. Finally, in the case of Poisson PS-innovations, the error statistics have slightly smaller values, so they seem more suitable for fitting with the ZOPIS-INAR(1) model. Some of the mentioned facts can also be seen in Figure 6, where the empirical and fitted frequencies of both INAR-based models are shown, whereby parameter estimates obtained by the PGF method were used.
Finally, for both of INAR-based models, as well as the both estimation procedures, the forecast accuracy analysis of the obtained models was checked. To that end, the time interval from 1 January 2023 to 28 February 2023 was taken as the forecast horizon of length . The testing procedure was conducted using the one-sided Diebold–Mariano prediction accuracy test [56]. The null hypothesis was that the time series fitted with the INAR and ZOIPS-INAR models had the same forecast accuracy, while the alternative was that the ZOIPS-INAR model had better accuracy. The test statistic, denoted as DM, along with the appropriate p-values, was computed using the R-package “forecast”, authored by Hyndman [57]. They both are shown in the lower parts of Table 4 and Table 5, and indicate that ZOIPS-INAR models have better forecast accuracy; that is, the alternative hypothesis is valid. This is particularly evident in the case of the Poisson PS-innovations, where for both CLS and PGF estimation procedures the obtained p-values are less than the significance level of .
7. Conclusions
In this paper, a generalized zero-and-one inflated ZOIPS-INAR(1) process, based on power series (PS) distributed innovations, was presented. As already noted, zero-and-one inflationary data are of particular interest in contemporary real-world data research. Let us emphasize once again that there are only two contributions in this direction: the ZOINAR model with Poisson [21] and another model with Poisson–Lindley innovations [22]. The ZOIPS-INAR(1) process proposed here, according to the general form of its PS distributions, can be viewed as a generalization of the previous models. Thus, for instance, the Poisson innovations represent only a special case of the PS-distributed innovation series. In a similar way, the ZOIPS-INAR(1) process with any other PS innovations (such as, for example, geometrically distributed innovations) may be suitable for estimating and fitting different kinds of time series. However, it should be noted that there are distributions of discrete types that do not belong to the PS family, which can be a certain limitation of this model.
The stochastic properties of the ZOIPS-INAR(1) process were considered in detail, and two parameter estimation methods were proposed. As a more contemporary method, we once again emphasize the estimation procedure based on probability generating functions (PGF method). It was shown here that the PGF estimators have slightly better asymptotic properties as well as efficiency compared to the widely used conditional least-squares (CLS) estimators. Additionally, the application of the ZOIPS-INAR(1) model to fitting real-life data on the number of deaths from the COVID-19 pandemic in the Republic of Serbia was presented. In order to determine the effectiveness of the proposed ZOIPS-INAR(1) model, it was compared with the standard INAR(1) model. In doing so, it was shown that the ZOIPS-INAR(1) model provides a better fit with the considered data; that is, it has greater efficiency and predictive accuracy compared to the standard INAR(1) model. Finally, we emphasize that two particular cases of the ZOIPS-INAR(1) model were obtained, and for both of them the fitting procedures were checked with different aspects, along with the predicting accuracy. The results obtained in this way indicate the appropriateness of the proposed model in fitting zero-and-one processes, both from a theoretical and a practical point of view. This can also be a motivation for some further research.
Author Contributions
Conceptualization, V.S.S. and H.S.B.; methodology, V.S.S. and H.S.B.; software, V.S.S. and H.S.B.; validation, E.L. and N.Q.; formal analysis, V.S.S. and H.S.B.; data curation, V.S.S. and H.S.B.; writing—original draft preparation, V.S.S., H.S.B. and E.L.; writing—review and editing, E.L. and N.Q.; visualization, V.S.S. and H.S.B.; supervision, V.S.S. and E.L.; project administration, E.L. and N.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R376), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Official data on deaths from the disease COVID-19 can be found on the website of the World Health Organization (https://covid19.who.int/data, accessed on 19 March 2023).
Acknowledgments
The authors gratefully acknowledge Princess Nourah bint Abdulrahman University Researchers’ Supporting Project number (PNURSP2023R376), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia, for the financial support for this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Johnson, N.L.; Kemp, A.W.; Kotz, S. Univariate Discrete Distributions, 3rd ed.; Wiley Series in Probability and Statistics; John Wiley & Sons: Washington, DC, USA, 2005. [Google Scholar]
- Xu, H.-Y.; Xie, M.; Goh, T.N.; Fu, X. A Model for Integer–Valued Time Series with Conditional Overdispersion. Comput. Stat. Data Anal. 2012, 56, 4229–4242. [Google Scholar] [CrossRef]
- Weiß, C.H.; Pollet, P.K. Binomial Autoregressive Processes with Density-Dependent Thinning. J. Time Ser. Anal. 2014, 35, 115–132. [Google Scholar] [CrossRef]
- Martin, V.L.; Tremayne, A.R.; Jung, R.C. Efficient Method of Moments Estimators for Integer Time Series Models. J. Time Ser. Anal. 2014, 35, 491–516. [Google Scholar] [CrossRef]
- Graziadei, H.; Lijoi, A.; Lopes, H.F.; Marques, F.P.C.; Prünster, I. Prior Sensitivity Analysis in a Semi-Parametric Integer-Valued Time Series Model. Entropy 2020, 22, 69. [Google Scholar] [CrossRef] [PubMed]
- Al-Osh, M.A.; Alzaid, A.A. First-Order Integer-Valued Autoregressive (INAR(1)) Process. J. Time Ser. Anal. 1987, 8, 261–275. [Google Scholar] [CrossRef]
- Silva, M.E.; Oliveira, V.L. Difference Equations for the Higher-Order Moments and Cumulants of the INAR(1) Model. J. Time Ser. Anal. 2004, 25, 317–333. [Google Scholar] [CrossRef]
- Jung, R.C.; Ronning, G.; Tremayne, A.R. Estimation in Conditional First Order Autoregression with Discrete Support. Stat. Pap. 2005, 46, 195–224. [Google Scholar] [CrossRef]
- Ristić, M.; Bakouch, H.S.; Nastić, A. A New Geometric First-Order Integer-Valued Autoregressive (NGINAR(1)) Process. J. Stat. Plan. Infer. 2009, 139, 2218–2226. [Google Scholar] [CrossRef]
- Schweer, S.; Weiß, C.H. Compound Poisson INAR(1) Processes: Stochastic Properties and Testing for Over-Dispersion. Comput. Stat. Data Anal. 2014, 77, 267–284. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Bakouch, H.S.; Nadarajah, S.; Sharafi, F. A New Weighted Lindley Distribution with Application. Braz. J. Probab. Stat. 2016, 30, 1–27. [Google Scholar]
- Mohammadpour, M.; Bakouch, H.S.; Shirozhan, M. Poisson–Lindley INAR(1) Model with Applications. Braz. J. Probab. Stat. 2018, 32, 262–280. [Google Scholar] [CrossRef]
- Bermúdez, L.; Karlis, D. Multivariate INAR(1) Regression Models Based on the Sarmanov Distribution. Mathematics 2021, 9, 505. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Liu, X. A New Bivariate Random Coefficient INAR(1) Model with Applications. Symmetry 2022, 14, 39. [Google Scholar] [CrossRef]
- Maya, R.; Chesneau, C.; Krishna, A.; Irshad, M.R. Poisson Extended Exponential Distribution with Associated INAR(1) Process and Applications. Stats 2022, 5, 755–772. [Google Scholar] [CrossRef]
- Maya, R.; Irshad, M.R.; Chesneau, C.; Nitin, S.L.; Shibu, D.S. On Discrete Poisson–Mirra Distribution: Regression, INAR(1) Process and Applications. Axioms 2022, 11, 193. [Google Scholar] [CrossRef]
- Khoo, W.C.; Ong, S.H.; Atanu, B. Coherent Forecasting for a Mixed Integer-Valued Time Series Model. Mathematics 2022, 10, 2961. [Google Scholar] [CrossRef]
- Saito, M.Y.; Rodrigues, J. A Bayesian Analysis of Zero and One Inflated Distributions. Rev. Mat. Estatíst. 2005, 23, 47–57. [Google Scholar]
- Zhang, C.; Tian, G.; Ng, K. Properties of the Zero-and-One Inflated Poisson Distribution and Likelihood-Based Inference Methods. Stat. Interface 2016, 9, 11–32. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, G.-L.; Yuen, K.C.; Wu, Q.; Li, T. Multivariate Zero-and-One Inflated Poisson Model with Applications. J. Comput. Appl. Math. 2020, 365, 112356. [Google Scholar] [CrossRef]
- Qi, X.; Li, Q.; Zhu, F. Modeling Time Series of Count with Excess Zeros and Ones Based on INAR(1) Model with Zero-and-One Inflated Poisson Innovations. J. Comput. Appl. Math. 2019, 346, 572–590. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Sajjadnia, Z.; Bakouch, H.S.; Sharafi, M. Zero-and-One Inflated Poisson–Lindley INAR(1) Process for Modelling Count Time Series with Extra Zeros and Ones. J. Stat. Comput. Simulat. 2022, 92, 2018–2040. [Google Scholar] [CrossRef]
- Franke, J.; Seligmann, T.H. Conditional Maximum Likelihood Estimates for INAR(1) Processes and Their Application to Modelling Epileptic Seizure Counts; Developments in Time Series; Chapman & Hall: London, UK, 1993; pp. 310–330. [Google Scholar]
- Du, J.-G.; Li, Y. The Integer-Valued Autoregressive (INAR(p)) Model. J. Time Ser. Anal. 1991, 12, 129–142. [Google Scholar]
- Latour, A. Existence and Stochastic Structure of a Non-negative Integer-valued Autoregressive Process. J. Time Ser. Anal. 1998, 19, 439–455. [Google Scholar] [CrossRef]
- Silva, I.; Silva, M.E. Asymptotic Distribution of the Yule-Walker Estimator for INAR(p) Processes. Stat. Prob. Lett. 2006, 76, 1655–1663. [Google Scholar] [CrossRef]
- Esquìvel, M.L. Some Applications of Probability Generating Function Based Methods to Statistical Estimation. Discuss. Math. 2009, 29, 131–153. [Google Scholar] [CrossRef]
- Stojanović, V.; Randjelović, D.; Kuk, K. Noise-Indicator Non-negative Integer-Valued Autoregressive Time Series of the First Order. Braz. J. Probab. Stat. 2018, 32, 147–171. [Google Scholar] [CrossRef]
- Stojanović, V.; Ljajko, E.; Tošić, M. Parameters Estimation in Non-Negative Integer-Valued Time Series: Approach Based on Probability Generating Functions. Axioms 2023, 12, 112. [Google Scholar] [CrossRef]
- Bourguignon, M.; Vasconcellos, K.L.P. First Order Non-Negative Integer Valued Autoregressive Processes with Power Series Innovations. Braz. J. Probab. Stat. 2015, 29, 71–93. [Google Scholar] [CrossRef]
- Weiß, C.H. Thinning Operations for Modelling Time Series of Counts—A Survey. Adv. Statist. Anal. 2008, 92, 319–341. [Google Scholar] [CrossRef]
- Kella, O.; Löpker, A. On Binomial Thinning and Mixing. Indag. Math. 2022, in press. [Google Scholar] [CrossRef]
- Alzaid, A.A.; Al-Osh, M.A. An Integer-Valued pth-order Autoregressive Structure (INAR(p)) Process. J. App. Prob. 1990, 27, 314–324. [Google Scholar] [CrossRef]
- Jazi, M.A.; Jones, G.; Lai, C.D. First-Order Integer-Valued Ar Processes with Zero-Inflated Poisson Innovations. J. Time Ser. Anal. 2012, 33, 954–963. [Google Scholar] [CrossRef]
- Li, C.; Wang, D.; Zhang, H. First-Order Mixed Integer-Valued Autoregressive Processes with Zero-Inflated Generalized Power Series Innovations. J. Korean Stat. Soc. 2015, 44, 232–246. [Google Scholar] [CrossRef]
- Knight, J.L.; Yu, J. Empirical Characteristic Function in Time Series Estimation. Econ. Theory 2002, 18, 691–721. [Google Scholar] [CrossRef]
- Yu, J. Empirical Characteristic Function Estimation and Its Applications. Econ. Rev. 2004, 23, 93–123. [Google Scholar] [CrossRef]
- Newey, W.K.; McFadden, D. Large Sample Estimation and Hypothesis Testing. In Handbook of Econometrics; Elsevier: Amsterdam, The Netherlands, 1994; Volume 4. [Google Scholar]
- Stojanović, V.; Milovanović, G.V.; Jelić, G. Distributional Properties and Parameters Estimation of GSB Process: An Approach Based on Characteristic Functions. ALEA Lat. Am. J. Probab. Math. Stat. 2016, 13, 835–861. [Google Scholar] [CrossRef]
- Stojanović, V.; Popović, B.Č.; Milovanović, G.V. The Split-SV Model. Comput. Statist. Data Anal. 2016, 100, 560–568. [Google Scholar] [CrossRef]
- Billingsley, P. Probability and Measure; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Klimko, L.A.; Nelson, P.I. On Conditional Least Squares Estimation for Stochastic Processes. Ann. Stat. 1978, 6, 629–642. [Google Scholar] [CrossRef]
- Tjøstheim, D. Estimation in Non-linear Time Series Models. Stochastic Process. Appl. 1986, 21, 251–273. [Google Scholar] [CrossRef]
- Cvetković, A.S.; Milovanović, G.V. The Mathematica Package “Orthogonal Polynomials”. Facta Univ. Ser. Math. Inform. 2004, 19, 17–36. [Google Scholar]
- Lange, K. Numerical Analysis for Statisticians; Statistics and Computing; Springer: New York, NY, USA, 2001. [Google Scholar]
- Gross, L. Tests for Normality. R Package Version 1.0-2. 2013. Available online: http://CRAN.R-project.org/package=nortest (accessed on 28 February 2023).
- Vaz, S.; Torres, D.F.M. A Discrete-Time Compartmental Epidemiological Model for COVID-19 with a Case Study for Portugal. Axioms 2021, 10, 314. [Google Scholar] [CrossRef]
- Ghosh, S.; Volpert, V.; Banerjee, M. An Epidemic Model with Time Delay Determined by the Disease Duration. Mathematics 2022, 10, 2561. [Google Scholar] [CrossRef]
- Sivakumar, B.; Deepthi, B. Complexity of COVID-19 Dynamics. Entropy 2022, 24, 50. [Google Scholar] [CrossRef] [PubMed]
- Hassan, S.M.; Riveros Gavilanes, J.M. First to React Is the Last to Forgive: Evidence from the Stock Market Impact of COVID 19. J. Risk Financ. Manag. 2021, 14, 26. [Google Scholar] [CrossRef]
- Zakharov, V.; Balykina, Y.; Ilin, I.; Tick, A. Forecasting a New Type of Virus Spread: A Case Study of COVID-19 with Stochastic Parameters. Mathematics 2022, 10, 3725. [Google Scholar] [CrossRef]
- Jovanović, M.; Stojanović, V.; Kuk, K.; Popović, B.; Čisar, P. Asymptotic Properties and Application of GSB Process: A Case Study of the COVID-19 Dynamics in Serbia. Mathematics 2022, 10, 3849. [Google Scholar] [CrossRef]
- Stapper, M. Count Data Time Series Modelling in Julia—The CountTimeSeries.jl Package and Applications. Entropy 2021, 23, 666. [Google Scholar] [CrossRef]
- World Health Organization. Available online: https://covid19.who.int/data (accessed on 3 March 2023).
- Weiß, C.H.; Homburg, A.; Puig, P. Testing for Zero Inflation and Overdispersion in INAR(1) Models. Stat. Pap. 2019, 60, 823–848. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar]
- Hyndman, R. Forecasting Functions for Time Series and Linear Models. R Package Version 7.1. 2016. Available online: http://CRAN.R-project.org/package=forecast (accessed on 3 March 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).