Neural Attractor-Based Adaptive Key Generator with DNA-Coded Security and Privacy Framework for Multimedia Data in Cloud Environments

Abstract

Cloud services offer doctors and data scientists access to medical data from multiple locations using different devices (laptops, desktops, tablets, smartphones, etc.). Therefore, cyber threats to medical data at rest, in transit and when used by applications need to be pinpointed and prevented preemptively through a host of proven cryptographical solutions. The presented work integrates adaptive key generation, neural-based confusion and non-XOR, namely DNA diffusion, which offers a more extensive and unique key, adaptive confusion and unpredictable diffusion algorithm. Only authenticated users can store this encrypted image in cloud storage. The proposed security framework uses logistics, tent maps and adaptive key generation modules. The adaptive key is generated using a multilayer and nonlinear neural network from every input plain image. The Hopfield neural network (HNN) is a recurrent temporal network that updates learning with every plain image. We have taken Amazon Web Services (AWS) and Simple Storage Service (S3) to store encrypted images. Using benchmark evolution metrics, the ability of image encryption is validated against brute force and statistical attacks, and encryption quality analysis is also made. Thus, it is proved that the proposed scheme is well suited for hosting cloud storage for secure images.

1. Introduction

In recent decades, the world of computing has grown tremendously. The revolution in modern gadgets is completely rebuilding information sharing and storing in the public sector. In reflection, the security and privacy of information sharing have become a challenge [1]. Additionally, the incremental impact of data storage platforms such as cloud [1], fog [2], edge [3], etc., has led to development in the field of information technology (IT). The rapid increase in Internet of Things-centric engineering applications also demands platforms such as cloud and edge [4,5]. However, information security is a significant concern during transit, and the rest of the multimedia data are shared in the public domain. Confidentiality, integrity, authentication and nonrepudiation are security components that structure the security solutions to share and store multimedia data. The cloud paradigm has recently enabled worldwide organisations to host and run their business applications and IT services in cloud environments (public, private and hybrid). The consistent growth of the cloud paradigm makes it a cornerstone for efficient and affordable multimedia data storage for various applications. Owing to the multitenant nature of the cloud, addressing the security and privacy concerns of multimedia data is essential. Authentication is one solution to ensure the tightest security for confidential and customer data. Images are a significant segment of multimedia data. Multimedia data are captured and transmitted to geographically distributed cloud environments. One such solution is proven and potential image encryption.

Cloud computing plays a commendable role in shaping the IT infrastructure [6]. Cloud computing is the consolidated, centralised/federated, automated and shared computing model representing IT industrialisation. Due to the shared environment, anybody can access cloud services globally to host their data. The pay-per-usage model has created a string of newer possibilities and opportunities for business houses, IT service providers, governments and other establishments across the globe.

The cloud environment offers infrastructure, a platform and storage as a service. Storage is the superior service and backbone for e-commerce and online finance applications (e.g., Salesforce CRM and Netflix) [7]. However, security and privacy are unbeatable challenges for the cloud storage environment, particularly for images as multimedia data. In addition, tamper resistance and data protection are significant challenges [8]. The new shape for image encryption schemes is vital in this concern. Ciphering images is the solution to protect the images in the public cloud storage area. The art of the image encryption approach is to make the image unreadable by unauthorised users. Due to the uniqueness of the image, such as high correlation among neighbouring pixels, conventional crypto solutions cannot be advised for image ciphering [9].

Chaos theory supports image encryption to break neighbouring pixels’ correlation after encryption. Chaotic maps [10], attractors [11], etc. have specific properties such as periodicity, greater keyspace, sensitivity to initial parameters, etc. [12], which played a commendable role in the substitution and transposition process of image encryption [13]. Ponuma et al. proposed compressive sensing-based image encryption with the key matrix generated from the chaotic measurement approach [14].

2. Related Works

The confusion process using a chaotic Arnold’s cat map (ACM) has a flaw: the specific number of rotations fetches the original image again [15]. Along with ACM, the diffusion process using chaotic nature keys increases impulsiveness [16]. Belazi et al. proposed a new 1D map for a permutation-substitution network attained through chaotic linear fractional transformation (LFT) along with the interleaved diffusion process [17]. Huang et al. suggested plain image-dependent encryption through N-dimensional chaotic maps [18]. Broumandnia experimented with image ciphering using multidimensional nonlinear chaos equations to enhance the keyspace [19]. Finally, Chen et al. proposed an image ciphering technique which tolerates brute-force attacks. Nonlinear fractional Tchebyshev moments are used to achieve the fractal permutation to enrich the security level of a colour image [20].

DNA blended image encryption has become a remarkable strategy for data privacy [21]. Substitution rules of DNA coding agree that chaos offers better diffusion in image encryption, which increases the keyspace and entropy, and the correlation results are meagre [22]. Hu et al. suggested a spatiotemporal chaos system constructed using a logistic-sine system (LSS) in the coupled map lattice (CML) for diffusion and DNA-based shuffling in the encryption process and obtained good entropy [23]. Chai et al. experimented with the DNA blended chaos-based grey image encryption where 1D chaotic maps and cipher block chaining approaches are used to obtain near-zero correlation and maximum entropy [24]. Enayatifar et al. proposed DNA XORing for diffusing the image followed by confusion through three-dimensional logistic maps. Still, the diagonal correlation of the encrypted image is near zero compared to the vertical and horizontal correlation of the same. Additionally, the entropy value needs to be improved [25]. A multidimensional hyperchaotic system generates the random key for colour image encryption blended with a DNA-based diffusion process at block and bit levels [26,27]. Wenjie et al. experimented with plaintext-specific key generation for image encryption. The SHA-512 hash value is generated for every plain image as a random key for bit-level scrambling and diffusion [28]. Pavithran et al. suggested DNA-based image encryption using a hyperchaotic key generator [29]. Yousif et al. experimented with an image encryption algorithm comprising bit-level permutation and diffusion using DNA addition to improve the resistivity against known attacks in the cryptosystem [30].

Qin et al. suggested a fully homomorphic encryption (FHE) scheme for image encryption linked with cloud storage where complexity and overhead are very high, even for small images [31]. Chidambaram et al. proposed the DNA blended chaos-based image encryption to offer a secure image repository in the public cloud. Due to coupled chaos and cipher block chaining approaches, the image entropy after encryption was increased, but the keyspace was small, which may not be entertained [32].

Zhang et al. proposed an image encryption algorithm for the Internet of Multimedia Things (IoMT), a combination of Arnold transform-based scrambling followed by XOR-based diffusion using the key generated through cascade chaotic maps [33]. The neural-based works have concluded that it is well suited for all images, namely grey, colour and medical images, which are more feasible for cloud-based storage. In cloud storage, the user is not restricted from uploading these types of images. In addition, neural-based works contribute metrics equivalent to the chaos and attractors [34,35,36,37].

It is observed from the literature that the image encryption approaches [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] linked with cloud storage have become essential, and there are few such algorithms in the literature. Utility-specific algorithms to offer multimedia security to cloud storage demand cloud computing. This proposed algorithm can be a solution for secure image storage in the public cloud network. This security framework experimented with DNA coding blended with chaotic maps to cipher grey images before storing them in a public repository. Any authenticated user can download the decrypted image from the cloud. Later, with the valid keys, the image is decrypted to attain the original image, with confidentiality and authentication. The proposed algorithm is an enhanced approach for managing cloud repositories with utmost image security.

From the survey, offering security for sharing information in the public domain is essential. The uniqueness of the proposed encryption scheme has been enriched with adaptive key generation and chaos key generation for image encryption. As all multimedia data are unique, including their dimensions, value range, nature of the value, properties of the data, randomness and redundancy, at the same time, the key should be random, and it should not be predicted easily. With consideration, the proposed scheme has been inaugurated with adaptive key generation using the back propagation neural (BPN) model, which should be a supervised learning model. As the input of the neural network should be extracted from the features of the multimedia data, such as images and outputs, the initial seed has limited chaotic range. Future prediction is an inherent property of the artificial neural network. The BPN model includes precise selection for the adaptive key generation; during the training, BPN can learn about the randomness and redundancy nature of the image from the extracted image features. After the training, BPN can adapt to any image, producing the adaptive key. The proposed security framework mainly focuses on securely sharing and storing images in the cloud. The significant contributions of the proposed solution are:

• Neural–DNA–chaos permutation-based image encryption.
• Adaptive key generation based on plain image.
• Neural-based confusion of grey image.
• Establishment of a public cloud interface with the security framework.
• Validation of user authenticity to access the cloud-ciphered image.
• Improved protection for image sharing in multimedia communication.

3. Pre-Requisites

3.1. DNA Approach

Nucleic acid bases A (adenine), C (cytosine), G (guanine) and T (thymine) form a DNA sequence. It produces a DNA-coded value for every two-bit binary value, i.e., 00, 01, 10, 11. Based on Watson and Crick’s complementary rule, A complements T and G complements C. Thus, the possible combinations of DNA coding and operations result in 24 DNA rules in which only 8 rules are appropriate for image encryption, as shown in Table 1.

Table 1. DNA encoding rules.

Binary Stream (DNA Rules)	00	01	10	11
I	A	C	G	T
II	A	G	C	T
III	T	G	C	A
IV	T	C	G	A
V	C	A	T	G
VI	C	T	A	G
VII	G	A	T	C
VIII	G	T	A	C

In DNA space, addition, subtraction and XORing operations are carried out to offer diffusion. DNA XORing reflects the binary XOR operation rule in DNA space. DNA addition and subtraction are performed as follows:

DNAX(OUT) = mod((DNAX(IN1) + DNAX(IN2)), 4)

DNAX(OUT) = DNAX(IN1) − DNAX(IN2); if DNAX(IN1) − DNAX(IN2)

= (4 + DNAX(IN1)) − DNAX(IN2); else

DNAX(OUT) is the output DNA value in the ruleset X after addition/subtraction.

DNAX(IN1) and DNAX(IN2) are the input values in DNA space at the rule set X.

3.2. Chaotic System

The chaotic system offers a good impact in ciphering the images due to its properties of ergodicity, keyspace and chaotic behaviour. The proposed work used 1D logistic and tent chaotic maps. The initial parameters for the chaotic maps X₀ and Y₀ vary from 0 to 1. The control parameter for the 1D logistic map is 3.57 ≤ α ≤ 4 and, for the tent map, 2 ≤ µ ≤ 4. The chaotic equations for a 1D logistic map and tent map are expressed through (1) and (2).

$$F\left(\alpha ,X_{n+1}\right) \hspace{0.17em}=\hspace{0.17em}\left(\alpha \times X_n\right)\times \left(1-X_n\right)$$

(1)

$$\hspace{0.17em}F\left(\mu ,Y_{n+1}\right)\hspace{0.17em}=\hspace{0.17em}\{\begin{array}{l}\left(\frac{\mu Y_n}{2}\right);\hspace{1em}\hspace{1em}{Y}_n\hspace{0.17em}<\hspace{0.17em}0.5\\ \left(\frac{\mu \left(1-Y_n\right)}{2}\right);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{Y}_n\ge \hspace{0.17em}0.5\hspace{0.17em}\end{array}$$

(2)

The Suitability of Chaotic Sequences for the Image Encryption Algorithm

The chaotic system consistently exhibits disordered behaviour due to chaos properties. In addition, it shows a direct relation with properties expected for cryptographic functions, namely confusion and diffusion [38]. Even if there is a slight change in the initial condition value, the chaos sequences will diverge to the extreme after some iteration. The ergodicity property in the diverged sequences will give uncorrelated neighbouring values, making the chaos system genuinely dynamic. Regarding the property of sensitivity to initial condition value, two very close initial condition values, such as 0.949 and 0.950, have been taken as input and iterated 20 times, as illustrated in Figure 1.

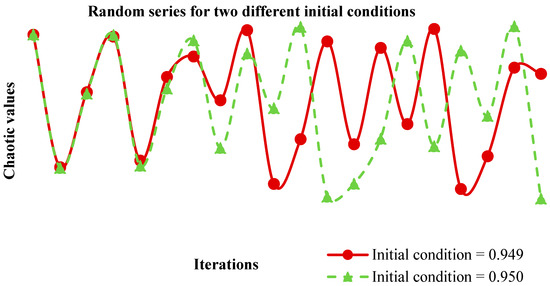
Figure 1. Random series for two different initial conditions.

3.3. Hyperchaotic HNN

The presented work employed a four-node HNN. All the nodes are interconnected with all others, along with self-connection. Every node produces the output based on its previous state and the external bias input. The connection paths between the nodes are weighted, and the updated weights depend on the Hebb rule with a hyperbolic activation function, which exhibits the desired chaotic behaviour. Since the proposed HNN has four nodes, there are 16 weight values, namely W₁–W₁₆ (3).

$${\mathrm{W}}_{\mathrm{i}\mathrm{j}}=\left[\begin{array}{cccc}{\mathrm{w}}_1& {\mathrm{w}}_2& {\mathrm{w}}_3& {\mathrm{w}}_4\\ {\mathrm{w}}_5& {\mathrm{w}}_6& {\mathrm{w}}_7& {\mathrm{w}}_8\\ {\mathrm{w}}_9& {\mathrm{w}}_{10}& {\mathrm{w}}_{11}& {\mathrm{w}}_{12}\\ {\mathrm{w}}_{13}& {\mathrm{w}}_{14}& {\mathrm{w}}_{15}& {\mathrm{w}}_{16}\end{array}\right]$$

(3)

Converged weight values decide the accuracy of obtained output compared to the actual output. Based on the activation function, the weight values can be integer/floating decimal values. The HNN generates random sequences with chaotic behaviour using Equations (4) and (5).

$${\mathrm{x}}_{\mathrm{i}+1}=-{\mathrm{c}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{i}}+{\displaystyle \sum _{\mathrm{j}=1}^4{\mathrm{w}}_{\mathrm{i}\mathrm{j}}{\mathrm{v}}_{\mathrm{j}}}$$

(4)

$${\mathrm{v}}_{\mathrm{i}}=\tanh \hspace{0.17em}({\mathrm{x}}_{\mathrm{i}})$$

(5)

where C_i is constant and C₁ = C₂ = C₃ = 1; C₄ = 100; X_i is the previous state and w_ij is the weight matrix.

Nonlinearity analysis of HNN

The proposed hyperchaotic HNN weight matrix is given below:

$${\mathrm{w}}_{\mathrm{i}\mathrm{j}}=\left[\begin{array}{cccc}1& 0.5& -3& -1\\ 0& 2+\mathrm{p}& 3& 0\\ 3& -3& 1& 0\\ 100& 0& 0& 170\end{array}\right]$$

where p is the control parameter.

The weight matrix must be asymmetrical, and the control parameter p = 0.3 is fixed to achieve the chaotic behaviour. With control parameter p = 0.3, the chaotic behaviour is depicted using Figure 2. The chaotic behaviour shown in Figure 2 depends on the initial seed X_i, weight values and the control parameter p.

Figure 2. Chaotic behaviour of HNN with p = 0.3. (a–c) Between nodes X₁ and all other three nodes. (d,e) Between nodes X₂ with X₃ and X₄. (f) Between nodes X₃ and X₄.

4. Proposed Approach

The proposed approach consists of transposition followed by two DNA-based diffusion process stages. For the confusion and diffusion processes, keys are vital. In this proposed framework, two key generator modules are available to generate the keys, which are random sequences. One is to change the pixels’ position in an image, and the other is to change the pixel’s value. A neural attractor-based key is generated specifically for the images, so no two non-identical images have the same key for transposition. A chaotic-based key generation generates the random numbers through which image pixel values are diffused.

First, the adaptive key is generated through neural networks for the confusion process. Second, features extracted from the plain image influence the key generation. Hence, generated keys are image specific. The advantage is that cryptanalysis cannot guess the key without knowing the image features and features unique to the images. Third, the Hopfield neural network confuses the image irrespective of the modality or pixel intensity of the plain image; the knowledge database of the confusion model is updated to the plain image. Hence, image-specific confusion is carried out; as a result, interpixel redundancy is removed, which enhances the resistance against statistical attacks.

Adaptive key generation can be implemented with supervised learning, the BPN model. The model training data set is considered a significant feature of the image and required range of chaotic seeds. The proposed model enhances security using artificial intelligence. Firstly, adaptive key generation using the BPN model and image confusion with the Hopfield neural attractor are carried out. The BPN model is a multilayer feedforward architecture that can be learned through back propagating the error and with the gradient descent method. The Hopfield neural attractor is a recurrent random auto-associator architecture. The Hopfield neural attractor is stimulated with initial inputs, then inputs are removed and the attractor moves towards a stable state. With the initial input, the Hopfield neural attractor has a finite number of pseudo-random states. The pseudo-random states govern the confusion process adaptively. The proposed method is a hybrid technique which creates artificial intelligence-assisted DNA blended security.

Diffusion stages are called cipher block chaining, where pixels are ciphered sequentially. The diffusion operation uses the random keys generated by the chaos key generator. The encrypted image is pushed into a storage area available in the public cloud environment and can be retrieved as the original only with the encryption key(s). The proposed framework establishes secure storage of grey images in the cloud, as shown in Figure 3. The proposed security framework for the cloud-based grey image repository consists of various phases in the image encryption process, namely,

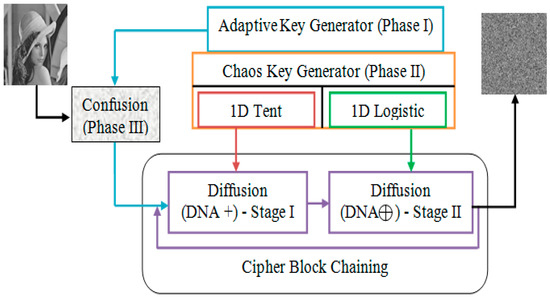
Figure 3. Proposed Security Framework.

Phase I: Adaptive key generator.

Phase II: Chaos key generator.

Phase III: Hopfield neural network-based confusion process.

Phase IV: Cipher block chaining-based diffusion process.

Phase V: Interfacing cloud and the security framework.

Phase VI: Image decryption—cipher block chaining process.

Phase VII: Image decryption—Hopfield-based reassembling.

4.1. Image Ciphering and Deciphering Process

The various phases incorporated in the image ciphering and deciphering process are given as Algorithms 1–4 below:

Algorithm 1: Adaptive random sequence generation using discrete Hopfield attractor

Input: Multiplicative identity matrix (Β)[4,4], sampling rate Tw, random initiator h[1,4] Output: Nonlinear random sequence Ω Initialise wij ← [w w/2 σ − w; Ψ 2w 3w 0; 3w ϕ w 0; mw 0 0 nw] ← [1 0.5 −5 −1; −0.37 2 3 0; 3 −13 1 0; 100 0 0 170] Update the wij with new σ, Ψ, ϕ   Get H(0) ← [h]T   Repeat $$\begin{gathered} f(H(r))=\tanh H(r) \\ \mathrm{H}\left(r+1\right)=(1-\mathrm{B}{T}_w) \mathrm{H}\left(r\right)+T_{w}wf\left(\mathrm{H}\left(r\right)\right) \\ \mathrm{D}\mathrm{h}=\hspace{0.17em}\left|\left(\mathrm{H}(\mathrm{r}+1)-\lfloor \hspace{0.17em}\left|\mathrm{H}(\mathrm{r}+1)\right|\hspace{0.17em}\rfloor \hspace{0.17em}\right)\hspace{0.17em}\right| \end{gathered}$$    Set r ← r + 1    Until r ≤ (Image size/4)    Initialise Ω ← {}    for f ← 1 to 16,384     for i ← 1 to 4       Ω ((4 × (f − 1)) + i) = Dh(i)     end     end   Return (Ω)

Algorithm 2: Chaos key generator

Input: Initial parameters (KLD(0), KT(0)) control parameters (γ, μ) and image size N 3.4 ≤ α2 ≤ 4; 0 ≤ γ ≤ 2; 0 ≤ KLD(0) and KT(0) ≤ 1 Output: Chaos sequence KLDM and KTM as key for size N and DNA rule selectors R1, R2 1D tent map-based sequence as key for Diffusion I      Initialise KTM = { }; θ = 1/2       for i ← 1 to N do   if KT(i − 1) ≥ θ then Set KT(i) ← (μ × (1 − KT(i − 1)))          else Set KT(i) ← (μ × KT(i − 1)) Set KTM(i) ← mod (KT × 1014, 256) end       Return (KTM) 1D logistic map-based sequence as key for Diffusion II       Set KLD(1) ← (γ × KLD(0)) × (1 − KLD(0))       Initialise KLDM = { }        for i ← 2 to N do           Set KLD(i) ← (γ × KLD(i −1)) × (1- KLD(i − 1))           Set KLDM(i) ← mod (KLD × 1014, 256) end       Return (KLDM)

Algorithm 3: Image encryption—Hopfield based permutation

Input: Original image I of size (X) [M, N], Nonlinear random sequence Ω Output: Scrambled image matrix C     Get $[R,\forall ] \leftarrow sort (\mathsf{\Omega }, ‘ascend’)$ where R is the ascending order of key stream $\mathsf{\Omega }$; ∀ is the index of the sorted key stream $\mathsf{\Omega }$        Repeat          Set $C\left(j\right) \leftarrow {\rm I} (\forall \left(j\right))$          Set j ← j + 1        Until j < (M × N)        Return (C)

Algorithm 4: Image encryption—cipher block chaining process

Input: Shuffled image C, Key sequences KTM, KLDM, rule for DNA encoding R1, R2 and 8-bit secret key K1 Output: Encrypted image E Set E(1) ← C(1) ⊕ K1 for i← 2 to N do   Cd(i) ← C(i) ⊕ E(i − 1) Diffusion Stage I:     Set CdDNA(i) $\stackrel{{\mathrm{R}}_1}{\leftarrow }$ DNAEncode (Cd(i))     Set KTMDNA(i) $\stackrel{{\mathrm{R}}_1}{\leftarrow }$ DNAEncode (KTM(i))     Set List ← [0, 2, 4, 6]     for j ← 1 to 4 do       Set n ← List[j]       Set Cd1(i)[n:n + 1] ← mod ((CdDNA(i) [n:n + 1] + KTMDNA (i) [n:n + 1]), 4);    end   Diffusion Stage II:     Set Cd1DNA(i)$\stackrel{{\mathrm{R}}_2}{\leftarrow }$ DNAEncode (Cd1(i))     Set KLDMDNA(i) $\stackrel{{\mathrm{R}}_2}{\leftarrow }$ DNAEncode (KLDM(i))     Set List ← [0, 2, 4, 6]     for j ← 1 to 4 do       Set n ← List[j] Set E(i)[n:n + 1] ← Cd1DNA (i) [n:n + 1] ⊕ KLDMDNA (i) [n:n + 1]      end  end Return (E)

The aim is to store the secure image in a public repository called the cloud. So, the ciphered images are uploaded into the private storage area allotted by Amazon’s public cloud, availed with access privileges and credentials. Algorithm 5 pseudo-code describes the security framework and cloud storage interface. First, the authenticity verification process is carried out with invalid credentials.

Algorithm 5: Authenticated cloud access process

Input: Encrypted image E of size X, login credentials of AWS, identity and access management (IAM) key pairs Output: Uploaded encrypted image E in the cloud storage Set AWS login credentials: username ← “username” and password←“password”    Set IAM key pairs:      access key ← “AAAAAAA” and secret key ← “SSSSSSS”    if (username = “username” && password = “password”) then     if (access key = “AAAAAAA” && secret key = “SSSSSSS”) then       captcha = randomgen (captcha) and user expect to type it on the screen       if captcha matched then Access = “Access Granted”         Push S3: Bucket ← Encrypted images        else Return (“Invalid CAPTCHA”)       else Return (“Invalid Credentials”)      else Return (Access = “Access Denied”)

The cloud is accessed to download the ciphered images with valid credentials. Then, the ciphered images are decrypted using the algorithms described in Algorithms 6 and 7.

Algorithm 6: Image decryption—cipher block chaining process

Input: Encrypted image of size (E) [M, N], key sequences KTM, KLDM, rule for DNA encoding R1, R2 and 8-bit secret key K1 Output: Shuffled image C   Diffusion Stage I:     Set EDNA(i) $\stackrel{{\mathrm{R}}_2}{\leftarrow }$ DNAEncode (E(i))     Set KLDMDNA(i) $\stackrel{{\mathrm{R}}_2}{\leftarrow }$ DNAEncode (KLDM(i))     Set List ← [0, 2, 4, 6]     for j ← 1 to 4 do       Set n ← List[j]       Set Cd1(i)[n:n + 1] ← EDNA (i) [n:n + 1] ⊕ KLDMDNA (i) [n:n + 1]     end Diffusion Stage II:     Set Cd1DNA(i) $\stackrel{{\mathrm{R}}_1}{\leftarrow }$ DNAEncode (Cdi(i))     Set KTMDNA(i) $\stackrel{{\mathrm{R}}_1}{\leftarrow }$ DNAEncode (KTM(i))            Set List ← [0, 2, 4, 6]     for j ← 1 to 4 do       Set n ← List[j]       Set Cd(i)[n:n + 1] ← mod ((Cd1DNA (i) [n:n + 1] − KTMDNA (i) [n:n + 1]), 4) end Set C(1) ← Cd(1) ⊕ K1 for i ← 2 to N do Set C(i) ← Cd(i) ⊕ Cd(i − 1) end Return (C)

Algorithm 7: Image decryption—Hopfield-based reassembling

Input: Scrambled image matrix C of size (X) [M, N], nonlinear random sequence Ω Output: Original image I         Get [R, A] ← sort (Ω, “ascend”)         where R is the ascending order of key stream $\mathsf{\Omega }$; A is the index of the sorted key stream $\mathsf{\Omega }$       Repeat          Set I (A(j)) ← C(j)          Set j ← j + 1       Until j < (M × N)        Return (I)

4.2. Security Framework Interface with Public Cloud

In this proposed approach, the S3 service from Amazon Web Services (AWS) is used as a public repository to store the grey images in encrypted form. The proposed approach offers third-level authentication because one of the contributions of the work is improved protection for image sharing in multimedia communication over public repositories. A user registers with AWS to obtain the S3 service and credentials as a cloud user. Every registered user is provided with a username and password as a level 1 authentication credential. At level 2 authentication, the secret key pairs validate the user’s identity. Third-level authentication employs CAPTCHA verification. During data access, the user’s authenticity is verified. If the credentials fail to be correct at any level of authentication, the user access is denied with the warning “Invalid credentials”. The interface between the proposed framework and the AWS is illustrated in Figure 4a. Figure 4b illustrates the uploading process of cipher images into AWS S3 storage. The view of the S3 bucket with uploaded ciphered images is shown in Figure 5.

Figure 4. (a) Block diagram view: Storing ciphered image in S3 bucket. (b) Block diagram view: Retrieving ciphered image from S3 bucket with three-tier authentication.

Figure 5. View of the ciphered image in AWS S3 bucket.

5. Results and Discussion

The performance of the proposed encryption approach was analysed using different grey images of size [256, 256] with the Waterloo image databases (https://links.uwaterloo.ca/Repository.html (accessed on 8 December 2022)). It was implemented using the LabVIEW platform on an Intel Core i5 system configured with a 2.5 GHz CPU, 500 GB of main memory and 4 GB of RAM. The ability of the encryption approach against attacks such as brute force, statistical and chosen plaintext was analysed. The proposed scheme is influenced by adaptive key generation using the BPN model, which generates the adaptive key based on the randomness and redundant nature of the images. Furthermore, the security framework resists known plaintext attacks due to image-specific key generation for transposition. In addition, encryption quality analyses were carried out to prove the fitness of the proposed image encryption algorithm for secure image storage in the cloud.

5.1. Brute Force Attack

5.1.1. Keyspace Analysis

According to Kerckhoff’s cipher principle, the key must be vital and secure even if the encryption algorithm is public access. Keeping a longer key for the encryption process increased the key searching space, increasing the time to find the correct key [25]. In this security framework, six keys were generated adaptively with a precision of 10¹⁴. Hence, 10¹¹² is the keyspace for keys generated through the HNN. For the diffusion process, three different keys, K1, K2 and K3, are used of which two keys have chaotic behaviour, requiring four initial parameters, with precision of 10¹⁴ and one key is a fixed 8-bit key. Thus, the total keyspace is 10² × 10¹⁴ × 10¹⁴ × 10¹⁴ × 10¹⁴ × 10¹¹² = 10¹⁷⁰. In our earlier research on DNA blended chaos-based image encryption [24], the keyspace was 10⁸⁶. Compared to earlier work, this proposed approach exhibits greater keyspace, making the brute force attack even more complex.

5.1.2. Key Sensitivity Analysis

Chaotic sequence generators such as a hyperchaotic HNN and logistic and tent maps are used in the proposed security framework because they are sensitive to the initial conditions. Furthermore, an independent and adaptive key for each image makes the key search complex. Image features used to generate the adaptive keys through the HNN make the search even more complex. For example, a change in one bit out of 256 × 256 × 8 bits in the diffusion stage II key produces an entirely different image due to the chaotic behaviour of the key generated through the 1D logistic map. This is evident for the anti-brute force attack approach of the proposed security algorithm. Figure 6 shows the Lena image before and after encryption with correct and incorrect keys as evidence of the key sensitivity analysis.

Figure 6. Key sensitivity analysis through various images: (a) Plain; (b) ciphered (E1); (c) ciphered (one-bit change in original key) (E2); (d) E1 XOR E2; (e) decrypted E1 with correct key; (f) decrypted E1 with an incorrect key.

5.2. Statistical Attack Analysis

Images with statistical properties are subject to vulnerability when stored in public environments such as the cloud. The images before their storage are expected to have zero correlation to avoid such a security breach. The resistivity of the encryption algorithm against statistical attacks is tested through histogram, correlation and entropy analysis.

5.2.1. Histogram Analysis

The intensity of pixels in the greyscale must be distributed uniformly over the image plane for any encrypted image. However, due to the proposed DNA diffusion process, the histogram obtained for the test images is flat in response. Thus, an image’s unpredictability is proved. The histogram analysis for the test images of the proposed method is illustrated in Figure 7. Figure 7 shows that the pixels are uniformly distributed after encryption, and histograms of plain and cipher images are completely different.

Figure 7. Representation of Histogram for Plain and Cipher images.

5.2.2. Neighbouring Pixel Correlation Analysis

The co-located pixels in the original image are extremely correlated. Ideally, the correlation is zero for an encrypted image, i.e., a near-zero correlation [25]. After employing the proposed encryption algorithm on the images, the randomness of co-occurring pixels is high. Randomness in the encrypted images is calculated using a relation among co-located pixels. The dependency among the pixels is measured using the following expressions ((6)–(8)):

$$\mathrm{Corr}\left({\mathrm{Y}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{j}}\right)= \frac{\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left({\mathrm{Y}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{j}}\right)}{{\mathsf{\sigma }}_{{\mathrm{Y}}_{\mathrm{i}}}\times {\mathsf{\sigma }}_{{\mathrm{Y}}_{\mathrm{j}}}}$$

(6)

where standard deviation ${\mathsf{\sigma }}_{{\mathrm{E}}_{\mathrm{i}}}$ is obtained by

$${\mathrm{\sigma }}_{{\mathrm{Y}}_{\mathrm{i}}}=\sqrt{\frac{1}{\mathrm{M}\times \mathrm{N}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}\times \mathrm{N}}{\left({\mathrm{Y}}_{\mathrm{i}}\text{-}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\right)\right)}^2}}$$

(7)

Co-variance of an image is computed by

$$\mathrm{C}\mathrm{o}\text{-}\mathrm{variance}\left({\mathrm{Y}}_{\mathrm{i}},{\mathrm{Y}}_{\mathrm{j}}\right) = \frac{1}{\mathrm{M}\times \mathrm{N}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{M}\times \mathrm{N}}\left({\mathrm{Y}}_{\mathrm{i}}\text{-}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\right)\right)\times \left({\mathrm{Y}}_{\mathrm{j}}\text{-}\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{e}\right)\right)}$$

(8)

where Yi and Yj are two nearby pixel values of the ciphered image. The correlation among neighbouring pixels in all three directions of plain and encrypted images is illustrated in Figure 8. Figure 8 reveals that the correlation with the adjacent pixel values of the ciphered image is very low. Thus, the proposed neural-based adaptive key generation used for confusion offers near-zero correlation among the neighbouring pixels compared to other state of the art works shown in Table 2, which proves the ability of attack mitigation in the spatial domain.

Figure 8. Pixel distribution in horizontal, vertical and diagonal directions.

Table 2. Correlation analysis of Proposed versus Existing methods.

Test Images	Method	Correlation Direction
		Horizontal	Vertical	Diagonal
Lena	Plain	0.9106	0.9507	0.8849
	Proposed	0.0003	0.0042	−0.0049
	Ref. [12]	0.0011	0.0098	−0.0227
	Ref. [13]	0.00352	0.00648	0.00355
	Ref. [16]	−0.0066	−0.0089	0.0424
	Ref. [17]	−0.0048	−0.0112	−0.0045
	Ref. [19] Arnold Cat Map	0.0003	0.0145	0.0841
	Ref. [19] 2D Modular Chaotic Map	0.0287	0.0217	0.0179
	Ref. [19] 3D Modular Chaotic Map	0.0269	0.0038	0.0094
	Ref. [25]	0.0023	0.0019	0.0011
	Ref. [28]	0.0028	−0.0027	−0.0032
	Ref. [39]	−0.0287	0.0071	0.0007
	Ref. [40]	0.0054	−0.0073	0.0021
	Ref. [41]	− 0.0126	− 0.0048	0.0054
	Ref. [42]	0.0070	−0.0180	−0.0033
	Ref. [43]	−0.0042	-0.0028	0.0027
	Ref. [44]	−0.002153	−0.0000901	−0.0006059
	Ref. [45]	0.0090266	−0.0059255	0.0055227
	Ref. [46]	−0.0067	−0.0038	0.0063
	Ref. [47]	0.001348	0.00016	0.002236
	Ref. [48]	0.0018	0.0028	0.0016
	Ref. [49]	0.0049	−0.0022	−0.0042
	Ref. [50]	0.0015	−0.0021	−0.0020
	Ref. [51]	0.0016	−0.0034	−0.0032
	Ref. [52]	0.0003	−0.0021	−0.0030
	Ref. [53]	0.000033	−0.000295	−0.000085
Baboon	Plain	0.8423	0.8213	0.7408
	Proposed	0.0050	0.0022	−0.0048
	Ref. [13]	0.00083	0.00660	0.00159
	Ref. [14]	0.0003	−0.0162	0.0134
	Ref. [25]	0.0059	0.0041	0.0028
Cameraman	Plain	0.9303	0.9590	0.9048
	Proposed	−0.0055	0.0073	−0.0072
	Ref. [12]	−0.0047	−0.0195	0.0279
	Ref. [13]	0.00954	0.01908	0.00568
	Ref. [16]	0.0063	−0.0142	0.0168
	Ref. [17]	−0.0095	−0.0170	−0.0119
	Ref. [25]	0.0198	0.0132	0.0032
Barbara	Plain	0.8319	0.9483	0.7880
	Proposed	−0.0072	0.0002	0.0088
	Ref. [12]	−0.0187	−0.0016	0.0001
	Ref. [16]	−0.0212	−0.0161	−0.0110
	Ref. [17]	−0.0033	−0.0269	−0.0121
House	Plain	0.9782	0.9529	0.9361
	Proposed	0.0062	−0.0014	0.0074
	Ref. [12]	−0.0339	0.0186	−0.0001
	Ref. [13]	0.01659	0.01531	0.00034
	Ref. [16]	0.0023	−0.0187	−0.0225
	Ref. [17]	−0.0095	−0.0259	−0.0094

The neighbouring correlation values in Table 2 prove that the neural-based confusion model breaks the correlation between the adjacent pixels and the desired level. Due to neural-based adaptive confusion, all the images are equally confused, and pixels are dislocated repeatedly until the expected correlation is achieved.

5.2.3. Information Entropy

After encryption of an image, robustness and randomness are analysed using information entropy [25]. Global Shannon entropy E(s) is obtained using the following expression (9):

$$\mathrm{E}\left(\mathrm{s}\right)\hspace{0.17em}=\hspace{0.17em}-{\displaystyle \sum _{\mathrm{i}=1}^{256}\mathrm{I}\left({\mathrm{s}}_{\mathrm{i}}\right){\log }_2\mathrm{I}\left({\mathrm{s}}_{\mathrm{i}}\right)}$$

(9)

where I(S_i) is the probability of symbol (S_i). The pixel bit depths for grey images are always 8, so the entropy exists in the range [0 to 8]. For an ideally encrypted image, the entropy is always 8 [25]. This proposed neural-assisted DNA-based image encryption algorithm makes the pixel distribution over an image plane highly random. Therefore, the entropy value of an encrypted image is very close to 8. If the entropy value is less than 8 or close to 0 then the randomness effect in the encrypted image is significantly less and the vulnerability to attack is high. Table 3 shows that the proposed neural-based image encryption algorithm results in an entropy of almost eight, irrespective of the input image. The entropy value of the proposed encryption is compared with other state of the art works and exhibits the maximum unpredictability of the plain image.

Table 3. Entropy Analysis of Proposed versus Existing methods.

Test Images		Lena	Peppers	Baboon	Boat	Cameraman	Barbara	House
Plain		7.48183	7.60129	7.23399	7.26437	7.12881	7.51504	6.49614
Cipher	Proposed	7.9970	7.9973	7.9976	7.9972	7.9977	7.9973	7.9973
	Ref. [12]	7.9965	7.9958	NA	7.9959	7.9964	7.9957	7.9952
	Ref. [13]	7.99802	7.99852	7.99712	NA	7.99662	NA	7.99781
	Ref. [16]	7.9951	7.9965	NA	7.9960	7.9955	7.9937	7.9978
	Ref. [25]	7.9975	7.9958	7.9938	7.9941	7.9939	NA	NA
	Ref. [28]	NA	NA	7.9972	7.9962	7.9972	7.9969	NA
	Ref. [31]	7.9975	7.9972	NA	NA	7.9973	NA	7.9973
	Ref. [32]	7.9973	7.9972	7.9972	7.9972	7.9974	7.9972	7.9970
	Ref. [39]	7.9914	NA	7.9914	NA	NA	NA	7.9914

* NA—Not Available.

5.3. Encryption Quality Analysis

5.3.1. Chi-Square Test

The chi-square test measures pixel distribution in ciphered images [18]. The variation in the histogram is quantitatively obtained using a statistical metric called chi squared (${\chi }^2$), which is expressed as follows:

$${\chi }^2\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{\mathrm{i}=0}^{255}\frac{{\left(\mathrm{P}\mathrm{I}\left(\mathrm{i}\right)\hspace{0.17em}-\hspace{0.17em}256\right)}^2\hspace{0.17em}}{256}}$$

(10)

where PI is the pixel intensity value in the interval of 0 to 255. “i” is the intensity value in the encrypted pixels. The chi-square values that were found for encrypted images are verified with the distribution probability for 1% and 5% significance levels. The critical values for the 1% and 5% significance level with a degree of freedom of 255 are 310.457 and 293.2478, respectively. Therefore, the χ² value must be lower than the critical values for the ideally encrypted image. Table 4 reveals the uniform distributions of pixels in an encrypted image through low chi-square values compared to essential values.

Table 4. Chi-square test: Pixel distribution test.

Test Image	Plain		Cipher
	χ2 Value	H0 Test	χ2 Value	H0 Test
Airplane	168,463	Fail	258.172	Pass
Baboon	58,247.8	Fail	213.781	Pass
Barbara	35,001.2	Fail	242.57	Pass
Boat	85,621.8	Fail	255.305	Pass
Cameraman	97,215.8	Fail	212.992	Pass
Girl	93,817.1	Fail	240.836	Pass
House	300,852	Fail	242.477	Pass
Lena	37,973	Fail	276.633	Pass
Peppers	30,024.6	Fail	248.867	Pass
Splash	86,407.1	Fail	269.953	Pass

5.3.2. Histogram Maximum Deviation

The histogram maximum deviation is a measure of diffusion efficiency and encryption quality. Histogram maximum deviation is the difference in histogram values between the ciphered and plain image at every pixel intensity [17]. For an ideally encrypted image, the value must be close to the total size of the image. A histogram maximum deviation value close to the size of an image proves the randomness of pixel distribution through the encryption process. Histogram maximum deviation (HM) is obtained using the following Equation (11):

$${\mathrm{H}}_{\mathrm{M}}\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{d}\mathrm{i}\mathrm{f}\left(0\right)+\mathrm{d}\mathrm{i}\mathrm{f}\left(255\right)}{2}\hspace{0.17em}+{\displaystyle \sum _{\mathrm{j}=1}^{254}\mathrm{d}\mathrm{i}\mathrm{f}\left(\mathrm{j}\right)}$$

(11)

where dif(j) is the difference between the plain and cipher image histogram at the jth index. After encryption, the histogram deviation between the plain and cipher image is high, as shown in Table 5. From Table 5, it is proven that the strength of the encryption algorithm is well suited for secure image sharing and storing compared to other state of the art works. This is because, after ciphering the image, its statistical properties do not reveal any significant detail about the plain image.

Table 5. Histogram Maximum Deviation.

Test Image/Method	Histogram Maximum Deviation
	Barbara	Boat	Cameraman	Lena	Peppers
Proposed	40,694.5	53,452.5	60,413	40,921.5	36,169
Ref. [12]	17,944	25,367	16,674	20,811	22,648
Ref. [16]	19,384	25,193	16,803	19,931	22,966
Ref. [17]	18,148	25,442	18,007	21,339	22,935
Ref. [28]	NA	NA	64,119	41,458	36,391
Ref. [31]	158,258	148,597	64,300	NA	NA

* NA—Not Available.

5.3.3. Irregular Deviation

Encryption quality is analysed using irregular deviation. The linearity of the pixel distribution may be reflected in a differential attack. In any image encryption algorithm, the pixel intensities are expected to be uniformly distributed in the cipher image [17]. The irregular deviation is calculated through Equations (12)–(14), given below:

$$\mathrm{d}=\hspace{0.17em}\mathrm{i}\mathrm{m}\mathrm{h}\mathrm{i}\mathrm{s}\mathrm{t}\left(\mathrm{a}\mathrm{b}\mathrm{s}\left(\left(\mathrm{P}\right)\hspace{0.17em}-\left(\mathrm{C}\right)\right)\right)$$

(12)

The mean for the histogram of the difference in pixel intensities between the plain and cipher images (d) is calculated through the following expression:

$${\mathrm{M}}_{\mathrm{d}}\hspace{0.17em}=\hspace{0.17em}\frac{1}{256}{\displaystyle \sum _{\mathrm{i}=0}^{255}{\mathrm{d}}_{\mathrm{i}}}$$

(13)

where d_i is the ith element in the array d.

Irregular deviation (H_I) is obtained using Equation (14).

$${\mathrm{H}}_{\mathrm{I}}\hspace{0.17em}=\hspace{0.17em}{\displaystyle \sum _{\mathrm{i}=0}^{255}\left|{\mathrm{d}}_{\mathrm{i}}-{\mathrm{M}}_{\mathrm{d}}\right|}$$

(14)

Table 6 reveals that the proposed encryption algorithm distributes the pixel intensities uniformly without bias in the plain image.

Table 6. Irregular Deviation.

Test Image/Method	Irregular Deviation
	Barbara	Boat	Cameraman	Lena	Peppers
Proposed	43,446	46,218	39,020	44,748	41,394
Ref. [12]	42,556	36,124	39,380	40,820	34,824
Ref. [16]	43,014	36,220	39,414	40,768	34,706
Ref. [17]	42,708	36,226	39,244	40,480	35,088
Ref. [28]	NA	NA	38,959	44,465	41,184
Ref. [31]	129,765	137,793	39,668	NA	NA

5.3.4. Deviation from Ideality

Deviation from ideality must be minimal after encryption to prove the algorithm is promising for attacks [17]. Deviation of the originally encrypted image histogram from ideally encrypted images is estimated by the following Equation (15):

$$H_{DI}=\frac{{{\displaystyle \sum }}_{\mathrm{i}=0}^{255}\left|\mathrm{imhist}{\left(\mathrm{Idealcipher}\right)}_{\mathrm{i}}-\mathrm{imhist}{\left(\mathrm{Originalcipher}\right)}_{\mathrm{i}}\right|}{\mathrm{M}\times \mathrm{N}}$$

(15)

where M × N is the total size of the image.

Near-zero HDI proves the quality of the encryption algorithm. Table 7 depicts the existence of a very low deviation from ideality between plain and ciphered images. Thus, the proposed encryption algorithm produces low deviation from ideality compared to the existing literature, as shown in Table 7.

Table 7. Deviation from Ideality.

Test Image/Method	Deviation from Ideality
	Barbara	Boat	Cameraman	House	Lena	Peppers
Proposed	0.04834	0.05002	0.04437	0.04889	0.05182	0.04916
Ref. [12]	0.0928	0.0985	0.092	0.0994	0.0934	0.0977
Ref. [16]	0.1012	0.0995	0.1065	0.1141	0.1001	0.0979
Ref. [17]	0.0976	0.0958	0.0942	0.0882	0.0994	0.0917
Ref. [28]	NA	NA	NA	0.0485	0.0468	0.0496
Ref. [31]	0.0522	0.0528	0.0502	NA	NA	NA

5.4. Chosen Plaintext Attack

Diffusion employed in the encryption through XOR alone as an operation is subject to a chosen plaintext attack. The chosen plaintext attack results in the key used for diffusion; the encryption algorithm is compromised. Any encryption algorithms against the chosen plaintext attack need to satisfy the following condition:

P1 ⊕ P2 ≠ E1 ⊕ E2

Any two plain grey images, as P1 and P2, are XORed. Similarly, the encrypted versions of P1 and P2 as E1 and E2 are XORed. If both the XORed values are equal, it is vulnerable to chosen plaintext attack. Otherwise, breaking the image encryption algorithm is impossible, and its fitness against the chosen plaintext attack is proved. The ability of this security algorithm is analysed and it is shown that the DNA diffusion approach acts against the chosen plaintext attack. Figure 9a shows the XORed result of two plain images; the encrypted version of the same plain images is XORed, as shown in Figure 9b. Figure 9a,b are not identical, which indicates that the proposed diffusion process is not vulnerable to the chosen plaintext attack. A known plaintext attack becomes unviable in the proposed security framework due to the image-specific adaptive key generation using a neural network.

Figure 9. (a) P1 ⊕ P2; (b) E1 ⊕ E2.

5.5. Bit Distribution Analysis at Plane Level

The potency of the diffusion process is further analysed using the equality test over every bit plane. For any encrypted image, the distribution of zeros and ones in each bit plane must be equal, i.e., 50% of zeros and ones must be present in each plane to prove the unpredictability of the plain image after encryption. The diffusion strategy proposed in the algorithm outfit for the image encryption are shown, where the bits 1 and 0 of an encrypted image are equally distributed and tabulated in Table 8. Table 8 shows the bit “1” percentage in each plain and encrypted test image’s bit plane. Table 8 shows that each plane’s bit “1” in an encrypted image is equally distributed. So, the proposed DNA-based diffusion offers strong enough image encryption.

Table 8. Bit distribution analysis at plane level.

Planes Test Images		1	2	3	4	5	6	7	8
Airplane	P	50.383	49.817	49.355	51.842	53.865	24.394	78.969	81.544
	E	50.191	50.134	49.817	50.22	49.763	50.531	50.034	49.969
Baboon	P	50.247	50.075	50.378	50.563	53	55.841	44.63	53.096
	E	49.834	50.006	50.09	49.844	50.102	50.092	49.715	49.782
Barbara	P	49.928	49.916	50.075	50.272	48.856	48.956	47.932	35.727
	E	50.041	50.259	49.825	50.356	50.066	49.71	49.623	50.128
Boat	P	49.924	50	49.974	49.364	50.856	39.584	22.548	67.471
	E	49.889	50.281	49.783	50.168	49.977	49.974	49.911	49.98
Cameraman	P	49.841	49.379	50.844	52.199	42.644	50.958	18.71	60.005
	E	50.145	49.895	49.931	49.965	49.867	50.336	49.782	50.058
Girl	P	50.175	50.787	50.722	49.904	46.37	50.824	26.7	8.197
	E	49.586	49.832	49.916	49.887	49.77	50.003	50.111	49.713
House	P	50.035	49.631	52.985	65.085	67.981	71.492	52.217	48.505
	E	49.921	50.359	50.259	49.77	49.988	50.05	49.829	50.122
Lena	P	50.009	50.108	49.728	49.901	49.777	50.337	41.794	51.187
	E	50.247	49.968	49.486	49.768	50.113	50.005	50.536	50.444
Peppers	P	49.979	49.715	49.796	49.933	53.462	46.248	44.778	47.327
	E	49.925	50.201	49.954	50.281	49.966	49.78	50.204	50.194

P—Plain image; E—Encrypted image.

5.6. Computational Complexity

The overhead of the proposed security framework includes significant operations called key generation, confusion and DNA-based diffusions. The greyscale image used in this research is of size [M, N], where M = N = 256. The random number generated using the HNN takes the complexity of O {n(M × N)}. The transposition process complexity is O {M × N}. The proposed algorithm contains two DNA-based diffusion stages, which take O {4(M × N)}. So, the total computational complexity of the proposed framework takes O {(n + 5)(M × N)}. Table 9 compares the proposed system and other state of the art works with various aspects such as system configuration, tool used for implementation, the approach suggested and execution time. This proposed work has been implemented using the LabVIEW platform on an Intel Core i5 system configured with a 2.5 GHz CPU, 500 GB of main memory and 4 GB of RAM. Total execution time taken by this proposed approach, including key generation and cipher block chaining encryption, is calculated as 219.5 ms, comparable with Ref. [32]. The file is pushed into the AWS S3 bucket via a Wi-Fi network with 144.4 Mbps speed, which takes an uploading time of 0.4056 sec. Network speed influences propagation delay, which means they are inversely proportional.

Table 9. Computational complexity comparison with existing literature.

	Parameters	Tool Used for Implementation	System Configuration	Proposed Approach	Execution Time (s)
Existing Work
Ref. [17]		MATLAB	Intel Core i3-3227U 1.9 CPU and 4 GB of RAM	LFT-based S-box using a new chaotic map, P-S network	0.095
Ref. [18]		MATLAB R2011b	Intel(R) Core (TM) i3–2350, 2.30 GHz CPU	Plain image-dependent keystream using 2D logistic map	0.0343
Ref. [19]		MATLAB R2017a	Intel Core i7–7500 U, 3.5 GHz CPU, 4GB RAM	3D modular chaotic map permutation process for image encryption	0.8271
Ref. [25]		MATLAB 8	Intel Core i7, 2.3 GHz CPU, 8 GB RAM	Logistic chaos system, DNA encoding and operations.	0.281
Ref. [30]		MATLAB 2013a	Intel Core i3, 2.4 GHz CPU and 4 GB RAM	Bit-level permutation and diffusion using DNA addition	0.54
Ref. [32]		Virtual instrumentation tool	Core i5, 2.5 GHz CPU, 4 GB RAM	Chaos-based key generation system, DNA encoding and operations for secure image storage in the cloud	0.2188
Ref. [33]		MATLAB2011b	AMD A6-3420M and 2 GB RAM	Secure sampling through cascade chaotic map followed by confusion using Arnold transform and single-stage XOR-based diffusion	1.663661
Proposed		Virtual instrumentation tool	Core i5, 2.5 GHz CPU, 4 GB RAM	Neural attractor-based image-specific key generation and chaos key generation for image scrambling and DNA-based diffusion	0.2195

5.7. Discussion

The proposed algorithm is tested with ten test images of size [256, 256]. The algorithm achieves average entropy of 7.996098 and offers better entropy when compared to Refs. [12,16,39] and is comparable with [40,41,42,43,44,45,46,47,48,49,50,51,52,53]. The near-zero correlation offered by the proposed algorithm is better than the previous works, which is also given in the findings. The obtained average bit distribution at the plane level for the test images is 50.00364 and shows that the encrypted images are highly randomised. Therefore, the proposed image encryption is cryptographically efficient and can withstand statistical and chosen plaintext attacks. Furthermore, the presented work can restore useful images from captured versions of images under various environmental conditions. The suggested methodology is the best for analysing an image across a wireless medium and is sufficiently robust to interference.

6. Conclusions

Cloud storage is trendy and inevitable in many applications. However, data stored in the cloud are always under threat due to their multitenancy. So, it is essential to construct a security solution to ensure the security of cloud-hosted data. The proposed Hopfield attractor-based permutation blended DNA diffusion provides tightened security for grey images hosted in public cloud storage during when at rest, in transit and used by other applications. The proposed security framework exhibits greater potency to defend against various attacks. This proposed work uses a Hopfield attractor and chaotic maps, resulting in the keyspace of 10¹⁷⁰. The key generated for the confusion process is adaptive and image specific; hence, attackers cannot find the key using a chosen plaintext attack and a known plaintext attack. The proposed security algorithm yielded an average entropy value of 7.9973 and an average correlation value of 0.0008; hence, attackers cannot find the plain image using a statistical attack. This framework can be enhanced in future by using a reconfigurable hardware platform.