1. Introduction
The striving by companies to gain market share has promoted a continuous advance in their production processes. Several operational practices have been tested to obtain better performance in quality and productivity in manufacturing processes. This endless search for improvement compels academics to explore and apply the use of real-world instances in more depth to contribute to understanding and adapting these practices and help managers to make more adequate decisions. The use of a warm-up period is a conventional but effective practice in production processes. The basic notion of warm-up is used in many fields, such as high-intensity activities such as CNC machines. This practice allows the machinery a brief period of operation prior to the main production cycle; within this prior period, it is possible to adjust operating parameters, validate the quality level of the products generated, and, above all, prepare the system to withstand the high pressure of a lengthy task. The evaluation of this approach in the operational research field has not been the subject of many studies even though there exists some evidence to support the use of the warm-up in many manufacturing processes. In fact, actual production runs have variable schedules, and facilities and machinery go through schedule changes based on diverse circumstances. Unintended actions and unanticipated human behavior on the production line cause the schedule to become unpredictable, and, consequently, the states in which the machines are turned on and off vary. In addition, the warm-up period is dependent not only on the system’s features but also on the downtime of the equipment prior to its reactivation for a new production cycle. From this perspective, relevant research fails to illuminate this behavior. Thus, this study examines the effect of machine downtime on the warm-up period.
The definition of machine downtime is that the facilities or machinery are turned off after a production cycle, and no extra products are manufactured during this period. As soon as the production of the scheduled lot size is finished, consumption and demand fulfillment are covered with stock items. Thus, in the context of this study, anywhere the term “machine downtime” is used, it means that production has been finished but products manufactured previously continue to be shipped to customers or retailers.
Economic production quantity is an area for discussing these issues; although some studies have concentrated on the concept of warm-ups, it is still necessary to examine a wider variety of conditions. This study has the same orientation as a novel perspective that is common in the production process research area, as it starts with a general idea, and later, an innovative approach is introduced. The warm-up process runs in an economic production quantity environment, and the system stays in different out-of-state ranges. According to each range, the proper warm-up period is defined, and the mathematical model and the solution method are discussed. Overall, the optimal solution is provided, and the robustness of the results, with the changes in the system parameters, is analyzed. The conclusions and managerial insights help the reader and managers easily understand the concept and its applications.
In the day-to-day operations of a manufacturing system, it is common for the system to function in a variety of initial states, and operators and management seek to have a strategy in place to solve problems and achieve their production goals. These events are studied by researchers to determine the optimal strategy for organizations. Every time the system follows a new scheme, and the prior scenarios are no longer valid, it is necessary to have an overview of these concerns and provide a solution. Consideration of the warm-up process has emerged as a new trend in the manufacturing industry over the last several years; nevertheless, more work is required to illuminate these new concerns. In most research works, the warm-up length is implicitly specified or defined as a random variable. The warm-up period should be determined based on the amount of time that facilities or machinery spend out-of-state, meaning that the warm-up time must be proportional to the system’s out-of-state time. Therefore, if the system is off, the need for warm-up time increases.
The importance of establishing a warm-up period dependent on the machine’s downtime is supported by a series of research that has demonstrated its high impact on the energy consumption of production operations. Warm-up duration as a decision variable is a unique area of research that began in 2019; increasingly, the relationship between the warm-up period and the efficiency of the manufacturing process is being questioned. Beyond this notion, the area of machine downtime can generate more questions and research opportunities. Machine downtime’s contribution to the warm-up practice enables the system to be more flexible in terms of scheduling and planning for any operations, including maintenance or unanticipated events. As a complement, this study considers two approaches to defective products in the production process: (a) rejecting defective items or (b) restoring their quality. Leaving aside the manufacturing process and factoring in the extra cost for the systems, both options are a loss to the systems. Nevertheless, the analysis performed states that the former strategy is more expensive than the latter.
The rest of the study is organized as follows:
Section 2 presents a literature overview of the most current studies related to the main topics.
Section 3 explains the problem and the mathematical operations required to solve it.
Section 4 offers numerical examples for each defective product type. Using sensitivity analysis,
Section 5 investigates the robustness of the model’s parameters. Some managerial and environmental findings are discussed in
Section 6. The main conclusions and some future research ideas are presented in
Section 7.
2. Literature Review
Harris pioneered the scientific field of inventory management in 1913. Several years later, Taft introduced the economic order quantity (EOQ). These initiatives offered a solid framework for researchers to expand the inventory management field in accordance with any real-world applications (Glock and Grosse [
1]). Recent studies have focused on illuminating gaps between theoretical and practitioner points of view and enhancing their findings in inventory management decisions. Jaber et al. [
2] examined lot size problems according to the learning effect. They evaluated papers included in the inventory management field, categorized them, and made recommendations for future works. Farahani and Tohidi [
3] evaluated maintenance and quality-related literature in inventory models. Gautam et al. [
4] comprehensively assessed EPQ problems with defective items. The scope of EPQ challenges has been expanded to include several characteristics of real-world situations. Numerous scientists have committed huge amounts of time in developing diverse aspects of these disciplines.
Any manufacturing process generates a small percentage of defective products; these low-quality products cause difficulties, such as item delivery delays and inventory management problems. In addition, these defective items must be handled through a different process, such as remanufacturing, repair, reworking, or, in the worst-case scenario, they are discarded as scrap items. Tsao et al. [
5] evaluated a defective manufacturing system with reworking and predicted maintenance. Karim and Nakade [
6] examined sustainable EPQ models with an emphasis on carbon emissions and product recycling. Biswas and Schultz [
7] examined an imperfect manufacturing system by addressing the possibility of reworking or discarding products. These systems produce items that are not in satisfactory condition based on a quality standard. Hauck et al. [
8] used two screening phases to identify defective products. Given that a second phase in the production line is more expensive and time-consuming, they added an initial screening procedure in earlier stages.
The integration of the rework process into this field is presented in the following studies. Garg et al. [
9] proposed a model in which a proportion of products includes defective items of high quality and low quality; the latter products are considered scrap items represented by a uniform distribution. They utilized fuzzy algorithms to find the optimal solution. Fallahi et al. [
10] incorporated several constraints into an economic order quantity multi-item manufacturing system. Their study determined the optimal replenishment quantity and an item reuse approach. Alsawafy and Selim [
11] presented a discrete production system where the sequence of manufacturing perfect items and defective items is difficult to track. They studied the time needed to fulfill customer demands. Askari et al. [
12] considered warehouse space and budget constraints in an economic production quantity problem. The study focused on inspection, various inspection errors, and defective items. In their model, defective items are categorized according to the type of operation performed on them. Asadkhani et al. [
13] investigated four economic order quantity models that produced different types of defective items, labeled as salvage, repairable, scrap, and rejected items. They studied the optimal policy for each case and used the inspection process to screen the products. Furthermore, a learning rate for the inspector is considered in the models. Asadkhani et al. [
14] studied the contribution of several parameters to an inventory problem based on supply chains, quality requirements, and environmental issues. In their model, there is no value in following the repair approach, so they provided a decision to address the optimal retirement policy.
The maintenance cost and schedule are inherent components of any corporation. Researchers often use the phrase “consideration of maintenance combined with other characteristics such as production or quality.” During machine downtime, production is stopped, and numerous maintenance actions are executed based on the system’s deterioration. Zheng et al. [
15] incorporated EPQ optimization with condition-based maintenance. Wan et al. [
16] introduced production, maintenance, and quality control decisions and issues into their approach. They adopted continuous-flow production and demonstrated that the combination of these elements reduces costs. Salmasnia et al. [
17] merged three principles into an imperfect system: statistical process monitoring, maintenance scheduling, and production cycle length. Their findings indicated that the variable sampling approach and rework procedure result in fewer damaged products. In addition, they showed an assessment of financial profits over time and product degradation in the practical implementation of the research results.
Even if the production of low-quality items is not desirable, they have value. One alternative that can reduce environmental damage and cut costs is reworking defective items. This is a standard practice in the industrial sector, and its adoption has been integrated into many inventory management applications. Gharaei et al. [
18] expanded an EPQ model to include partial backordering and reworkable items. They employed both linear and fixed costs in their model and considered that imperfect products might deteriorate with time. Shee and Chakrabarti [
19] implemented an EPQ model with a markdown policy. This strategy is a practical approach to reducing the amount of inventory on hand, as opposed to increasing the outcome or selling more items. The model is fully backordered and permits shortages throughout the lead period. Al-Salamah [
20] established an EPQ model with variable rework rates and two types of reworkable products. The asynchronous plan permits imperfect items to remain in a lot until production is complete; after that, the rework process starts. In the alternate plan, defective items are reworked as soon as they are manufactured in a synchronous system.
Other researchers have centered their work on machine downtime relevance, as represented by the following authors. Biswas and Sarker [
21] evaluated the operation time in a manufacturing process and determined the best running duration to prevent imperfect matching within the production. Tiwari et al. [
22] suggested a green production quantity model with a trade–credit strategy to reduce the overall cost. They discovered that setup time had a considerable impact on the cycle time. Nwanya et al. [
23] examined the impact of machine downtime on industrial practices using a case study. Employing multiple regression analysis, they compared downtime with other components, such as cycle time, and found that lowering machine downtime had a significant influence on improving productivity.
Countless production devices, such as CNC machines, operate and are set up in different manners. Nobil et al. [
24] noted that warm-up periods offer several advantages, such as workload reduction, as fewer faulty products are generated by manufacturing lines, and lower maintenance costs, as machines reach better and stable operational conditions during the warm-up phase. In addition, they stated that it is feasible to fabricate products during the warm-up stage, although at a slower pace. If any defective item is generated during the warm-up period, it may be reconditioned in the main production cycle. Frigerio and Matta [
25] employed a time-dependent warm-up phase to illustrate the varying energy requirements of each manufacturing phase. A proper trade-off is necessary between the machine starting and shutdown to reduce overall energy usage. They noted that the warm-up period is generally nondeterministic and dependent on the machine’s off-state time. They observed that the warm-up phase is dependent on how long the machine remains in a low energy usage condition. The warm-up length determined the correct approach to reducing overall energy consumption; for instance, if the warm-up time is growing, they proposed keeping the machinery operating for long periods. Mouzon and Yildirim [
26] employed a variety of dispatching techniques available to a controller to reduce equipment power consumption. They implemented a warm-up phase as a crucial element in machinery operation, which may be repeated several times. In their research, the warm-up length influences the selection of each dispatching rule. Additionally, the selection rule might vary based on the downtime period. Chen et al. [
27] optimized a system with an efficient scheduling trade-off between the startup and shutdown states. Mashaei and Lennartson [
28] investigated a design for a closed-loop flow shop control approach. They focused on lowering the energy consumption of the machine during idle states based on a deterministic warm-up phase.
Frigerio and Matta [
29] considered four energy consumption management policies: in-service, out-of-service, working, and warm-up. They used a real-world case scenario to demonstrate the impact of each strategy on energy usage. The study states that a machine that has been out of service for an extended period must be preheated before a production period; moreover, a warm-up interval is required after maintenance activity. The articles reviewed so far reveal the importance of predicting the correct length of the warm-up time; furthermore, the amount of time allowed for the machine to rest is also relevant to the calculation of the warm-up period. Nevertheless, the warm-up time, in terms of economic production quantity, is a new and under-researched topic. The common approach is to consider the warm-up length to be deterministic. Nobil et al. [
24] applied the warm-up notion to an imperfect manufacturing system in which defective products are reworked as the first phase of their EPQ problem. They listed several advantages of adopting warm-up for machinery, such as extending the life of the equipment, fabricating fewer low-quality items, and the potential of producing goods during the warm-up phase. Two advantages of a warm-up are saving money with less waste output and boosting equipment efficiency. Nobil et al. [
30] divided an EPQ problem into three parts: two single-item EPQ inventory problems and one multi-item, single-machine EPQ inventory problem. They identified the optimal cycle time to reduce the overall cost. Ganesan and Uthayakumar [
31] reassured managers and corporations that the warm-up procedure is a genuine technique that can increase production efficiency and product quality. Their study examined two production inventory issues, including a hybrid maintenance schedule, item shortages, and reworking defective goods, and it assumed fixed and variable forms for the warm-up time. In the end, they advised defining the duration of the warm-up phase to make a more accurate inventory decision. Ganesan and Uthayakumar [
32] established three inventory models for a faulty system with partial backordering and reworking operations for defective products. During the production process, an arbitrary number of defective items are generated. The warm-up notion and maintenance schedules work together to form a faulty system. In their research, they deemed the warm-up to be defined as a strategic decision. Nobil et al. [
33] examined warm-up duration as a decision variable in an EPQ model. They assumed that the defective item quantity is a function of the warm-up time, so the model selects the appropriate warm-up time to obtain fewer low-quality items in the system.
The use of the warm-up concept in a manufacturing process is an innovative issue in inventory management literature. In most studies, the warm-up length is assumed to be fixed; nevertheless, its duration may be altered by other variables, such as machinery downtime. Frigerio and Matta [
25] focused on leveraging warm-up time as a decision variable and the influence of machine downtime to fill this knowledge gap. Finally,
Table 1 presents a summary of recent studies related to the warm-up concept and their main features.
3. Problem Definition
This section presents model notations and explains the idea behind the warm-up schemes. First, the parameters, dependent variables, and decision variables are as follows:
Parameters:
: Warm-up categories index based on downtime length;
: Unit production cost ($/unit)
: Unit defective (scrapped/reworked) cost ($/unit)
: Setup cost per cycle ($/cycle)
: Corrective maintenance cost per cycle ($/cycle)
: Unit holding cost per unit time ($/unit/unit time)
: Demand rate per unit time ($/unit time)
: Production rate per unit time during the warm-up period ($/unit time)
: Production rate per unit time during the primary manufacturing process ($/unit time);
: Rework rate per unit time for defective items ($/unit time)
: The fraction of defective (scrap or rework) items produced during the warm-up period
: The fraction of defective (scrap or rework) items produced during the primary manufacturing process;
: Breakpoint of downtime or consumption length;
: Warm-up period in the jth interval (year);
Dependent Variables:
: Maximum on-hand inventory level per cycle (unit)
: Production quantity per cycle during the warm-up period (unit)
: Production quantity per cycle during the primary manufacturing period (unit)
: Total production quantity per cycle (unit);
: Primary production period per cycle (unit time)
: Consumption or downtime period per cycle (unit time)
: Rework period per cycle (unit time)
: Minimum point of cycle length in the jth interval;
: Maximum point of cycle length in the jth interval;
: Total cost ($/unit time)
Decision Variables:
: Cycle length (unit time)
The model finds the optimal warm-up period based on different downtimes. In this context, the machine warm-up period is connected to (dependent on) the downtime length. Downtime or machine downtime is defined as the period in which production stops, machines are shut down, and the system continues to fulfill the demand with previously stored items. Essentially, the model correlates the lengths of the warm-up and cool-down periods; then, relevant warm-up intervals are provided for different downtime criteria. Under this strategy, prolonging the machine downtime increases the warm-up period, which means that
.
Table 2 presents the warm-up time diagram. Based on the aforesaid strategy, two inventory models are devised. In the first model, presented in
Section 3.1, it is presumed that defective products are scrap and are handled just after manufacturing. The second model assumes that all defective products are repaired and reconditioned as perfect products after reworking, described in
Section 3.3. It is noted that, during the warm-up period, the machinery is adjusted and prepared for the production cycle. These adjustments include cleaning, lubrication, and the adjustment of operating parameters, among others. Corrective maintenance, mentioned in this study, is also considered to be part of those adjustments, and it is a common part of the warm-up process.
3.1. Scrap Model
This section highlights an inventory problem with a warm-up period based on machine downtime. In the production process, defective products are scrapped and removed from the system.
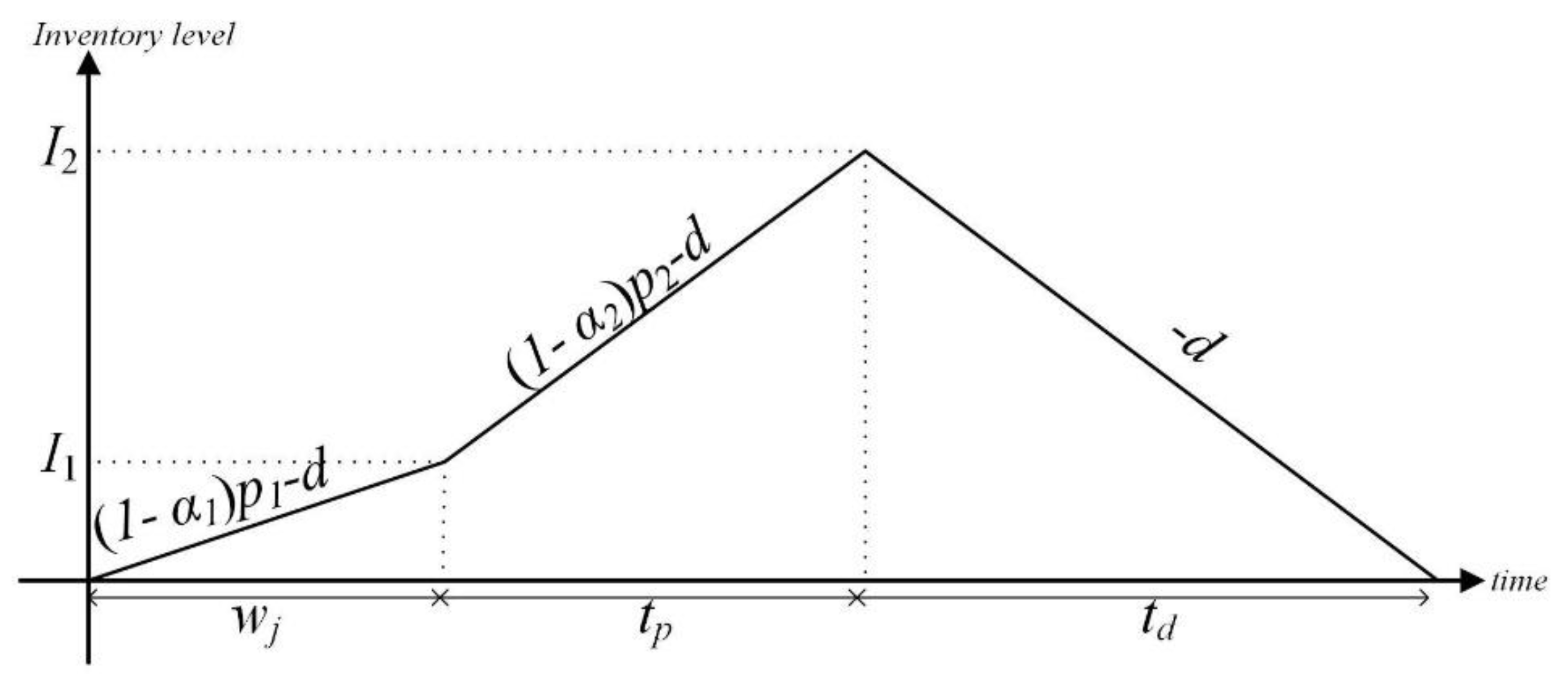
Figure 1 describes the resulting inventory graph, and the solution method is described next. Before the main production process, which is reliant on machine downtime (
, the system needs a warm-up period (
). In the warm-up stage, the machines run at a lower production rate than during the main manufacturing process as they are geared up to withstand heavy-duty operations. In addition, any essential maintenance operations are performed during the warm-up period. Then, the inventory system operates flawlessly under these conditions. Due to the fine-tuning of the adjustments, the inventory system generates more defective items during the warm-up stage than in the main production process. In other words,
. In this model, defective products are manufactured during the warm-up and main process and later discarded at an extra cost at the end of the production phase. In summary, the system undergoes a warm-up phase (
) at the start of production, and it generates perfect products at a rate of
. As soon as the warm-up phase concludes, the main process begins with a time length of
and a production rate of
. As the main process ends, the system is turned off, and customer demand is met until the available inventory level equals zero. In addition, shortages are not permitted in this system, as
and
; therefore, the result is
.
As seen in
Figure 1, the following equations represent the total production quantities generated throughout the warm-up and main production periods:
The inventory levels at the end of the warm-up and main production processes are then calculated as follows:
As stated before, the warm-up length is
. On the other hand, the production and downtime durations are computed as follows:
Thus, the cycle length is
Substituting
from Equation (1) into Equation (7), the number of products fabricated in the main production process is obtained as
The setup and corrective maintenance costs in each cycle are
and
, respectively. Therefore, the following equations represent these costs per unit of time:
Each cycle’s total production quantity,
, is equal to the sum of the quantities generated during the warm-up (
) and production (
) processes. Mathematical speaking,
. Given the expected manufacturing cost per unit, the production cost per unit of time is as follows:
In addition, the total number of defective items produced in each cycle is equal to
, where
and
are the defective items produced in the warm-up and main production processes, respectively. Since the defective item scrap cost per unit is
, then the scrap cost per unit time is obtained as follows:
According to
Figure 1, the holding cost per unit of time is computed based on the area below the inventory level graph:
Therefore, the total inventory cost, including setup, maintenance, production, scrap, and holding costs is as follows:
As aforementioned, increasing the downtime period increases the warm-up period, so the downtime range is represented by
Since
is equal to
, the cycle length range is
Substituting
from Equation (4) into Equation (16)
Therefore, the breaking point of the cycle length,
, is obtained as follows:
Finally, according to Equations (18) and (19),
Table 2 is rewritten into
Table 3 to report the warm-up time diagram based on the cycle length.
3.2. Solution Algorithm for Scrap Model
The total cost in Equation (14) depends on two decision variables: the warm-up time (
) and the cycle length (
). The first step is to demonstrate that the objective function’s Hessian matrix in Equation (14) is positive. The partial derivations of the objective function are computed in
Appendix A. After some simplification, the Hessian matrix becomes
Given that the Hessian matrix in Equation (20) is always positive, the total cost in Equation (14) is convex. As previously stated, this problem has a diversity of potential downtime durations. The warm-up duration depends on these values, so the ideal cycle length for each range is calculated as follows:
Since there are several optimal cycle lengths, the lowest cost is the optimal result. The solution method to find the optimal solution is as follows:
Forward-solving the model is required. Starting with the lowest warm-up period, calculate the values of , , and from Equations (18), (19), and (21), respectively.
If is obtained from , stop at the desired distance, i.e., the allowed distance, (). Otherwise, go to the next time, that is, , which is greater than .
Whenever is at the allowed distance, determine the total cost. Then, calculate the exact cost for the left breakpoint at that point, i.e., for the time . The lowest cost is the problem’s optimal answer.
3.3. Rework Model
This section presents the second case of the inventory study, which includes a warm-up period that depends on machine downtime and allows for the reworking of defective items. In this system, all defective items produced during the warm-up and main production processes are reconditioned immediately after the end of the main production period, and all defective items regain a good-quality status after the rework phase.
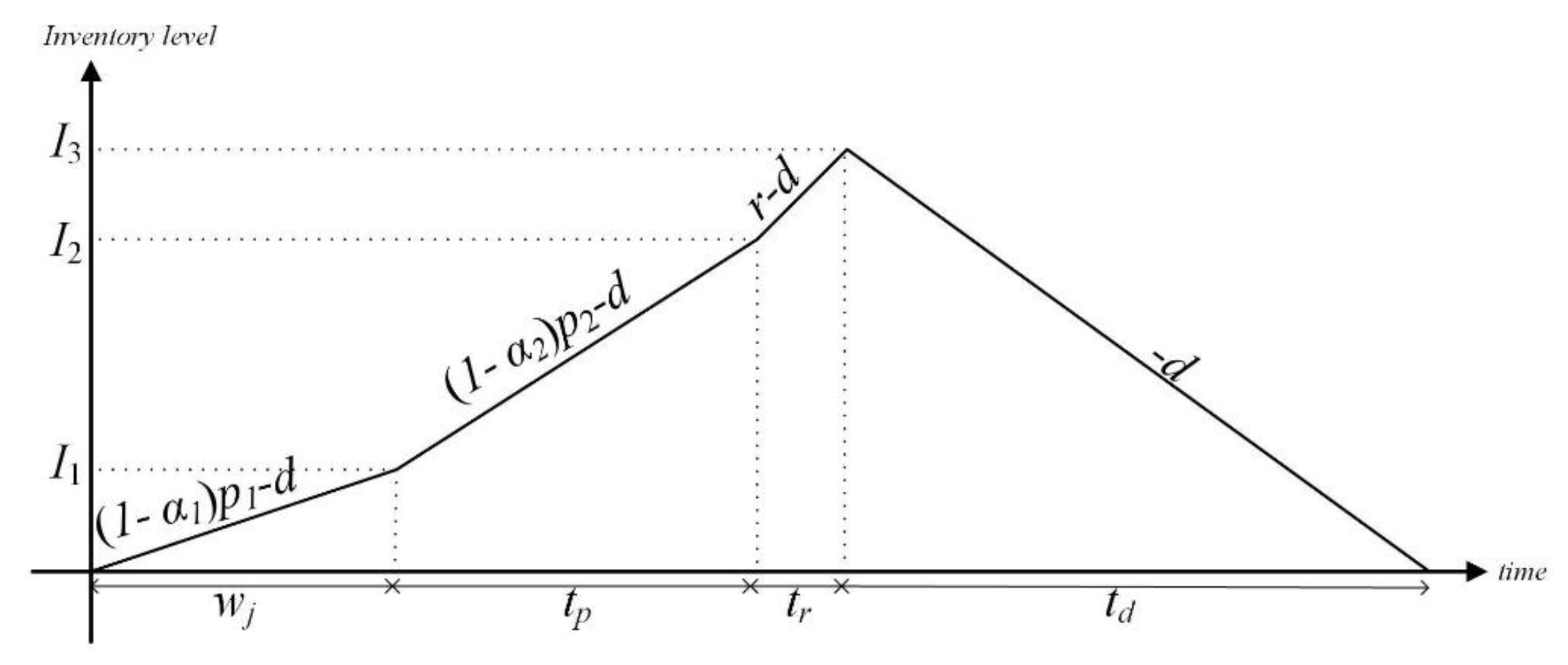
Figure 2 illustrates the inventory system with the rework procedure. As soon as the main production process is finished, the rework process (
) begins. The rework rate is greater than the production rate, as no faulty goods are produced during this phase. The warm-up proportion of faulty items is the same as the first case and higher than the main production process. From a mathematical point of view,
and
. Since shortage is not allowed in this model, then
.
The total production quantities generated in the warm-up and production periods are equal to
and
, respectively. Then, based on
Figure 2, inventory levels at the end of the warm-up, main production, and rework periods are calculated as follows:
Then, the production, downtime, and rework period lengths are defined as
As a result, the cycle length is defined as
As stated in
Section 3.1, the setup, maintenance, and production costs are
In addition, the total re-workable items manufactured in each cycle is equal to
. Since the defective item rework cost per unit is
, the rework cost per unit time is obtained as follows:
Additionally, the holding cost per unit of time is
Finally, the total inventory cost including setup, maintenance, production, rework, and holding costs, is obtained as follows:
Given that, the downtime range is
, and
is equal to
, the cycle length range is written as
. Replacing
from Equation (24), this range is as follows:
Thus, the range of the breakpoint of the cycle length,
, is as follows:
3.4. Solution Algorithm for Rework Model
The total cost in Equation (35) depends on two decision variables: the warm-up duration (
) and the cycle length (
). The next step is to show the convexity of the objective function in Equation (35) by obtaining its Hessian matrix. The partial derivations of the objective function are provided in
Appendix B. Thus, with some simplification, the Hessian matrix is computed as
As the Hessian matrix in Equation (39) is always positive, the total cost is undoubtedly convex. It is understood that along with the different ranges of downtime length, the warm-up period comes up with a defined value based on these ranges. Hence, solving the problem requires obtaining the optimal cycle length value for each range.
To solve this case, the steps of the solution algorithm stated in
Section 3.2 is rewritten as follows:
Forward-solving the model is required. Starting with the lowest warm-up period, calculate the values of , , and from Equations (37), (38), and (40), respectively.
If is obtained from , stop at the desired distance, i.e., the allowed distance, (). Otherwise, go to the next time, that is, , which is greater than .
Whenever is at the allowed distance, determine the total cost, calculate the same cost for the left breakpoint at that point, i.e., for the time . The lowest cost is the problem’s optimal solution.
4. Numerical Examples
4.1. Numerical Example for Scrap Model
To illustrate the relevance of the inventory problem with scrap items, an example is presented next: consider
;
;
unit/day;
unit/day;
unit/day;
unit/day;
$/cycle;
$/cycle;
$/unit;
$/defective unit; and
$/unit/day. The downtime range that is used to determine each warm-up period is shown in
Table 4. As stated in Equation (17), it is possible to determine the warm-up period based on the cycle length range instead of the downtime range using Equations (18) and (19); therefore,
Table 4 is converted into
Table 5 to show the warm-up period based on the cycle length range.
The optimal solutions are obtained based on the procedure stated in
Section 3.2. This algorithm is a forward procedure, so the value of the cycle length for the first range, based on Equation (21), is equal to
. Since
is greater than the maximum range of the cycle length according to
Table 5 (
), the cycle length and the total cost for the first range are
. Go to the next breakpoint of this range, and repeat the same procedure. The cycle length and the total cost values are
. Go to the third breakpoint; thus, the values of the cycle length and the total cost are
. As the cycle length of the third breakpoint is between its range, it does not need to go to the next breakpoint. Finally, based on the three cycle lengths obtained, the optimal solution belongs to the breakpoint with the lowest total cost. The lowest total cost is located in the second breakpoint with
(
); the optimal warm-up and cycle length are equal to
days and
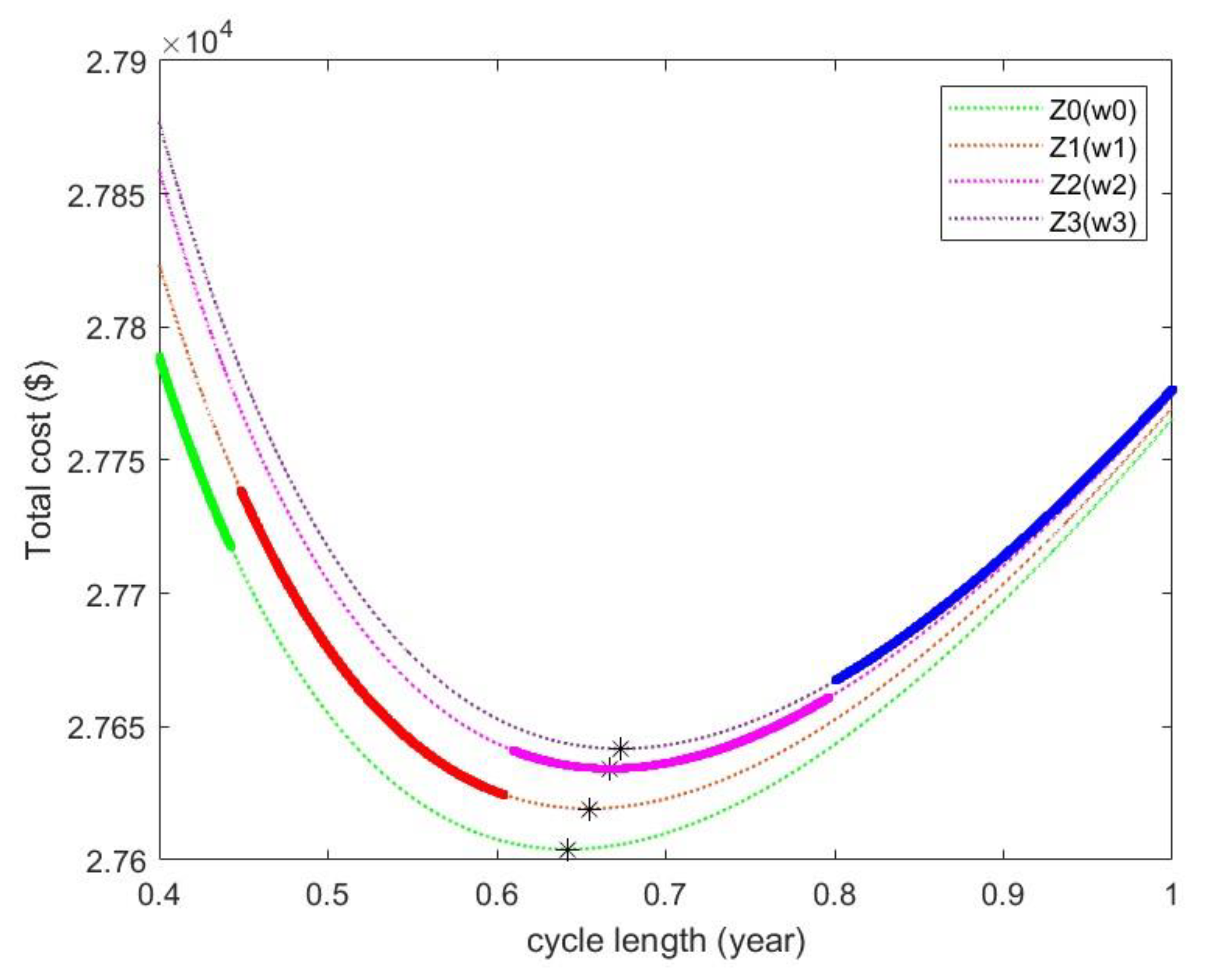
. Based on the optimal solution, the values of production quantity during warm-up and main production are equal to 20 and 326.7 units, respectively. Therefore, total production quantity, production time, and downtime (consumption) time are 346.7 units, 0.38 days, and 0.22 days, respectively. The graph of the total cost value concerning the cycle length for each breakpoint is illustrated in
Figure 3.
4.2. Numerical Example for Rework Model
To verify the application of the inventory model for the defective production system with a rework phase, the numerical example presented in
Section 4.1 is analyzed with the parameters stated before, adding that all defective items produced in the warm-up and production processes are reconditioned at a rework rate of 2000 unit/day. Based on Equations (37) and (38), a warm-up period based on the cycle length range instead of the downtime range is determined. Hence,
Table 4 converts to
Table 6 to show a warm-up period based on the cycle length range.
The optimal solutions are obtained based on the procedure stated in
Section 3.4; the value of the cycle length for the first range according to Equation (40) is equal to
. As it exceeds the maximum value of the cycle length from
Table 6 (
), the cycle length and the total cost are obtained for the first range as
. Then, go to the next breakpoint of this range, and repeat the previous procedure; therefore, the cycle length and the total cost are as follows:
. Next, the procedure progresses to the third breakpoint; the cycle length and the total cost are
. The procedure ends if the cycle length is located within its range, as it is in this instance. In the end, the optimal solution is located at any breakpoint that has the lowest total cost among all cycle lengths. In this example, the lowest total cost is obtained from the second breakpoint:
(
). Thus, the optimal warm-up and the cycle length are equal to
days and
. Next, according to the optimal solutions, the values of production quantity during warm-up and main production are 20 and 280 units, respectively. Therefore, total production quantity, production time, downtime (consumption) time, and rework time are 300 units, 0.19 days, 0.38 days, and 0.02 days, respectively. Furthermore, the graph of the total cost value concerning the cycle length for each breakpoint is illustrated in
Figure 4.
5. Sensitivity Analysis
This section aims to examine the system’s robustness, so the input parameters are changed to reflect the response in the cycle length, the total cost, and the difference in total cost between both proposed models. This study examines two techniques for defective products: scrapping and reworking. In
Section 3.1 and
Section 3.3, the total cost of the scrap and rework models are shown, while the difference between them is stated in Equation (41). Depending on the specifics of each scenario, their differences reveal which model is preferable and associated with the lowest system cost. The second model has a lower cost when Equation (41) is greater than zero. If the result is smaller than zero, the first model is less expensive. Moreover, a change in any input parameter influences both costs. The disposal and operation costs for the rework process are the same in both cases. In the second model, the rate of rework (
r) is applied to the items discarded in the first model.
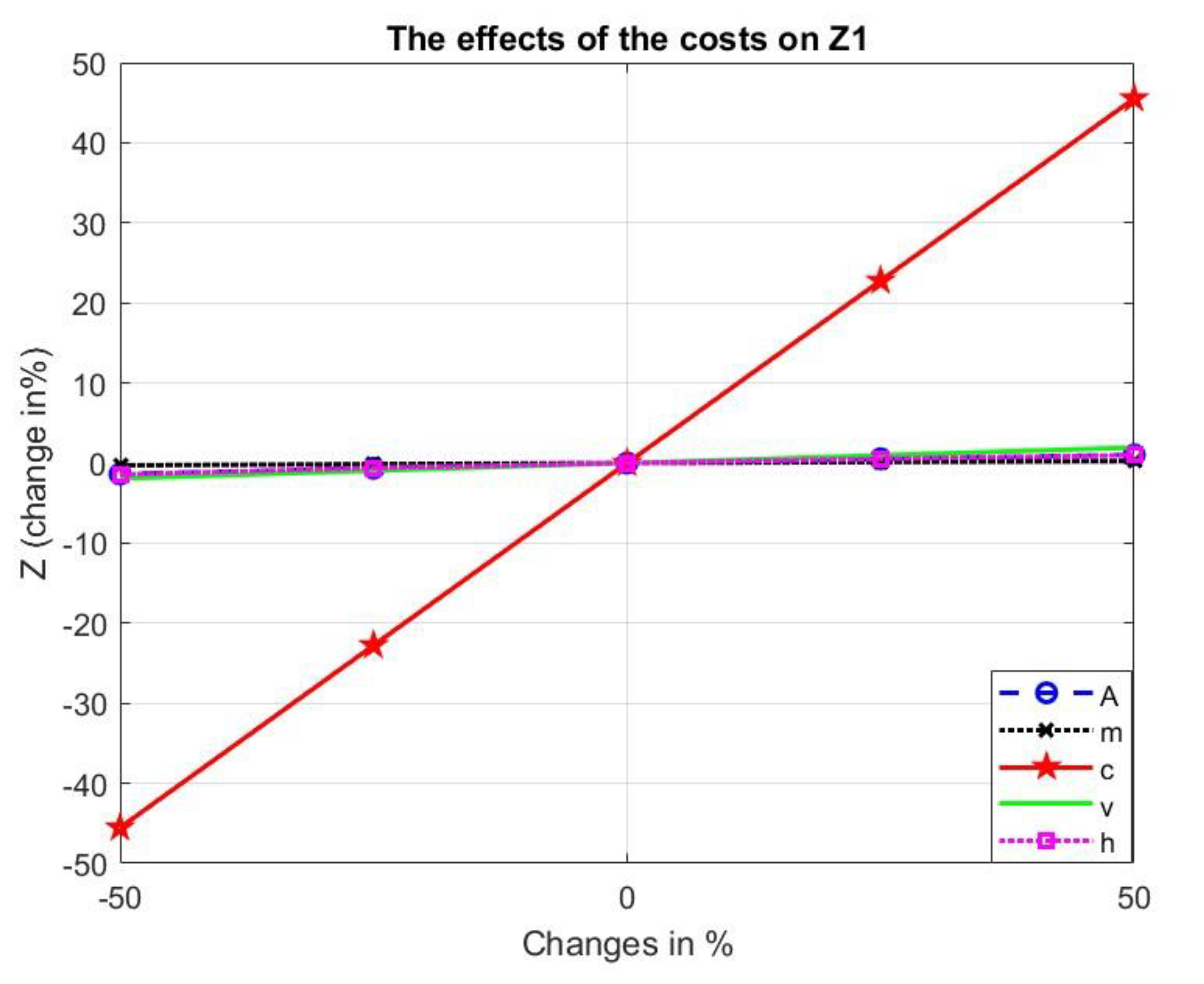
Table 7 displays individual model analyses. The cost parameters account for any changes in the cycle length (
T) and the total cost. Even though the second model is more sensitive to changes in the cost parameters, both models respond in a similar way. Changes in the following parameters have less than a 2% effect on the overall cost: the setup cost (
A), the corrective maintenance cost (
m), the defective cost (
), and the holding cost (
h). In contrast, the total cost is influenced by the same proportion of changes in the manufacturing cost (
c). The cycle length is less sensitive to variations in the corrective maintenance cost (
m), the defective cost (
), and the production cost (
c), while the setup cost has a significant impact on its duration. In addition, the inverse trend of the cycle length demonstrates a noticeable reaction to any holding cost adjustments.
Figure 5,
Figure 6,
Figure 7 and
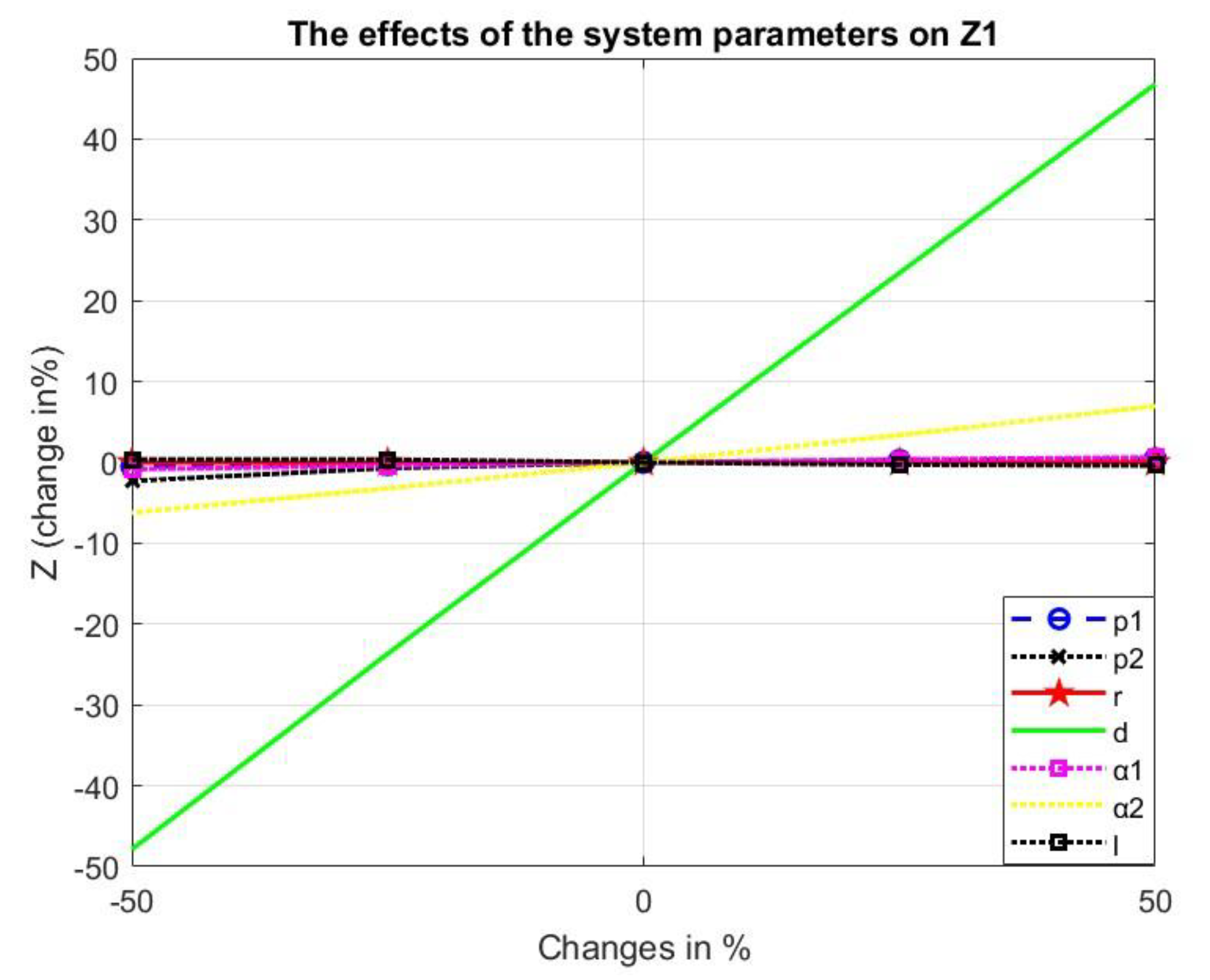
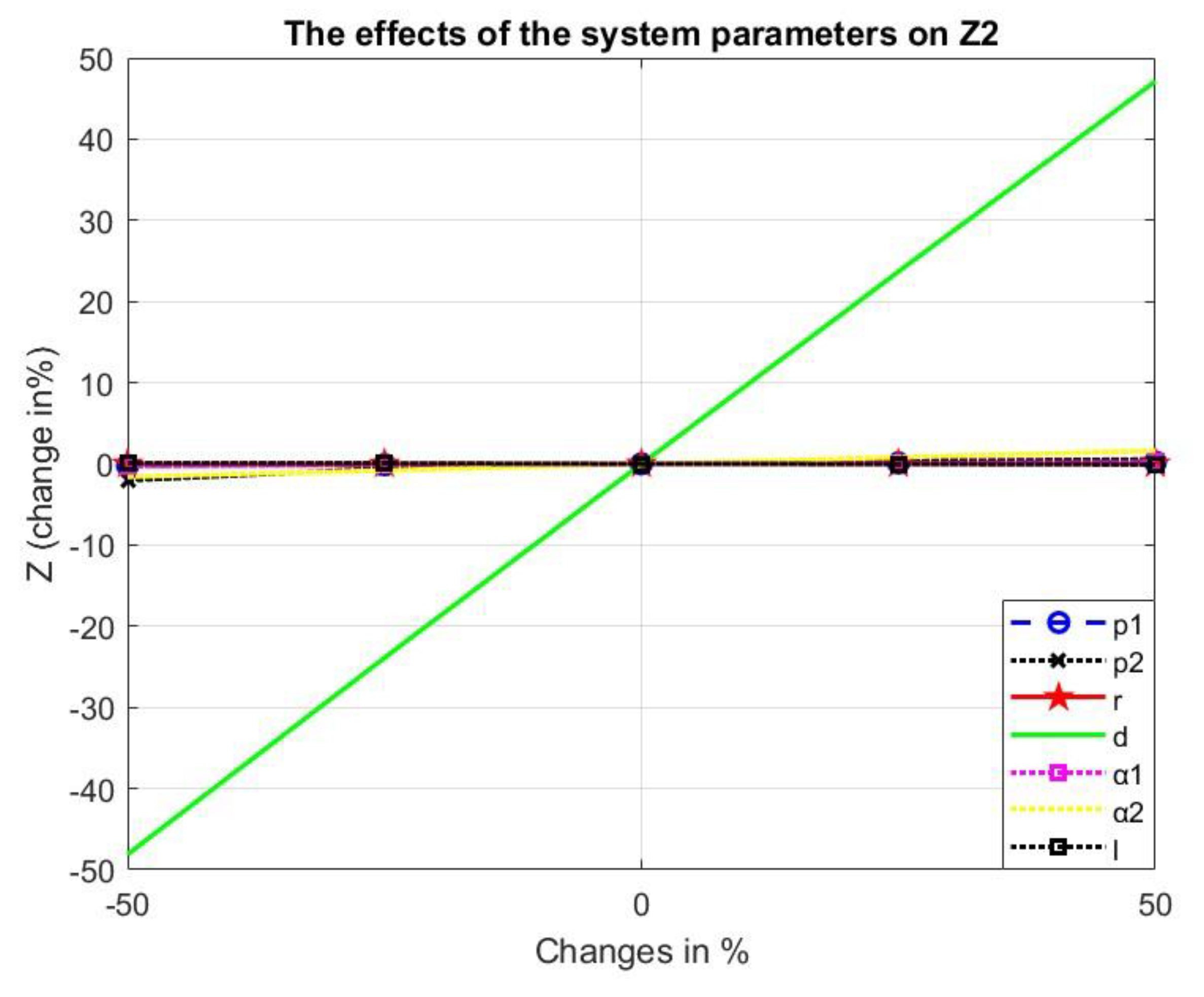
Figure 8 indicate the effect on the total cost for each model. In addition,
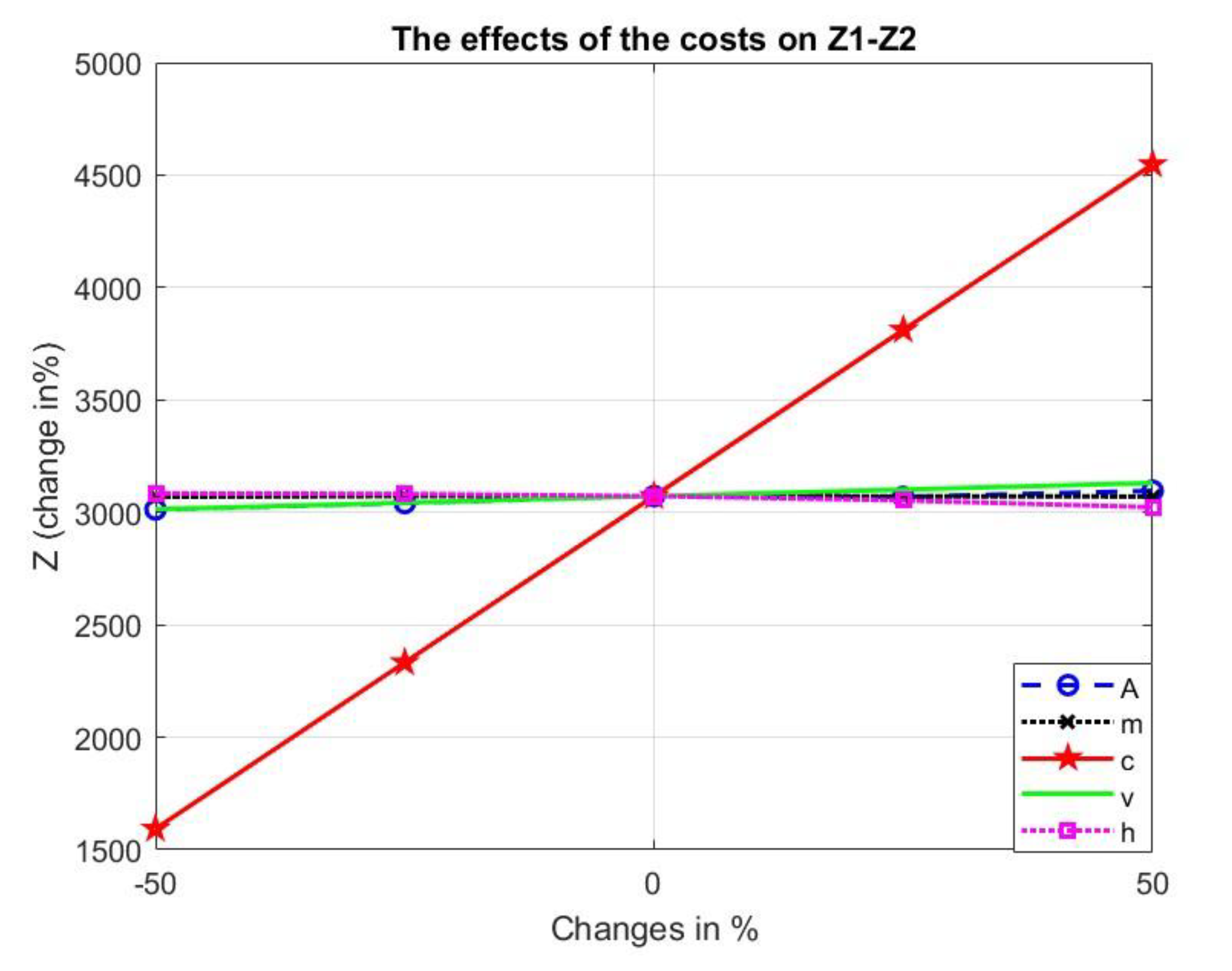
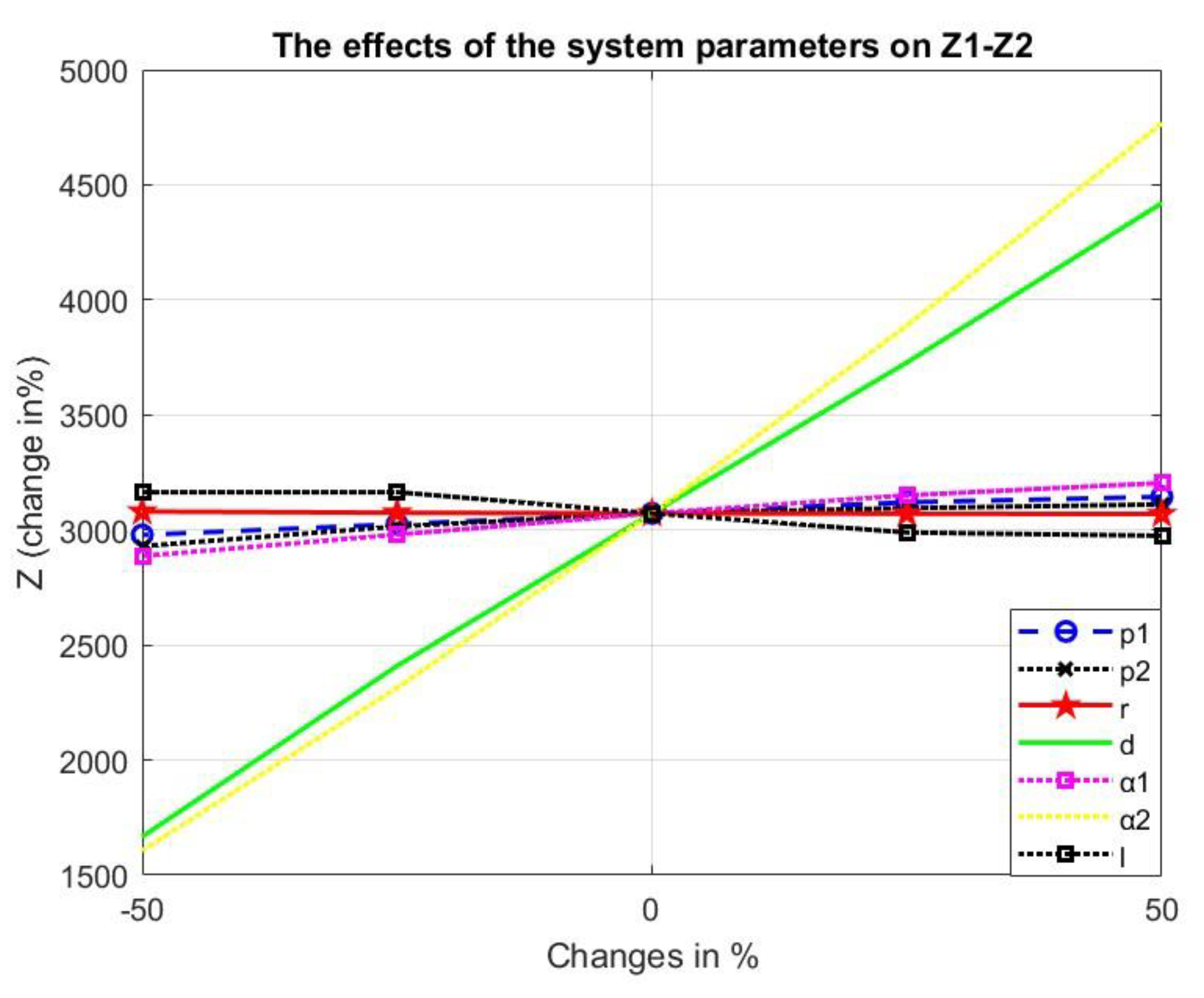
Figure 9 and
Figure 10 depict the effect of diverse parameters on the difference between the two total costs.
Table 8 indicates the sensitivity of the models’ total costs and cycle lengths to inherent system parameters. In general, the rework model is less sensitive to changes in the relevant parameters. Variations in the production rate during the warm-up phase (
), the production rate during the main production process (
), the proportion of defective (scrap or rework) items produced during the warm-up period (
), and the breakpoint of the downtime duration (
) have a less than 1% impact on the total cost. In contrast, the proportion of defective (scrap or rework) products generated during the main production process (
) affects the total cost.
In inventory management models, the demand rate (
) is a crucial element that has a significant impact on the total cost, as is the case in this analysis. The cycle length of the system responds inversely to variations in the production rate during the warm-up phase (
), the production rate during the main production process (
), and the proportion of defective (scrap or rework) items produced during the warm-up period (
). In addition, it has a significant response to changes in the demand rate, the proportion of defective (scrap or rework) products generated during the main production process, and the threshold of downtime length. In the second model, the rework rate for defective items has a minor influence on the cycle length. Finally,
Figure 5,
Figure 6,
Figure 7 and
Figure 8 illustrate the impacts of fundamental system parameters on the total cost, while
Figure 9 and
Figure 10 show their influence on the difference between the two total costs.
6. Managerial and Environmental Insights
Overseeing facilities and machinery under stable conditions and circumstances allows managers to plan and schedule manufacturing operations with a high degree of confidence. The introduction of the warm-up concept to the inventory management model was proposed recently, and its benefits have been discussed by some studies; however, the machinery downtime effect has been absent in those studies. This study integrates the warm-up concept with real-world observed conditions, as its length is dependent on the time that the machine is off. Overall, this research extends the warm-up concept with a realistic assumption that provides a solution according to the state in which the machine remained. Undoubtedly, as machines spend more time out of state, they will require more time in the warm-up phase. This study considers these operating conditions and provides a model (and its exact optimal solution), helping managers test and understand several approaches in their search for better results.
Moreover, this research offers the comprehensive development of an EPQ model with a warm-up time. The model is constructed under some special conditions: (a) the warm-up length is regarded as being dependent on machine downtime; (b) a range of machine downtimes determines the necessary warm-up duration; and (c) two different approaches are used to generate defective products. In the end, two models are presented as part of the analysis. The first model discards low-quality items as scrap, while the second model reworks them to regain their quality and return them to the inventory as good-quality items. Based on the machinery’s downtime, managers can swiftly decide on the warm-up period. The study reveals the least expensive strategy for their system and recommends a production schedule. In addition, a sensitivity analysis investigates the influence of some relevant model parameters on the system’s total cost, allowing managers to explore some of the initial conditions of the system (model parameters) to search for more profits.
The manufacturing process has two alternatives to deal with defective products: pay money and dedicate effort to restore their quality or discard them as scrap. Both have an adverse effect on the environment. As a response to machinery downtime, managers can select an appropriate warm-up period that leads to fewer defective items in the production process; therefore, the “warm-up” notion guarantees that manufacturing processes are more cost-efficient and more environmentally friendly. Finally, the sensitivity analysis presented in
Section 5 states that the rework model is less expensive than the scrap model (see
Table 7 and
Table 8); therefore, managers should evaluate this approach regarding defective items as their first option.
From this perspective, the production costs, the proportion of defective (scrap or rework) products generated during the main manufacturing process, and the demand rate reduce the cost of the system in the rework strategy. Diverse warm-up durations and variable machine downtimes enable managers to use this strategy broadly and across various sectors. Overall, the outcome provides insights into the scheduling and planning of manufacturing equipment operations. This approach answers some managerial concerns about the prospective aspects of production processes and provides some insights based on a numerical comparison between two defective item strategies.
7. Conclusions
The warm-up process provides benefits to the manufacturing system. However, to capture these benefits, the concept must be correctly applied to integrate the effect of other factors. Frigerio and Matta [
25] suggested that machinery downtime significantly affects the warm-up process, as they analyzed the energy consumption of the machine in different operational states. Based on these results, the relationship between the warm-up process and machine downtime is considered in the proposed models as a novel contribution to the literature on economic production quantity science.
This study investigates the adoption of an appropriate warm-up period based on machine downtime. An economic production quantity (EPQ) model generates defective products and benefits from a warm-up period. Several downtime ranges correspond to the optimal value of the warm-up period, so the warm-up time is contingent on machine downtime. The defective goods in the system are handled in two ways. In one model, the system takes away low-quality goods as waste or scrap. In the second model, the system employs a process of reworking to increase their worth and regain their good-quality level. Both cases are modeled and solved as an EPQ problem; furthermore, an algorithm procedure and an exact mathematical solution are provided. Each mathematical scenario is supported by a numerical illustration. The solutions are compared to one another, and a summary is presented.
The key novelty is the consideration of a range for machine downtime; in addition, the warm-up duration is a dependent variable whose value is determined by machine downtime. The approach to solving the problem is unique, and it relaxes different constraints to reach a solution where the warm-up is determined according to machine downtime, and the optimized total cost is obtained. In other words, this study fills the gap in the literature on the warm-up period and highlights the significance of the relationship between the warm-up process and machine downtime.
Even though this research can be applied to many industrial settings, further ideas can enhance and expand the understanding and use of these concepts. Several inventory management elements reinforce the warm-up notion, such as shortage strategies. In addition, the products used by enterprises take many forms, such as deteriorating products. Pricing policy is an important idea in inventory management that may be used in the future for this system. Therefore, there is a wide set of options to develop more research on the integration of such features throughout the warm-up phase.
Moreover, the consideration of carbon emissions is another avenue of study for the further extension of this research. Different methods are available to be applied in this model such as carbon taxes, cap-and-trade, and greenhouse gas emissions (GHGs). Furthermore, analyzing the effect of the warm-up process in reducing defective items and the attenuation of energy consumption fit well as future research tracks (Mala et al. [
34], Marchi and Zanoni [
35], Marchi et al. [
36], Malleeswaran and Uthayakumar [
37], and Fajrianto et al. [
38]).
Author Contributions
Conceptualization, E.N., L.E.C.-B., G.T.-G. and A.H.N.; Methodology, E.N., L.E.C.-B., D.G.-N., G.T.-G., A.C.-M., I.d.J.L.-H., N.R.S. and A.H.N.; Software, E.N. and A.H.N.; Validation, E.N., L.E.C.-B., D.G.-N., A.C.-M., I.d.J.L.-H., N.R.S. and A.H.N.; Formal analysis, E.N., L.E.C.-B., D.G.-N., G.T.-G., A.C.-M., I.d.J.L.-H., N.R.S. and A.H.N.; Investigation, E.N., L.E.C.-B., D.G.-N., G.T.-G., A.C.-M., I.d.J.L.-H., N.R.S. and A.H.N.; Data curation, E.N., L.E.C.-B., D.G.-N., G.T.-G., A.C.-M., I.d.J.L.-H. and A.H.N.; Writing—original draft, E.N.; Writing—review & editing, L.E.C.-B.; Visualization, E.N.; Supervision, L.E.C.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is included in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Partial Derivations of the Total Cost Equation (14)
According to Equation (14), the partial derivations of Equation (14) for the cycle length and the warm-up period are as follows:
Appendix B. Partial Derivations of the Total Cost Equation (35)
According to Equation (35), the partial derivations of Equation (35) with the respect to the cycle length and the warm-up period are as follows:
References
- Glock, C.H.; Grosse, E.H. The impact of controllable production rates on the performance of inventory systems: A systematic review of the literature. Eur. J. Oper. Res. 2020, 288, 703–720. [Google Scholar] [CrossRef]
- Jaber, M.; Peltokorpi, J.; Smunt, T. The lot size problem and the learning curve: A review of mathematical modeling (1950′s–2020). Appl. Math. Model. 2022, 105, 832–859. [Google Scholar] [CrossRef]
- Farahani, A.; Tohidi, H. Integrated optimization of quality and maintenance: A literature review. Comput. Ind. Eng. 2020, 151, 106924. [Google Scholar] [CrossRef]
- Gautam, P.; Maheshwari, S.; Kausar, A.; Jaggi, C.K. Advances in Interdisciplinary Research in Engineering and Business Management. In Inventory Models for Imperfect Quality Items: A Two-Decade Review; Springer: Singapore, 2021; pp. 185–215. [Google Scholar] [CrossRef]
- Tsao, Y.-C.; Lee, P.-L.; Liao, L.-W.; Zhang, Q.; Vu, T.-L.; Tsai, J. Imperfect economic production quantity models under predictive maintenance and reworking. Int. J. Syst. Sci. Oper. Logist. 2019, 7, 347–360. [Google Scholar] [CrossRef]
- Karim, R.; Nakade, K. A Literature Review on the Sustainable EPQ Model, Focusing on Carbon Emissions and Product Recycling. Logistics 2022, 6, 55. [Google Scholar] [CrossRef]
- Biswas, P.; Schultz, S.R. An EPQ model for an imperfect production system with rework, scrap and backorder. Int. J. Ind. Syst. Eng. 2021, 37, 411–431. [Google Scholar] [CrossRef]
- Hauck, Z.; Rabta, B.; Reiner, G. Impact of early inspection on the performance of production systems–insights from an EPQ model. Appl. Math. Model. 2022, 107, 670–687. [Google Scholar] [CrossRef]
- Garg, H.; Sugapriya, C.; Kuppulakshmi, V.; Nagarajan, D. Optimization of fuzzy inventory lot-size with scrap and defective items under inspection policy. Soft Comput. 2023, 27, 2231–2250. [Google Scholar] [CrossRef]
- Fallahi, A.; Bani, E.A.; Niaki, S.T.A. A constrained multi-item EOQ inventory model for reusable items: Reinforcement learning-based differential evolution and particle swarm optimization. Expert Syst. Appl. 2022, 207, 118018. [Google Scholar] [CrossRef]
- Alsawafy, O.G.; Selim, S.Z. Discrete production workstation with two types of imperfect items: Determining the optimal promise time. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2180689. [Google Scholar] [CrossRef]
- Askari, R.; Sebt, M.V.; Amjadian, A. A multi-product EPQ model for defective production and inspection with single machine, and operational constraints: Stochastic programming approach. In Logistics and Supply Chain Management, Proceedings of the 7th International Conference LSCM 2020, Tehran, Iran, 23–24 December 2020; Springer International Publishing: Cham, Switzerland, 2021; Revised Selected Papers 7; pp. 161–193. [Google Scholar]
- Asadkhani, J.; Mokhtari, H.; Tahmasebpoor, S. Optimal lot-sizing under learning effect in inspection errors with different types of imperfect quality items. Oper. Res. 2021, 22, 2631–2665. [Google Scholar] [CrossRef]
- Asadkhani, J.; Fallahi, A.; Mokhtari, H. A sustainable supply chain under VMI-CS agreement with withdrawal policies for imperfect items. J. Clean. Prod. 2022, 376, 134098. [Google Scholar] [CrossRef]
- Zheng, R.; Zhou, Y.; Gu, L.; Zhang, Z. Joint optimization of lot sizing and condition-based maintenance for a production system using the proportional hazards model. Comput. Ind. Eng. 2021, 154, 107157. [Google Scholar] [CrossRef]
- Wan, Q.; Chen, L.; Zhu, M. A reliability-oriented integration model of production control, adaptive quality control policy and maintenance planning for continuous flow processes. Comput. Ind. Eng. 2023, 176, 108985. [Google Scholar] [CrossRef]
- Salmasnia, A.; Hajihosseini, Z.; Maleki, M.R. An economic manufacturing quantity model with rework process for deteriorating products under maintenance-quality policy. Int. J. Model. Simul. 2022, 42, 946–965. [Google Scholar] [CrossRef]
- Gharaei, A.; Shekarabi, S.A.H.; Karimi, M.; Pourjavad, E.; Amjadian, A. An integrated stochastic EPQ model under quality and green policies: Generalised cross decomposition under the separability approach. Int. J. Syst. Sci. Oper. Logist. 2019, 8, 119–131. [Google Scholar] [CrossRef]
- Shee, S.; Chakrabarti, T. An EPQ Model for Imperfect Production System with Deteriorating Items, Price-Dependent Demand, Rework and Lead Time Under Markdown Policy. In Data Analytics and Artificial Intelligence for Inventory and Supply Chain Management; Springer: Singapore, 2022; pp. 81–96. [Google Scholar]
- Al-Salamah, M. Economic production quantity in an imperfect manufacturing process with synchronous and asynchronous flexible rework rates. Oper. Res. Perspect. 2019, 6, 100103. [Google Scholar] [CrossRef]
- Biswas, P.; Sarker, B. Operational planning of supply chains in a production and distribution center with just-in-time delivery. J. Ind. Eng. Manag. 2020, 13, 2. [Google Scholar] [CrossRef]
- Tiwari, S.; Ahmed, W.; Sarkar, B. Multi-item sustainable green production system under trade-credit and partial backordering. J. Clean. Prod. 2018, 204, 82–95. [Google Scholar] [CrossRef]
- Nwanya, S.; Udofia, J.; Ajayi, O. Optimization of machine downtime in the plastic manufacturing. Cogent Eng. 2017, 4, 1335444. [Google Scholar] [CrossRef]
- Nobil, A.H.; Tiwari, S.; Tajik, F. Economic production quantity model considering warm-up period in a cleaner production environment. Int. J. Prod. Res. 2019, 57, 4547–4560. [Google Scholar] [CrossRef]
- Frigerio, N.; Matta, A. Energy Efficient Control Strategy for Machine Tools with Stochastic Arrivals and Time Dependent Warm-up. Procedia CIRP 2014, 15, 56–61. [Google Scholar] [CrossRef]
- Mouzon, G.; Yildirim, M.B.; Twomey, J. Operational methods for minimization of energy consumption of manufacturing equipment. Int. J. Prod. Res. 2007, 45, 4247–4271. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, L.; Arinez, J.; Biller, S. Energy-Efficient Production Systems Through Schedule-Based Operations. IEEE Trans. Autom. Sci. Eng. 2012, 10, 27–37. [Google Scholar] [CrossRef]
- Mashaei, M.; Lennartson, B. Energy Reduction in a Pallet-Constrained Flow Shop Through On–Off Control of Idle Machines. IEEE Trans. Autom. Sci. Eng. 2012, 10, 45–56. [Google Scholar] [CrossRef]
- Frigerio, N.; Matta, A. Machine Control Policies for Energy Saving in Manufacturing. In Proceedings of the CASE 2013-IEEE International Conference on Automation Science and Engineering, Madison, WI, USA, 17–21 August 2013; pp. 663–668. [Google Scholar]
- Nobil, A.H.; Kazemi, A.; Taleizadeh, A.A. Economic lot-size problem for a cleaner manufacturing system with warm-up period. RAIRO Oper. Res. 2020, 54, 1495–1514. [Google Scholar] [CrossRef]
- Ganesan, S.; Uthayakumar, R. EPQ models for an imperfect manufacturing system considering warm-up production run, shortages during hybrid maintenance period and partial backordering. Adv. Ind. Manuf. Eng. 2020, 1, 100005. [Google Scholar] [CrossRef]
- Ganesan, S.; Uthayakumar, R. EPQ models with bivariate random imperfect proportions and learning-dependent production and demand rates. J. Manag. Anal. 2021, 8, 134–170. [Google Scholar] [CrossRef]
- Nobil, E.; Cárdenas-Barrón, L.E.; Loera-Hernández, I.D.J.; Smith, N.R.; Treviño-Garza, G.; Céspedes-Mota, A.; Nobil, A.H. Sustainability Economic Production Quantity with Warm-Up Function for a Defective Production System. Sustainability 2023, 15, 1397. [Google Scholar] [CrossRef]
- Mala, P.; Palanivel, M.; Priyan, S.; Jirawattanapanit, A.; Rajchakit, G.; Kaewmesri, P. Sustainable Supply Chain System for Defective Products with Different Carbon Emission Strategies. Sustainability 2022, 14, 16082. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S. Technical note on “Inventory management in supply chains with consideration of Logistics, green investment and different carbon emissions policies”. Comput. Ind. Eng. 2023, 175, 108870. [Google Scholar] [CrossRef]
- Marchi, B.; Zanoni, S.; Zavanella, L.; Jaber, M. Green supply chain with learning in production and environmental investments. IFAC PapersOnLine 2018, 51, 1738–1743. [Google Scholar] [CrossRef]
- Malleeswaran, B.; Uthayakumar, R. A Vendor-Managed Inventory Model for Imperfect Production Process Using Sustainability Investment and Energy Consumption Under Different Carbon Policies. Process. Integr. Optim. Sustain. 2022, 6, 707–722. [Google Scholar] [CrossRef]
- Fajrianto, A.; Jauhari, W.A.; Rosyidi, C.N. A Three-Echelon Inventory Model for Deteriorated and Imperfect Items with Energy Usage and Carbon Emissions. In iMEC-APCOMS 2019, Proceedings of the 4th International Manufacturing Engineering Conference and The 5th Asia Pacific Conference on Manufacturing Systems, Putrajaya, Malaysia, 21–22 August 2019; Springer: Singapore, 2020; pp. 305–312. [Google Scholar]
Figure 1.
Scrap model inventory level, including scrap items.
Figure 1.
Scrap model inventory level, including scrap items.
Figure 2.
The inventory level of the first model, including reworked items.
Figure 2.
The inventory level of the first model, including reworked items.
Figure 3.
The scrap model total cost versus cycle length for each breakpoint. Bold line: permissible limits of each range, *: the answers for each range are obtained from Equation (21).
Figure 3.
The scrap model total cost versus cycle length for each breakpoint. Bold line: permissible limits of each range, *: the answers for each range are obtained from Equation (21).
Figure 4.
The rework model’s total cost versus the cycle length for each breakpoint. Bold line: permissible limits of each range, *: the answers for each range are obtained from Equation (40).
Figure 4.
The rework model’s total cost versus the cycle length for each breakpoint. Bold line: permissible limits of each range, *: the answers for each range are obtained from Equation (40).
Figure 5.
The effects of the costs of the numerical example on the total cost of the first model.
Figure 5.
The effects of the costs of the numerical example on the total cost of the first model.
Figure 6.
The effects of the system parameters of the numerical example on the total cost of the first model.
Figure 6.
The effects of the system parameters of the numerical example on the total cost of the first model.
Figure 7.
The effects of the cost of the numerical example on the total cost of the second model.
Figure 7.
The effects of the cost of the numerical example on the total cost of the second model.
Figure 8.
The effects of the system parameters of the numerical example on the total cost of the second model.
Figure 8.
The effects of the system parameters of the numerical example on the total cost of the second model.
Figure 9.
The effects of the cost of the numerical example on the difference between the two models.
Figure 9.
The effects of the cost of the numerical example on the difference between the two models.
Figure 10.
The effects of the system parameters of the numerical example on the difference between the two models.
Figure 10.
The effects of the system parameters of the numerical example on the difference between the two models.
Table 1.
A comparison of recent studies related to the warm-up concept.
Table 1.
A comparison of recent studies related to the warm-up concept.
| Paper | Objective Function | Warm-Up Period | Defective Items | Solution Method | Warm-Up-Dependent Machine Downtime |
|---|
| Cost | Profit | Fixed | Variable | Scrap | Rework | Closed-Form | Analytical | Meta-Heuristic |
|---|
| Nobil et al. [24] | * | | * | | | * | | * | | |
| Nobil et al. [30] | * | | * | | | | * | | | |
| Ganesan and Uthayakumar [31] | * | | * | * | | * | | * | | |
| Ganesan and Uthayakumar [32] | | * | * | | | * | | * | * | |
| Nobil et al. [33] | * | | | * | * | | | * | | |
| This study | * | | | * | * | * | | * | | * |
Table 2.
Warm-up time diagram based on downtime length.
Table 2.
Warm-up time diagram based on downtime length.
| Range Number | Downtime Range | Warm-Up Time |
|---|
| 0 | | |
| 1 | | |
| 2 | | |
| | |
| | |
| | |
| | |
Table 3.
Warm-up time diagram based on the cycle length.
Table 3.
Warm-up time diagram based on the cycle length.
| Range Number | Downtime Range | Cycle Length Range | Warm-Up Time |
|---|
| 0 | | | |
| 1 | | | |
| 2 | | | |
| | | |
| | | |
| | | |
| | | |
Table 4.
Warm-up time diagram based on the downtime range.
Table 4.
Warm-up time diagram based on the downtime range.
| Range Number | Downtime Range | Warm-Up Time |
|---|
| 0 | | |
| 1 | | |
| 2 | | |
| 3 | | |
Table 5.
Warm-up time diagram based on the downtime range with scrap items.
Table 5.
Warm-up time diagram based on the downtime range with scrap items.
| Range Number | Downtime Range | Cycle Time Range | Warm-Up Time |
|---|
| 0 | | | |
| 1 | | | |
| 2 | | | |
| 3 | | | |
Table 6.
Warm-up time diagram based on the downtime range with a rework phase.
Table 6.
Warm-up time diagram based on the downtime range with a rework phase.
| Range Number | Downtime Range | Cycle Time Range | Warm-Up Time |
|---|
| 0 | | | |
| 1 | | | |
| 2 | | | |
| 4 | | | |
Table 7.
Sensitivity analysis of the cost parameters.
Table 7.
Sensitivity analysis of the cost parameters.
| Change in % | Model I with Scrap Items | Model II with Rework | Z(1)* − Z(2)*
|
|---|
| Breakpoint of | | | Breakpoint of | | |
|---|
| Initial | 2 | 0 | 0 | 2 | 0 | 0 | 3072.317 |
|---|
| 50 | 3 | 31.965 | 1.030 | 4 | 32.437 | 1.059 | 3095.999 |
| 25 | 2 | 0 | 0.528 | 2 | 0 | 0.599 | 3069.011 |
| −25 | 1 | −26.812 | −0.641 | 2 | −2.194 | −0.600 | 3041.354 |
| −50 | 1 | −26.812 | −1.363 | 1 | −26.784 | −1.299 | 3012.737 |
| 50 | 2 | 0 | 0.264 | 2 | 0 | 0.299 | 3070.664 |
| 25 | 2 | 0 | 0.132 | 2 | 0 | 0.149 | 3071.491 |
| −25 | 2 | 0 | −0.132 | 2 | 0 | −0.149 | 3073.144 |
| −50 | 1 | −26.812 | −0.280 | 2 | 0 | −0.299 | 3069.049 |
| 50 | 1 | −26.812 | 45.526 | 2 | 0 | 45.249 | 4547.566 |
| 25 | 2 | 0 | 22.769 | 2 | 0 | 22.624 | 3811.821 |
| −25 | 2 | 0 | −22.769 | 2 | 0 | −22.624 | 2332.813 |
| −50 | 2 | 0 | −45.538 | 2 | 0 | −45.249 | 1593.310 |
| 50 | 2 | 0 | 1.927 | 2 | 0 | 1.929 | 3130.816 |
| 25 | 2 | 0 | 0.963 | 2 | 0 | 0.964 | 3101.567 |
| −25 | 2 | 0 | −0.963 | 2 | 0 | −0.964 | 3043.068 |
| −50 | 2 | 0 | −1.927 | 2 | 0 | −1.929 | 3013.818 |
| 50 | 1 | −26.812 | 0.980 | 2 | −11.519 | 1.267 | 3022.997 |
| 25 | 1 | −26.812 | 0.530 | 2 | −3.086 | 0.658 | 3053.375 |
| −25 | 2 | 0 | −0.606 | 4 | 32.437 | −0.709 | 3082.212 |
| −50 | 4 | 79.738 | −1.437 | 4 | 57.448 | −1.638 | 3083.884 |
Table 8.
The sensitivity analysis of the system parameters.
Table 8.
The sensitivity analysis of the system parameters.
| Change in % | Model I with Scrap Items | Model II with Rework | Z(1)* − Z(2)*
|
|---|
| | | | | |
|---|
| Initial | 2 | 0 | 0 | 2 | 0 | 0 | 3072.317 |
|---|
| 0.50 | 1 | −27.576 | 0.427 | 2 | −1.590 | 0.214 | 3144.201 |
| 0.25 | 2 | −0.763 | 0.252 | 2 | −0.795 | 0.106 | 3120.303 |
| −0.25 | 2 | 0.763 | −0.249 | 2 | 0.795 | −0.106 | 3025.045 |
| −0.50 | 2 | 1.526 | −0.495 | 2 | 1.590 | −0.211 | 2978.469 |
| 0.50 | 2 | −15.542 | 0.613 | 2 | −13.782 | 0.542 | 3110.980 |
| 0.25 | 2 | −9.979 | 0.369 | 2 | −8.788 | 0.328 | 3095.127 |
| −0.25 | 1 | −9.595 | −0.701 | 2 | 19.555 | −0.572 | 3015.190 |
| −0.50 | infeasible |
| 0.50 | 2 | 0 | 0 | 2 | −1.366 | 0.011 | 3069.206 |
| 0.25 | 2 | 0 | 0 | 2 | −0.824 | 0.006 | 3070.482 |
| −0.25 | 2 | 0 | 0 | 2 | 1.402 | −0.010 | 3075.160 |
| −0.50 | 2 | 0 | 0 | 2 | 4.322 | −0.027 | 3080.003 |
| 0.50 | 1 | 3.681 | 46.807 | 1 | 1.578 | 47.133 | 4420.445 |
| 0.25 | 1 | −14.194 | 23.444 | 2 | 4.876 | 23.678 | 3727.799 |
| −0.25 | 3 | 15.046 | −23.659 | 3 | 15.779 | −23.891 | 2409.420 |
| −0.50 | 4 | 58.080 | −47.864 | 4 | 38.583 | −48.100 | 1666.951 |
| 0.50 | 1 | −26.622 | 0.625 | 2 | 0.257 | 0.217 | 3204.230 |
| 0.25 | 1 | −26.717 | 0.353 | 2 | 0.128 | 0.108 | 3150.737 |
| −0.25 | 2 | −0.190 | −0.400 | 2 | −0.128 | −0.109 | 2979.539 |
| −0.50 | 3 | 2.325 | −0.844 | 3 | 4.3115 | −0.266 | 2886.611 |
| 0.50 | 2 | 3.398 | 6.968 | 2 | 1.855 | 1.606 | 4767.729 |
| 0.25 | 2 | 1.620 | 3.381 | 2 | 0.918 | 0.803 | 3888.441 |
| −0.25 | 2 | −1.483 | −3.193 | 2 | −0.900 | −0.803 | 2314.082 |
| −0.50 | 1 | −28.932 | −6.220 | 2 | −1.784 | −1.607 | 1606.814 |
| 0.50 | 1 | 9.255 | −0.384 | 1 | 6.276 | −0.074 | 2974.806 |
| 0.25 | 1 | −8.778 | −0.288 | 2 | 8.339 | −0.019 | 2989.180 |
| −0.25 | 4 | 27.159 | 0.356 | 4 | 11.411 | 0.062 | 3164.379 |
| −0.50 | 4 | 27.159 | 0.356 | 4 | 11.411 | 0.062 | 3164.379 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).