Abstract
Zero-shot super-resolution (ZSSR) has generated a lot of interest due to its flexibility in various applications. However, the computational demands of ZSSR make it ineffective when dealing with large-scale low-resolution image sets. To address this issue, we propose a novel meta-learning model. We treat the set of low-resolution images as a collection of ZSSR tasks and learn meta-knowledge about ZSSR by leveraging these tasks. This approach reduces the computational burden of super-resolution for large-scale low-resolution images. Additionally, through multiple ZSSR task learning, we uncover a general super-resolution model that enhances the generalization capacity of ZSSR. Finally, using the learned meta-knowledge, our model achieves impressive results with just a few gradient updates when given a novel task. We evaluate our method using two remote sensing datasets with varying spatial resolutions. Our experimental results demonstrate that using multiple ZSSR tasks yields better outcomes than a single task, and our method outperforms other state-of-the-art super-resolution methods.
MSC:
68T05; 68T07
1. Introduction
High-resolution (HR) images are important in remote sensing, such as object detection and satellite imaging, as they contain more detailed information than low-resolution (LR) images. However, due to equipment limitations, researchers have turned to using image processing techniques to transform LR images into visually pleasing HR images. Super-resolution is one such technique that generates HR images from LR ones using algorithms. Image super-resolution has extensive applications in various fields, such as medical imaging [1], military remote sensing [2], remote sensing satellite image processing, multimedia communication, surveillance video, and security [3]. It also helps to improve other computer vision tasks, such as image retrieval and image segmentation [4,5], etc. Image super-resolution has long been a highly sought-after research topic. Dong et al. [6] were the first to propose a super-resolution algorithm that incorporated convolutional neural networks. Haque et al. [7] proposed a lightweight enhanced SR CNN (LESRCNN), which extracts hierarchical low-resolution features and aggregates the obtained features step-by-step to increase memory ability. Subsequently, Zhang et al. [8] improved perceptual quality by designing a generative adversarial network for image super-resolution. A series of super-resolution models with deep learning capabilities have achieved remarkable results in the super-resolution of natural images.
Remote sensing images are primarily captured at high altitudes, and their acquisition is affected by various factors such as atmospheric disturbances, physical limitations of imaging systems, and changes in scene motion. As a result, remote sensing images are often more intricate and blurrier than ordinary images, containing a variety of surface details. This makes it challenging for existing methods suitable for regular image super-resolution to effectively super-resolve remote sensing images. To address this issue, Zheng et al. [9] proposed a Spatial Spectral Residual Attention Network (SSRAN) to reconstruct hyperspectral images (HIS), which can explore both the spatial and spectral information of multispectral (MSI). Dong et al. [10] not only explored the potential of reference-based image super-resolution (RefSR) methods for remote sensing images but also proposed an end-to-end reference-based remote sensing GAN (RRSGAN) for super-resolution. Generative Adversarial Networks (GANs) have made tremendous progress in the task of natural image super-resolution, for remote sensing images, there are more low-frequency components than in natural images, making it difficult for the discriminator to accurately distinguish low-frequency regions. To address this issue, Lei et al. [11] proposed a super-resolution algorithm known as Coincidental Discriminative GAN (CDGAN) for remote sensing images. Additionally, Feng et al. [12] proposed a remote sensing image recursive residual network (WTCRR) combined with wavelet transform. However, deep learning-based super-resolution methods rely on LR-HR training sample pairs, which can be challenging to obtain in practice for remote sensing images. Therefore, using the internal reproducibility of information within each image has long been a robust prior for natural images, making it a widely used technique in tasks, such as image denoising [13,14] and image super-resolution [8,15]. Additionally, network performance can be further enhanced by implicitly learning strong image priors for non-local attributes, which are then integrated into the network architecture [16,17]. Some researchers also proposed learning internal distributions [18,19], while others explored combining the advantages of both internal and external information in image restoration and super-resolution [20,21].
Zero-shot super-resolution has emerged as a flexible image processing technique in recent years, attracting significant attention from researchers for its ability to leverage internal image information to address LR-HR mismatches without relying on prior training. This approach can also be well adapted to test images. To improve the super-resolution of remote sensing images, we propose a zero-shot super-resolution method that capitalizes on the unique characteristics of zero-shot learning to address challenges specific to remote sensing imagery. However, when multiple images are provided for zero-shot super-resolution, the network must be trained multiple times. As a result, the zero-shot super-resolution network requires retraining for each image, which increases computational complexity.
Meta-learning has gained significant attention from researchers due to its ability to leverage previous tasks to extract meta-knowledge that possesses strong representation capabilities and can be generalized to new tasks. As one of the mainstream approaches to solve few-shot learning problems, meta-learning has been combined with few-shot learning, leading to the proposal of many methods such as those listed in [22,23,24]. Notably, model-agnostic meta-learning (MAML) [22] has had a large impact by learning optimal initialization parameters that allow for rapid adaptation of basic learners to new tasks with only a few gradient steps. MAML leverages gradient updates as a meta-learner and shows that gradient descent can approximate any learning algorithm [25]. Additionally, Soh et al. [21] introduced meta-transfer into the field of image super-resolution, bringing new insights to the domain.
Based on previous work, we propose a novel meta-learning model where we treat each remote sensing image as a separate task and learn meta-knowledge during the ZSSR process for that image. This approach not only reduces the computational cost of super-resolution for large-scale low-resolution images, but also improves generalization through multi-task learning. By leveraging the acquired meta-knowledge, our model achieves impressive results with just a few gradient updates on any new task.
In the paper, the main contributions are as follows:
- For the first time, a meta-learning framework was introduced into zero-shot remote sensing image super-resolution, and we propose a new solution;
- We learn to perform zero-shot super-resolution on remote sensing images from the task level, and learn meta-knowledge of the task through meta-learning, achieving good results with zero-shot remote sensing image super-resolution;
- We take full advantage of the advantages of MAML and ZSSR, so solving the mismatch between low-resolution remote sensing images and high-resolution remote sensing images.
2. Related Work
In this section, we briefly introduce some representative works on image super-resolution as well as meta-learning.
2.1. Zero-Shot Super-Resolution
According to the characteristics of the training dataset, image super-resolution can be broadly classified into supervised and unsupervised methods. With the development of deep learning, increasing deep learning-based super-resolution models have been proposed, including ESPCN [6], VDSR [26], SRGAN [8], RCAN [27], and more. Deep learning has made significant progress in this field. Generally, deep learning SR algorithms may differ in various aspects, such as network architectures [26,27], loss functions [28,29], learning rules, and strategies [30,31]. Meanwhile, most existing works mainly focused on supervised learning. Specifically, supervised super-resolution involves using matched low-resolution (LR) and high-resolution (HR) image pairs to learn the mapping from LR to HR images.
Compared to supervised learning, unsupervised learning can generate more accurate models when applied to real-world situations. Shocher et al. [19] proposed the first “zero-shot” super-resolution technique, which employs a convolutional neural network (CNN) in an unsupervised manner and takes advantage of the internal information of a single image. Unlike supervised methods, ZSSR can perform training and testing on-the-fly without requiring any prior training. By downsampling the test images to create LR counterparts, corresponding LR-HR pairs are generated. After continuous training on LR-HR pairs, SR images are generated, which is the process by which ZSSR improves the resolution of low-resolution images. However, for zero-shot super-resolution, the network needs to be retrained for each new input image. Soh et al. [21] proposed a meta-transfer zero-shot super-resolution method that uses both external and internal information. This approach finds a suitable initialization parameter for internal learning and can produce impressive results with only a single gradient update, in comparison with ZSSR’s gradient update. To address the issue of the current image SR methods not generalizing well to real-world scenarios due to the degradation process of the model, Xi et al. [32] proposed a zero-shot image super-resolution for depth-guided internal degradation learning. This method combines an image-specific degradation simulation network (DSN) with an image-specific super-resolution network (SRN) to learn, and uses depth information from images to extract unpaired high-resolution and low-resolution patch sets for training. Furthermore, zero-shot learning is not limited to natural images. Cheng et al. [33] proposed zero-shot light field super-resolution, which extracts samples from the input LR light field itself to learn input-specific super-resolution maps. They also present different learning strategies through zero-shot learning and offer a strategy for efficient learning with extremely limited training data.
2.2. Meta-Learning
Meta-learning, also known as learning to learn, aims to equip a model with the ability to acquire the aptitude to learn to learn. By doing so, the model can gain meta-knowledge from prior tasks, which it can use to quickly adapt to new tasks, thus improving the efficiency and effectiveness of the model. Meta-learning is mainly used for few-shot learning [22] and transfer learning [21]. Further details are available in [34]. Recently, an increasing number of meta-learning algorithms have been proposed, which can be divided into four categories.
The first category is Bayesian meta-learning [35,36], which uses Bayesian inference to learn prior and posterior distributions and infer parameters for new tasks. The second category is memory-based meta-learning [37,38], which adapts to new tasks using experience from previous tasks. The third category is reinforcement learning-based meta-learning [39,40], which learns reinforcement learning algorithms on meta-learning tasks to adjust model parameters for new tasks. The fourth category is gradient-based meta-learning [22,41], which adjusts model parameters by learning gradient descent on meta-learning tasks to enable the learner to better adapt to various tasks. MAML is the most influential and representative method in this category. These categories are not mutually exclusive, and some meta-learning algorithms may combine multiple techniques. We are proud to introduce meta-learning into zero-shot remote sensing image super-resolution, leveraging the advantages of MAML. MAML learns from tasks, with the goal of enabling the model to identify an optimal initialization parameter that is effective for all tasks. However, the initialization parameters may not be optimal for every task. Depending on the learned initialization parameters, only one or a few gradient updates are necessary to obtain optimal results for a given new task.
Meta-learning is a useful approach for facilitating few-shot learning, and previous studies [42,43] have applied meta-learning techniques to the field of image super-resolution. Meta-learning offers new perspectives for addressing the super-resolution challenge, and we, therefore, introduce the Model-Agnostic Meta-Learning (MAML) algorithm to zero-shot remote sensing image super-resolution, based on its unique characteristics.
3. Proposed Method
In practical scenarios, acquiring images of varying resolutions within a single scene can prove to be challenging. Therefore, LR (low-resolution) images are frequently obtained by downsampling HR (high-resolution) images, as demonstrated in Equation (1) and cited by [44].
where and refer to the low-resolution and high-resolution images, ⊗ denotes convolution, k represents the blur kernel, signifies downsampling with a scale factor of s, and n denotes the presence of noise. It is worth mentioning that real-world scenarios often exhibit a multitude of degraded conditions, including a wide range of unknown values for k, , and n.
Convolutional Neural Networks (CNNs) have remarkable capabilities in image super-resolution (SR) due to their spatial invariance, feature extraction, multi-scale processing, and residual learning. However, they heavily rely on external supervised data for training, which prevents them from exploiting the intrinsic data within images. One of the major challenges faced by current SR techniques is the lack of supervised samples. To address this issue, our method is based on the assumption that images possess inherent reproducible factors. This implies that small blocks (such as 5 × 5 or 3 × 3) can be repeated with the same or different scales within a single image to enhance visual effects, reduce computational costs, and improve network generalization performance.
To address the challenge of super-resolving unsupervised images, researchers have introduced a versatile technique called Zero-Shot (ZSSR), which has gained attention. However, the ease of use of ZSSR also brings some drawbacks. For instance, when multiple images are given to ZSSR for super-resolution, the calculation becomes complex as ZSSR needs to be trained several times. In contrast, Meta-Learning has captivated researchers with its noteworthy advantages, particularly its ability to enable models to learn how to learn.
Building on the aforementioned discussion, we propose a novel meta-learning model that combines Meta-Learning MAML with Zero-Shot Remote Sensing Image Super-Resolution to tackle the challenges related to ZSSR. Specifically, our aim is to leverage the benefits of MAML to learn how to perform Zero-Shot remote sensing Image Super-Resolution on Remote Sensing images at the task level, using ZSSR for each remote sensing image in the task. During this process, the model can acquire meta-knowledge about ZSSR, which can subsequently reduce the time required for ZSSR on subsequent images. Additionally, learning from multiple tasks can reduce the complexity of applying ZSSR. For a new task, the model only requires a few gradient updates to produce satisfactory results. The neural network diagram for our proposed method is illustrated in Figure 1.
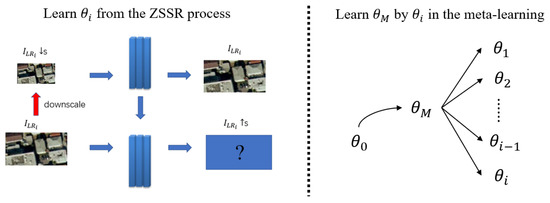
Figure 1.
Inner: Learning meta-knowledge in the process of ZSSR within the task. External: Let the network learn an optimal representation of through the meta-knowledge .
In Figure 1, we begin by downsampling the low-resolution image to obtain a lower version (where s represents the scaling factor required for super-resolution). We then use a lightweight CNN that has been trained to reconstruct from . This trained CNN, along with the given image , is used to produce the desired super-resolution result and learn meta-knowledge for training the parameters in the ZSSR process outlined above. Ultimately, we use meta-learning MAML to enable to learn the optimal representation from the different .
In our approach, we define the data D as a task distribution , and sample tasks from the task distribution . We use the model , which is parameterized by , to represent the trained CNN for the super-resolution of a given image. We measure the similarity between the low-resolution LR image and the super-resolution SR image by minimizing the loss. Based on the image quality loss discussed in this paper and [43], we propose the loss function shown in Equation (2):
where represents the network parameters that Meta-learning aims to optimize. On receiving a new task , the parameters of the model are updated to . Subsequently, the updated parameters are used to process the input image and its reduced version . After computing one or more gradients on the task , is then computed. The adaptation formulation of updating rules is shown in Equations (3) and (4):
where controls the learning rate of the inner update procedure. Additionally, ▽ denotes the gradient operator. Once the gradient update of is finished, the meta-learning parameter needs to be updated through . To achieve this, we adopt the stochastic gradient descent method to update the parameter . The update rule that we propose is illustrated in Equation (5):
where controls the meta-update step, and represents the parameter trained in meta-learning. These update procedures are iteratively repeated in meta-learning until convergence is achieved. Finally, we obtain an optimal parameter , which can be easily applied to any differentiable SR network.
4. Algorithm
To perform a new task , we first perform batch distribution for the task according to . We then downsample the test image using Equation (1) to obtain . Next, we employ stochastic gradient descent (SGD) for batches of for each task, calculating the value of using Equations (3) and (4). We then randomly initialize the parameters and use and to calculate and update the value of through Equation (5), resulting in the model . By inputting the subsampled image of the test image, the super-resolution image after image quality restoration can be output. The specific algorithm is presented in Algorithm 1.
| Algorithm 1: Meta-learning Zero-shot Image Super-resolution. |
 |
5. Experiments
In this section, we introduce two baseline datasets and three image quality evaluation indices. The primary objective of the experiments is to answer the following research questions: (1) How does our method perform compared to previous super-resolution methods when dealing with diverse types of remote sensing images, such as aircraft, parking lots, and buildings? (2) How does our approach compare to previous super-resolution methods in terms of PSNR, SSIM, and GSSIM on the two datasets? (3) What is the computational advantage of our method compared to ZSSR in terms of computational burden?
Our approach is implemented on a deep learning server via OpenCV (http://opencv.org/ (accessed on 8 March 2023)) and Pytorch (http://pytorch.org/ (accessed on 8 March 2023)), The server is powered by a GeForce GTX 1050Ti GPU, 8 GB RAM, and 4 GB VRAM. Our experiment code will be available at (https://github.com/elessarsnow/czz001).
5.1. Dataset, Evaluation Indicators, and Training Details
Dataset: The UC Merced Land Use dataset [45] is a well-known and widely used dataset in research. It consists of 21 object categories, including aircraft, buildings, parking lots, forests, and more, with 100 images per category. In our experiments, we focused on the aircraft, buildings, and parking lots categories from this dataset, as shown in Figure 2. It should be noted that the aircraft category may contain one or more similar images, while the parking lot category includes images featuring vehicles of various colors and models. The buildings category exhibits a variety of structures in each image, making these three categories representative for evaluation.

Figure 2.
Representative class images in the UC Merced dataset.
To evaluate how well our model performs on remote sensing data with different spatial resolutions, we incorporated the NWPU-RESISC45 dataset [46], which was compiled by Northwestern Polytechnical University, in our experiments. This dataset is shown in Figure 3 and contains 45 categories of remote sensing scenarios, each consisting of 700 images. These scenarios depict a range of environments, including aircraft, railway stations, airports, clouds, and more. For our experiment, we specifically focused on the aircraft, buildings, and parking lot categories.

Figure 3.
Partial sample display of NWPU-RESISC45 dataset.
Evaluation Indicators: The peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and gradient-based structural similarity index (GSSIM) are commonly used evaluation metrics for super-resolution images. Higher experimental values indicate a superior super-resolution effect. Equations (6) and (7) show the computation of PSNR.
where h and w denote the height and width of the image, respectively, and refers to the mean squared error between the original image and the super-resolution image . The parameters a and b correspond to the horizontal and vertical axes, respectively. Equation (8) illustrates the calculation formula for SSIM.
where , and , , respectively, represent the average gray value and variance of the original image and the super-resolution image , and represent the covariance of the original image and the super-resolution image.
The spatial structure of a scene can capture its structural information, which is often shared among remote sensing images of the same region, displaying similar or identical patterns [47]. The gradient-based structural similarity index (GSSIM) is a metric that effectively measures the similarity between structural information and features of images. It does so by integrating measures of luminance comparison , contrast comparison , and gradient-based structural comparison in the equation below:
where
where and denote the mean value of the two images, respectively, and reflect the luminance comparison information. The standard deviations and correspond to the contrast comparison information of the two images, respectively. and represent the gradient value of the pixel at row i and column j in the two images, respectively. The small constants , , and are used to prevent the denominator from being zero, with , , and and , . The parameters , , and are greater than zero. In this paper, we set , , and . A higher GSSIM value indicates greater similarity between the two images.
Training Details: To process the UC Merced and NWPU-RESISC45 remote sensing datasets for segmentation, we selected three specific image categories and randomly allocated 80% and 20% of each category to the training and test sets, respectively. We set the image size to 128 × 128 and adjusted the weights using the Adam optimizer with a learning rate of 0.001. Next, we randomly selected five images from the training set for each task, and applied ZSSR to each image while learning meta-knowledge during the process. This is because the relationship between low-resolution (LR) and high-resolution (HR) is relatively simple for a single image, which facilitates the learning of meta-knowledge. Moreover, our approach involves using ZSSR on the same category of images with the help of meta-knowledge, resulting in faster ZSSR speeds over time.
In this paper, we used an eight-layer convolutional neural network as our image-specific model. The network consisted of eight hidden layers, each comprising 64 channels, with ReLU serving as the activation function for each layer. To accelerate training and avoid the impact of test image size during network execution, we randomly selected fixed-size crops of dimensions 128 × 128 from a pair of selected samples during each iteration. For our experiments, we set the learning rate to 0.001 and performed linear fitting for the reconstruction errors. Whenever the accuracy of linear fitting fell below the standard deviation, we divided the learning rate by 10. We performed zero-lens superresolution processing on the image until the learning rate reached , resulting in a corresponding superresolution reconstruction image. We used Adam as the optimizer and stochastic gradient descent (SGD) for gradient updates to optimize the model. For the inner loop of the experiment, we employed 15-step gradient updates, enabling the adaptation of parameters through only 15 expansion steps. We subjected remote sensing data to and magnification, respectively, to effectively test each model’s performance. These tasks also facilitated the acquisition of useful meta-knowledge that could be employed in novel tasks.
5.2. Visualize Images and Results
In this section, we compare the peak signal-to-noise ratio (PSNR) of our proposed approach with several classic methods, such as Bicubic, SRCNN [6], VDSR [26], LGCNet [48] and ZSSR, among others. We selected three distinct image types - building, parking lot, and airplane - and evaluated our approach using and super-resolution images to gauge its efficacy.
Figure 4 shows the comparison of the super-resolution visualization results of “airplane00” by in different methods. Figure 5 shows the comparison of super-resolution visualization results of “airplane00” on different methods.

Figure 4.
Select the “airplane00” image from the airplane class data to display the visual effects of super-resolution on different methods.

Figure 5.
Select the “airplane00” image from the airplane class data to display the visual effects of super-resolution on different methods.
Figure 6 shows the comparison of the super-resolution visualization results of “parkinglot00” by in different methods. Figure 7 shows the comparison of super-resolution visualization results of “parkinglot00” on different methods.

Figure 6.
Select the “parkinglot00” image from the parkinglot class data to display the visual effects of super-resolution on different methods.

Figure 7.
Select the “parkinglot00” image from the parkinglot class data to display the visual effects of super-resolution on different methods.
Figure 8 shows the comparison of the super-resolution visualization results of “building05” by in different methods. Figure 9 shows the comparison of super-resolution visualization results of “building05” on different methods.

Figure 8.
Select the “building05” image from the building class data to display the visual effects of super-resolution on different methods.

Figure 9.
Select the “building05” image from the building class data to display the visual effects of super-resolution on different methods.
From Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, we can easily observe that the super-resolution images generated by our approach are more visually similar to the real images, providing further evidence of its efficiency. To provide a quantitative comparison, Table 1 displays the average PSNR results of the three types of data from the UC Merced land use dataset at different scale factors, obtained using various methods.

Table 1.
Average PNSR values of the UC Merced dataset under different methods and different scale factors.
Table 1 presents the PSNR values of the super-resolution images obtained by our approach and other SR techniques, showing that our method consistently achieves higher PSNR scores. Moreover, we conducted and super-resolution on both the UC Merced land use dataset and the NWPU-RESISC45 remote sensing dataset using various SR methods to assess the effectiveness of our approach at different spatial resolutions. To quantitatively evaluate the results, we used SSIM, PSNR, and GSSIM as three indicators, which are presented in Table 2.

Table 2.
Comparison of PSNR, SSIM, and GSSIM values between UC Merced data set and NWPU-RESISC45 data set.
As shown in Table 2, a comparison of and super-resolution images using various methods on two different remote sensing datasets reveals that our approach achieves the highest PSNR, SSIM, and GSSIM values across both datasets and resolutions. This outcome demonstrates the robustness of our technique and its ability to produce satisfactory results across diverse remote sensing datasets. Moreover, the image generated using meta-learning for zero-shot remote sensing image super-resolution more closely approximates the original image, therefore better meeting user requirements.
While our approach only provides a marginal improvement in image quality restoration compared to ZSSR, it has a clear advantage in terms of speed. As shown in Table 3, during the training of five tasks, our approach took slightly longer than ZSSR, but during testing, it was two-thirds faster than ZSSR. Furthermore, as we trained for 10 tasks, the training time for each task progressively decreased, resulting in a total training time even shorter than that of ZSSR. Our approach demonstrated even more significant testing advantages, as it required only about half the time. Therefore, when dealing with a substantial number of tasks in practical scenarios, our approach generally outperforms ZSSR in both performance and efficiency.

Table 3.
Comparing the training and testing time of ZSSR and our method for the same task, where time is in minutes.
Furthermore, after completing the three types of tasks on the UC Merced dataset, we directly tested our model on “river00” and “river01”. Due to the meta-knowledge learned by our model regarding the connections between remote sensing images, we only needed to perform a few gradient updates to achieve satisfactory super-resolution results, as shown in Figure 10.

Figure 10.
“River00” image and “River01” image display the visual effects of ×2 super-resolution.
The results clearly demonstrate the effectiveness of zero-shot super-resolution of images at the task level. Our meta-learning approach for zero-shot remote sensing image super-resolution effectively resolves the mismatch issue between low-resolution and high-resolution remote sensing images.
6. Conclusions
This paper presents a meta-learning-based approach to zero-shot remote sensing image super-resolution. Using Model-Agnostic Meta-Learning (MAML), we can learn zero-shot super-resolution at the task level. Specifically, we define zero-shot super-resolution for each remote sensing image as a task, and our model learns meta-knowledge by performing zero-shot super-resolution on multiple tasks. This meta-knowledge can be used to construct a general model that is applicable to various tasks, simplifying the application of ZSSR. Our network does not require any prior training and instead uses a given image to generate LR-HR sample pairs. Leveraging the small diversity of LR-HR sample pairs, we employ an eight-layer convolutional neural network as an image-specific network. Through meta-learning zero-shot remote sensing image super-resolution, we solve the problem of mismatching high-resolution and low-resolution remote sensing images. Furthermore, by learning zero-shot super-resolution at the task level, our method can adapt to any new task based on the learned meta-knowledge. Experimental results demonstrate that our approach outperforms state-of-the-art SR methods in both qualitative and quantitative metrics, making it the first to introduce meta-learning into zero-shot remote sensing image super-resolution.
Author Contributions
Conception, Z.C. and D.X.; methodology, Y.T., Z.C. and Z.J.; software, D.X. and Z.C.; validation, Y.T., Z.J., Z.C. and D.X.; formal analysis, Y.T., Z.J. and Z.C.; investigation, Z.C., D.X. and Y.T.; resource, Z.J.; data, Z.C. and D.X.; writing—original draft preparation, D.X., Z.C., Y.T. and Z.J.; writing—review and editing, D.X., Z.C., Y.T. and Z.J.; projection administration, Y.T. and Z.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 61866040); Special Support Plan for High-Level Talents of Guangdong Province (No. 2019TQ05X571), Project of Guangdong Province Innovative Team (No. 2020WCXTD011).
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Chen, Z.; Guo, X.; Woo, P.Y.M.; Yuan, Y. Super-Resolution Enhanced Medical Image Diagnosis with Sample Affinity Interaction. IEEE Trans. Med Imaging 2021, 40, 1377–1389. [Google Scholar] [CrossRef]
- Ran, Q.; Xu, X.; Zhao, S.; Li, W.; Du, Q. Remote sensing images super-resolution with deep convolution networks. Multimed. Tools Appl. 2020, 79, 8985–9001. [Google Scholar] [CrossRef]
- Zhang, M.; Xin, J.; Zhang, J.; Tao, D.; Gao, X. Curvature Consistent Network for Microscope Chip Image Super-Resolution. IEEE Trans. Neural Networks Learn. Syst. 2022, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Feng, Y.; Dai, T.; Bai, J.; Jiang, Y.; Xia, S.T.; Wang, X. Adversarial Examples Generation for Deep Product Quantization Networks on Image Retrieval. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 1388–1404. [Google Scholar] [CrossRef]
- Wu, X.; Wu, Z.; Ju, L.; Wang, S. A One-Stage Domain Adaptation Network with Image Alignment for Unsupervised Nighttime Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 58–72. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolu tional network for image super-resolution. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar]
- Haque, W.A.; Arefin, S.; Shihavuddin, A.S.M.; Hasan, M.A. DeepThin: A novel lightweight CNN architecture for traffic sign recognition without GPU requirements. Expert Syst. Appl. 2021, 168, 114481. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Dong, C.; Qiao, Y. RankSRGAN: Super Resolution Generative Adversarial Networks with Learning to Rank. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7149–7166. [Google Scholar] [PubMed]
- Zheng, X.; Chen, W.; Lu, X. Spectral super-resolution of multi spectral images using spatial–spectral residual attention network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Dong, R.; Zhang, L.; Fu, H. Rrsgan: Reference-based super resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Coupled adversarial training for remote sensing image super-resolution. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3633–3643. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, W.; Su, X.; Xu, Z. Optical Remote Sensing Image Denoising Furthermore, Super-Resolution Reconstructing Using Optimized Generative Network in Wavelet Transform Domain. Remote Sens. 2021, 13, 1858. [Google Scholar] [CrossRef]
- Wan, Y.; Ma, A.; He, W.; Zhong, Y. Accurate Multiobjective Low-Rank and Sparse Model for Hyperspectral Image Denoising Method. IEEE Trans. Evol. Comput. 2023, 27, 37–51. [Google Scholar] [CrossRef]
- Ning, Q.; Dong, W.; Li, X.; Wu, J.; Li, L.; Shi, G. Searching Efficient Model-Guided Deep Network for Image Denoising. IEEE Trans. Image Process. 2023, 32, 668–681. [Google Scholar] [CrossRef]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image Super-Resolution via Iterative Refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 4713–4726. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Yao, Q.; Li, C.; Yokoya, N.; Zhao, Q.; Zhang, H.; Zhang, L. Non-Local Meets Global: An Iterative Paradigm for Hyperspectral Image Restoration. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2022, 44, 2089–2107. [Google Scholar] [CrossRef] [PubMed]
- Zha, Z.; Yuan, X.; Wen, B.; Zhou, J.; Zhu, C. Group Sparsity Residual Constraint with Non-Local Priors for Image Restoration. IEEE Trans. Image Process. 2020, 29, 8960–8975. [Google Scholar] [CrossRef] [PubMed]
- Fei, N.; Li, G.; Wang, X.; Li, J.; Hu, X.; Hu, Y. Deep Learning-Based Auto-Segmentation of Spinal Cord Internal Structure of Diffusion Tensor Imaging in Cervical Spondylotic Myelopathy. Diagnostics 2023, 13, 817. [Google Scholar] [CrossRef]
- Shocher, A.; Cohen, N.; Irani, M. “Zero-Shot” Super-Resolution Using Deep Internal Learning. Comput. Vis. Pattern Recognit. 2018, 3118–3126. [Google Scholar]
- Fu, Y.; Zhang, T.; Wang, L.; Huang, H. Coded Hyperspectral Image Reconstruction Using Deep External and Internal Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3404–3420. [Google Scholar] [CrossRef]
- Soh, J.W.; Cho, S.; Cho, N.I. Meta-transfer learning for zero shot super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3516–3525. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Ye, H.; Han, L.; Zhan, D. Revisiting Unsupervised Meta-Learning via the Characteristics of Few-Shot Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 3721–3737. [Google Scholar] [CrossRef]
- Jiang, H.; Gao, M.; Li, H.; Jin, R.; Miao, H.; Liu, J. Multi-Learner Based Deep Meta-Learning for Few-Shot Medical Image Classification. IEEE J. Biomed. Health Inform. 2023, 27, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Flennerhag, S.; Rusu, A.A.; Pascanu, R.; Visin, F.; Yin, H.; Hadsell, R. Meta-Learning with Warped Gradient Descent. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Ahn, N.; Kang, B.; Sohn, K.-A. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 252–268. [Google Scholar]
- Li, J.; Wu, C.; Song, R.; Li, Y.; Xie, W.; He, L.; Gao, X. Deep Hybrid 2-D–3-D CNN Based on Dual Second-Order Attention with Camera Spectral Sensitivity Prior for Spectral Super-Resolution. IEEE Trans. Neural Networks Learn. Syst. 2023, 34, 623–634. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Jin, Z.; Zhao, Y. SRDRL: A Blind Super-Resolution Framework with Degradation Reconstruction Loss. IEEE Trans. Multimed. 2022, 24, 2877–2889. [Google Scholar] [CrossRef]
- Chen, H.; He, X.; Yang, H.; Wu, Y.; Qing, L.; Sheriff, R.E. Self-supervised cycle-consistent learning for scale-arbitrary real-world single image super-resolution. Expert Syst. Appl. 2023, 212, 118657. [Google Scholar] [CrossRef]
- Song, J.; Liu, K.; Sowmya, A.; Sun, C. Super-Resolution Phase Retrieval Network for Single-Pattern Structured Light 3D Imaging. IEEE Trans. Image Process. 2023, 32, 537–549. [Google Scholar] [CrossRef]
- Cheng, X.; Fu, Z.; Yang, J. Zero-shot image super-resolution with depth guided internal degradation learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 265–280. [Google Scholar]
- Cheng, Z.; Xiong, Z.; Chen, C.; Liu, D.; Zha, Z.-J. Light field super resolution with zero-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10005–10014. [Google Scholar]
- Huisman, M.; Rijn, J.N.V.; Plaat, A. A survey of deep metalearning. Artif. Intell. Rev. 2021, 54, 4483–4541. [Google Scholar] [CrossRef]
- Patacchiola, M.; Turner, J.; Crowley, E.J.; O’Boyle, M.; Storkey, A. Bayesian Meta-Learning for the Few-Shot Setting via Deep Kernels. In Proceedings of the Conference on Neural Information Processing Systems, Online, 6–12 December 2020; Volume 33, pp. 16108–16118. [Google Scholar]
- Dai, Z.; Chen, Y.; Yu, H.; Low, B.K.H.; Jaillet, P. On provably robust meta-Bayesian optimization. In Proceedings of the International Conference on Uncertainty in Artificial Intelligence, Eindhoven, The Netherlands, 1–5 August 2022; pp. 475–485. [Google Scholar]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T.P. Meta-Learning with Memory-Augmented Neural Networks. J. Mach. Learn. Res. 2016, 48, 1842–1850. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R.S. Prototypical Networks for Few-shot Learning. In Proceedings of the Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 4080–4090. [Google Scholar]
- Gupta, A.; Mendonca, R.; Liu, Y.; Abbeel, P.; Levine, S. Meta-Reinforcement Learning of Structured Exploration Strategies. In Proceedings of the Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31, pp. 5307–5316. [Google Scholar]
- Nagabandi, A.; Clavera, I.; Liu, S.; Fearing, R.S.; Abbeel, P.; Levine, S.; Finn, C. Learning to Adapt in Dynamic, Real-World Environments through Meta-Reinforcement Learning. arXiv 2018, arXiv:1803.11347. [Google Scholar]
- Grant, E.; Finn, C.; Levine, S.; Darrell, T.; Griffiths, T. Recasting gradient-based meta-learning as hierarchical bayes. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wu, W.; Wang, T.; Wang, Z.; Cheng, L.; Wu, H. Meta transfer learning-based super-resolution infrared imaging. Digit. Signal Process. 2022, 131, 103730. [Google Scholar] [CrossRef]
- Park, S.; Yoo, J.; Cho, D.; Kim, J.; Kim, T.H. Fast adaptation to super-resolution networks via meta-learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 754–769. [Google Scholar]
- Yang, Z.; Shi, P.; Pan, D. A survey of super-resolution based on deep learning. In Proceedings of the 2020 International Conference on Culture-Oriented Science and Technology (ICCST), Beijing, China, 30–31 October 2020; pp. 514–518. [Google Scholar]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, H. The Temperature Vegetation Dryness Index (TVDI) Based on Bi-Parabolic NDVI-Ts Space and Gradient-Based Structural Similarity (GSSIM) for Long-Term Drought Assessment Across Shaanxi Province China (2000–2016). Remote Sens. 2018, 10, 959. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Super-Resolution for Remote Sensing Images via Local-Global Combined Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).