Data-Driven pH Model in Raceway Reactors for Freshwater and Wastewater Cultures
Abstract
1. Introduction
2. Materials and Methods
2.1. Modelled Photobioreactors
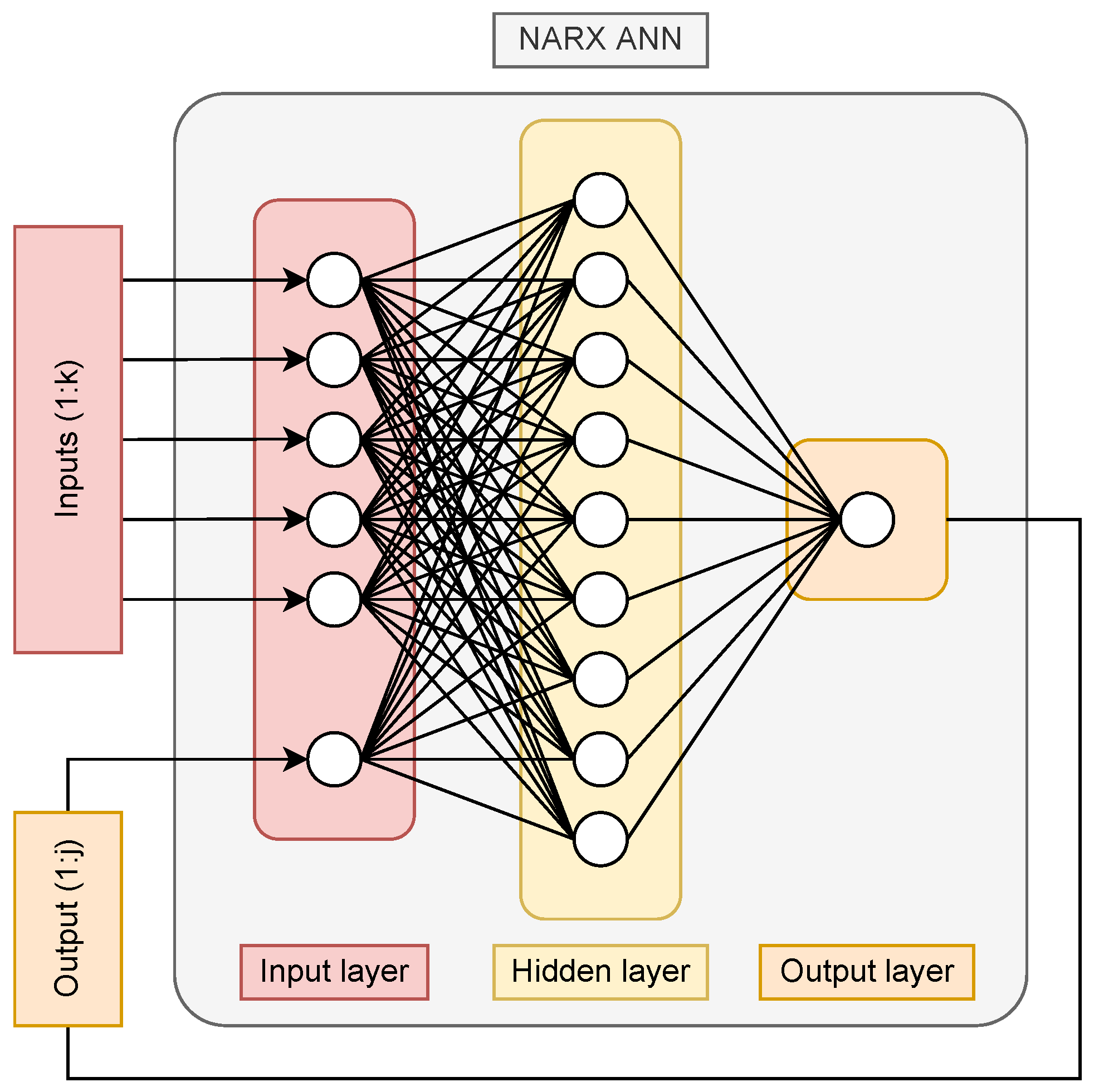
2.2. Artificial Neural Networks
2.3. Deep Learning Toolbox
2.4. Performance Metrics
3. Results
3.1. Model Development
3.1.1. Data Processing
- Modification of the data sample time to 1 min.
- Selection of valid spans for training.
- Outlier filtering.
3.1.2. Model Structure
3.1.3. Model Training
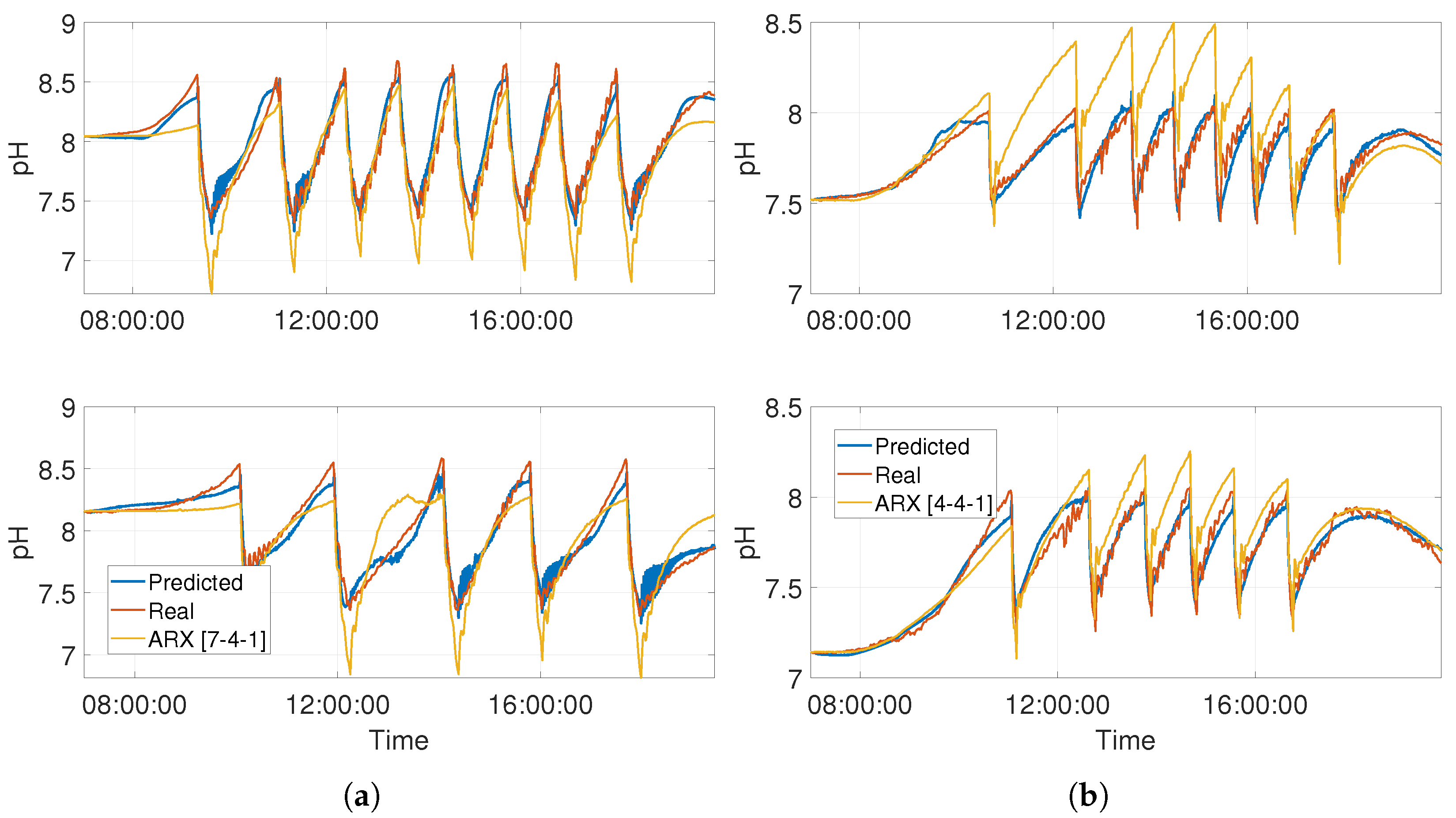
3.2. Model Performance Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DO | Dissolved Oxygen |
| ANN | Artificial Neural Network |
| MPC | Model Predictive Control |
| LSTM | Long Short-Term Memory |
| NARX | Nonlinear AutoRegressive with eXogenous inputs |
| TDL | Tapped Delay Line |
| MSE | Mean Squared Error |
References
- Guzmán, J.L.; Acién, F.G.; Berenguel, M. Modelling and control of microalgae production in industrial photobioreactors. Rev. Iberoam. Autom. Inform. Ind. 2020, 18, 1–18. [Google Scholar] [CrossRef]
- Acién Fernández, F.G.; Fernández Sevilla, J.M.; Molina Grima, E. Contribución de las microalgas al desarrollo de la bioeconomía. Mediterr. Econ. 2018, 31, 309–332. [Google Scholar]
- Hernández-Pérez, A.; Labbé, J.I. Microalgae, culture and benefits. Rev. Biol. Mar. Oceanogr. 2014, 49, 157–173. [Google Scholar] [CrossRef]
- Pittman, J.K.; Dean, A.P.; Osundeko, O. The potential of sustainable algal biofuel production using wastewater resources. Bioresour. Technol. 2011, 102, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Raouf, N.; Al-Homaidan, A.A.; Ibraheem, I.B. Microalgae and wastewater treatment. Saudi J. Biol. Sci. 2012, 19, 257–275. [Google Scholar] [CrossRef]
- De Andrade, G.A.; Berenguel, M.; Guzmán, J.L.; Pagano, D.J.; Acién, F.G. Optimization of biomass production in outdoor tubular photobioreactors. J. Process. Control. 2016, 37, 58–69. [Google Scholar] [CrossRef]
- Barceló-Villalobos, M.; Serrano, C.G.; Zurano, A.S.; García, L.A.; Maldonado, S.E.; Peña, J.; Fernández, F.G. Variations of culture parameters in a pilot-scale thin-layer reactor and their influence on the performance of Scenedesmus almeriensis culture. Bioresour. Technol. Rep. 2019, 6, 190–197. [Google Scholar] [CrossRef]
- Banerjee, S.; Ramaswamy, S. Dynamic process model and economic analysis of microalgae cultivation in open raceway ponds. Algal Res. 2017, 26, 330–340. [Google Scholar] [CrossRef]
- Sfez, S.; Van Den Hende, S.; Taelman, S.E.; De Meester, S.; Dewulf, J. Environmental sustainability assessment of a microalgae raceway pond treating aquaculture wastewater: From up-scaling to system integration. Bioresour. Technol. 2015, 190, 321–331. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, X.; Guo, D.; Ye, T.; Xiong, M.; Zhu, L.; Liu, C.; Jin, S.; Hu, Z. Operation of a vertical algal biofilm enhanced raceway pond for nutrient removal and microalgae-based byproducts production under different wastewater loadings. Bioresour. Technol. 2018, 253, 323–332. [Google Scholar] [CrossRef]
- Sánchez-Zurano, A.; Rodríguez-Miranda, E.; Guzmán, J.L.; Acién-Fernández, F.G.; Fernández-Sevilla, J.M.; Molina Grima, E. Abaco: A new model of microalgae-bacteria consortia for biological treatment of wastewaters. Appl. Sci. 2021, 11, 998. [Google Scholar] [CrossRef]
- Mairet, F.; Muñoz-Tamayo, R.; Bernard, O. Adaptive control of light attenuation for optimizing microalgae production. J. Process. Control. 2015, 30, 117–124. [Google Scholar] [CrossRef]
- Sompech, K.; Chisti, Y.; Srinophakun, T. Design of raceway ponds for producing microalgae. Biofuels 2012, 3, 387–397. [Google Scholar] [CrossRef]
- Kazbar, A.; Cogne, G.; Urbain, B.; Marec, H.; Le-Gouic, B.; Tallec, J.; Takache, H.; Ismail, A.; Pruvost, J. Effect of dissolved oxygen concentration on microalgal culture in photobioreactors. Algal Res. 2019, 39, 101432. [Google Scholar] [CrossRef]
- De-Luca, R.; Bezzo, F.; Béchet, Q.; Bernard, O. Exploiting meteorological forecasts for the optimal operation of algal ponds. J. Process. Control. 2017, 55, 55–65. [Google Scholar] [CrossRef]
- González, J.; Rodríguez-Miranda, E.; Guzmán, J.L.; Acién, F.G.; Visioli, A. Temperature optimization in microalgae raceway reactors by depth regulation. Rev. Iberoam. Autom. Inform. Ind. 2022, 19, 164–173. [Google Scholar] [CrossRef]
- Posadas, E.; Morales, M.d.M.; Gomez, C.; Acién, F.G.; Muñoz, R. Influence of pH and CO2 source on the performance of microalgae-based secondary domestic wastewater treatment in outdoors pilot raceways. Chem. Eng. J. 2015, 265, 239–248. [Google Scholar] [CrossRef]
- Bernard, O.; Mairet, F.; Chachuat, B. Modelling of Microalgae Culture Systems with Applications to Control and Optimization. In Microalgae Biotechnology; Posten, C., Feng, C.S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 59–87. [Google Scholar] [CrossRef]
- García-Mañas, F.; Guzmán, J.L.; Berenguel, M.; Acién, F.G. Biomass estimation of an industrial raceway photobioreactor using an extended Kalman filter and a dynamic model for microalgae production. Algal Res. 2019, 37, 103–114. [Google Scholar] [CrossRef]
- Fernández, I.; Acién, F.G.; Berenguel, M.; Guzmán, J.L. First principles model of a tubular photobioreactor for microalgal production. Ind. Eng. Chem. Res. 2014, 53, 11121–11136. [Google Scholar] [CrossRef]
- Pawlowski, A.; Guzmán, J.L.; Berenguel, M.; Acién, F.G. Control system for pH in raceway photobioreactors based on Wiener models. IFAC-PapersOnLine 2019, 52, 928–933. [Google Scholar] [CrossRef]
- Pawlowski, A.; Fernández, I.; Guzmán, J.L.; Berenguel, M.; Acién, F.G.; Dormido, S. Event-based selective control strategy for raceway reactor: A simulation study. IFAC-PapersOnLine 2016, 49, 478–483. [Google Scholar] [CrossRef]
- Fernández, I.; Acién, F.G.; Fernández, J.M.; Guzmán, J.L.; Magán, J.J.; Berenguel, M. Dynamic model of microalgal production in tubular photobioreactors. Bioresour. Technol. 2012, 126, 172–181. [Google Scholar] [CrossRef] [PubMed]
- Fernández, I.; Acién, F.G.; Guzmán, J.L.; Berenguel, M.; Mendoza, J.L. Dynamic model of an industrial raceway reactor for microalgae production. Algal Res. 2016, 17, 67–78. [Google Scholar] [CrossRef]
- Rodríguez-Miranda, E.; Acién, F.G.; Guzmán, J.L.; Berenguel, M.; Visioli, A. A new model to analyze the temperature effect on the microalgae performance at large scale raceway reactors. Biotechnol. Bioeng. 2021, 118, 877–889. [Google Scholar] [CrossRef]
- Ifrim, G.A.; Titica, M.; Cogne, G.; Boillereaux, L.; Legrand, J.; Caraman, S. Dynamic pH model for autotrophic growth of microalgae in photobioreactor: A tool for monitoring and control purposes. AIChE J. 2014, 60, 585–599. [Google Scholar] [CrossRef]
- Pawlowski, A.; Mendoza, J.L.; Guzman, J.L.; Berenguel, M.; Acien, F.G.; Dormido, S. Effective utilization of flue gases in raceway reactor with event-based pH control for microalgae culture. Bioresour. Technol. 2014, 170, 1–9. [Google Scholar] [CrossRef]
- Rodríguez-Miranda, E.; Guzmán, J.; Berenguel, M.; Acién, F.; Visioli, A. Diurnal and nocturnal pH control in microalgae raceway reactors by combining classical and event-based control approaches. Water Sci. Technol. 2020, 82, 1155–1165. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Sci. 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Rajendra, P.; Brahmajirao, V. Modeling of dynamical systems through deep learning. Biophys. Rev. 2020, 12, 1311–1320. [Google Scholar] [CrossRef]
- Kiš, K.; Klaučo, M. Neural network based explicit MPC for chemical reactor control. Acta Chim. Slovaca 2020, 12, 218–223. [Google Scholar] [CrossRef]
- Pon Kumar, S.S.; Tulsyan, A.; Gopaluni, B.; Loewen, P. A deep learning architecture for predictive control. IFAC-PapersOnLine 2018, 51, 512–517. [Google Scholar] [CrossRef]
- Correa, I.; Drews, P.; Botelho, S.; De Souza, M.S.; Tavano, V.M. Deep learning for microalgae classification. In Proceedings of the 16th IEEE International Conference on Machine Learning and Applications, ICMLA 2017, Cancun, Mexico, 18–21 December 2017; Volume 2017, pp. 20–25. [Google Scholar] [CrossRef]
- Otálora, P.; Guzmán, J.L.; Acién, F.G.; Berenguel, M.; Reul, A. Microalgae classification based on machine learning techniques. Algal Res. 2021, 55, 102256. [Google Scholar] [CrossRef]
- Otálora, P.; Guzmán, J.L.; Berenguel, M.; Acién, F.G. Dynamic Model for the pH in a Raceway Reactor using Deep Learning techniques. In Proceedings of the CONTROLO 2020. Lecture Notes in Electrical Engineering; Gonçalves, J.A., Braz-César, M., Coelho, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 695, pp. 190–199. [Google Scholar]
- Caparroz, M.; Otálora, P.; Guzmán, J.L.; Berenguel, M. Modelado y control adaptativo del pH en reactores raceway para la producción de microalgas. In Proceedings of the XLIII Jornadas de Automática, Logroño, Spain, 7–9 September 2022; pp. 333–340. [Google Scholar]
- Kay, R.A.; Barton, L.L. Microalgae as Food and Supplement. Crit. Rev. Food Sci. Nutr. 1991, 30, 555–573. [Google Scholar] [CrossRef]
- Xie, H.; Tang, H.; Liao, Y.H. Time series prediction based on NARX neural networks: An advanced approach. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009; Volume 3, pp. 1275–1279. [Google Scholar] [CrossRef]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Mrabet Bellaaj, N. A Nonlinear Autoregressive Exogenous (NARX) Neural Network Model for the Prediction of the Daily Direct Solar Radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef]
- Cerinski, D.; Baleta, J.; Mikulčić, H.; Mikulandrić, R.; Wang, J. Dynamic modelling of the biomass gasification process in a fixed bed reactor by using the artificial neural network. Clean. Eng. Technol. 2020, 1, 100029. [Google Scholar] [CrossRef]
- Song, H.; Shan, X.; Zhang, L.; Wang, G.; Fan, J. Research on identification and active vibration control of cantilever structure based on NARX neural network. Mech. Syst. Signal Process. 2022, 171, 108872. [Google Scholar] [CrossRef]
- Kim, P. MATLAB Deep Learning; Apress: Berkeley, CA, USA, 2017. [Google Scholar] [CrossRef]
- Ljung, L. System Identification Toolbox; Math Works: Natick, MA, USA, 1995. [Google Scholar]


| Measurement | Model | Range | Precision |
|---|---|---|---|
| pH | Crison 5342T | [0–14] | 0.01 |
| Medium temperature | Crison 5342T | [0–80] °C | 0.1 °C |
| Dissolved oxygen | Mettler Toledo InPro 6050 | [30–Sat.] ppb | 30 ppb |
| Medium level | Wenglor UMD402U035 | [0–30] cm | 0.1 mm |
| injection | SMC PFM725S-C8-F | [0.5–25] L/min | 0.1 L/min |
| Air injection | SMC PFMB7501-F04-F | [5–500] L/min | 1 L/min |
| Ambient temperature | ONSET S-THB-M008 | [−40–75] | 0.21 °C |
| Humidity | ONSET S-THB-M008 | [10–90] % | 0.1% |
| Solar radiation | ONSET S-LIB-M003 | [0–1280] | 10 |
| Variable | Maximum (Freshwater) | Minimum (Freshwater) | Maximum (Wastewater) | Minimum (Wastewater) |
|---|---|---|---|---|
| pH | 11.33 | 7.13 | 8.07 | 7.11 |
| Medium level | 19.20 cm | 13.16 cm | 15.23 cm | 13.29 cm |
| injection | 13.49 L/min | 0 L/min | 12.00 L/min | 0 L/min |
| Solar radiation | 1080.94 W/ | 0 W/ | 1060.39 W/ | 0 W/ |
| Variable | TDL |
|---|---|
| pH | (k−1):(k−2) |
| Medium level | (k−1):(k−2) |
| injection | (k−5):(k−6) |
| Solar radiation | (k−1):(k−2) |
| Hidden Layer Size | Freshwater Model | Wastewater Model | Number of Parameters |
|---|---|---|---|
| 5 | 0.0208 | 0.0130 | 51 |
| 6 | 0.0341 | 0.0409 | 61 |
| 7 | 0.0195 | 0.0500 | 71 |
| 8 | 0.0429 | 0.0106 | 81 |
| 9 | 0.0367 | 0.0836 | 91 |
| 10 | 0.0291 | 0.0449 | 101 |
| 11 | 0.0404 | 0.0532 | 111 |
| 12 | 0.0417 | 0.0325 | 121 |
| 13 | 0.0384 | 0.0225 | 131 |
| 14 | 0.0383 | 0.0517 | 141 |
| 15 | 0.0192 | 0.0601 | 151 |
| Freshwater Model | Wastewater Model | |
|---|---|---|
| Test Model Fit (%) | 71.34 | 73.75 |
| General Model Fit (%) | 63.91 | 62.76 |
| Test MSE | 0.0192 | 0.0106 |
| [4-4-1] ARX Model Fit (%) | −19.43 | 10.64 |
| [4-4-1] ARX MSE | 0.1531 | 0.0301 |
| [8-8-1] ARX Model Fit (%) | −2.32 | −198.00 |
| [8-8-1] ARX MSE | 0.1102 | 0.3406 |
| Best-fit ARX Model Fit (%) | 41.76 | −60.26 |
| Best-fit ARX MSE | 0.0357 | 0.0971 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otálora, P.; Guzmán, J.L.; Berenguel, M.; Acién, F.G. Data-Driven pH Model in Raceway Reactors for Freshwater and Wastewater Cultures. Mathematics 2023, 11, 1614. https://doi.org/10.3390/math11071614
Otálora P, Guzmán JL, Berenguel M, Acién FG. Data-Driven pH Model in Raceway Reactors for Freshwater and Wastewater Cultures. Mathematics. 2023; 11(7):1614. https://doi.org/10.3390/math11071614
Chicago/Turabian StyleOtálora, Pablo, José Luis Guzmán, Manuel Berenguel, and Francisco Gabriel Acién. 2023. "Data-Driven pH Model in Raceway Reactors for Freshwater and Wastewater Cultures" Mathematics 11, no. 7: 1614. https://doi.org/10.3390/math11071614
APA StyleOtálora, P., Guzmán, J. L., Berenguel, M., & Acién, F. G. (2023). Data-Driven pH Model in Raceway Reactors for Freshwater and Wastewater Cultures. Mathematics, 11(7), 1614. https://doi.org/10.3390/math11071614









