Undirected Structural Markov Property for Bayesian Model Determination
Abstract
1. Introduction
2. Preliminaries
2.1. Graphical Terminologies and Notation
- (i)
- is prime, and
- (ii)
- s.t. , is reducible.
2.2. Independence Model and Collapsibility
- for all , , and ;
- if , then ;
- if , and , then ;
- if , and , then ;
- if , and , then .
- 1.
- G is graphical collapsible onto D;
- 2.
- is CI-collapsible onto D;
- 3.
- is M-collapsible onto D.
- 1.
- G can be graphical collapsible onto;
- 2.
- ;
- 3.
- .
3. Structural Markov Graph Laws for Full Bayesian Inference
3.1. Basic Concepts and Properties
- 1.
- and ;
- 2.
- if is structural Markov on , then
3.2. Joint Distribution Law
- 1.
- if is weak hyper Markov with respect to G, then
- 2.
- if is strong hyper Markov, then
- 1.
- if is weak hyper Markov, then
- 2.
- if is strong hyper Markov, then
- 1.
- if is weak hyper Markov, then
- 2.
- if is strong hyper Markov, then
- 1.
- if is weak hyper Markov, then
- 2.
- if is strong hyper Markov, then
- 1.
- if is weak hyper Markov, then
- 2.
- if is strong hyper Markov, then
3.3. Posterior Updating for Graph Law
- 1.
- The posterior graph law obtained by conditioning on data is structural Markov with respect to ;
- 2.
- The marginal data distribution of is Markov with respect to ;
- 3.
- The posterior law of θ conditioning on is Markov with respect to .
4. Two Special Cases
4.1. Graphical Gaussian Models and the Inverse Wishart Law
4.2. Multinomial Models and the Dirichlet Law
4.3. An Example on Simulated Data
4.3.1. Dataset Description
- inc: The income of the respondents.
- deg: Tespondents’ highest educational degree.
- chi: The number of children of the respondents.
- pin: The income of the respondents’ parents.
- pde: The highest educational degree of respondents’ parents.
- pch: The number of children of respondents’ parents.
- age: Respondents’ age in years.
4.3.2. Experiments and Results
- ;
- .
5. Computations
5.1. Ratio for Graph Law
- 1.
- if u and v are contained in exactly one maximal prime subgraph of G, then
- 2.
- if u and v are contained in both two neighboring maximal prime subgraphs of G, thenwherein G.
- 1.
- if u and v are contained in exactly one incomplete prime subgraph , then
- 2.
- if and are the two distinct maximal prime subgraphs of G, then there are some prime components such thatwhere.
- 1.
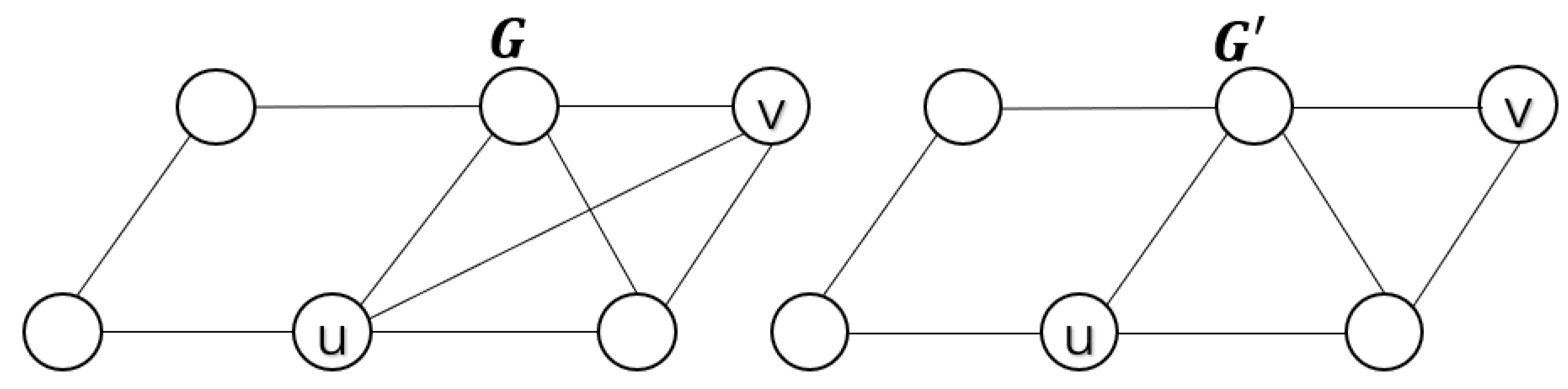
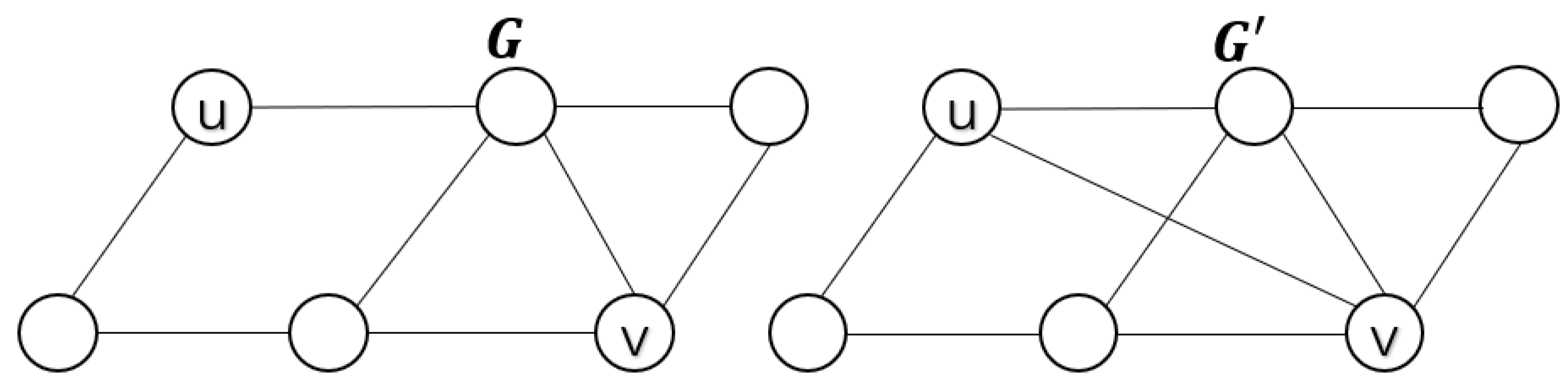
- If is obtained from G by removing the edge , then u and v must belong to a clique of G;
- 2.
- If is obtained from G by adding the edge , then there exist two different cliques and such that is complete and separates and .
- 1.
- If is obtained from G by removing the edge within , thenwhere, and ;
- 2.
- If is obtained from G by adding the edge such that and , then the ratio iswhere,,and.
5.2. Sampling Decomposable Graphs from Structural Markov Graph Laws
| Algorithm 1 A Metropolis–Hastings algorithm for sampling decomposable graphs from a structural Markov graph law. |
| Input: An ER random graph . Output: A set of decomposable graph from . Set for do if and then set with probability else if and then set with probability else end if end for return A set of decomposable graphs. |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs of Some Main Theorems and Propositions
References
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Lauritzen, S.L. Graphical Models; Oxford University Press: New York, NY, USA, 1996. [Google Scholar]
- Richardson, T. A factorization criterion for acyclic directed mixed graphs. In Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–21 June 2009. [Google Scholar]
- Richardson, T.; Spirtes, P. Ancestral graph Markov models. Ann. Stat. 2002, 30, 962–1030. [Google Scholar] [CrossRef]
- Iqbal, K.; Buijsse, B.; Wirth, J. Gaussian Graphical Models Identify Networks of Dietary Intake in a German Adult Population. J. Nutr. Off. Organ Am. Inst. Nutr. 2016, 146, 646–652. [Google Scholar] [CrossRef] [PubMed]
- Larranaga, P.; Moral, S. Probabilistic graphical models in artificial intelligence. Appl. Soft Comput. 2011, 11, 1511–1528. [Google Scholar] [CrossRef]
- Verzilli, C.J.; Stallard, N.; Whittaker, J.C. Bayesian graphical models for genomewide association studies. Am. J. Hum. Genet. 2006, 79, 100–112. [Google Scholar] [CrossRef] [PubMed]
- Giudici, P.; Green, P.J. Decomposable graphical Gaussian model determination. Biometrika 1999, 86, 785–801. [Google Scholar] [CrossRef]
- Madigan, D.; Raftrey, A.E. Model selection and accounting for model uncertainty in graphical models using Occam’s window. J. Amer. Stat. Assoc. 1994, 89, 1535–1546. [Google Scholar] [CrossRef]
- Byrne, S.; Dawid, A.P. Structural Markov graph laws for Bayesian model uncertainty. Ann. Stat. 2015, 43, 1647–1681. [Google Scholar] [CrossRef]
- Li, B.C. Support condition for equivalent characterization of graph laws. Sci. Sin. Math. 2022, 52, 467–474. [Google Scholar]
- Dawid, A.P.; Lauritzen, S.L. Hyper Markov laws in the statistical analysis of decomposable graphical models. Ann. Stat. 1993, 21, 1272–1317. [Google Scholar] [CrossRef]
- Green, P.J.; Thomas, A. A structural Markov property for decomposable graph laws that allows control of clique intersections. Biometrika 2018, 105, 19–29. [Google Scholar] [CrossRef]
- Leimer, H.G. Optimal decomposition by clique separators. Discret. Math. 1993, 113, 99–123. [Google Scholar] [CrossRef]
- Dawid, A.P. Conditional independence in statistical theory. J. R. Stat. Soc. B. 1979, 41, 1–15. [Google Scholar] [CrossRef]
- Dawid, A.P. Conditional independence for statistical operations. Ann. Stat. 1980, 8, 598–617. [Google Scholar] [CrossRef]
- Meek, C. Strong Completeness and Faithfulness in Bayesian Networks; Morgan Kaufmann: San Francisco, CA, USA, 1995. [Google Scholar]
- Hoff, P.D. Extending the rank likelihood for semiparametric copula estimation. Ann. Appl. Stat. 2007, 23, 103–122. [Google Scholar]
- Frydennberg, M.; Lauritzen, S.L. Decomposition of maximum likelihood in mixed graphical interaction models. Biometrika 1989, 76, 539–555. [Google Scholar] [CrossRef]
- Asmussen, S.; Edwards, D. Collapsibility and response variables in contingency tables. Biometrika 1983, 70, 567–578. [Google Scholar] [CrossRef]
- Wang, X.F.; Guo, J.H. Junction trees of general graphs. Front. Math. China 2008, 3, 399–413. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, X.; Hu, Y.; Sun, Y. Undirected Structural Markov Property for Bayesian Model Determination. Mathematics 2023, 11, 1590. https://doi.org/10.3390/math11071590
Kang X, Hu Y, Sun Y. Undirected Structural Markov Property for Bayesian Model Determination. Mathematics. 2023; 11(7):1590. https://doi.org/10.3390/math11071590
Chicago/Turabian StyleKang, Xiong, Yingying Hu, and Yi Sun. 2023. "Undirected Structural Markov Property for Bayesian Model Determination" Mathematics 11, no. 7: 1590. https://doi.org/10.3390/math11071590
APA StyleKang, X., Hu, Y., & Sun, Y. (2023). Undirected Structural Markov Property for Bayesian Model Determination. Mathematics, 11(7), 1590. https://doi.org/10.3390/math11071590







