Author Contributions
Conceptualization, H.M.A., Z.A. and C.B.A.; Methodology, H.M.A., Z.A. and C.B.A.; Software, H.M.A., Z.A., H.A.-M. and S.K.K.; Validation, Z.A. and H.A.-M.; Formal analysis, H.M.A., H.A.-M. and S.K.K.; Data curation, H.M.A. and Z.A.; Writing—original draft, H.M.A., Z.A., H.A.-M., C.B.A. and S.K.K.; Visualization, H.A.-M. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Plots of of the WS-Weibull distribution for different values of and .
Figure 1.
Plots of of the WS-Weibull distribution for different values of and .
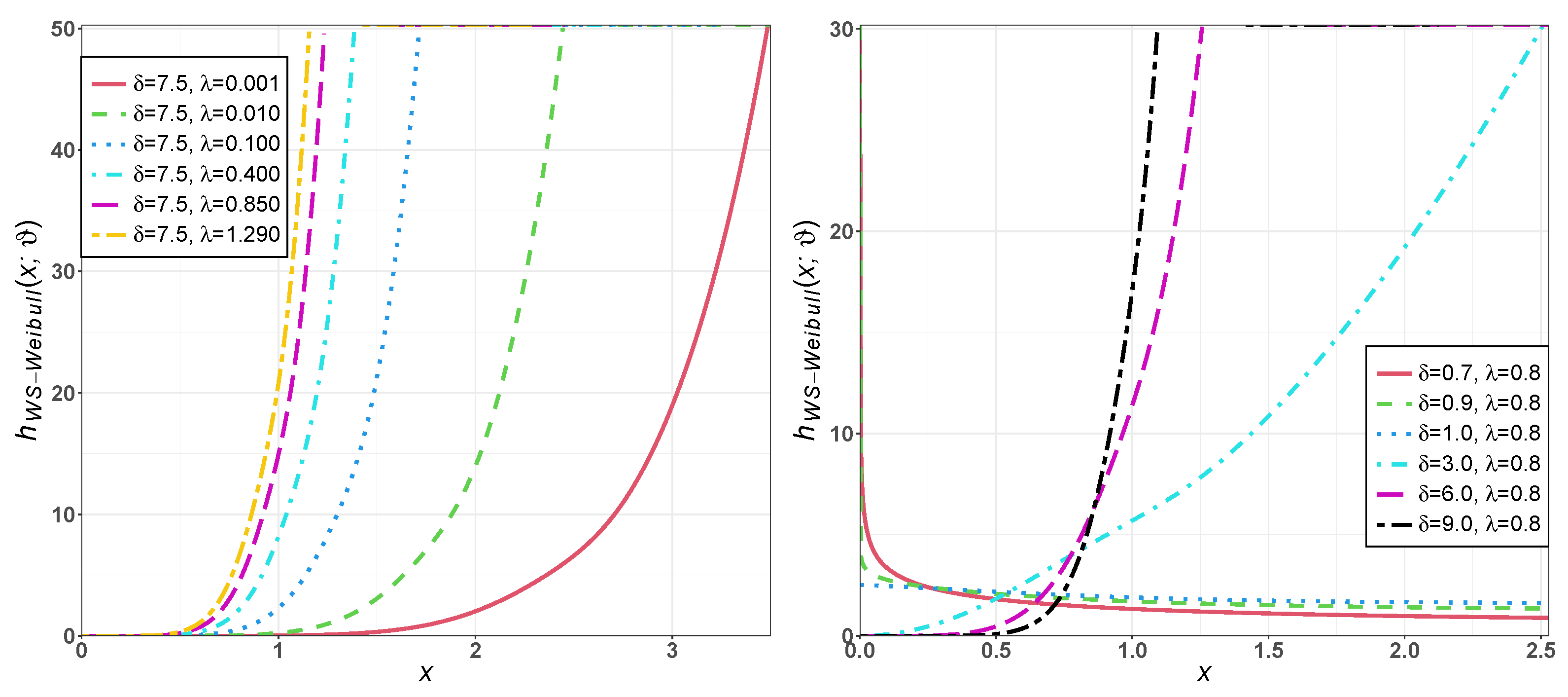
Figure 2.
Plots of of the WS-Weibull distribution for different values of and .
Figure 2.
Plots of of the WS-Weibull distribution for different values of and .
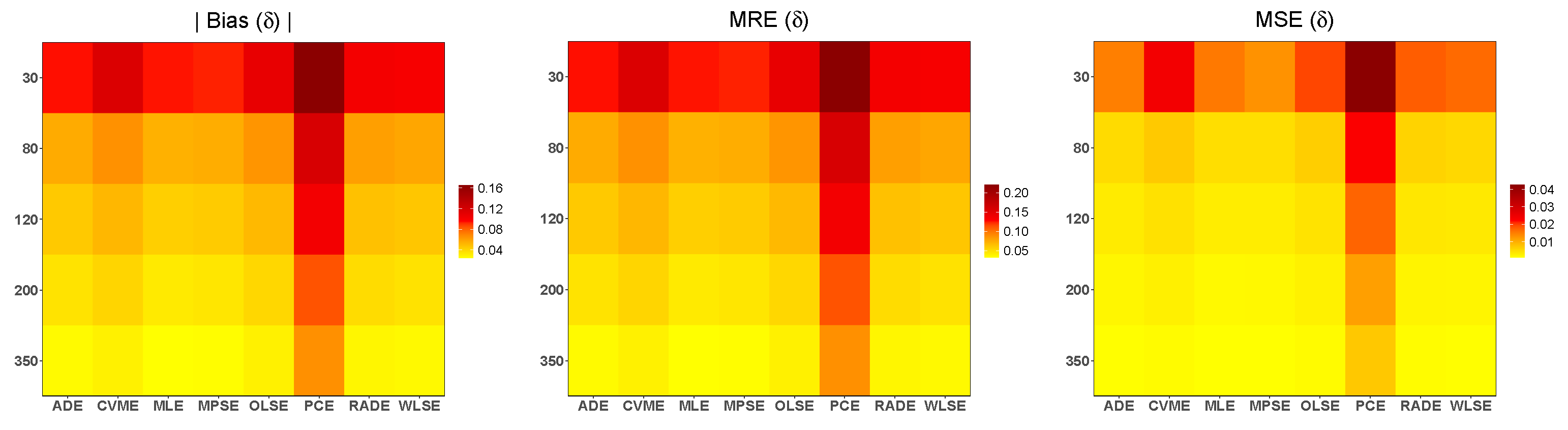
Figure 3.
The heatmaps of the simulated biases, MSE and MRE of the eight simulation methods for and .
Figure 3.
The heatmaps of the simulated biases, MSE and MRE of the eight simulation methods for and .
Figure 4.
The heatmaps of the simulated biases, MSE and MRE of the eight simulation methods for and .
Figure 4.
The heatmaps of the simulated biases, MSE and MRE of the eight simulation methods for and .
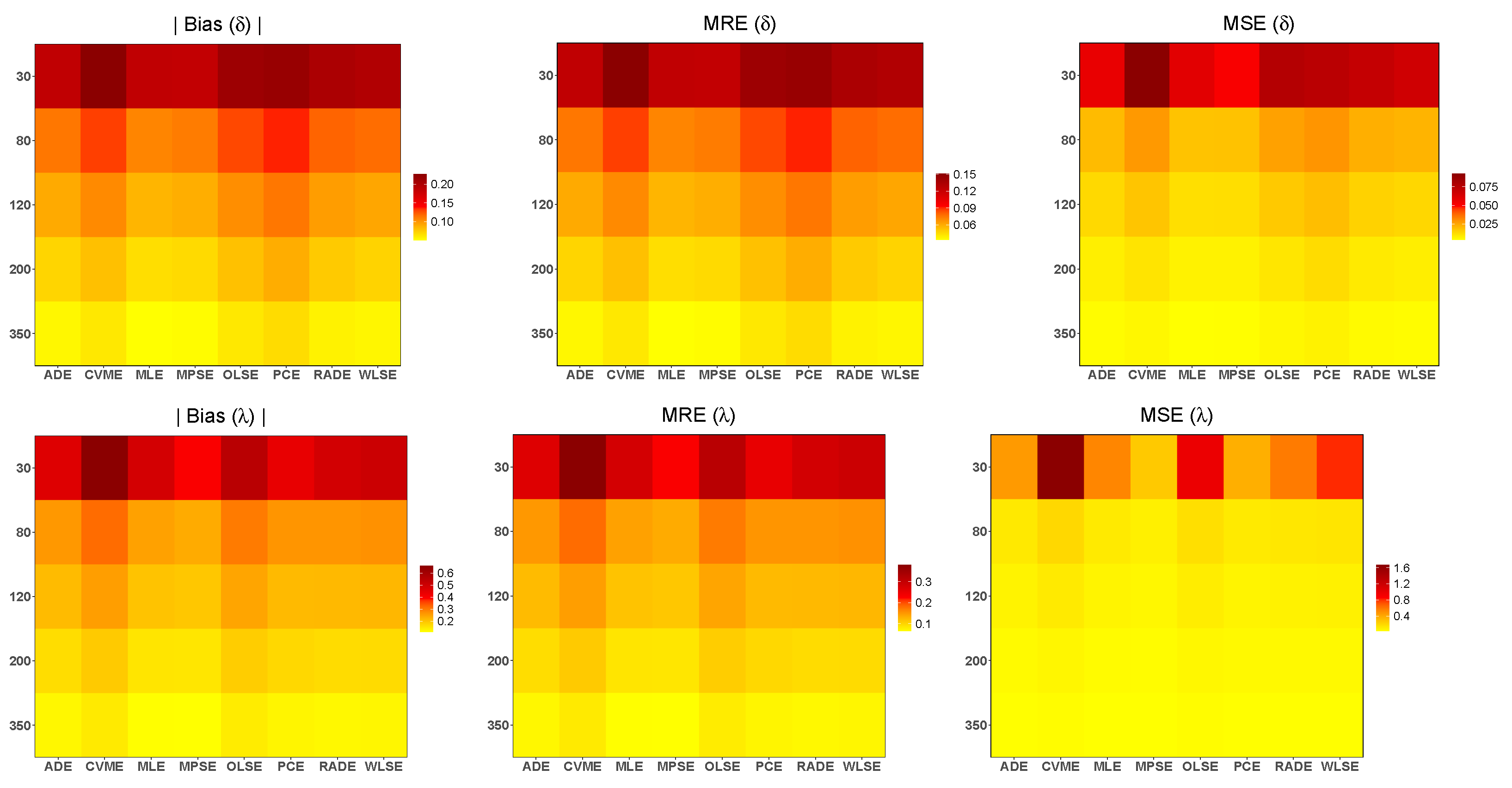
Figure 5.
The heatmaps of the simulated biases, MSE and MRE, of the eight simulation methods for and .
Figure 5.
The heatmaps of the simulated biases, MSE and MRE, of the eight simulation methods for and .
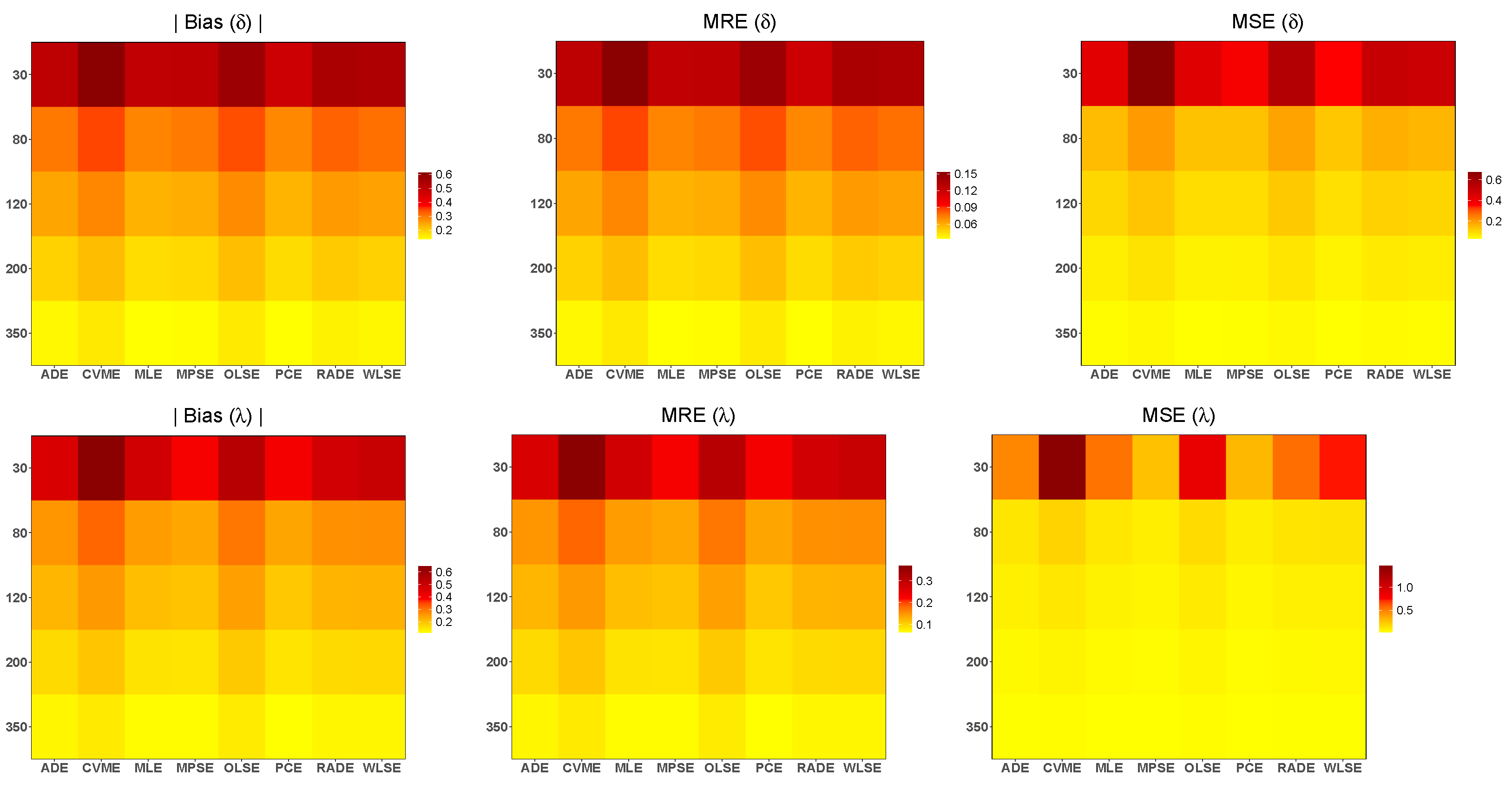
Figure 6.
The heatmaps of the simulated biases, MSE and MRE, of the eight simulation methods for and .
Figure 6.
The heatmaps of the simulated biases, MSE and MRE, of the eight simulation methods for and .
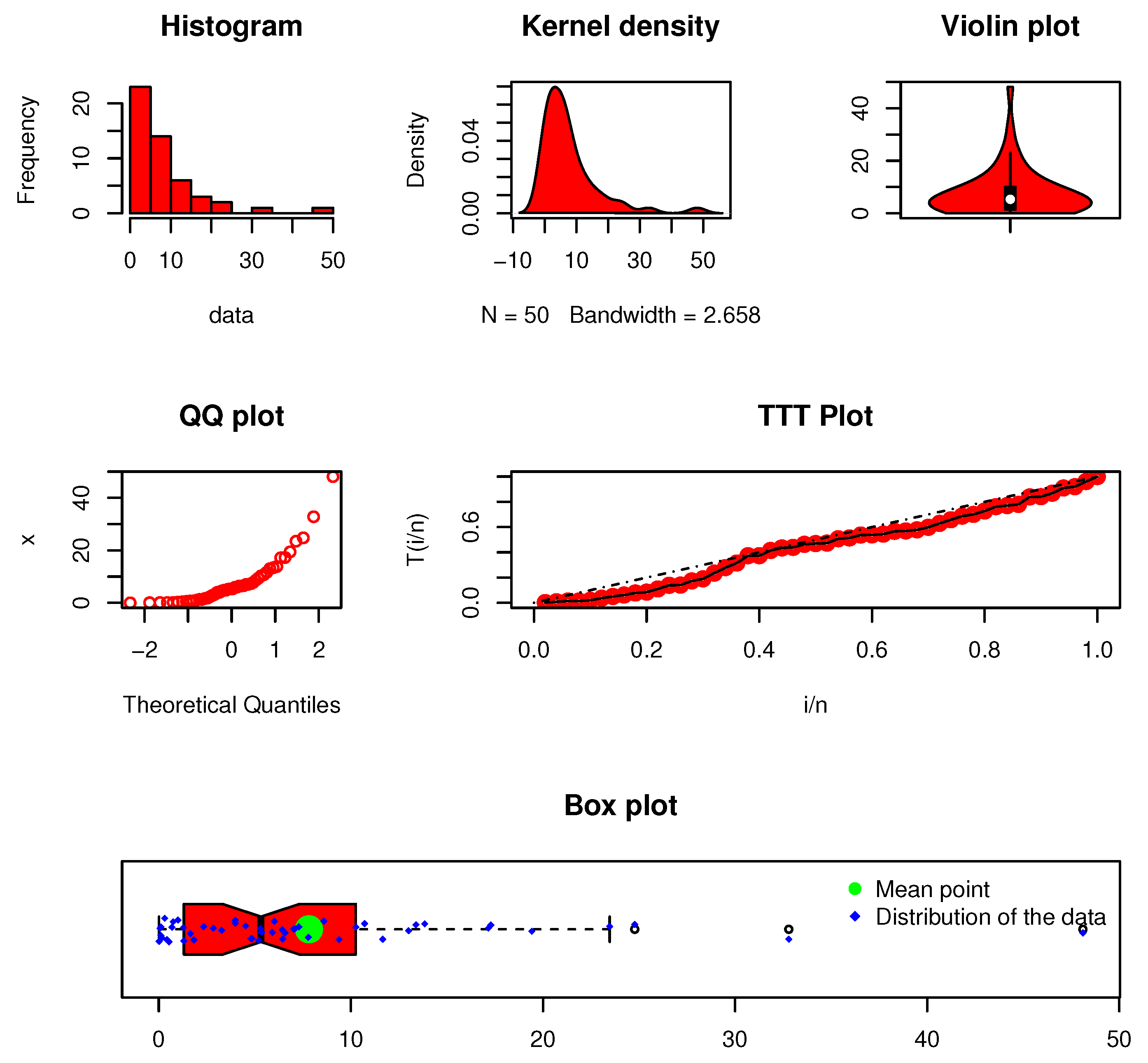
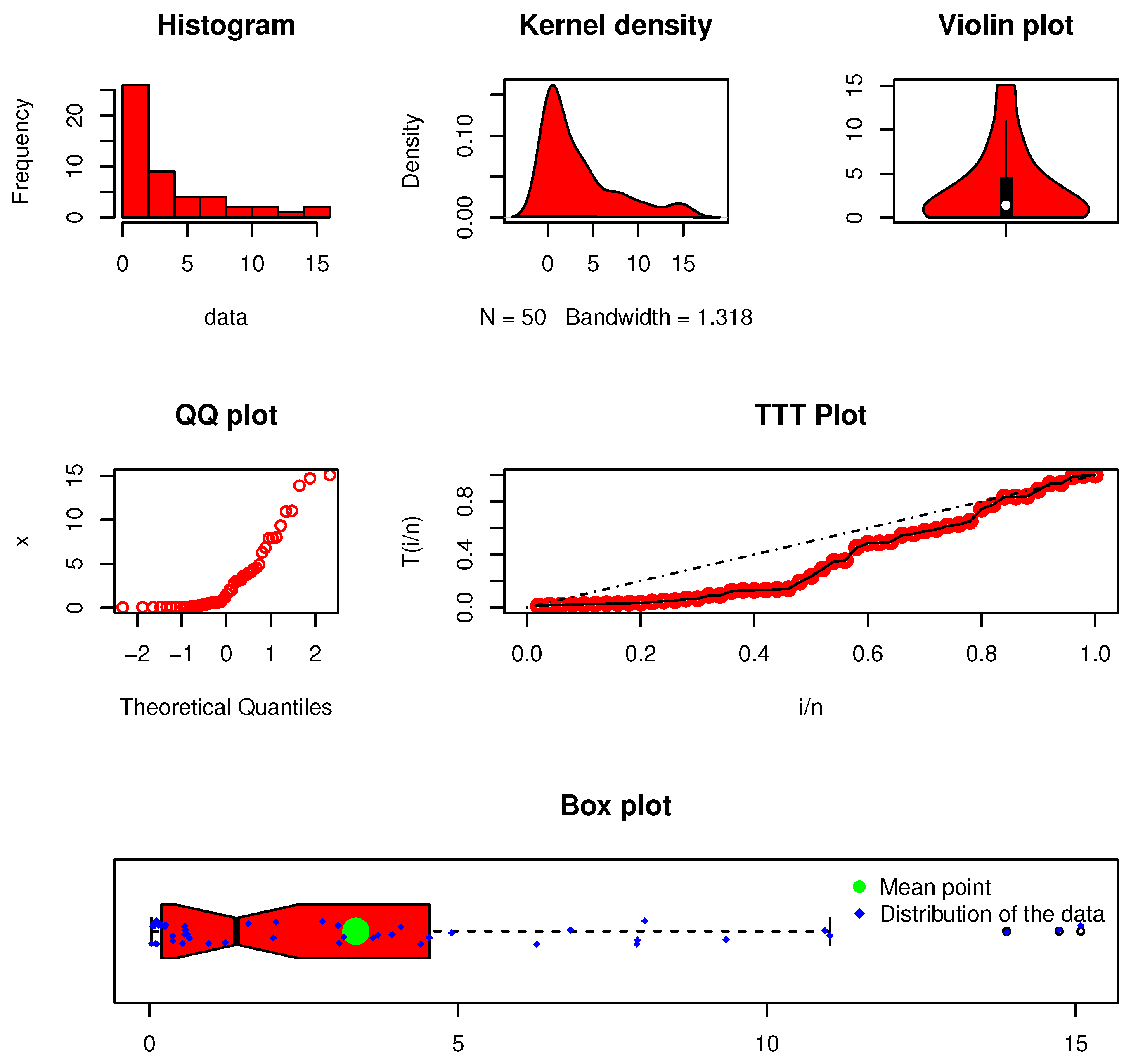
Figure 7.
Visual description of the first failure times data set.
Figure 7.
Visual description of the first failure times data set.
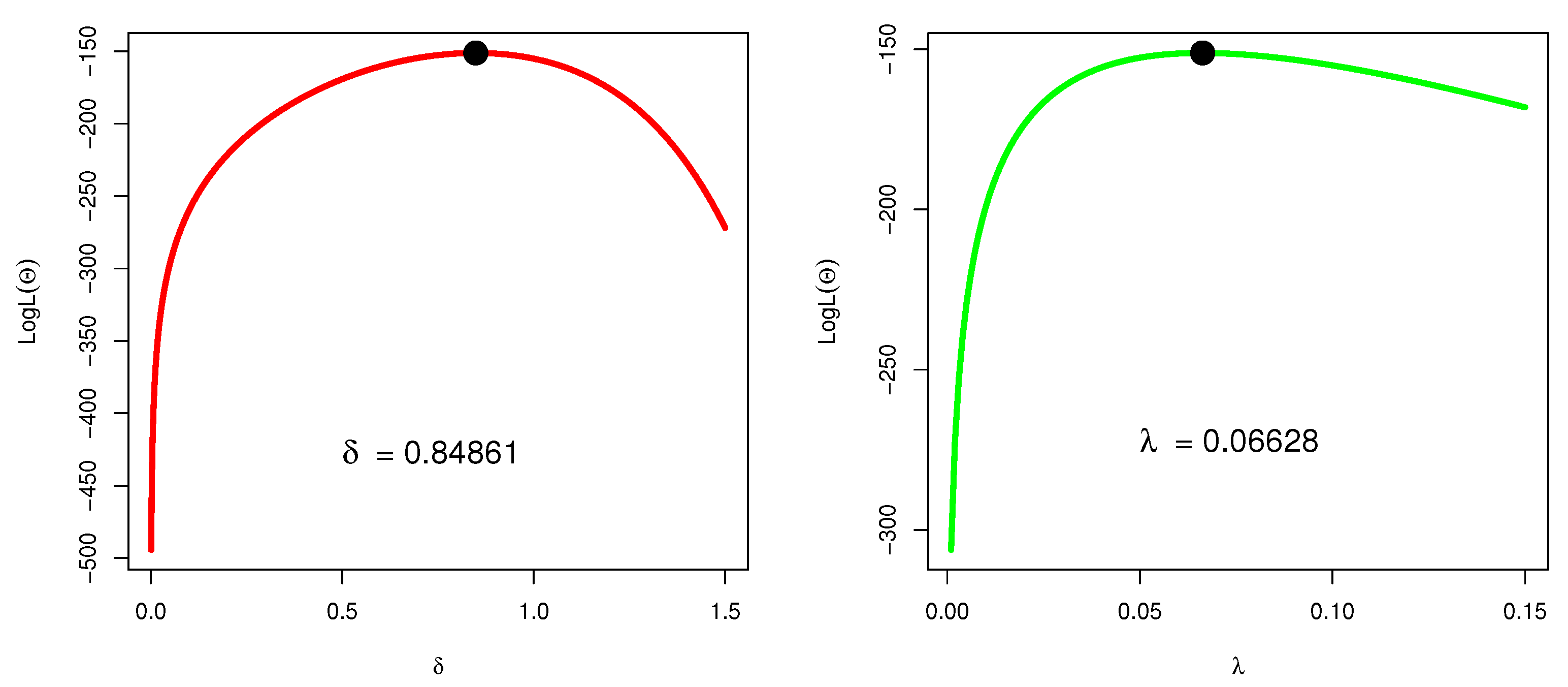
Figure 8.
The profiles of the LLF of and of WS-Weibull using the first failure times data.
Figure 8.
The profiles of the LLF of and of WS-Weibull using the first failure times data.
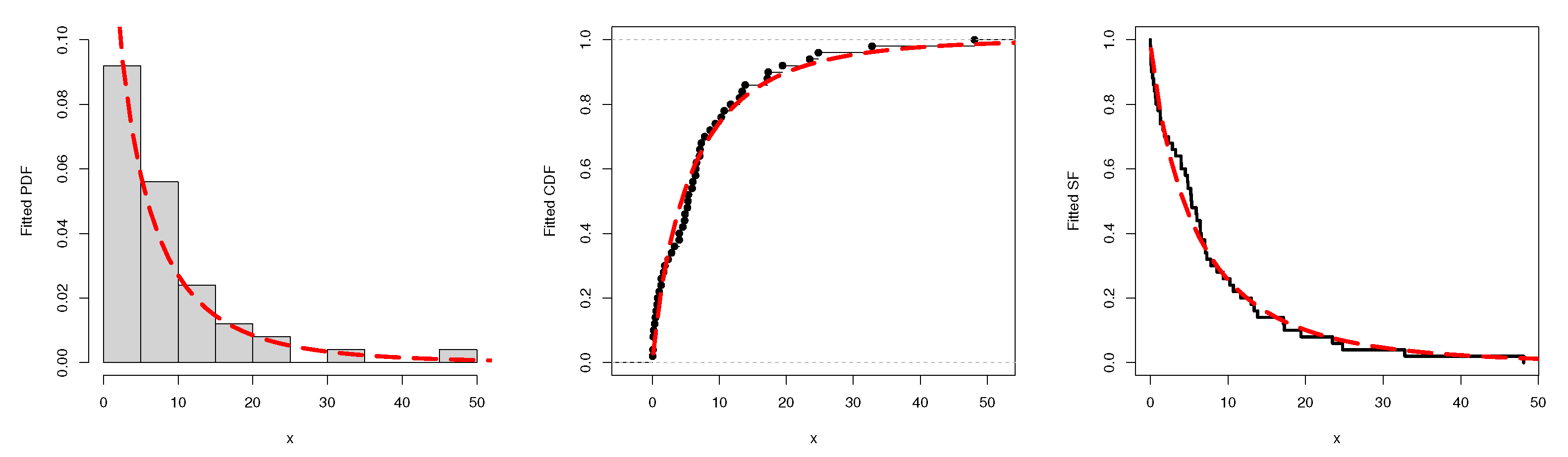
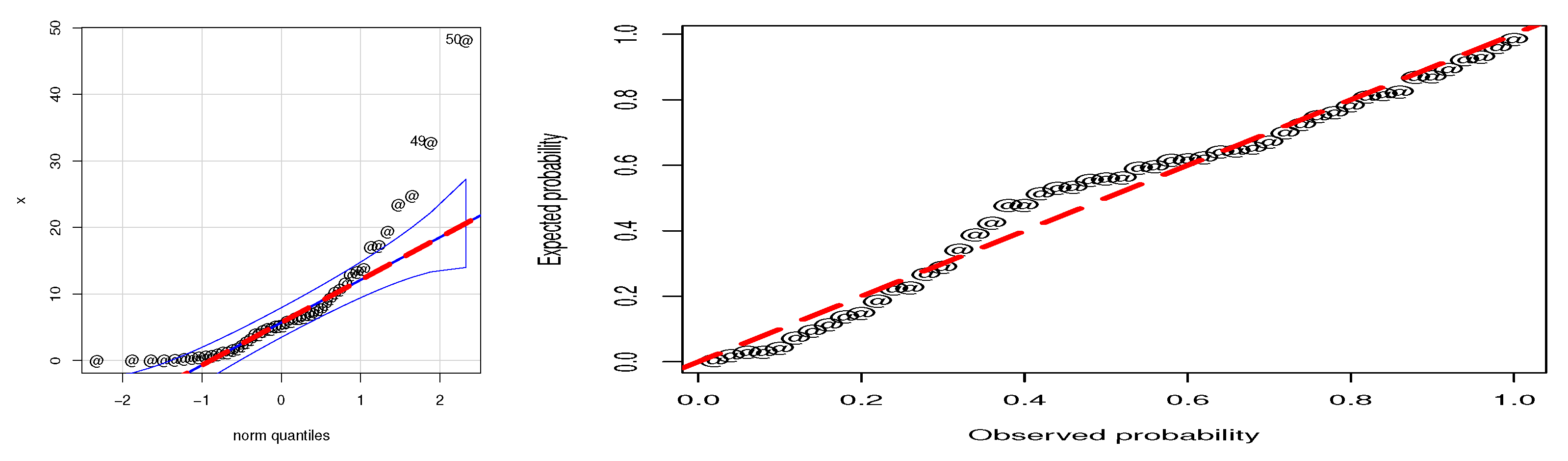
Figure 9.
A visual illustration of the WS-Weibull distribution using the first failure times data.
Figure 9.
A visual illustration of the WS-Weibull distribution using the first failure times data.
Figure 10.
Visual description of the second failure times data set.
Figure 10.
Visual description of the second failure times data set.
Figure 11.
The profiles of the LLF of and of WS-Weibull using the second failure times data.
Figure 11.
The profiles of the LLF of and of WS-Weibull using the second failure times data.
Figure 12.
A visual illustration of the WS-Weibull distribution using the second failure times data.
Figure 12.
A visual illustration of the WS-Weibull distribution using the second failure times data.
Table 1.
The summation formula and the exact value for the PDFs of WS-Weibull, Weibull, and sin-Weibull distributions for different values of x, , and at truncated N terms.
Table 1.
The summation formula and the exact value for the PDFs of WS-Weibull, Weibull, and sin-Weibull distributions for different values of x, , and at truncated N terms.
| x | | | N | WS-Weibull | sin-Weibull | Weibull |
|---|
| Summation | Exact Value | Summation | Exact Value | Exact Value |
|---|
| 0.5 | 0.8 | 1.2 | 2 | 0.4090627 | | 0.6170058 | | |
| | | | 4 | 0.3950064 | 0.3946863 | 0.6167320 | 0.6167320 | 0.5535454 |
| | | | 10 | 0.3946863 | | 0.6167320 | | |
| | | 2.2 | 2 | 0.1841287 | | 0.3880394 | | |
| | | | 4 | 0.1718327 | 0.1714237 | 0.3855453 | 0.3855445 | 0.5714233 |
| | | | 10 | 0.1714237 | | 0.3855445 | | |
| | 1.5 | 1.2 | 2 | 1.0064660 | | 1.1198750 | | |
| | | | 4 | 0.9908311 | 0.9906327 | 1.1198280 | 1.1198280 | 0.8327257 |
| | | | 10 | 0.9906327 | | 1.1198280 | | |
| | | 2.2 | 2 | 0.6842317 | | 1.1132750 | | |
| | | | 4 | 0.6566751 | 0.6559729 | 1.1124090 | 1.1124090 | 1.0720057 |
| | | | 10 | 0.6559729 | | 1.1124090 | | |
| 1.0 | 0.8 | 1.2 | 2 | 0.1009522 | | 0.2080368 | | |
| | | | 4 | 0.0945207 | 0.0943092 | 0.2069571 | 0.2069568 | 0.2891464 |
| | | | 10 | 0.0943092 | | 0.2069568 | | |
| | | 2.2 | 2 | 0.0230105 | | 0.0560985 | | |
| | | | 4 | 0.0201815 | 0.0201114 | 0.0530495 | 0.0530471 | 0.1950136 |
| | | | 10 | 0.0201114 | | 0.0530471 | | |
| | 1.5 | 1.2 | 2 | 0.1892854 | | 0.3900691 | | |
| | | | 4 | 0.1772264 | 0.1768297 | 0.3880446 | 0.3880440 | 0.5421496 |
| | | | 10 | 0.1768297 | | 0.3880440 | | |
| | | 2.2 | 2 | 0.0431448 | | 0.1051847 | | |
| | | | 4 | 0.0378403 | 0.0377088 | 0.0994678 | 0.0994634 | 0.3656504 |
| | | | 10 | 0.0377088 | | 0.0994634 | | |
| 2.5 | 0.8 | 1.2 | 2 | 0.0058948 | | 0.0145537 | | |
| | | | 4 | 0.0049978 | 0.0049798 | 0.0133140 | 0.0133129 | 0.0657602 |
| | | | 10 | 0.0049798 | | 0.0133129 | | |
| | | 2.2 | 2 | 0.0003286 | | 0.0008248 | | |
| | | | 4 | 0.0001409 | 0.0001402 | 0.0003815 | 0.0003809 | 0.0150408 |
| | | | 10 | 0.0001402 | | 0.0003809 | | |
| | 1.5 | 1.2 | 2 | 0.0005063 | | 0.0012709 | | |
| | | | 4 | 0.0001970 | 0.0001960 | 0.0005335 | 0.0005326 | 0.0247858 |
| | | | 10 | 0.0001960 | | 0.0005326 | | |
| | | 2.2 | 2 | 0.0000110 | | 0.0000277 | | |
| | | | 4 | 0.0000001 | 0.0000001 | 0.0000004 | 0.0000004 | 0.0008725 |
| | | | 10 | 0.0000001 | | 0.0000004 | | |
Table 2.
The summary of the HF limits for the WS-Weibull, Weibull, and sin-Weibull distributions.
Table 2.
The summary of the HF limits for the WS-Weibull, Weibull, and sin-Weibull distributions.
| Distributions | Limit as | Limit as |
|---|
| | | | | |
|---|
| WS-Weibull | ∞ | | 0 | 0 | | ∞ |
| Weibull | ∞ | | 0 | 0 | | ∞ |
| sin-Weibull | ∞ | | 0 | 0 | | ∞ |
Table 3.
The summation formula and the numerical integration values for the non-central moments of the WS-Weibull, Weibull, and sin-Weibull distributions for different values of r, , and at truncated N terms.
Table 3.
The summation formula and the numerical integration values for the non-central moments of the WS-Weibull, Weibull, and sin-Weibull distributions for different values of r, , and at truncated N terms.
| r | | | N | WS-Weibull | sin-Weibull | Weibull |
|---|
| Summation | NI | Summation | NI | Exact Integration |
|---|
| 1.0 | 0.8 | 1.2 | 2 | 0.2712448 | | 0.4416135 | | |
| | | | 4 | 0.2560016 | 0.2556559 | 0.4294283 | 0.4294168 | 0.9020998 |
| | | | 10 | 0.2556559 | | 0.4294168 | | |
| | | 2.2 | 2 | 0.1271481 | | 0.2070096 | | |
| | | | 4 | 0.1200027 | 0.1198406 | 0.2012978 | 0.2012924 | 0.4228660 |
| | | | 10 | 0.1198406 | | 0.2012924 | | |
| | 1.5 | 1.2 | 2 | 0.4124430 | | 0.5530663 | | |
| | | | 4 | 0.3983605 | 0.3980281 | 0.5457003 | 0.5456939 | 0.7994250 |
| | | | 10 | 0.3980281 | | 0.5456939 | | |
| | | 2.2 | 2 | 0.2753402 | | 0.3692180 | | |
| | | | 4 | 0.2659389 | 0.2657171 | 0.3643006 | 0.3642963 | 0.5336831 |
| | | | 10 | 0.2657171 | | 0.3642963 | | |
| 2.0 | 0.8 | 1.2 | 2 | 0.2331464 | | 0.4881900 | | |
| | | | 4 | 0.2027422 | 0.2022463 | 0.4433054 | 0.4432577 | 2.1067990 |
| | | | 10 | 0.2022463 | | 0.4432577 | | |
| | | 2.2 | 2 | 0.0512301 | | 0.1072717 | | |
| | | | 4 | 0.0445493 | 0.0444403 | 0.0974091 | 0.0973986 | 0.4629345 |
| | | | 10 | 0.0444403 | | 0.0973986 | | |
| | 1.5 | 1.2 | 2 | 0.2609388 | | 0.4347446 | | |
| | | | 4 | 0.2453182 | 0.2449682 | 0.4215772 | 0.4215647 | 0.9336954 |
| | | | 10 | 0.2449682 | | 0.4215647 | | |
| | | 2.2 | 2 | 0.1162921 | | 0.1937518 | | |
| | | | 4 | 0.1093305 | 0.1091745 | 0.1878835 | 0.1878779 | 0.4161181 |
| | | | 10 | 0.1091745 | | 0.1878779 | | |
| 3.0 | 0.8 | 1.2 | 2 | 0.4160335 | | 0.9762510 | | |
| | | | 4 | 0.3061227 | 0.3051022 | 0.7563797 | 0.7561286 | 8.3717721 |
| | | | 10 | 0.3051022 | | 0.7561286 | | |
| | | 2.2 | 2 | 0.0428522 | | 0.1005556 | | |
| | | | 4 | 0.0315312 | 0.0314261 | 0.0779084 | 0.0778826 | 0.8623072 |
| | | | 10 | 0.0314261 | | 0.0778826 | | |
| | 1.5 | 1.2 | 2 | 0.2236855 | | 0.4328695 | | |
| | | | 4 | 0.2024038 | 0.2019931 | 0.4071599 | 0.4071336 | 1.3888889 |
| | | | 10 | 0.2019931 | | 0.4071336 | | |
| | | 2.2 | 2 | 0.0665511 | | 0.1287876 | | |
| | | | 4 | 0.0602193 | 0.0600971 | 0.1211385 | 0.1211307 | 0.4132231 |
| | | | 10 | 0.0600971 | | 0.1211307 | | |
Table 4.
The summation formula and the numerical integration values for the Rényi entropy of WS-Weibull, Weibull, and sin-Weibull distributions for different values of , , and at truncated N terms.
Table 4.
The summation formula and the numerical integration values for the Rényi entropy of WS-Weibull, Weibull, and sin-Weibull distributions for different values of , , and at truncated N terms.
| | | N | WS-Weibull | sin-Weibull | Weibull |
|---|
| Summation | NI | Summation | NI | Exact Value |
|---|
| 0.5 | 0.8 | 1.2 | 2 | 0.3572427 | | 0.7321667 | | |
| | | | 4 | 0.2645767 | 0.2631333 | 0.6566993 | 0.6564579 | 1.4347754 |
| | | | 10 | 0.2631333 | | 0.6564579 | | |
| | | 2.2 | 2 | −0.4004269 | | −0.0255028 | | |
| | | | 4 | −0.4930927 | −0.4945364 | −0.1009705 | −0.1012118 | 0.6771066 |
| | | | 10 | −0.4945364 | | −0.1012118 | | |
| | 1.5 | 1.2 | 2 | 0.3055993 | | 0.4904644 | | |
| | | | 4 | 0.2511143 | 0.2501745 | 0.4488667 | 0.4487522 | 0.8705198 |
| | | | 10 | 0.2501745 | | 0.4487522 | | |
| | | 2.2 | 2 | −0.0984913 | | 0.0863738 | | |
| | | | 4 | −0.1529758 | −0.1539160 | 0.0447768 | 0.0446617 | 0.4664292 |
| | | | 10 | −0.1539160 | | 0.0446617 | | |
| 2.0 | 0.8 | 1.2 | 2 | −1.0818547 | | −0.3444082 | | |
| | | | 4 | −1.0767934 | −1.0767260 | −0.3439980 | −0.3439978 | 0.3118210 |
| | | | 10 | −1.0767261 | | −0.3439978 | | |
| | | 2.2 | 2 | −1.8395245 | | −1.1020779 | | |
| | | | 4 | −1.8344632 | −1.8343958 | −1.1016677 | −1.1016675 | −0.4458487 |
| | | | 10 | −1.8343958 | | −1.1016675 | | |
| | 1.5 | 1.2 | 2 | −0.2044980 | | 0.1123635 | | |
| | | | 4 | −0.1918153 | −0.1916098 | 0.1136098 | 0.1136103 | 0.5103751 |
| | | | 10 | −0.1916098 | | 0.1136103 | | |
| | | 2.2 | 2 | −0.6085886 | | −0.2917271 | | |
| | | | 4 | −0.5959058 | −0.5957003 | −0.2904808 | −0.2904803 | 0.1062845 |
| | | | 10 | −0.5957004 | | −0.2904803 | | |
| 4.0 | 0.8 | 1.2 | 2 | −1.7438683 | | −0.9049445 | | |
| | | | 4 | −1.7437275 | −1.7437268 | −0.9049410 | −0.9049410 | −0.3185747 |
| | | | 10 | −1.7437268 | | −0.9049410 | | |
| | | 2.2 | 2 | -2.5015382 | | −1.6626142 | | |
| | | | 4 | -2.5013973 | -2.5013966 | −1.6626107 | −1.6626107 | −1.0762445 |
| | | | 10 | -2.5013966 | | −1.6626107 | | |
| | 1.5 | 1.2 | 2 | −0.3274484 | | 0.0083556 | | |
| | | 4 | −0.3237034 | −0.3236696 | 0.0085064 | 0.0085064 | | 0.3971834 |
| | | | 10 | −0.3236696 | | 0.0085064 | | |
| | | 2.2 | 2 | −0.7315390 | | −0.3957349 | | |
| | | | 4 | −0.7277940 | −0.7277602 | −0.3955842 | −0.3955842 | −0.0069071 |
| | | | 10 | −0.7277602 | | −0.3955842 | | |
Table 5.
Simulation results for .
Table 5.
Simulation results for .
| n | Est. | Est. Par. | WLSE | OLSE | MLE | MPSE | CVME | ADE | RADE | PCE |
|---|
| 30 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 80 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 120 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 200 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 350 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
Table 6.
Simulation results for .
Table 6.
Simulation results for .
| n | Est. | Est. Par. | WLSE | OLSE | MLE | MPSE | CVME | ADE | RADE | PCE |
|---|
| 30 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 80 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 120 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 200 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 350 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
Table 7.
Simulation results for .
Table 7.
Simulation results for .
| n | Est. | Est. Par. | WLSE | OLSE | MLE | MPSE | CVME | ADE | RADE | PCE |
|---|
| 30 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 80 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 120 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 200 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 350 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
Table 8.
Simulation results for .
Table 8.
Simulation results for .
| n | Est. | Est. Par. | WLSE | OLSE | MLE | MPSE | CVME | ADE | RADE | PCE |
|---|
| 30 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 80 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 120 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 200 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
| 350 | | | | | | | | | | |
| | | | | | | | | | | |
| | MSE | | | | | | | | | |
| | | | | | | | | | | |
| | MRE | | | | | | | | | |
| | | | | | | | | | | |
| | | | | | | | | | | |
Table 9.
Partial and overall ranks of the classical estimation methods for several parametric values.
Table 9.
Partial and overall ranks of the classical estimation methods for several parametric values.
| n | WLSE | OLSE | MLE | MPSE | CVME | ADE | RADE | PCE |
|---|
| | 30 | 5 | 6 | 3 | 1 | 7 | 2 | 4 | 8 |
| | 80 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| 120 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 200 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 350 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 30 | 5 | 7 | 3 | 1 | 8 | 2 | 4 | 6 |
| | 80 | 5 | 6 | 2 | 1 | 8 | 3 | 4 | 7 |
| 120 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 200 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 350 | 5 | 6 | 1 | 2 | 7 | 3 | 4 | 8 |
| | 30 | 5 | 7 | 3 | 1 | 8 | 2 | 4 | 6 |
| | 80 | 4.5 | 6 | 2 | 1 | 8 | 3 | 4.5 | 7 |
| 120 | 4.5 | 6 | 2 | 1 | 7.5 | 3 | 4.5 | 7.5 |
| | 200 | 5 | 6 | 1.5 | 1.5 | 7.5 | 3 | 4 | 7.5 |
| | 350 | 5 | 6 | 1.5 | 1.5 | 7.5 | 3 | 4 | 7.5 |
| | 30 | 4.5 | 6 | 3 | 1 | 7 | 2 | 4.5 | 8 |
| | 80 | 4 | 6 | 2 | 1 | 7 | 3 | 5 | 8 |
| 120 | 4 | 6 | 1.5 | 1.5 | 7 | 3 | 5 | 8 |
| | 200 | 4.5 | 6 | 1.5 | 1.5 | 7 | 3 | 4.5 | 8 |
| | 350 | 4.5 | 6 | 1.5 | 1.5 | 7 | 3 | 4.5 | 8 |
| | 30 | 5 | 6 | 3.5 | 1 | 8 | 2 | 3.5 | 7 |
| | 80 | 5 | 6 | 2 | 1 | 7 | 3 | 4 | 8 |
| 120 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 200 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 350 | 5 | 6 | 1.5 | 1.5 | 7 | 3 | 4 | 8 |
| | 30 | 5.5 | 7 | 3 | 1 | 8 | 2 | 4 | 5.5 |
| | 80 | 5.5 | 7 | 2 | 1 | 8 | 3 | 4 | 5.5 |
| 120 | 5 | 7 | 2 | 1 | 8 | 3 | 5 | 5 |
| | 200 | 5 | 7 | 2 | 1 | 8 | 3 | 4 | 6 |
| | 350 | 5 | 7 | 1.5 | 1.5 | 8 | 3 | 4 | 6 |
| | 30 | 5 | 7 | 3 | 1 | 8 | 2 | 4 | 6 |
| | 80 | 4.5 | 6 | 2 | 1 | 8 | 3 | 4.5 | 7 |
| 120 | 4.5 | 6 | 1.5 | 1.5 | 8 | 3 | 4.5 | 7 |
| | 200 | 4.5 | 6 | 1.5 | 1.5 | 8 | 3 | 4.5 | 7 |
| | 350 | 4.5 | 6 | 1.5 | 1.5 | 7 | 3 | 4.5 | 8 |
| | 30 | 5 | 6 | 3 | 1 | 8 | 2 | 4 | 7 |
| | 80 | 4.5 | 6 | 1.5 | 1.5 | 7 | 3 | 4.5 | 8 |
| 120 | 4 | 6 | 1.5 | 1.5 | 7 | 3 | 5 | 8 |
| | 200 | 4 | 6 | 1.5 | 1.5 | 7 | 3 | 5 | 8 |
| | 350 | 4 | 6 | 1.5 | 1.5 | 7 | 3 | 5 | 8 |
| | 30 | 6 | 7 | 4 | 1 | 8 | 2 | 5 | 3 |
| | 80 | 6 | 7 | 2 | 1 | 8 | 3 | 5 | 4 |
| 120 | 5.5 | 7 | 2 | 1 | 8 | 3 | 4 | 5.5 |
| | 200 | 5.5 | 7 | 2 | 1 | 8 | 3 | 4 | 5.5 |
| | 350 | 5 | 7 | 1.5 | 1.5 | 8 | 3 | 4 | 6 |
| | 30 | 6 | 7 | 3 | 1 | 8 | 2 | 5 | 4 |
| | 80 | 5 | 7 | 2 | 1 | 8 | 3 | 5 | 5 |
| 120 | 5 | 7 | 2 | 1 | 8 | 3 | 5 | 5 |
| | 200 | 5 | 7 | 1.5 | 1.5 | 8 | 3 | 4 | 6 |
| | 350 | 5 | 7 | 1.5 | 1.5 | 8 | 3 | 4 | 6 |
| | 30 | 5.5 | 7 | 3 | 1 | 8 | 2 | 5.5 | 4 |
| | 80 | 4.5 | 7 | 1.5 | 1.5 | 8 | 3 | 4.5 | 6 |
| 120 | 4.5 | 7 | 1.5 | 1.5 | 8 | 3 | 4.5 | 6 |
| | 200 | 4.5 | 6 | 1.5 | 1.5 | 8 | 3 | 4.5 | 7 |
| | 350 | 5 | 6 | 1.5 | 1.5 | 8 | 3 | 4 | 7 |
| | 30 | 5.5 | 7 | 3 | 1 | 8 | 2 | 5.5 | 4 |
| | 80 | 4 | 6.5 | 2 | 1 | 8 | 3 | 5 | 6.5 |
| 120 | 4 | 6.5 | 1.5 | 1.5 | 8 | 3 | 5 | 6.5 |
| | 200 | 4 | 6 | 1.5 | 1.5 | 8 | 3 | 5 | 7 |
| | 350 | 4 | 6 | 1.5 | 1.5 | 8 | 3 | 5 | 7 |
| | 30 | 5 | 7 | 5 | 2 | 8 | 3 | 5 | 1 |
| | 80 | 6 | 7 | 3 | 2 | 8 | 4 | 5 | 1 |
| 120 | 6 | 7 | 3 | 2 | 8 | 4 | 5 | 1 |
| | 200 | 6 | 7 | 2 | 2 | 8 | 4 | 5 | 2 |
| | 350 | 6 | 7 | 2 | 1 | 8 | 4 | 5 | 3 |
| | 30 | 6 | 7 | 4 | 1 | 8 | 3 | 5 | 2 |
| | 80 | 6 | 7 | 3 | 1.5 | 8 | 4 | 5 | 1.5 |
| 120 | 5.5 | 7 | 2 | 3 | 8 | 4 | 5.5 | 1 |
| | 200 | 6 | 7 | 1 | 2 | 8 | 4 | 5 | 3 |
| | 350 | 6 | 7 | 1 | 2 | 8 | 4 | 5 | 3 |
| | 30 | 6 | 7 | 4 | 2 | 8 | 3 | 5 | 1 |
| | 80 | 5.5 | 7 | 3 | 2 | 8 | 4 | 5.5 | 1 |
| 120 | 5.5 | 7 | 2.5 | 2.5 | 8 | 4 | 5.5 | 1 |
| | 200 | 6 | 7 | 2 | 3 | 8 | 4 | 5 | 1 |
| | 350 | 5.5 | 7 | 2 | 3 | 8 | 4 | 5.5 | 1 |
| | 30 | 5.5 | 7 | 4 | 1.5 | 8 | 3 | 5.5 | 1.5 |
| | 80 | 5 | 7 | 3 | 2 | 8 | 4 | 6 | 1 |
| 120 | 5.5 | 7 | 3 | 2 | 8 | 4 | 5.5 | 1 |
| | 200 | 5 | 7 | 2 | 2 | 8 | 4 | 6 | 2 |
| | 350 | 5.5 | 7 | 3 | 2 | 8 | 4 | 5.5 | 1 |
| ∑ Ranks
| | 404 | 523 | 171 | 117.5 | 616.5 | 244 | 369.5 | 434.5 |
| Overall Rank | | 5 | 7 | 2 | 1 | 8 | 3 | 4 | 6 |
Table 10.
Using the first failure times data, the values of and of the fitted distributions.
Table 10.
Using the first failure times data, the values of and of the fitted distributions.
| Models | | | | | | |
|---|
| WS-Weibull | 0.84861 | 0.06628 | - | - | - | - |
| E-Weibull | 0.32947 | 1.39376 | 5.28710 | - | - | - |
| L-Weibull | 0.55268 | 0.55492 | - | 0.48751 | 1.22066 | - |
| NEC-Weibull | 0.42927 | 1.03216 | - | - | - | 2.96768 |
Table 11.
For the first failure times data, the values of selection criteria of the competing distributions.
Table 11.
For the first failure times data, the values of selection criteria of the competing distributions.
| Models | AIC | CAIC | BIC | HQIC |
|---|
| WS-Weibull | 306.28000 | 306.53530 | 310.10400 | 307.73620 |
| E-Weibull | 315.68840 | 316.21010 | 321.42440 | 317.87270 |
| L-Weibull | 309.23860 | 310.12750 | 316.88670 | 312.15110 |
| NEC-Weibull | 310.05400 | 310.57570 | 315.79000 | 312.23830 |
Table 12.
Using the second failure times data, the values of and of the fitted distributions.
Table 12.
Using the second failure times data, the values of and of the fitted distributions.
| Models | | | | | | |
|---|
| WS-Weibull | 0.69934 | 0.18176 | - | - | - | - |
| E-Weibull | 0.53984 | 0.76136 | 1.37903 | - | - | - |
| L-Weibull | 0.10962 | 0.64226 | - | 5.09788 | 8.88077 | - |
| NEC-Weibull | 0.52723 | 0.57884 | - | - | - | 0.69887 |
Table 13.
For the second failure time data, the values of selection criteria of the competing distributions.
Table 13.
For the second failure time data, the values of selection criteria of the competing distributions.
| Models | AIC | CAIC | BIC | HQIC |
|---|
| WS-Weibull | 208.60920 | 209.86460 | 213.43330 | 211.06550 |
| E-Weibull | 210.90750 | 211.42920 | 216.64350 | 213.09180 |
| L-Weibull | 212.46140 | 213.35030 | 220.10950 | 215.37390 |
| NEC-Weibull | 210.69880 | 211.22050 | 216.43490 | 212.88310 |