Abstract
The design of pumping stations in a water distribution network determines the investment costs and affects a large part of the operating costs of the network. In recent years, it was shown that it is possible to use flow distribution to optimize both costs concurrently; however, the methodologies proposed in the literature are not applicable to real-sized networks. In these cases, the space of solutions is huge, a small number of feasible solutions exists, and each evaluation of the objective function implies significant computational effort. To avoid this gap, a new method was proposed to reduce the search space in the problem of pumping station design. This method was based on network preprocessing to determine in advance the maximum and minimum flow that each pump station could provide. According to this purpose, the area of infeasibility is limited by ranges of the decision variable where it is impossible to meet the hydraulic constraints of the model. This area of infeasibility is removed from the search space with which the algorithm works. To demonstrate the benefits of using the new technique, a new real-sized case study was presented, and a pseudo-genetic algorithm (PGA) was implemented to resolve the optimization model. Finally, the results show great improvement in PGA performance, both in terms of the speed of convergence and quality of the solution.
MSC:
90-08; 68Uxx
1. Introduction
Unquestionably, the water distribution service directly affects the quality of life of people around the world [1,2]. However, this process constitutes one of the most significant expenses in the budget of any city [3,4]. The main reason is the high energy consumption of the water distribution network (WDN). Specifically, pumping stations (PSs) require a significant amount of energy to transport water to consumers [4]. Therefore, improving the efficiency of these systems allows for significant energy and economic savings [2,5]. Furthermore, the price of electricity has been increasing globally. Consequently, optimizing PS design and operations is crucial for achieving a cost-effective WDN.
The design of PSs has short- and long-term consequences [6]. In the immediate term, determining the investment cost for constructing physical structures and acquiring equipment can be done. In the long term, establishing most of the operating conditions throughout the life of the project is performed. Thus, the design of PSs must be optimized after considering the operational variables in the network [7,8]. The design of a PS includes selecting the number, model, type of pump, accessories, and control system [6]. This set of decisions involves many possible combinations and, therefore, can be expressed as a mathematical optimization problem to minimize the investment and operating costs [7].
Different optimization problems were proposed to achieve a minimal amount of energy consumed by PSs from different perspectives [1,2,7]. These models differ in the decision variables used to build their objective functions and constraints. For this purpose, the authors used different approaches, such as the trade-off method between reliability and energy efficiency [9], maximizing energy production [10], minimizing maintenance and energy costs [11,12], location and minimization of the leakage [13], multi-criteria-based approach to minimize the operational costs and operational lack of service and maximize the pressure uniformity and network resilience [14], individual analysis for each design and operation option available by using binary variables [15], and/or calculating the equivalent flow and equivalent volume to approximate the annual costs [8], among other techniques. However, despite all efforts, this problem has not been fully resolved due to its complexity, high level of non-linearity, and the vast space of solutions restricted by hydraulic conditions that ensure a minimum quality of service (minimum pressure) [1,2,16]. Consequently, the development of effective operational strategies in addition to appropriate mathematical models based on comprehensive knowledge about the system and efficient computationally guided search methods are essential for the application of these techniques to real-world WDN problems.
More recently, interest in the determination of the optimal flow distribution as an effective tool in the design of PSs has been growing [5,7,17], mainly when this calculation is driven through the setpoint curve (SC) [18]. The setpoint curve represents the required dynamic head (Hc) for every flow rate (Q) in the PS to satisfy the minimum pressure service in the nodes of the network. The main characteristic of this curve is that the resistance produced by consumption nodes is replaced by a constant value that is the minimum service pressure for consumption nodes at any time instant. More details about its mathematical construction can be found in [19].
In particular, Gutiérrez et al. [7] implemented a novel methodology based on the concurrent minimization of capital expenditures (CAPEX) and operating expenses (OPEX) using the optimization of flow distribution. They proposed a mathematical optimization model with three types of decision variables: (1) the fractions of flow provided by each PS, (2) the model of the pumps, and (3) the number of fixed and variable speed pumps. To solve the model, a pseudo-genetic algorithm proposed by [20] was used. The authors presented a case study to demonstrate the advantages of the method. The results indicate that despite the large number of combinations presented in the network, it appears to be possible to find feasible solutions, avoid oversizing the pumps, and adjust the flows contributed by the PSs to the changes in the consumption pattern of the network for 24 h. However, this methodology still has room for improvement. First, using the SC in each objective function evaluation ensures that the solution fulfills the minimum head by using the minimum energy expenditure. Nevertheless, each evaluation of a solution involves examining all nodes in an iterative way. Thus, the computational cost is high, and the optimization algorithm loses search capacity as the network grows. Second, each solution to the problem includes a decision variable that determines the flow contribution of each pumping station. This variable can take values between 0% and 100% of the total flow demanded by the network in each period, but depending on the topology of the network, many of these solutions are a priori infeasible.
In general terms, real water distribution networks contain many nodes, pipes, and accessories. One of the significant challenges faced by state-of-the-art methods used to optimize the design of pumping stations is the application of the methods described above in networks of real size [1,2,16]. Traditionally, the pumps are selected based on an operation point and, later, their operation is optimized once the equipment is selected. In contrast, this work proposed an approximation to the operation mode of the pump in the planning phase based on optimizing the energy and cost in the WDN. This new approach can help to better select the pumping equipment. In this context, the method proposed by Gutiérrez-Bahamondes et al. [7] is limited by the size of the network. To avoid this problem, this study proposed an automatic pre-processing strategy to accelerate the heuristic search processes of evolutionary algorithms applied to the problem posed in [7]. Several main advantages of this strategy can be described: (1) it reduces the computational burden, (2) it rules out infeasible solutions during the evaluation process in any period, and (3) it finds a set of solutions close to the optimal design of the pumping station. The newly proposed method was validated using a real-world case study, and its performance was evaluated and compared with the original method. EPANET [21] was used to evaluate the hydraulic behavior of the hydraulic network, while the optimization model was solved using a pseudo-genetic algorithm (PGA).
The remainder of the paper is organized into several sections: (1) Section 2 describes the mathematical model of the original method and the infeasibility problem, followed by an explanation of the pre-processing strategy. The developed methodology was then applied to a case study, and an optimization method was implemented. (2) Section 3 provides the results in which 100 experiments were executed and analyzed. The use of the preprocessing strategy improved the quality of solutions and speed of convergence. (3) The conclusions of the research can be found in Section 4.
2. Materials and Methods
This work proposed a new method to accelerate the process of searching for solutions to the problem posed by [7] and includes several improvements:
- −
- A new constraint was added to the mathematical optimization model. For each PS, this equation allows us to discard all pump models that, due to their specifications, did not manage to supply at least the maximum flow rate during the analysis period.
- −
- The method used network preprocessing to determine in advance the maximum and minimum flow that each PS could provide. This procedure made it possible to limit the search space for solutions to the problem, thus eliminating areas of total infeasibility. An area of infeasibility is limited by ranges of the decision variable where it is impossible to meet the hydraulic constraints of the model. Our proposed method maps these ranges before starting the optimization process, accelerating the convergence of the algorithm using infeasibility maps (IMs).
- −
- This study combined the use of the SC with the mapping of infeasibility zones to rule out unfeasible solutions during the evaluation process in any period, thus avoiding unnecessary hydraulic simulations when it was detected that part of the solution was not viable. Consequently, the IMs reduce the search space of the optimization algorithm. Reducing the search space to increase computational efficiency is a significant challenge faced when optimizing water networks
2.1. Mathematical Model
First, for a better understanding, the mathematical optimization model proposed by [7] is briefly presented in this section. This model was based on the optimization of flow rate injection, which was based on the use of the SC concept. The SC curve can be defined as a theoretical curve that indicates the minimum energy (in terms of pressure head) required for pumping stations to meet the minimum pressure required for each demand in the network, namely, it is a representation of the pressure head versus the flow at a given point in the system.
Next, the main assumptions, simplifications, and limitations of the model are detailed. First, it should be understood that the SC concept does not deal explicitly with pumps as hydraulic machines; therefore, we started with the assumption that all the related curves (such as flow rate versus pumping head, efficiency, and power) were not known. The use of the SC allowed us to determine the energy required at the source without considering specific pump head-flow curves. That is, we were only dealing with the energy supplied by the pumping station. One SC curve was available for each supply source. Second, this work assumed that a direct injection network was optimized. That is, the network was fed directly from groundwater or did not have a high enough elevation for tanks to be installed. Third, the location of each possible pumping station was defined previously and was not part of the problem. Fourth, the method required a pump model database containing all the characteristic coefficients of each pump and the purchase costs of all accessories and control systems necessary to build the physical structure. Finally, it is important to note that to simplify the calculation of the total costs, the design of the stations was parameterized according to the established modular design. The mathematical notation, decision variables, objective function, and constraints are presented below.
2.1.1. Mathematical Notation
- −
- Nt: total number of time steps in the optimization process.
- −
- Nps: total number of PSs in the network.
- −
- Nb: total number of pump models available in the data set.
- −
- Fa: amortization factor.
- −
- r: interest rate.
- −
- Np: total number of project life periods.
- −
- H0,i, Ai: characteristic coefficients of the pump head installed in PSi.
- −
- Ei, Fi: characteristic coefficients of the performance curve of the pump installed in PSi.
- −
- Qi,j,k: represents the discharge of pump k during time step j in PSi.
- −
- pi,j: energy cost in PSi during the time step j.
- −
- ϒ: specific gravity of water.
- −
- Δtj: discretization interval of the optimization period.
- −
- mi,j: the number of FSPs running in PSi at time step j.
- −
- ni,j: the number of VSPs running in PSi at time step j. These values depend on the selected pump model and the system selected to control the operation point.
- −
- NB,i: total number of total pumps.
- −
- HBmax: maximum head of the largest pump available in the data set.
- −
- Hmax,i: maximum head supplied by PSi during time analysis.
- −
- Cpump, i: purchase cost of a pump installed in PSi.
- −
- ni: number of frequency inverters in PSi.
- −
- Cfacility,i: cost of accessories including pipes in PSi.
- −
- Ccontrol,i: sum of a pressure transducer, flowmeter, and programmable logic controller cost for PSi.
2.1.2. Decision Variables
- −
- Xij: percentage of the flow supplied from PSi at each time step j.
- −
- mi: number of fixed speed pumps in PSi.
- −
- bi: ID of the pump model to be installed in PSi in the range [1,Nb].
2.1.3. Objective Function
The optimization model minimizes the sum of the capital (CAPEX) and operational (OPEX) costs at the same time. Equation (1) presents the total annualized cost of the project in which Fa is the amortization factor, which applies an interest rate r during Np periods.
The CAPEX and OPEX are calculated according to Equations (3) and (4), respectively.
2.1.4. Constraints
The optimization model is restricted by continuity and momentum equations and by minimum head requirements in the demand nodes. Equations (5) and (6) guarantee that the total flow supplied by the PS will be equal to the flow demand.
Equation (7) was incorporated into this work. The new method determines a subset made up only of the pump models capable of delivering the minimum head and flow to reach the service levels required by the network. The search range of the decision variable associated with the pump model, i.e., bi, is then limited to the previously defined set.
All intermediate details about the hydraulic calculations of the objective function can be found in reference [7].
2.2. Infeasibility Maps
The decision variable xij determines the fraction of flow that PSi contributes during period j. This variable can have a range from 0 to 100 (expressed as a percentage) for which 0 indicates that the PS did not supply water in that period; in contrast, a value of 100 indicated that all the flow was supplied by a single PS in the period. Therefore, a huge number of possible combinations exist, and many of them are infeasible solutions.
The main causes of infeasibility are listed below:
- The distribution of flow generates sectors of the network where it is not possible to reach the minimum required pressures.
- Some of the PSs must provide a pressure greater than the maximum head of the largest pump that exists in the available catalog.
- The sum of the flows supplied is greater than the demand.
Each additional evaluation of the objective function supposes an increase in the computational effort made by the optimization algorithm. For this reason, this study proposed to analyze the network previously used to establish minimum and maximum limits for the variable xi,j. Thus, it was possible to avoid the evaluation of infeasible solutions, which could be ruled out using hydraulic criteria before starting the optimization process. Unfortunately, the non-linearity of the relationships between the hydraulic variables did not allow these values to be fixed, but this value could be expressed as a function of the piezometric head of a reference PS (PSref). This reference pumping station could be any of the pumping stations in the network. Furthermore, PSref supplied all the water that was not provided by the rest of the PSs.
Before executing the optimization algorithm, for each PSi different from PSref, it was possible to build a graph called the “Infeasibility Map” (IM), such as the one presented in Figure 1.
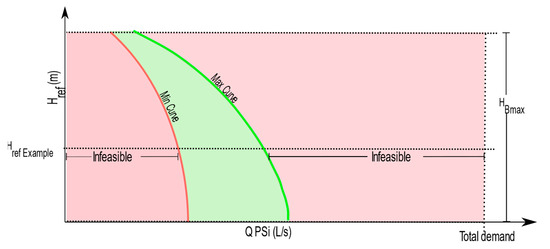
Figure 1.
Infeasibility map for PSi.
The horizontal axis represents the flow provided by PSi (QPSi). It could have values between zero and the total flow demanded by the network.
The vertical axis represents the head of PSref (Href). For any Href, all points to the left of the minima curve (red color) are infeasible. This infeasibility was due to the fact that it was not possible to reach the minimum height required in all the nodes of the network. Similarly, at any point to the right of the maximum curve (green color), the head required by PSi always exceeded the maximum head of the largest pump available in the catalog (HBmax), and therefore, it would also be infeasible.
The green area of the graph is the bounded search region (BSR), which represents a set of combinations for which it was not possible to previously check infeasibility. That is, the BSR contained both feasible and infeasible points. Therefore, the optimization algorithm was in charge of traversing this space. Consequently, it was possible to use an IM to rule out a large number of combinations by previously limiting the range of the variable xij.
Finding these curves for all possible combinations can generate a high computational cost. Specifically, the number of hydraulic simulations increases significantly as the number of pumping stations grows. However, it is possible to estimate the maximum and minimum curves via randomly sampling combinations of pumping station flows using the Monte Carlo method [22]. Using this method greatly simplifies the proposed method.
The curves are used by the optimization algorithm in each evaluation of the objective function. In this new method, the value of xij represents a fraction of the difference between the highest value of the maximum flow curve and the lowest value of the minimum flow curve. It is important to note that this range is always less than the total demand. Therefore, it represents a search space reduction for any network, regardless of the topology.
Figure 2 shows the use of the IM with two PSs. The red line represents the SC calculated for a PSi different from PSref [18]. From the solution, the intersection of the input flow xij and the respective SC could be obtained. If the resulting point was within the blue region, the solution could not be discarded. Otherwise, the solution was irrefutably infeasible. Outside this range, it would have been impossible to achieve a technically feasible solution.
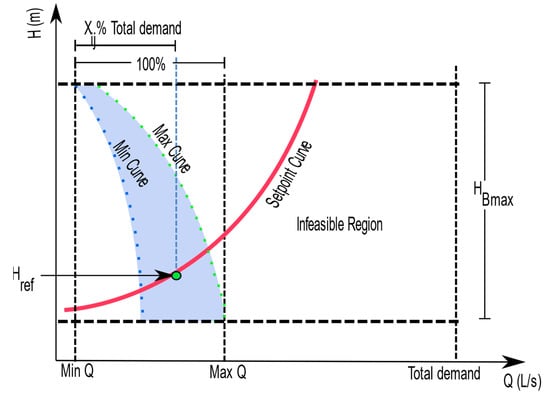
Figure 2.
Decoding a solution for a 2-PS problem.
The method presented in this work does not depend on the number of pumping stations. It could be applied to any problem with at least two PSs. For example, Figure 3 shows the decoding process in a network with three PSs: (1) PS1, (2) PS2, and (3) PS3.
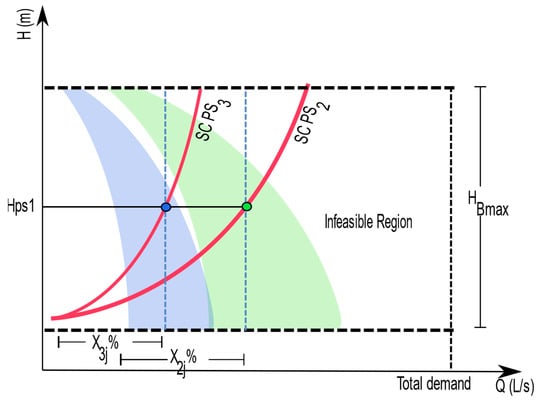
Figure 3.
Decoding a solution for a 3-PS problem.
Analogous to the case of Figure 2, it was necessary to select a PSref. PS1 was selected as the reference station after which the minimum and maximum curves for PS2 and PS3 were calculated. The limits defined by the curves allowed for generating the BSR for each PSi. In Figure 3, blue and green areas represent the BSRs for PS3 and PS2, respectively. Regarding the flow supplied by each PSi, x3j, and x2j represent the total percentage of flow supplied by PS3 and PS2, respectively. Consequently, PS1 must supply the remaining flow with the head Hps1. Note that each supply source had its own SC. Consequently, the SC was found for both pumping stations.
The use of IMs allows for reducing the number of hydraulic simulations carried out during the optimization process. The newly proposed method involves using IMs to rule out solutions during the evaluation of a solution when at least one period is infeasible. In this way, the hydraulic calculation stops, and the solution is penalized depending on the number of periods elapsed until finding the infeasibility.
The number of nodes and pipes in the network is the main cause of computational slowdown because the hydraulic motor calculates each node and each pipe in each iteration of the algorithm. This new procedure saves a large number of hydraulic simulations. This is important in the case of large networks because the computing time can be extremely high. Consequently, the application of the presented method is aimed at optimizing large networks. However, it could also be used in small networks without the need for changes.
2.3. Case Study
To apply the methodology described above, one case study was conducted. Figure 4a shows the topology of a WDN located in the city of Curicó (Chile). The network model was proposed by [23]. The network contained 7630 nodes and 8359 pipes. The network had 2 pumping stations working, PS1 and PS2. However, due to the growth of the city, the pumping equipment was old and susceptible to replacement. There is the possibility of putting a third water source into operation, located at PS3. The node with the lowest elevation was 190 m, and the elevation of the largest node was approximately 295 m. The minimum operating pressure was 15 m for all network nodes. Information about the nodes and pipelines can be found in the Supplementary Materials.
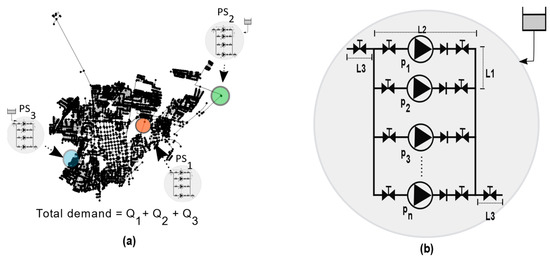
Figure 4.
Case study. (a) Curicó water distribution network; (b) modular design for PSi.
The total demand of the network was provided by the three pumping stations, where Q1 was the flow provided by PS1, Q2 was the flow provided by PS2, and Q3 was the flow provided by PS3. Figure 4b shows the modular design proposed by [7]. This scheme was used later to carry out the CAPEX calculations.
The hydraulic analysis was conducted for one day, and the time was divided into periods of one hour. A time pattern was used to characterize the time variation in demand, providing multipliers that were applied to the base demand to determine the actual demand in a given period. Figure 5 shows the 24 h use pattern.
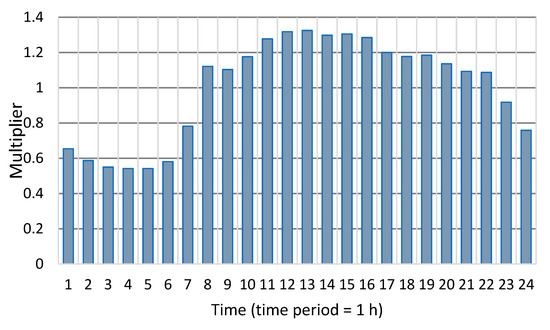
Figure 5.
Demand pattern for the Curicó network.
To calculate the OPEX, Table 1 shows the hourly electricity rate used for each PS in the network. On the other hand, all the necessary coefficients to estimate the CAPEX were obtained from [7].

Table 1.
Electricity for the case study (EUR/kWh).
To perform the optimization process, a database with 67 pump models was used. The maximum flow rate of the pumps in the database varied between 9 L/s and 50.7 L/s. The annualized costs of these models were calculated using an interest rate of 5% per year and a projection time of 20 years. This led to an amortization factor of Fa = 7.92%.
2.4. Optimization Method
The solution space of the case study was 10104. Consequently, the use of a computational method was required to solve the optimization model. Specifically, this work used a pseudo-genetic algorithm (PGA) developed by the authors of [20] to solve problems of an integer nature. Unlike a traditional genetic algorithm (GA), the PGA is based on an integer coding of the solution, and each decision variable can store different values represented by alphanumeric variables.
The objective of the work was to demonstrate that the use of IMs improves the performance of the optimization algorithm. For this comparison to be fair, the resolution of the proposed model was carried out using the same algorithm used by [7]. In this way, it was possible to directly compare the proposed methodologies and avoid unnecessary biases. In addition, the same parameters of population size (P), crossover frequency (Pc), and mutation frequency (Pm) recommended by the authors in previous works [24] were considered, specifically, population size (P = 100), crossover frequency (Pc = 90%), and mutation frequency (Pm = 5%).
The PGA was implemented using JMetalPy, which is an open-source Python library for solving single-objective and multi-objective optimization problems. It was inspired by the JMetal library, written in Java, and it implements evolutionary, local-search-based, and hybrid algorithms to solve various optimization problems [25]. Specifically, the Python 3.8 programming language was used. The objective function call was implemented according to the guidelines described in [12]. The hydraulic simulations were carried out using the programmer’s toolkit of EPANET [21]. This system can conduct massive simulations and is integrated with the hydraulic network solver. To ensure a minimum level of statistical confidence in the results, 100 experiments were performed and analyzed.
Finally, to carry out the experiments, a computer with an Intel(R) Xeon(R) Gold 5218 CPU @ 2.30 GHz, 2300 Mhz, 16 main processors, and 32 logical processors equipped with the Windows 10 Pro operating system was used. The average time per execution was 21 h.
3. Results
The results compared the performance of the PS design method with and without IMs. First, PS1 was selected as PSref and the IMs for the 24 periods were calculated for each PSi. For example, Figure 6 shows the resulting IM for PS2 in the period of greatest water demand (hour = 12). The orange zone represents the BSR and the remaining area represents hydraulically infeasible solutions that were not used by the PGA in the optimization process.
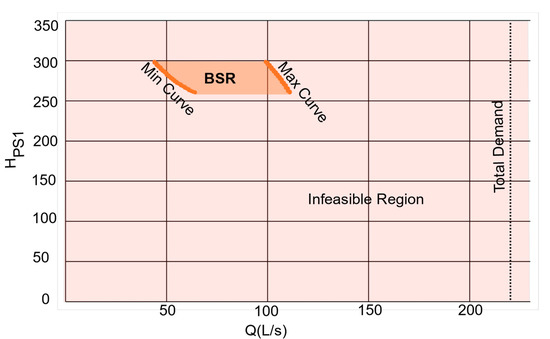
Figure 6.
Calculated IM of PS2.
Once the IMs were constructed, the algorithm searched only within the BSR. In this space, it was not possible to determine in advance whether the solutions were feasible/infeasible. This choice depended exclusively on the characteristics of the network and the hydraulic simulation to be executed. Both methods were compared. To increase the statistical reliability of the results, 100 experiments were performed. Each experiment ran 100,000 objective function evaluations, and the final values obtained for each method were compared. Note that the method presented in [7] performed one hydraulic simulation for each period analyzed. Consequently, each full day (24 h) led to 24 hydraulic simulations. However, the number of hydraulic simulations of the novel method presented in this work depended on the number of feasible periods of the analyzed solution. Figure 7 shows the results.
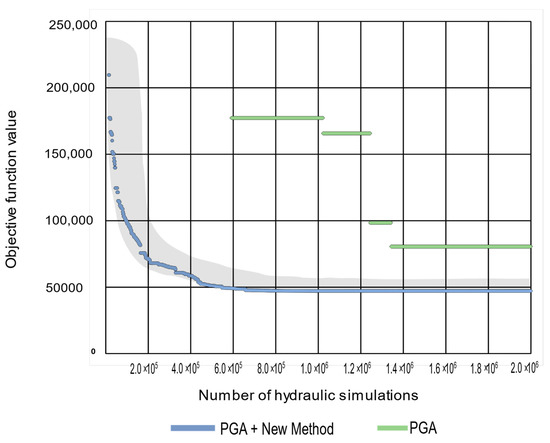
Figure 7.
Comparison of the results with and without IMs.
The blue dots represent the best solution obtained using the PGA with a search space limited by the IMs. The green dots show the best solution obtained using the PGA with the original method presented by [7], which utilized the complete search space. Additionally, the shaded area represents the complete distribution of all experiments simulated using IMs.
Note that the optimization algorithm converged to feasible solutions much faster when IMs were used, and the value of the objective function in all experiments when using IMs was less than the best solution using the complete search space. Consequently, the results demonstrate great improvement in the PGA performance when it was guided by IMs.
It is important to highlight that the construction of the IMs also requires computational effort prior to the optimization process. The number of hydraulic simulations of this pre-processing will depend mainly on the number of pumping stations in the network. Specifically, in the case study, 4.0 × 105 hydraulic simulations were needed. However, this preprocessing was only executed once for the entire experiment and represented a small percentage of the total simulations. For example, for the case study in which 100 experiments were executed, the generation of IMs represented approximately 2% of the total number of simulations (2.0 × 108) and decreased in an inversely proportional manner with the number of experiments executed.
Previously, the monetary difference in the solutions obtained by each method was highlighted. Next, we focused on the hydraulic difference between both solutions. Figure 8 and Figure 9 show the 24 h analysis of the pumping scheme of each PSi for the best solution obtained by the PGA with and without IMs, respectively.
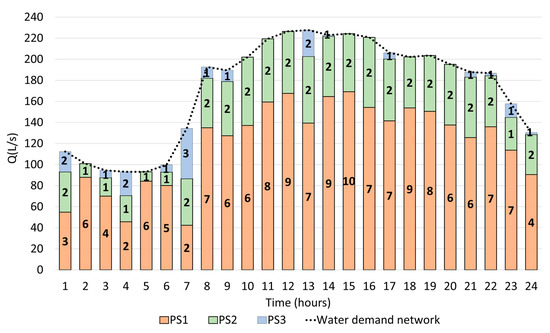
Figure 8.
Best solution without IMs.
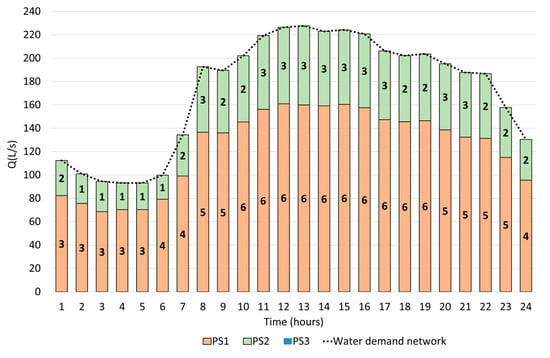
Figure 9.
Best solution using IMs.
In both figures, the bars represent the number of active pumps during each period, and the dotted lines represent the total flow required by the network according to the consumption pattern in Figure 5.
The best solution obtained using the PGA without IMs (Figure 7) would have required the operation of the third pumping station to meet the operating conditions of the network. Notably, PS1, PS2, and PS3 would have had to be at least ten, two, and two pumps, respectively. In contrast, when using the IMs, the PGA found many solutions in which only PS1 and PS2 were needed. Both solutions were hydraulically feasible, but the solution found using IMs was found to be more efficient, cheaper, and perfectly fit the network requirements. This feature is important for decision-making because if the search space is not correctly explored, unnecessary energy and building costs can be incurred. Table 2details the total yearly costs for the best solutions achieved by the PGA without and with IMs (Figure 8 and Figure 9, respectively).

Table 2.
Cost comparison between the best solutions with and without IMs.
The use of IMs led to a reduction in the cost of the solution by 71% relative to previous solutions found without using a reduced search space. When analyzing the objective function in detail, the main difference occurred in the CAPEX term. First, pumping stations are expensive structures. Consequently, it is not profitable to activate the operation of PS3 because it requires a high level of investment. Second, the optimized design without IMs required 10 pumps running on PS1. This feature implies a high cost of purchasing this equipment.
Consequently, the best solution would supply all water demands from stations PS1 and PS2, and it would not be necessary to activate a third pumping station. According to the scheme in Figure 4, Table 3 shows the design specifications for pumping stations 1 and 2.

Table 3.
Pump station designs for the case study.
ND1, ND2, and ND3 are the nominal diameters of the corresponding pipe p, which is used for defining the diameters of elements such as isolation valves or check valves according to the modular design presented in Figure 4b. Similarly, L1, L2, and L3 are the lengths of pipes. Furthermore, Table 3 shows the number of fixed-speed pumps (mi) and the number of variable-speed pumps (ni). H0, A, E, and F represent the characteristic and efficiency curve coefficients. Finally, the last row displays the selected model pump from the database. It is important to note that the final solution only considered variable-speed pumps and ruled out fixed-speed pumps. The higher cost of this equipment could be offset by the reduction in energy consumption during the years of the project’s life.
4. Conclusions
In the current context, improving the energy efficiency of pumping systems is a priority since these pumping systems represent a considerable percentage of the operating costs of any water supply company. Several approaches are described in the literature for optimizing the energy consumption of a PS. One possibility is approximating the operation mode of the pump(s) in the planning phase and optimizing the energy and cost in the WDN. This approach can help to make a better selection of pumping equipment. However, the computational cost is high, and the optimization algorithm loses search capacity as the network grows.
This work presents a new pumping station design method that considers the use of IMs for a better exploration of the search space. The method was applied to a real case study and was compared with the same design method without considering the use of IMs. The use of IMs eliminates infeasible areas in the optimization process and improves the performance of the algorithm, both in terms of convergence speed and in the quality of the solutions. It is possible to highlight several findings after comparing the optimization methods with and without IMs:
- −
- The exhaustive construction of the IMs required a significant number of hydraulic simulations. However, this procedure only needed to be done once, representing only 2% of the total number of simulations.
- −
- When IMs were not used, the search space was too large, and the algorithm took a long time to find feasible regions, which were usually local minima. The use of IMs allowed for accelerating the convergence of the optimization algorithms, rapidly evolving toward better solutions. Specifically, the number of simulations required by the IM-guided algorithm managed to reduce the number of hydraulic simulations necessary to achieve convergence in the case study by 60%.
- −
- The use of IMs in the case study achieved savings of 71% compared with the solutions obtained by the optimization algorithm when considering the complete search space. Additionally, the 100 experiments ran using IMs had better solutions than the best solution obtained using the PGA when no IMs were used. An inadequate exploration of the solution space implies unnecessary cost overruns and non-optimal solutions for a given problem.
Additionally, a new constraint was added to the model. In each evaluation of the objective function, the variable that determines the pump model in each PS only allows for selecting models from the catalog that have the maximum head required according to the flow distribution established by the solution. This mechanism allows the changes made by the PGA operators in these genes to always give rise to a new feasible solution.
The use of IMs guarantees that outside the bounded search region (BSR), there are no feasible solutions. However, it is not possible to determine the feasibility or infeasibility of solutions within this zone. In general terms, the search for global optima within the BSR continues to be a complex problem.
Finally, in small networks in which hydraulic simulation is not very computationally expensive, it could be possible to obtain solutions close to the global optimum by running a considerable number of evaluations of the objective function in a very short time. The construction of the IMs requires preprocessing of the network. Consequently, a limitation of the method could be a decrease in efficiency in small networks. Therefore, the use of IMs is only highly recommended when the analyzed network has a high number of nodes, pipes, and components.
Supplementary Materials
The following supporting information can be downloaded from https://www.mdpi.com/article/10.3390/math11071582/s1, Case Study S1.
Author Contributions
Conceptualization, J.H.G.-B., P.L.I.-R. and D.M.-M.; data curation, J.H.G.-B. and B.V.-M.; formal analysis, J.H.G.-B., D.M.-M., P.L.I.-R. and B.V.-M.; funding acquisition D.M.-M.; investigation, J.H.G.-B., D.M.-M., P.L.I.-R., B.V.-M. and F.S.-A.; methodology, J.H.G.-B., D.M.-M., P.L.I.-R. and B.V.-M.; project administration J.H.G.-B. and D.M.-M.; resources, J.H.G.-B., D.M.-M., P.L.I.-R., B.V.-M. and F.S.-A.; software, J.H.G.-B., D.M.-M. and B.V.-M.; supervision, D.M.-M. and P.L.I.-R.; validation, J.H.G.-B., D.M.-M., P.L.I.-R., B.V.-M. and F.S.-A.; visualization, J.H.G.-B., D.M.-M., P.L.I.-R., B.V.-M. and F.S.-A.; writing—original draft, J.H.G.-B. and D.M.-M.; writing—review and editing, J.H.G.-B., D.M.-M. and P.L.I.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Program Fondecyt Regular, grant number 1210410. It was also funded by the Ministry of Universities (Spain) and the Program European Union–Next Generation EU.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the Program Fondecyt Regular (project 1210410) of the Agencia Nacional de Investigación y Desarrollo (ANID), Chile. It was also supported by the Ministry of Universities (Spain) and the Program European Union–Next Generation EU and CONICYT PFCHA/DOCTORADO BECAS CHILE/2018—21182013.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? a literature review of system design. Water 2018, 10, 307. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? a literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef]
- Gupta, A.; Kulat, K.D. A selective literature review on leak management techniques for water distribution system. Water Resour. Manag. 2018, 32, 3247–3269. [Google Scholar] [CrossRef]
- Bordea, D.; Pro, O.; Filip, I.; Drăgan, F.; Va, C. Modelling, Simulation and Controlling of a Multi-Pump System with Water Storage Powered by a Fluctuating and Intermittent Power Source. Mathematics 2022, 10, 4019. [Google Scholar] [CrossRef]
- León-Celi, C.F.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Savic, D. Operation of multiple pumped-water sources with no storage. J. Water Resour. Plan Manag. 2018, 144, 04018050. [Google Scholar] [CrossRef]
- Blinco, L.J.; Simpson, A.R.; Lambert, M.F.; Marchi, A. Comparison of pumping regimes for water distribution systems to minimize cost and greenhouse gases. J. Water Resour. Plan Manag. 2016, 142, 04016010. [Google Scholar] [CrossRef]
- Gutiérrez-Bahamondes, J.H.; Mora-Meliá, D.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Salgueiro, Y. Pumping station design in water distribution networks considering the optimal flow distribution between sources and capital and operating costs. Water 2021, 13, 3098. [Google Scholar] [CrossRef]
- Martin-Candilejo, A.; Santillan, D.; Iglesias, A.; Garrote, L. Optimization of the design of water distribution systems for variable pumping flow rates. Water 2020, 12, 359. [Google Scholar] [CrossRef]
- Oshurbekov, S.; Kazakbaev, V.; Prakht, V.; Dmitrievskii, V. Improving reliability and energy efficiency of three parallel pumps by selecting trade-off operating points. Mathematics 2021, 9, 1297. [Google Scholar] [CrossRef]
- Nagkoulis, N.; Katsifarakis, K.L. Minimization of Total Pumping Cost from an Aquifer to a Water Tank, Via a Pipe Network. Water Resour. Manag. 2020, 34, 4147–4162. [Google Scholar] [CrossRef]
- Makaremi, Y.; Haghighi, A.; Ghafouri, H.R. Optimization of Pump Scheduling Program in Water Supply Systems Using a Self-Adaptive NSGA-II; a Review of Theory to Real Application. Water Resour. Manag. 2017, 31, 1283–1304. [Google Scholar] [CrossRef]
- Gutiérrez-Bahamondes, J.H.; Salgueiro, Y.; Silva-Rubio, S.A.; Alsina, M.A.; Mora-Meliá, D.; Fuertes-Miquel, V.S. jHawanet: An open-source project for the implementation and assessment of multi-objective evolutionary algorithms on water distribution networks. Water 2019, 11, 2018. [Google Scholar] [CrossRef]
- Fecarotta, O.; McNabola, A. Optimal location of pump as turbines (pats) in water distribution networks to recover energy and reduce leakage. Water Resour. Manag. 2017, 31, 5043–5059. [Google Scholar] [CrossRef]
- Carpitella, S.; Brentan, B.; Montalvo, I.; Izquierdo, J.; Certa, A. Multi-criteria analysis applied to multi-objective optimal pump scheduling in water systems. Water Sci. Technol. Water Supply 2019, 19, 2338–2346. [Google Scholar] [CrossRef]
- Weber, J.B.; Lorenz, U. Optimizing Booster Stations. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Berlin, Germany, 15–19 July 2017; pp. 1303–1310. [Google Scholar] [CrossRef]
- Predescu, A.; Truică, C.O.; Apostol, E.S.; Mocanu, M.; Lupu, C. An advanced learning-based multiple model control supervisor for pumping stations in a smart water distribution system. Mathematics 2020, 8, 887. [Google Scholar] [CrossRef]
- Gil, F.A.A.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Cortes, J.V.L.; Mora-Meliá, D. Methodology for Projects Of Pumping Stations Directly Connected To The Network Considering The Operation Strategy. In Proceedings of the 22nd International Congress on Project management and Engineering, Madrid, Spain, 11–13 July 2018; 2018; pp. 551–563. Available online: http://dspace.aeipro.com/xmlui/handle/123456789/1728 (accessed on 20 March 2023).
- León-Celi, C.F.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Mora-Melia, D. The Setpoint Curve as a Tool for the Energy and Cost Optimization of Pumping Systems in Water Networks. Water 2022, 14, 2426. [Google Scholar] [CrossRef]
- Briceño-León, C.X.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Creaco, E. Integrating Demand Variability and Technical, Environmental, and Economic Criteria in Design of Pumping Stations Serving Closed Distribution Networks. J. Water Resour. Plan Manag. 2023, 149, 4023002. [Google Scholar] [CrossRef]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martinez-Solano, F.J.; Fuertes-Miquel, V.S. Design of water distribution networks using a pseudo-genetic algorithm and sensitivity of genetic operators. Water Resour. Manag. 2013, 27, 4149–4162. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2.0 User’s Manual (EPA/600/R-00/057); National Risk Management Research Laboratory: Cincinnatti, OH, USA, 2000. [Google Scholar]
- Lučin, I.; Lučin, B.; Čarija, Z.; Sikirica, A. Data-driven leak localization in urban water distribution networks using big data for random forest classifier. Mathematics 2021, 9, 672. [Google Scholar] [CrossRef]
- Negrete, M. Modelación Computacional en EPANET de un Sector de la Red de Abastecimiento de Agua Potable de Curicó; Universidad de Talca, Facultad de Ingeniería: Curicó, Chile, 2021. [Google Scholar]
- Mora-Melia, D.; Iglesias-Rey, P.L.; Martínez-Solano, F.J.; Muñoz-Velasco, P. The efficiency of setting parameters in a modified shuffled frog leaping algorithm applied to optimizing water distribution networks. Water 2016, 8, 182. [Google Scholar] [CrossRef]
- Benítez-Hidalgo, A.; Nebro, A.J.; García-Nieto, J.; Oregi, I.; Del Ser, J. jMetalPy: A Python framework for multi-objective optimization with metaheuristics. Swarm Evol. Comput. 2019, 51, 100598. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).