Efficient Method for Derivatives of Nonlinear Stiffness Matrix
Abstract
1. Introduction
2. Analytical Formulation
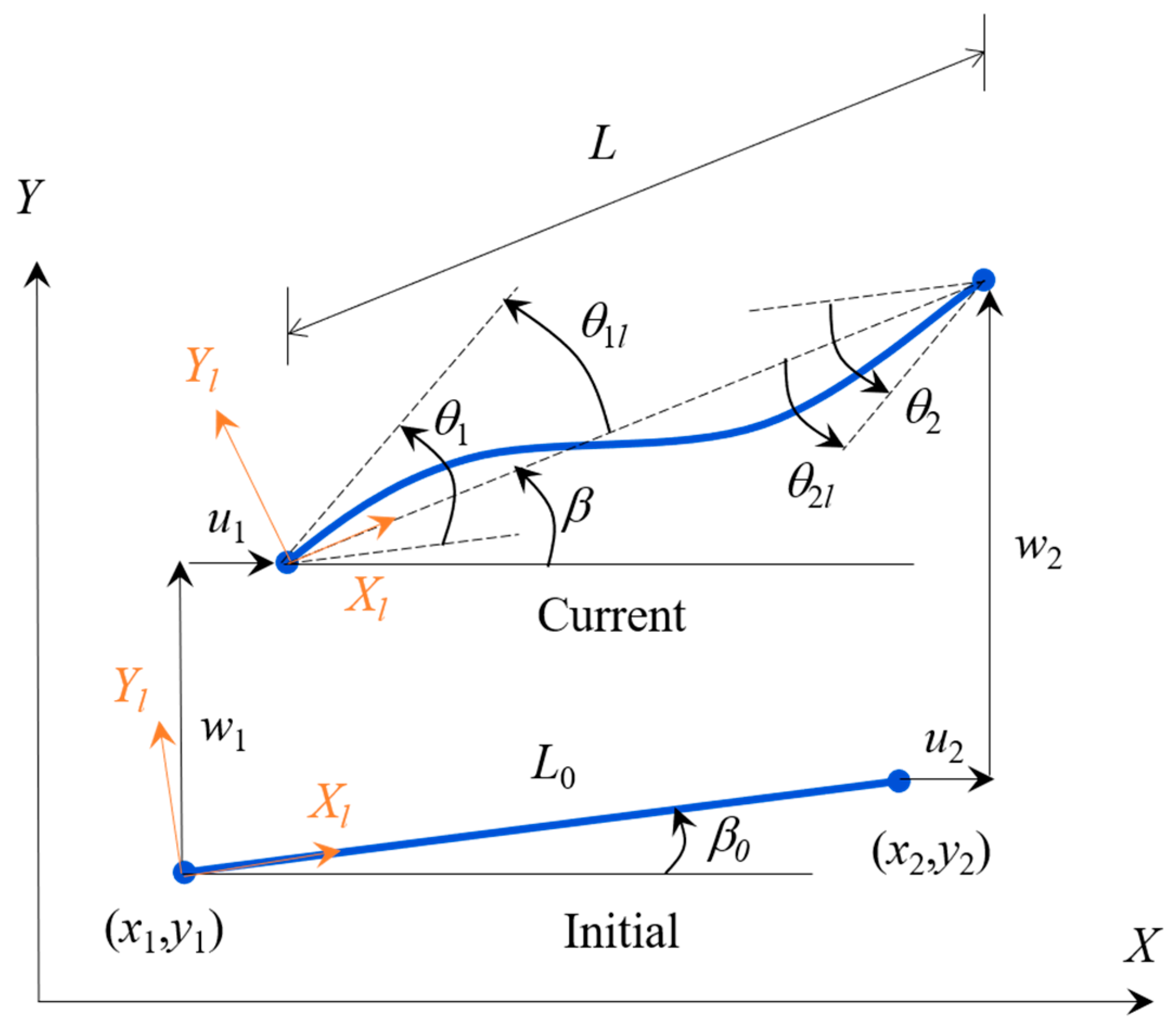
2.1. Nonlinear Stiffness Matrix
2.2. Reduced Stiffness
2.3. Analytical Derivative Formulation
3. Numerical Derivatives of Nonlinear Stiffness
3.1. Finite Difference Methods
| Algorithm 1 Algorithm to calculate the second-order derivative of nonlinear stiffness by forward difference method |
|
3.2. Complex Step Method
3.3. Hyper-Dual Step
4. Results
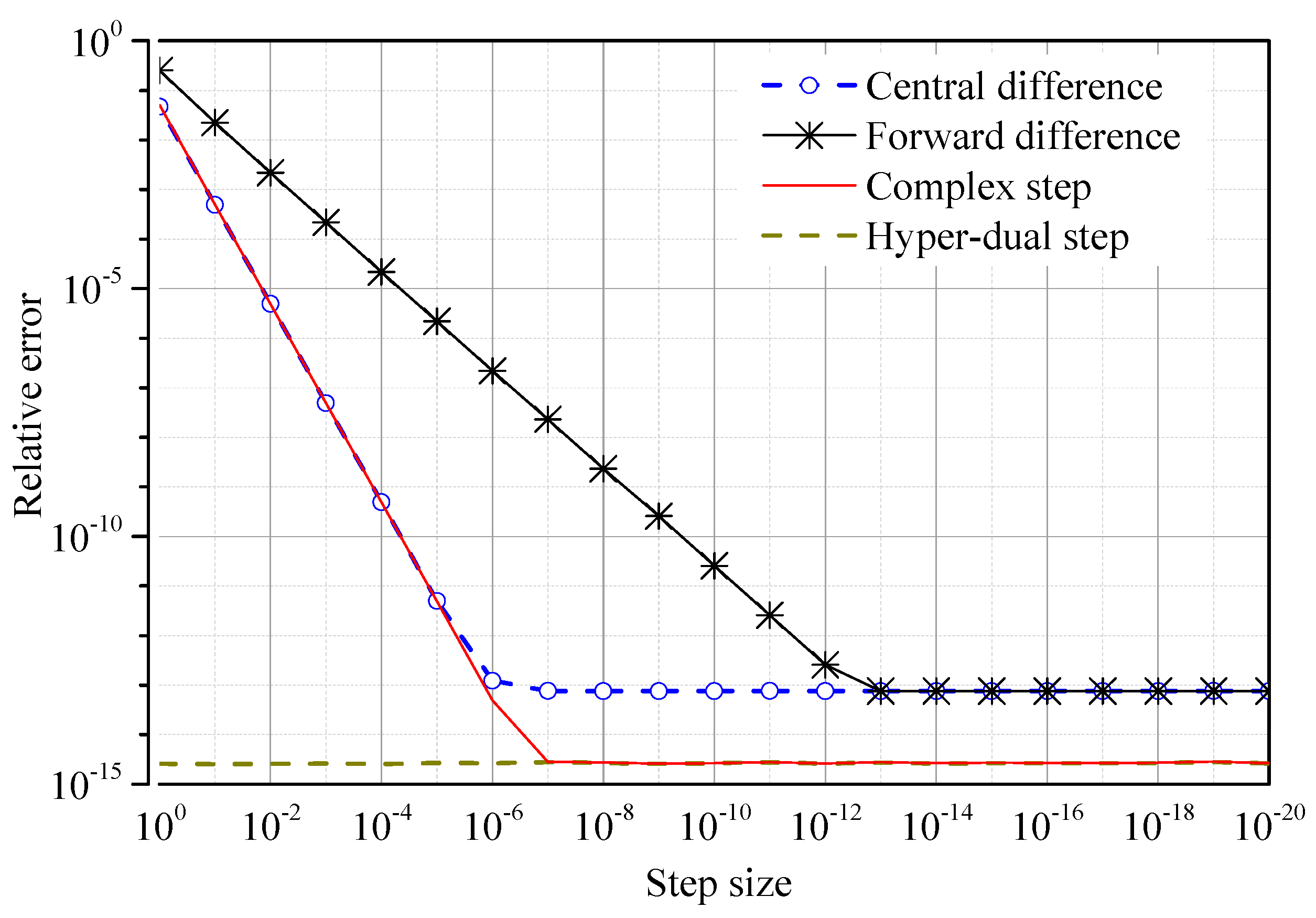
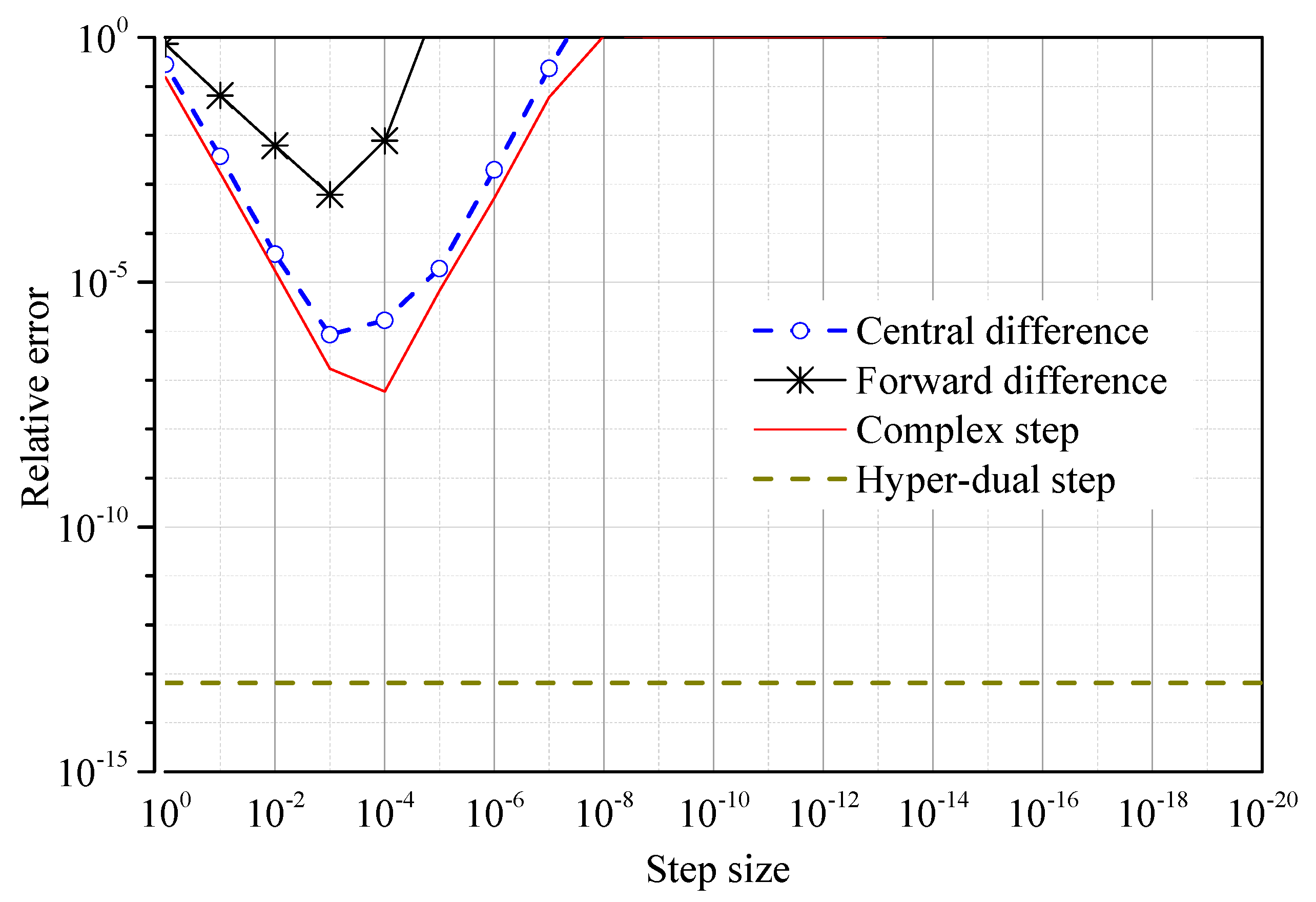
4.1. Accuracy of Derivatives of Nonlinear Stiffness
4.2. Accuracy of NLROM
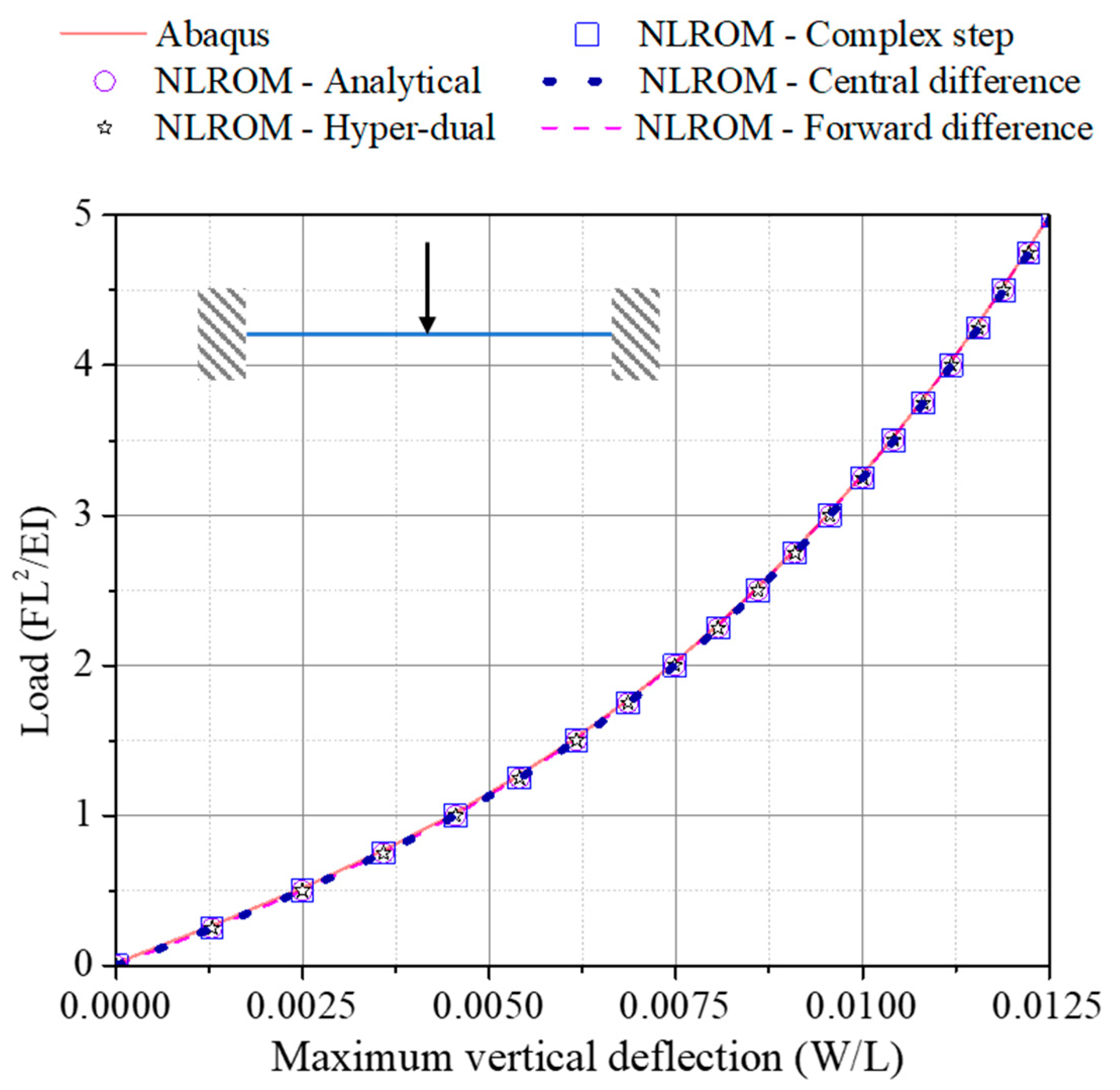
4.2.1. Clamped-Clamped Beam
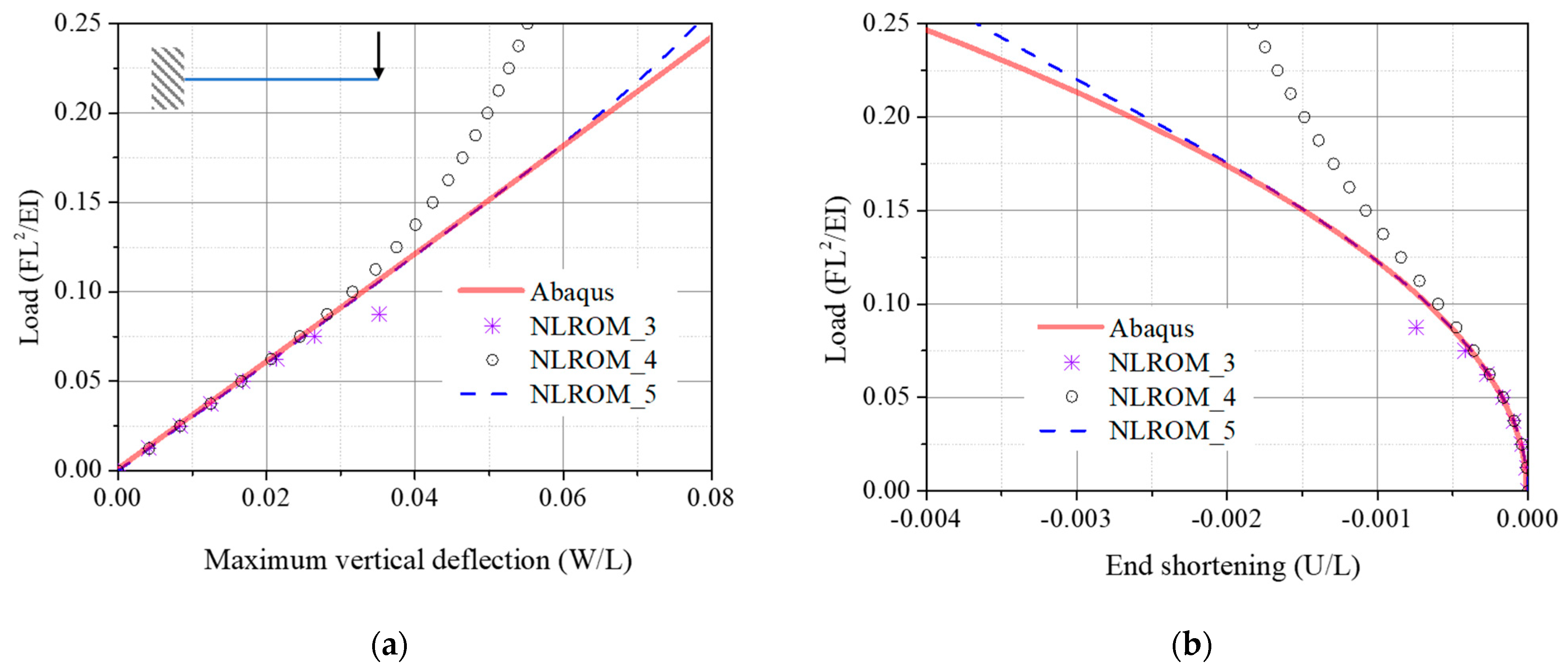
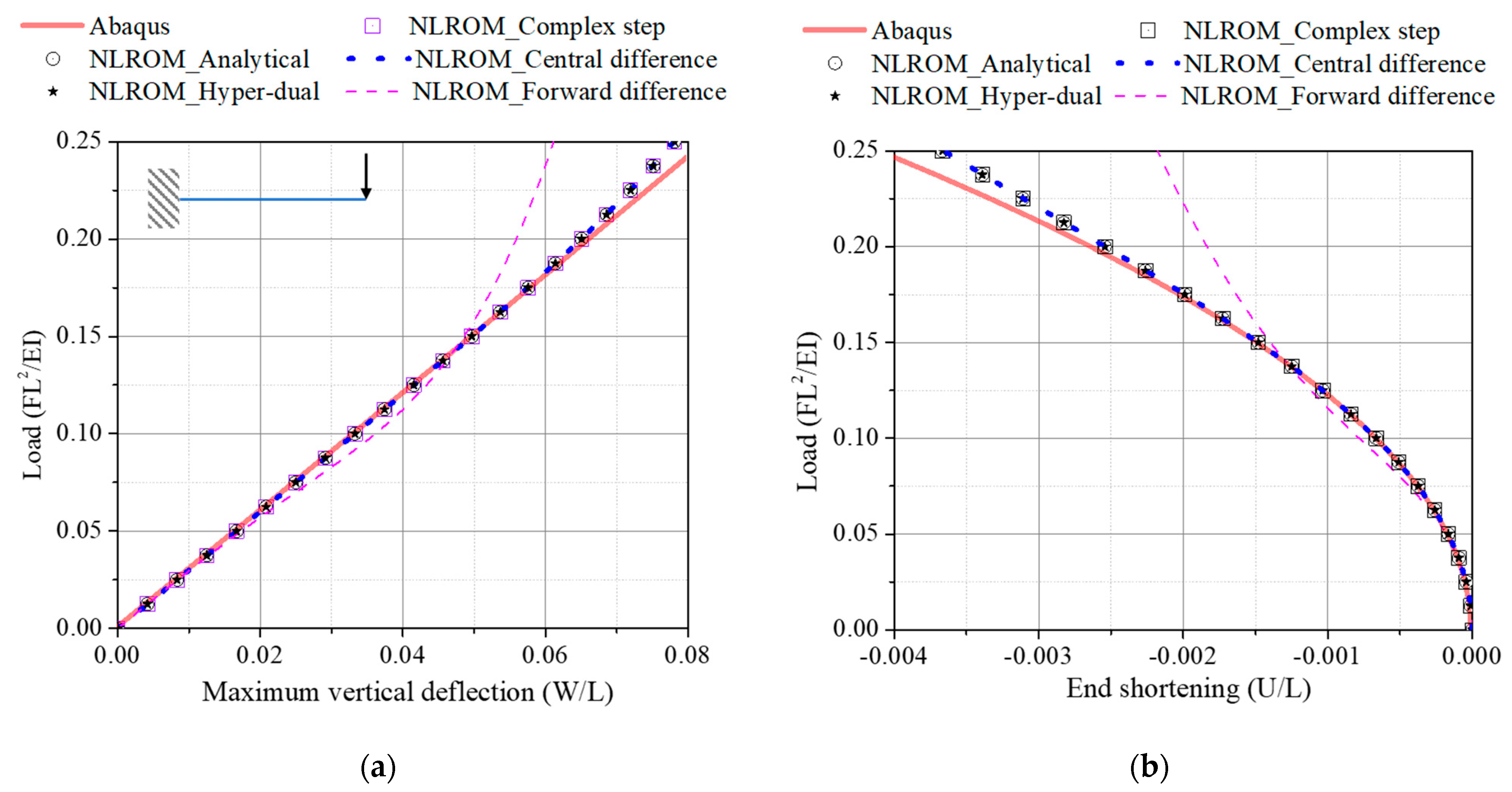
4.2.2. Cantilever Beam
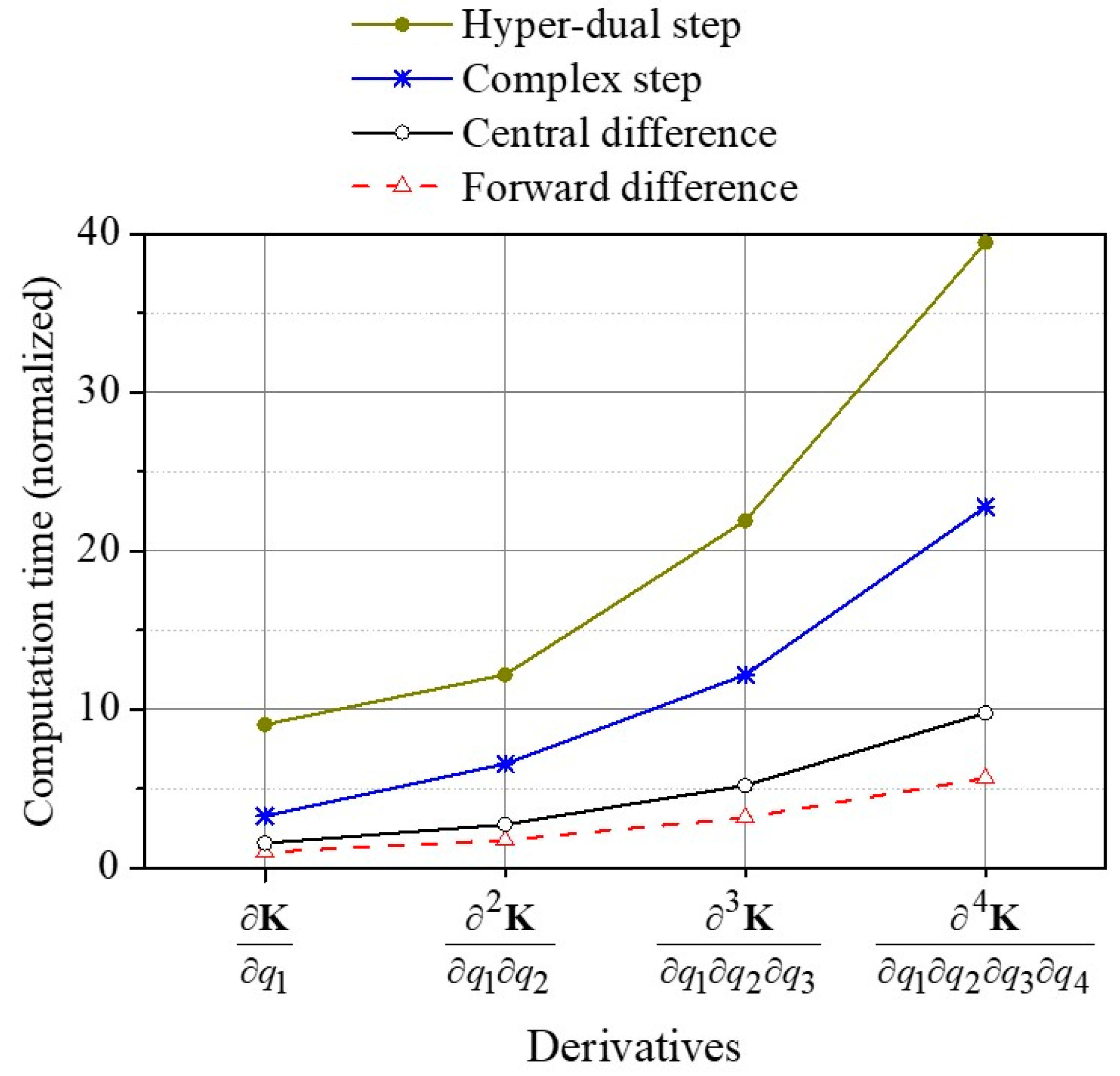
4.3. Computation Cost
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- Rutzmoser, J. Model Order Reduction for Nonlinear Structural Dynamics. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2018. [Google Scholar]
- Muravyov, A.A.; Rizzi, S.A. Determination of nonlinear stiffness with application to random vibration of geometrically nonlinear structures. Comput. Struct. 2003, 81, 1513–1523. [Google Scholar] [CrossRef]
- Perez, R.; Wang, X.Q.; Mignolet, M.P. Nonintrusive structural dynamic reduced order modeling for large deformations: Enhancements for complex structures. J. Comput. Nonlinear Dyn. 2014, 9, 031008. [Google Scholar] [CrossRef]
- Cai, M.; Li, C. Numerical approaches to fractional integrals and derivatives: A review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef]
- Treanţă, S. Recent advances of constrained variational problems involving second-order partial derivatives: A review. Mathematics 2022, 10, 2599. [Google Scholar] [CrossRef]
- Kirsch, U.; Bogomolni, M.; Keulen, F.V. Efficient finite difference design sensitivities. AIAA J. 2005, 43, 399–405. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Ma, Y. Residual stress constrained self-support topology optimization for metal additive manufacturing. Comput. Methods Appl. Mech. Eng. 2022, 389, 114380. [Google Scholar] [CrossRef]
- Lyness, J.N.; Moler, C.B. Numerical differentiation of analytic functions. SIAM J. Numer. Anal. 1967, 4, 202–210. [Google Scholar] [CrossRef]
- Lyness, J.N. Numerical algorithms based on the theory of complex variables. In Proceedings of the 22nd ACM National Conference, Washington, DC, USA, 1 January 1967. [Google Scholar] [CrossRef]
- Squire, W.; Trapp, G. Using complex variables to estimate derivatives of real functions. SIAM Rev. 1998, 10, 100–112. [Google Scholar] [CrossRef]
- Lai, K.L.; Crassidis, J.L. Extensions of the first and second complex-step derivative approximations. J. Comput. Appl. Math. 2008, 219, 276–293. [Google Scholar] [CrossRef]
- Abreu, R.; Stich, D.; Morales, J. On the generalization of the Complex Step Method. J. Comput. Appl. Math. 2013, 241, 84–102. [Google Scholar] [CrossRef]
- Pérez-Foguet, A.; Rodríguez-Ferran, A.; Huerta, A. Numerical differentiation for local and global tangent operators in computational plasticity. Comput. Meth. Appl. Mech. Eng. 2000, 189, 277–296. [Google Scholar] [CrossRef]
- Kim, S.; Ryu, J.; Cho, M. Numerically generated tangent stiffness matrices using the complex variable derivative method for nonlinear structural analysis. Comput. Meth. Appl. Mech. Eng. 2011, 200, 403–413. [Google Scholar] [CrossRef]
- Tanaka, M.; Fujikawa, M.; Balzani, D.; Schröder, J. Robust numerical calculation of tangent moduli at finite strains based on complex-step derivative approximation and its application to localization analysis. Comput. Meth. Appl. Mech. Eng. 2014, 269, 454–470. [Google Scholar] [CrossRef]
- Fike, J.A. Multi-Objective Optimization Using Hyper-Dual Numbers. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2013. [Google Scholar]
- Tanaka, M.; Sasagawa, T.; Omote, R.; Fujikawa, M.; Balzani, D.; Schröder, J. A highly accurate 1st- and 2nd-order differentiation scheme for hyperelastic material models based on hyper-dual numbers. Comput. Meth. Appl. Mech. Eng. 2015, 283, 22–45. [Google Scholar] [CrossRef]
- Kiran, R.; Khandelwal, K. Automatic implementation of finite strain anisotropic hyperelastic models using hyper-dual numbers. Comput. Mech. 2015, 55, 229–248. [Google Scholar] [CrossRef]
- Lantoine, G.; Russell, R.P.; Dargent, T. Using multicomplex variables for automatic computation of high-order derivatives. ACM Trans. Math. Softw. 2012, 38, 1–21. [Google Scholar] [CrossRef]
- Aristizabal, M.; Ramirez-Tamayo, D.; Garcia, M.; Aguirre-Mesa, A.; Montoya, A.; Millwater, H. Quaternion and octonion-based finite element analysis methods for computing multiple first order derivatives. J. Comput. Phys. 2019, 397, 108831. [Google Scholar] [CrossRef]
- Rutzmoser, J.B.; Rixen, D.J.; Tiso, P.; Jain, S. Generalization of quadratic manifolds for reduced order modeling of nonlinear structural dynamics. Comput. Struct. 2017, 192, 196–209. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2021, 103, 3335–3370. [Google Scholar] [CrossRef]
- Mahdiabadi, M.K.; Tiso, P.; Brandt, A.; Rixen, D.J. A non-intrusive model-order reduction of geometrically nonlinear structural dynamics using modal derivatives. Mech. Syst. Signal Process. 2021, 147, 107126. [Google Scholar] [CrossRef]
- Jeong, Y.M.; Kim, J.S. On the stable mode selection for efficient component mode synthesis of geometrically nonlinear beams. J. Mech. Sci. Technol. 2020, 34, 2961–2973. [Google Scholar] [CrossRef]
- Talebitooti, R.; Zarastvand, M.R. The effect of nature of porous material on diffuse field acoustic transmission of the sandwich aerospace composite doubly curved shell. Aerosp. Sci. Technol. 2018, 78, 157–170. [Google Scholar] [CrossRef]
- Seilsepour, H.; Zarastvand, M.; Talebitooti, R. Acoustic insulation characteristics of sandwich composite shell systems with double curvature: The effect of nature of viscoelastic core. J. Vib. Control 2023, 29, 1076–1090. [Google Scholar] [CrossRef]
- Yaw, L.L. 2D Corotational Beam Formulation; Walla Walla University: Washington, DC, USA, 2009. [Google Scholar]
- Sombroek, C.S.M.; Tiso, P.; Renson, L.; Kerschen, G. Numerical computation of nonlinear normal modes in a modal derivative subspace. Comput. Struct. 2018, 195, 34–46. [Google Scholar] [CrossRef]
- Kim, K.; Radu, A.G.; Wang, X.Q.; Mignolet, M.P. Nonlinear reduced order modeling of isotropic and functionally graded plates. Int. J. Non-Linear Mech. 2013, 49, 100–110. [Google Scholar] [CrossRef]
- Rizzi, S.A.; Przekop, A. System identification-guided basis selection for reduced-order nonlinear response analysis. J. Sound Vib. 2008, 315, 467–485. [Google Scholar] [CrossRef]
- Olver, P.J. Finite Differences. In Introduction to Partial Differential Equations, 2nd ed.; Sheldon, A., Kenneth, R., Eds.; Springer: Cham, Switzerland, 2020; pp. 181–214. [Google Scholar] [CrossRef]
- Wang, X.Q.; Khanna, V.; Kim, K.; Mignolet, M.P. Nonlinear Reduced-Order Modeling of Flat Cantilevered Structures: Identification Challenges and Remedies. J. Aerosp. Eng. 2021, 34, 04021085. [Google Scholar] [CrossRef]





| Parameter | Selection |
|---|---|
| Internal force | K(1)q + K(2)qq + K(3)qqq |
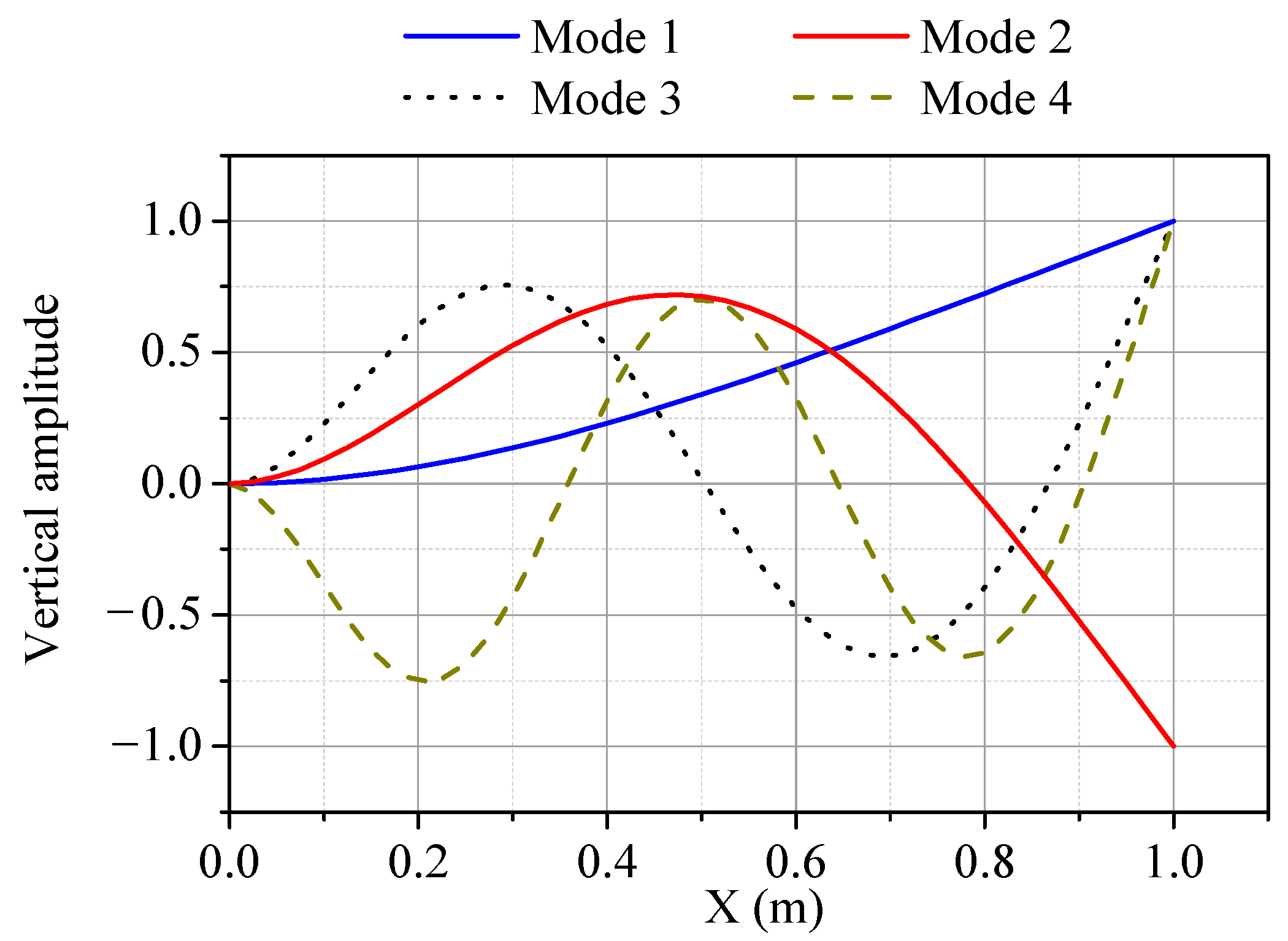
| Reduction base | 4 VMs + 10 MDs |
| Derivative method | Optional |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, T.A.; Kim, J.-S.; Park, J. Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics 2023, 11, 1572. https://doi.org/10.3390/math11071572
Bui TA, Kim J-S, Park J. Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics. 2023; 11(7):1572. https://doi.org/10.3390/math11071572
Chicago/Turabian StyleBui, Tuan Anh, Jun-Sik Kim, and Junyoung Park. 2023. "Efficient Method for Derivatives of Nonlinear Stiffness Matrix" Mathematics 11, no. 7: 1572. https://doi.org/10.3390/math11071572
APA StyleBui, T. A., Kim, J.-S., & Park, J. (2023). Efficient Method for Derivatives of Nonlinear Stiffness Matrix. Mathematics, 11(7), 1572. https://doi.org/10.3390/math11071572







