1. Introduction
A space-time panel dataset is one sample collected from a number of spatial units over time periods (Li et al. [
1]). Such datasets widely exist in economics, management, geography, environmental science and other research fields. How to effectively analyze space-time panel datasets and construct space-time panel data regression models has great theoretical and empirical significance. The space-time panel data regression models are a natural extension of panel data regression models. In the early 19th century, “regression” was first mentioned in the works of Legendre and Gauss. Later, at the turn of the 19th and 20th centuries, Galton and Pearson conceptualized regression, there were a number of regression models for analyzing panel data and exploring the association between dependent variable and regressors (Hsiao [
2]; Baltagi [
3]; Porter et al. [
4]; Zamanzade [
5]; Imai and Kim [
6]). Among them, parametric panel data regression models have been widely used to study linear influence of regressors. Since the 1990s, nonparametric methods have been gradually applied into regression analysis (Fan and Gijbels [
7]; Luo et al. [
8]; Ullah et al. [
9]; Dai et al. [
10]), Li and Stengos [
11] first proposed nonparametric panel data regression models to explore nonlinear influence of regressors. However, such models have their drawbacks. Parametric panel data regression models need to be precisely pre-specified, misspecified model forms can lead to inconsistent estimates as well as incorrect policy prescriptions. Although nonparametric panel data regression models are useful whenever we are not certain what the correct functional forms are, they may face the “curse of dimensionality” when the dimension of regressors is higher (Fan and Gijbels [
7]), namely, the estimation accuracy decreases rapidly with the number of regressors increasing. Therefore, scholars proposed a number of non/semiparametric panel data regression models with a dimension reduction function to more flexibly overcome the “curse of dimensionality” encountered in practice, for example, partially linear additive panel data regression model, partially linear single-index panel data regression model and partially linear varying coefficient panel data regression model. In recent years, a series of their estimation methods have been also developed, including profile least squares estimation (Baltagi et al. [
12]; Chen et al. [
13]; Huang et al. [
14]; Yong et al. [
15]; Zhou et al. [
16]; Zhang and Shen [
17]), profile quasi-maximum likelihood estimation (Li et al. [
18]; Su and Ullah [
19]; Wu et al. [
20]; Hu [
21]), generalized method of moment estimation (GMM) (Tran and Tsionas [
22]; Su and Ullah [
23]), and others (Liu and Zhuang [
24]).
All those modeling techniques and corresponding statistical inference methods for the above-mentioned semiparametric panel data regression models need the assumption that there is no correlation among the individuals or time periods. Elhorst [
25] pointed out that two problems hampering the modeling of space-time panel data are serial correlation between the observations on each spatial unit over time and spatial correlation between the observations on the spatial units at each point in time. Furthermore, Baltagi et al. [
12] mentioned that ignoring the serial correlation in the errors will result in consistent, but inefficient estimates of the regression coefficients and biased standard errors. Therefore, some scholars added nonseparable space-time filters, that is, space-time error correlation are modeled jointly, or separable space-time filters, that is, space-time error correlation are modeled independently from one another, under the framework of semi/parametric panel data regression models. The estimation, testing and empirical analysis of these models have been studied in recent years. Baltagi et al. [
26] derived joint and conditional Lagrange Multiplier (LM) and Likelihood Ratio (LR) test statistics of random effects parametric panel regression model with separable space-time correlations and presented their small sample performance using Monte Carlo experiments. Elhorst [
25] constructed a random effects parametric panel regression model with nonseparable space-time filters and presented its maximum likelihood estimation. Parent and LeSage [
27] explored the Markov Chain Monte Carlo method of random effects parametric panel regression model with separable space-time filters—both Monte Carlo simulation and an application were used to illustrate the method. Lee and Yu [
28] investigated quasi-maximum likelihood estimation for fixed effects parametric panel regression model with separable or nonseparable space-time filters, which might be spatially stable or unstable. They also derived consistency and asymptotic normality of the estimators under some regular conditions. Bai et al. [
29] proposed a random effects partially linear varying coefficient panel model with separable space-time filters and derived consistency and asymptotic normality of weighted semiparametric least squares estimators. Zhao et al. [
30] constructed weighted semiparametric least squares estimators and generalized F-type test statistic for random effects partially linear single-index panel model with separable space-time filters. They also derived the asymptotic properties of estimators and the asymptotic distribution of F-type test statistic. Li et al. [
1] studied profile quasi-maximum likelihood estimation and generalized F-type test of random effects partially linear nonparametric panel model with separable space-time filters and obtained the consistency and asymptotic normality of parametric and nonparametric estimators as well as asymptotic distribution of generalized F-type test statistic. Monte Carlo simulation and Indonesian rice farming data were used to illustrate their methods.
To the best of our knowledge, there are no non/semiparametric spatiotemporal econometric models that study both fixed effects and nonseparable space-time filters in the existing literature. In this paper, we attempt to propose a fixed effects partially linear varying coefficient panel data regression model (PLVCPDRM) with nonseparable spacetime filters. It can simultaneously capture the linear and nonlinear effects of regressors, spatial and serial correlations of error structure, and individual fixed effects. Our aim is to construct profile quasi-maximum likelihood estimators (PQMLE) of this model and systematically study their asymptotic properties and finite sample performance. Furthermore, the proposed estimation method is illustrated by using a real dataset.
The rest of this paper is organized as follows:
Section 2 presents a fixed effects PLVCPDRM with nonseparable space-time filters and its PQMLEs.
Section 3 lays out some regular assumptions and asymptotic properties.
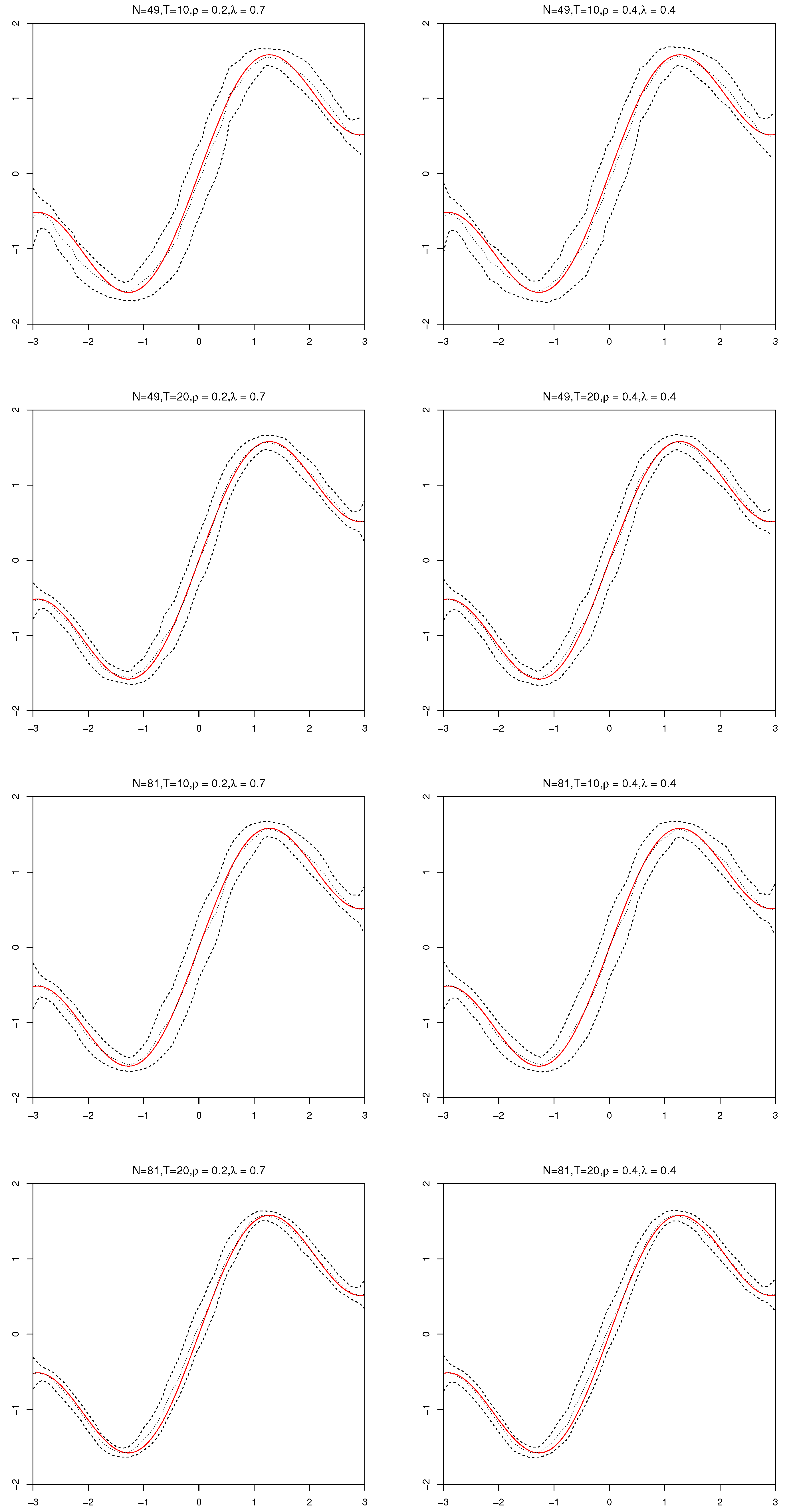
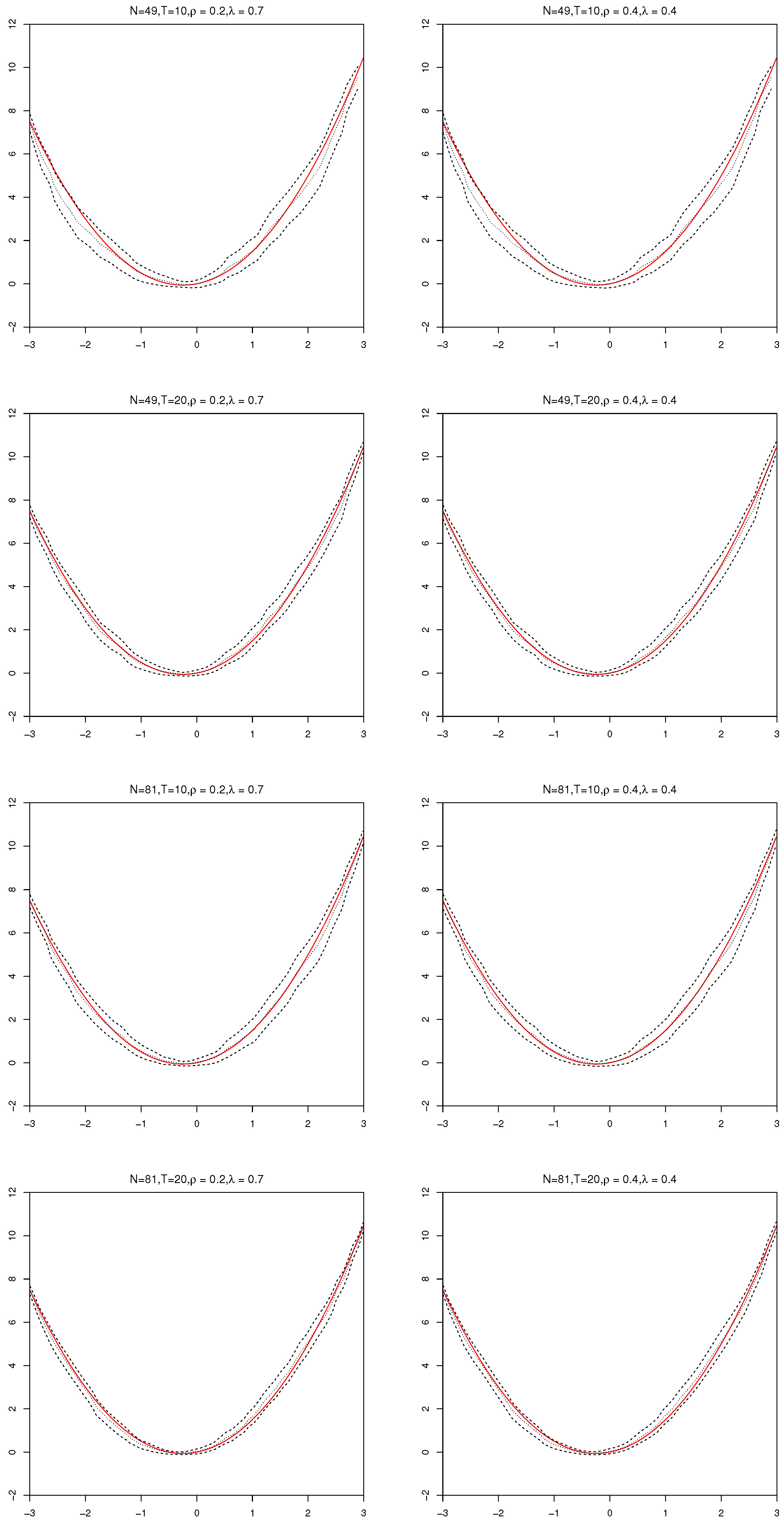
Section 4 reports simulation results for examining the finite sample performance of the proposed estimators.
Section 5 shows the empirical study for illustrating the proposed methodology. Conclusions are summarized in
Section 6.
Appendix A presents a lemma and proofs of the main theorems.
2. Model and Estimation
Consider a fixed effects PLVCPDRM with nonseparable space-time filters:
where
,
are observations of a response variable,
;
,
,
and
are observations of
p-dimensional and
q-dimensional exogenous regressors, respectively;
is a regression coefficient vector of
,
is an unknown univariate varying coefficient function vector,
are smoothing functions of
u,
u is an intermediate univariate variable;
are fixed effects satisfying
for identification purpose;
W is an
row-normalized non-negative spatial weights matrix with zero diagonals;
is an
vector of disturbance term,
is an
vector of random error term which is assumed to be
. In order to keep the stationarity of the model (1)–(2), serial correlation coefficient
and spatial correlation coefficient
should belong to parameter space
(Elhorst [
25]; Lee and Yu [
28]), see
Figure 1.
For the model (1)–(2), it is necessary to identify an appropriate estimation method to obtain estimators of the unknown parameter vector and varying coefficient functions .
Before proceeding to the estimation procedure, the fitting problem of the varying coefficient functions needs to be solved priority. Polynomial spline method is efficient in function approximation and numerical computation. Polynomial splines are piecewise polynomials with the polynomial pieces joining together smoothly at a set of interior knot points (see De Boor [
31]; Huang and Shen [
32]; Zou and Zhu [
33]). B-spline is a special form of polynomial spline. Considering that the B-spline basis has better numerical properties than other basis functions, we use the B-spline method to approximate the varying coefficient functions
in the model (
1). To be precise, let
,
and
be a partition of interval
. Using the
as knots, we have
normalized B-spline basis function of order
that forms a basis function for the linear spline space
on
. Denote B-spline basis function
, we can approximate
by some spline function in
:
, where
is an unknown
spline coefficient vector. Thus, the model (
1) can be written as
where
,
,
and
is a
matrix,
.
For any
vector
, denote
as the first order difference. By first difference of the model (2)–(3) to eliminate the fixed effects, we have
Note that
is observable for
,
can’t be observed. Let
,
,
,
,
and
is an
identity matrix. The Equation (5) can be rewritten as
for all
t. With backward substitution, we have
, where
. By denoting
and
the matrix form of the Equation (5) can be simply expressed as
,
. As
, where
and
, we can obtain
with
Note that the only unknown element of
is
. In order to obtain determinant and inverse of
, we define a confirmable block matrix (Hsiao et al [
34]; Lee and Yu [
28]) as
From straight calculation, we know that
Thus, the determinant
and the inverse
. Therefore, the quasi-log-likelihood function can be written as
where
,
,
,
,
with
as the first order difference transformation matrix of dimension
.
Motivated by Su and Jin [
35], we obtain PQMLEs of parameter vector
and varying coefficient functions
by the following the two-step estimation procedure:
Step 1: Assuming the parameter
is known, the initial estimators of
can be obtained by maximizing quasi-log-likelihood function (
6):
Step 2: With the estimated
,
and
, PQMLE of
can be obtained by maximizing the concentrated quasi-log-likelihood function of
:
The final estimator of
is given by
. With the estimated
, update
and
, we can obtain the final PQMLEs as
where
I is an identity matrix of dimension
,
. Then, the estimator of the nonparametric function
can be written as
3. Asymptotic Properties
To derive the asymptotic properties of the estimators, we first introduce some regular assumptions. For clear exposition, denote , and as the true parameter vector of , and , respectively, and as the true varying coefficient function vector of .
Assumption 1. (i) The sequences ,
and are nonstochastic, and they have bounded support set on ,
and
respectively. In addition,
forms a sequence of designs such that they are analogous to a positive and bounded “design density“ (Su and Jin [35]). (ii) For any bounded continuous function ,
it holds that (iii) The parameter in a neighborhood of satisfies , where is a positive constant.
Assumption 2. The disturbances are with zero mean, variance and for some .
Assumption 3. (i) For every K, the smallest eigenvalue of and are bounded away from zero uniformly in K.
(ii) There is a sequence of constants satisfying such that as .
(iii) For any -th continuously differentiable bounded function satisfying the normalization of , there exist some such that as and as .
Assumption 4. (i) W is a row-normalized and prespecified spatial weights matrix.
(ii) Row and column sums of W in absolute value are uniformly bounded (i.e., UB).
(iii) is invertible for all , where is compact and the true parameter is in the interior of . Additionally, is UB for .
Assumption 5. (i) is UB, where and .
(ii) is UB.
(iii) The limit of the information matrix (A4) in Appendix A is nonsingular. (iv) is nonsingular.
Assumption 6. for , where is defined in (A1). Remark 1. The fixed bounded design in Assumption 1 is typically assumed in spatial econometric literature, see Kelejian and Prucha [36], Kelejian and Prucha [37], Su and Jin [35] and Cheng and Chen [38]. Assumption 1 (ii) parallels Assumption 1 of Su and Jin [35] and Assumption 2.1 (iv) of Hu et al. [39]. It means that if are with the density , the Equation (9) holds with probability 1. Assumption 2 presents regularity assumptions for error terms . Assumption 3 is a set of mild conditions on the B-spline method (see Newey [40]; Hu et al. [39]; Yong et al. [15]; Zhang [41]). Assumption 3(i) ensures that and are asymptotically nonsingular, which parallels Assumption 3 of Zhang [41] and Assumption 2(i) of Newey [40]. Newey [40] gave some primitive conditions for power series and splines such that Assumption 3(ii)–(iii) hold. In addition, Assumption 3(iii) is the counterpart assumption in the kernel method. Assumption 4 provides the basic features of the spatial weight matrix. The uniform boundedness of W and limits the spatial correlation to a manageable degree in Assumptions 4(ii)–(iii). Assumption 5(i) is the absolute summability condition and row/column sum boundedness condition for disturbances, which will play an important role for the proofs of asymptotic properties. To prove the absolute summability of , a sufficient condition is for any matrix norm (see Corollary 5.6.16 in Horn and Johnson [42]) that satisfies . When , exists and can be defined as . Under the condition that the inverse of the variance matrix of is UB for and , Assumption 5(ii) can be certified. Assumption 5(iii)–(iv) is used for establishing the uniqueness identification and asymptotic normality of the proposed estimators. Assumption 6 specifies an identification condition for the estimators of parameters when Assumption 5(iv) is not satisfied. In order to prove consistency of the parametric estimators, we need to obtain the expected value function for the quasi-log-likelihood function (
6) divided by the effective sample size
. The relationship
between
and
(the first block of
N in
e are not exactly the original
and all the entries are i.i.d. under normality) would be used frequently, where
and
. Thus,
and
under the normality of disturbances. Split
into four block matrices, one of which is
. Utilizing the formula
for inversion of a block matrix, we have that
Define
, then
However, when
are not normally distributed, elements in
are uncorrelated but not necessarily independent of each other even though they are independent with
(
). Consider the case that the process starts at a finite past period, such as
. Denote
, which includes the original
disturbances vectors, we have
, where
is UB. Under non-normality, we can obtain
To show the consistency of
, we follow Lee [
43] by identifying
based upon the maximum value of
and showing the uniform convergence of
to zero, consistency of
follows.
Theorem 1. Suppose Assumptions 1–6 hold, is globally identifiable and is consistent with .
Theorem 2. Suppose Assumptions 1–6 hold, as simultaneously, we havewhere “” means convergence in distribution, is an expected Hessian matrix showed in (A5) and with defined in (A6). Theorem 3. Suppose Assumptions 1–5 hold, we have Remark 2. The term essentially corresponds to a variance term and to a bias term. When K is chosen as so that these two terms go to zero at the same rate, which occurs when K goes to infinity at the same rate as (and the side condition is satisfied), the convergence rate will be .
Theorem 4. Suppose Assumptions 1–5 hold, as simultaneously, we havewhere , , is an identity matrix of dimension K. 5. Real Data Analysis
In this section, we employ the proposed model and its estimation method to study the driving forces of Chinese resident consumption rate. This dataset was collected on 1 August 2022) from the
China Statistical Yearbook (
http://www.stats.gov.cn/sj/ndsj/) for 2008 to 2020 and covers 30 provincial administrative regions (except Tibet, Taiwan, Hong Kong and Macau). Based on the research results drawn by Ding and Chen [
45] and Ding [
46], let
be response variable and
,
,
,
and
be regressors. There is no doubt that per capita disposable income has an important impact on the resident consumption rate. Therefore, we assume that the impacts of the above regressors on resident consumption rate may be realized through per capita disposable income and
is selected as their intermediate variable. The definitions of these variables and their meanings are given in
Table 5.
Firstly,
Table 6 and
Figure 4 show the descriptive statistics of the response variable, five regressors and intermediate variable. From observing
Table 6, we can draw the conclusion that
,
,
,
,
and
are steady, as well as concluding that
has a small fluctuation range. In addition,
Figure 4 presents the scatter plots between
versus each regressor (
,
,
,
and
). It can be found that the regressor
has a linear effect on the response variable
. The rest of the regressors have nonlinear effects on the response variable
.
Based on the above comprehensive analysis, the study on driving forces of Chinese resident consumption rate can be analyzed by establishing the following PLVCPDRM with nonseparable space-time filters:
where
is a normalized spatial weight matrix calculated by the Euclidean distance in the light of the longitude and latitude coordinates of any two provinces.
Table 7 reports the estimation results of parameters in the model (
16). It can be seen that
and
are significant. Namely, it indicates that there exist strong and positive spatial and serial correlations among the disturbance terms in the model (
16). Furthermore,
is significant, which means that the linear effect of
on the resident consumption rate is negative.
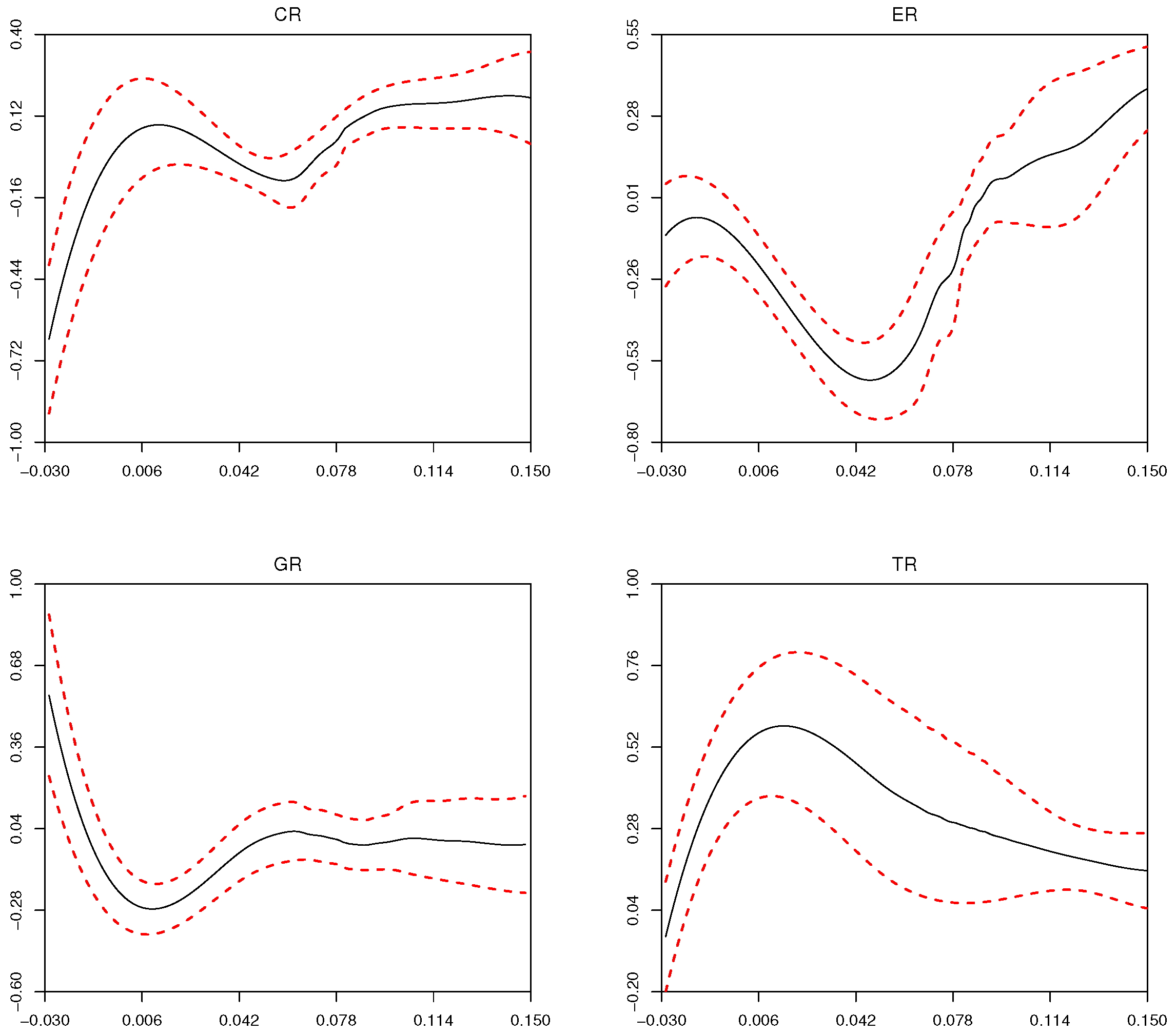
Figure 5 shows the varying coefficient effects of
,
,
and
to
and their
confidence intervals. It can be seen that
,
,
and
have obvious nonlinear effects on resident consumption rate with
.
6. Concluding Remarks
In order to sufficiently use the information of spatial and serial correlations in the disturbances when modeling space-time data by regression models, we propose a fixed effects PLVCPDRM with nonseparable space-time filters. It can not only simultaneously capture non/linear effects of regressors and space-time correlations of error structure, but also overcome the “curse of dimensionality” in multivariate nonparametric regression models.
In this paper, the PQMLEs of unknown parameters and varying coefficient functions for this model are constructed. Under the regular assumptions, we prove that the estimators satisfy consistency and asymptotic normality. Monte Carlo simulations show that the proposed estimators have good finite sample performances. In addition, ignoring spatial and serial correlations in errors of the model would result in inconsistent and inefficient estimators. Finally, a Chinese resident consumption rate dataset is used to illustrate our estimation method.
This paper mainly focuses on the estimation of a fixed effects PLVCPDRM with nonseparable space-time filters. In the future, we may study the methods of variable selection, Bayesian estimation and quantile regression for the proposed model in our paper; we can also use the proposed method to study similar semiparametric panel data regression models with space-time filters.