Mathematical Circuit Root Simplification Using an Ensemble Heuristic–Metaheuristic Algorithm
Abstract
:1. Introduction
- Introducing a combined mathematical modeling and optimization technique for the extraction and simplification of symbolic poles and zeros in OTAs.
- Proposing an enhanced root splitting technique, named ERS, to accurately extract the exact pole/zero expressions.
- Applying a combined heuristic–metaheuristic optimization algorithm to solve the proposed symbolic root simplification problem, utilizing the heuristic knowledge available in the circuit model and SA.
- Programming the proposed method in a MATLAB m-file, wherein simplified root equations are automatically generated from the circuit netlist.
- Successfully driving symbolic pole/zero expressions for three OTAs.
2. Literature Review
2.1. Symbolic Simplification Techniques
2.2. Symbolic Pole/Zero Extraction Techniques
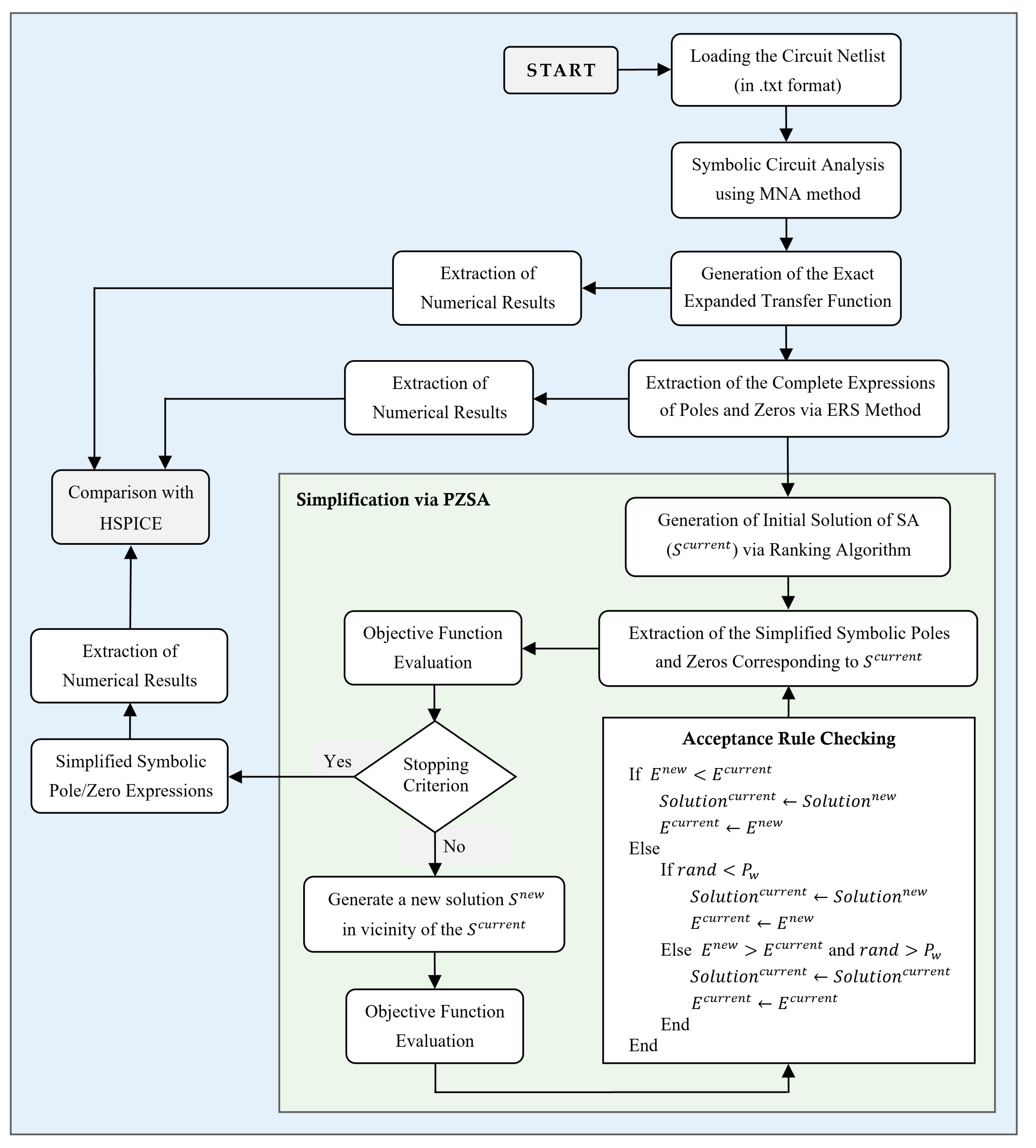
3. Proposed Method
- The input circuit netlist is loaded as a text file (in .txt format).
- All transistors are replaced via proper small-signal modeling.
- The symbolic circuit is solved via a modified nodal analysis (MNA).
- The exact transfer function (TF) is achieved in the expanded symbolic form.
- The exact expressions of poles and zeroes are derived using ERS.
- The numerical results of the exact symbolic pole/zero expressions are stored.
- A heuristic algorithm is performed to generate a near-optimal solution, utilizing the circuit-based knowledge available in the exact poles and zeroes.
- SA is performed to improve further the quality of the heuristic solution in order to generate the final simplified symbolic pole/zero expressions.
- The numerical results of the obtained simplified symbolic pole/zero expressions are calculated.
- The numerical results of the exact and simplified poles/zeroes are compared against HSPICE and other simplification algorithms.
3.1. Symbolic Pole/Zero Extraction via ERS
| Algorithm 1. Symbolic Pole/Zero Extraction using ERS |
| Inputs: |
| Symbolic exact expanded transfer function |
| Numerical values of the circuit parameters in the nominal point |
| ) |
| Output: |
| Symbolic expressions of poles and zeros |
| Numerical Analysis: |
| 1. ) |
| 2. Numerically evaluate the exact expanded transfer function in the nominal point |
| 3. |
| 4. ) by their magnitude |
| Extraction of Symbolic Zeros: |
| 5. |
| 6. Numerically estimate the position of zero j as |
| 7. |
| 8. |
| 9. else |
| 10. in one cluster 11. |
| 12. |
| 13. |
| 14. |
| 15. else |
| 16. |
| 17. end if 18. end if 19. end for |
| Extraction of Symbolic Poles: |
| 20. |
| 21. |
| 22. |
| 23. |
| 24. else |
| 25. in one cluster 26. |
| 27. |
| 28. |
| 29. |
| 30. else |
| 31. |
| 32. end if 34. end if 35. end for |
3.2. Symbolic Pole/Zero Simplification via PZSA
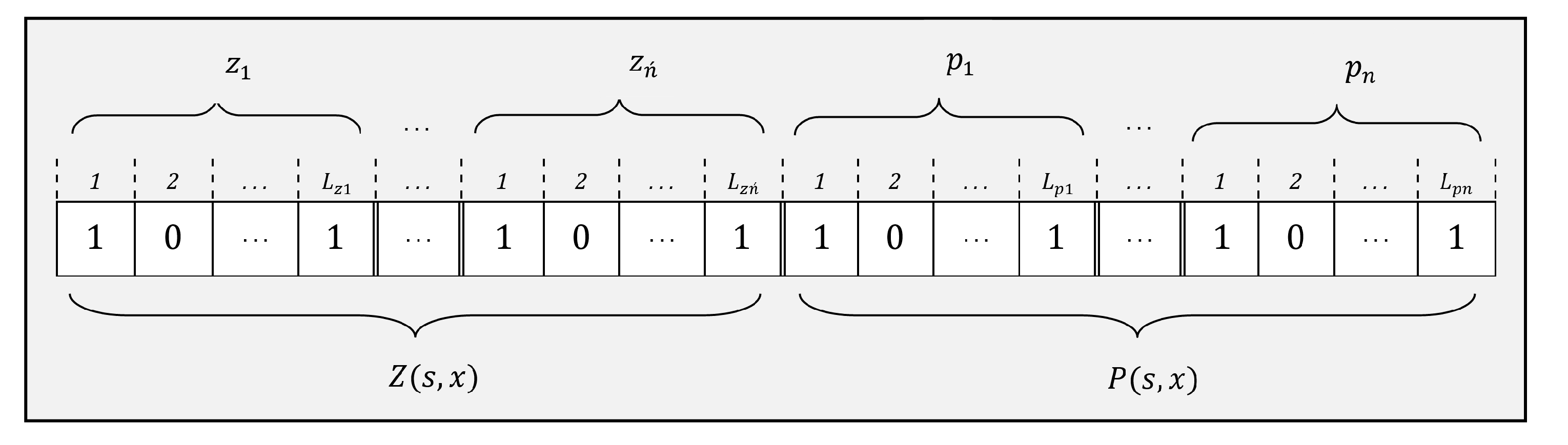
3.2.1. Solution Encoding/Decoding
3.2.2. Generation of the Initial Solution
3.2.3. Objective Function Evaluation
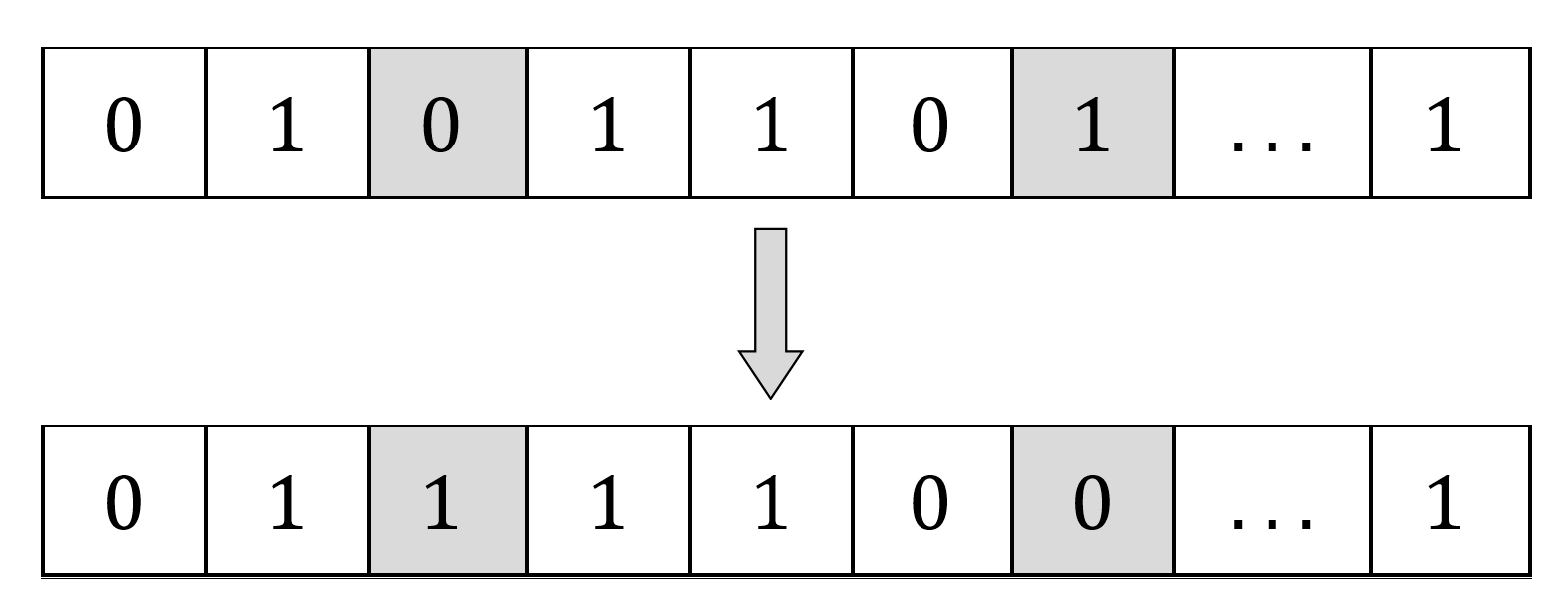
3.2.4. Generation of a New Solution
3.2.5. Acceptance Rule Checking
4. Performance Evaluation
4.1. Results for a Three-Stage Amplifier in the RCgm Model (Circuit 1)
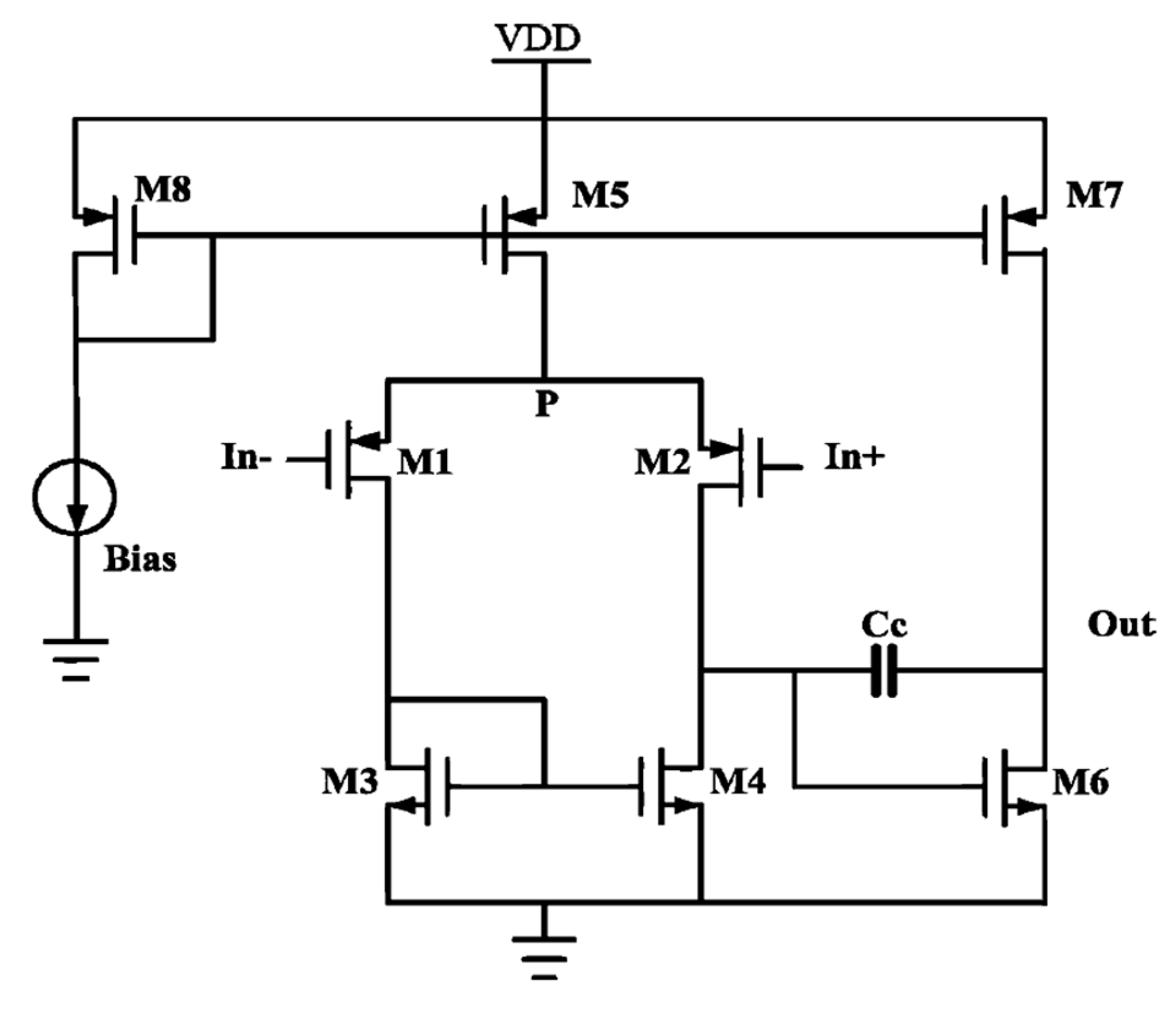
4.2. Results for a Two-Stage Miller Compensated Amplifier (Circuit 2)
4.3. Results for a Three-Stage Amplifier in Transistor Model (Circuit 3)
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gielen, G.; Sansen, W.M. Symbolic Analysis for Automated Design of Analog Integrated Circuits; Springer Science + Business Media: Berlin, Germany, 2012; Volume 137. [Google Scholar]
- Riad, J.; Soto-Aguilar, S.; Estrada-López, J.J.; Moreira-Tamayo, O.; Sánchez-Sinencio, E. Design Trade-Offs in Common-Mode Feedback Implementations for Highly Linear Three-Stage Operational Transconductance Amplifiers. Electronics 2021, 10, 991. [Google Scholar] [CrossRef]
- Akbari, M.; Shokouhifar, M.; Hashemipour, O.; Jalali, A.; Hassanzadeh, A. Systematic design of analog integrated circuits using ant colony algorithm based on noise optimization. Analog. Integr. Circuits Signal Process. 2016, 86, 327–339. [Google Scholar] [CrossRef]
- Rodovalho, L.H.; Toledo, P.; Mir, F.; Ebrahimi, F. Hybrid Inverter-Based Fully Differential Operational Transconductance Amplifiers. Chips 2023, 2, 1–19. [Google Scholar] [CrossRef]
- Akbari, M.; Hussein, S.M.; Hashim, Y.; Khateb, F.; Kulej, T.; Tang, K.T. Implementation of a Multipath Fully Differential OTA in 0.18-μm CMOS Process. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 31, 147–151. [Google Scholar] [CrossRef]
- Aminzadeh, H.; Grasso, A.D.; Palumbo, G. A methodology to derive a symbolic transfer function for multistage amplifiers. IEEE Access 2022, 10, 14062–14075. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Jalali, A. Simplified symbolic transfer function factorization using combined artificial bee colony and simulated annealing. Appl. Soft Comput. 2017, 55, 436–451. [Google Scholar] [CrossRef]
- Grasso, A.D.; Marano, D.; Pennisi, S.; Vazzana, G. Symbolic factorization methodology for multistage amplifier transfer functions. Int. J. Circuit Theory Appl. 2015, 44, 38–59. [Google Scholar] [CrossRef]
- Shi, G.; Tan, S.X.D.; Tlelo-Cuautle, E. Advanced Symbolic Analysis for VLSI Systems; Springer: Berlin, Germany, 2014. [Google Scholar]
- Shokouhifar, M.; Jalali, A. An evolutionary-based methodology for symbolic simplification of analog circuits using genetic algorithm and simulated annealing. Expert Syst. Appl. 2015, 42, 1189–1201. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Jalali, A. Simplified symbolic gain, CMRR and PSRR analysis of analog amplifiers using simulated annealing. J. Circuits Syst. Comput. 2016, 25, 1650082. [Google Scholar] [CrossRef]
- Sathasivam, S.; Mamat, M.; Kasihmuddin, M.S.M.; Mansor, M.A. Metaheuristics approach for maximum k satisfiability in restricted neural symbolic integration. Pertanika J. Sci. Technol. 2020, 28, 545–564. [Google Scholar]
- Ali, S.; Bhargava, A.; Saxena, A.; Kumar, P. A Hybrid Marine Predator Sine Cosine Algorithm for Parameter Selection of Hybrid Active Power Filter. Mathematics 2023, 11, 598. [Google Scholar] [CrossRef]
- Dziedziewicz, S.; Warecka, M.; Lech, R.; Kowalczyk, P. Self-Adaptive Mesh Generator for Global Complex Roots and Poles Finding Algorithm. IEEE Trans. Microw. Theory Tech. 2023, 66, 7198–7205. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Hennig, E. Symbolic Approximation and Modeling Techniques for Analysis and Design of Analog Circuits; Shaker Verlag: Herzogenrath, Germany, 2000. [Google Scholar]
- Toumazou, C.; Moschytz, G.S.; Gilbert, B. Trade-Offs in Analog Circuit Design: The Designer’s Companion; Kluwer Academic Publishers: New York, NY, USA, 2014. [Google Scholar]
- Wierzba, G.; Srivastava, A.; Joshi, V.; Noren, K.; Svoboda, J. SSPICE-A symbolic SPICE program for linear active circuits. Midwest Symp. Circuits Syst. 1989, 2, 1197–1201. [Google Scholar]
- Fernández, F.V.; Rodríguez-Vázquez, A.; Huertas, J.L. Interactive AC modeling and characterization of analog circuits via symbolic analysis. Kluwer J. Analog. Integr. Circuits Signal Process. 1991, 1, 183–208. [Google Scholar]
- Gielen, G.; Walscharts, H.; Sansen, W. ISAAC: A symbolic simulator for analog integrated circuits. IEEE J. Solid-State Circuits 1989, 24, 1587–1597. [Google Scholar] [CrossRef]
- Fakhfakh, M.; Cuautle, E.T.; Fernandez, F.V. Design of Analog Circuits through Symbolic Analysis; Bentham Science Publishers: Sharjah, United Arab Emirates, 2012. [Google Scholar]
- Shokouhifar, M.; Jalali, A. Automatic Simplified Symbolic Analysis of Analog Circuits Using Modified Nodal Analysis and Genetic Algorithm. J. Circuits Syst. Comput. 2015, 24, 1–20. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Jalali, A. Evolutionary based simplified symbolic PSRR analysis of analog integrated circuits. Analog. Integr. Circuits Signal Process. 2016, 86, 189–205. [Google Scholar] [CrossRef]
- Panda, M.; Kumar Patnaik, S.; Kumar Mal, A.; Ghosh, S. Fast and optimised design of a differential VCO using symbolic technique and multi objective algorithms. IET Circuits Devices Syst. 2019, 13, 1187–1195. [Google Scholar] [CrossRef]
- Panda, M.; Patnaik, S.K.; Mal, A.K. An efficient method to compute simplified noise parameters of analog amplifiers using symbolic and evolutionary approach. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 34, e2790. [Google Scholar] [CrossRef]
- Zhou, R.; Poechmueller, P.; Wang, Y. An Analog Circuit Design and Optimization System with Rule-Guided Genetic Algorithm. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2022, 41, 5182–5192. [Google Scholar] [CrossRef]
- Hayes, M. Lcapy: Symbolic linear circuit analysis with Python. PeerJ Comput. Sci. 2022, 8, e875. [Google Scholar] [CrossRef] [PubMed]
- Guerra, O.; Rodriguez-Garcia, J.D.; Fernandez, F.V.; Rodríguez-Vázquez, A. A symbolic pole/zero extraction methodology based on analysis of circuit time-constants. Analog. Integr. Circuits Signal Process. 2002, 31, 101–118. [Google Scholar] [CrossRef]
- Gomes, J.L.; Nunes, L.C.; Gonçalves, C.F.; Pedro, J.C. An accurate characterization of capture time constants in GaN HEMTs. IEEE Trans. Microw. Theory Tech. 2019, 67, 2465–2474. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Y.; Han, Z.; Shao, X.; Gao, J.; Huang, K.; Shi, Y.; Tang, J.; Shen, C.; Liu, J. Temperature compensation circuit design and experiment for dual-mass MEMS gyroscope bandwidth expansion. IEEE/ASME Trans. Mechatron. 2019, 24, 677–688. [Google Scholar] [CrossRef]
- Coşkun, K.Ç.; Hassan, M.; Drechsler, R. Equivalence Checking of System-Level and SPICE-Level Models of Linear Circuits. Chips 2022, 1, 54–71. [Google Scholar] [CrossRef]
- Evnin, O. Melonic dominance and the largest eigenvalue of a large random tensor. Lett. Math. Phys. 2021, 111, 66. [Google Scholar] [CrossRef]
- Gheorghe, A.G.; Constantinescu, F. Pole/Zero Computation for Linear Circuits. In Proceedings of the 2012 Sixth UKSim/AMSS European Symposium on Computer Modeling and Simulation, Valletta, Malt, 14–16 November 2012; pp. 477–480. [Google Scholar]
- Sohrabi, M.; Zandieh, M.; Shokouhifar, M. Sustainable inventory management in blood banks considering health equity using a combined metaheuristic-based robust fuzzy stochastic programming. Socio-Econ. Plan. Sci. 2022, 86, 101462. [Google Scholar] [CrossRef]
- Razavi, B. Fundamentals of Microelectronics; John Wiley & Sons: New York, NY, USA, 2021. [Google Scholar]
- Ghasemi Darehnaei, Z.; Shokouhifar, M.; Yazdanjouei, H.; Rastegar Fatemi, S.M.J. SI-EDTL: Swarm intelligence ensemble deep transfer learning for multiple vehicle detection in UAV images. Concurr. Comput. Pract. Exp. 2022, 34, e6726. [Google Scholar] [CrossRef]
- Aziz, R.M.; Mahto, R.; Goel, K.; Das, A.; Kumar, P.; Saxena, A. Modified Genetic Algorithm with Deep Learning for Fraud Transactions of Ethereum Smart Contract. Appl. Sci. 2023, 13, 697. [Google Scholar] [CrossRef]




| Sets/Parameters | Definition |
|---|---|
| Index of poles, | |
| Index of zeroes, | |
| Degree of the denominator within the exact expanded TF | |
| Degree of the numerator within the exact expanded TF | |
| Index of the symbolic terms, | |
| Number of symbolic terms within all pole/zero expressions | |
| Defined frequency bound range for the pole/zero extraction | |
| A binary parameter: 1 if the -th term is presented; 0 otherwise | |
| Percentage of the selected symbolic terms | |
| Set of poles in the frequency range of | |
| ZeroSet | Set of zeroes in the frequency range of |
| -th pole within the exact expanded TF | |
| -th extracted pole via ERS | |
| -th simplified pole via SA | |
| Mean pole displacements | |
| -the zero of the exact expanded TF | |
| -th extracted zero via ERS | |
| -th simplified zero via SA | |
| Mean zero displacements | |
| Maximum allowable pole/zero extraction error via ERS | |
| Maximum allowable pole/zero simplification error via SA |
| Phase | Parameter | Value/Description |
|---|---|---|
| Model Parameters | 1 Hz | |
| 10 × | ||
| in Equations (32) and (33) | 10% | |
| in Equations (39) and (40) | 20% | |
| in Equation (35) | 0.99 | |
| in Equation (35) | 0.005 | |
| in Equation (35) | 0.005 |
| Phase | Parameter | Parameter Levels | Selected Value | ||
|---|---|---|---|---|---|
| SA Parameters | Maximum iterations | L | 5 × L | 10 × L | 5 × L |
| Local search operators | Swap | Exchange | Swap/Exchange | Swap/Exchange | |
| in Equation (42) | 10−5 | 10−4 | 10−3 | 10−5 | |
| in Equation (42) | 0 | 10−8 | 10−10 | 0 | |
| Expression | Expanded TF (Exact) | Ref. [26] | Ref. [29] | Ref. [31] | Proposed Exact (ERS) | Proposed Simplified (SA) |
|---|---|---|---|---|---|---|
| P1 | - | - | 1 | 10 | 10 | 1 |
| P2 | - | - | 4 | 26 | 26 | 3 |
| P3 | - | - | 5 | 25 | 25 | 3 |
| Z1 | - | - | 2 | 9 | 3 | 2 |
| Z2 | - | - | 2 | 9 | 4 | 2 |
| Overall TF | 40 | 10 | - | - | - | - |
| Parameter | HSPICE | Expanded TF (Exact) | Ref. [26] | Ref. [29] | Ref. [31] | Proposed Exact | Proposed Simplified |
|---|---|---|---|---|---|---|---|
| P1 (Hz) | −12.8 | −12.8 | −13.3 | −13.2 | −12.8 | −12.8 | −13.2 |
| P2 (MHz) | −3.19 | −3.19 | −3.49 | −3.19 | −2.96 | −2.96 | −3.18 |
| P3 (MHz) | −40.6 | −40.6 | −36.3 | −43.9 | −43.8 | −43.8 | −39.8 |
| Z1 (MHz) | 2.72 | 2.72 | 2.72 | 3.18 | 3.36 | 3.18 | 3.18 |
| Z2 (MHz) | −18.6 | −18.6 | −18.6 | −15.9 | −17.5 | −15.9 | −15.9 |
| Mean pole displacement (%) | - | - | 7.8 | 3.8 | 5 | 5 | 1.9 |
| Max pole displacement (%) | - | - | 10.6 | 8.36 | 7.9 | 7.9 | 3.5 |
| Mean zero displacement (%) | - | - | 0.03 | 15.9 | 14.7 | 15.8 | 15.9 |
| Max zero displacement (%) | - | - | 0.04 | 17.1 | 23.6 | 17.1 | 17.1 |
| Expression | Expanded TF (Exact) | Ref. [26] | Ref. [29] | Ref. [31] | Proposed Exact (ERS) | Proposed Simplified (SA) |
|---|---|---|---|---|---|---|
| P1 | - | - | 5 | 104 | 104 | 5 |
| P2 | - | - | 7 | 82 | 82 | 2 |
| Z | - | - | 4 | 18 | 18 | 2 |
| Overall TF | 134 | 11 | - | - | - | - |
| Parameter | HSPICE | Expanded TF (Exact) | Ref. [26] | Ref. [29] | Ref. [31] | Proposed Exact | Proposed Simplified |
|---|---|---|---|---|---|---|---|
| P1 (KHz) | −177.1 | −178.5 | −192 | −152.8 | −178.4 | −178.4 | −152.8 |
| P2 (MHz) | −377.4 | −435.4 | −409.1 | −341 | −435.6 | −435.6 | −409.3 |
| Z (MHz) | 407.2 | 409.3 | 409.3 | 409.3 | 409.3 | 409.3 | 409.3 |
| Mean pole displacement (%) | - | - | 6.8 | 18 | 0.04 | 0.04 | 10.2 |
| Max pole displacement (%) | - | - | 7.5 | 21.7 | 0.04 | 0.04 | 14.4 |
| Zero displacement (%) | - | - | 0.01 | 0.01 | 0 | 0 | 0.01 |
| Expression | Expanded TF (Exact) | Ref. [26] | Ref. [29] | Ref. [31] | Proposed Exact (ERS) | Proposed Simplified (SA) |
|---|---|---|---|---|---|---|
| P1 | - | - | 29 | 714 | 714 | 9 |
| P2 | - | - | 21 | 837 | 837 | 3 |
| P3 | - | - | 23 | 330 | 330 | 3 |
| Z1 | - | - | 15 | 75 | 75 | 2 |
| Z2 | - | - | 13 | 105 | 105 | 2 |
| Overall TF | 1320 | 18 | - | - | - | - |
| Parameter | HSPICE | Expanded TF (Exact) | Ref. [26] | Ref. [29] | Ref. [31] | Proposed Exact | Proposed Simplified |
|---|---|---|---|---|---|---|---|
| P1 (Hz) | −27.7 | −27.9 | −20.6 | −20.5 | −27.9 | −27.9 | −22.8 |
| P2 (MHz) | −1.84 | −1.84 | −2.03 | −2.16 | −1.76 | −1.76 | −2.07 |
| P3 (MHz) | −36.6 | −40.2 | −36.3 | −36.1 | −42.1 | −42.1 | −35.7 |
| Z1 (MHz) | 1.4 | 1.4 | 1.4 | 2.23 | 1.62 | 1.62 | 1.62 |
| Z2 (MHz) | −10.3 | −10.2 | −10.5 | −7.37 | −8.81 | −8.81 | −9.1 |
| Mean pole displacement (%) | - | - | 15.6 | 18 | 3 | 3 | 14.2 |
| Max pole displacement (%) | - | - | 26.4 | 26.5 | 4.6 | 4.6 | 18.4 |
| Mean zero displacement (%) | - | - | 1.7 | 43.5 | 14.8 | 14.8 | 13.5 |
| Max zero displacement (%) | - | - | 2.9 | 59.3 | 15.9 | 15.9 | 16.1 |
| Circuit/Objective | En | Ep | Ez |
|---|---|---|---|
| Circuit 1 | 0.1617 | 0.019 | 0.159 |
| Circuit 2 | 0.0441 | 0.102 | 0.0001 |
| Circuit 3 | 0.0092 | 0.142 | 0.135 |
| Circuit/Objective | Circuit 1 | Circuit 2 | Circuit 3 |
|---|---|---|---|
| Run 1 | 0.1619 | 0.0447 | 0.0119 |
| Run 2 | 0.162 | 0.0451 | 0.013 |
| Run 3 | 0.1618 | 0.0448 | 0.0128 |
| Run 4 | 0.1766 | 0.045 | 0.0123 |
| Run 5 | 0.162 | 0.0447 | 0.0114 |
| Run 6 | 0.1767 | 0.0445 | 0.0115 |
| Run 7 | 0.1617 | 0.0446 | 0.012 |
| Run 8 | 0.1616 | 0.0449 | 0.0129 |
| Run 9 | 0.1473 | 0.0398 | 0.0117 |
| Run 10 | 0.1621 | 0.0447 | 0.0121 |
| Average | 0.1634 | 0.0443 | 0.0122 |
| Standard Deviation | 0.0083 | 0.0016 | 0.0006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Behmanesh-Fard, N.; Yazdanjouei, H.; Shokouhifar, M.; Werner, F. Mathematical Circuit Root Simplification Using an Ensemble Heuristic–Metaheuristic Algorithm. Mathematics 2023, 11, 1498. https://doi.org/10.3390/math11061498
Behmanesh-Fard N, Yazdanjouei H, Shokouhifar M, Werner F. Mathematical Circuit Root Simplification Using an Ensemble Heuristic–Metaheuristic Algorithm. Mathematics. 2023; 11(6):1498. https://doi.org/10.3390/math11061498
Chicago/Turabian StyleBehmanesh-Fard, Navid, Hossein Yazdanjouei, Mohammad Shokouhifar, and Frank Werner. 2023. "Mathematical Circuit Root Simplification Using an Ensemble Heuristic–Metaheuristic Algorithm" Mathematics 11, no. 6: 1498. https://doi.org/10.3390/math11061498
APA StyleBehmanesh-Fard, N., Yazdanjouei, H., Shokouhifar, M., & Werner, F. (2023). Mathematical Circuit Root Simplification Using an Ensemble Heuristic–Metaheuristic Algorithm. Mathematics, 11(6), 1498. https://doi.org/10.3390/math11061498







